Testing and Numerical Analysis of the Anti-Blast Performance of Curved Steel-Concrete-Steel Composite Slab Using Headed Stud Connectors
-
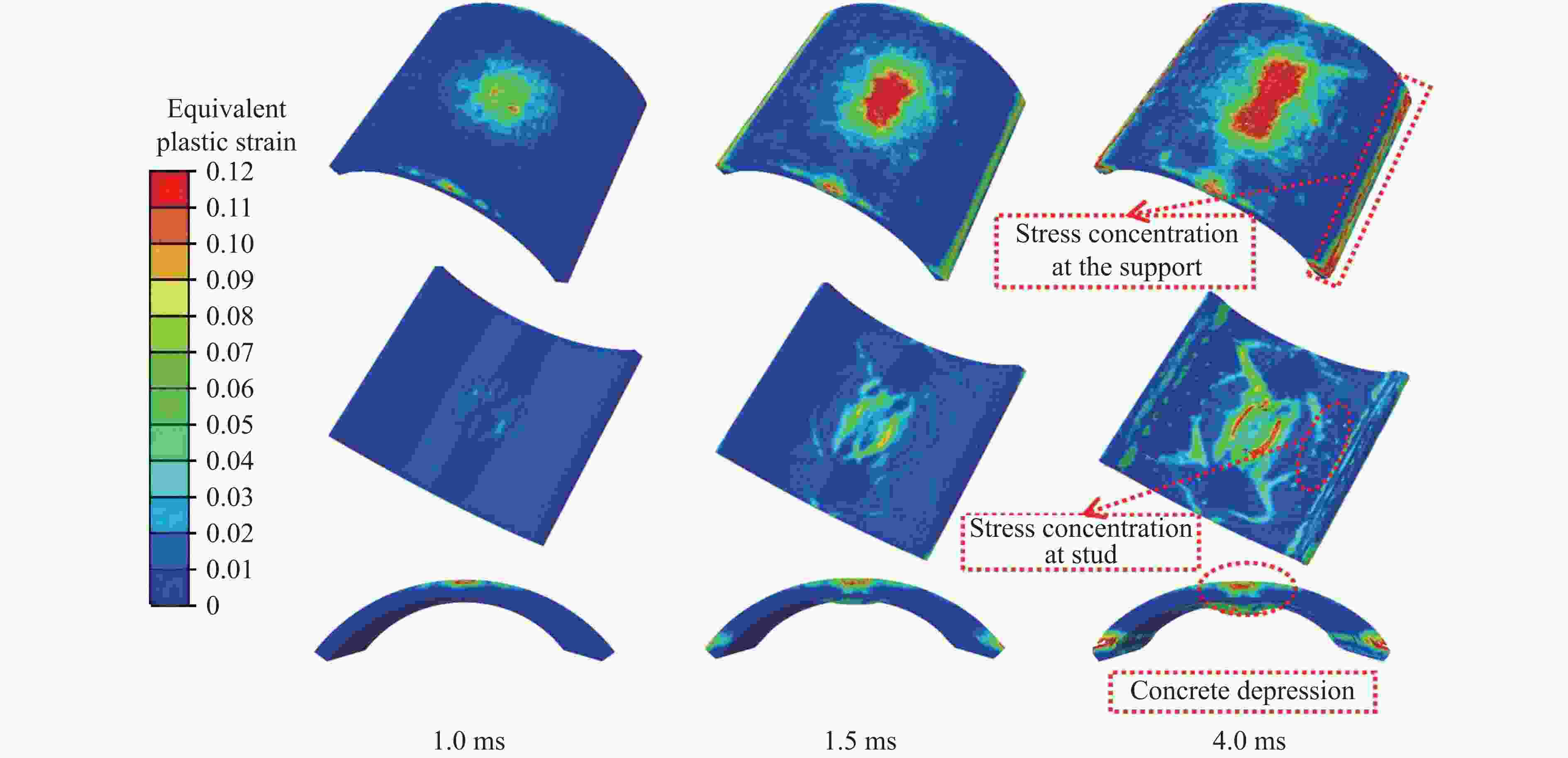
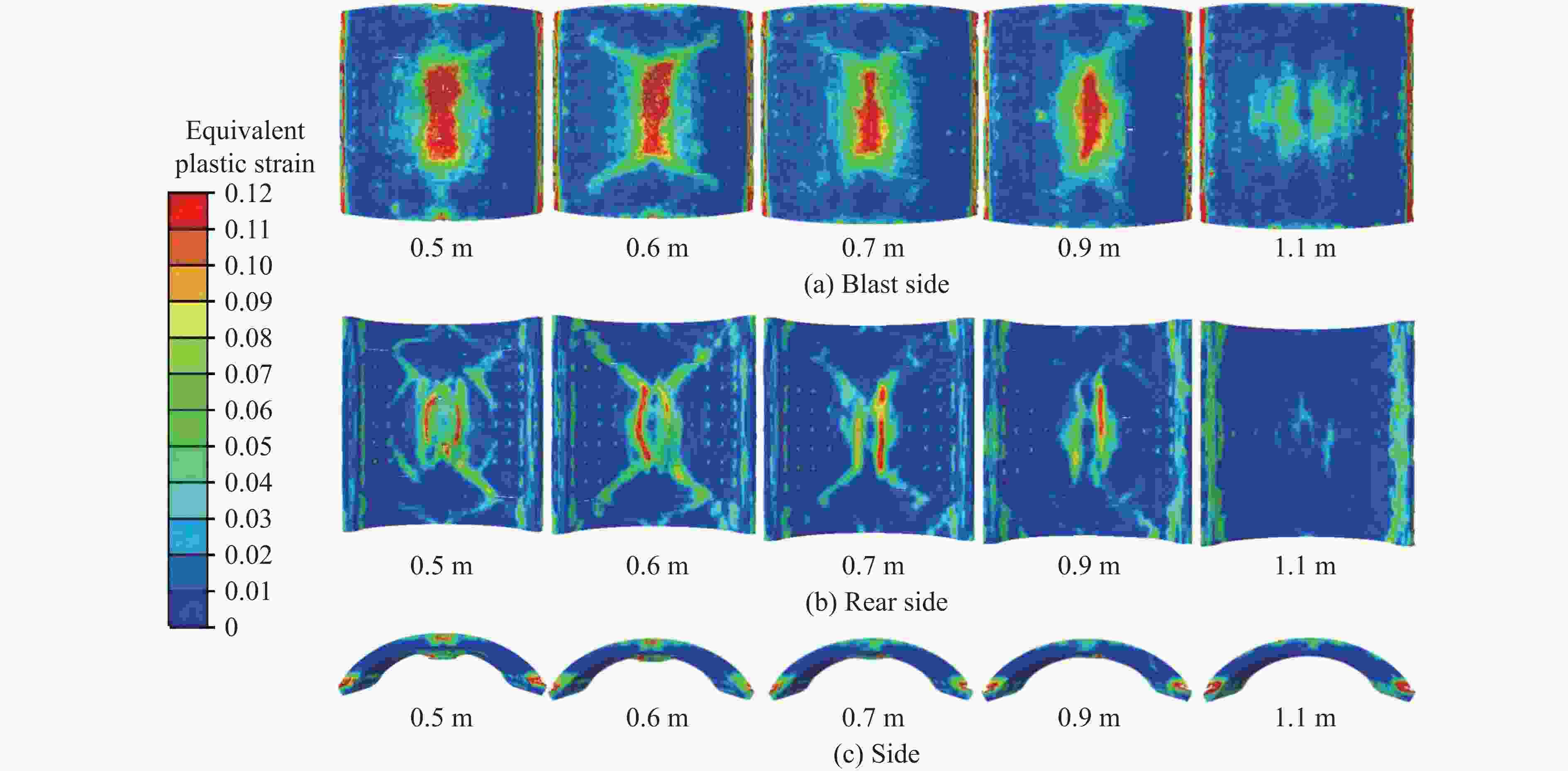
摘要: 弧形双钢板混凝土组合结构由钢板、混凝土与连接件协同作用，具有更优异的抗震和抗爆性能，被应用于超高层结构、海洋平台和核电设施中。利用试验和数值分析方法研究了栓钉型弧形双钢板混凝土组合结构的破坏模式和损伤机理，参数化分析了爆炸距离、钢板厚度、拱高和栓钉间距对其抗爆性能的影响。结果表明：在爆炸荷载下，栓钉型弧形双钢板混凝土组合板整体表现良好，仍具有较高的承载能力。增加爆炸距离和钢板厚度能有效减小混凝土的损伤和组合板的跨中挠度；减小拱高，混凝土损伤区域从以压缩破坏为主逐渐转换为以拉伸破坏为主，混凝土损伤更严重，组合板跨中挠度变大；减小栓钉间距会增大混凝土塑性损伤程度，但组合板的跨中挠度减小。研究结果可为弧形双钢板混凝土组合结构的设计提供参考。
-
关键词:
- 爆炸荷载 /
- 栓钉型弧形双钢板混凝土组合板 /
- 抗爆性能 /
- 参数分析
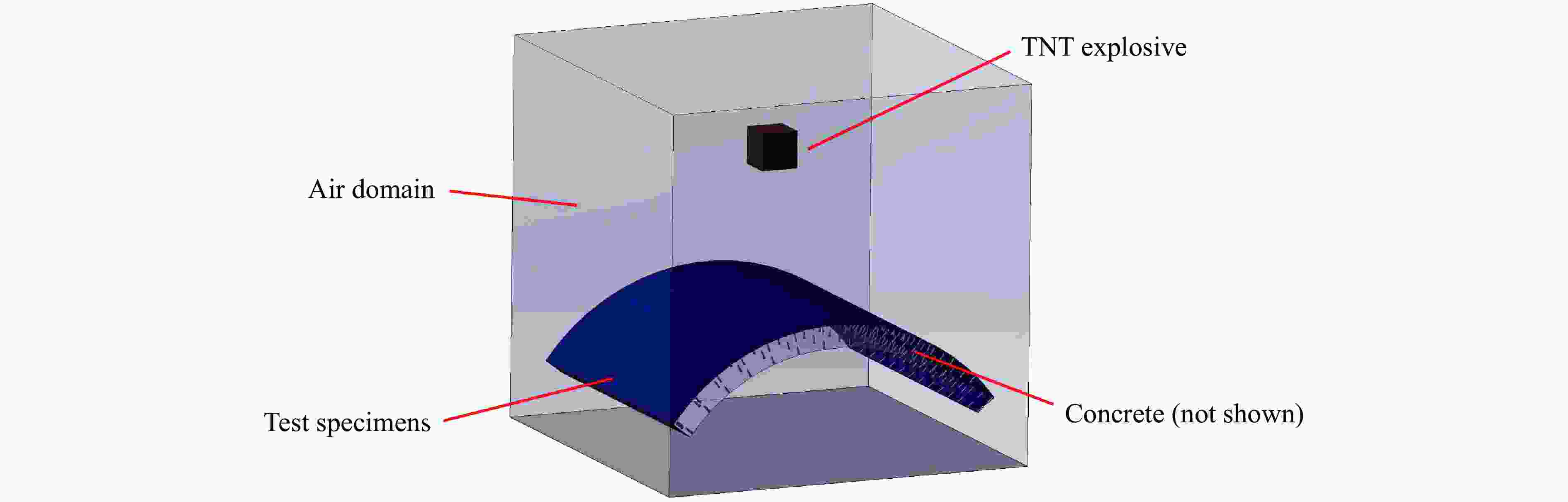
Abstract: The curved steel-concrete-steel composite structure is a sandwiched structural member, consisting of two curved steel plates and concrete core. Headed studs are used to connect the steel plates and concrete to achieve the composite effect. This type of structure is promising for improving earthquake resistance and anti-blast performance, and has been applied in super high-rise structures, offshore platforms, and nuclear power facilities. This paper conducts experimental and numerical analysis to investigate the damage mode and mechanism of the curved steel-concrete-steel composite slab. Additionally, a parametrically analysis is conducted to explore the impact of blast distance, steel plate thickness, arch heights, and stud spacing on its anti-blast performance. The results indicate that the curved steel-concrete-steel composite structure performs well globally and retains their structural load-bearing capacity without failure after subjecting to blast loading. Increasing the blast distance and steel plate thickness can effectively reduce the concrete damage and the span deflection of the composite slab. Reducing arch heights causes a switch in concrete damage from compression damage to tensile damage, which is more severe and results in larger span deflection of the slab. Although reducing stud spacing increases the concrete plastic damage, it reduces the span deflection of the composite slab. The research results can contribute to the design and applications of curved steel-concrete-steel composite structures. -
图 8 采用不同网格尺寸得到的位移时程曲线
Figure 8. Time history curves of displacement for models with different mesh sizes
图 13 不同爆炸距离下混凝土的等效塑性应变
Figure 13. Equivalent plastic strain of concrete at different blast distances
图 14 不同爆炸距离下钢板的跨中挠度
Figure 14. Mid-span deflection of steel platesat different blast distances
图 15 不同钢板厚度下混凝土的等效塑性应变
Figure 15. Equivalent plastic strain for concrete with different steel plate thicknesses
图 16 不同钢板厚度下钢板的跨中挠度
Figure 16. Mid-span deflection of steel platesat different plate thicknesses
图 17 不同拱高下混凝土的等效塑性应变
Figure 17. Equivalent plastic strain for concrete with different arch heights
图 18 不同拱高下钢板的跨中挠度
Figure 18. Mid-span deflection of steel plates for modelswith different arch heights
图 19 不同栓钉间距下混凝土的等效塑性应变
Figure 19. Equivalent plastic strain of concrete for models with different stud spacing
图 20 不同栓钉间距下钢板的跨中挠度
Figure 20. Mid-span deflection of steel platewith different stud spacing
表 1 材料属性
Table 1. Material properties
Material Modulus of elasticity/GPa Compressive strength/MPa Yield strength/MPa Tensile strength/MPa C50 concrete 30 52.4 Q345 steel 200 370 462 A2-50 stud 200 210 500 
下载: 导出CSV
表 2 混凝土的CDP模型参数
Table 2. Parameters of CDP model for concrete
Expansion angle/(°) Eccentricity Compressive strength ratio Stress invariant ratio Viscosity coefficient 30 0.1 1.16 0.667 0.005
下载: 导出CSV
表 3 试验结果与数值模拟结果的对比
Table 3. Comparison of experimental results and numerical results
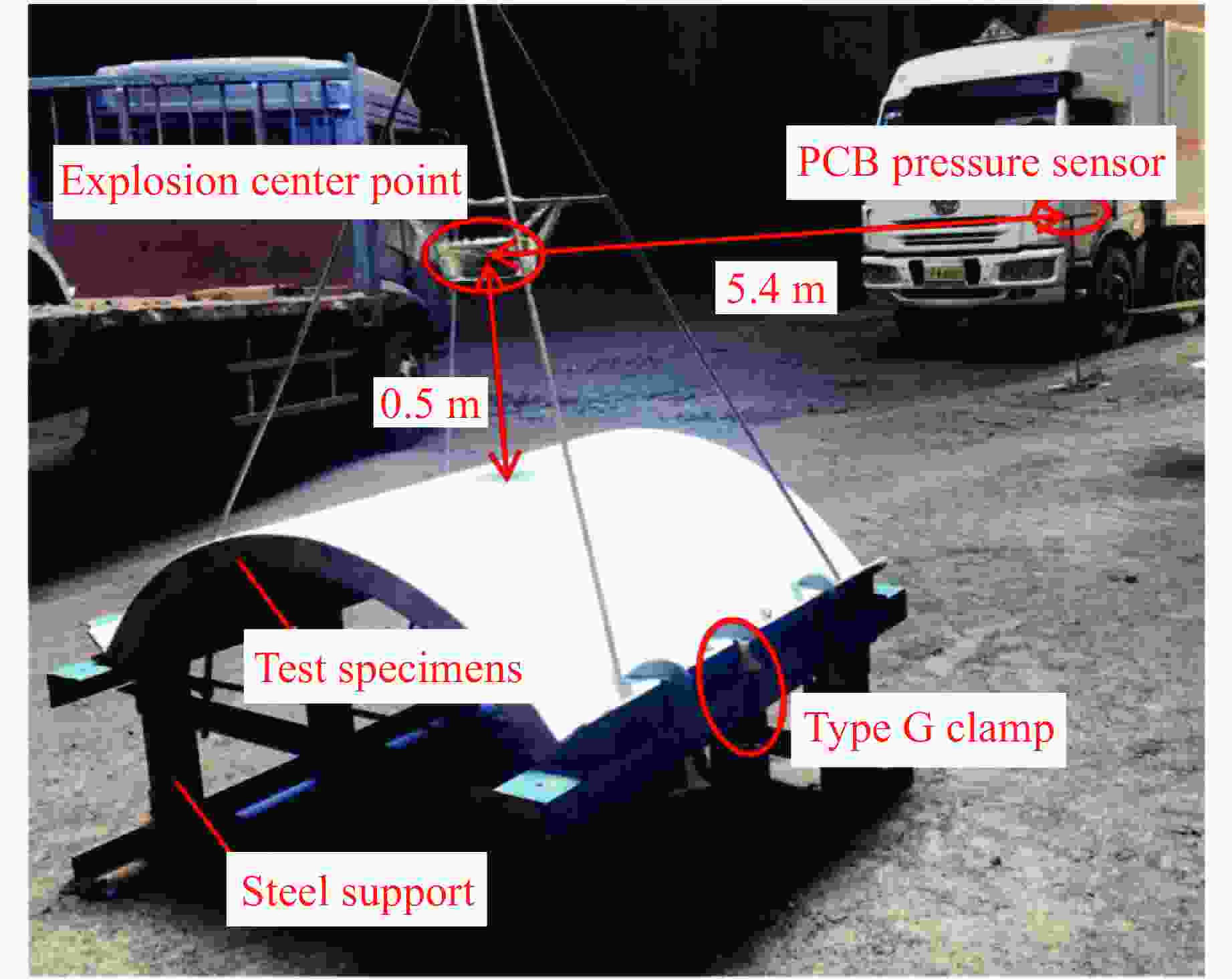
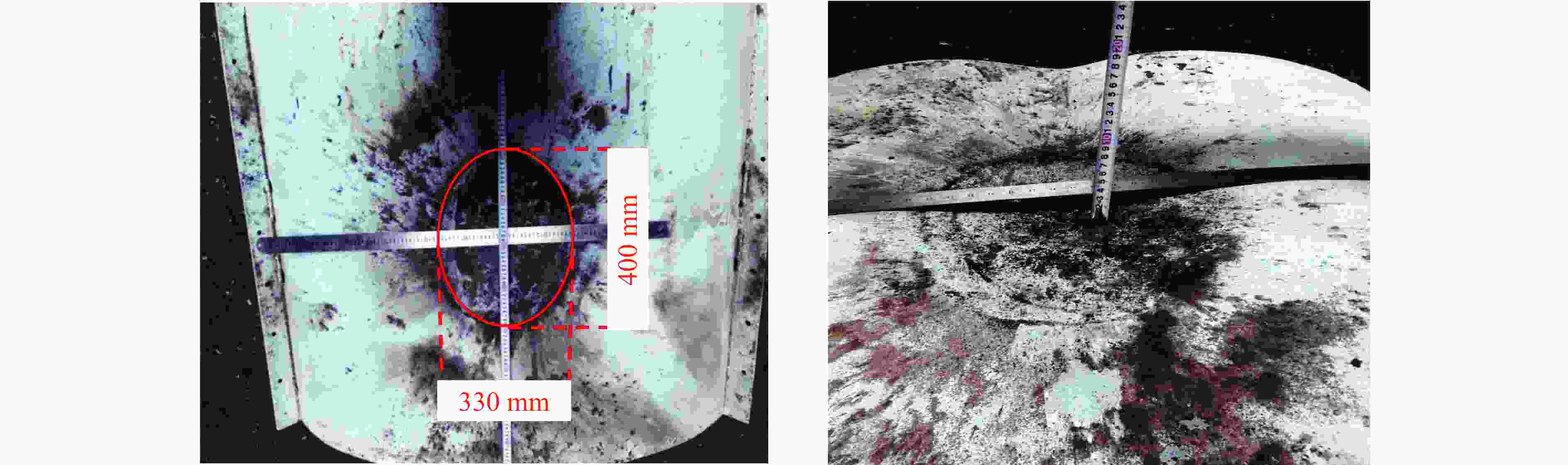
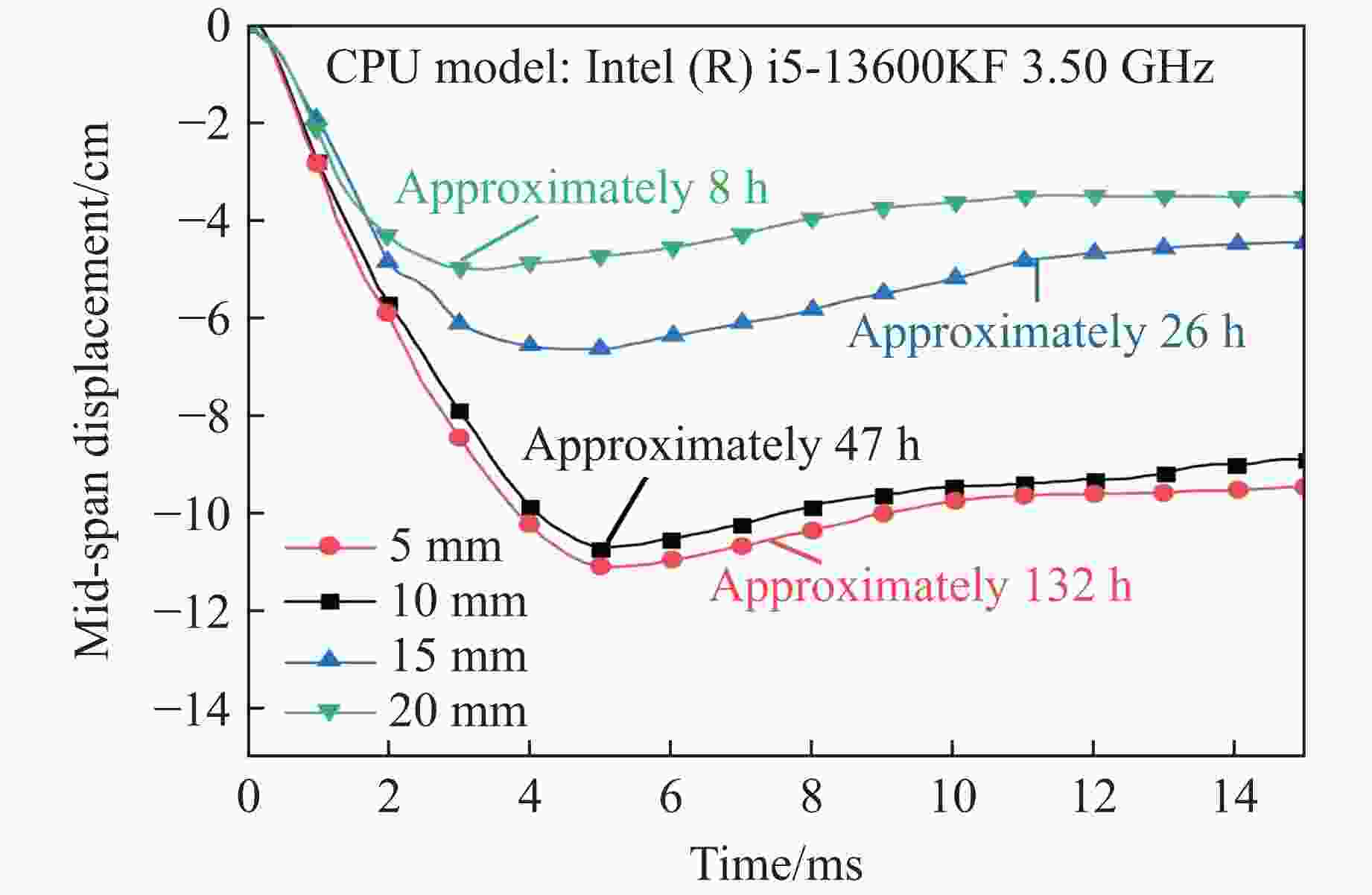
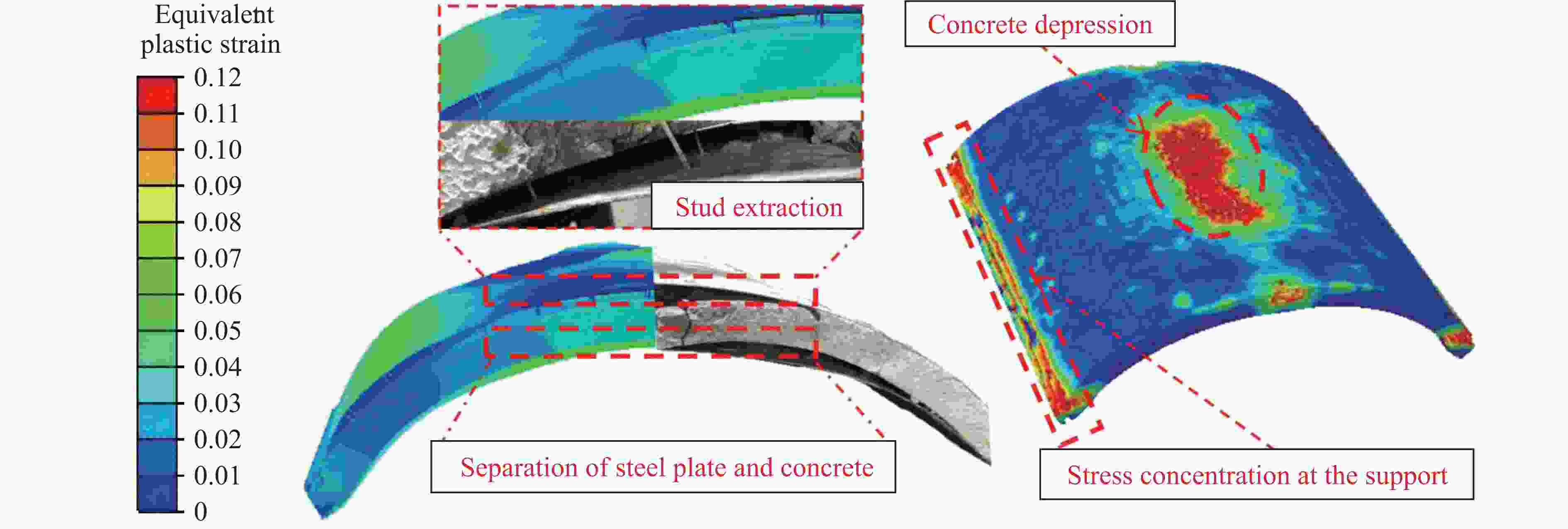
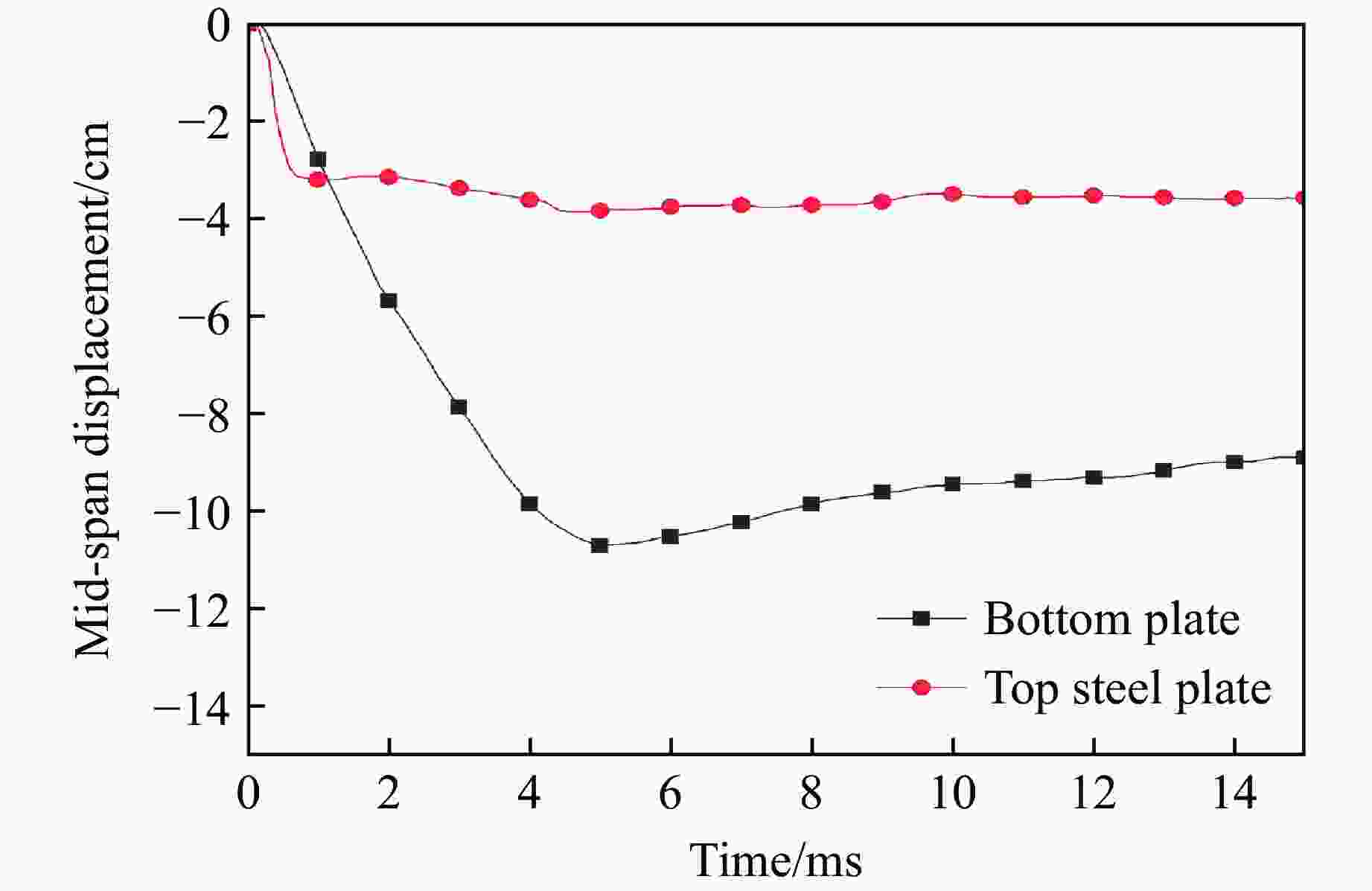
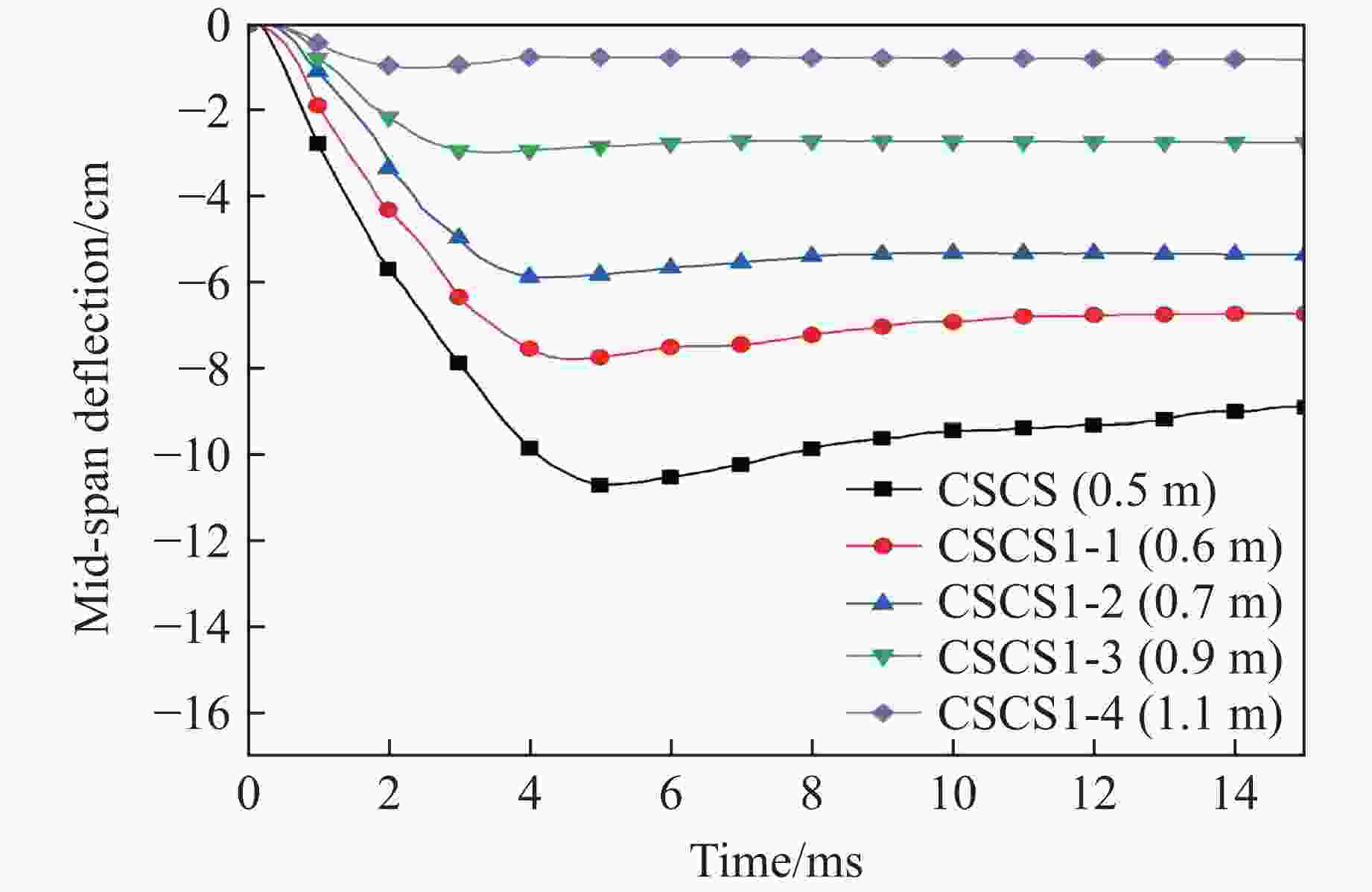
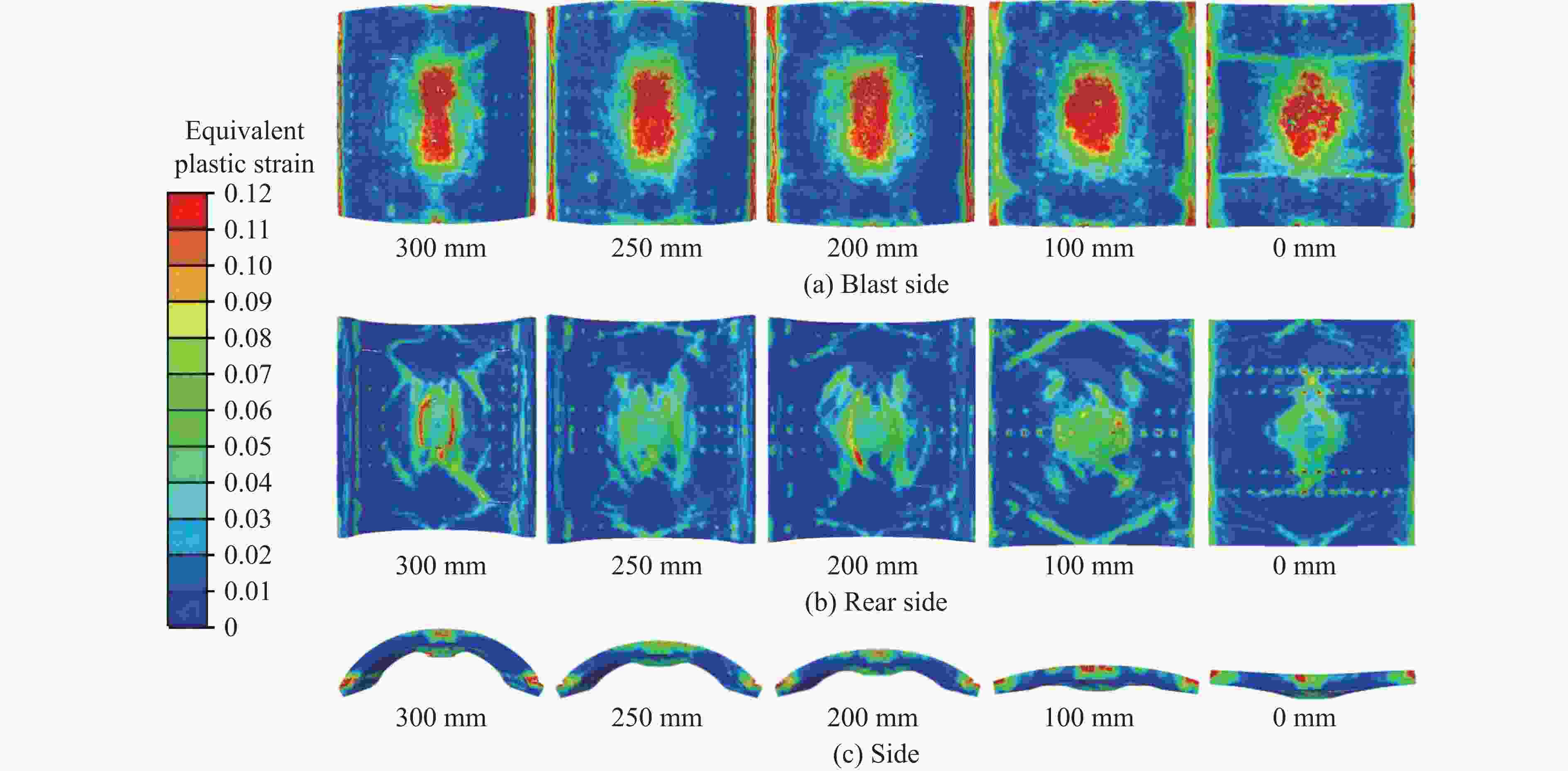
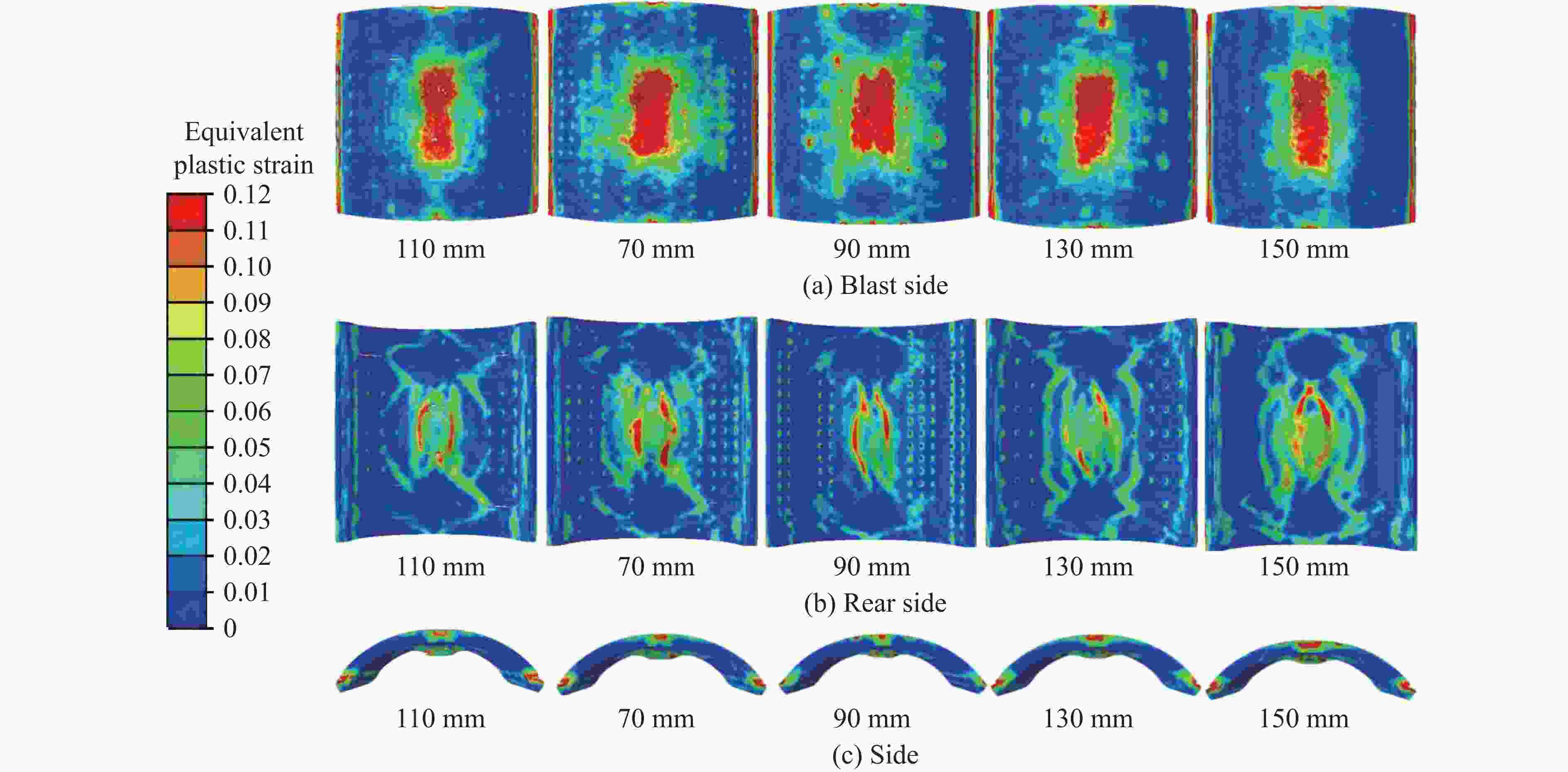
Part Deformation Residual deflection Explosion pressure Test/(mm×mm) Sim./(mm×mm) Error/% Test/mm Sim./mm Error/% Test/MPa Sim./MPa Error/% Top steel plate 330×400 310×470 9.4 38 35 7.9 Bottom plate 640×610 770×560 9.5 100 88 12.0 Measurement points 0.08 0.078 2.5
下载: 导出CSV
表 4 参数模拟工况
Table 4. Parameters for simulation
Simulated
specimenExplosion
distance/mTop steel plate
thickness/mmBottom steel plate
thickness/mmArch heights/
mmStud spacing/
mmCSCS1-1 0.6 3 3 300 110 CSCS1-2 0.7 3 3 300 110 CSCS1-3 0.9 3 3 300 110 CSCS1-4 1.1 3 3 300 110 CSCS2-1 0.5 4 4 300 110 CSCS2-2 0.5 5 5 300 110 CSCS2-3 0.5 5 3 300 110 CSCS2-4 0.5 3 5 300 110 CSCS3-1 0.5 3 3 250 110 CSCS3-2 0.5 3 3 200 110 CSCS3-3 0.5 3 3 100 110 CSCS3-4 0.5 3 3 0 110 CSCS4-1 0.5 3 3 300 70 CSCS4-2 0.5 3 3 300 90 CSCS4-3 0.5 3 3 300 130 CSCS4-4 0.5 3 3 300 150
下载: 导出CSV
-
[1] QU Y D, LI X, KONG X Q, et al. Numerical simulation on dynamic behavior of reinforced concrete beam with initial cracks subjected to air blast loading [J]. Engineering Structures, 2016, 128: 96–110. doi: 10.1016/j.engstruct.2016.09.032 [2] KONG X Q, QI X J, GU Y H, et al. Numerical evaluation of blast resistance of RC slab strengthened with AFRP [J]. Construction and Building Materials, 2018, 178: 244–253. doi: 10.1016/j.conbuildmat.2018.05.081 [3] 武钰朋, 张天辉, 刘志芳, 等. 横向爆炸载荷下泡沫铝夹芯管的动态响应与多目标优化 [J]. 高压物理学报, 2023, 37(4): 044202.WU Y P, ZHANG T H, LIU Z F, et al. Dynamic response and multi-objective optimization of aluminum foam-filled sandwich tube under lateral blast loading [J]. Chinese Journal of High Pressure Physics, 2023, 37(4): 044202. [4] 李忠献, 任其武, 师燕超, 等. 重要建筑结构抗恐怖爆炸设计爆炸荷载取值探讨 [J]. 建筑结构学报, 2016, 37(3): 51–58.LI Z X, REN Q W, SHI Y C, et al. Research on blast load value in design of important building structures against terrorist explosions [J]. Journal of Building Structures, 2016, 37(3): 51–58. [5] 王万月, 耿少波, 王华, 等. 近场多发爆炸荷载作用下方钢管构件的动态响应及其损伤 [J]. 高压物理学报, 2022, 36(3): 034104.WANG W Y, GENG S B, WANG H, et al. Dynamic response and damage of square steel tubular structural components by near-field multiple blast loads [J]. Chinese Journal of High Pressure Physics, 2022, 36(3): 034104. [6] HUANG Z Y, LIEW J Y R. Experimental and analytical studies of curved steel-concrete-steel sandwich panels under patch loads [J]. Materials & Design, 2016, 93: 104–117. [7] YAN C, WANG Y H, ZHAI X M. Low velocity impact performance of curved steel-concrete-steel sandwich shells with bolt connectors [J]. Thin-Walled Structures, 2020, 150: 106672. doi: 10.1016/j.tws.2020.106672 [8] MENG L Z, WANG Y H, ZHAI X M. Modeling and dynamic response of curved steel-concrete-steel sandwich shells under blast loading [J]. International Journal of Steel Structures, 2020, 20(5): 1663–1681. doi: 10.1007/s13296-020-00403-8 [9] 卢欣. 钢-混凝土组合墙板抗接触爆炸性能试验及数值研究 [D]. 合肥: 合肥工业大学, 2020.LU X. Experimental and numerical study on contact explosion resistance of steel-concrete composite wallboard [D]. Hefei: Hefei University of Technology, 2020. [10] ZHAO C F, LU X, WANG Q, et al. Experimental and numerical investigation of steel-concrete (SC) slabs under contact blast loading [J]. Engineering Structures, 2019, 196: 109337. doi: 10.1016/j.engstruct.2019.109337 [11] ZHAO C F, WANG Q, LU X, et al. Numerical study on dynamic behaviors of NRC slabs in containment dome subjected to close-in blast loading [J]. Thin-Walled Structures, 2019, 135: 269–284. doi: 10.1016/j.tws.2018.11.013 [12] ZHAO C F, WANG Q, LU X, et al. Blast resistance of small-scale RCS in experimental test and numerical analysis [J]. Engineering Structures, 2019, 199: 109610. doi: 10.1016/j.engstruct.2019.109610 [13] 赵唯以, 高泽鹏, 王琳, 等. 集中荷载作用下四边简支双钢板混凝土组合板的力学性能研究 [J]. 工程力学, 2022, 39(3): 158–170, 192.ZHAO W Y, GAO Z P, WANG L, et al. Mechanical performance of two-way simply supported steel-plate composite slabs under concentrated load [J]. Engineering Mechanics, 2022, 39(3): 158–170, 192. [14] 赵唯以, 王琳, 郭全全, 等. 双钢板混凝土组合结构抗冲击性能的研究进展 [J]. 钢结构(中英文), 2020, 35(3): 26–36.ZHAO W Y, WANG L, GUO Q Q, et al. Research advances of impact resistance of steel-concrete composite structures [J]. Steel Construction (Chinese & English), 2020, 35(3): 26–36. [15] 严辰, 王永辉, 翟希梅, 等. 集中荷载作用下拱形双钢板混凝土组合墙板的有限元分析 [J]. 建筑结构学报, 2019, 40(Suppl 1): 78–83.YAN C, WANG Y H, ZHAI X M, et al. Finite element anlysis of curved steel-concrete-steel composite panels subjected to concentrated load [J]. Journal of Building Structures, 2019, 40(Suppl 1): 78–83. [16] WANG Y H, ZHAI X M, LEE S C, et al. Responses of curved steel-concrete-steel sandwich shells subjected to blast loading [J]. Thin-Walled Structures, 2016, 108: 185–192. doi: 10.1016/j.tws.2016.08.018 [17] 赵春风, 何凯城, 卢欣, 等. 弧形与平面双钢板混凝土组合板抗爆性能对比研究 [J]. 建筑钢结构进展, 2021, 23(7): 89–96.ZHAO C F, HE K C, LU X, et al. A comparison study on the blast resistance of curved and flat steel-concrete-steel composite panels [J]. Progress in Steel Building Structures, 2021, 23(7): 89–96. [18] 赵春风, 何凯城, 李晓杰, 等. L型隔板弧形双钢板组合墙板抗爆性能试验与数值研究 [J/OL]. 工程力学, (2023-04-28)[2023-10-17]. http://engineeringmechanics.cn/cn/article/doi/10.6052/j.issn.1000-4750.2022.07.0612.ZHAO C F, HE K C, LI X J, et al. Experimental and numerical study on anti-explosion performance of curved double steel concrete composite wallboard with L-shaped connector [J/OL]. Engineering Mechanics, (2023-04-28)[2023-10-17]. http://engineeringmechanics.cn/cn/article/doi/10.6052/j.issn.1000-4750.2022.07.0612. [19] 中华人民共和国住房和城乡建设部. 钢板剪力墙技术规程: JGJ/T 380—2015 [S]. 北京: 中国建筑工业出版社, 2016.Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical specification for steel plate shear walls: JGJ/T 380—2015 [S]. Beijing: China Architecture & Building Press, 2016. [20] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 金属材料 拉伸试验 第1部分: 室温试验方法: GB/T 228.1—2010 [S]. 北京: 中国标准出版社, 2011.General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. Metallic materials–tensile testing–Part 1: method of test at room temperature: GB/T 228.1—2010 [S]. Beijing: Standards Press of China, 2011. [21] LEE J, FENVES G L. Plastic-damage model for cyclic loading of concrete structures [J]. Journal of Engineering Mechanics, 1998, 124(8): 892–900. doi: 10.1061/(ASCE)0733-9399(1998)124:8(892) [22] LUBLINER J, OLIVER J, OLLER S, et al. A plastic-damage model for concrete [J]. International Journal of Solids and Structures, 1989, 25(3): 299–326. doi: 10.1016/0020-7683(89)90050-4 [23] 过镇海, 时旭东. 钢筋混凝土原理和分析 [M]. 北京: 清华大学出版社, 2003.GUO Z H, SHI X D. Reinforced concrete theory and analyse [M]. Beijing: Tsinghua University Press, 2003. [24] Comité Euro-International du Béton. CEB-FIP model code 1990: Design code [M]. London: Thomas Telford Publishing, 1993. [25] MALVAR L J, CRAWFORD J E. Dynamic increase factors for concrete [R]. Proceedings of the Twenty-Eighth DoD Explosives Safety Seminar. Orlando: Naval Facilities Engineering Service Center, 1998. [26] BENSELAMA A M, WILLIAM-LOUIS M J P, MONNOYER F. A 1D–3D mixed method for the numerical simulation of blast waves in confined geometries [J]. Journal of Computational Physics, 2009, 228(18): 6796–6810. doi: 10.1016/j.jcp.2009.06.010 [27] 周涛, 袁宝慧, 梁争锋. 聚能射流引爆屏蔽PBX的实验研究 [J]. 火炸药学报, 2006, 29(4): 10–13. doi: 10.3969/j.issn.1007-7812.2006.04.003ZHOU T, YUAN B H, LIANG Z F. Experimental study of jet initiation of shield PBX [J]. Chinese Journal of Explosives & Propellants, 2006, 29(4): 10–13. doi: 10.3969/j.issn.1007-7812.2006.04.003 -
下载:
点击查看大图
计量
- 文章访问数: 52
- HTML全文浏览量: 11
- PDF下载量: 18
