Translational-Rotational Decoupling Dynamics of High-Pressure Liquid Water under Quasi-Isentropic Compression
-
摘要: 水广泛存在于地球、海洋行星、冰巨行星以及星际空间中，其在广泛热力学区间内的物态和物性是生化反应、环境气候及行星结构等众多问题的核心。尽管极端压力下的液态水表现出丰富的反常行为，但其相关研究长期受限于实验测量技术的瓶颈与理论计算的复杂性，可用的原子尺度数据极为匮乏，限制了对其微观机制的深入理解。为此，基于高精度第一性原理数据构建的深度学习相互作用模型，利用分子动力学模拟将液态水沿等熵线压缩至数万倍大气压强，计算并分析其在不同压强下的结构和动力学性质。结果表明，高压下液态水中固有的四面体局域配位环境被打破，使得水分子的旋转运动能力随着压强增大而显著提高。与此相反，在更加“凝聚”的高压环境下，水分子的平移运动能力受到强烈限制，并且高压下水分子的均方位移呈现出类似玻璃态的3段区域式行为，即弹道输运区、平台区以及扩散区。宏观上，这种平移运动能力的下降表现为剪切黏度的大幅提高。尤为关键的是，与环境压力下过冷水平移-旋转运动高度耦合的特性不同，动态高压下的液态水展现出本征的平移和旋转运动解耦现象。研究结果有望为材料在动态载荷下的响应、亚稳液体凝固等重要科学问题研究提供有意义的微观见解。Abstract: The ubiquitous presence of water, from Earth and planetary bodies to interstellar space, renders its phase behavior across an extensive thermodynamic range fundamental to understanding key scientific phenomena such as biochemical reactions, climate dynamics, and planetary evolution. Nevertheless, although liquid water exhibits distinct anomalous behaviors under extreme pressure, research has been hampered by experimental limitations and computational complexity, resulting in scarce atomic-scale data and hindered understanding of its microscopic mechanisms. To address this, our study employed a deep learning interaction model trained on high-precision ab initio data. Employing molecular dynamics simulations, we compressed liquid water isentropically to tens of thousands of atmospheres. Systematic analysis of its structural and dynamic properties revealed that elevated pressure significantly disrupts the inherent tetrahedral local coordination of water molecules, enhancing their rotational mobility. Conversely, translational mobility is severely suppressed in this highly condensed state. The mean squared displacement of water molecules under high pressure exhibits a characteristic three-stage behavior which is typical of glassy systems: ballistic transport, a plateau, and diffusion. Macroscopically, this reduced translational mobility manifests as a substantial increase in shear viscosity. A critical finding is that, unlike supercooled water under ambient pressure where translational and rotational motions are strongly coupled, liquid water under dynamic high pressure exhibits an intrinsic decoupling of these motions. The insights from this work are expected to offer significant microscopic understanding for crucial scientific questions, including the response of materials under dynamic loading and the solidification of metastable liquids.
-
图 1 高压液态水的O-O RDF和 O-O 配位数
Figure 1. O-O RDF and O-O coordination number of high-pressure liquid water
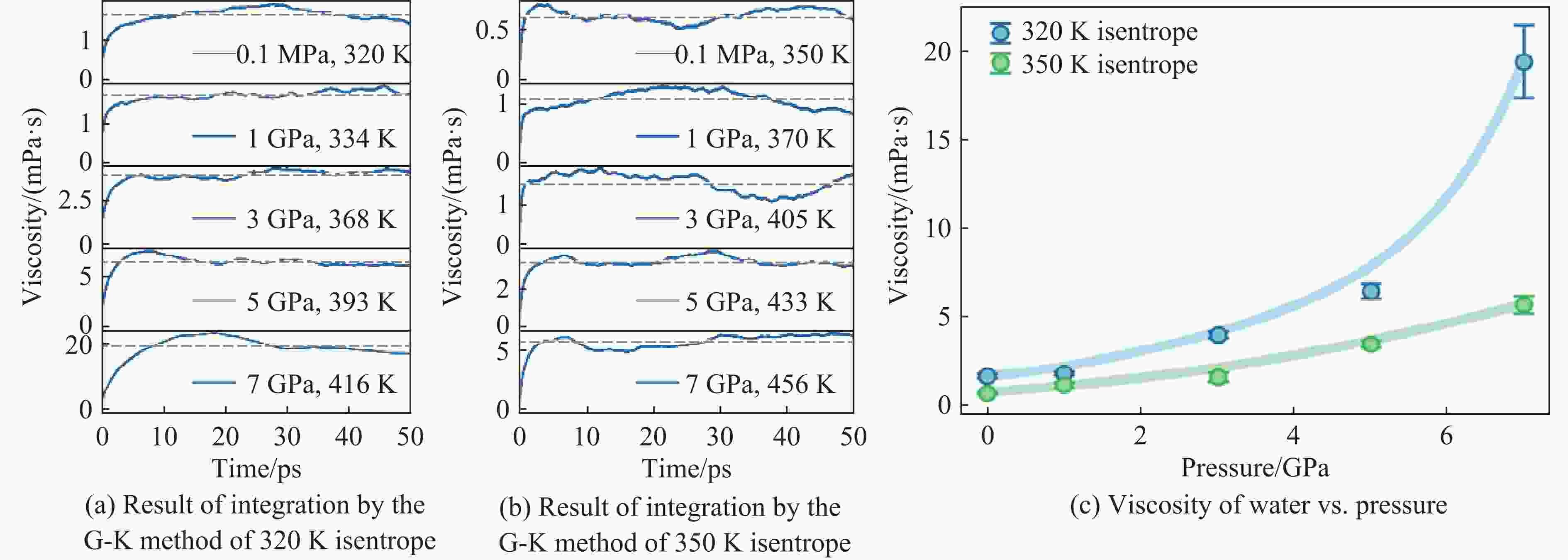
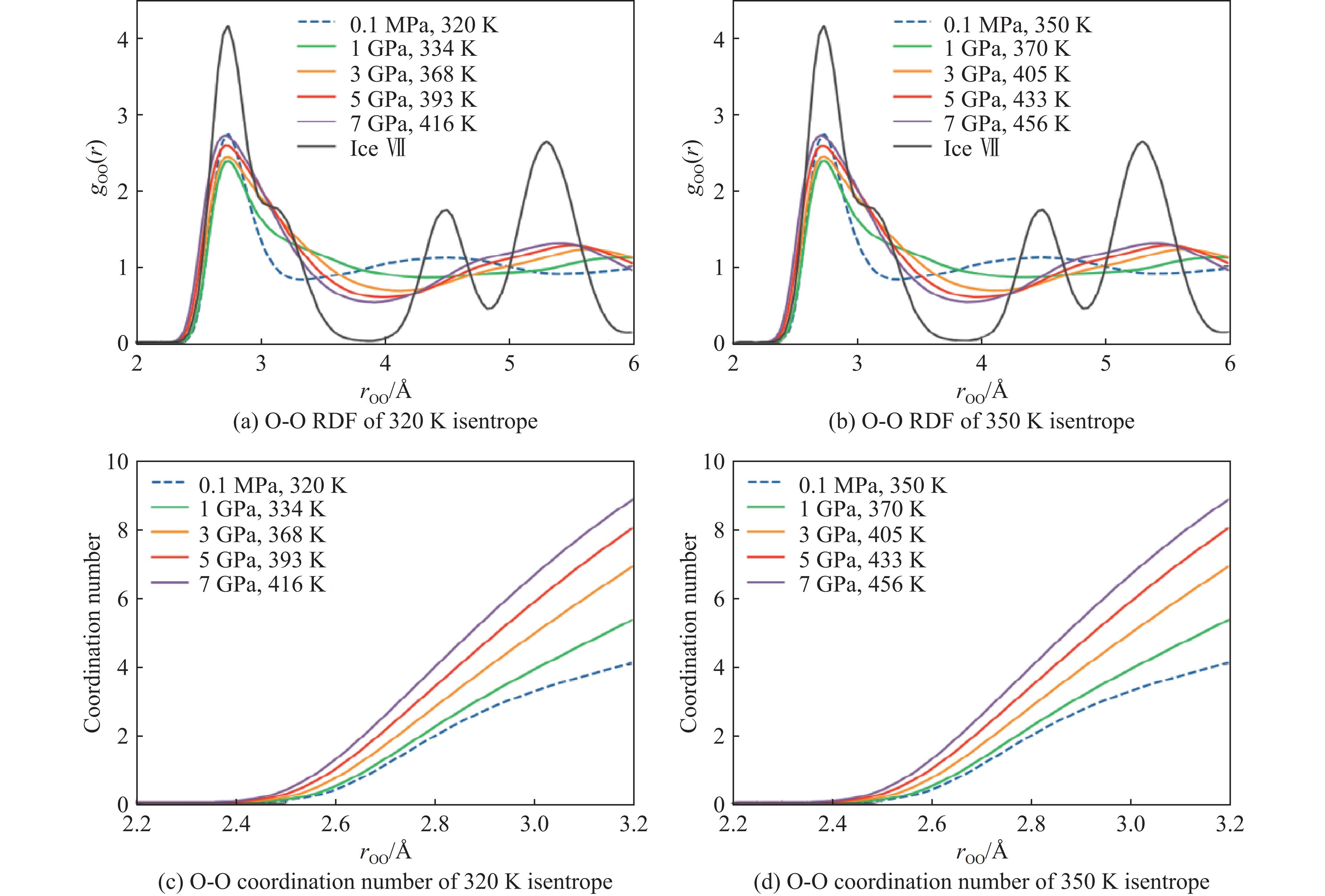
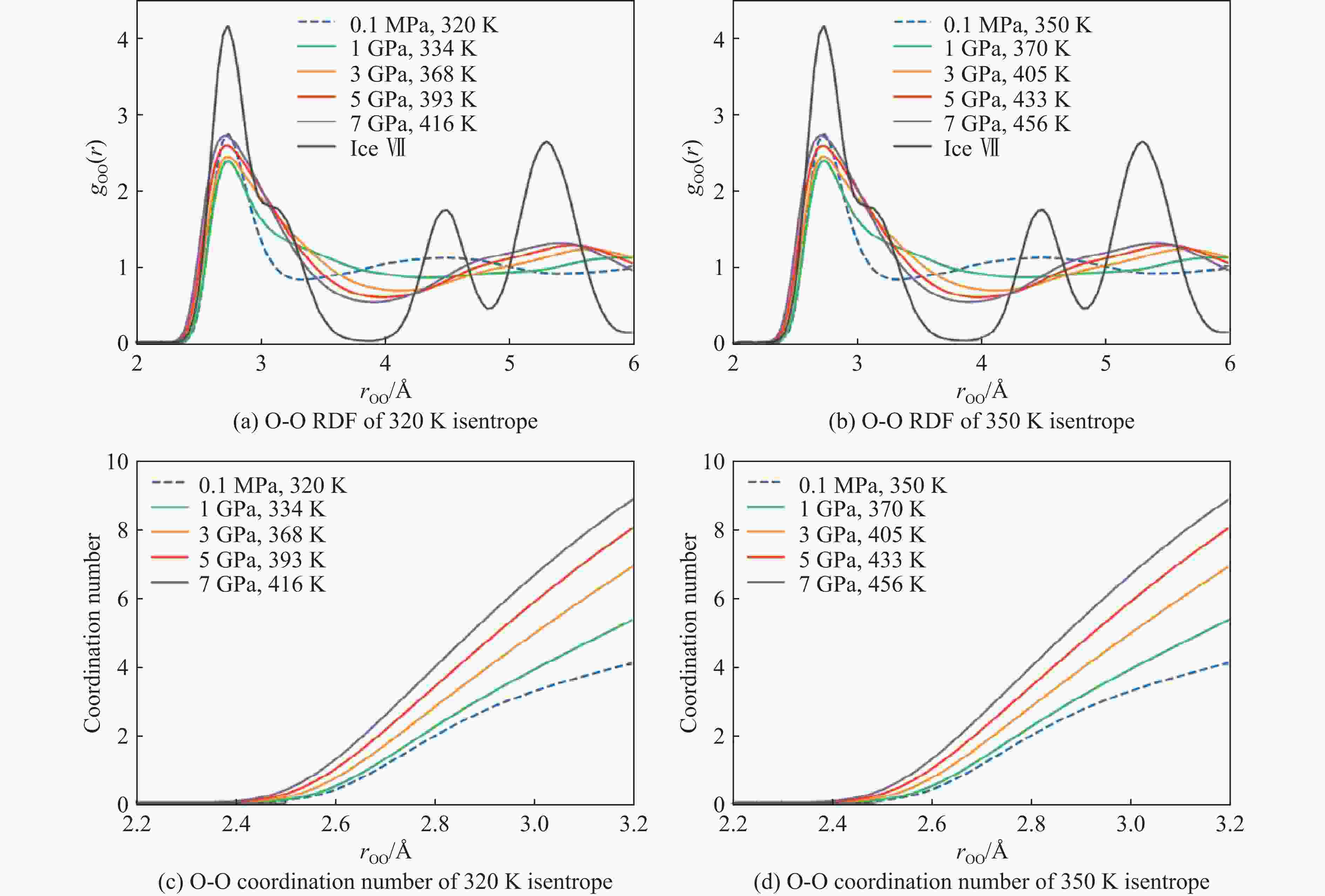
图 2 高压液态水的剪切黏度（图2(a)、图2(b)中灰色水平虚线为积分平台区的数据平均值，即估计的黏度值；图2(c)中的误差为标准差，蓝色和绿色实线为使用贝塞尔方法拟合对应数据得到的结果）
Figure 2. Shear viscosity of high-pressure liquid water (Gray horizontal dashed lines represent the mean value of data within the platform region, which corresponds to the estimated viscosity in Fig.2(a) and Fig.2(b); the error bars indicate standard deviations, while the blue and green lines represent results obtained by fitting the corresponding data using Bessel’s method in Fig.2(c).)
图 3 高压液态水中水分子的平动动力学性质（图3(c)中蓝色和绿色实线为使用贝塞尔方法拟合对应颜色数据得到的结果）
Figure 3. Translational dynamics of water molecules under high-pressure (The blue and green lines represent results obtained by fitting the corresponding data using Bessel’s method in Fig.3(c))
图 4 高压液态水中水分子的旋转动力学性质（图4(c)中蓝色和绿色的实线是使用贝塞尔方法拟合对应颜色的数据所得到的结果）
Figure 4. Rotational dynamics of water molecules under high-pressure (The blue and green lines represent results obtained by fitting the corresponding data using Bessel’s method in Fig.4(c))
图 5 环境压力下不同工作中液态水的O-O RDF结果对比
Figure 5. Comparison of calculated O-O RDF with other works under ambient pressure
表 1 高压下液态水的性质
Table 1. Properties of liquid water under high pressure
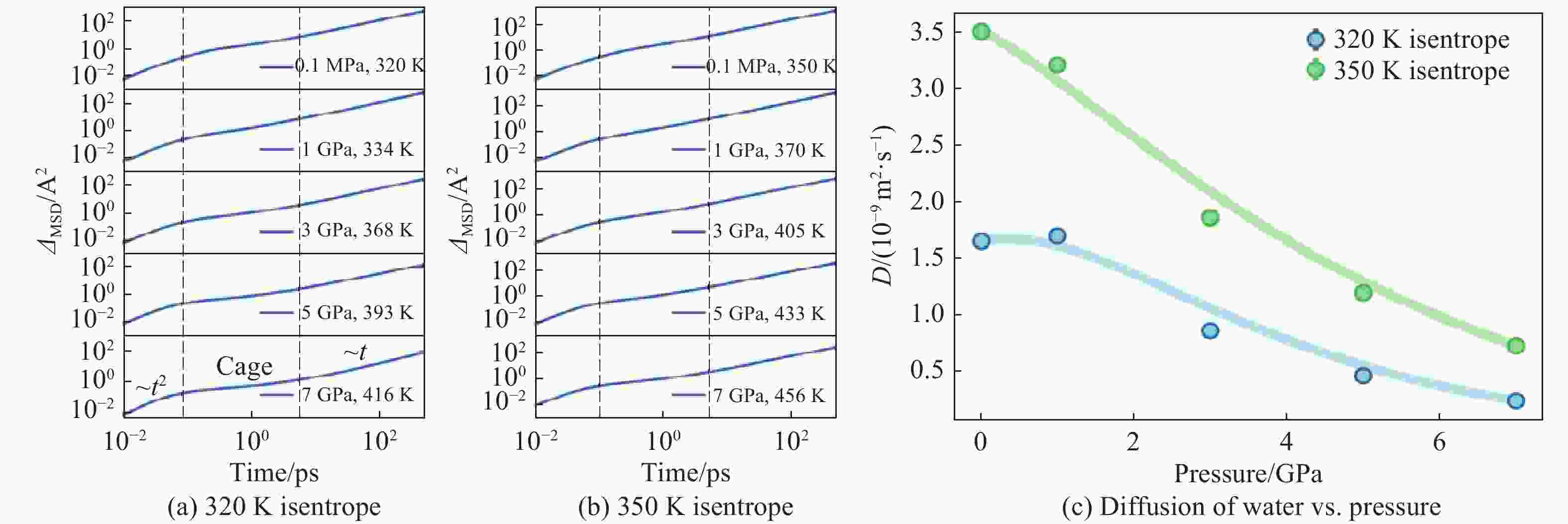
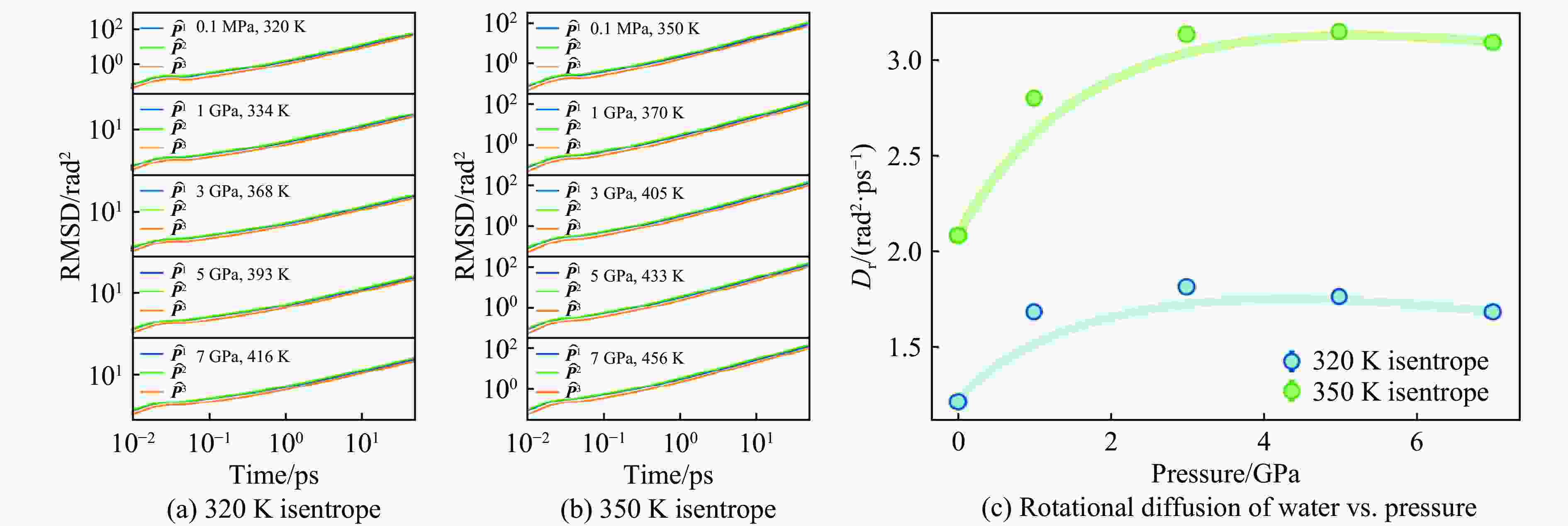
Pressure/GPa Density/(g·cm−3) $ {N}_{\mathrm{c}} $(cutoff is 3.2 Å) D/(10−9 m2·s−1) $ {D}_{\mathbf{r}}/ $(rad2·ps−1) $ \eta $/(mPa·s) 320 K 350 K 320 K 350 K 320 K 350 K 320 K 350 K 320 K 350 K 10−4 1.007 1.005 4.051 4.053 1.652 3.503 1.216 2.084 1.612 0.633 1 1.269 1.251 5.297 5.295 1.699 3.209 1.687 2.803 1.723 1.089 3 1.459 1.437 6.837 6.835 0.845 1.857 1.817 3.139 3.932 1.532 5 1.574 1.557 7.953 7.953 0.443 1.182 1.766 3.150 6.408 3.426 7 1.667 1.647 8.789 8.789 0.222 0.706 1.685 3.096 19.410 5.644 
下载: 导出CSV
表 2 环境压力下本研究与其他工作结果的对比
Table 2. Comparison of our MD simulation results with other works under ambient pressure
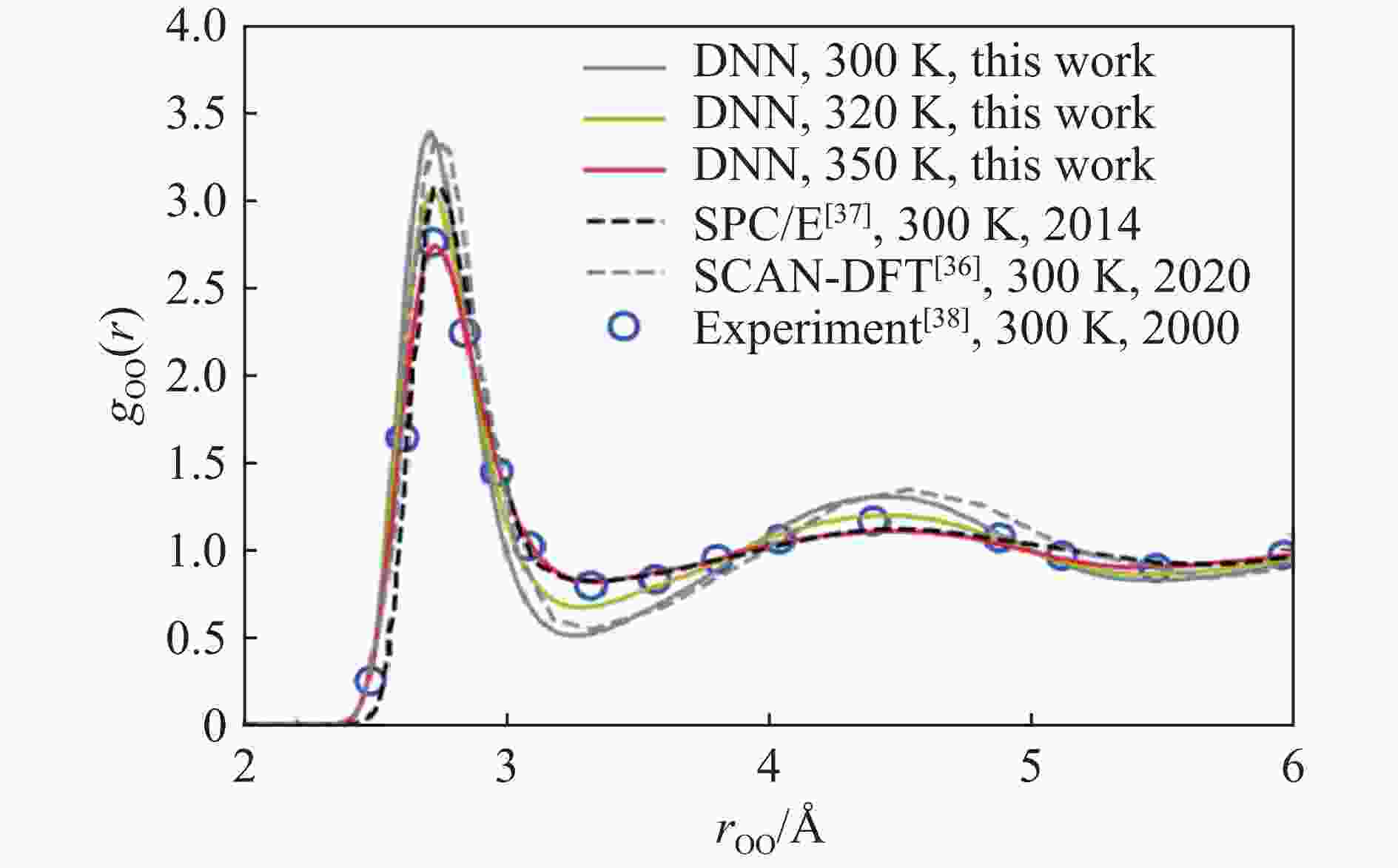
Condition Temperature/K Density/(g·cm−3) $ {N}_{\mathbf{c}} $(cutoff is 3.2 Å) D/(10−9 m2·s−1) $ {D}_{\mathbf{r}}/ $(rad2·ps−1) $ \eta $/(mPa·s) This work 320 1.007 4.051 1.652 1.216 1.612 This work 350 1.005 4.053 3.503 2.084 0.633 Exp.[33–34] 298 0.997 2.300 0.892 Exp.[33] 333 0.467 Exp.[34] 343 5.610 SCAN-DFT[35–36] 300 0.860 2.300 SCAN-DFT[35–36] 330 3.360 0.600 SCAN-DFT[35–36] 360 5.750 0.500 TIP4P/2005[37] 300 2.600 0.800 TIP4P/2005[37] 330 4.530 5.000 TIP4P/2005[37] 360 6.650 3.500
下载: 导出CSV
-
[1] GALLO P, AMANN-WINKEL K, ANGELL C A, et al. Water: a tale of two liquids [J]. Chemical Reviews, 2016, 116(13): 7463–7500. doi: 10.1021/acs.chemrev.5b00750 [2] BERNAL J D, FOWLER R H. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions [J]. The Journal of Chemical Physics, 1933, 1(8): 515–548. doi: 10.1063/1.1749327 [3] PALLARES G, EL MEKKI AZOUZI M, GONZÁLEZ M A, et al. Anomalies in bulk supercooled water at negative pressure [J]. Proceedings of the National Academy of Sciences of the United States of America, 2014, 111(22): 7936–7941. doi: 10.1073/pnas.1323366111 [4] GARTNER Ⅲ T E, PIAGGI P M, CAR R, et al. Liquid-liquid transition in water from first principles [J]. Physical Review Letters, 2022, 129(25): 255702. doi: 10.1103/PhysRevLett.129.255702 [5] EICHLER J, STEFANSKI J, ROCA J M, et al. Shear and bulk viscosities of water up to 1.6 GPa and anomaly in the structural relaxation time [J]. Physical Review Letters, 2025, 134(13): 134101. doi: 10.1103/PhysRevLett.134.134101 [6] DOLAN D H, KNUDSON M D, HALL C A, et al. A metastable limit for compressed liquid water [J]. Nature Physics, 2007, 3(5): 339–342. doi: 10.1038/nphys562 [7] DUFFY T S, SMITH R F. Ultra-high pressure dynamic compression of geological materials [J]. Frontiers in Earth Science, 2019, 7: 23. doi: 10.3389/feart.2019.00023 [8] MARSHALL M C, MILLOT M, FRATANDUONO D E, et al. Metastability of liquid water freezing into ice Ⅶ under dynamic compression [J]. Physical Review Letters, 2021, 127(13): 135701. doi: 10.1103/PhysRevLett.127.135701 [9] PÉPIN C M, ANDRÉ R, OCCELLI F, et al. Metastable water at several compression rates and its freezing kinetics into ice Ⅶ [J]. Nature Communications, 2024, 15(1): 8239. doi: 10.1038/S41467-024-52576-Z [10] BERENDSEN H J C, GRIGERA J R, STRAATSMA T P. The missing term in effective pair potentials [J]. Journal of Physical Chemistry, 1987, 91(24): 6269–6271. doi: 10.1021/j100308a038 [11] JORGENSEN W L, CHANDRASEKHAR J, MADURA J D, et al. Comparison of simple potential functions for simulating liquid water [J]. The Journal of Chemical Physics, 1983, 79(2): 926–935. doi: 10.1063/1.445869 [12] YAGASAKI T, MATSUMOTO M, TANAKA H. Phase diagrams of TIP4P/2005, SPC/E, and TIP5P water at high pressure [J]. The Journal of Physical Chemistry B, 2018, 122(31): 7718–7725. doi: 10.1021/acs.jpcb.8b04441 [13] CAR R, PARRINELLO M. Unified approach for molecular dynamics and density-functional theory [J]. Physical Review Letters, 1985, 55(22): 2471–2474. doi: 10.1103/PhysRevLett.55.2471 [14] 邓莉, 刘红, 田华, 等. 高温高压下MgSiO3熔体结构的第一性原理分子动力学研究 [J]. 高压物理学报, 2014, 28(3): 273–282. doi: 10.11858/gywlxb.2014.03.003DENG L, LIU H, TIAN H, et al. First-principles molecular dynamics study of the structure of MgSiO3 melt at high temperatures and high pressures [J]. Chinese Journal of High Pressure Physics, 2014, 28(3): 273–282. doi: 10.11858/gywlxb.2014.03.003 [15] ZHANG L F, WANG H, CAR R, et al. Phase diagram of a deep potential water model [J]. Physical Review Letters, 2021, 126(23): 236001. doi: 10.1103/PhysRevLett.126.236001 [16] CHANG X J, CHEN B, ZENG Q Y, et al. Theoretical evidence of H-He demixing under Jupiter and Saturn conditions [J]. Nature Communications, 2024, 15(1): 8543. doi: 10.1038/s41467-024-52868-4 [17] QIU R, ZENG Q Y, WANG H, et al. Anomalous thermal transport across the superionic transition in ice [J]. Chinese Physics Letters, 2023, 40(11): 116301. doi: 10.1088/0256-307X/40/11/116301 [18] YANG F H, ZENG Q Y, CHEN B, et al. Lattice thermal conductivity of MgSiO3 perovskite and post-perovskite under lower mantle conditions calculated by deep potential molecular dynamics [J]. Chinese Physics Letters, 2022, 39(11): 116301. doi: 10.1088/0256-307X/39/11/116301 [19] CHEN T, LIU Q R, LIU Y, et al. Combining stochastic density functional theory with deep potential molecular dynamics to study warm dense matter [J]. Matter and Radiation at Extremes, 2024, 9(1): 015604. doi: 10.1063/5.0163303 [20] CHEN M H, KO H Y, REMSING R C, et al. Ab initio theory and modeling of water [J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(41): 10846–10851. doi: 10.1073/pnas.1712499114 [21] RAVELO R, HOLIAN B L, GERMANN T C. High strain rates effects in quasi-isentropic compression of solids [J]. AIP Conference Proceedings, 2009, 1195(1): 825–828. doi: 10.1063/1.3295269 [22] THOMPSON A P, AKTULGA H M, BERGER R, et al. LAMMPS—a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales [J]. Computer Physics Communications, 2022, 271: 108171. doi: 10.1016/j.cpc.2021.108171 [23] ZENG J Z, ZHANG D, LU D H, et al. DeePMD-kit V2: a software package for deep potential models [J]. The Journal of Chemical Physics, 2023, 159(5): 054801. doi: 10.1063/5.0155600 [24] GREEN M S. Markoff random processes and the statistical mechanics of time-dependent phenomena. Ⅱ. irreversible processes in fluids [J]. The Journal of Chemical Physics, 1954, 22(3): 398–413. doi: 10.1063/1.1740082 [25] KUBO R, YOKOTA M, NAKAJIMA S. Statistical-mechanical theory of irreversible processes. Ⅱ. response to thermal disturbance [J]. Journal of the Physical Society of Japan, 1957, 12(11): 1203–1211. doi: 10.1143/JPSJ.12.1203 [26] MAGINN E J, MESSERLY R A, CARLSON D J, et al. Best practices for computing transport properties 1. self-diffusivity and viscosity from equilibrium molecular dynamics [article v1.0] [J]. Living Journal of Computational Molecular Science, 2019, 1(1): 6324–6324. doi: 10.33011/livecoms.1.1.6324 [27] MAZZA M G, GIOVAMBATTISTA N, STARR F W, et al. Relation between rotational and translational dynamic heterogeneities in water [J]. Physical Review Letters, 2006, 96(5): 057803. doi: 10.1103/PhysRevLett.96.057803 [28] SILVESTRELLI P L. Transport properties in liquids from first-principles: the case of liquid water and liquid argon [J]. The Journal of Chemical Physics, 2023, 158(13): 134503. doi: 10.1063/5.0144353 [29] GOSLING E M, MCDONALD I R, SINGER K. On the calculation by molecular dynamics of the shear viscosity of a simple fluid [J]. Molecular Physics, 1973, 26(6): 1475–1484. doi: 10.1080/00268977300102631 [30] BOWMAN R W, GIBSON G M, PADGETT M J, et al. Optical trapping at gigapascal pressures [J]. Physical Review Letters, 2013, 110(9): 095902. doi: 10.1103/PhysRevLett.110.095902 [31] MATHAROO G S, RAZUL M S G, POOLE P H. Structural and dynamical heterogeneity in a glass-forming liquid [J]. Physical Review E, 2006, 74(5): 050502. doi: 10.1103/PhysRevE.74.050502 [32] ZHANG X, YAO Y F, LI H Y, et al. Fast crystal growth of ice Ⅶ owing to the decoupling of translational and rotational ordering [J]. Communications Physics, 2023, 6(1): 164. doi: 10.1038/s42005-023-01285-y [33] HARRIS K R, WOOLF L A. Temperature and volume dependence of the viscosity of water and heavy water at low temperatures [J]. Journal of Chemical & Engineering Data, 2004, 49(4): 1064–1069. doi: 10.1021/je049668+ [34] KRYNICKI K, GREEN C D, SAWYER D W. Pressure and temperature dependence of self-diffusion in water [J]. Faraday Discussions of the Chemical Society, 1978, 66: 199–208. doi: 10.1039/DC9786600199 [35] HERRERO C, PAULETTI M, TOCCI G, et al. Connection between water’s dynamical and structural properties: insights from ab initio simulations [J]. Proceedings of the National Academy of Sciences of the United States of America, 2022, 119(21): e2121641119. doi: 10.1073/pnas.2121641119 [36] YAO Y, KANAI Y. Temperature dependence of nuclear quantum effects on liquid water via artificial neural network model based on SCAN meta-GGA functional [J]. The Journal of Chemical Physics, 2020, 153(4): 044114. doi: 10.1063/5.0012815 [37] ORSI M. Comparative assessment of the ELBA coarse-grained model for water [J]. Molecular Physics, 2014, 112(11): 1566–1576. doi: 10.1080/00268976.2013.844373 [38] SOPER A K. The radial distribution functions of water and ice from 220 to 673 K and at pressures up to 400 MPa [J]. Chemical Physics, 2000, 258(2/3): 121–137. doi: 10.1016/S0301-0104(00)00179-8 -
下载:
图(5) / 表(2)
计量
- 文章访问数: 69
- HTML全文浏览量: 16
- PDF下载量: 5
