Optimization and Uncertainty Quantification of High-Fidelity Material Model Parameters for Dynamic Loading Simulation
-
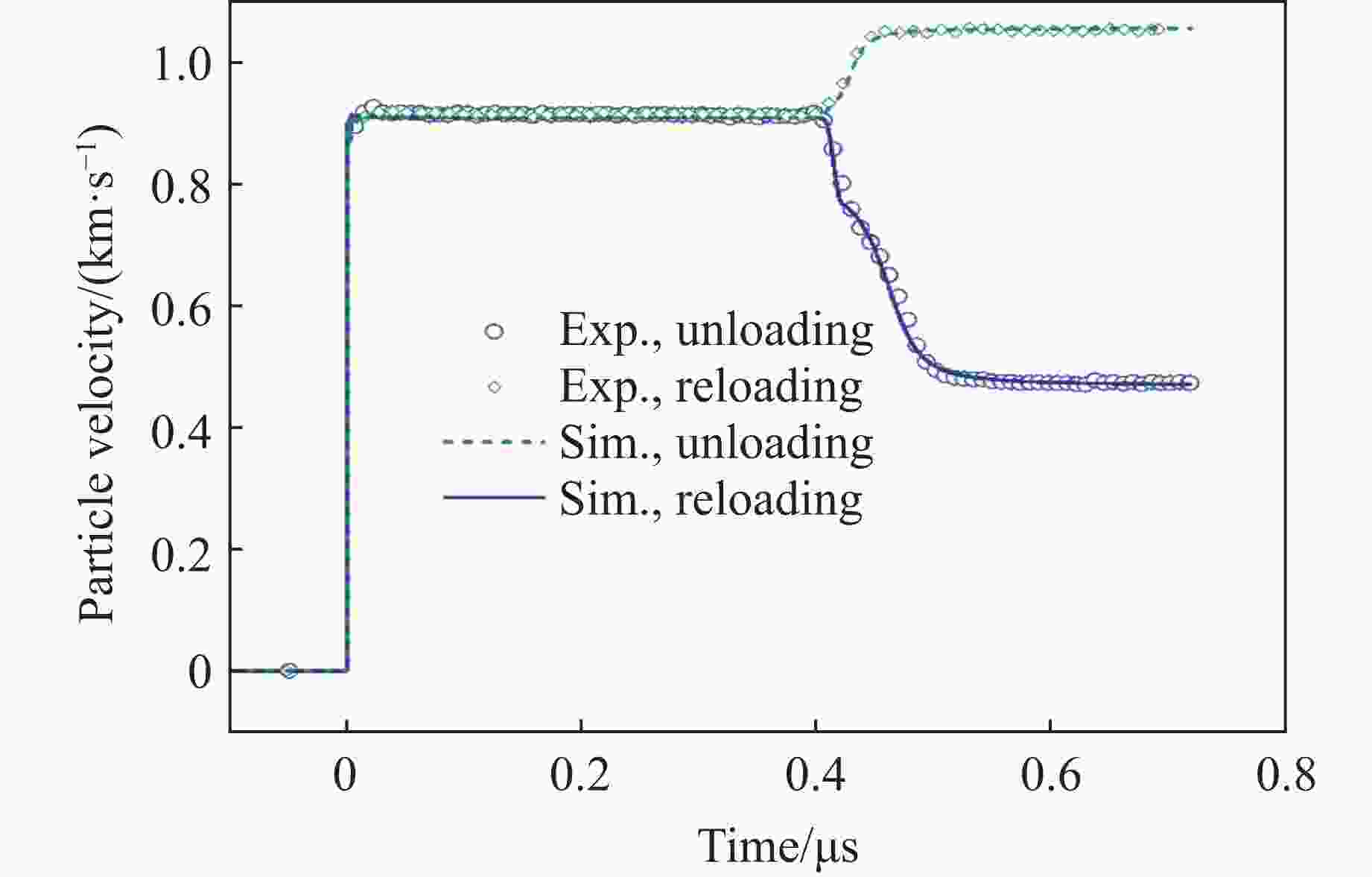
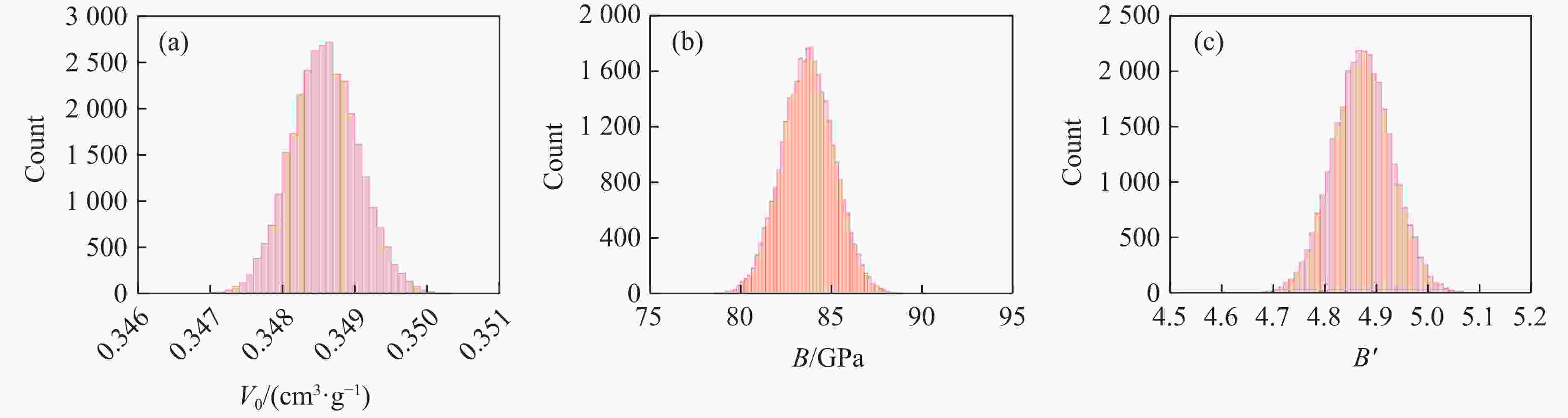
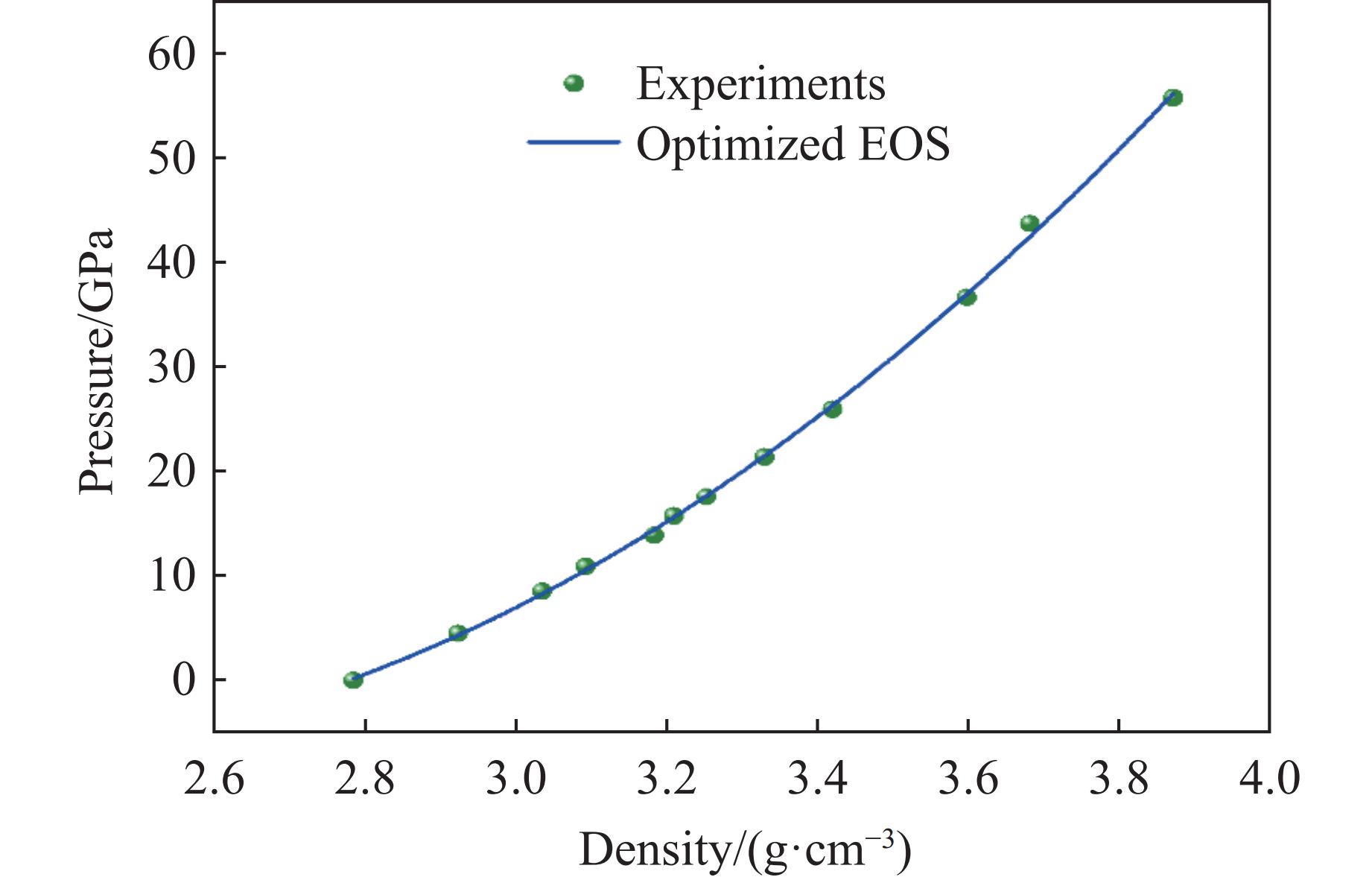
摘要: 高保真材料模型的系统性构建、优化和验证对于动态载荷仿真至关重要。详述了在大禹数字平台上构建和验证此类模型的方法:首先,构建参数化状态方程(equation of state, EOS)框架,整合所有可用的含相关不确定度的实验数据,并采用全局优化方法确定最优EOS参数;然后,将优化后的EOS与包含待定参数的本构模型耦合,开展复现实验条件的一维或二维数值模拟;进而,利用优化算法迭代调整本构模型参数,以实现模拟波形与实验波形的全局最优匹配,从而精确标定本构参数;最后,整合优化后的EOS与标定后的本构模型,形成完整的材料模型,并为自研及商业仿真软件开发标准化接口。通过模拟预测新的实验条件下的材料性质并与实验结果进行对比,完成材料模型的验证。利用自主研发的新型重要性交叉优化算法,实现了实验数据约束下的理论模型参数优化,采用贝叶斯不确定性量化程序对材料模型参数的不确定性及其向计算物理量的传递进行严格量化。Abstract: Systematic construction, optimization, and validation of high-fidelity material models are crucial for dynamic load simulations. This study details a methodology for building and validating such models on the Dayu Digital Platform. First, a parameterized equation of state (EOS) framework is constructed, integrating all available experimental data with associated uncertainties. Global optimization methods are then employed to determine the optimal EOS parameters. Second, the optimized EOS is coupled with a constitutive model containing undetermined parameters. One-dimensional or two-dimensional numerical simulations are conducted, reproducing experimental conditions. Optimization algorithms iteratively adjust the constitutive model parameters to achieve a globally optimal match between simulated waveforms and experimental waveforms, thereby precisely calibrating the constitutive parameters. Finally, the optimized EOS and calibrated constitutive model are integrated to form a complete material model, and standardized interfaces are developed for both in-house and commercial simulation software. The validation of material models is accomplished by comparing simulated predictions under new experimental conditions with experimental results. Within this process, the optimization of theoretical model parameters constrained by experimental data is achieved using the self-developed novel importance cross-optimization (ICON) algorithm. The uncertainty in material model parameters and its propagation to computed physical quantities are rigorously quantified using a self-developed Bayesian uncertainty quantification (UQ) program.
-
-
[1] 刘朋, 王黎钦, 张传伟, 等. 航空发动机主轴轴承状态监测研究现状与发展趋势 [J]. 航空动力学报, 2022, 37(2): 330–343.LIU P, WANG L Q, ZHANG C W, et al. Research status and development trend of condition monitoring on main-shaft bearings used in aircraft engines [J]. Journal of Aerospace Power, 2022, 37(2): 330–343. [2] 向士凯, 耿华运, 孙毅, 等. Yudb V1.0: 2025SR1194507 [P]. 2025. [3] XIAN Y T, XIANG S K, LIU L, et. al. Accurate equation of state of rhenium as pressure cale up to 130 GPa and 3 200 K [J]. AIP Advances, 2022, 12(5): 055313. doi: 10.1063/5.0089292 [4] IKUTA D, OHTANI E, FUKUI H, et al. Large density deficit of Earthʼs core revealed by a multi-megabar primary pressure scale [J]. arXiv, 2021: 210402076. [5] STEINBERG D J, LUND C M. A constitutive model for strain rates from 10−4 to 106 s−1 [J]. Journal of Applied Physics, 1989, 65(4): 1528–1533. doi: 10.1063/1.342968 [6] MARSH S P. LASL shock Hugoniot data [M]. Berkeley, USA: University of California Press, 1980. [7] GAN Y C, NAN X L, WU D. Dynamic yield behaviors of aluminum under shock and ramp compression: experiments and models [J]. Journal of Applied Physics, 2025, 137: 215902. doi: 10.1063/5.0270423 [8] YAO S L, PEI X Y, YU J D, et al. A dislocation-based explanation of quasi-elastic release in shock-loaded aluminum [J]. Journal of Applied Physics, 2017, 121: 035101. doi: 10.1063/1.4974055 [9] JOHNSON J N, HIXSON R S, GRAY G T, et al. Quasielastic release in shock-compressed solids [J]. Journal of Applied Physics, 1992, 72(2): 429–441. doi: 10.1063/1.351871 -






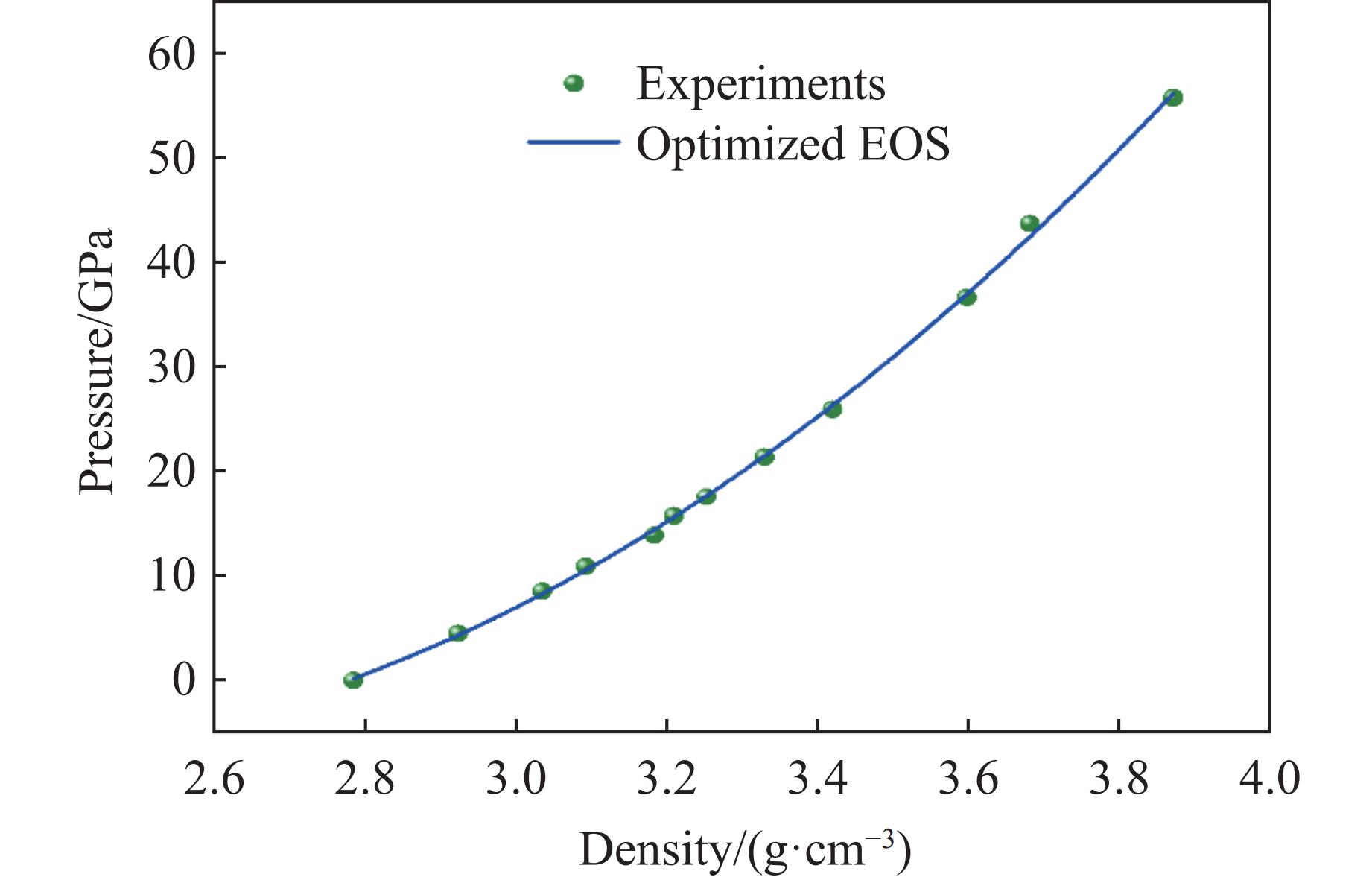
 下载:
下载: