A Review of Machine Learning Potentials in the Study of Materials Properties
-
摘要: 随着人工智能技术与计算硬件的迅速发展,人工智能技术已逐渐成为推动多个科学研究领域变革的革命性工具。在材料科学领域,机器学习方法在材料高通量设计与性能预测方面均发挥着重要作用。近十余年来,基于机器学习构建材料原子间相互作用势的方法已被广泛应用于材料物性研究中,为新型材料的理论设计及微观机制的深入揭示提供了重要支撑。系统梳理了机器学习势的发展历程,介绍其基本流程,概述主流机器学习势的原理及其在材料物性研究中的应用场景,简要评述新兴通用势模型的进展,总结当前面临的挑战及未来发展方向。Abstract: With the rapid advancement of artificial intelligence (AI) technologies and hardware capabilities, AI has gradually become a revolutionary tool driving transformative changes across multiple scientific research domains. In the field of materials science, machine learning methods are significant in high-throughput materials design and property prediction. Over the past decade, machine learning-based approaches for constructing interatomic potentials have been widely applied in the study of material properties, and are providing crucial support for the theoretical design of novel materials and in-depth understanding of their underlying microscopic mechanisms. This article reviews the development of machine learning potentials, and introduces their fundamental workflows. The principles of mainstream methods and their applications in materials property research are outlined. Moreover, recent progress in emerging universal potential models is briefly discussed, then concludes with an analysis of current challenges and future research directions.
-
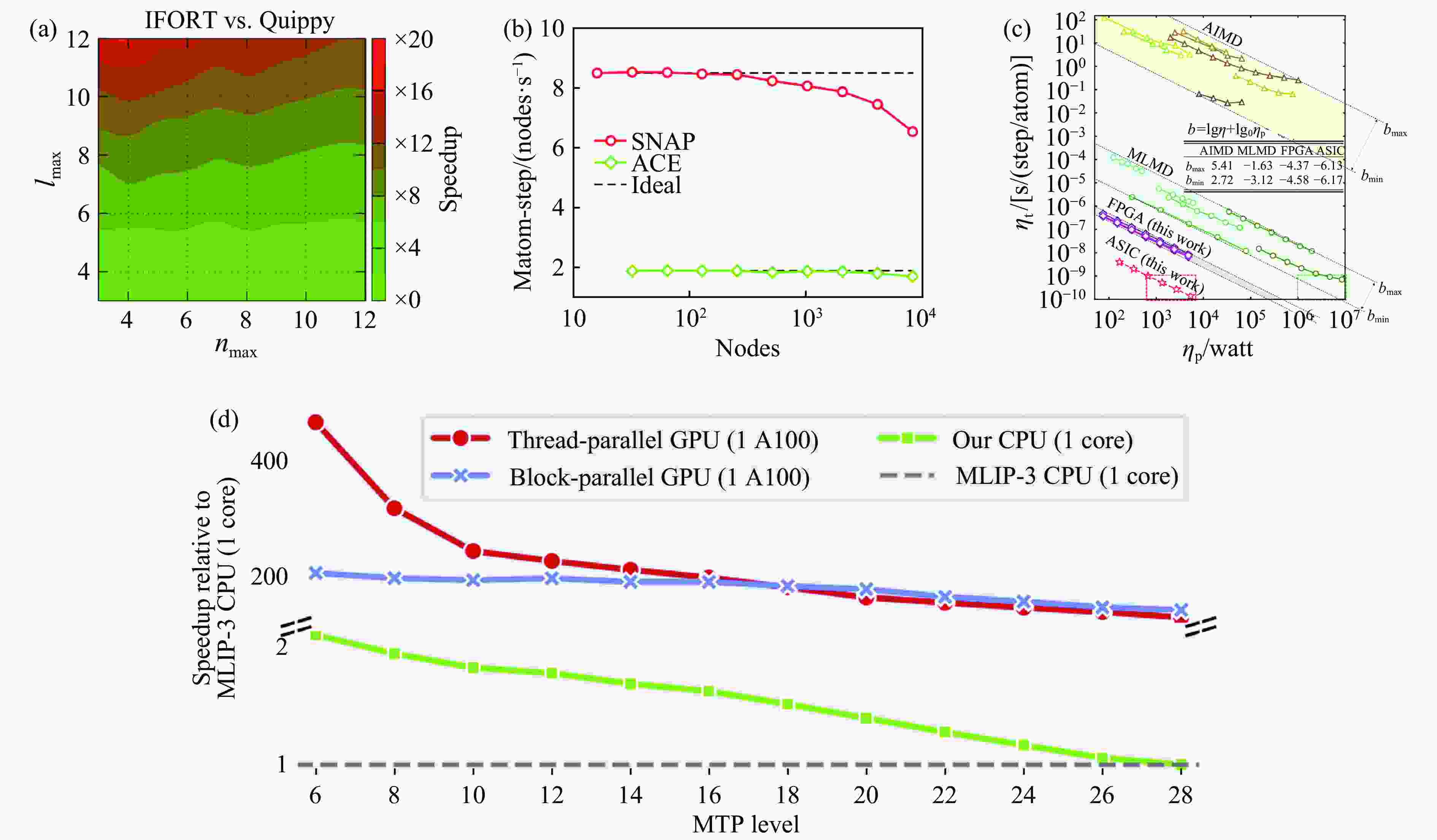
图 7 通过算法、硬件等重新优化下的机器学习势速度提升:(a) Speedup是指用IFORT编译的新SOAP计算与Quippy实现的时序的倒数(tQuippy/tIfort)[28];(b) 基于GPU的超算平台上液态碳1×109原子的分子动力学模拟中SNAP和ACE的计算效率[36];(c) AIMD、MLMD与MDPU平台MD的能效对比[37];(d) 基于Kokkos加速下MTP势计算效率相比原MLIP-3 CPU版本的效率提升[38]
Figure 7. Acceleration of machine learning potentials through optimizations in algorithms and hardware: (a) speedup is defined as the inverse of the time ratio (tQuippy/tIfort) between the new SOAP calculations compiled with IFORT and the implementation by Quippy[28]; (b) the computational efficiency of SNAP and ACE force fields in large-scale molecular dynamics simulations of liquid carbon containing 1×109 atoms on GPU-based supercomputing platforms[36]; (c) a comparison of energy efficiencies among ab initio molecular dynamics (AIMD), machine learning molecular dynamics (MLMD), and MD approaches on the MDPU platform[37]; (d) efficiency gains in MTP potential computations facilitated by Kokkos, as compared to the original CPU version of MLIP-3[38]
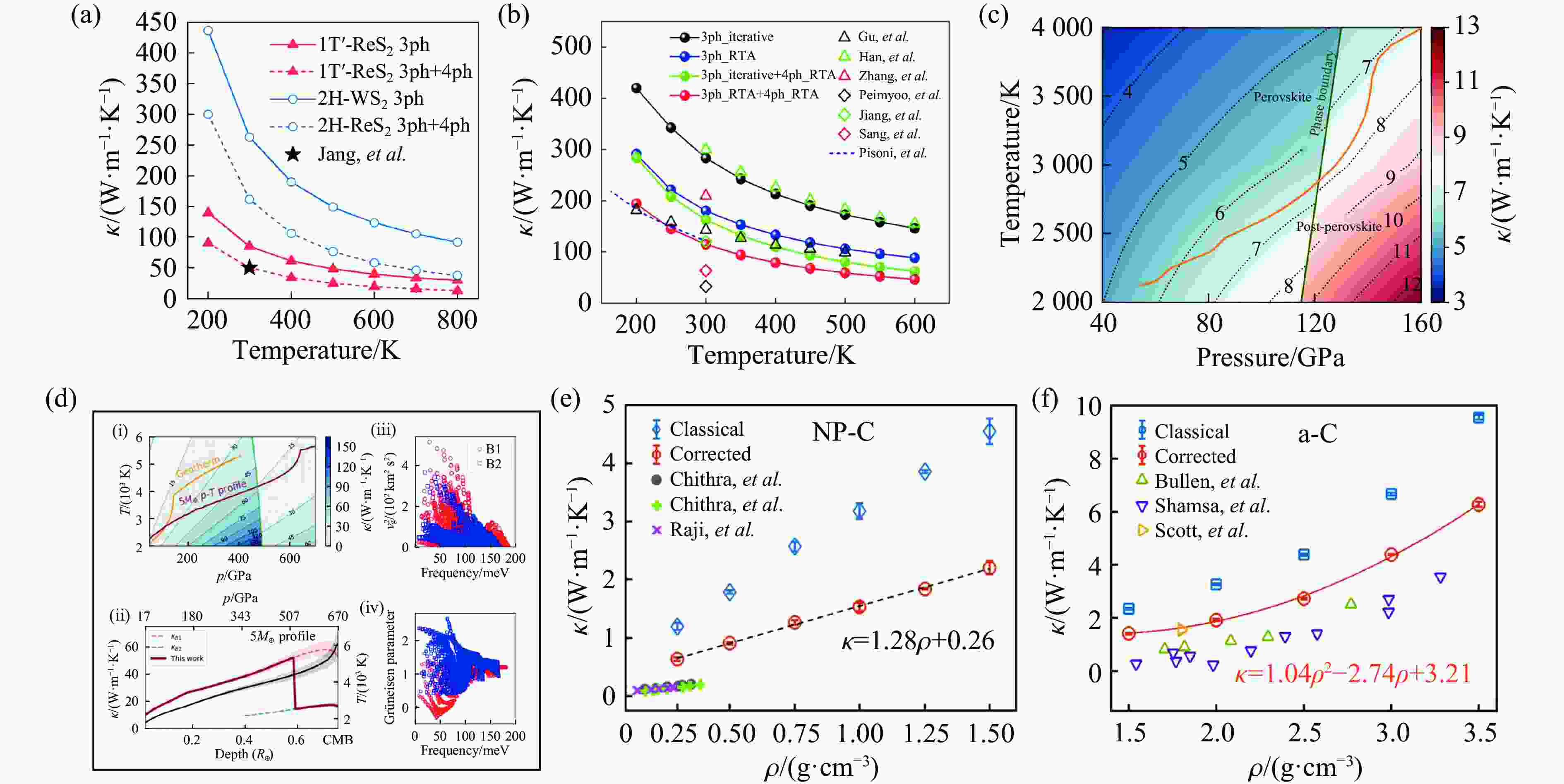
图 9 基于机器学习势的材料热输运性质研究:(a) 基于MTP+Boltzmann输运方程给出的二维 ReS2的热导率[80];(b) 基于GAP和Boltzmann输运方程给出的二维-WS2的热导率[81];(c)~(d) DP和EMD方法给出的MgSiO3和MgO在高温高压下的热导率图像[82–83];(e)~(f) 基于NEP+HNEMD方法计算的纳米多孔和非晶碳热导率的密度依赖性[84]
Figure 9. A study of the thermal transport properties of materials based on machine learning potential: (a) thermal conductivity of 2D-ReS2 calculated by the MTP with Boltzmann transport equation[80]; (b) thermal conductivity of 2D-WS2 calculated using the GAP with Boltzmann transport equation[81]; (c)−(d) thermal conductivity map of MgSiO3 at high temperature and pressure calculated by the DP+EMD method[82–83]; (e)−(f) density dependence of the thermal conductivity of nanoporous and amorphous carbon calculated by the NEP+HNEMD method[84]
表 1 常见机器学习势及下载地址
Table 1. Common machine learning potentials and download links
Machine learning potential Download website MTP[13] https://gitlab.com/ashapeev/mlip-2 GAP[18] https://github.com/libAtoms/GAP SNAP[19] https://github.com/FitSNAP/FitSNAP Materials potential library (MatPL) https://github.com/LonxunQuantum/MatPL Machine learning force filed based on VASP (VASP-MLFF)[12] https://www.vasp.at DP[20] https://github.com/deepmodeling/deepmd-kit NEP[22] https://github.com/brucefan1983/GPUMD High-dimensional neural network potential (HDNNP)[7] https://github.com/CompPhysVienna/n2p2 NequIP https://github.com/mir-group/nequip MACE https://github.com/ACEsuit/mace Polarizable atom interaction neural network (PaiNN)[25] https://github.com/atomistic-machine-learning/schnetpack 表 2 基于机器学习势的部分材料相变研究汇总[41–42, 44–49, 52–79]
Table 2. A partial overview of studies on machine learning potentials in material phase transitions[41–42, 44–49, 52–79]
MLP Materials Phase transition References MTP U SS/SL Kruglov, et al.[42] (2019) TaVCrW SL Zhu, et al.[52] (2024) Ti-6Al-4V SS/SL Nitol, et al.[53] (2025) Ag-Pd alloy SL Rosenbrock, et al.[54] (2021) Ti, Zr, Hf SS Jung, et al.[55] (2023) U-6%Nb SS Huang, et al.[56] (2025) GAP 2D Ga2O3 SS Zhao, et al.[57] (2021) SiO2 SS Erhard, et al.[58] (2022) Ga2O3 SS/SL Zhao, et al.[59] (2023) Zr SS/SL Zong, et al.[48–49] (2018, 2019) SNAP Carbon SS/SL Willman, et al.[41] (2022) Ni-Mo SS Li, et al.[60] (2018) Au SS/SL Richard, et al.[61] (2023) Co SS Bideault, et al.[62] (2024) VASP-MLFF ZrO2 SS Liu, et al.[63] (2022) Zr SS Liu, et al.[64] (2021) DeepMD H2O SS/SL Zhang, et al.[44] (2021) Hydrogen SS/SL Niu, et al.[65] (2023) H-He LG Dai, et al.[46] (2024) Sn SS/SL Chen, et al.[66] (2023) MgSiO3 SS/SL Deng, et al.[67] (2023) Ag-Pd alloy SS Guo, et al.[68] (2023) MgO SL Wisesa, et al.[69] (2023) SrTiO3 SS He, et al.[70] (2022) Ti SS/SL Wen, et al.[71] (2021) Ga SS/SL Niu, et al.[72] (2020) NEP Coesite SS Feng, et al.[73] (2025) BaZrS3 SS Kayastha, et al.[74] (2025) Oxygen SS/SL Wang, et al.[45] (2025) SiO2 SS Pan, et al.[75] (2024) CsPbBr3, MAPbI3 SS Fransson, et al.[76] (2023) Carbon SS/SL Shi, et al.[47] (2023) MgO-H2O SS Pan, et al.[77] (2023) NequIP Hydrogen LL Istas, et al.[78] (2025) MACE Hydrogen SL LY, et al.[79] (2025) 表 3 机器学习势在材料热输运性质上的部分研究汇总[81–83, 85–119]
Table 3. Selected studies on machine learning potentials for materials thermal transport properties[81–83, 85–119]
MLP Materials Method References MTP BAs BTE Ouyang, et al.[85] (2022) CoSb3 EMD-GK Korotaev, et al.[86] (2019) SrTiO3 BTE Wang, et al.[87] (2021) 2D materials BTE Mortazavi, et al.[88] (2021) Pb3Bi2S6 BTE Wang, et al.[89] (2025) SnSe EMD-GK Liu, et al.[90] (2021) Cs3Bi2Br9 EMD-GK Li, et al.[91] (2024) 2D ReS2 BTE Yang, et al.[80] (2024) GAP 2D h-BN BTE Zhang, et al.[92] (2021) TiO2 EMD-GK Ren, et al.[93] (2025) h-BN BTE Tang, et al.[94] (2023) 2D-WS2 BTE Zhang, et al.[81] (2023) (vacancies) Si BTE Babaei, et al.[96] (2019) c-BAs BTE Tang, et al.[95] (2023) SNAP MoSSe alloy EMD-GK Gu, et al.[97] (2019) ZrB2 EMD-GK Zhang, et al.[98] (2020) VASP-MLFF CsPbBr3 NEMD Lahnsteiner, et al.[99] (2024) meta-stable Si BTE Cui, et al.[100] (2023) DeepMD MgO EMD-GK Qiu, et al.[83] (2025) Ice EMD-GK Qiu, et al.[101] (2023) Ir EMD-GK Bhatt, et al.[102] (2024) La2Hf2O7 BTE Che, et al.[103] (2024) V EMD-GK Malgope, et al.[104] (2024) MgSiO3-H2O EMD-GK Peng, et al.[105] (2024) SnSe BTE Zhang, et al.[106] (2024) Ice EMD-GK Qiu, et al.[101] (2023) Wadsleyite NEMD Wang, et al.[107] (2022) 2D NiN2 BTE Mirchi, et al.[108] (2024) Bi2Te3 EMD-GK Zhang, et al.[109] (2022) MgSiO3 EMD-GK Yang, et al.[82] (2022) NEP MoS2/WSe2 HNEMD Hu, et al.[110] (2025) ICOF-Li/Na HNEMD Li, et al.[111] (2025) MECs HNEMD Zhou, et al.[112] (2025) BaTiS3 HNEMD Wang, et al.[113] (2025) HECs HNEMD Liu, et al.[114] (2025) 2D PCn HNEMD Cao, et al.[115] (2024) Amorphous Si HNEMD Yang, et al.[116] (2025) HKUST-1 HNEMD Fan, et al.[117] (2024) Mg3(Sb, Bi)2 HNEMD Huang, et al.[118] (2024) Ga2O3/h-BN NEMD So, et al.[119] (2024) 表 4 机器学习势在材料力学性质上的部分研究汇总[98, 125–126, 129–158]
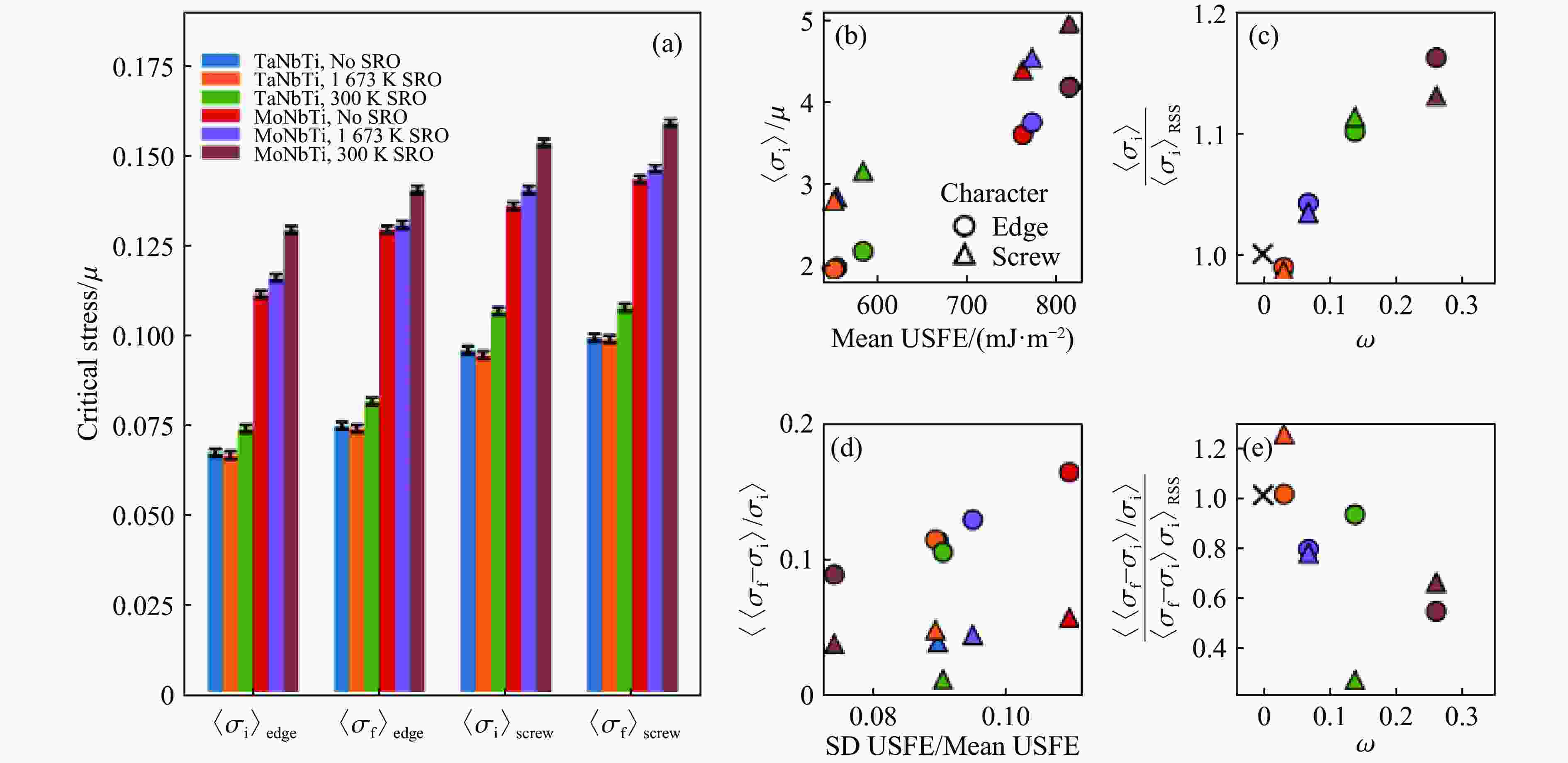
Table 4. Selected studies on machine learning potentials for mechanical properties of materials[98, 125–126, 129–158]
MLP Materials Properties References MTP β-Ti Elastic Shapeev, et al.[129] (2020) Nb Dislocation Zotov, et al.[130] (2024) U Elastic Wang, et al.[125] (2022) TiZrHfTax Elastic Gubaev, et al.[131] (2021) Poly-carbon Elastic Jalolov, et al.[132] (2024) α-Ag2S Plasticity Yang, et al.[133] (2025) CNTs Mechanical Choyal, et al.[134] (2025) h-BN sheet Strength Choyal, et al.[135] (2025) Ti-Nb-Zr Elastic Mukhamedov, et al.[136] (2025) FeRh Elastic Ourdani, et al.[137] (2024) GAP W/W-Mo Dislocation Koskenniemi, et al.[138] (2023) SNAP Mo, Nb, Ta, W GSFE Wang, et al.[139] (2021) UO2 GSFE Dubois, et al.[140] (2024) Ti3SiC2 MAX Dislocation Hossain, et al.[141] (2023) Mo-Re Elastic Yang, et al.[142] (2024) ZrB2 Elastic Zhang, et al.[98] (2020) Si/MoS2 Friction Wan, et al.[143] (2025) VASP-MLFF CaSiO3 Elastic Zhang, et al.[126] (2025) DeepMD W Mechanical Wang, et al.[144] (2022) MgSiO3 Elastic Wan, et al.[145] (2024) MOF CALF-20 Mechanical Fan, et al.[146] (2024) Cu Dislocation Deng, et al.[147] (2023) CdTe Dislocation Li, et al.[148] (2023) ZrO2 Plasticity Zhang, et al.[149] (2024) MgAlSi Elastic Zhu, et al.[150] (2024) V Mechanical Wang, et al.[151] (2022) H2O Plastic Matusalem, et al.[152] (2022) Ti Dislocation Wen, et al.[153] (2023) Fe Elastic Li, et al.[154] (2022) NEP BeGeN2 Elastic Li, et al.[155] (2025) Ti-Al-Nb GSFE Zhao, et al.[156] (2024) fullerene Strength Ying, et al.[157] (2023) diamane Strength Zhang, et al.[158] (2024) -
[1] CAR R, PARRINELLO M. Unified approach for molecular dynamics and density-functional theory [J]. Physical Review Letters, 1985, 55(22): 2471–2474. doi: 10.1103/PhysRevLett.55.2471 [2] ALDER B J, WAINWRIGHT T E. Phase transition for a hard sphere system [J]. The Journal of Chemical Physics, 1957, 27(5): 1208–1209. doi: 10.1063/1.1743957 [3] SHARIFI H, WICK C D. Developing interatomic potentials for complex concentrated alloys of Cu, Ti, Ni, Cr, Co, Al, Fe, and Mn [J]. Computational Materials Science, 2025, 248: 113595. doi: 10.1016/j.commatsci.2024.113595 [4] MUELLER T, HERNANDEZ A, WANG C H. Machine learning for interatomic potential models [J]. The Journal of Chemical Physics, 2020, 152(5): 050902. doi: 10.1063/1.5126336 [5] BEDOLLA E, PADIERNA L C, CASTAÑEDA-PRIEGO R. Machine learning for condensed matter physics [J]. Journal of Physics: Condensed Matter, 2020, 33(5): 053001. doi: 10.1088/1361-648X/abb895 [6] CARLEO G, CIRAC I, CRANMER K, et al. Machine learning and the physical sciences [J]. Reviews of Modern Physics, 2019, 91(4): 045002. doi: 10.1103/RevModPhys.91.045002 [7] BEHLER J, PARRINELLO M. Generalized neural-network representation of high-dimensional potential-energy surfaces [J]. Physical Review Letters, 2007, 98(14): 146401. doi: 10.1103/PhysRevLett.98.146401 [8] SATORRAS V G, HOOGEBOOM E, WELLING M. E(n) equivariant graph neural networks [C]//Proceedings of the 38th International Conference on Machine Learning. PMLR, 2021: 9323–9332. [9] NOVIKOV I S, GUBAEV K, PODRYABINKIN E V, et al. The MLIP package: moment tensor potentials with MPI and active learning [J]. Machine Learning: Science and Technology, 2021, 2(2): 025002. doi: 10.1088/2632-2153/abc9fe [10] ZHANG Y Z, WANG H D, CHEN W J, et al. DP-GEN: a concurrent learning platform for the generation of reliable deep learning based potential energy models [J]. Computer Physics Communications, 2020, 253: 107206. doi: 10.1016/j.cpc.2020.107206 [11] STENCZEL T K, EL-MACHACHI Z, LIEPUONIUTE G, et al. Machine-learned acceleration for molecular dynamics in CASTEP [J]. The Journal of Chemical Physics, 2023, 159(4): 044803. doi: 10.1063/5.0155621 [12] JINNOUCHI R, KARSAI F, KRESSE G. On-the-fly machine learning force field generation: application to melting points [J]. Physical Review B, 2019, 100(1): 014105. doi: 10.1103/PhysRevB.100.014105 [13] SHAPEEV A V. Moment tensor potentials: a class of systematically improvable interatomic potentials [J]. Multiscale Modeling & Simulation, 2016, 14(3): 1153–1173. doi: 10.1137/15M1054183 [14] GUBAEV K, PODRYABINKIN E V, SHAPEEV A V. Machine learning of molecular properties: locality and active learning [J]. The Journal of Chemical Physics, 2018, 148(24): 241727. doi: 10.1063/1.5005095 [15] WEN T Q, ZHANG L F, WANG H, et al. Deep potentials for materials science [J]. Materials Futures, 2022, 1(2): 022601. doi: 10.1088/2752-5724/ac681d [16] BARTÓK A P, KONDOR R, CSÁNYI G. On representing chemical environments [J]. Physical Review B, 2013, 87(18): 184115. doi: 10.1103/PhysRevB.87.184115 [17] BEHLER J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials [J]. The Journal of Chemical Physics, 2011, 134(7): 074106. doi: 10.1063/1.3553717 [18] BARTÓK A P, PAYNE M C, KONDOR R, et al. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons [J]. Physical Review Letters, 2010, 104(13): 136403. doi: 10.1103/PhysRevLett.104.136403 [19] THOMPSON A P, SWILER L P, TROTT C R, et al. Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials [J]. Journal of Computational Physics, 2015, 285: 316–330. doi: 10.1016/j.jcp.2014.12.018 [20] ZHANG L F, HAN J Q, WANG H, et al. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics [J]. Physical Review Letters, 2018, 120(14): 143001. doi: 10.1103/PhysRevLett.120.143001 [21] WANG H, ZHANG L F, HAN J Q, et al. DeePMD-kit: a deep learning package for many-body potential energy representation and molecular dynamics [J]. Computer Physics Communications, 2018, 228: 178–184. doi: 10.1016/j.cpc.2018.03.016 [22] FAN Z Y, ZENG Z Z, ZHANG C Z, et al. Neuroevolution machine learning potentials: combining high accuracy and low cost in atomistic simulations and application to heat transport [J]. Physical Review B, 2021, 104(10): 104309. doi: 10.1103/PhysRevB.104.104309 [23] HAN J, CEN J C, WU L M, et al. A survey of geometric graph neural networks: data structures, models and applications [J]. Frontiers of Computer Science, 2025, 19(11): 1911375. doi: 10.1007/s11704-025-41426-w [24] BATZNER S, MUSAELIAN A, SUN L X, et al. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials [J]. Nature Communications, 2022, 13(1): 2453. doi: 10.1038/s41467-022-29939-5 [25] SCHÜTT K T, UNKE O T, GASTEGGER M. Equivariant message passing for the prediction of tensorial properties and molecular spectra [C]//Proceedings of the 38th International Conference on Machine Learning. PMLR, 2021: 9377–9388. [26] KLAWOHN S, DARBY J P, KERMODE J R, et al. Gaussian approximation potentials: theory, software implementation and application examples [J]. The Journal of Chemical Physics, 2023, 159(17): 174108. doi: 10.1063/5.0160898 [27] DERINGER V L, BARTÓK A P, BERNSTEIN N, et al. Gaussian process regression for materials and molecules [J]. Chemical Reviews, 2021, 121(16): 10073–10141. doi: 10.1021/acs.chemrev.1c00022 [28] CARO M A. Optimizing many-body atomic descriptors for enhanced computational performance of machine learning based interatomic potentials [J]. Physical Review B, 2019, 100(2): 024112. doi: 10.1103/PhysRevB.100.024112 [29] YING P H, QIAN C, ZHAO R, et al. Advances in modeling complex materials: the rise of neuroevolution potentials [J]. Chemical Physics Reviews, 2025, 6(1): 011310. doi: 10.1063/5.0259061 [30] GILMER J, SCHOENHOLZ S S, RILEY P F, et al. Neural message passing for quantum chemistry [C]//Proceedings of the 34th International Conference on Machine Learning. Sydney: JMLR. org, 2017: 1263–1272. [31] SCHÜTT K T, SAUCEDA H E, KINDERMANS P J, et al. SchNet-a deep learning architecture for molecules and materials [J]. The Journal of Chemical Physics, 2018, 148(24): 241722. doi: 10.1063/1.5019779 [32] BATATIA I, KOVÁCS D P, SIMM G N C, et al. MACE: higher order equivariant message passing neural networks for fast and accurate force fields [C]//Proceedings of the 36th International Conference on Neural Information Processing Systems. New Orleans: Curran Associates Inc. , 2022: 830. [33] YANG Z D, WANG X, LI Y F, et al. Efficient equivariant model for machine learning interatomic potentials [J]. NPJ Computational Materials, 2025, 11(1): 49. doi: 10.1038/s41524-025-01535-3 [34] ZUO Y X, CHEN C, LI X G, et al. Performance and cost assessment of machine learning interatomic potentials [J]. The Journal of Physical Chemistry A, 2020, 124(4): 731–745. doi: 10.1021/acs.jpca.9b08723 [35] FAN Z Y, WANG Y Z, YING P H, et al. GPUMD: a package for constructing accurate machine-learned potentials and performing highly efficient atomistic simulations [J]. The Journal of Chemical Physics, 2022, 157(11): 114801. doi: 10.1063/5.0106617 [36] WILLMAN J T, GONZALEZ J M, NGUYEN-CONG K, et al. Accuracy, transferability, and computational efficiency of interatomic potentials for simulations of carbon under extreme conditions [J]. The Journal of Chemical Physics, 2024, 161(8): 084709. doi: 10.1063/5.0218705 [37] MO P H, ZHANG Y J, ZHAO Z Y, et al. High-speed and low-power molecular dynamics processing unit (MDPU) with ab initio accuracy [J]. NPJ Computational Materials, 2024, 10(1): 253. doi: 10.1038/s41524-024-01422-3 [38] MENG Z J, ZONGO K, TORRES E, et al. A Kokkos-accelerated moment tensor potential implementation for LAMMPS [EB/OL]. arXiv: 2510.00193. (2025-09-30)[2025-08-26]. https://arxiv.org/abs/2510.00193. [39] HUANG J, RATHOD V, SUN C, et al. Speed/accuracy trade-offs for modern convolutional object detectors [C]//Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017: 3296–3297. [40] WANG J T, LIU P T, ZHU H Y, et al. Efficient moment tensor machine-learning interatomic potential for accurate description of defects in Ni-Al alloys [J]. Physical Review Materials, 2025, 9(5): 053805. doi: 10.1103/PhysRevMaterials.9.053805 [41] WILLMAN J T, NGUYEN-CONG K, WILLIAMS A S, et al. Machine learning interatomic potential for simulations of carbon at extreme conditions [J]. Physical Review B, 2022, 106(18): L180101. doi: 10.1103/PhysRevB.106.L180101 [42] KRUGLOV I A, YANILKIN A, OGANOV A R, et al. Phase diagram of uranium from ab initio calculations and machine learning [J]. Physical Review B, 2019, 100(17): 174104. doi: 10.1103/PhysRevB.100.174104 [43] CHIRKOV P V, ELTSOV G S, KICHIGIN R M, et al. Machine learning enhanced quantum molecular dynamics assessment of the phase diagram of uranium [J]. Physical Review B, 2025, 112(2): 024104. doi: 10.1103/8w5w-f3kd [44] ZHANG L F, WANG H, CAR R, et al. Phase diagram of a deep potential water model [J]. Physical Review Letters, 2021, 126(23): 236001. doi: 10.1103/PhysRevLett.126.236001 [45] WANG Y L, SHI J Y, LIANG Z X, et al. Machine learning simulations reveal oxygen’s phase diagram and thermal properties at conditions relevant to white dwarfs [J]. Nature Communications, 2025, 16(1): 5504. doi: 10.1038/s41467-025-61390-0 [46] CHANG X J, CHEN B, ZENG Q Y, et al. Theoretical evidence of H-He demixing under Jupiter and Saturn conditions [J]. Nature Communications, 2024, 15(1): 8543. doi: 10.1038/s41467-024-52868-4 [47] SHI J Y, LIANG Z X, WANG J J, et al. Double-shock compression pathways from diamond to BC8 carbon [J]. Physical Review Letters, 2023, 131(14): 146101. doi: 10.1103/PhysRevLett.131.146101 [48] ZONG H X, LUO Y F, DING X D, et al. hcp→ω phase transition mechanisms in shocked zirconium: a machine learning based atomic simulation study [J]. Acta Materialia, 2019, 162: 126–135. doi: 10.1016/j.actamat.2018.09.067 [49] ZONG H X, PILANIA G, DING X D, et al. Developing an interatomic potential for martensitic phase transformations in zirconium by machine learning [J]. NPJ Computational Materials, 2018, 4(1): 48. doi: 10.1038/s41524-018-0103-x [50] ZHU S C, CHEN G W, YUAN X H, et al. Key for hexagonal diamond formation: theoretical and experimental study [J]. Journal of the American Chemical Society, 2025, 147(2): 2158–2167. doi: 10.1021/jacs.4c16312 [51] CHEN B, ZENG Q Y, WANG H, et al. Atomistic mechanism of phase transition in shock compressed gold revealed by deep potential [EB/OL]. arXiv: 2006.13136. (2021-07-19)[2025-08-26]. https://arxiv.org/abs/2006.13136. [52] ZHU L F, KÖRMANN F, CHEN Q, et al. Accelerating ab initio melting property calculations with machine learning: application to the high entropy alloy TaVCrW [J]. NPJ Computational Materials, 2024, 10(1): 274. doi: 10.1038/s41524-024-01464-7 [53] NITOL M S, MISHRA A, XU S Z, et al. Moment tensor potential and its application in the Ti-Al-V multicomponent system [J]. Physical Review Materials, 2025, 9(6): 063601. doi: 10.1103/PhysRevMaterials.9.063601 [54] ROSENBROCK C W, GUBAEV K, SHAPEEV A V, et al. Machine-learned interatomic potentials for alloys and alloy phase diagrams [J]. NPJ Computational Materials, 2021, 7(1): 24. doi: 10.1038/s41524-020-00477-2 [55] JUNG J H, FORSLUND A, SRINIVASAN P, et al. Dynamically stabilized phases with full ab initio accuracy: thermodynamics of Ti, Zr, Hf with a focus on the hcp-bcc transition [J]. Physical Review B, 2023, 108(18): 184107. doi: 10.1103/PhysRevB.108.184107 [56] HUANG Y F, YAO S L, CHEN H J, et al. An atomistic study of γ→γ0→α" martensitic transformation in uranium-6 wt% niobium [J]. Journal of Nuclear Materials, 2025, 606: 155617. doi: 10.1016/j.jnucmat.2025.155617 [57] ZHAO J L, BYGGMÄSTAR J, ZHANG Z F, et al. Phase transition of two-dimensional ferroelectric and paraelectric Ga2O3 monolayers: a density functional theory and machine learning study [J]. Physical Review B, 2021, 104(5): 054107. doi: 10.1103/PhysRevB.104.054107 [58] ERHARD L C, ROHRER J, ALBE K, et al. A machine-learned interatomic potential for silica and its relation to empirical models [J]. NPJ Computational Materials, 2022, 8(1): 90. doi: 10.1038/s41524-022-00768-w/ [59] ZHAO J L, BYGGMÄSTAR J, HE H, et al. Complex Ga2O3 polymorphs explored by accurate and general-purpose machine-learning interatomic potentials [J]. NPJ Computational Materials, 2023, 9(1): 159. doi: 10.1038/s41524-023-01117-1 [60] LI X G, HU C Z, CHEN C, et al. Quantum-accurate spectral neighbor analysis potential models for Ni-Mo binary alloys and fcc metals [J]. Physical Review B, 2018, 98(9): 094104. doi: 10.1103/PhysRevB.98.094104 [61] RICHARD P, CASTELLANO A, BÉJAUD R, et al. Ab initio phase diagram of gold in extreme conditions [J]. Physical Review Letters, 2023, 131(20): 206101. doi: 10.1103/PhysRevLett.131.206101 [62] BIDEAULT M, CREUZE J, ASAHI R, et al. Polyvalent machine-learned potential for cobalt: from bulk to nanoparticles [J]. Physical Review Materials, 2024, 8(12): 123803. doi: 10.1103/PhysRevMaterials.8.123803 [63] LIU P T, VERDI C, KARSAI F, et al. Phase transitions of zirconia: machine-learned force fields beyond density functional theory [J]. Physical Review B, 2022, 105(6): L060102. doi: 10.1103/PhysRevB.105.L060102 [64] LIU P T, VERDI C, KARSAI F, et al. α−β phase transition of zirconium predicted by on-the-fly machine-learned force field [J]. Physical Review Materials, 2021, 5(5): 053804. doi: 10.1103/PhysRevMaterials.5.053804 [65] NIU H W, YANG Y B, JENSEN S, et al. Stable solid molecular hydrogen above 900 K from a machine-learned potential trained with diffusion quantum Monte Carlo [J]. Physical Review Letters, 2023, 130(7): 076102. doi: 10.1103/PhysRevLett.130.076102 [66] CHEN T, YUAN F B, LIU J C, et al. Modeling the high-pressure solid and liquid phases of tin from deep potentials with ab initio accuracy [J]. Physical Review Materials, 2023, 7(5): 053603. doi: 10.1103/PhysRevMaterials.7.053603 [67] DENG J, NIU H Y, HU J W, et al. Melting of MgSiO3 determined by machine learning potentials [J]. Physical Review B, 2023, 107(6): 064103. doi: 10.1103/PhysRevB.107.064103 [68] GUO L F, JIN T, SHAN S, et al. Structural transformations in single-crystalline AgPd nanoalloys from multiscale deep potential molecular dynamics [J]. The Journal of Chemical Physics, 2023, 159(2): 024702. doi: 10.1063/5.0158918 [69] WISESA P, ANDOLINA C M, SAIDI W A. Machine-learning accelerated first-principles accurate modeling of the solid-liquid phase transition in MgO under mantle conditions [J]. The Journal of Physical Chemistry Letters, 2023, 14(39): 8741–8748. doi: 10.1021/acs.jpclett.3c02424 [70] HE R, WU H Y, ZHANG L F, et al. Structural phase transitions in SrTiO3 from deep potential molecular dynamics [J]. Physical Review B, 2022, 105(6): 064104. doi: 10.1103/PhysRevB.105.064104 [71] WEN T Q, WANG R, ZHU L Y, et al. Specialising neural network potentials for accurate properties and application to the mechanical response of titanium [J]. NPJ Computational Materials, 2021, 7(1): 206. doi: 10.1038/s41524-021-00661-y [72] NIU H Y, BONATI L, PIAGGI P M, et al. Ab initio phase diagram and nucleation of gallium [J]. Nature Communications, 2020, 11(1): 2654. doi: 10.1038/s41467-020-16372-9 [73] FENG X K, PAN S N, KATAGIRI K, et al. Nanosecond structural evolution in shocked coesite [J]. Science Advances, 2025, 11(17): eads3139. doi: 10.1126/sciadv.ads3139 [74] KAYASTHA P, FRANSSON E, ERHART P, et al. Octahedral tilt-driven phase transitions in BaZrS3 chalcogenide perovskite [J]. The Journal of Physical Chemistry Letters, 2025, 16(8): 2064–2071. doi: 10.1021/acs.jpclett.4c03517 [75] PAN S N, SHI J Y, LIANG Z X, et al. Shock compression pathways to pyrite silica from machine learning simulations [J]. Physical Review B, 2024, 110(22): 224101. doi: 10.1103/PhysRevB.110.224101 [76] FRANSSON E, RAHM J M, WIKTOR J, et al. Revealing the free energy landscape of halide perovskites: metastability and transition characters in CsPbBr3 and MAPbI3 [J]. Chemistry of Materials, 2023, 35(19): 8229–8238. doi: 10.1021/acs.chemmater.3c01740 [77] PAN S N, HUANG T H, VAZAN A, et al. Magnesium oxide-water compounds at megabar pressure and implications on planetary interiors [J]. Nature Communications, 2023, 14(1): 1165. doi: 10.1038/s41467-023-36802-8 [78] ISTAS M, JENSEN S, YANG Y B, et al. Liquid-liquid phase transition of hydrogen and its critical point: analysis from ab initio simulation and a machine-learned potential [J]. Physical Review E, 2025, 111(4): 045307. doi: 10.1103/PhysRevE.111.045307 [79] LY K K, CEPERLEY D M. Melting curves of atomic hydrogen and deuterium calculated using path-integral Monte Carlo [J]. Physical Review B, 2025, 111(10): 104102. doi: 10.1103/PhysRevB.111.104102 [80] YANG X, CHEN Y S, ZHENG Y H, et al. Understanding the importance of four-phonon scattering in low-symmetry monolayer 1T′-ReS2 using machine learning potential [J]. Applied Physics Letters, 2024, 124(7): 072204. doi: 10.1063/5.0190570 [81] ZHANG G W, DONG S L, YANG C, et al. Revisiting four-phonon scattering in WS2 monolayer with machine learning potential [J]. Applied Physics Letters, 2023, 123(5): 052205. doi: 10.1063/5.0159517 [82] YANG F H, ZENG Q Y, CHEN B, et al. Lattice thermal conductivity of MgSiO3 perovskite and post-perovskite under lower mantle conditions calculated by deep potential molecular dynamics [J]. Chinese Physics Letters, 2022, 39(11): 116301. doi: 10.1088/0256-307X/39/11/116301 [83] QIU R, ZENG Q Y, HAN J S, et al. Coupled temperature-density dependence of lattice thermal conductivity of MgO at extreme conditions [J]. Physical Review B, 2025, 111(6): 064103. doi: 10.1103/PhysRevB.111.064103 [84] WANG Y Z, FAN Z Y, QIAN P, et al. Density dependence of thermal conductivity in nanoporous and amorphous carbon with machine-learned molecular dynamics [J]. Physical Review B, 2025, 111(9): 094205. doi: 10.1103/PhysRevB.111.094205 [85] OUYANG Y L, YU C Q, HE J, et al. Accurate description of high-order phonon anharmonicity and lattice thermal conductivity from molecular dynamics simulations with machine learning potential [J]. Physical Review B, 2022, 105(11): 115202. doi: 10.1103/PhysRevB.105.115202 [86] KOROTAEV P, NOVOSELOV I, YANILKIN A, et al. Accessing thermal conductivity of complex compounds by machine learning interatomic potentials [J]. Physical Review B, 2019, 100(14): 144308. doi: 10.1103/PhysRevB.100.144308 [87] WANG Q, ZENG Z Z, CHEN Y. Revisiting phonon transport in perovskite SrTiO3: anharmonic phonon renormalization and four-phonon scattering [J]. Physical Review B, 2021, 104(23): 235205. doi: 10.1103/PhysRevB.104.235205 [88] MORTAZAVI B, PODRYABINKIN E V, NOVIKOV I S, et al. Accelerating first-principles estimation of thermal conductivity by machine-learning interatomic potentials: a MTP/ShengBTE solution [J]. Computer Physics Communications, 2021, 258: 107583. doi: 10.1016/j.cpc.2020.107583 [89] WANG D Y, ZHAO K, HONG T, et al. Intrinsically low lattice thermal conductivity and multivalley band structure induced promising high thermoelectric performance in Pb3Bi2S6 [J]. Materials Today Physics, 2025, 51: 101654. doi: 10.1016/j.mtphys.2025.101654 [90] LIU H, QIAN X, BAO H, et al. High-temperature phonon transport properties of SnSe from machine-learning interatomic potential [J]. Journal of Physics: Condensed Matter, 2021, 33(40): 405401. doi: 10.1088/1361-648X/ac13fd [91] LI Y H, LI X, WEI B, et al. Phonon coherence in bismuth-halide perovskite Cs3Bi2Br9 with ultralow thermal conductivity [J]. Advanced Functional Materials, 2024, 34(52): 2411152. doi: 10.1002/adfm.202411152 [92] ZHANG Y X, SHEN C, LONG T, et al. Thermal conductivity of h-BN monolayers using machine learning interatomic potential [J]. Journal of Physics: Condensed Matter, 2021, 33(10): 105903. doi: 10.1088/1361-648X/abcf61 [93] REN J L, ZHANG G H, WANG X M, et al. Research on machine learning interatomic potentials for titanium oxide ceramic materials [J]. Physica B: Condensed Matter, 2025, 711: 417281. doi: 10.1016/j.physb.2025.417281 [94] TANG J L, LI G T, WANG Q, et al. Effect of four-phonon scattering on anisotropic thermal transport in bulk hexagonal boron nitride by machine learning interatomic potential [J]. International Journal of Heat and Mass Transfer, 2023, 207: 124011. doi: 10.1016/j.ijheatmasstransfer.2023.124011 [95] TANG J L, LI G T, WANG Q, et al. Competition between phonon-vacancy and four-phonon scattering in cubic boron arsenide by machine learning interatomic potential [J]. Physical Review Materials, 2023, 7(4): 044601. doi: 10.1103/PhysRevMaterials.7.044601 [96] BABAEI H, GUO R Q, HASHEMI A, et al. Machine-learning-based interatomic potential for phonon transport in perfect crystalline Si and crystalline Si with vacancies [J]. Physical Review Materials, 2019, 3(7): 074603. doi: 10.1103/PhysRevMaterials.3.074603 [97] GU X K, ZHAO C Y. Thermal conductivity of single-layer MoS2(1−x)Se2x alloys from molecular dynamics simulations with a machine-learning-based interatomic potential [J]. Computational Materials Science, 2019, 165: 74–81. doi: 10.1016/j.commatsci.2019.04.025 [98] ZHANG Y H, LUNGHI A, SANVITO S. Pushing the limits of atomistic simulations towards ultra-high temperature: a machine-learning force field for ZrB2 [J]. Acta Materialia, 2020, 186: 467–474. doi: 10.1016/j.actamat.2019.12.060 [99] LAHNSTEINER J, RANG M, BOKDAM M. Tuning einstein oscillator frequencies of cation rattlers: a molecular dynamics study of the lattice thermal conductivity of CsPbBr3 [J]. The Journal of Physical Chemistry C. Nanomaterials and Interfaces, 2024, 128(3): 1341–1349. doi: 10.1021/acs.jpcc.3c06590 [100] CUI C F, ZHANG Y W, OUYANG T, et al. On-the-fly machine learning potential accelerated accurate prediction of lattice thermal conductivity of metastable silicon crystals [J]. Physical Review Materials, 2023, 7(3): 033803. doi: 10.1103/PhysRevMaterials.7.033803 [101] QIU R, ZENG Q Y, WANG H, et al. Anomalous thermal transport across the superionic transition in ice [J]. Chinese Physics Letters, 2023, 40(11): 116301. doi: 10.1088/0256-307X/40/11/116301 [102] BHATT N, KARNA P, THAKUR S, et al. Pressure-driven enhancement of phonon contribution to the thermal conductivity of Iridium [J]. International Journal of Heat and Mass Transfer, 2024, 229: 125673. doi: 10.1016/j.ijheatmasstransfer.2024.125673 [103] CHE J W, HUANG W J, REN G L, et al. Dual-channel phonon transport leads to low thermal conductivity in pyrochlore La2Hf2O7 [J]. Ceramics International, 2024, 50(13): 22865–22873. doi: 10.1016/j.ceramint.2024.04.011 [104] MALGOPE S, GUPTA M K, BAG S, et al. Untangling high-temperature thermal expansion and lattice thermal conductivity behavior of vanadium using machine-learned molecular dynamics [J]. Physical Review B, 2024, 110(5): 054301. doi: 10.1103/PhysRevB.110.054301 [105] PENG Y H, DENG J. Thermal conductivity of MgSiO3-H2O system determined by machine learning potentials [J]. Geophysical Research Letters, 2024, 51(5): e2023GL107245. doi: 10.1029/2023GL107245 [106] ZHANG P, JIN D, QIN M, et al. Effects of four-phonon interaction and vacancy defects on the thermal conductivity of the low-temperature phase of SnSe [J]. Physical Review Applied, 2024, 21(2): 024043. doi: 10.1103/PhysRevApplied.21.024043 [107] WANG D, WU Z Q, DENG X. Thermal conductivity of hydrous wadsleyite determined by non-equilibrium molecular dynamics based on machine learning [J]. Geophysical Research Letters, 2022, 49(22): e2022GL100337. doi: 10.1029/2022GL100337 [108] MIRCHI P, ADESSI C, MERABIA S, et al. Lattice thermal conductivity and mechanical properties of the single-layer penta-NiN2 explored by a deep-learning interatomic potential [J]. Physical Chemistry Chemical Physics, 2024, 26(19): 14216–14227. doi: 10.1039/D4CP00997E [109] ZHANG P, ZHANG Z H, LIU Y, et al. Phonon thermal transport in Bi2Te3 from a deep-neural-network interatomic potential [J]. Physical Review Applied, 2022, 18(5): 054022. doi: 10.1103/PhysRevApplied.18.054022 [110] HU S, GU X K. Approaching to low thermal conductivity limit in layered materials through full-spectrum phonon band engineering [J]. Materials Today Physics, 2025, 52: 101669. doi: 10.1016/j.mtphys.2025.101669 [111] LI K, MA H. Decoding the thermal conductivity of ionic covalent organic frameworks: optical phonons as key determinants revealed by neuroevolution potential [J]. Materials Today Physics, 2025, 54: 101724. doi: 10.1016/j.mtphys.2025.101724 [112] ZHOU X T, XU Y J, CHEN Y, et al. Mechanism on lattice thermal conductivity of carbon-vacancy and porous medium entropy ceramics [J]. Scripta Materialia, 2025, 259: 116568. doi: 10.1016/j.scriptamat.2025.116568 [113] WANG Y, XIE L, YANG H B, et al. Strong orbital-lattice coupling induces glassy thermal conductivity in high-symmetry single crystal BaTiS3 [J]. Physical Review X, 2025, 15(1): 011066. doi: 10.1103/PhysRevX.15.011066 [114] LIU Y W, FU Y M, GU F C, et al. Lattice-distortion-driven reduced lattice thermal conductivity in high-entropy ceramics [J]. Advanced Science, 2025, 12(19): 2501157. doi: 10.1002/advs.202501157 [115] CAO C Y, CAO S, ZHU Y X, et al. Thermal transports of 2D phosphorous carbides by machine learning molecular dynamics simulations [J]. International Journal of Heat and Mass Transfer, 2024, 224: 125359. doi: 10.1016/j.ijheatmasstransfer.2024.125359 [116] YANG J, ZHU X Y, MCGAUGHEY A J H, et al. Two-mode terms in Wigner transport equation elucidate anomalous thermal transport in amorphous silicon [J]. Physical Review B, 2025, 111(9): 094206. doi: 10.1103/PhysRevB.111.094206 [117] FAN H Z, YING P H, FAN Z Y, et al. Anomalous strain-dependent thermal conductivity in the metal-organic framework HKUST-1 [J]. Physical Review B, 2024, 109(4): 045424. doi: 10.1103/PhysRevB.109.045424 [118] HUANG X F, LI C Z, YUAN M H, et al. Unphysical grain size dependence of lattice thermal conductivity in Mg3(Sb, Bi)2: an atomistic view of concentration dependent segregation effects [J]. Materials Today Physics, 2024, 43: 101386. doi: 10.1016/j.mtphys.2024.101386 [119] SO S, LEE J H. Unraveling interfacial thermal transport in β-Ga2O3/h-BN van der Waals heterostructures [J]. Materials Today Physics, 2024, 46: 101506. doi: 10.1016/j.mtphys.2024.101506 [120] LI W, CARRETE J, KATCHO N A, et al. ShengBTE: a solver of the Boltzmann transport equation for phonons [J]. Computer Physics Communications, 2014, 185(6): 1747–1758. doi: 10.1016/j.cpc.2014.02.015 [121] KUBO R. Statistical-mechanical theory of irreversible processes. Ⅰ. general theory and simple applications to magnetic and conduction problems [J]. Journal of the Physical Society of Japan, 1957, 12(6): 570–586. doi: 10.1143/JPSJ.12.570 [122] LI Z, XIONG S Y, SIEVERS C, et al. Influence of thermostatting on nonequilibrium molecular dynamics simulations of heat conduction in solids [J]. The Journal of Chemical Physics, 2019, 151(23): 234105. doi: 10.1063/1.5132543 [123] FAN Z Y, DONG H K, HARJU A, et al. Homogeneous nonequilibrium molecular dynamics method for heat transport and spectral decomposition with many-body potentials [J]. Physical Review B, 2019, 99(6): 064308. doi: 10.1103/PhysRevB.99.064308 [124] DONG H K, SHI Y B, YING P H, et al. Molecular dynamics simulations of heat transport using machine-learned potentials: a mini-review and tutorial on GPUMD with neuroevolution potentials [J]. Journal of Applied Physics, 2024, 135(16): 161101. doi: 10.1063/5.0200833 [125] WANG H, PAN X L, WANG Y F, et al. Lattice dynamics and elastic properties of α-U at high-temperature and high-pressure by machine learning potential simulations [J]. Journal of Nuclear Materials, 2022, 572: 154029. doi: 10.1016/j.jnucmat.2022.154029 [126] ZHANG C, YANG J Y, SUN T, et al. Strong precursor softening in cubic CaSiO3 perovskite [J]. Proceedings of the National Academy of Sciences of the United States of America, 2025, 122(5): e2410910122. doi: 10.1073/pnas.2410910122 [127] ZHENG H, FEY L T W, LI X G, et al. Multi-scale investigation of short-range order and dislocation glide in MoNbTi and TaNbTi multi-principal element alloys [J]. NPJ Computational Materials, 2023, 9(1): 89. doi: 10.1038/s41524-023-01046-z [128] WU L P, LI T. A machine learning interatomic potential for high entropy alloys [J]. Journal of the Mechanics and Physics of Solids, 2024, 187: 105639. doi: 10.1016/j.jmps.2024.105639 [129] SHAPEEV A V, PODRYABINKIN E V, GUBAEV K, et al. Elinvar effect in β-Ti simulated by on-the-fly trained moment tensor potential [J]. New Journal of Physics, 2020, 22(11): 113005. doi: 10.1088/1367-2630/abc392 [130] ZOTOV N, GUBAEV K, WÖRNER J, et al. Moment tensor potential for static and dynamic investigations of screw dislocations in bcc Nb [J]. Modelling and Simulation in Materials Science and Engineering, 2024, 32(3): 035032. doi: 10.1088/1361-651X/ad2d68 [131] GUBAEV K, IKEDA Y, TASNÁDI F, et al. Finite-temperature interplay of structural stability, chemical complexity, and elastic properties of bcc multicomponent alloys from ab initio trained machine-learning potentials [J]. Physical Review Materials, 2021, 5(7): 073801. doi: 10.1103/PhysRevMaterials.5.073801 [132] JALOLOV F N, PODRYABINKIN E V, OGANOV A R, et al. Mechanical properties of single and polycrystalline solids from machine learning [J]. Advanced Theory and Simulations, 2024, 7(5): 2301171. doi: 10.1002/adts.202301171 [133] YANG G L, PENG H X, HUANG J, et al. Atomic perspective on plasticity mechanism of ionic-covalent silver sulfide [J]. International Journal of Mechanical Sciences, 2025, 300: 110471. doi: 10.1016/j.ijmecsci.2025.110471 [134] CHOYAL V, MISHRA S, LUHADIYA N, et al. Development and evaluation of machine-learned interatomic potentials for carbon nanotubes for molecular dynamics simulations [J]. Carbon Letters, 2025, 35(3): 1311–1326. doi: 10.1007/s42823-025-00867-w [135] CHOYAL V, PATIL M, LUHADIYA N, et al. Machine-learned interatomic potentials for accurate analysis of the mechanical properties of boron nitride sheets [J]. Journal of Physics: Materials, 2025, 8(1): 015003. doi: 10.1088/2515-7639/ad9635 [136] MUKHAMEDOV B, TASNÁDI F, ABRIKOSOV I A. Machine learning interatomic potential for the low-modulus Ti-Nb-Zr alloys in the vicinity of dynamical instability [J]. Materials & Design, 2025, 253: 113865. doi: 10.1016/j.matdes.2025.113865 [137] OURDANI D, CASTELLANO A, VYTHELINGUM A K, et al. Experimental determination of the temperature- and phase-dependent elastic constants of FeRh [J]. Physical Review B, 2024, 110(1): 014427. doi: 10.1103/PhysRevB.110.014427 [138] KOSKENNIEMI M, BYGGMÄSTAR J, NORDLUND K, et al. Efficient atomistic simulations of radiation damage in W and W-Mo using machine-learning potentials [J]. Journal of Nuclear Materials, 2023, 577: 154325. doi: 10.1016/j.jnucmat.2023.154325 [139] WANG X W, XU S Z, JIAN W R, et al. Generalized stacking fault energies and Peierls stresses in refractory body-centered cubic metals from machine learning-based interatomic potentials [J]. Computational Materials Science, 2021, 192: 110364. doi: 10.1016/j.commatsci.2021.110364 [140] DUBOIS E T, TRANCHIDA J, BOUCHET J, et al. Atomistic simulations of nuclear fuel UO2 with machine learning interatomic potentials [J]. Physical Review Materials, 2024, 8(2): 025402. doi: 10.1103/PhysRevMaterials.8.025402 [141] HOSSAIN R, KIMIZUKA H, OGATA S. Asymmetry in core structure and mobility of basal dislocations in a Ti3SiC2 MAX phase: an atomistic study with machine-learned force fields [J]. Physical Review Materials, 2023, 7(5): 053608. doi: 10.1103/PhysRevMaterials.7.053608 [142] YANG W, YE J W, BI P, et al. Mechanical properties of Mo-Re alloy based on first-principles and machine learning potential function [J]. Materials Today Communications, 2024, 38: 107796. doi: 10.1016/j.mtcomm.2023.107796 [143] WAN S J, TONG R T, HAN B, et al. Machine learning interatomic potential for friction study in silicon and molybdenum disulfide [J]. Computational Materials Science, 2025, 248: 113608. doi: 10.1016/j.commatsci.2024.113608 [144] WANG X Y, WANG Y N, ZHANG L F, et al. A tungsten deep neural-network potential for simulating mechanical property degradation under fusion service environment [J]. Nuclear Fusion, 2022, 62(12): 126013. doi: 10.1088/1741-4326/ac888b [145] WAN T Q, LUO C X, SUN Y, et al. Thermoelastic properties of bridgmanite using deep-potential molecular dynamics [J]. Physical Review B, 2024, 109(9): 094101. doi: 10.1103/PhysRevB.109.094101 [146] FAN D, NASKAR S, MAURIN G. Unconventional mechanical and thermal behaviours of MOF CALF-20 [J]. Nature Communications, 2024, 15(1): 3251. doi: 10.1038/s41467-024-47695-6 [147] DENG F L, WU H Y, HE R, et al. Large-scale atomistic simulation of dislocation core structure in face-centered cubic metal with deep potential method [J]. Computational Materials Science, 2023, 218: 111941. doi: 10.1016/j.commatsci.2022.111941 [148] LI J, LUO K, AN Q. Atomic structure, stability, and dissociation of dislocations in cadmium telluride [J]. International Journal of Plasticity, 2023, 163: 103552. doi: 10.1016/j.ijplas.2023.103552 [149] ZHANG J Y, HUYNH G, DAI F Z, et al. A deep-neural network potential to study transformation-induced plasticity in zirconia [J]. Journal of the European Ceramic Society, 2024, 44(6): 4243–4254. doi: 10.1016/j.jeurceramsoc.2024.01.007 [150] ZHU C S, DONG W J, GAO Z H, et al. Deep potential fitting and mechanical properties study of MgAlSi alloy [J]. Computational Materials Science, 2024, 239: 112966. doi: 10.1016/j.commatsci.2024.112966 [151] WANG R, MA X X, ZHANG L F, et al. Classical and machine learning interatomic potentials for BCC vanadium [J]. Physical Review Materials, 2022, 6(11): 113603. doi: 10.1103/PhysRevMaterials.6.113603 [152] MATUSALEM F, REGOJ S, DE KONING M. Plastic deformation of superionic water ices [J]. Proceedings of the National Academy of Sciences of the United States of America, 2022, 119(45): e2203397119. doi: 10.1073/pnas.2203397119 [153] WEN T Q, LIU A W, WANG R, et al. Modelling of dislocations, twins and crack-tips in HCP and BCC Ti [J]. International Journal of Plasticity, 2023, 166: 103644. doi: 10.1016/j.ijplas.2023.103644 [154] LI Z, SCANDOLO S. Elasticity and viscosity of hcp iron at Earth’s inner core conditions from machine learning-based large-scale atomistic simulations [J]. Geophysical Research Letters, 2022, 49(24): e2022GL101161. doi: 10.1029/2022GL101161 [155] LI Z D, HAN L W, OUYANG T, et al. Thermal and mechanical properties of deep-ultraviolet light sources candidate materials BeGeN2 by machine-learning molecular dynamics simulations [J]. Physical Review Materials, 2025, 9(3): 033804. doi: 10.1103/PhysRevMaterials.9.033804 [156] ZHAO Z Q, YI M, GUO W L, et al. General-purpose neural network potential for Ti-Al-Nb alloys towards large-scale molecular dynamics with ab initio accuracy [J]. Physical Review B, 2024, 110(18): 184115. doi: 10.1103/PhysRevB.110.184115 [157] YING P H, DONG H K, LIANG T, et al. Atomistic insights into the mechanical anisotropy and fragility of monolayer fullerene networks using quantum mechanical calculations and machine-learning molecular dynamics simulations [J]. Extreme Mechanics Letters, 2023, 58: 101929. doi: 10.1016/j.eml.2022.101929 [158] ZHANG G Q, ZHAO S W, QIN H S, et al. A unified strength criterion of diamane grain boundaries [J]. Extreme Mechanics Letters, 2024, 68: 102146. doi: 10.1016/j.eml.2024.102146 [159] ZENG Q Y, CHEN B, YU X X, et al. Towards large-scale and spatiotemporally resolved diagnosis of electronic density of states by deep learning [J]. Physical Review B, 2022, 105(17): 174109. doi: 10.1103/PhysRevB.105.174109 [160] ZENG Q Y, CHEN B, ZHANG S, et al. Full-scale ab initio simulations of laser-driven atomistic dynamics [J]. NPJ Computational Materials, 2023, 9(1): 213. doi: 10.1038/s41524-023-01168-4 [161] FU X, WOOD B M, BARROSO-LUQUE L, et al. Learning smooth and expressive interatomic potentials for physical property prediction [C]//Proceedings of the 42nd International Conference on Machine Learning. PMLR, 2025: 17875–17893. [162] YANG H, HU C X, ZHOU Y C, et al. MatterSim: a deep learning atomistic model across elements, temperatures and pressures [EB/OL]. arXiv: 2405.04967. (2024-03-10)[2025-08-26]. https://arxiv.org/abs/2405.04967. [163] ZHANG D, PENG A Y, CAI C, et al. A graph neural network for the era of large atomistic models [EB/OL]. arXiv: 2506.01686. (2025-06-02)[2025-08-26]. https://arxiv.org/abs/2506.01686. [164] BATATIA I, BENNER P, CHIANG Y, et al. A foundation model for atomistic materials chemistry [EB/OL]. arXiv: 2401.00096. (2025-09-04)[2025-08-26]. https://arxiv.org/abs/2401.00096. [165] LIANG T, XU K, LINDGREN E, et al. NEP89: universal neuroevolution potential for inorganic and organic materials across 89 elements [EB/OL]. arXiv: 2504.21286. (2025-06-10)[2025-08-26]. https://arxiv.org/abs/2504.21286. [166] ZHANG L F, WANG H, MUNIZ M C, et al. A deep potential model with long-range electrostatic interactions [J]. The Journal of Chemical Physics, 2022, 156(12): 124107. doi: 10.1063/5.0083669 [167] CHENG B Q. Latent Ewald summation for machine learning of long-range interactions [J]. NPJ Computational Materials, 2025, 11(1): 80. doi: 10.1038/s41524-025-01577-7 [168] XIA J F, ZHANG Y L, JIANG B. The evolution of machine learning potentials for molecules, reactions and materials [J]. Chemical Society Reviews, 2025, 54(10): 4790–4821. doi: 10.1039/D5CS00104H [169] YANG T, CAI Z F, HUANG Z T, et al. Deep learning illuminates spin and lattice interaction in magnetic materials [J]. Physical Review B, 2024, 110(6): 064427. doi: 10.1103/PhysRevB.110.064427 [170] NOVIKOV I, GRABOWSKI B, KÖRMANN F, et al. Magnetic moment tensor potentials for collinear spin-polarized materials reproduce different magnetic states of bcc Fe [J]. NPJ Computational Materials, 2022, 8(1): 13. doi: 10.1038/s41524-022-00696-9 [171] KOTYKHOV A S, HODAPP M, TANTARDINI C, et al. Actively trained magnetic moment tensor potentials for mechanical, dynamical, and thermal properties of paramagnetic CrN [J]. Physical Review B, 2025, 111(9): 094438. doi: 10.1103/PhysRevB.111.094438 [172] ZHANG Y Z, GAO C, LIU Q R, et al. Warm dense matter simulation via electron temperature dependent deep potential molecular dynamics [J]. Physics of Plasmas, 2020, 27(12): 122704. doi: 10.1063/5.0023265 [173] SRINIVASAN P, DEMURIYA D, GRABOWSKI B, et al. Electronic moment tensor potentials include both electronic and vibrational degrees of freedom [J]. NPJ Computational Materials, 2024, 10(1): 41. doi: 10.1038/s41524-024-01222-9 [174] LIU Q R, LI J Y, CHEN M H. Thermal transport by electrons and ions in warm dense aluminum: a combined density functional theory and deep potential study [J]. Matter and Radiation at Extremes, 2021, 6(2): 026902. doi: 10.1063/5.0030123 [175] HINTON G, VINYALS O, DEAN J. Distilling the knowledge in a neural network [EB/OL]. arXiv: 1503.02531. (2025-03-09)[2025-08-26]. https://arxiv.org/abs/1503.02531. [176] GARDNER J L A, DU TOIT D F T, MAHMOUD C B, et al. Distillation of atomistic foundation models across architectures and chemical domains [EB/OL]. arXiv: 2506.10956. (2025-06-12)[2025-08-26]. https://arxiv.org/abs/2506.10956. -






 下载:
下载: