The Disappearing Quartz-Coesite Path: the Phase Transition Mechanism of Silicon Dioxide from Machine Learning Simulations
-
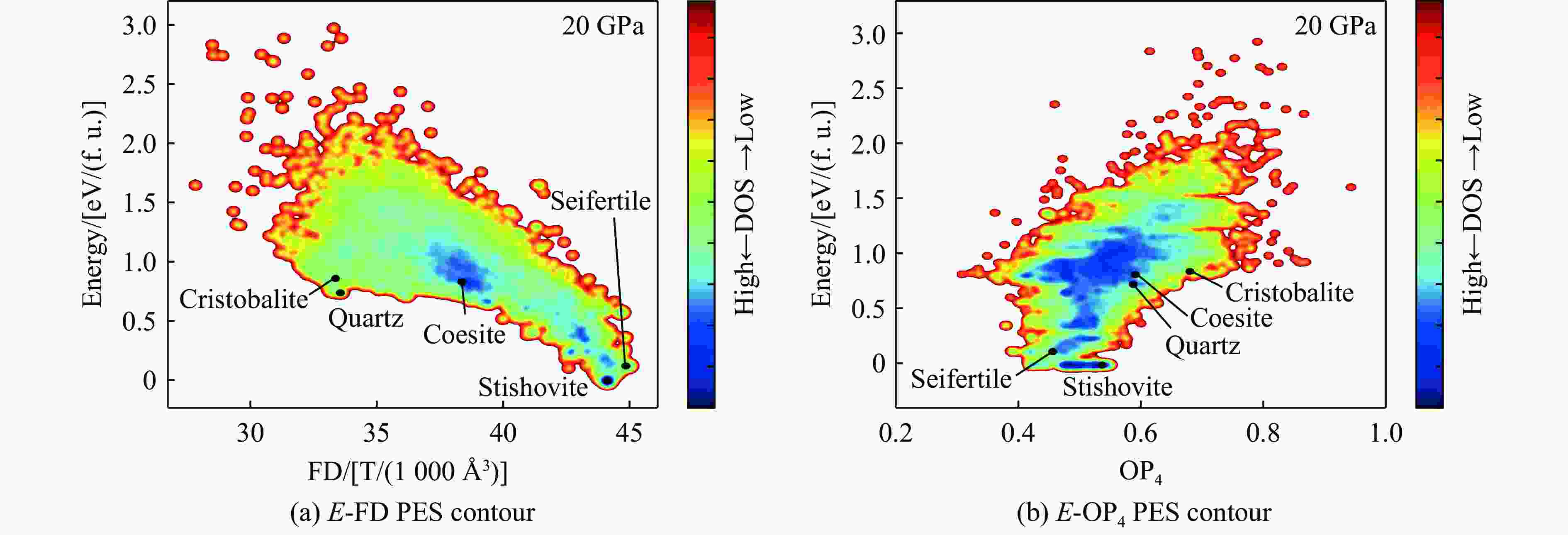
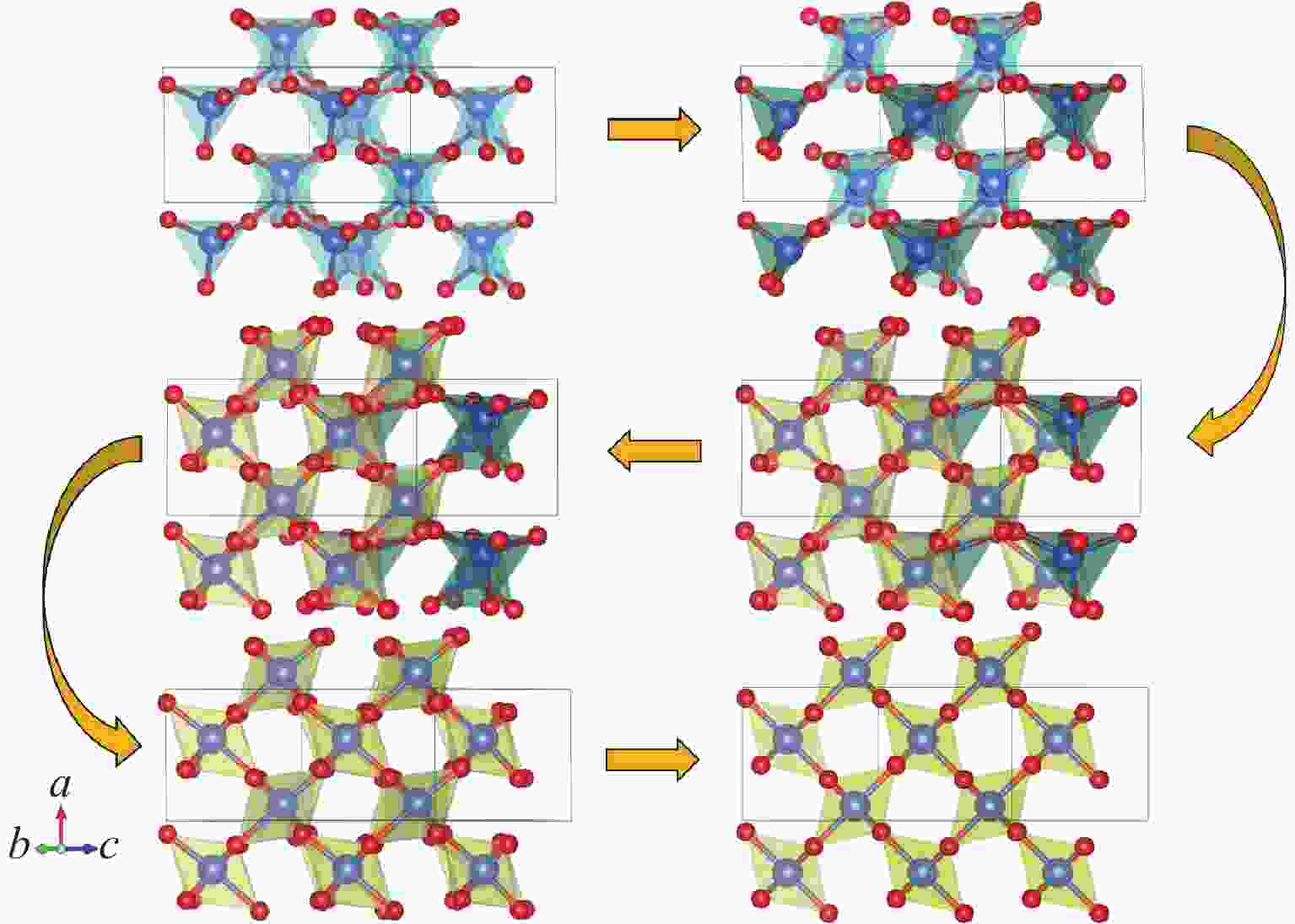
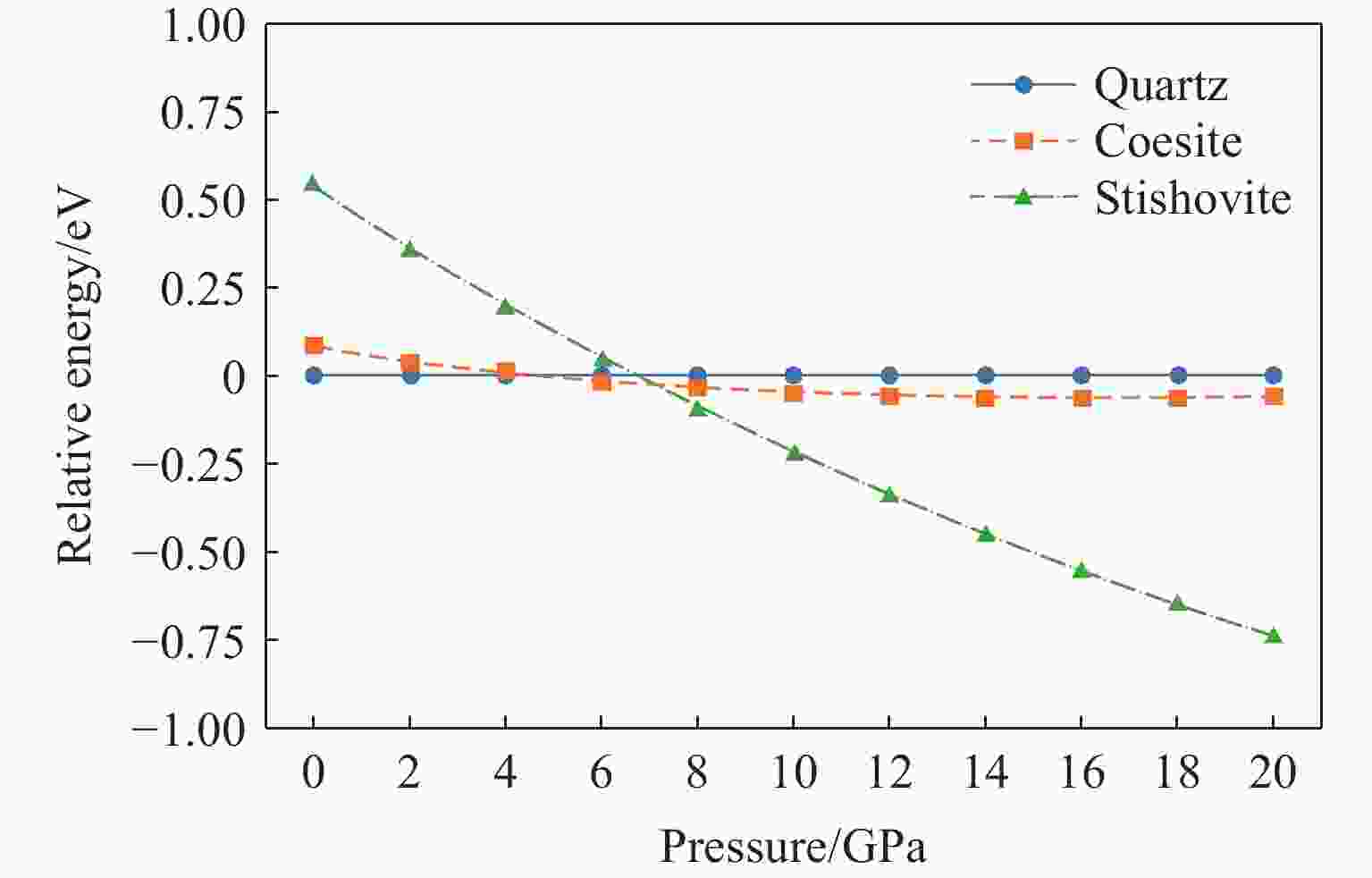
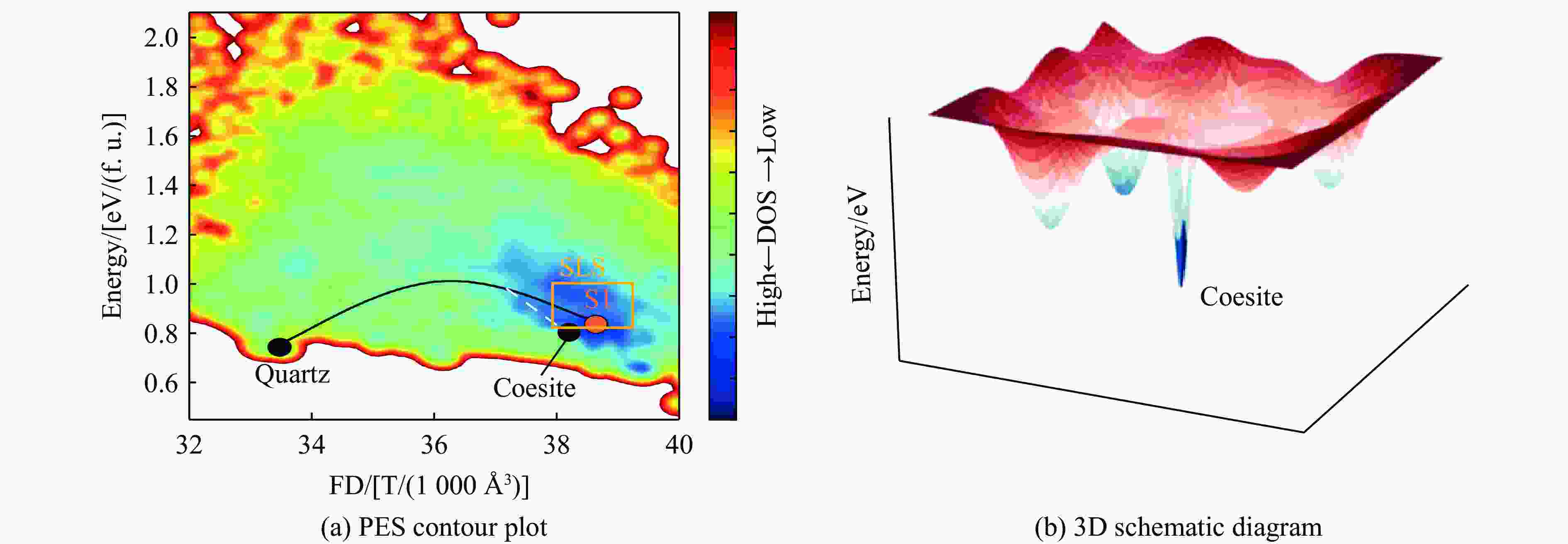
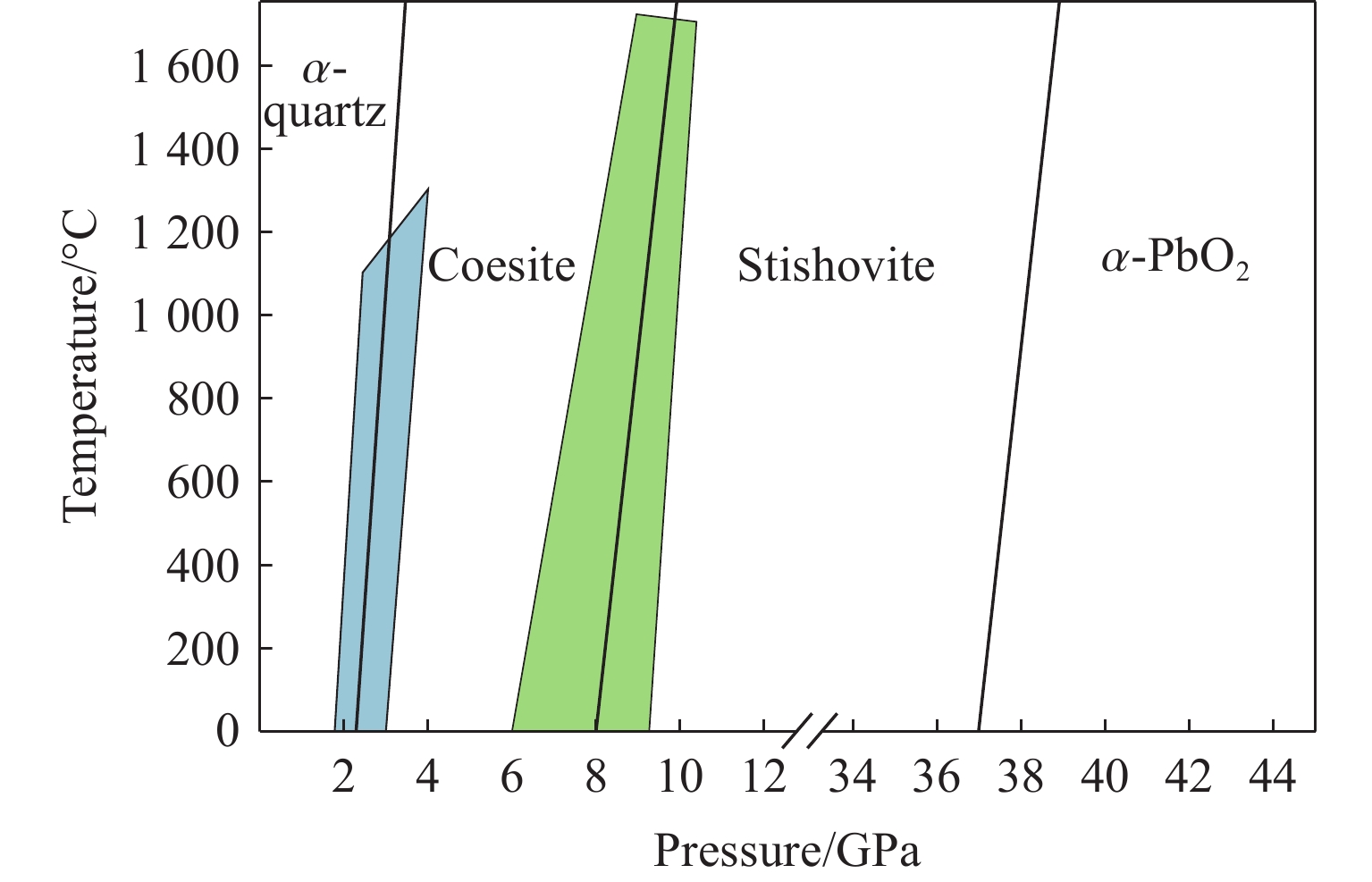
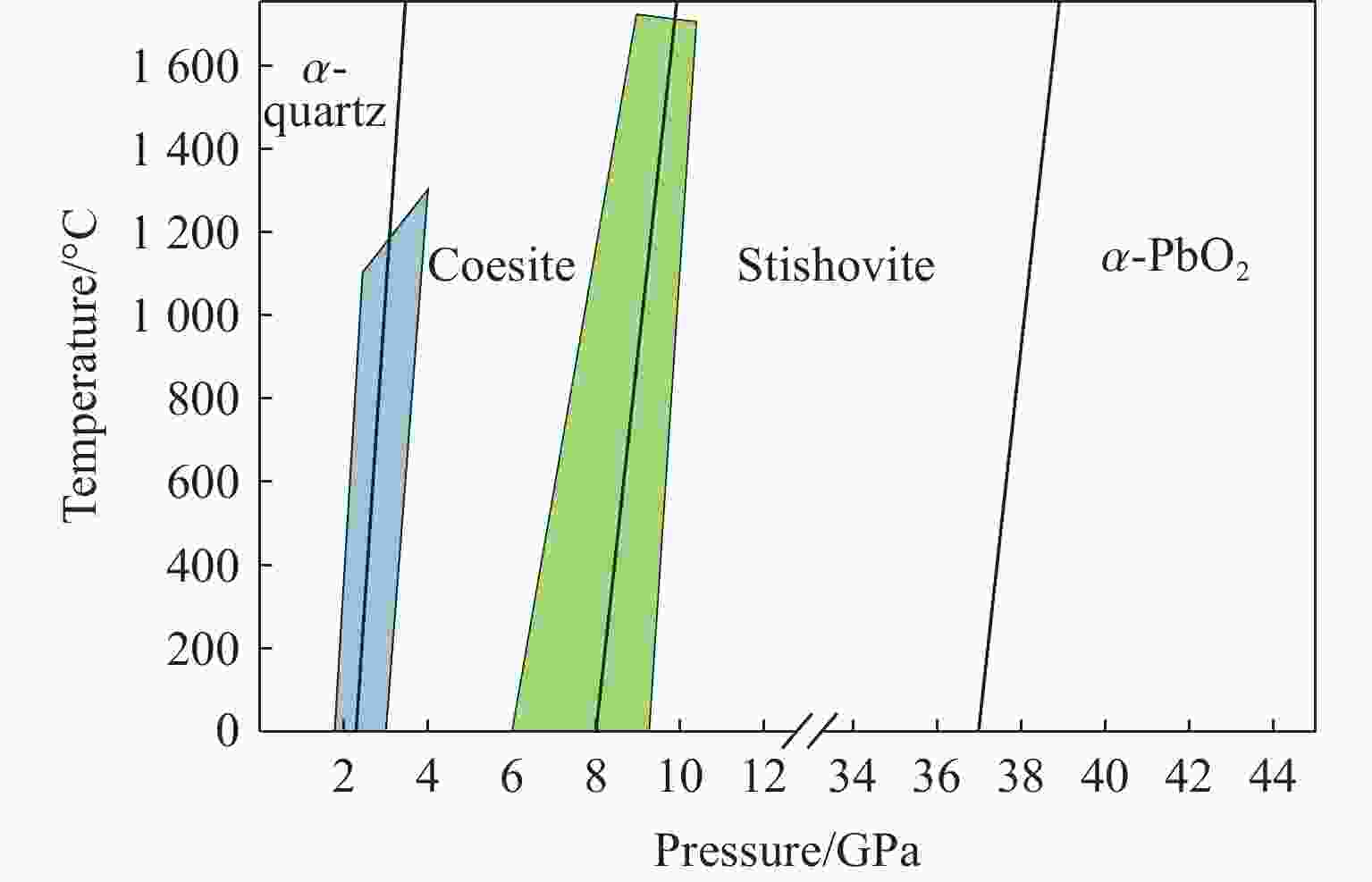
摘要: 基于高维神经网络势能模型与随机表面行走算法，系统研究了二氧化硅在高压条件下的结构相变机理。首先，构建了覆盖石英、柯石英、斯石英及非晶态的全局势能面，绘制出热力学相图。进一步分析发现，对于石英到斯石英的相变路径，高压下能垒显著降低，表现出较强的动力学可行性；而柯石英至斯石英的相变路径则为单步机制，能垒随压力升高略有上升。在非晶化相变方面，通过采样与识别低对称性结构群，明确了低对称性结构群在石英高压非晶化中的关键作用，揭示了“短程有序—中程无序—拓扑有序”结构作为非晶态的关键特征。值得注意的是，研究过程中未发现有效的石英-柯石英相变路径，进一步研究表明，非晶路径在动力学上的优势“截断”了石英向柯石英的直接演化路径，揭示了石英-柯石英路径缺失的本质原因。该工作系统探究了高压下二氧化硅的晶态与非晶态相变机理，为复杂氧化物的高压模拟研究提供了理论依据和方法范式。Abstract: This study systematically investigates the structural phase transition mechanisms of silicon dioxide under high pressure by using the high-dimensional neural network potential model combined with the stochastic surface walking algorithm. First, a global potential energy surface of quartz, coesite, stishovite, and amorphous states was constructed, and the thermodynamic phase diagram reveals the thermodynamic stability advantage of stishovite in high-pressure regions. Further analysis demonstrated that the energy barrier for the quartz-to-stishovite transition path shows a significant decrease under high pressure, which exhibits strong kinetic feasibility; while for the coesite-to-stishovite pathway, it follows a single transition state mechanism and the energy barrier displays a slightly increase under high pressure. Regarding the amorphization transition, the low symmetry structure group plays a key role in the high-pressure amorphization of quartz based on sampling and identification, and the “short-range order−middle range-disorder−topological order” structure was unveiled as a defining characteristic of the amorphous state. Notably, we did not observe effective quartz-coesite transition path during the study and further confirmed that the advantage of kinetic dynamics in the amorphization transition inhibits this transformation pathway, revealing the origin of the absence of the quartz-coesite transition. This work systematically explores the mechanisms of crystalline and amorphous phase transitions in silicon dioxide under high pressure and provides theoretical foundations and methodological paradigms for high-pressure simulation studies of complex oxides.
-
图 3 石英至斯石英相变路径与能垒分析
Figure 3. Phase transition pathway and energy barrier analysis from quartz to stishovite
图 5 柯石英至斯石英的相变路径与能垒分析
Figure 5. Phase transition pathway and energy barrier analysis from coesite to stishovite
图 8 石英至非晶相S1的相变路径、能垒及配位数分析
Figure 8. Phase transition pathway, energy barriers and coordination numbers from quartz to S1
图 10 柯石英和斯石英相对于石英的相对能量随压力的变化关系
Figure 10. Relative energies of coesite and stishovite as a function of pressure (relative to quartz)
图 11 柯石英与SLS在势能面上的位置关系
Figure 11. Locations of coesite and SLS on the potential energy surface
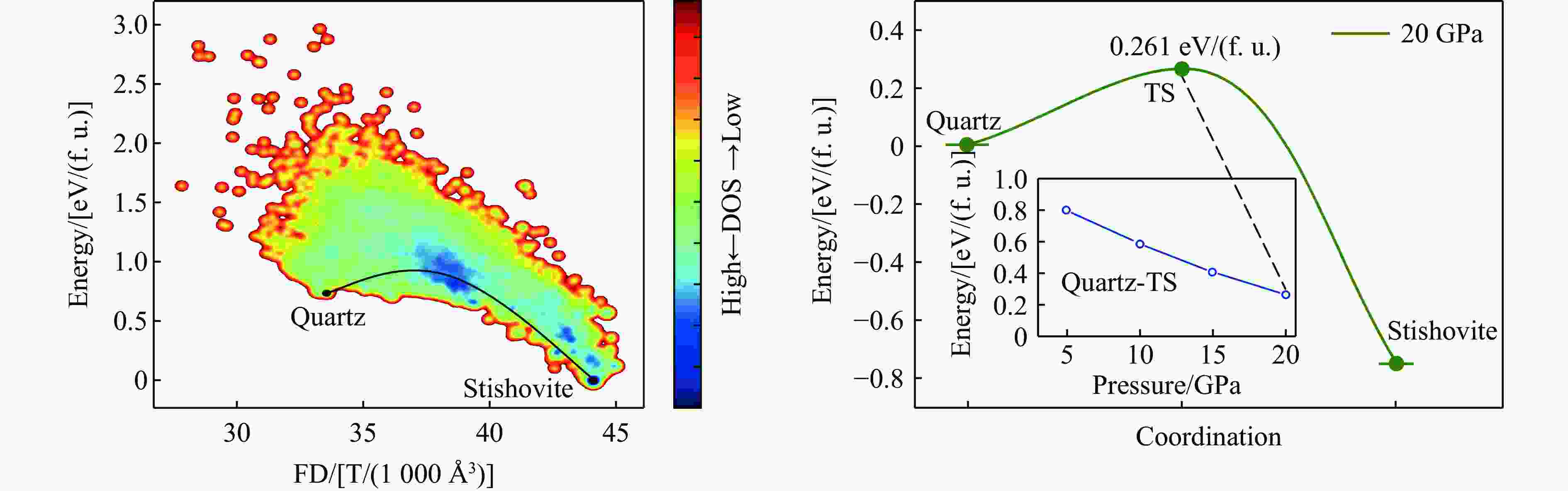
表 1 石英至斯石英的相变在不同压力下的能量分析
Table 1. Energy of the quartz-to-stishovite phase transition under different pressures
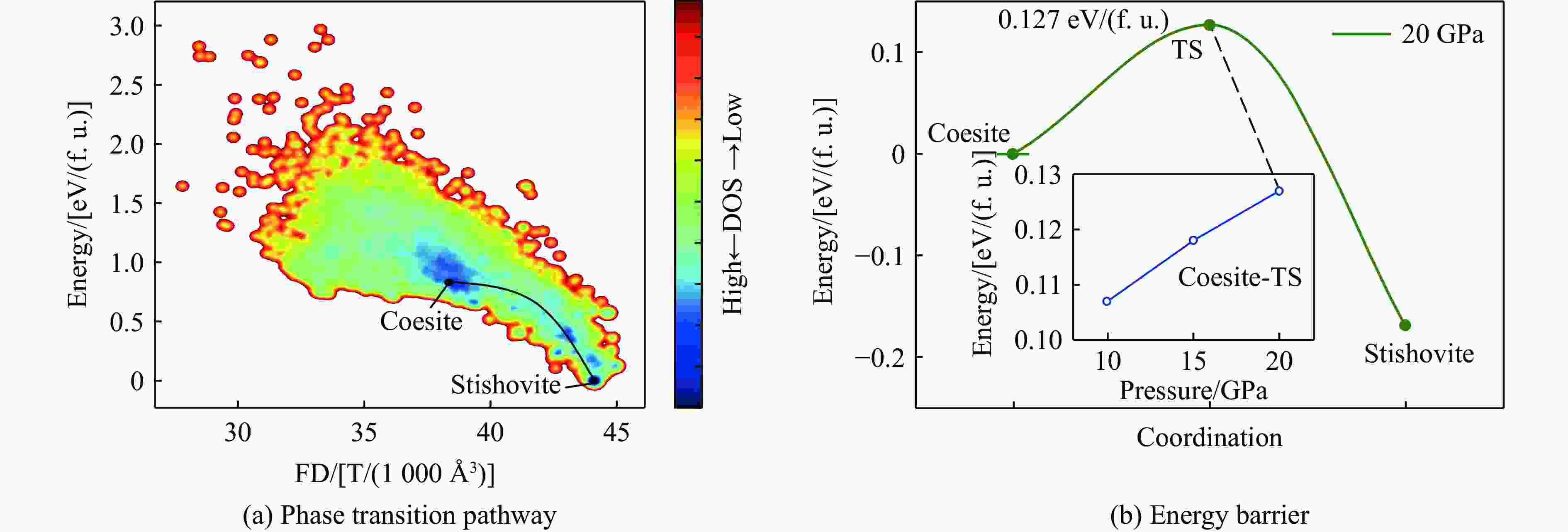
Pressure/GPa Energy barrier/[eV/(f. u.)] Final state energy/[eV/(f. u.)] 5 0.793 0.118 10 0.581 −0.225 15 0.402 −0.510 20 0.261 −0.752 
下载: 导出CSV
表 2 柯石英至斯石英的相变在不同压力下的能量分析
Table 2. Energy of the coesite-to-stishovite phase transition under different pressures
Pressure/GPa Energy barrier/[eV/(f. u.)] Final state energy/[eV/(f. u.)] 10 0.107 −0.160 15 0.118 −0.165 20 0.127 −0.169
下载: 导出CSV
表 3 石英至S1的相变在不同压力下的能量分析
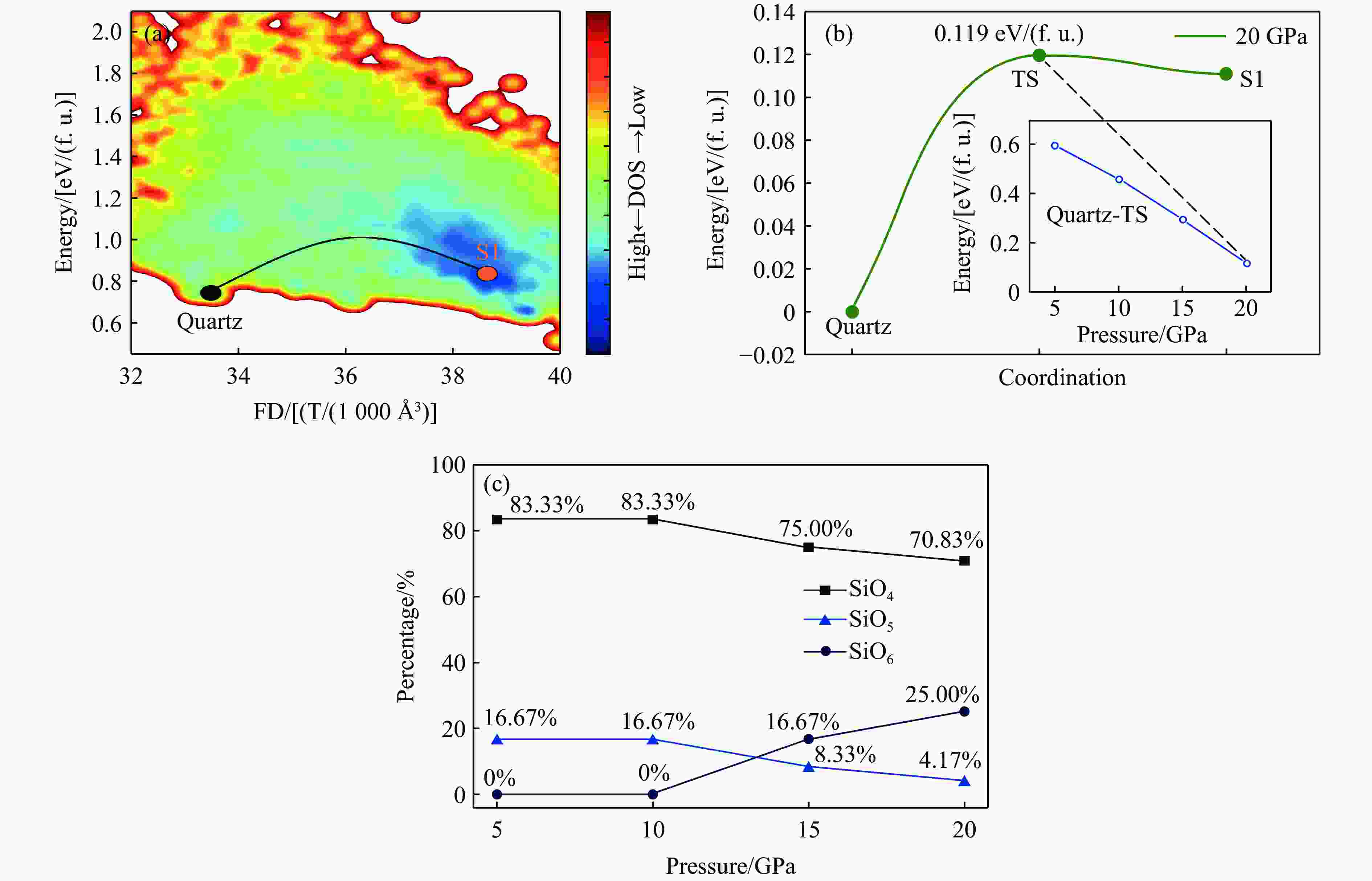
Table 3. Energy of the quartz-to-S1 phase transition under different pressures
Pressure/GPa Energy barrier/[eV/(f. u.)] Final state energy/[eV/(f. u.)] 5 0.597 0.452 10 0.462 0.341 15 0.296 0.240 20 0.119 0.111
下载: 导出CSV
-
[1] HEANEY P J, PREWITT C T, GIBBS G V. Silica: physical behavior, geochemistry and materials applications [M]. Washigton: Mineralogical Society of America, 1994: 309. [2] MOLAEI F, SIAVOSHI H. Molecular dynamics studies of thermal conductivity and mechanical properties of single crystalline α-quartz [J]. Solid State Communications, 2020, 320: 114020. doi: 10.1016/j.ssc.2020.114020 [3] SKELTON A A, FENTER P, KUBICKI J D, et al. Simulations of the quartz (101̅1)/water interface: a comparison of classical force fields, ab initio molecular dynamics, and X-ray reflectivity experiments [J]. The Journal of Physical Chemistry C, 2011, 115(5): 2076–2088. doi: 10.1021/jp109446d [4] WANG J, RAJENDRAN A M, DONGARE A M. Atomic scale modeling of shock response of fused silica and α-quartz [J]. Journal of Materials Science, 2015, 50(24): 8128–8141. doi: 10.1007/s10853-015-9386-1 [5] LOPES P E M, MURASHOV V, TAZI M, et al. Development of an empirical force field for silica. application to the quartz-water interface [J]. The Journal of Physical Chemistry B, 2006, 110(6): 2782–2792. doi: 10.1021/jp055341j [6] MARCINKEVIČIUS A, JUODKAZIS S, WATANABE M, et al. Femtosecond laser-assisted three-dimensional microfabrication in silica [J]. Optics Letters, 2001, 26(5): 277. doi: 10.1364/OL.26.000277 [7] JIANG B Q, XIAO L, HU S F, et al. Optimization and kinetics of electroless Ni-P-B plating of quartz optical fiber [J]. Optical Materials, 2009, 31(10): 1532–1539. doi: 10.1016/j.optmat.2009.02.016 [8] TAY A, HO W K, SCHAPER C D, et al. Constraint feedforward control for thermal processing of quartz photomasks in microelectronics manufacturing [J]. Journal of Process Control, 2004, 14(1): 31–39. doi: 10.1016/S0959-1524(03)00069-6 [9] PERRY L A, CORONELL O. Reliable, bench-top measurements of charge density in the active layers of thin-film composite and nanocomposite membranes using quartz crystal microbalance technology [J]. Journal of Membrane Science, 2013, 429: 23–33. doi: 10.1016/j.memsci.2012.11.023 [10] HOU W J, ZHANG Y M, LIU T, et al. Graphene oxide coated quartz sand as a high performance adsorption material in the application of water treatment [J]. RSC Advances, 2015, 5(11): 8037–8043. doi: 10.1039/C4RA11430B [11] BEATO P, KRAEHNERT R, ENGELSCHALT S, et al. A micro-structured quartz reactor for kinetic and in situ spectroscopic studies in heterogeneous catalysis [J]. Chemical Engineering Journal, 2008, 135: S247–S253. doi: 10.1016/j.cej.2007.07.011 [12] DJURABEKOVA F, BACKHOLM M, BACKMAN M, et al. Amorphization of α-quartz and comparative study of defects in amorphized quartz and Si nanocrystals embedded in amorphous silica [J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2010, 268(19): 3095–3098. doi: 10.1016/j.nimb.2010.05.056 [13] NISHIYAMA N, WAKAI F, OHFUJI H, et al. Fracture-induced amorphization of polycrystalline SiO2 stishovite: a potential platform for toughening in ceramics [J]. Scientific Reports, 2014, 4(1): 6558. doi: 10.1038/srep06558 [14] BADRO J, BARRAT J L, GILLET P. Numerical simulation of α-quartz under nonhydrostatic compression: memory glass and five-coordinated crystalline phases [J]. Physical Review Letters, 1996, 76(5): 772–775. doi: 10.1103/PhysRevLett.76.772 [15] ZHANG X J, SHANG C, LIU Z P. Pressure-induced silica quartz amorphization studied by iterative stochastic surface walking reaction sampling [J]. Physical Chemistry Chemical Physics, 2017, 19(6): 4725–4733. doi: 10.1039/C6CP06895B [16] MACHON D, MEERSMAN F, WILDING M C, et al. Pressure-induced amorphization and polyamorphism: inorganic and biochemical systems [J]. Progress in Materials Science, 2014, 61: 216–282. doi: 10.1016/j.pmatsci.2013.12.002 [17] TOLÉDANO P, MACHON D. Structural mechanism leading to a ferroelastic glass state: interpretation of amorphization under pressure [J]. Physical Review B, 2005, 71(2): 024210. doi: 10.1103/PhysRevB.71.024210 [18] DEMUTH T, JEANVOINE Y, HAFNER J, et al. Polymorphism in silica studied in the local density and generalized-gradient approximations [J]. Journal of Physics: Condensed Matter, 1999, 11(19): 3833–3874. doi: 10.1088/0953-8984/11/19/306 [19] LAPITSKAYA V A, KUZNETSOVA T A, KHUDOLEY A L, et al. Influence of polishing technique on crack resistance of quartz plates [J]. International Journal of Fracture, 2021, 231(1): 61–77. doi: 10.1007/s10704-021-00564-5 [20] WRIGHT A F, LEHMANN M S. The structure of quartz at 25 and 590 ℃ determined by neutron diffraction [J]. Journal of Solid State Chemistry, 1981, 36(3): 371–380. doi: 10.1016/0022-4596(81)90449-7 [21] MILTON K L, DURRANT T R, COBOS FREIRE T, et al. Difference in structure and electronic properties of oxygen vacancies in α-quartz and α-cristobalite phases of SiO2 [J]. Materials, 2023, 16(4): 1382. doi: 10.3390/ma16041382 [22] MO C K, ZHAO J L, ZHANG D X. Real-time measurement of mechanical behavior of granite during heating-cooling cycle: a mineralogical perspective [J]. Rock Mechanics and Rock Engineering, 2022, 55(7): 4403–4422. doi: 10.1007/s00603-022-02867-y [23] TANG C H, ZHU J X, LI Z H, et al. Surface chemistry and reactivity of SiO2 polymorphs: a comparative study on α-quartz and α-cristobalite [J]. Applied Surface Science, 2015, 355: 1161–1167. doi: 10.1016/j.apsusc.2015.07.214 [24] TRACY S J, TURNEAURE S J, DUFFY T S. Structural response of α-quartz under plate-impact shock compression [J]. Science Advances, 2020, 6(35): eabb3913. doi: 10.1126/sciadv.abb3913 [25] YURTSEVEN H, ATEŞ S. Resonant frequency shifts related to the elastic constants near the α-β transition in quartz [J]. Journal of Molecular Structure, 2019, 1179: 421–424. doi: 10.1016/j.molstruc.2018.11.044 [26] YANG Z Y, XU X L, DOUGLAS J F, et al. Molecular dynamics investigation of the pressure dependence of glass formation in a charged polymer melt [J]. Macromolecules, 2023, 56(11): 4049–4064. doi: 10.1021/acs.macromol.3c00317 [27] HUANG S D, SHANG C, ZHANG X J, et al. Material discovery by combining stochastic surface walking global optimization with a neural network [J]. Chemical Science, 2017, 8(9): 6327–6337. doi: 10.1039/C7SC01459G [28] HUANG S D, SHANG C, KANG P L, et al. LASP: fast global potential energy surface exploration [J]. WIREs Computational Molecular Science, 2019, 9(6): e1415. doi: 10.1002/wcms.1415 [29] LIN Y H, HU Q Y, WALTER M J, et al. Hydrous SiO2 in subducted oceanic crust and H2O transport to the core-mantle boundary [J]. Earth and Planetary Science Letters, 2022, 594: 117708. doi: 10.1016/j.jpgl.2022.117708 [30] HUANG S D, SHANG C, KANG P L, et al. Atomic structure of boron resolved using machine learning and global sampling [J]. Chemical Science, 2018, 9(46): 8644–8655. doi: 10.1039/C8SC03427C [31] ZHU S C, CHEN G W, ZHANG D Z, et al. Topological ordering of memory glass on extended length scales [J]. Journal of the American Chemical Society, 2022, 144(16): 7414–7421. doi: 10.1021/jacs.2c01717 [32] ZHANG X J, SHANG C, LIU Z P. Double-ended surface walking method for pathway building and transition state location of complex reactions [J]. Journal of Chemical Theory and Computation, 2013, 9(12): 5745–5753. doi: 10.1021/ct4008475 [33] CHEN T, XIE J S, WEN B, et al. Inhibition of defect-induced α-to-δ phase transition for efficient and stable formamidinium perovskite solar cells [J]. Nature Communications, 2023, 14(1): 6125. doi: 10.1038/s41467-023-41853-y [34] GUET C, HOBZA P, SPEIGELMAN F, et al. Atomic clusters and nanoparticles: agregatsatomiques et nanoparticules [M]. Berlin: Springer, 2001. [35] PARRISH K, HU Q, ZHU Q Y. PyLRO: a python calculator for analyzing long-range structural order [J]. Journal of Applied Physics, 2025, 137(2): 025101. doi: 10.1063/5.0244012 [36] CAO X Y, HAN S S, LI J W, et al. Kinetic and thermodynamic transition pathways of silica by machine learning: implication for meteorite impacts [J]. Journal of Geophysical Research: Solid Earth, 2024, 129(3): e2024JB028656. doi: 10.1029/2024JB028656 -
下载:
图(11) / 表(3)
计量
- 文章访问数: 235
- HTML全文浏览量: 43
- PDF下载量: 18
