Hugoniot Equation of State Model for Mixtures
-
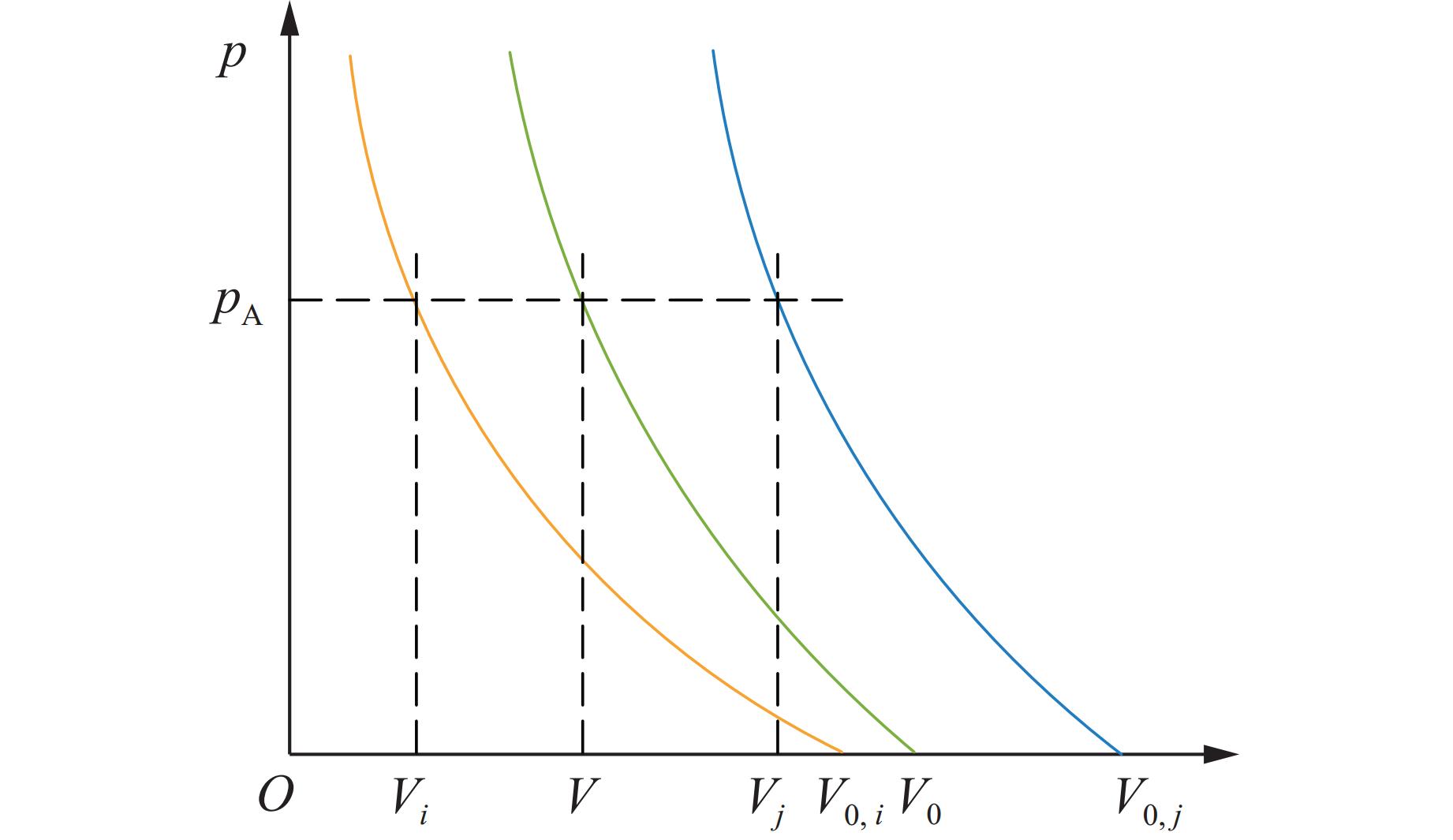
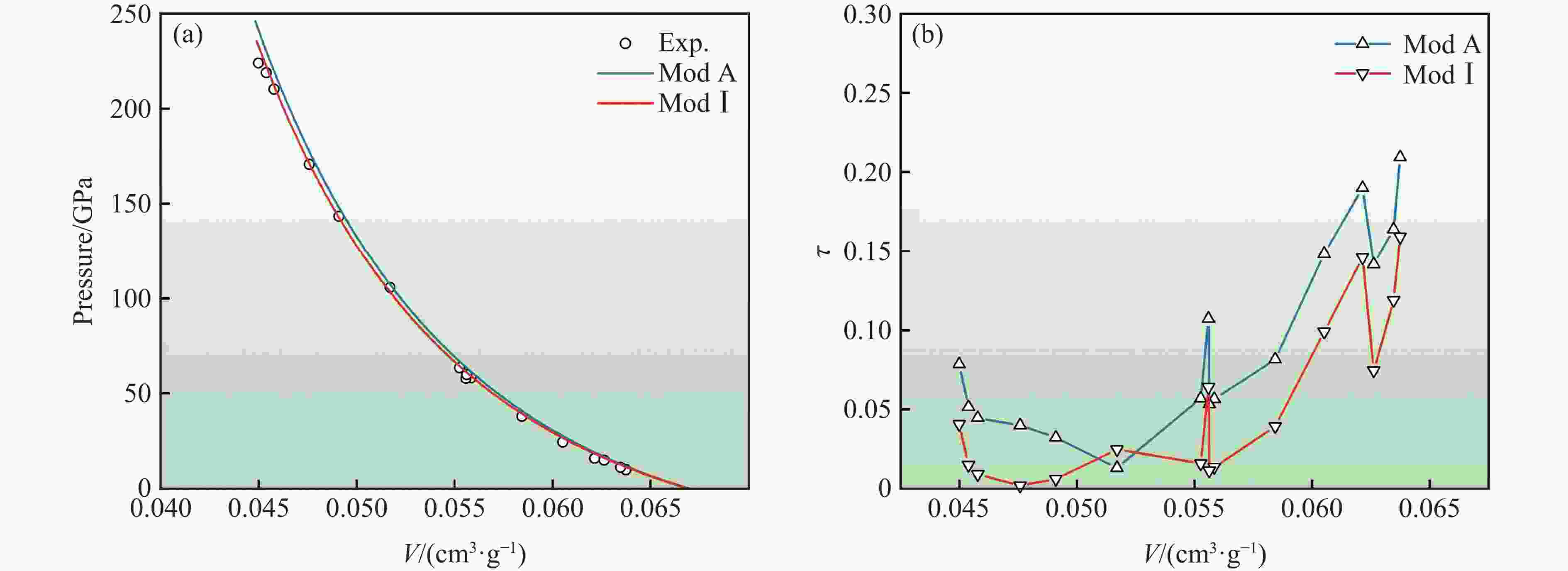
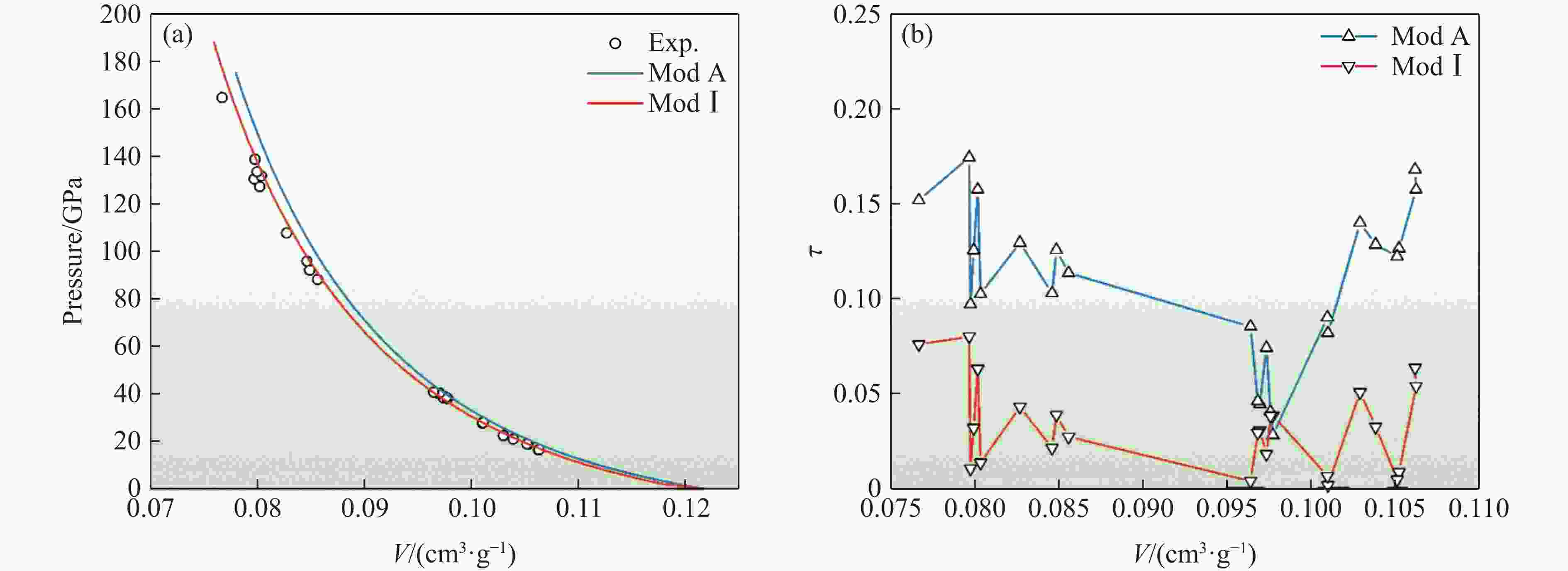
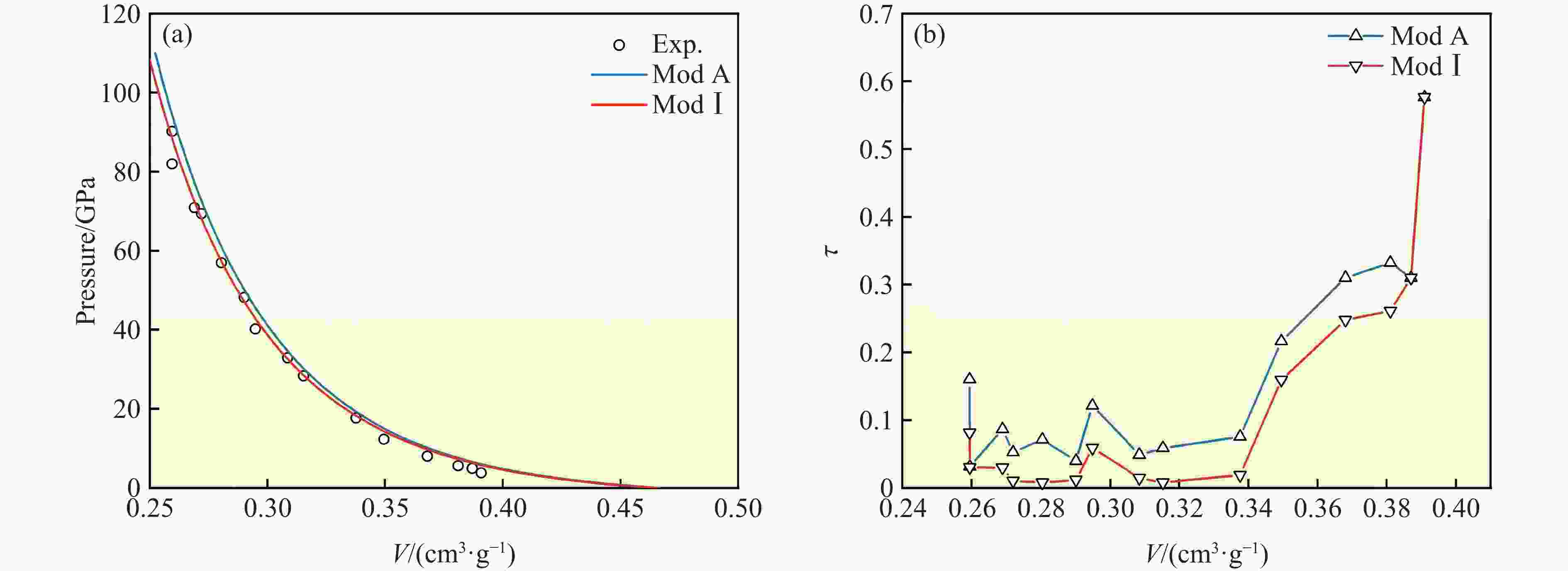
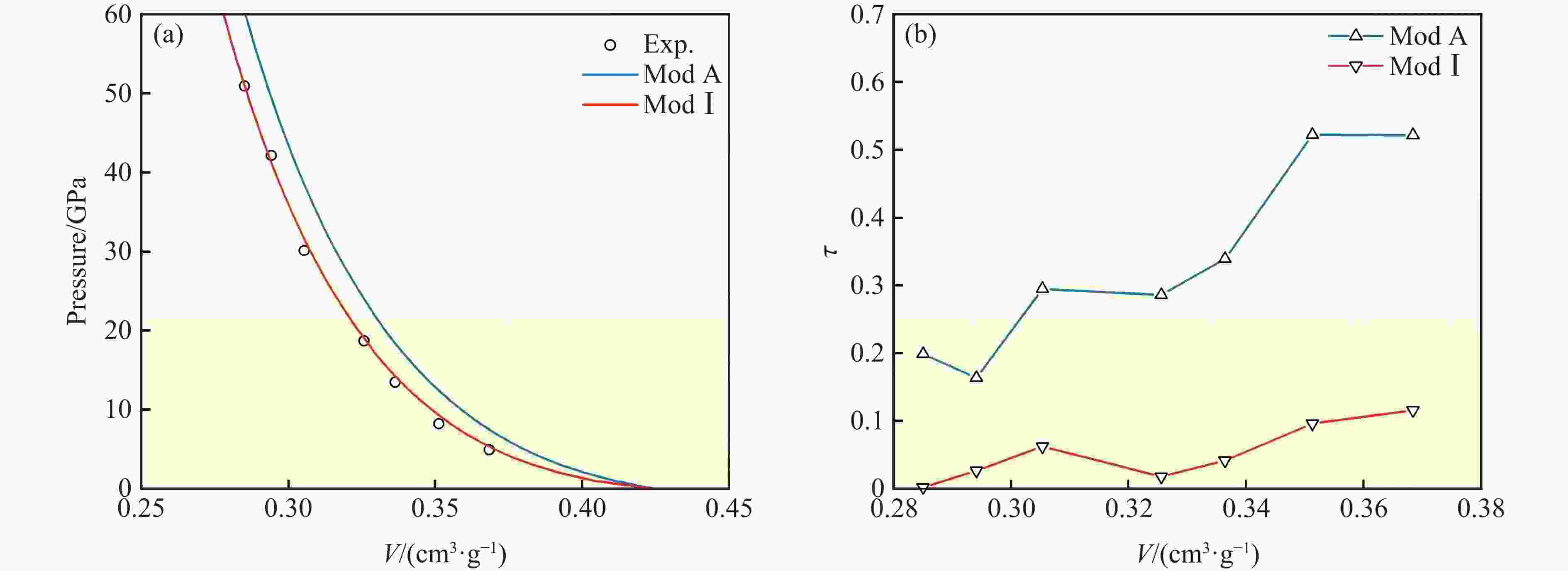
摘要: 高通量计算可显著提升材料的设计效率，推动冲击荷载下材料物性的前沿研究。混合物Hugoniot状态方程计算模型作为材料动力学数值模拟和材料高通量计算的关键，一直是研究热点。分别对体积可加模型和等温平均模型预估混合物Hugoniot状态方程的准确性进行了评估：前者基于热力学平衡条件，在计算混合物状态方程时并未考虑组分冲击压缩导致的温差效应；后者则利用0 K等温线，通过Mie-Grüneisen状态方程反推混合物Hugoniot冲击绝热线，等温平均模型可消除混合物中各组分因冲击压缩导致的温差效应。利用体积可加模型和等温平均模型，分别对二元合金、三元合金、二元混合物的Hugoniot状态方程进行预估，并与实测数据进行比对。计算结果表明：等温平均模型预估的混合物Hugoniot状态方程与实测数据的偏离度一般优于10%，准确度较体积可加模型更高；同时，两种模型都存在低压区预估准确性略差的现象。Abstract: High-throughput computing has become a cornerstone of modern materials design and is driving new advances in the study of shock-compressed matter. Central to these efforts is an accurate Hugoniot equation of state (EOS) for mixtures, yet existing mixture models continue to show sizeable scatter. Here we benchmarked two widely used schemes—the volume-additive model (Mod A) and the isothermal-average model (ModⅠ)—against experimental Hugoniot data for binary alloys, ternary alloys and granular mixtures. The Mod A model assumes full thermodynamic equilibrium and neglects the temperature rise of individual constituents under shock compression. The ModⅠ model, by contrast, removes this thermal contribution by deriving the mixture Hugoniot from 0 K isotherms via the Mie-Grüneisen EOS. Systematic comparison between the predicted Hugoniot EOS of binary alloy, ternary alloy, granular mixtures and the experimental data reveals that the ModⅠ model reproduces measured Hugoniot states within about 10% error across the entire pressure range studied, outperforming the Mod A model in both accuracy and robustness. Both approaches exhibit moderately larger discrepancies at low shock pressures, where thermal effects are most pronounced.
-
Key words:
- mixture /
- Hugoniot /
- equation of state /
- principle of volume additivity /
- isothermal average
-
图 1 冲击波阵面前后介质物性参数的突变
Figure 1. Sudden change in the physical parameters of the medium on either side of the shock front
图 2 Mod A的混合物p-V线与各组分p-V线
Figure 2. p-V curves for mixture and its component based on Mod A
图 3 (a) Mod A和ModⅠ预估钨铜烧结合金Hugoniot状态方程与实验数据的对比，(b) Mod A和ModⅠ预估模型的偏离度
Figure 3. (a) Comparison of the EOS of tungsten-copper alloy estimated by Mod A and ModⅠ with experimental data; (b) deviation degree of Mod A and ModⅠ
图 4 (a) Mod A和ModⅠ预估黄铜Hugoniot状态方程与实验数据的对比，(b) Mod A和ModⅠ预估模型的偏离度
Figure 4. (a) Comparison of the EOS of brass estimated by Mod A and ModⅠ with experimental data; (b) deviation degree of Mod A and ModⅠ
图 5 (a) Mod A和ModⅠ预估的环氧树脂-方镁石混合物的Hugoniot状态方程与实验数据的对比，(b) Mod A和ModⅠ预估模型的偏离度
Figure 5. (a) Comparison of the EOS of epoxy-periclase mixture estimated by Mod A and ModⅠ with experimental data; (b) deviation degree of Mod A and ModⅠ
图 6 (a) Mod A和ModⅠ预估的石蜡-方镁石混合物的Hugoniot状态方程与实验数据的对比，(b) Mod A和ModⅠ预估模型的偏离度
Figure 6. (a) Comparison of the EOS of paraffin-periclase mixture estimated by Mod A and ModⅠ with experimental data; (b) deviation degree of Mod A and ModⅠ
表 1 钨铜烧结合金和黄铜组分的物性参数
Table 1. Physical parameters for tungsten-copper mixture and brass alloy
下载: 导出CSV
-
[1] 经福谦. 实验物态方程导引 [M]. 2版. 北京: 科学出版社, 1999: 81−88.JING F Q. Experimental guide for the equation of state [M]. 2nd ed. Beijing: Science Press, 1999: 81−88. [2] WEN P, DU C X, TAO G, et al. Effect of Mn element on shock response in CoCrFeNiMnx high entropy alloys [J]. Chinese Physics B, 2024, 33(11): 116103. doi: 10.1088/1674-1056/ad7fd0 [3] ZHOU W Y, LI H R, CAO L X, et al. Shock hugoniot calculations of newly designed thermoplastic elastomers and comparison with classical binder estane [J]. The Journal of Physical Chemistry, 2024, 128(11): 2831–2840. doi: 10.1021/acs.jpcb.4c00062 [4] 李刚, 陈正汉, 谢云. 波在分层材料中的传播及防冲击波分层材料的设计 [J]. 振动与冲击, 2005, 24(2): 89–91, 105. doi: 10.3969/j.issn.1000-3835.2005.02.024LI G, CHEN Z H, XIE Y. Wave propagation in sandwich materials and design of anti-shockwave sandwith structure [J]. Journal of Vibration and Shock, 2005, 24(2): 89–91, 105. doi: 10.3969/j.issn.1000-3835.2005.02.024 [5] 梁汉良, 罗宁, 周嘉楠, 等. 多层金属复合材料界面微观结构特征数值计算研究 [J]. 稀有金属材料与工程, 2025, 54(1): 134–46. doi: 10.12442/j.issn.1002-185X.20240542LIANG H L, LUO N, ZHOU J N, et al. Numerical calculation study on interfacial microstructure characteristics of multilayer metal composite materials [J]. Rare Metal Materials and Engineering, 2025, 54(1): 134–46. doi: 10.12442/j.issn.1002-185X.20240542 [6] 高发光, 李永池, 王志海, 等. 新型聚酯材料状态方程的研究 [J]. 功能材料, 2012, 43(3): 287–289. doi: 10.3969/j.issn.1001-9731.2012.03.004GAO G F, LI Y C, WANG Z H, et al. Equations of state for a new type polyester material [J]. Journal of Functional Materials, 2012, 43(3): 287–289. doi: 10.3969/j.issn.1001-9731.2012.03.004 [7] 王世杰, 杨杰, 马硕, 等. 机器学习在功能梯度材料设计-制备中的应用综述 [J]. 材料导报, 2023, 37(21): 107–115. doi: 10.11896/cldb.22030237WANG S J, YANG J, MA S, et al. A review: applications of machine learning in design-fabrication of functionally graded materials [J]. Materials Reports, 2023, 37(21): 107–115. doi: 10.11896/cldb.22030237 [8] 戚兴怡, 胡耀峰, 王若愚, 等. 机器学习在新材料筛选方面的应用进展 [J]. 化学学报, 2023, 81(2): 158–174. doi: 10.6023/A22110446QI X Y, HU Y F, WANG R Y, et al. Recent advance of machine learning in selecting new materials [J]. Acta Chimica Sinica, 2023, 81(2): 158–174. doi: 10.6023/A22110446 [9] 张聪, 刘杰, 解树一, 等. 高通量计算与机器学习驱动高熵合金的研究进展 [J]. 材料工程, 2023, 51(3): 1–16. doi: 10.11868/j.issn.1001-4381.2022.000997ZHANG C, LIU J, XIE S Y, et al. Research progress in high-entropy alloys driven by high throughput computation and machine learning [J]. Journal of Materials Engineering, 2023, 51(3): 1–16. doi: 10.11868/j.issn.1001-4381.2022.000997 [10] JORDAN J L, BAER M R. Mixture model for determination of shock equation of state [J]. Journal of Applied Physics, 2012, 111(8): 083516. doi: 10.1063/1.3702873 [11] KINELOVSKII S A, MAEVSKII K K. Model of the behavior of the mixture with different properties of the species under high dynamic loads [J]. Journal of Applied Mechanics and Technical Physics, 2013, 54(4): 524–530. doi: 10.1134/S0021894413040020 [12] BOGACHEV G A. Calculation of the shock-wave adiabatics for some heterogeneous mixtures [J]. Journal of Applied Mechanics and Technical Physics, 1973, 14(4): 546–552. doi: 10.1007/BF01201248 [13] MEYERS M A. Dynamic behavior of materials [M]. New York: Wiley, 1994: 135–141. [14] 王学容, 王建国. 混合物物态方程的计算 [J]. 强激光与粒子束, 2011, 23(8): 2083–2089. doi: 10.3788/HPLPB20112308.2083WANG X R, WANG J G. Calculation of equation of state of material mixture [J]. High Power Laser and Particle Beams, 2011, 23(8): 2083–2089. doi: 10.3788/HPLPB20112308.2083 [15] 林华令, 黄风雷, 于万瑞. 混合物冲击温度的数值模拟 [J]. 高压物理学报, 2002, 16(1): 46–56. doi: 10.11858/gywlxb.2002.01.008LIN H L, HUANG F L, YU W R. Numerical simulation of shock temperature of mixtures during shock loading [J]. Chinese Journal of High Pressure Physics, 2002, 16(1): 46–56. doi: 10.11858/gywlxb.2002.01.008 [16] 周洪强, 于明, 孙海权, 等. 混合物状态方程的计算 [J]. 物理学报, 2015, 64(6): 064702. doi: 10.7498/aps.64.064702ZHOU H Q, YU M, SUN H Q, et al. Calculation of equation of state of a material mixture [J]. Acta Physica Sinica, 2015, 64(6): 064702. doi: 10.7498/aps.64.064702 [17] 谭华. 实验冲击波物理 [M]. 北京: 国防工业出版社, 2018: 40–47.TAN H. Experimental shock wave physics [M]. Beijing: National Defence Industry Press, 2018: 40–47. [18] MARSH S P. LASL shock Hugoniot data [M]. Berkeley: University of California Press, 1980. [19] MCQUEEN R G, MARSH S P, TAYLOR J W, et al. Chapter Ⅶ–the equation of state of solids from shock wave studies [M]//KINSLOW R. High-Velocity Impact Phenomena. New York: Academic Press, 1970: 293–417. [20] MITCHELL A C, NELLIS W J. Shock compression of aluminum, copper, and tantalum [J]. Journal of Applied Physics, 1981, 52(5): 3363–3374. doi: 10.1063/1.329160 [21] MILLETT J C F, BOURNE N K, BARNES N R. The behavior of an epoxy resin under one-dimensional shock loading [J]. Journal of Applied Physics, 2002, 92(11): 6590–6594. doi: 10.1063/1.1506389 -
下载:
计量
- 文章访问数: 134
- HTML全文浏览量: 49
- PDF下载量: 23
