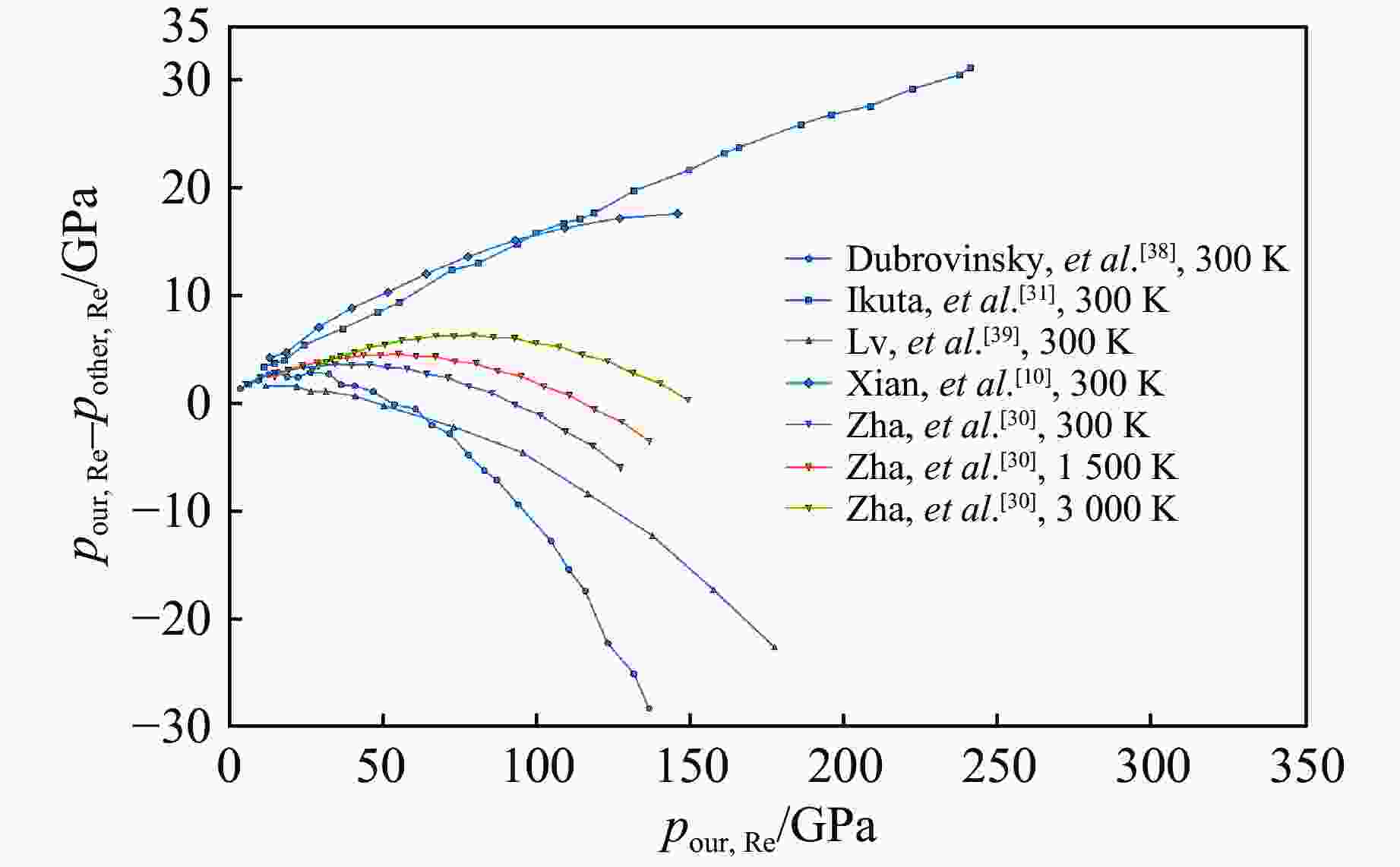
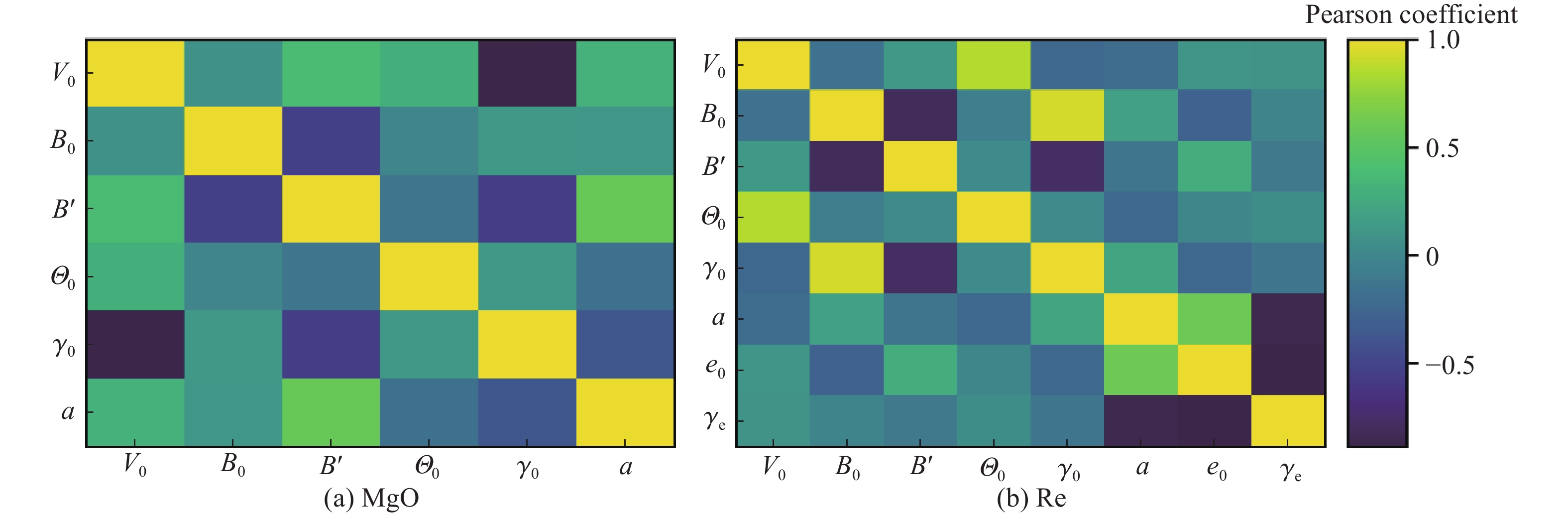
Quantification of Uncertainty in Magnesium Oxide and Rhenium Pressure Standards Based on Bayesian Statistical Methods
-
摘要: 静高压实验中精确的压力测量依赖于标准材料的物态方程,而物态方程参数的不确定度会显著影响压力预测的准确性。以氧化镁(MgO,B1相)和铼(Re,密排六方相)为研究对象,采用贝叶斯统计方法与马尔可夫链蒙特卡罗模拟技术,系统量化了其在金刚石对顶砧实验中的压力预测不确定度。通过均匀分布先验和正态似然函数构建贝叶斯框架,整合了多组实验数据进行参数校准。结果表明,贝叶斯统计方法成功量化了物态方程参数的后验分布,并揭示了参数间的强相关性,如MgO的Grüneisen参数与初始体积呈负相关,Re的体模量与Grüneisen参数呈正相关。MgO和Re的压力预测不确定度随着压力升高而显著增大;Re的压力预测不确定度随温度升高而显著增大,MgO则没有明显规律。研究结果为提升高压实验压力测量精度提供了具有不确定度的压标,可为提升材料科学和地球物理研究中的实验数据可靠性提供重要参考。Abstract: Accurate pressure measurement in static high-pressure experiments relies on the equation of state (EOS) of standard materials, where uncertainties in EOS parameters can significantly affect the accuracy of pressure predictions. This study focuses on magnesium oxide (MgO, B1 phase) and rhenium (Re, hexagonal close packed phase), employing Bayesian statistical methods and Markov Chain Monte Carlo (MCMC) simulation techniques to systematically quantify the uncertainty in pressure prediction during diamond anvil cell (DAC) experiments. By constructing a Bayesian framework with uniform prior distributions and normal likelihood functions, and integrating multiple sets of experimental data for parameter calibration, the results demonstrate that the Bayesian statistical approach successfully quantifies the posterior distribution of EOS parameters, revealing strong correlations between them, e.g., a negative correlation between Grüneisen parameter and initial volume for MgO, and a positive correlation between bulk modulus and Grüneisen parameter for Re. The uncertainty in pressure predictions for both MgO and Re increases significantly at higher pressures; for Re, this uncertainty also rises markedly with increasing temperature, whereas no clear trend is observed for MgO. This study provides pressure benchmarks with quantified uncertainties, contributing to improved accuracy in high-pressure experimental measurements. It holds significant reference value for ensuring the reliability of experimental data in materials science and geophysical research.
-
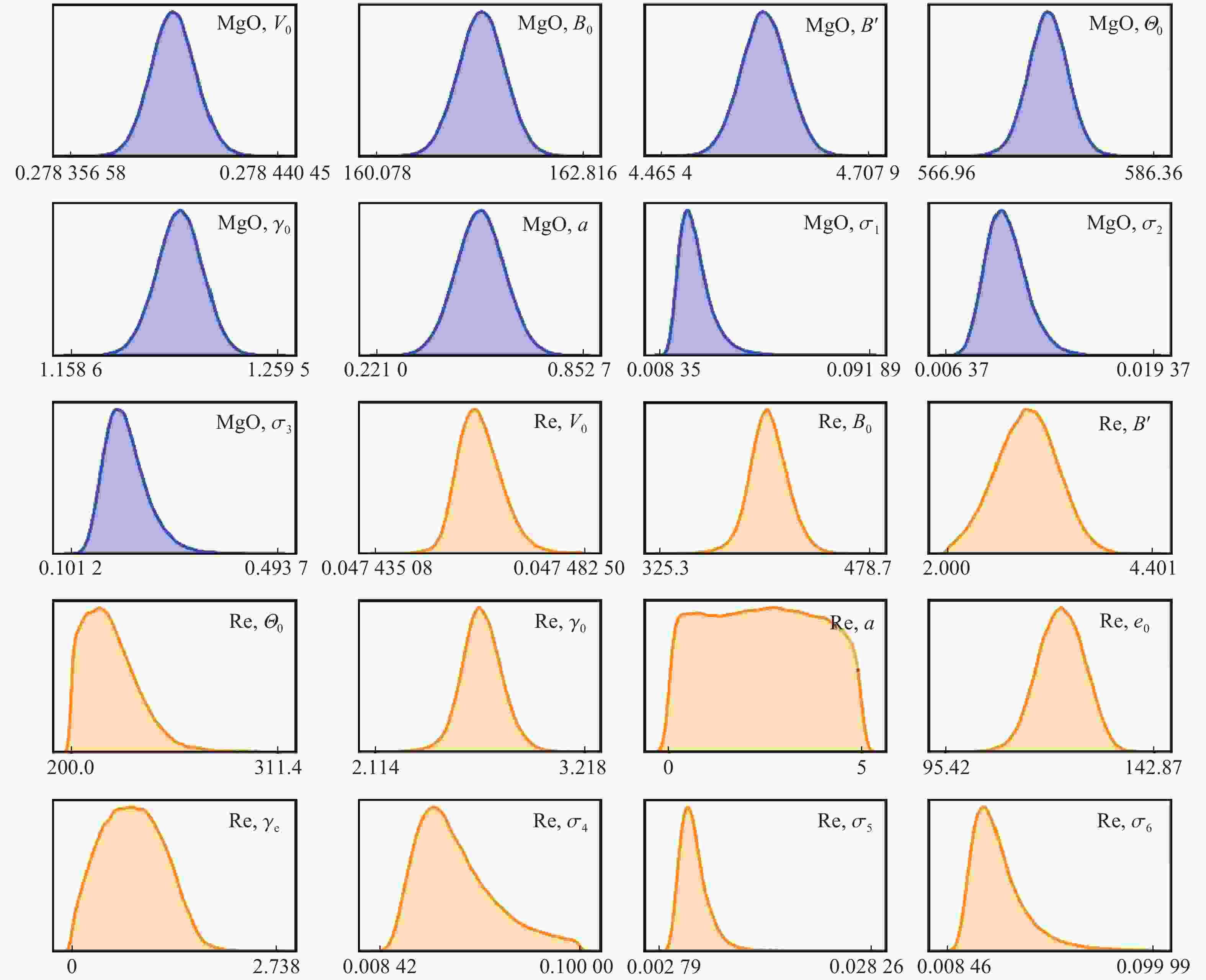
表 1 MgO和Re的物态方程参数和厌参数的最大后验概率估计以及自相关时间
Table 1. Parameters of the equation of state and nuisance parameters for MgO and Re including their maximum a posteriori estimates and autocorrelation times
Parameters MgO Re MAP Autocorrelation times MAP Autocorrelation times $ {V}_{0} $ 0.278 395 24 44.38 0.047 457 24 4 666.19 $ {B}_{0} $ 161.448 732 00 116.40 403.987 513 00 5 590.90 $ {B}{{{'}}} $ 4.584 482 53 117.47 3.056 576 91 4 144.78 $ {\varTheta }_{0} $ 576.196 100 00 131.41 214.846 678 00 5 757.61 $ {\gamma }_{0} $ 1.214 745 65 135.51 2.664 284 31 6 223.93 $ a $ 0.542 770 49 115.70 2.376 034 17 4 338.74 $ {\sigma }_{1} $ 0.018 744 43 135.76 $ {\sigma }_{2} $ 0.009 508 59 114.73 $ {\sigma }_{3} $ 0.178 798 18 123.73 $ {e}_{0} $ 122.204 570 00 4 493.19 $ {\gamma }_{\rm{e}} $ 0.776 681 40 4 826.82 $ {\sigma }_{4} $ 0.026 005 87 3 955.41 $ {\sigma }_{5} $ 0.005 416 86 3 328.32 $ {\sigma }_{6} $ 0.020 884 04 4 003.16 表 2 10 000个后验参数样本拟合的正态分布
Table 2. Normal distribution fitted from 10 000 posterior parameter samples
Parameter Mean value Standard deviation MgO Re MgO Re $ {V}_{0} $/(cm3·g−1) 0.278 398 15 0.047 458 54 0.000 009 02 0.000 004 91 $ {B}_{0} $/GPa 161.465 372 49 403.605 038 64 0.311 229 34 15.173 909 14 $ {B}{{{'}}} $ 4.585 703 90 2.945 016 63 0.027 343 49 0.358 836 98 $ {\varTheta }_{0} $/K 576.385 549 39 220.206 329 50 1.867 369 61 14.738 121 07 $ {\gamma }_{0} $ 1.211 618 31 2.669 167 99 0.011 137 87 0.116 507 98 $ a $ 0.537 953 01 2.465 206 65 0.074 877 68 1.413 728 35 $ {e}_{0} $/(10−6 K−1) 121.426 219 37 5.379 723 66 $ {\gamma }_{\mathrm{e}} $ 0.822 727 49 0.416 861 88 表 3 后验参数样本计算的不同压缩比和温度下MgO的平均压力及标准差
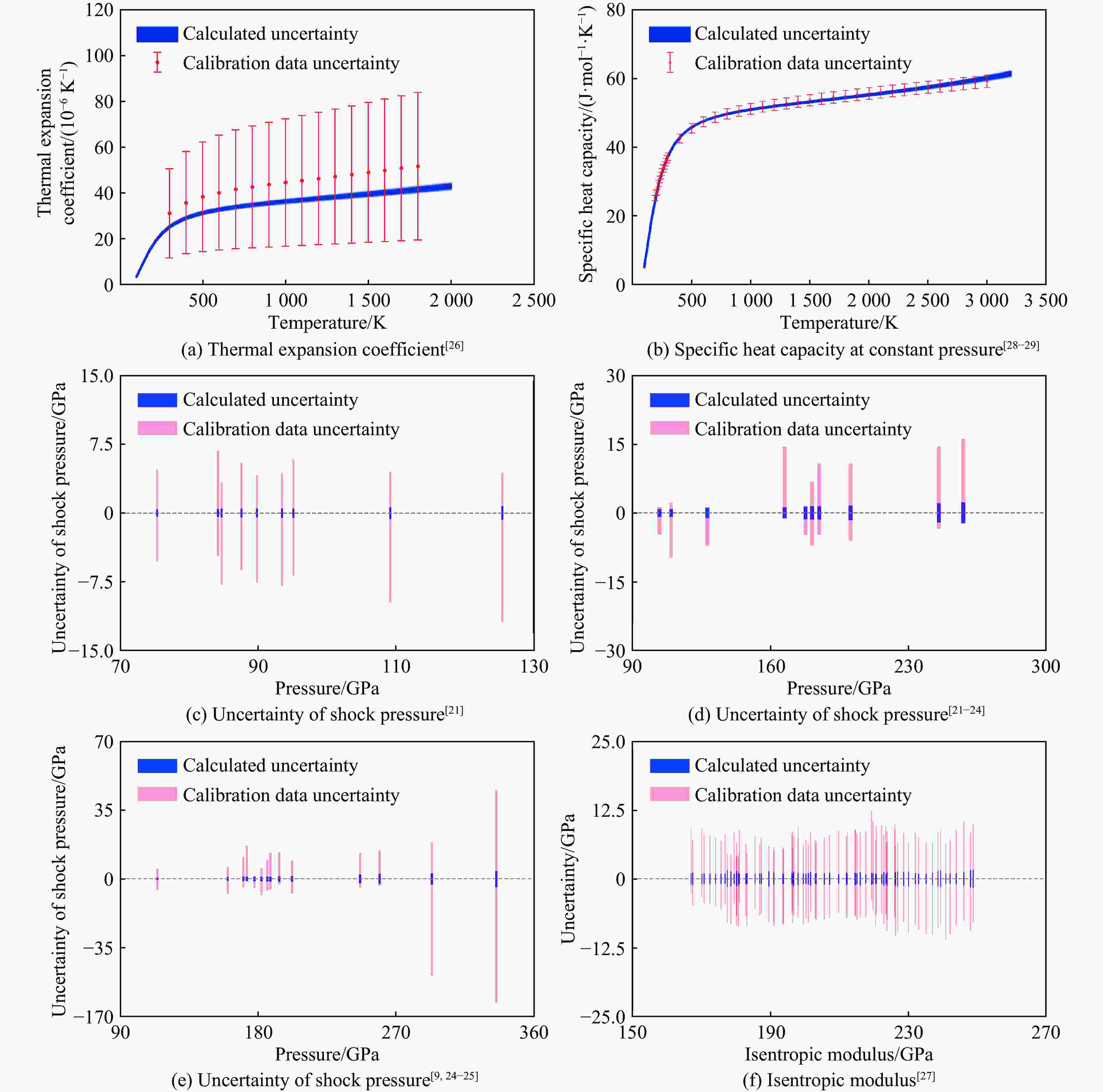
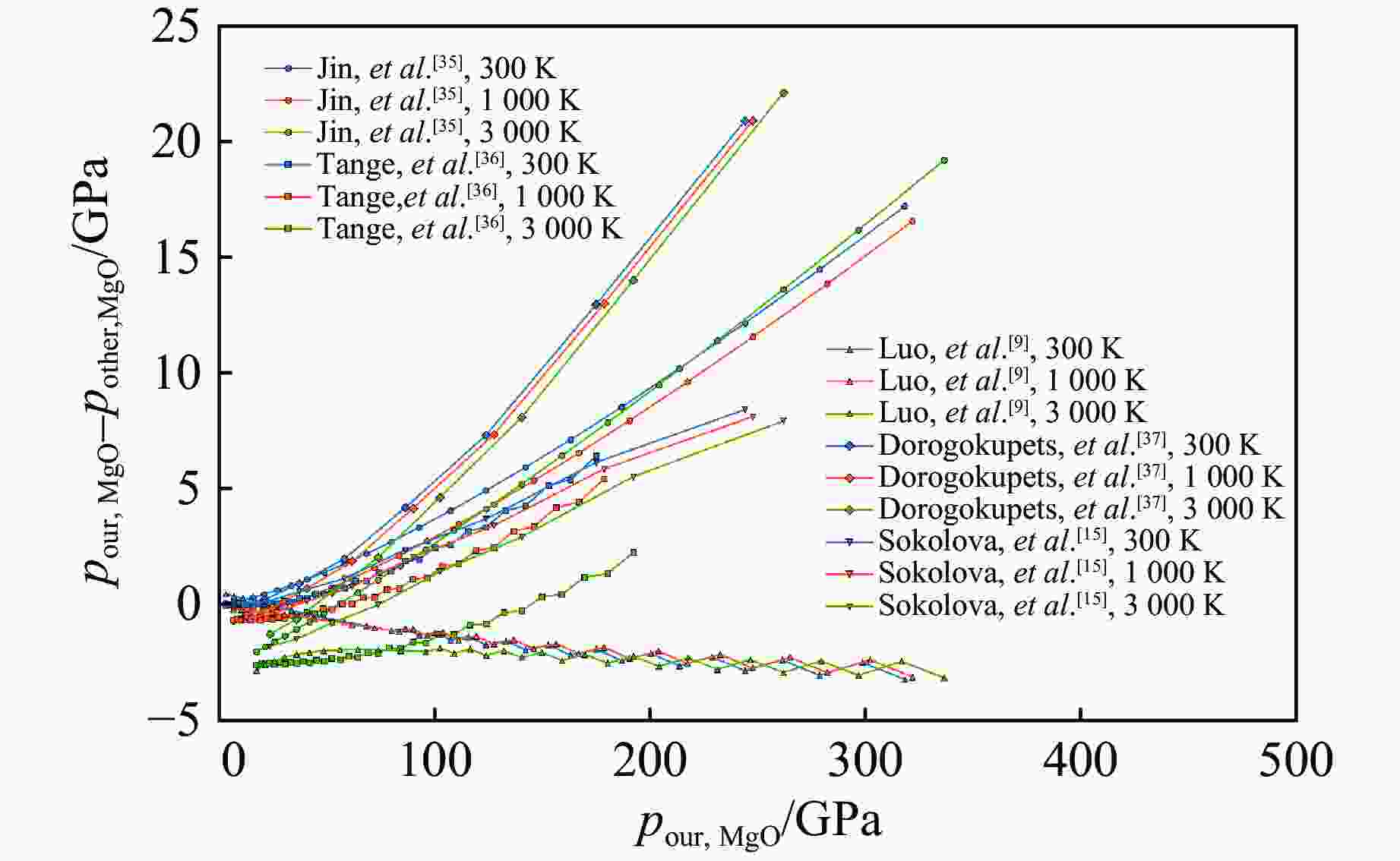
Table 3. Mean pressure and standard deviation of MgO at different compression ratios and temperatures calculated by posterior parameter samples
$ x=V/{V}_{0} $ Mean pressure/GPa Standard deviation/GPa 300 K 1 000 K 2 000 K 3 000 K 300 K 1 000 K 2 000 K 3 000 K 0.98 3.349 6.814 12.173 17.584 0.006 0.033 0.084 0.137 0.96 7.094 10.578 15.994 21.466 0.013 0.035 0.089 0.146 0.94 11.283 14.784 20.259 25.795 0.020 0.036 0.093 0.154 0.92 15.965 19.484 25.020 30.623 0.028 0.036 0.096 0.162 0.90 21.200 24.736 30.336 36.007 0.039 0.037 0.097 0.169 0.88 27.052 30.605 36.271 42.014 0.052 0.040 0.096 0.174 0.86 33.597 37.165 42.900 48.719 0.069 0.048 0.093 0.176 0.84 40.918 44.502 50.308 56.206 0.091 0.062 0.090 0.177 0.82 49.114 52.711 58.591 64.571 0.119 0.085 0.088 0.175 0.80 58.292 61.902 67.859 73.926 0.154 0.116 0.093 0.172 0.78 68.580 72.202 78.239 84.396 0.198 0.157 0.109 0.171 0.76 80.123 83.754 89.875 96.127 0.252 0.210 0.141 0.174 0.74 93.085 96.725 102.933 109.285 0.319 0.275 0.190 0.190 0.72 107.661 111.307 117.606 124.062 0.400 0.356 0.258 0.225 0.70 124.071 127.722 134.115 140.682 0.498 0.455 0.345 0.284 0.68 142.575 146.227 152.719 159.402 0.617 0.575 0.455 0.370 0.66 163.473 167.123 173.719 180.525 0.761 0.720 0.590 0.485 0.64 187.116 190.762 197.466 204.401 0.934 0.895 0.756 0.633 0.62 213.918 217.556 224.373 231.445 1.141 1.105 0.957 0.819 0.60 244.366 247.991 254.926 262.144 1.391 1.358 1.202 1.047 0.58 279.035 282.644 289.702 297.075 1.690 1.663 1.498 1.328 0.56 318.612 322.200 329.387 336.924 2.050 2.029 1.855 1.670 表 4 后验参数样本计算的不同压缩比和温度下Re的平均压力及标准差
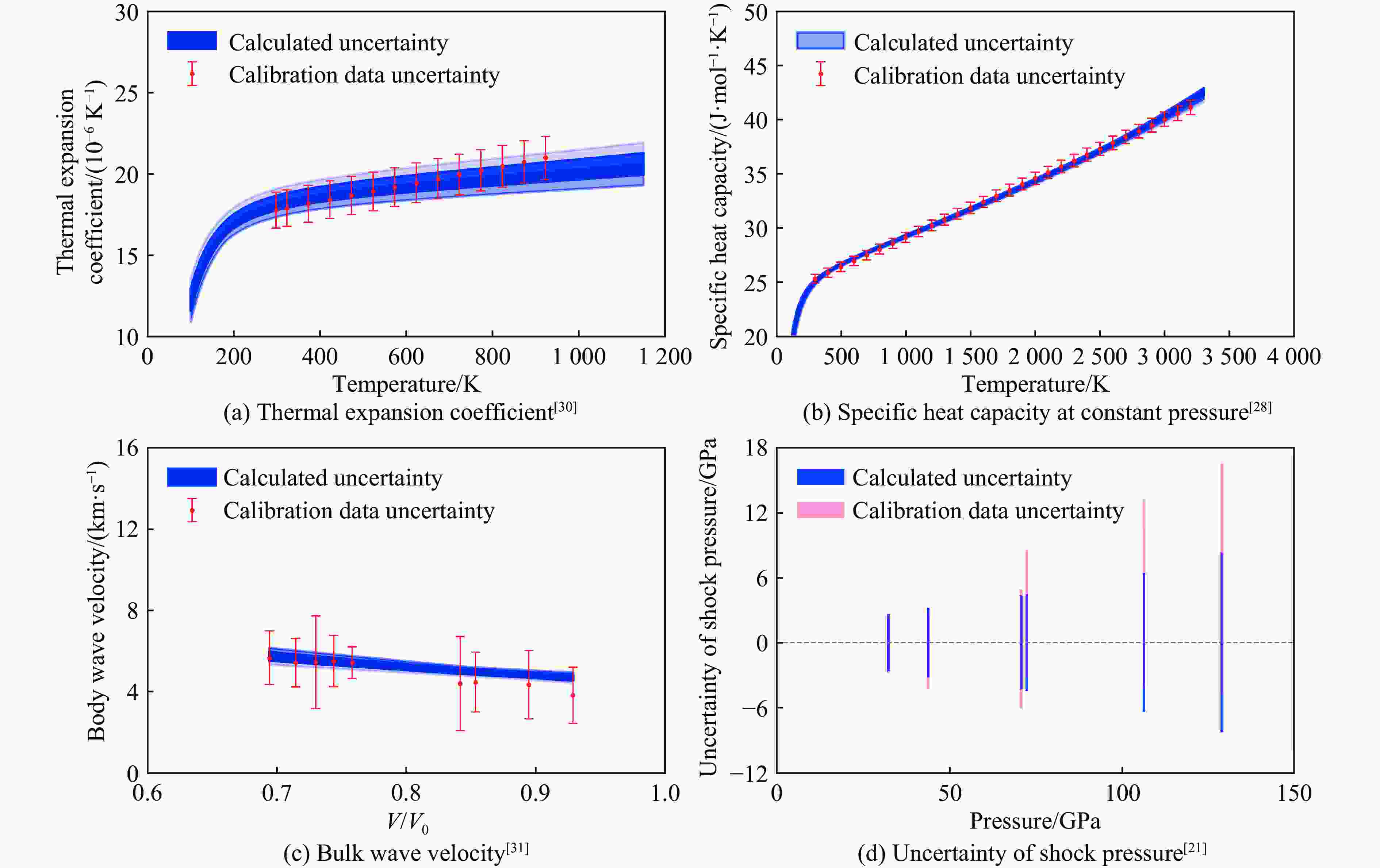
Table 4. Mean pressure and standard deviation of Re at different compression ratios and temperatures calculated by posterior parameter samples
$ x=V/{V}_{0} $ Mean pressure/GPa Standard deviation/GPa 300 K 1 000 K 2 000 K 3 000 K 300 K 1 000 K 2 000 K 3 000 K 0.98 8.292 13.624 21.566 29.795 0.297 0.514 0.868 1.291 0.96 17.268 22.605 30.558 38.798 0.572 0.784 1.147 1.599 0.94 26.990 32.331 40.295 48.547 0.824 1.030 1.406 1.889 0.92 37.525 42.869 50.846 59.111 1.059 1.257 1.645 2.164 0.90 48.949 54.296 62.284 70.562 1.284 1.470 1.869 2.427 0.88 61.343 66.692 74.693 82.986 1.513 1.682 2.090 2.687 0.86 74.800 80.151 88.166 96.472 1.767 1.914 2.324 2.958 0.84 89.424 94.776 102.804 111.126 2.077 2.197 2.600 3.264 0.82 105.330 110.681 118.723 127.061 2.478 2.568 2.952 3.634 0.80 122.646 127.995 136.051 144.406 3.010 3.068 3.422 4.107 0.78 141.517 146.863 154.933 163.305 3.710 3.738 4.055 4.725 0.76 162.106 167.445 175.531 183.921 4.614 4.617 4.894 5.536 0.74 184.596 189.927 198.028 206.436 5.760 5.741 5.979 6.583 0.72 209.195 214.514 222.630 231.058 7.183 7.148 7.351 7.913 0.70 236.139 241.441 249.572 258.021 8.927 8.880 9.051 9.572 0.68 265.696 270.977 279.122 287.592 11.041 10.984 11.129 11.611 0.66 298.172 303.425 311.584 320.076 13.580 13.517 13.639 14.085 0.64 333.916 339.135 347.307 355.822 16.611 16.544 16.648 17.062 0.62 373.334 378.508 386.692 395.231 20.214 20.144 20.233 20.619 0.60 416.888 422.009 430.202 438.765 24.481 24.411 24.488 24.849 0.58 465.119 470.174 478.372 486.960 29.524 29.454 29.522 29.862 0.56 518.653 523.628 531.827 540.439 35.476 35.407 35.467 35.789 -
[1] PEI S H, WANG Z H, XIA J. High pressure studies of 2D materials and heterostructures: a review [J]. Materials & Design, 2022, 213: 110363. doi: 10.1016/j.matdes.2021.110363 [2] LI Q J, ZHANG H F, LIU R, et al. Nanosize effects assisted synthesis of the high pressure metastable phase in ZrO2 [J]. Nanoscale, 2016, 84: 2412–2417. doi: 10.1039/C5NR07503C [3] SALAMAT A, FISCHER R A, BRIGGS R, et al. In situ synchrotron X-ray diffraction in the laser-heated diamond anvil cell: melting phenomena and synthesis of new materials [J]. Coordination Chemistry Reviews, 2014, 277/278: 15−30. [4] SHEN G Y, MAO H K. High-pressure studies with X-rays using diamond anvil cells [J]. Reports on Progress in Physics, 2017, 801: 016101. doi: 10.1088/1361-6633/80/1/016101 [5] DING Y J, SUN Y D, JIANG S Q, et al. Frontier in the diamond anvil cell techniques for ultrahigh pressure generation [J]. Journal of Physics: Condensed Matter, 2023, 3531: 313002. doi: 10.1088/1361-648X/acd15e [6] SEMAN S A H A, AHMAD R, AKIL H M. Meso-scale modelling and failure analysis of kenaf fiber reinforced composites under high strain rate compression loading [J]. Composites Part B: Engineering, 2019, 163: 403–412. doi: 10.1016/j.compositesb.2019.01.037 [7] DOROGOKUPETS P I. P-V-T equations of state of MgO and thermodynamics [J]. Physics and Chemistry of Minerals, 2010, 379: 677–684. doi: 10.1007/s00269-010-0367-2 [8] WU Z Q, WENTZCOVITCH R M, UMEMOTO K, et al. Pressure-volume-temperature relations in MgO: an ultrahigh pressure-temperature scale for planetary sciences applications [J]. Journal of Geophysical Research: Solid Earth, 2008, 113B6: B06204. [9] LUO Y, XIANG S K, LI J, et al. Equation of state of MgO up to 345 GPa and 8 500 K [J]. Physical Review B, 2023, 10713: 134116. doi: 10.1103/PhysRevB.107.134116 [10] XIAN Y T, XIANG S K, LIU L, et al. Accurate equation of state of rhenium as pressure scale up to 130 GPa and 3 200 K [J]. AIP Advances, 2022, 125: 055313. doi: 10.1063/5.0089292 [11] WU R, XIANG S K, SUN Y, et al. Obtaining the equation of state for multiphase iron under Earth’s core conditions using Bayesian statistics [J]. Journal of Applied Physics, 2025, 1373: 035904. doi: 10.1063/5.0240471 [12] LINDQUIST B A, JADRICH R B. Uncertainty quantification for a multi-phase carbon equation of state model [J]. Journal of Applied Physics, 2022, 13115: 155104. doi: 10.1063/5.0087210 [13] LINDQUIST B A, JADRICH R B. Uncertainty quantification for a multi-phase magnesium equation of state [J]. AIP Conference Proceedings, 2023, 28441: 310006. doi: 10.1063/12.0020372 [14] LINDQUIST B A, JADRICH R B, TICKNOR C. Uncertainty quantification for a TNT equation of state including the kinetic burn model [J]. AIP Conference Proceedings, 2024, 30661: 480010. doi: 10.1063/12.0028591 [15] SOKOLOVA T S, DOROGOKUPETS P I, LITASOV K D. Self-consistent pressure scales based on the equations of state for ruby diamond MgO B2-NaCl as well as Au Pt and other metals to 4 Mbar and 3 000 K [J]. Russian Geology and Geophysics, 2013, 542: 181–199. doi: 10.1016/j.rgg.2013.01.005 [16] JEANLOZ R, GODWAL B K, MEADE C. Static strength and equation of state of rhenium at ultra-high pressures [J]. Nature, 1991, 3496311: 687–689. doi: 10.1038/349687a0 [17] VAN DE, SCHOOT R, DEPAOLI S, KING R, et al. Bayesian statistics and modelling [J]. Nature Reviews Methods Primers, 2021, 11: 1. doi: 10.1038/s43586-020-00001-2 [18] VINET P, FERRANTE J, SMITH J R, et al. A universal equation of state for solids [J]. Journal of Physics C: Solid State Physics, 1986, 1920: L467–L473. doi: 10.1088/0022-3719/19/20/001 [19] BOUCHET J, MAZEVET S, MORARD G, et al. Ab initio equation of state of iron up to 1 500 GPa [J]. Physical Review B, 2013, 879: 094102. doi: 10.1103/PhysRevB.87.094102 [20] FOREMAN-MACKEY D, HOGG D W, LANG D, et al. EMCEE: the MCMC hammer [J]. Publications of the Astronomical Society of the Pacific, 2013, 125925: 306–312. doi: 10.1086/670067 [21] MARSH S P. LASL shock Hugoniot data [M]. Berkeley: University of California Press, 1980: 1–500. [22] ZHANG L, GONG Z Z, FEI Y W. Shock-induced phase transitions in the MgO-FeO system to 200 GPa [J]. Journal of Physics and Chemistry of Solids, 2008, 699: 2344–2348. doi: 10.1016/j.jpcs.2008.04.006 [23] VASSILIOU M S, AHRENS T J. Hugoniot equation of state of periclase to 200 GPa [J]. Geophysical Research Letters, 1981, 87: 729–732. doi: 10.1029/GL008i007p00729 [24] SVENDSEN B, AHRENS T J. Shock-induced temperatures of MgO [J]. Geophysical Journal International, 1987, 913: 667–691. doi: 10.1111/j.1365-246X.1987.tb01664.x [25] FAT'YANOV O V, ASIMOW P D, AHRENS T J. Thermodynamically complete equation of state of MgO from true radiative shock temperature measurements on samples preheated to 1 850 K [J]. Physical Review B, 2018, 972: 024106. doi: 10.1103/PhysRevB.97.024106 [26] REEBER R R, GOESSEL K, WANG K. Thermal expansion and molar volume of MgO periclase from 5 to 2 900 K [J]. European Journal of Mineralogy, 1995, 75: 1039–1047. doi: 10.1127/ejm/7/5/1039 [27] KONO Y, IRIFUNE T, HIGO Y, et al. P-V-T relation of MgO derived by simultaneous elastic wave velocity and in situ X-ray measurements: a new pressure scale for the mantle transition region [J]. Physics of the Earth and Planetary Interiors, 2010, 183(1/2): 196−211. [28] GARVIN D, PARKER V B, WHITE JR H J. CODATA thermodynamic tables [M]. Washington, USA: Hemisphere Pub, 1987: 1–200. [29] GMELIN E. Thermal properties of alcaline-earth-oxides Ⅰ. specific heat measurements 1-3 centre national de Recherches sur les Tres basses temperatures [J]. Zeitschrift für Naturforschung A, 1969, 2411: 1794–1800. doi: 10.1515/zna-1969-1120 [30] ZHA C S, BASSETT W A, SHIM S H. Rhenium an in situ pressure calibrant for internally heated diamond anvil cells [J]. Review of Scientific Instruments, 2004, 757: 2409–2418. doi: 10.1063/1.1765752 [31] IKUTA D, OHTANI E FUKUI H, et al. Density deficit of Earth’s core revealed by a multimegabar primary pressure scale [J]. Science Advances, 2023, 936: eadh8706. doi: 10.1126/sciadv.adh8706 [32] ZEL’DOVICH Y B, RAIZER Y P. Physics of shock waves and high-temperature hydrodynamic phenomena [M]. New York, USA: Dover Publications, 2002. [33] GELMAN A, RUBIN D B. A single series from the Gibbs sampler provides a false sense of security [M]//BERNARDO J M, BERGER J O, DAWID P, et al. Bayesian Statistics 4: Proceedings of the Fourth Valencia International Meeting Dedicated to the Memory of Morris H. DeGroot 1931–1989. Oxford: Oxford Academic, 1992: 625−632. [34] GOODMAN J, WEARE J. Ensemble samplers with affine invariance [J]. Communications in Applied Mathematics and Computational Science, 2010, 51: 65–80. doi: 10.2140/camcos.2010.5.65 [35] JIN K, LI X Z, WU Q, et al. The pressure-volume-temperature equation of state of MgO derived from shock Hugoniot data and its application as a pressure scale [J]. Journal of Applied Physics, 2010, 10711: 113518. doi: 10.1063/1.3406140 [36] TANGE Y, NISHIHARA Y, TSUCHIYA T. Unified analyses for P-V-T equation of state of MgO: a solution for pressure-scale problems in high P-T experiments [J]. Journal of Geophysical Research: Solid Earth, 2009, 114B3: B03208. [37] DOROGOKUPETS P I, DEWAELE A. Equations of state of MgO Au Pt NaCl-B1 and NaCl-B2: internally consistent high-temperature pressure scales [J]. High Pressure Research, 2007, 274: 431–446. doi: 10.1080/08957950701659700 [38] DUBROVINSKY L, DUBROVINSKAIA N, PRAKAPENKA V B, et al. Implementation of micro-ball nanodiamond anvils for high-pressure studies above 6 Mbar [J]. Nature Communications, 2012, 31: 1163. doi: 10.1038/ncomms2160 [39] LV M B, CHENG Y, QI Y Y, et al. Elastic properties and phonon dispersions of rhenium in hexagonal-close-packed structure under pressure from first principles [J]. Physica B: Condensed Matter, 2012, 4074: 778–783. doi: 10.1016/j.physb.2011.12.024 -






 下载:
下载: