锡的多相物态方程的第一性原理计算研究

陈凯乐; 王越超; 徐远骥; 刘瑜; 咸家伟; 王丽芳; 简单; 刘海风; 宋海峰

doi:10.11858/gywlxb.20251054

锡的多相物态方程的第一性原理计算研究

doi: 10.11858/gywlxb.20251054

陈凯乐^1,,
王越超¹,
徐远骥^2,*, ,,
刘瑜^1,*, ,,
咸家伟¹,
王丽芳¹,
简单³,
刘海风¹,
宋海峰¹

1.
北京应用物理与计算数学研究所计算物理全国重点实验室, 北京　100088
2.
北京科技大学应用物理研究所, 北京　100083
3.
中国工程物理研究院材料研究所表面物理与化学重点实验室, 四川绵阳　621908

基金项目: 国家重点研发计划（2021YFB3501503）；国家自然科学基金（U23A20537）；国家重大科研仪器研制专项（62327804）；计算物理全国重点实验室基金

详细信息

作者简介:
陈凯乐（2000－），男，硕士，主要从事材料物态方程研究. E-mail：chenkaile22@gscaep.ac.cn

通讯作者:
徐远骥（1990－），男，博士，讲师，主要从事高压强关联模拟研究. E-mail：yuanjixu@ustb.edu.cn

刘　瑜（1985－），男，博士，副研究员，主要从事强关联材料平衡态和动力学物性的理论计算与数值模拟研究. E-mail：liu_yu@iapcm.ac.cn

中图分类号: O521.2
计量
- 文章访问数: 384
- HTML全文浏览量: 91
- PDF下载量: 38
出版历程
- 收稿日期: 2025-03-20
- 修回日期: 2025-04-08
- 录用日期: 2025-09-08
- 网络出版日期: 2025-04-23

First-Principles Study on the Multiphase Equation of State of Tin

CHEN Kaile^1
,,
WANG Yuechao¹,
XU Yuanji^{2,*
, ,},
LIU Yu^{1,*
, ,},
XIAN Jiawei¹,
WANG Lifang¹,
JIAN Dan³,
LIU Haifeng¹,
SONG Haifeng¹

1.
National Key Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing 100088, China
2.
Institute for Applied Physics, University of Science and Technology Beijing, Beijing 100083, China
3.
Science and Technology on Surface Physics and Chemistry Laboratory, Institute of Materials, China Academy of Engineering Physics, Mianyang 621908, Sichuan, China

摘要

摘要: 金属锡是高压物理领域研究的热点，也是国防科技领域关注的重要材料。锡具有丰富的物相，无论是基础研究，还是工业应用，锡的多相物态方程和相界都至关重要。采用密度泛函理论结合平均场势方法，系统研究了锡的高温高压多相物态方程、相界、弹性模量、声速和Hugoniot线等，获得了高温高压下锡的多相物态方程，计算得到的β-γ相界、β-Sn的常压声速与实验结果吻合较好。此外，进一步研究了不同密度泛函对锡的高温高压物态方程的影响。结果表明：通过局域密度梯度近似（local density approximation，LDA）和PBEsol泛函得到的主Hugoniot线及常压弹性模量与实验结果具有较好的一致性；与其他泛函相比，通过SCAN（strongly constrained and appropriately normed）泛函描述的相界的偏差较大，但描述的β-Sn的常压声速与实验结果更接近。
- 多相物态方程 /
- 弹性模量 /
- 第一性原理计算 /
- 平均场势
Abstract: Metallic tin is a focal point in high-pressure physics research and a critical material of strategic importance in defense-related technologies. Due to the rich physical phases of tin, it is crucial to study the multiphase equation of state and phase boundaries of tin, whether in basic research or industrial applications. This work systematically investigates the high-temperature and high-pressure multiphase equation of state (EOS), phase boundaries, elastic modulus, sound velocities, and Hugoniot curves of tin using density functional theory (DFT) combined with the mean-field potential (MFP) method. The results not only provide the multiphase EOS of tin under extreme conditions but also demonstrate good agreement with experimental data for the β-γ phase boundary and ambient-pressure sound velocities of β-Sn. Furthermore, this study evaluates the effects of different density functionals (LDA, PBEsol, and SCAN) on the high-pressure EOS. The LDA and PBEsol functionals show superior consistency with experimental Hugoniot curves and ambient-pressure elastic moduli, while the SCAN functional exhibits larger deviations in phase boundary predictions but achieves closer agreement with experimental ambient-pressure sound velocities for β-Sn.
- multiphase equation of state /
- elastic modulus /
- first-principles calculations /
- mean-field potential

HTML全文

图 1 采用4种泛函计算得到的锡的4个相的E-V曲线

Figure 1. Calculated E-V curves of four phases of Sn using four exchange-correlation functionals

下载: 全尺寸图片幻灯片

图 2 采用PBE泛函分别计算4个固相得到的不同压力下的零温态密度

Figure 2. Calculated density of states at 0 K of four ground state at different pressures using PBE exchange-correlation functional

下载: 全尺寸图片幻灯片

图 3 采用4种交换-关联泛函计算得到的锡的不同相相对γ相的焓差随压力的变化曲线

Figure 3. Calculated ΔH-p curves of different phases (relative to γ phase) of Sn using four exchange-correlation functionals

下载: 全尺寸图片幻灯片

图 4 采用4种泛函计算得到零温下锡的4个相的p-V/V₀曲线（V₀为0 GPa下α-Sn的平衡体积）

Figure 4. Calculated p-V/V₀ curves of four different phases of Sn using four exchange-correlation functionals at 0 K(V₀ means equilibrium volume of α-Sn at 0 GPa)

下载: 全尺寸图片幻灯片

图 5 采用PBE泛函计算得到的锡的4个相的c/a随压强的变化

Figure 5. Calculated c/a-p curves of four structure of Sn calculated with PBE exchange-correlation functional

下载: 全尺寸图片幻灯片

图 6 采用4种泛函计算的300 K下Sn的4个相的p-V曲线与实验数据^{[3, 6–8, 67–68]}的对比

Figure 6. Comparision of the calculated p-V curves at 300 K of of four structure of Sn using four exchange-correlation functionals with experimental data^{[3, 6–8, 67–68]}

下载: 全尺寸图片幻灯片

图 7 采用4种泛函计算得到的Sn的β-γ-液相相图和Hugoniot线与实验及理论数据^{[3, 65–66, 69]}的对比

Figure 7. Comparision of calculated β-γ-liquid phase diagram and primary Hugoniot curves of tin using four exchange-correlation functionals with experimental and theoretical data^{[3, 65–66, 69]}

下载: 全尺寸图片幻灯片

图 8 采用4种泛函计算得到的β-Sn和γ-Sn在主Hugoniot线上的粒子速度（u）与冲击波速度（D）的关系与实验数据^[71]的对比

Figure 8. Comparision of calculated D-u curves of β-Sn and γ-Sn on the primary Hugoniot curve using four exchange-correlation functionals with the experimental data^[71]

下载: 全尺寸图片幻灯片

图 9 采用4种泛函计算的0 GPa下α-Sn的体弹模量与实验数据^{[18, 75–76]}的对比

Figure 9. Comparision of bulk modulus of α-Sn at 0 GPa calculated by four exchange-correlation functionals with the experimental data^{[18, 75–76]}

下载: 全尺寸图片幻灯片

图 10 采用4种泛函计算的0 GPa下β-Sn的体弹模量与实验数据^[77–85]的对比

Figure 10. Comparision of calculated bulk modulus of β-Sn at 0 GPa using four exchange-correlation functionals with the experimental data^[77–85]

下载: 全尺寸图片幻灯片

图 11 采用4种泛函计算的1 000 K下γ-Sn和δ-Sn的弹性模量

Figure 11. Calculated bulk modulus of γ-Sn and δ-Sn at 1 000 K using four exchange-correlation functionals

下载: 全尺寸图片幻灯片

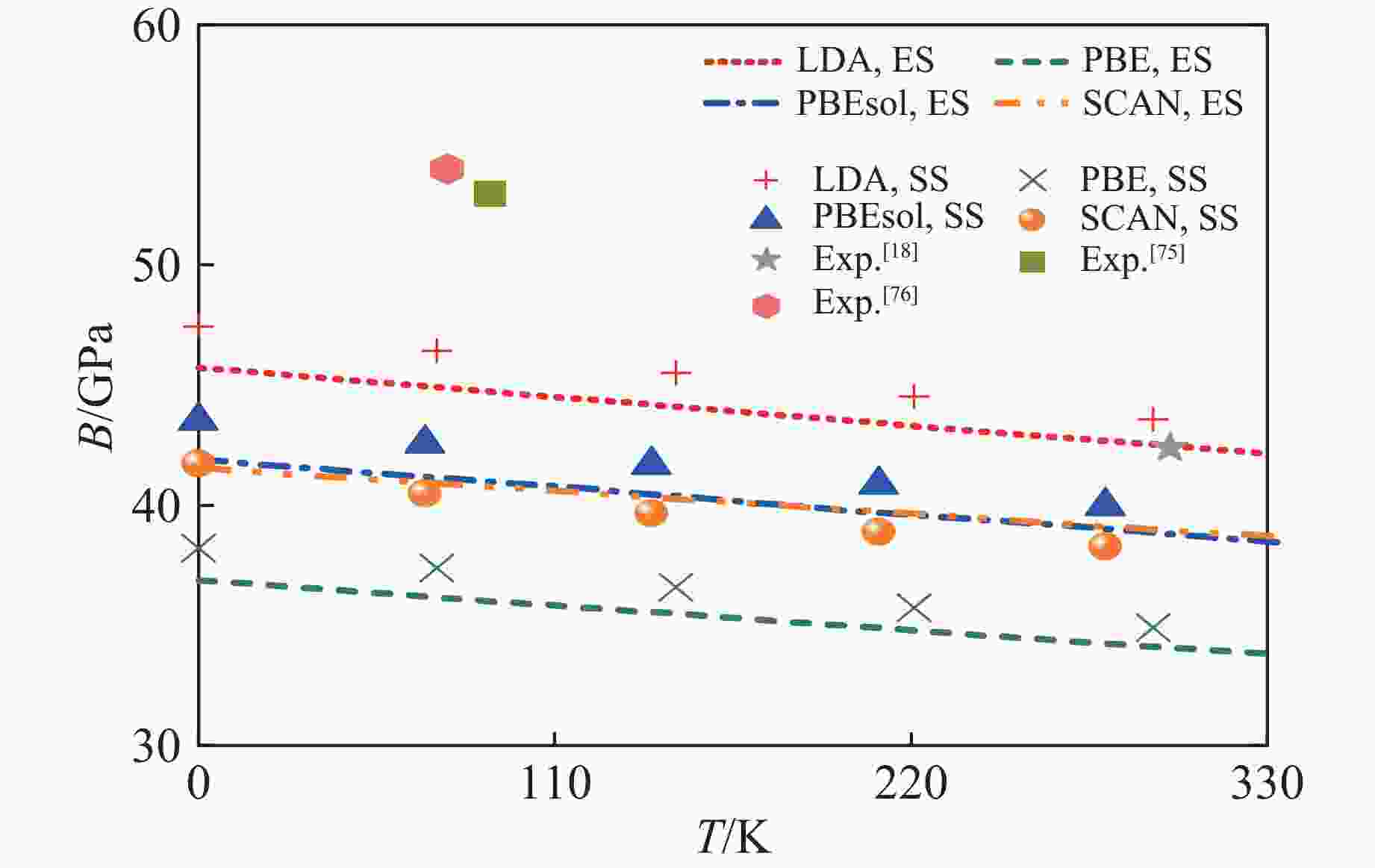
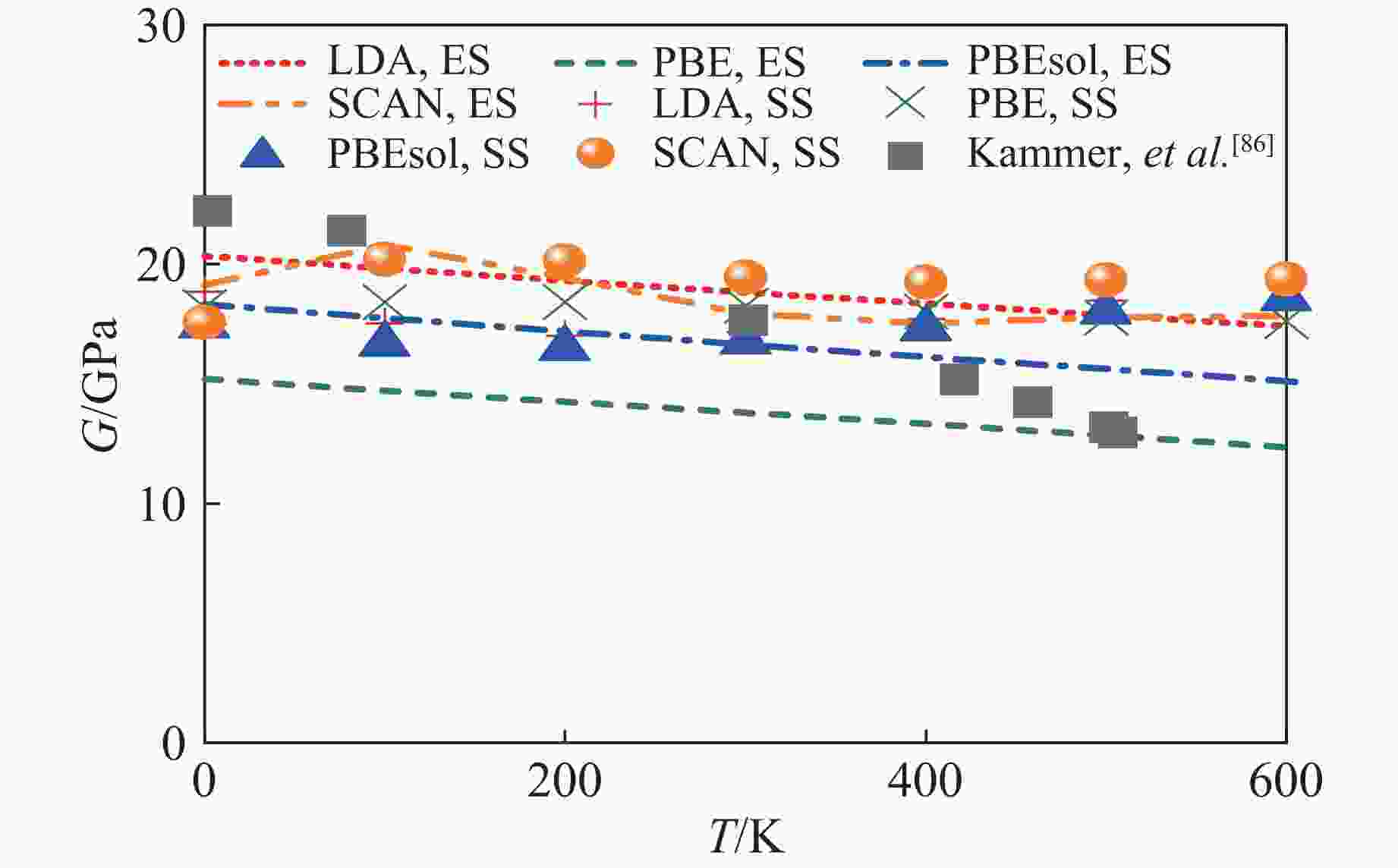
图 12 采用4种泛函计算的0 GPa下β-Sn的剪切模量（对比参考数据为Rehn等^[66]根据Kammer等^[86]得到的弹性常数计算得到）

Figure 12. Calculated shear modulus of β-Sn at 0 GPa using four exchange-correlation functionals (The data used for comparison were from Rehn, et al.^[66], calculated based on the elastic constants obtained from Kammer, et al.^[86])

下载: 全尺寸图片幻灯片

图 13 采用4种泛函计算得到的0 GPa下α-Sn的杨氏模量和泊松比

Figure 13. Calculated Young’s modulus and Possion’s ratio of α-Sn using four exchange-correlation functionals

下载: 全尺寸图片幻灯片

图 14 采用4种泛函结合能量-应变法计算的0 GPa下β-Sn的声速（对比实验数据来自文献[14]）

Figure 14. Calculated sound velocity of β-Sn at 0 GPa using four exchange-correlation functionals combined with energy-strain method (The experimental data used for comparison were from the literature [14])

下载: 全尺寸图片幻灯片

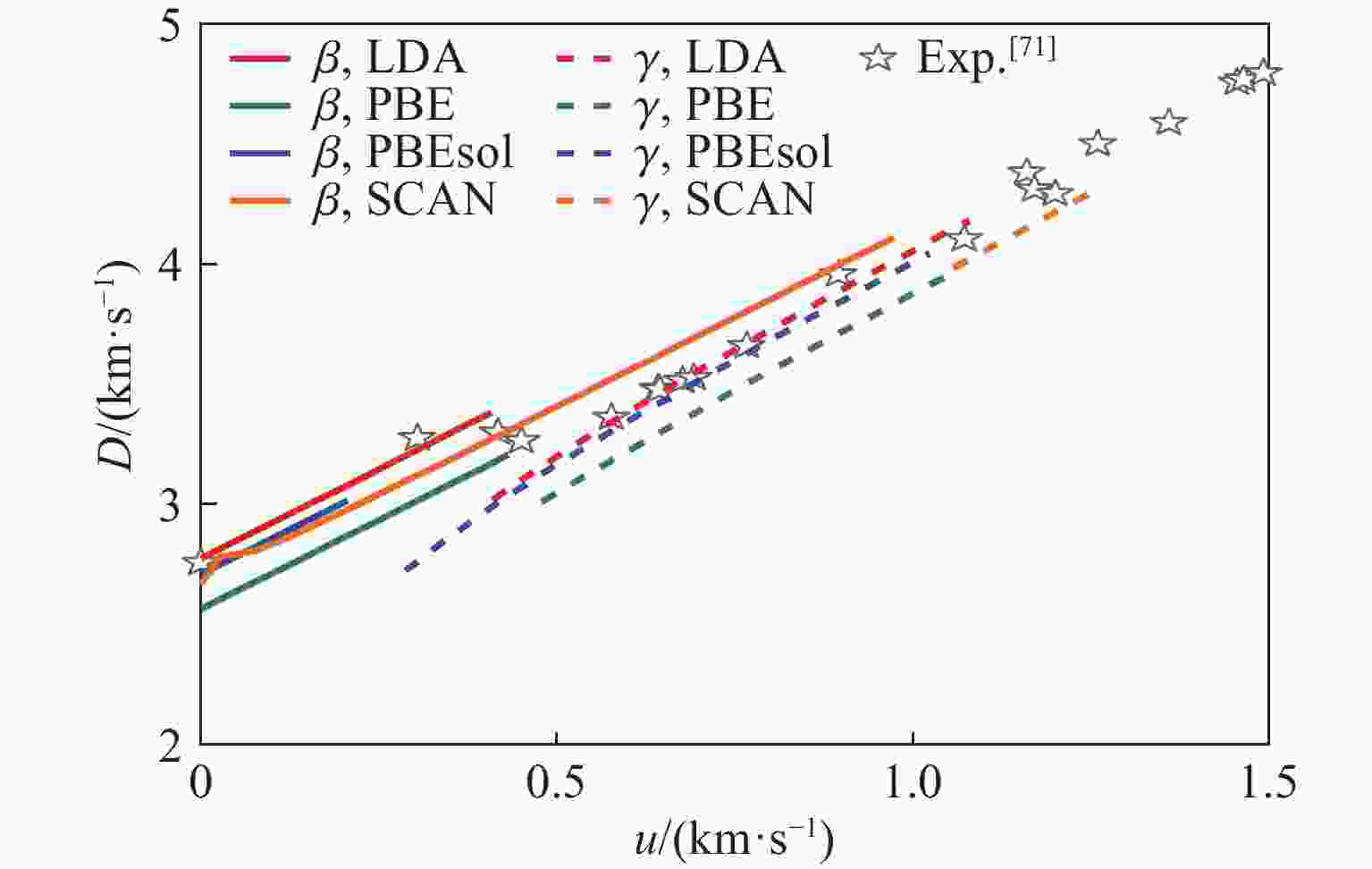
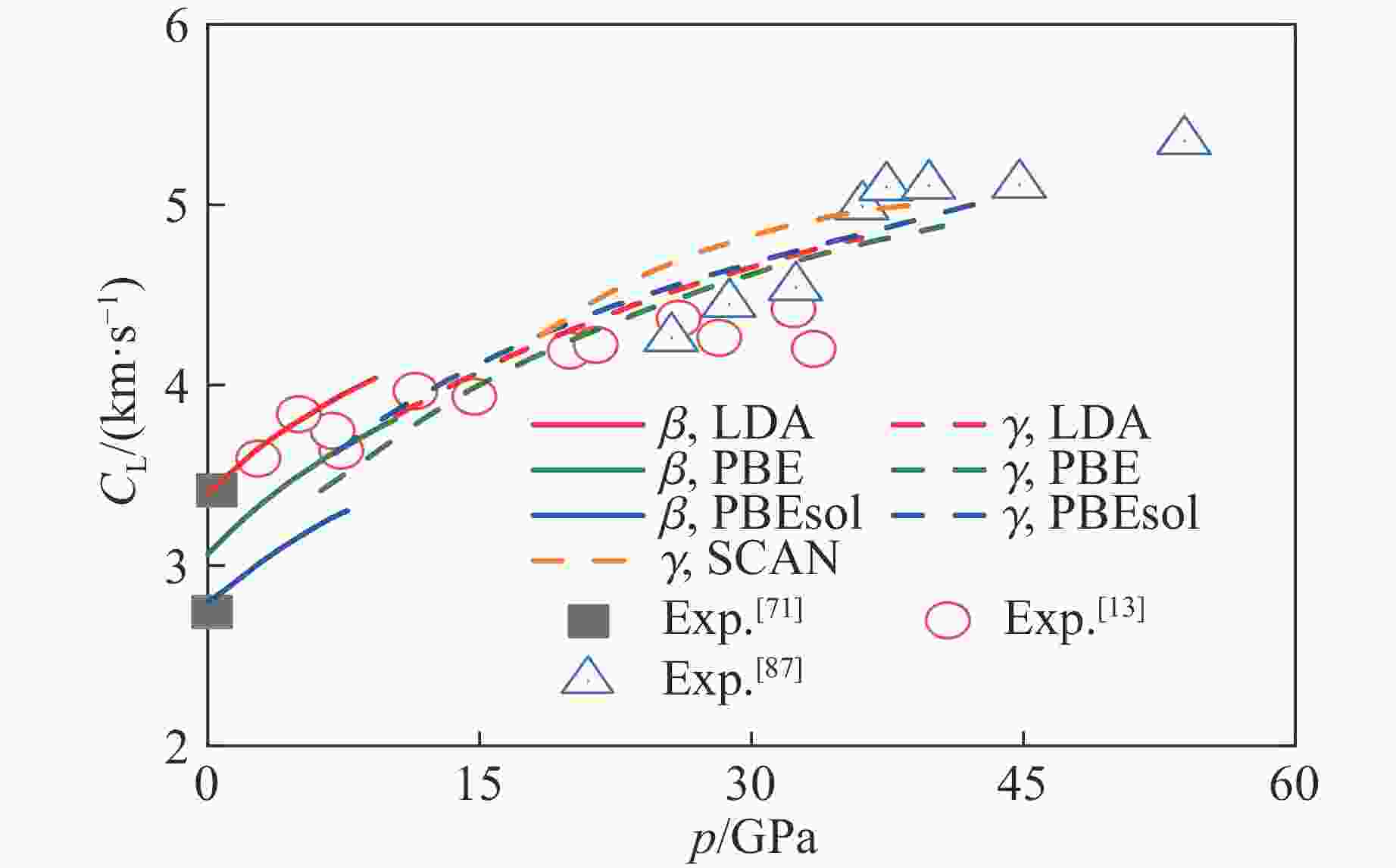
图 15 采用4种泛函结合能量-应变法计算的沿主Hugoniot线的β-Sn和γ-Sn的声速（对比实验数据来自文献[13, 71, 87]）

Figure 15. Calculated sound velocity of β-Sn and γ-Sn along primary Hugoniot curves using four exchange-correlation functionals combined with energy-strain method (The experimental data used for comparison were from the literature [13, 71, 87])

下载: 全尺寸图片幻灯片

表 1 采用不同交换-关联泛函计算得到的零温相变压力

Table 1. Pressures of zero temperature phase transition calculated by different exchange-correlation functional

Method	Phase transition pressure/GPa
Method	α-β	β-γ	γ-δ	δ-ε
LDA^[24]	0.80	23.5		>90
LDA^[25]	0.95	15.9	42.9	163
GGA^[26]	0.70	12.0	45.0	160
SCAN^[27]		16.2

下载: 导出CSV

表 2 基于冷能计算BM方程拟合的结构参数、平衡体积和体积模量

Table 2. Lattice parameters, equilibrium volumes, and bulk modulus from BM equation fitting

Phase	Method	a₀/Å	c₀/a₀	V₀/(Å³/atom)	E₀/(eV/atom)	B₀/GPa	$B'_0 $
	Exp.	6.483^[60]	1.000^[60]	34.06^[60]	3.140^[61]	42.6^[62]
	LDA	6.476	1.000	33.94	3.958	45.0	4.9
α-Sn	PBE	6.654	1.000	36.83	3.152	35.9	4.8
	PBEsol	6.539	1.000	34.95	3.509	41.7	4.8
	SCAN	6.549	1.000	35.11	3.414	41.5	4.6
	Exp.	5.831^[60]	0.546^[60]	27.07^[60]	3.100^[16]	57.0^[62]
	LDA	5.778	0.543	26.19	3.977	60.1	4.8
β-Sn	PBE	5.929	0.544	28.40	3.112	47.6	4.8
	PBEsol	5.827	0.543	26.87	3.536	56.1	4.8
	SCAN	5.868	0.544	27.45	3.335	52.7	4.8
	LDA	3.920	0.854	25.63	3.938	57.0	4.9
	PBE	4.041	0.846	27.80	3.091	45.5	4.9
γ-Sn	PBEsol	3.945	0.859	26.26	3.517	54.3	4.8
	SCAN	3.956	0.866	26.99	3.226	47.3	5.2
	Exp.					76.4^[9]	4.04^[9]
	LDA	3.708	1.000	25.48	3.928	59.4	4.8
δ-Sn	PBE	3.809	1.000	27.63	3.081	47.3	4.8
	PBEsol	3.738	1.000	26.12	3.507	55.8	4.8
	SCAN	3.770	1.000	26.78	3.215	51.4	4.8

下载: 导出CSV

表 3 采用4种交换-关联泛函计算得到的Sn的4个相分别稳定存在的压强范围

Table 3. Calculated stable pressure ranges of the four phases of tin using four different exchange-correlation functionals

Method	Pressure/GPa
Method	α	β	γ	δ
Exp.	0−0.6^[65]	0.6^[65]−9.8^[64]	9.8^[64]−19.0^[63]、50.0^[13]	19^[63]、50^[13]−146^[66]
LDA	Negative	0−10.7	10.7−31.3	31.3−50.0
PBE	0−0.8	0.8−5.3	5.3−21.1	21.1−50.0
PBEsol	Negative	0−5.2	5.2−50.0
SCAN	0−7.1	7.1−30.9		30.9−50.0

下载: 导出CSV

参考文献(87)

[1]	余克章. 锡(Sn)——金属在现代军事上的应用(十四) [J]. 金属世界, 1996(3): 18–19. YU K Z. The use of metals in modern military applications (14): tin (Sn) [J]. Metal World, 1996(3): 18–19.
[2]	BUTTLER W T, WILLIAMS R J R, NAJJAR F M. Foreword to the special issue on ejecta [J]. Journal of Dynamic Behavior of Materials, 2017, 3(2): 151–155. doi: 10.1007/s40870-017-0120-8
[3]	DEFFRENNES G, FAURE P, BOTTIN F, et al. Tin (Sn) at high pressure: review, X-ray diffraction, DFT calculations, and Gibbs energy modeling [J]. Journal of Alloys and Compounds, 2022, 919: 165675. doi: 10.1016/j.jallcom.2022.165675
[4]	CHEN T, YUAN F B, LIU J C, et al. Modeling the high-pressure solid and liquid phases of tin from deep potentials with ab initio accuracy [J]. Physical Review Materials, 2023, 7(5): 053603. doi: 10.1103/PhysRevMaterials.7.053603
[5]	CORNELIUS B, TREIVISH S, ROSENTHAL Y, et al. The phenomenon of tin pest: a review [J]. Microelectronics Reliability, 2017, 79: 175–192. doi: 10.1016/j.microrel.2017.10.030
[6]	SALAMAT A, BRIGGS R, BOUVIER P, et al. High-pressure structural transformations of Sn up to 138 GPa: angle-dispersive synchrotron X-ray diffraction study [J]. Physical Review B, 2013, 88(10): 104104. doi: 10.1103/PhysRevB.88.104104
[7]	LIU M, LIU L G. Compressions and phase transitions of tin to half a megabar [J]. High Temperatures High Pressures, 1986, 18(1): 79–85.
[8]	OLIJNYK H, HOLZAPFEL W B. Phase transitions in Si, Ge and Sn under pressure [J]. Journal de Physique Colloques, 1984, 45(C8): 153–156. doi: 10.1051/jphyscol:1984828
[9]	DESGRENIERS S, VOHRA Y K, RUOFF A L. Tin at high pressure: an energy-dispersive X-ray-diffraction study to 120 GPa [J]. Physical Review B, 1989, 39(14): 10359–10361. doi: 10.1103/PhysRevB.39.10359
[10]	SMIRNOV N A. Ab initio calculations of the phase diagrams of tin and lead under pressures up to a few TPa [J]. Journal of Physics: Condensed Matter, 2021, 33(3): 035402. doi: 10.1088/1361-648X/abbbc5
[11]	MABIRE C, HÉREIL P L. Shock induced polymorphic transition and melting of tin [J]. AIP Conference Proceedings, 2000, 505(1): 93–96. doi: 10.1063/1.1303429
[12]	CHAUVIN C, ZUCCHINI F, DE BARROS D P. Study on phase transformation in tin under dynamic compression [C]//2019 15th Hypervelocity Impact Symposium. Destin: American Society of Mechanical Engineers, 2019: V001T09A006.
[13]	HU J B, ZHOU X M, DAI C D, et al. Shock-induced bct-bcc transition and melting of tin identified by sound velocity measurements [J]. Journal of Applied Physics, 2008, 104(8): 083520. doi: 10.1063/1.3003325
[14]	XU L, BI Y, LI X H, et al. Phase diagram of tin determined by sound velocity measurements on multi-anvil apparatus up to 5 GPa and 800 K [J]. Journal of Applied Physics, 2014, 115(16): 164903. doi: 10.1063/1.4872458
[15]	HAFNER J. Ab initio calculation of the pressure-induced A4→A5→2 (distorted)→A3 phase transitions in tin [J]. Physical Review B, 1974, 10(10): 4151–4160. doi: 10.1103/PhysRevB.10.4151
[16]	IHM J, COHEN M L. Equilibrium properties and the phase transition of grey and white tin [J]. Physical Review B, 1981, 23(4): 1576–1579. doi: 10.1103/PhysRevB.23.1576
[17]	REDDY P J, SUBRAHMANYAM S V. Dependence on temperature of elastic moduli of tin [J]. Nature, 1960, 185(4705): 29. doi: 10.1038/185029a0
[18]	PRICE D L, ROWE J M, NICKLOW R M. Lattice dynamics of grey tin and indium antimonide [J]. Physical Review B, 1971, 3(4): 1268–1279. doi: 10.1103/PhysRevB.3.1268
[19]	CUI S X, CAI L C, FENG W X, et al. First-principles study of phase transition of tin and lead under high pressure [J]. Physica Status Solidi (b), 2008, 245(1): 53–57. doi: 10.1002/pssb.200743240
[20]	CHEN C C, APPLETON R J, NYKIEL K, et al. How accurate is density functional theory at high pressures? [J]. Computational Materials Science, 2025, 247: 113458. doi: 10.1016/j.commatsci.2024.113458
[21]	PERDEW J P, RUZSINSZKY A, CSONKA G I, et al. Restoring the density-gradient expansion for exchange in solids and surfaces [J]. Physical Review Letters, 2008, 100(13): 136406. doi: 10.1103/PhysRevLett.100.136406
[22]	KOHN W, SHAM L J. Self-consistent equations including exchange and correlation effects [J]. Physical Review, 1965, 140(4A): A1133–A1138. doi: 10.1103/PhysRev.140.A1133
[23]	PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [Phys. Rev. Lett. 77, 3865 (1996)] [J]. Physical Review Letters, 1997, 78(7): 1396. doi: 10.1103/PhysRevLett.78.1396
[24]	CORKILL J L, GARCA A, COHEN M L. Theoretical study of high-pressure phases of tin [J]. Physical Review B, 1991, 43(11): 9251–9254. doi: 10.1103/PhysRevB.43.9251
[25]	AGUADO A. First-principles study of elastic properties and pressure-induced phase transitions of Sn: LDA versus GGA results [J]. Physical Review B, 2003, 67(21): 212104. doi: 10.1103/PhysRevB.67.212104
[26]	YU C, LIU J Y, LU H, et al. Ab initio calculation of the properties and pressure induced transition of Sn [J]. Solid State Communications, 2006, 140(11/12): 538–543. doi: 10.1016/j.ssc.2006.09.026
[27]	SHAHI C, SUN J W, PERDEW J P. Accurate critical pressures for structural phase transitions of group Ⅳ, Ⅲ-Ⅴ, and Ⅱ-Ⅵ compounds from the SCAN density functional [J]. Physical Review B, 2018, 97(9): 094111. doi: 10.1103/PhysRevB.97.094111
[28]	ZHANG L, LI Y H, YU Y Y, et al. General construction of mean-field potential and its application to the multiphase equations of state of tin [J]. Physica B: Condensed Matter, 2011, 406(22): 4163–4169. doi: 10.1016/j.physb.2011.01.018
[29]	KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Physical Review B, 1999, 59(3): 1758–1775. doi: 10.1103/PhysRevB.59.1758
[30]	DONG W, KRESSE G, FURTHMÜLLER J, et al. Chemisorption of H on Pd(111): an ab initio approach with ultrasoft pseudopotentials [J]. Physical Review B, 1996, 54(3): 2157–2166. doi: 10.1103/PhysRevB.54.2157
[31]	KRESSE G, FURTHMÜLLER J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set [J]. Computational Materials Science, 1996, 6(1): 15–50. doi: 10.1016/0927-0256(96)00008-0
[32]	MONKHORST H J, PACK J D. Special points for Brillouin-zone integrations [J]. Physical Review B, 1976, 13(12): 5188–5192. doi: 10.1103/PhysRevB.13.5188
[33]	BLÖCHL P E. Projector augmented-wave method [J]. Physical Review B, 1994, 50(24): 17953–17979. doi: 10.1103/PhysRevB.50.17953
[34]	SUN J W, RUZSINSZKY A, PERDEW J P. Strongly constrained and appropriately normed semilocal density functional [J]. Physical Review Letters, 2015, 115(3): 036402. doi: 10.1103/PhysRevLett.115.036402
[35]	METHFESSEL M, PAXTON A T. High-precision sampling for Brillouin-zone integration in metals [J]. Physical Review B, 1989, 40(6): 3616–3621. doi: 10.1103/PhysRevB.40.3616
[36]	WANG Y. Classical mean-field approach for thermodynamics: ab initio thermophysical properties of cerium [J]. Physical Review B, 2000, 61(18): R11863–R11866. doi: 10.1103/PhysRevB.61.R11863
[37]	WANG Y, LI L. Mean-field potential approach to thermodynamic properties of metal: Al as a prototype [J]. Physical Review B, 2000, 62(1): 196–202. doi: 10.1103/PhysRevB.62.196
[38]	WANG Y, AHUJA R, JOHANSSON B. Mean-field potential approach to the quasiharmonic theory of solids [J]. International Journal of Quantum Chemistry, 2004, 96(5): 501–506. doi: 10.1002/qua.10769
[39]	WANG Y, AHUJA R, JOHANSSON B. Melting of iron and other metals at Earth’s core conditions: a simplified computational approach [J]. Physical Review B, 2001, 65(1): 014104. doi: 10.1103/PhysRevB.65.014104
[40]	SLATER J C. Introduction to chemical physics [M]. New York: McGraw-Hill, 1939.
[41]	DUGDALE J S, MACDONALD D K C. The thermal expansion of solids [J]. Physical Review, 1953, 89(4): 832–834. doi: 10.1103/PhysRev.89.832
[42]	VASHCHENKO V Y, ZUBAREV V N. Concerning the Grüneisen constant [J]. Soviet Physics-Solid State, 1963, 5: 653–655.
[43]	SONG H F, LIU H F. Modified mean-field potential approach to thermodynamic properties of a low-symmetry crystal: beryllium as a prototype [J]. Physical Review B, 2007, 75(24): 245126. doi: 10.1103/PhysRevB.75.245126
[44]	SONG H F, TIAN M F, LIU H F, et al. Theoretical study on equation of state of porous Mo and Sn [J]. Chinese Physics Letters, 2014, 31(1): 016402. doi: 10.1088/0256-307X/31/1/016402
[45]	WANG W Y, ZHANG S Y, LI G N, et al. Artificial intelligence enabled smart design and manufacturing of advanced materials: the endless Frontier in Al⁺ era [J]. Materials Genome Engineering Advances, 2024, 2(3): e56. doi: 10.1002/mgea.56
[46]	YU W, CHONG X Y, LIANG Y X, et al. Discovering novel γ-γ′ Pt-Al superalloys via lattice stability in Pt₃Al induced by local atomic environment distortion [J]. Acta Materialia, 2024, 281: 120413. doi: 10.1016/j.actamat.2024.120413
[47]	HAFNER J. Materials simulations using VASP—a quantum perspective to materials science [J]. Computer Physics Communications, 2007, 177(1/2): 6–13. doi: 10.1016/j.cpc.2007.02.045
[48]	ZHANG Q L, ZHANG P, SONG H F, et al. Mean-field potential calculations of high-pressure equation of state for BeO [J]. Chinese Physics B, 2008, 17(4): 1341–1348. doi: 10.1088/1674-1056/17/4/031
[49]	陈惠发, SALIPU A F. 弹性与塑性力学 [M]. 余天庆, 王勋文, 刘再华, 译. 北京: 中国建筑工业出版社, 2004. CHEN H F, SALIPU A F. Elasticity and plasticity [M]. Translated by YU T Q, WANG X W, LIU Z H. Beijing: China Architecture Publishing & Building Press, 2004.
[50]	简单. 铀和二氧化铀状态方程与弹性模量计算 [D]. 绵阳: 中国工程物理研究院, 2020. JIAN D. Calculation of equations of state and elastic modulus of uranium and uranium dioxide [D]. Mianyang: China Academy of Engineering Physics, 2020.
[51]	SWENSON C A. Equation of state of cubic solids; some generalizations [J]. Journal of Physics and Chemistry of Solids, 1968, 29(8): 1337–1348. doi: 10.1016/0022-3697(68)90185-6
[52]	WANG Y, WANG J J, ZHANG H, et al. A first-principles approach to finite temperature elastic constants [J]. Journal of Physics: Condensed Matter, 2010, 22(22): 225404. doi: 10.1088/0953-8984/22/22/225404
[53]	VOIGT W J T L. A determination of the elastic constants for beta-quartz lehrbuch de kristallphysik [J]. Terubner Leipzig, 1928, 40: 2856–2860.
[54]	REUSS A. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals [J]. Zeitschrift fur Angewandte Mathematik und Mechanik, 1929, 9: 49–58. doi: 10.1002/zamm.19290090104
[55]	谭华. 实验冲击波物理导引 [M]. 北京: 国防工业出版社, 2007. TAN H. Introduction to experimental shock-wave physics [M]. Beijing: National Defense Industry Press, 2007.
[56]	经福谦. 实验物态方程导引 [M]. 2版. 北京: 科学出版社, 1999. JING F Q. Introduction to experimental equation of state [M]. 2nd ed. Beijing: Science Press, 1999.
[57]	CHEN S, SUN Y, DUAN Y H, et al. Phase stability, structural and elastic properties of C15-type Laves transition-metal compounds MCo₂ from first-principles calculations [J]. Journal of Alloys and Compounds, 2015, 630: 202–208. doi: 10.1016/j.jallcom.2015.01.038
[58]	FENG J, XIAO B, WAN C L, et al. Electronic structure, mechanical properties and thermal conductivity of Ln₂Zr₂O₇ (Ln=La, Pr, Nd, Sm, Eu and Gd) pyrochlore [J]. Acta Materialia, 2011, 59(4): 1742–1760. doi: 10.1016/j.actamat.2010.11.041
[59]	BIRCH F. Finite elastic strain of cubic crystals [J]. Physical Review, 1947, 71(11): 809–824. doi: 10.1103/PhysRev.71.809
[60]	BARRETT C S, MASSALSKI T B. Structure of metals: crystallographic methods, principles and data [M]. 3rd ed. Oxford: Pergamon, 1980.
[61]	KITTEL C. Introduction to solid state physics [M]. New York: Wiley, 1976.
[62]	BRANDES E A, BROOK G B. Smithells metals reference book [M]. 7th ed. Oxford: Butterworth-Heinemann, 2013.
[63]	CHEONG B H, CHANG K J. First-principles study of the structural properties of Sn under pressure [J]. Physical Review B, 1991, 44(9): 4103–4108. doi: 10.1103/PhysRevB.44.4103
[64]	TONKOV E Y, PONYATOVSKY E G. Phase transformations of elements under high pressure [M]. Boca Raton: CRC Press, 2005.
[65]	BARNETT J D, BEAN V E, HALL H T. X-ray diffraction studies on tin to 100 kilobars [J]. Journal of Applied Physics, 1966, 37(2): 875–877. doi: 10.1063/1.1708275
[66]	REHN D A, GREEFF C W, BURAKOVSKY L, et al. Multiphase tin equation of state using density functional theory [J]. Physical Review B, 2021, 103(18): 184102. doi: 10.1103/PhysRevB.103.184102
[67]	SALAMAT A, GARBARINO G, DEWAELE A, et al. Dense close-packed phase of tin above 157 GPa observed experimentally via angle-dispersive X-ray diffraction [J]. Physical Review B, 2011, 84(14): 140104. doi: 10.1103/PhysRevB.84.140104
[68]	RAMBERT N, SITAUD B, FAURE P. Equation d’état multiphase et courbe de fusion de l’étain sous pression: une nouvelle approche expérimentale: rapport CEA A-22F00-00-10 [R]. Gif-sur-Yvette: CEA, 2003.
[69]	FRÉVILLE R, DEWAELE A, GUIGNOT N, et al. High-pressure-high-temperature phase diagram of tin [J]. Physical Review B, 2024, 109(10): 104116. doi: 10.1103/PhysRevB.109.104116
[70]	KIEFER B, DUFFY T S, UCHIDA T, et al. Melting of tin at high pressures [EB/OL]. [2025-04-05]. https://www.researchgate.net/publication/267709650_Melting_of_Tin_at_High_Pressures.
[71]	MARSH S P. LASL shock Hugoniot data [M]. Berkeley : University of California Press, 1980.
[72]	BORN M. On the stability of crystal lattices. I [J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1940, 36(2): 160–172. doi: 10.1017/S0305004100017138
[73]	BORN M, HUANG K. Dynamical theory of crystal lattices [M]. New York: Oxford University Press, 1996.
[74]	MOUHAT F, COUDERT F X. Necessary and sufficient elastic stability conditions in various crystal systems [J]. Physical Review B, 2014, 90(22): 224104. doi: 10.1103/PhysRevB.90.224104
[75]	PRICE D L, ROWE J M. The crystal dynamics of grey (α) tin at 90 °K [J]. Solid State Communications, 1969, 7(19): 1433–1438. doi: 10.1016/0038-1098(69)90318-4
[76]	BUCHENAUER C J, CARDONA M, POLLAK F H. Raman scattering in gray tin [J]. Physical Review B, 1971, 3(4): 1243–1244. doi: 10.1103/PhysRevB.3.1243
[77]	BRIDGMAN P W. The compressibility of thirty metals as a function of pressure and temperature [J]. Proceedings of the American Academy of Arts and Sciences, 1923, 58(5): 165–242. doi: 10.2307/20025987
[78]	BRIDGMAN P W. The viscosity of liquids under pressure [J]. Proceedings of the National Academy of Sciences of the United States of America, 1925, 11(10): 603–606. doi: 10.1073/pnas.11.10.603
[79]	PRASAD S C, WOOSTER W A. The study of the elastic constants of white tin by diffuse X-ray reflexion [J]. Acta Crystallographica, 1955, 8(11): 682–686. doi: 10.1107/S0365110X55002119
[80]	MASON W P, BÖMMEL H E. Ultrasonic attenuation at low temperatures for metals in the normal and superconducting states [J]. The Journal of the Acoustical Society of America, 1956, 28(5): 930–943. doi: 10.1121/1.1908524
[81]	HOUSE D G, VERNON E V. Determination of the elastic moduli of tin single crystals, and their variation with temperature [J]. British Journal of Applied Physics, 1960, 11(6): 254–259. doi: 10.1088/0508-3443/11/6/308
[82]	CARDINAL L C. NRL problem No: F03-01 [R]. Washington D C, USA: Naval Research Laboratory, 1963: 31.
[83]	KRAMER W, NÖLTING J. Anomale spezifische wärmen und fehlordnung der metalle indium, zinn, blei, zink, antimon und aluminium [J]. Acta Metallurgica, 1972, 20(12): 1353–1359. doi: 10.1016/0001-6160(72)90070-3
[84]	DU X P, ZHAO J C. Facile measurement of single-crystal elastic constants from polycrystalline samples [J]. NPJ Computational Materials, 2017, 3(1): 17. doi: 10.1038/s41524-017-0019-x
[85]	RAYNE J A, CHANDRASEKHAR B S. Elastic constants of beta tin from 4.2 K to 300 K [J]. Physical Review, 1960, 120(5): 1658–1663. doi: 10.1103/PhysRev.120.1658
[86]	KAMMER E W, CARDINAL L C, VOLD C L, et al. The elastic constants for single-crystal bismuth and tin from room temperature to the melting point [J]. Journal of Physics and Chemistry of Solids, 1972, 33(10): 1891–1898. doi: 10.1016/S0022-3697(72)80487-6
[87]	FURNISH M D, THADHANI N N, HORIE Y. Shock compression of condensed matter 2001 [C]//Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter. Melville: American Institute of Physics, 2002.