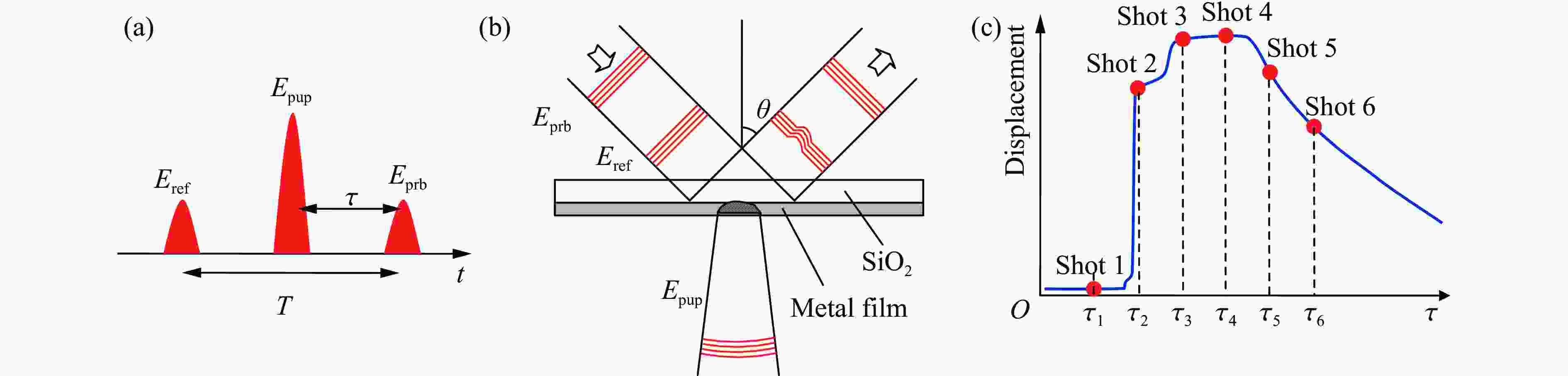
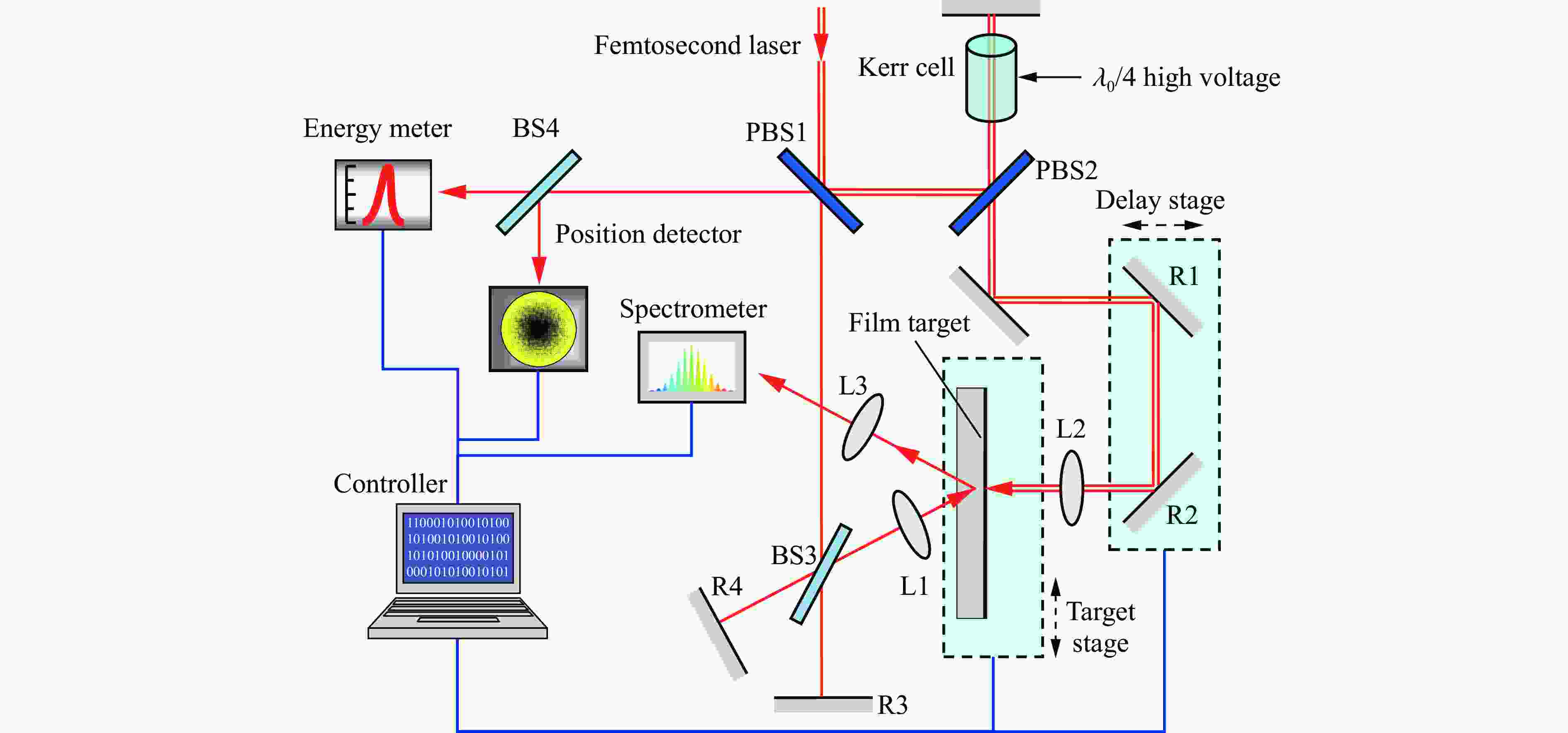
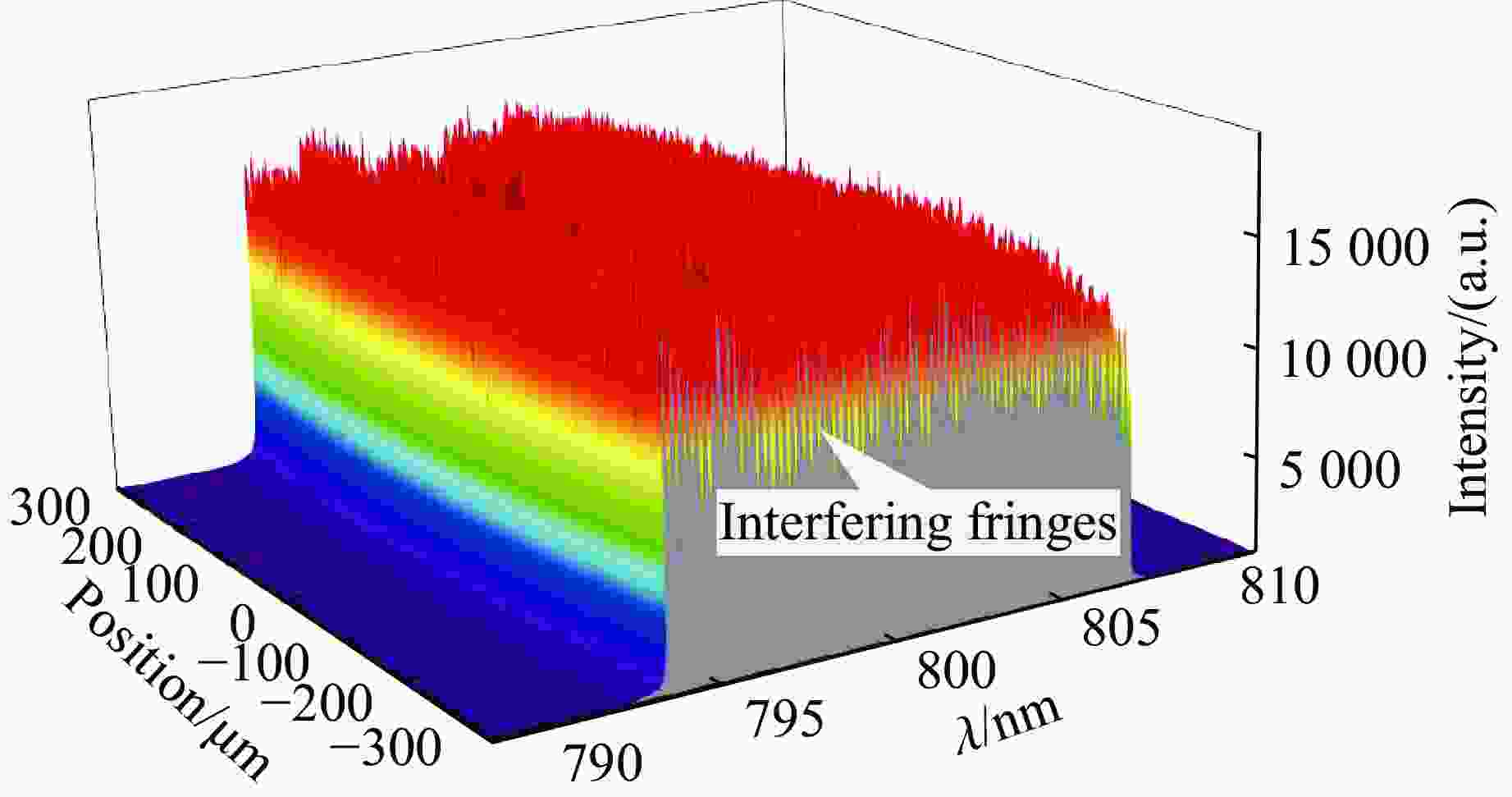
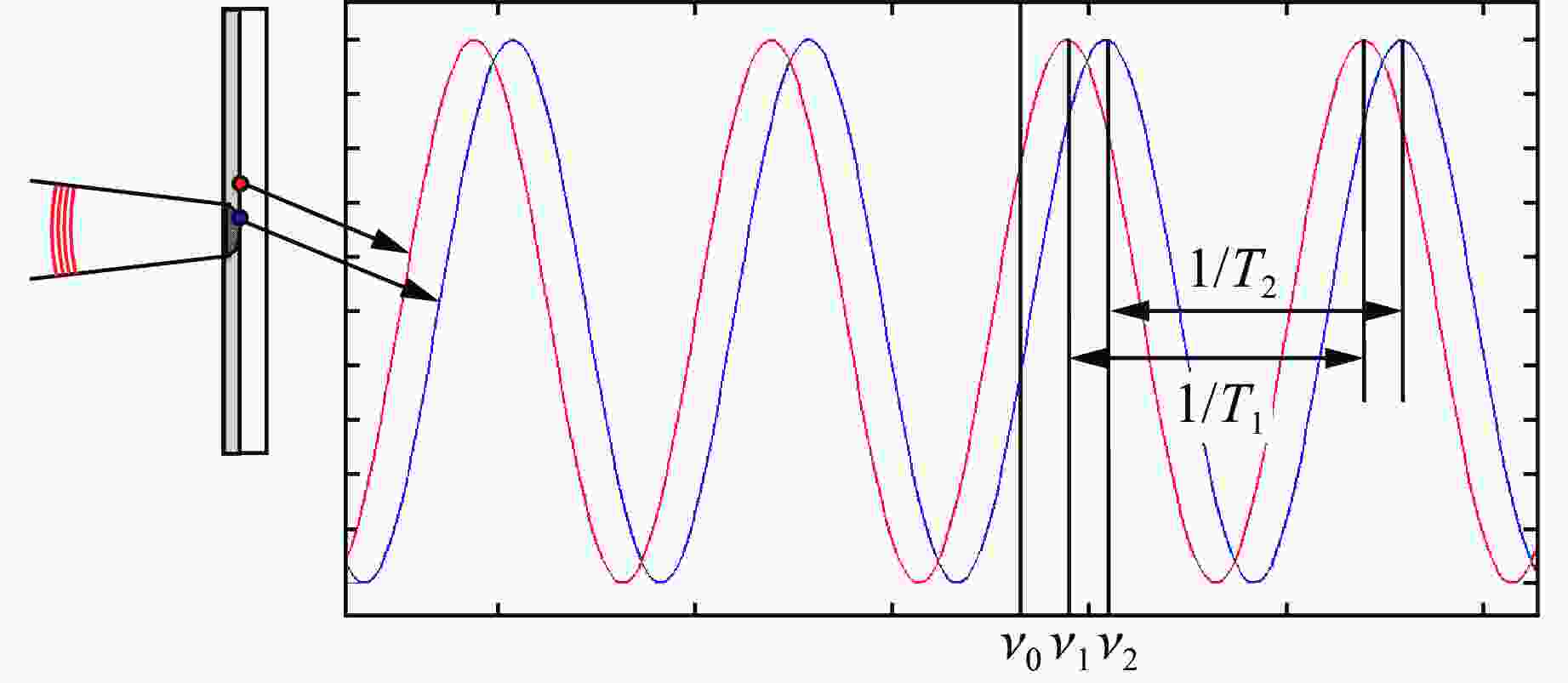
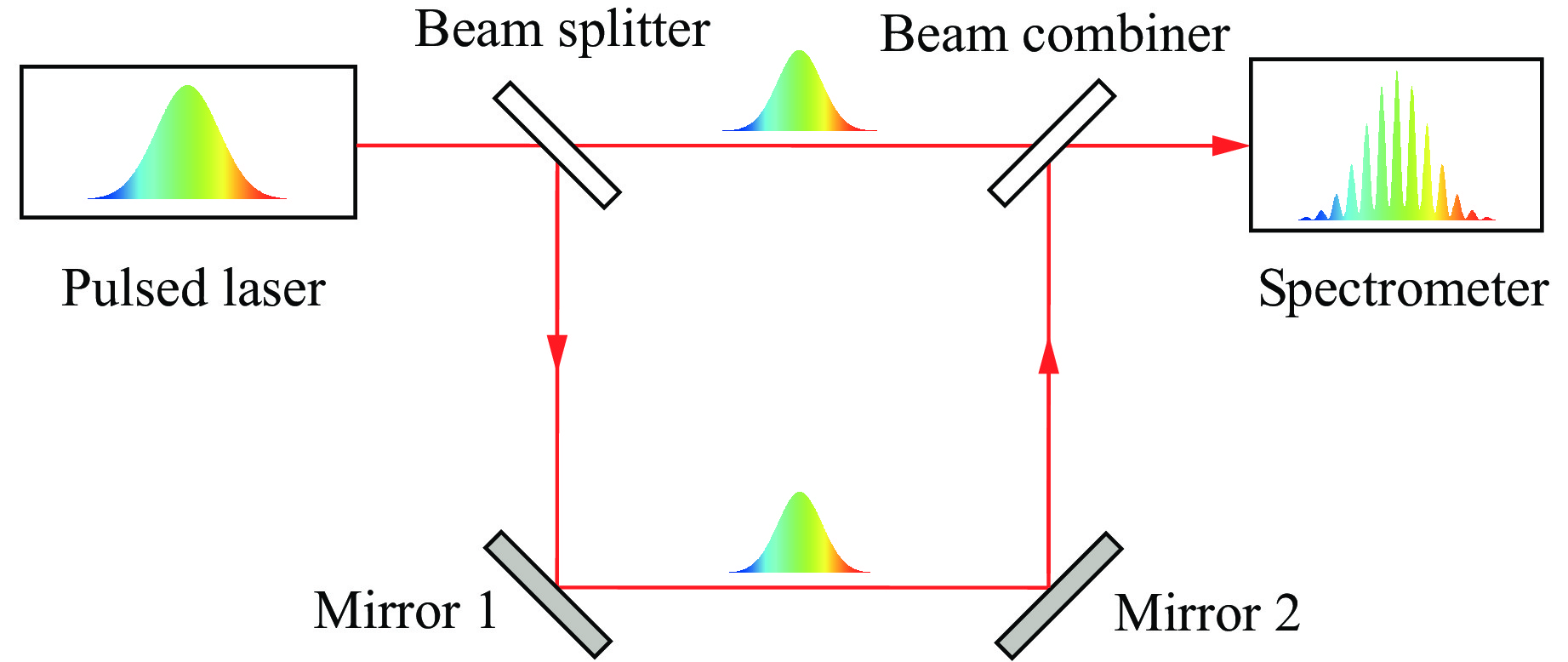
| [1] |
经福谦. 实验物态方程导引 [M]. 2版. 北京: 科学出版社, 1999.JING F Q. Introduction to experimental equation of state [M]. 2nd ed. Beijing: Science Press, 1999.
|
| [2] |
吴先前, 黄晨光. 强激光驱动爆炸与冲击效应 [J]. 强激光与粒子束, 2022, 34: 011003. doi: 10.11884/HPLPB202234.210326WU X Q, HUANG C G. Laser driven explosion and shock wave: a review [J]. High Power Laser and Particle Beams, 2022, 34: 011003. doi: 10.11884/HPLPB202234.210326
|
| [3] |
TOKUNAGA E, TERASAKI A, KOBAYASHI T. Frequency-domain interferometer for femtosecond time-resolved phase spectroscopy [J]. Optics Letters, 1992, 17(16): 1131–1133. doi: 10.1364/OL.17.001131
|
| [4] |
EVANS R, BADGER A D, FALLIÈS F, et al. Time- and space-resolved optical probing of femtosecond-laser-driven shock waves in aluminum [J]. Physical Review Letters, 1996, 77(16): 3359–3362. doi: 10.1103/PhysRevLett.77.3359
|
| [5] |
SALIÈRES P, DEROFF L L, AUGUSTE T, et al. Frequency-domain interferometry in the XUV with high-order harmonics [J]. Physical Review Letters, 1999, 83(26): 5483–5486. doi: 10.1103/PhysRevLett.83.5483
|
| [6] |
GAHAGAN K T, MOORE D S, FUNK D J, et al. Measurement of shock wave rise times in metal thin films [J]. Physical Review Letters, 2000, 85(15): 3205–3208. doi: 10.1103/PhysRevLett.85.3205
|
| [7] |
MOORE D S, GAHAGAN K T, BUELOW S T, et al. Time-and space-resolved optical probing of the shock rise time in thin aluminum films [J]. Shock Compression of Condensed Matter, 1999, 505(1): 1003–1006.
|
| [8] |
FUNK D J, MOORE D S, GAHAGAN K T, et al. Ultrafast measurement of the optical properties of aluminum during shock-wave breakout [J]. Physical Review B, 2001, 64(11): 115114. doi: 10.1103/PhysRevB.64.115114
|
| [9] |
MOORE D S, GAHAGAN K T, REHO J H, et al. Ultrafast nonlinear optical method for generation of planar shocks [J]. Applied Physics Letters, 2001, 78(1): 40–42. doi: 10.1063/1.1337629
|
| [10] |
CHEN J P, LI R X, ZENG Z N, et al. Experimental EOS determination of aluminum at Mbar pressure [J]. Science in China Series G: Physics, Mechanics and Astronomy, 2004, 47(4): 416–423. doi: 10.1360/03yw0059
|
| [11] |
HUANG L, YANG Y Q, WANG Y H, et al. Measurement of transit time for femtosecond-laser-driven shock wave through aluminium films by ultrafast microscopy [J]. Journal of Physics D: Applied Physics, 2009, 42(4): 045502. doi: 10.1088/0022-3727/42/4/045502
|
| [12] |
翁继东. 超快脉冲激光干涉技术及其在冲击动力学过程诊断中的应用[D]. 绵阳: 中国工程物理研究院, 2010.
|
| [13] |
WALSH J M, RICE M H, MCQUEEN P G, et al. Shock-wave compressions of twenty-seven metals: equations of state of metals [J]. Physical Review Journals Archive, 1957, 108(2): 196–216.
|
| [14] |
SESAME. The Los Alamos National Laboratory equation of state database: LA-UR-92-3407 [R]. Los Alamos, USA: Los Alamos National Laboratory, 1992.
|






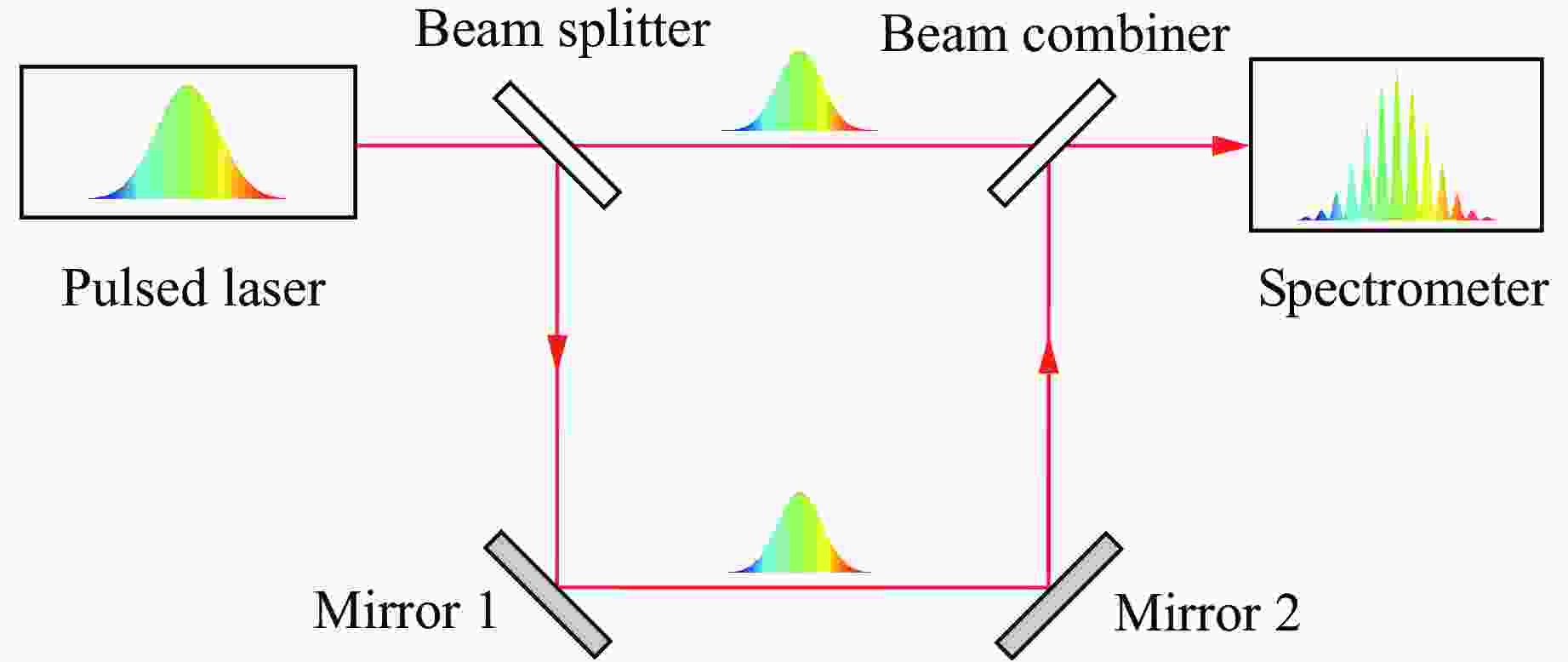
 下载:
下载: