基于颗粒流软件探究不同CFRP布层数对轴压煤圆柱能量演化的影响

李庆文; 潘创创; 张学磊; 钟宇奇; 李玲; 聂帆帆; 李雯霞; 徐梦娇

doi:10.11858/gywlxb.20240931

基于颗粒流软件探究不同CFRP布层数对轴压煤圆柱能量演化的影响

doi: 10.11858/gywlxb.20240931

1.
辽宁工业大学土木建筑工程学院, 辽宁锦州　121001
2.
中国建筑材料工业地质勘查中心辽宁总队, 辽宁沈阳　110004

基金项目: 辽宁省自然科学基金（2023-MS-298，20180550297）；辽宁省教育厅基本科研面上项目（JYTMS20230866）；辽宁省博士科研启动基金（2019-BS-120）

详细信息

作者简介:
李庆文（1987－），男，博士，副教授，主要从事岩石力学、新材料与新型组合结构及离散元-有限差分跨尺度耦合细观模拟研究. E-mail：lgjzlqw@163.com

通讯作者:
潘创创（1997－），男，硕士研究生，主要从事计算颗粒力学研究. E-mail：panguoguo0602@163.com

中图分类号: TU45; O521.9
计量
- 文章访问数: 86
- HTML全文浏览量: 35
- PDF下载量: 22
出版历程
- 收稿日期: 2024-11-05
- 修回日期: 2024-11-22
- 网络出版日期: 2025-03-25
- 刊出日期: 2025-04-05

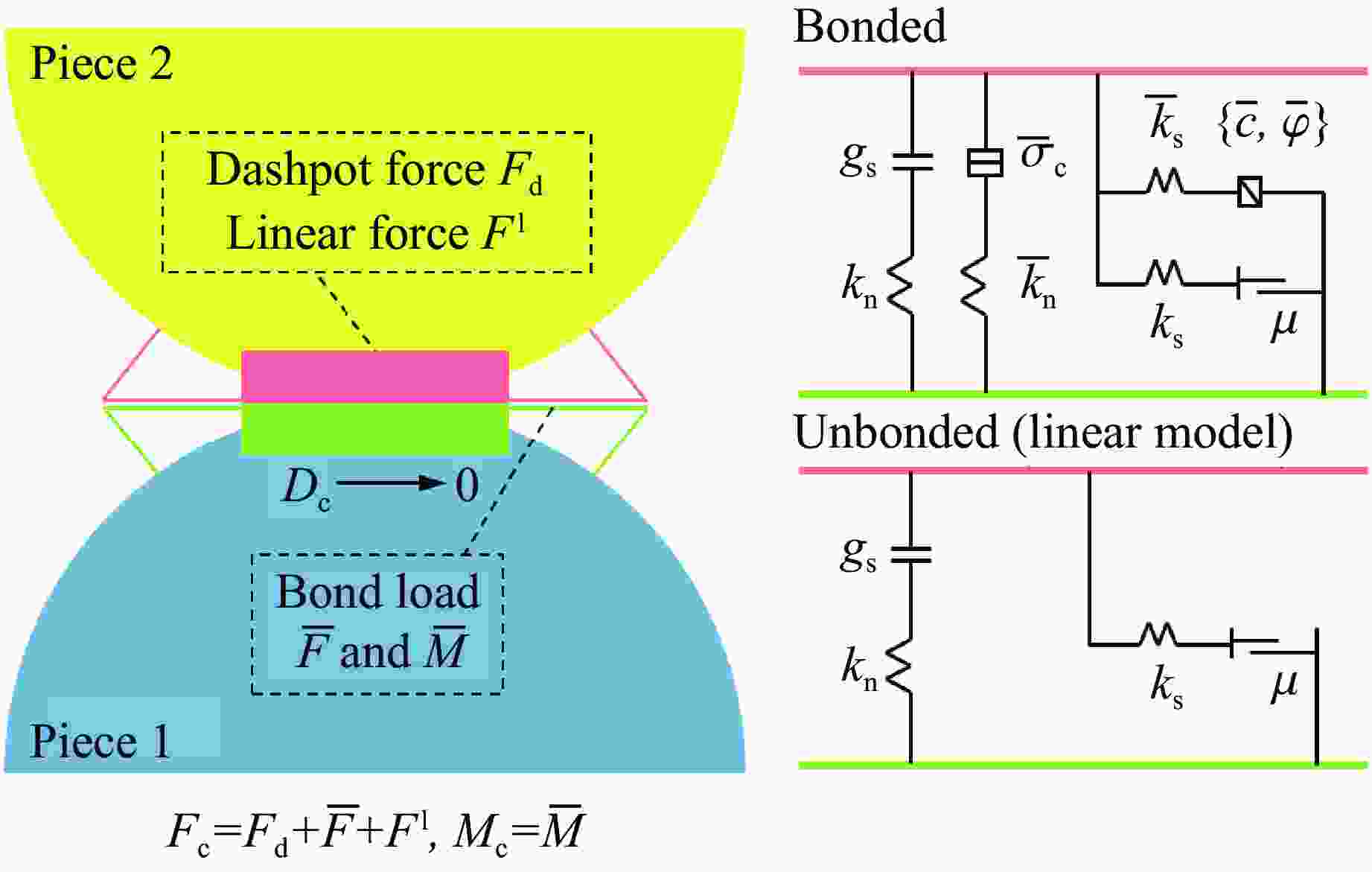
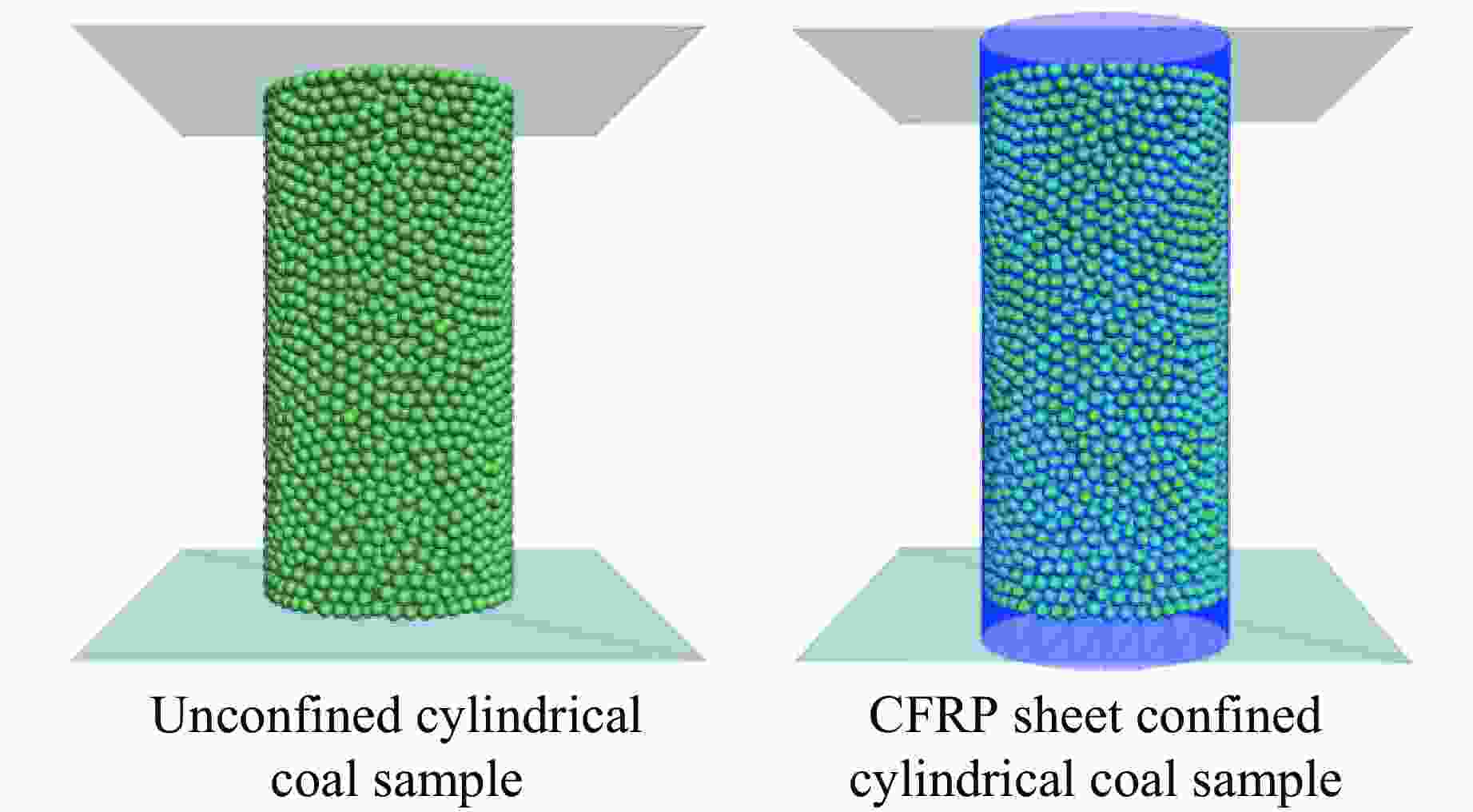
Effect of CFRP Layers on the Energy Evolution of Axial Compressed Cylindrical Coal Based on Particle Flow Software

1.
School of Civil and Architectural Engineering, Liaoning University of Technology, Jinzhou 121001, Liaoning, China
2.
China Building Materials Industry Geologic Exploration Center Liaoning Branch, Shenyang 110004, Liaoning, China

摘要

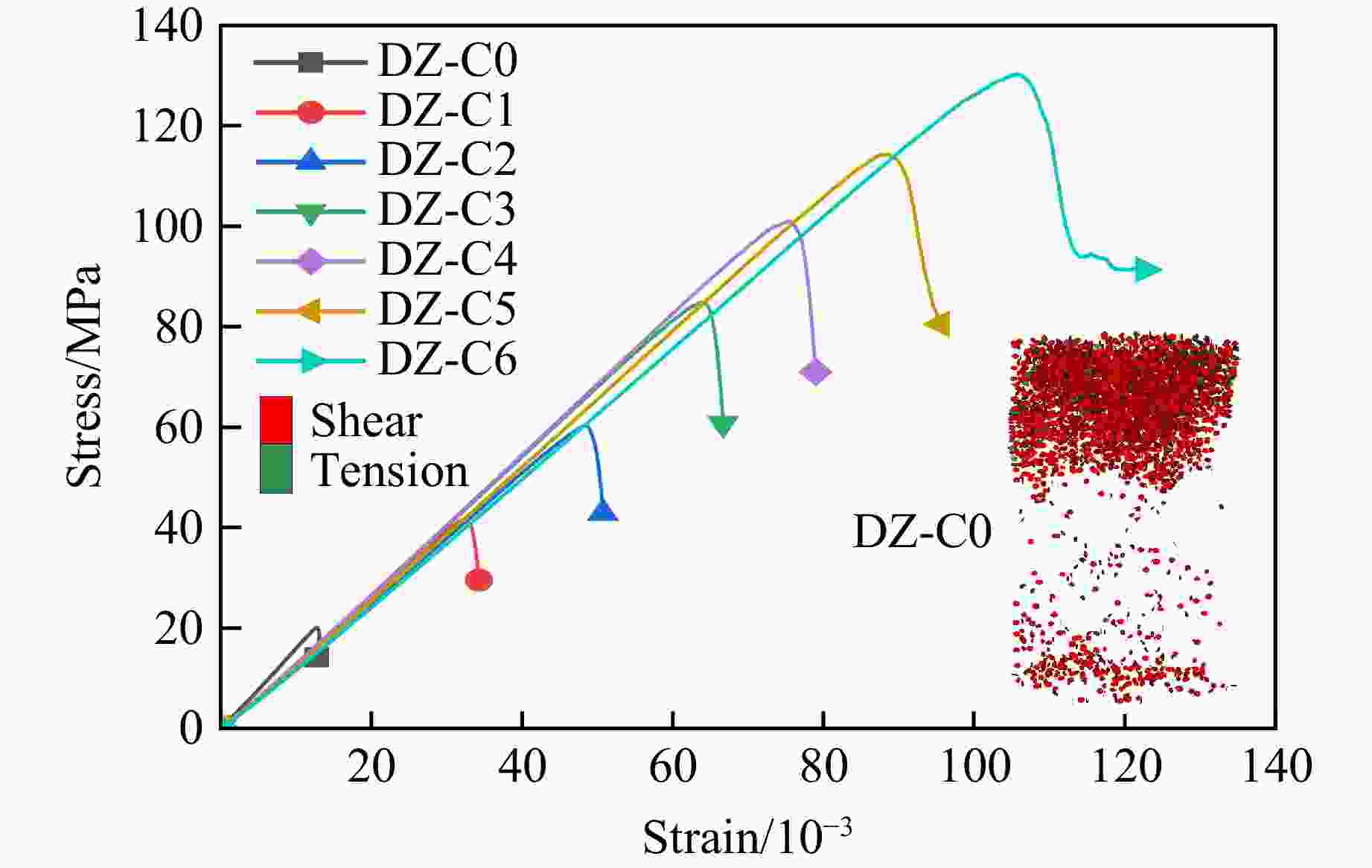
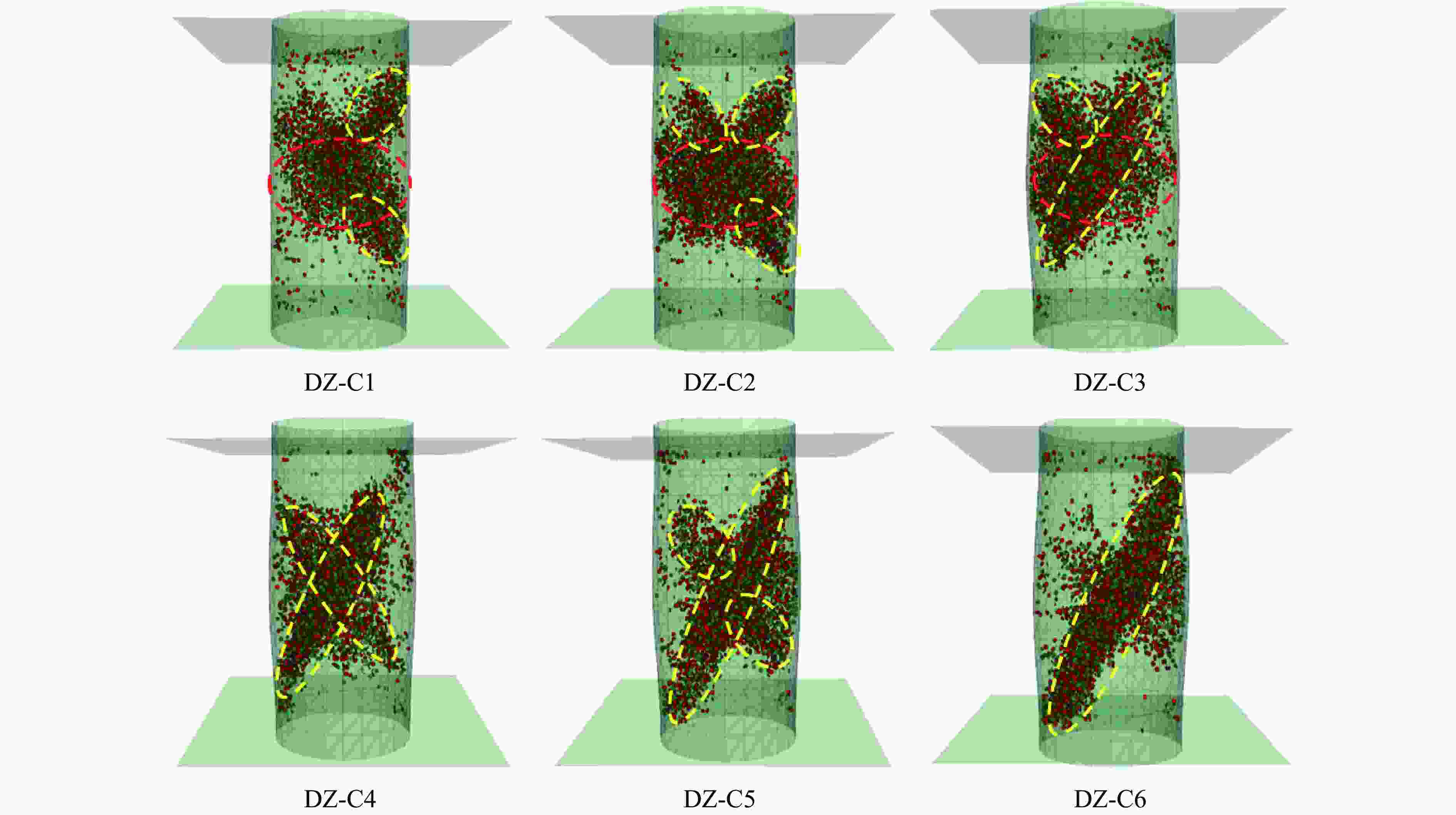
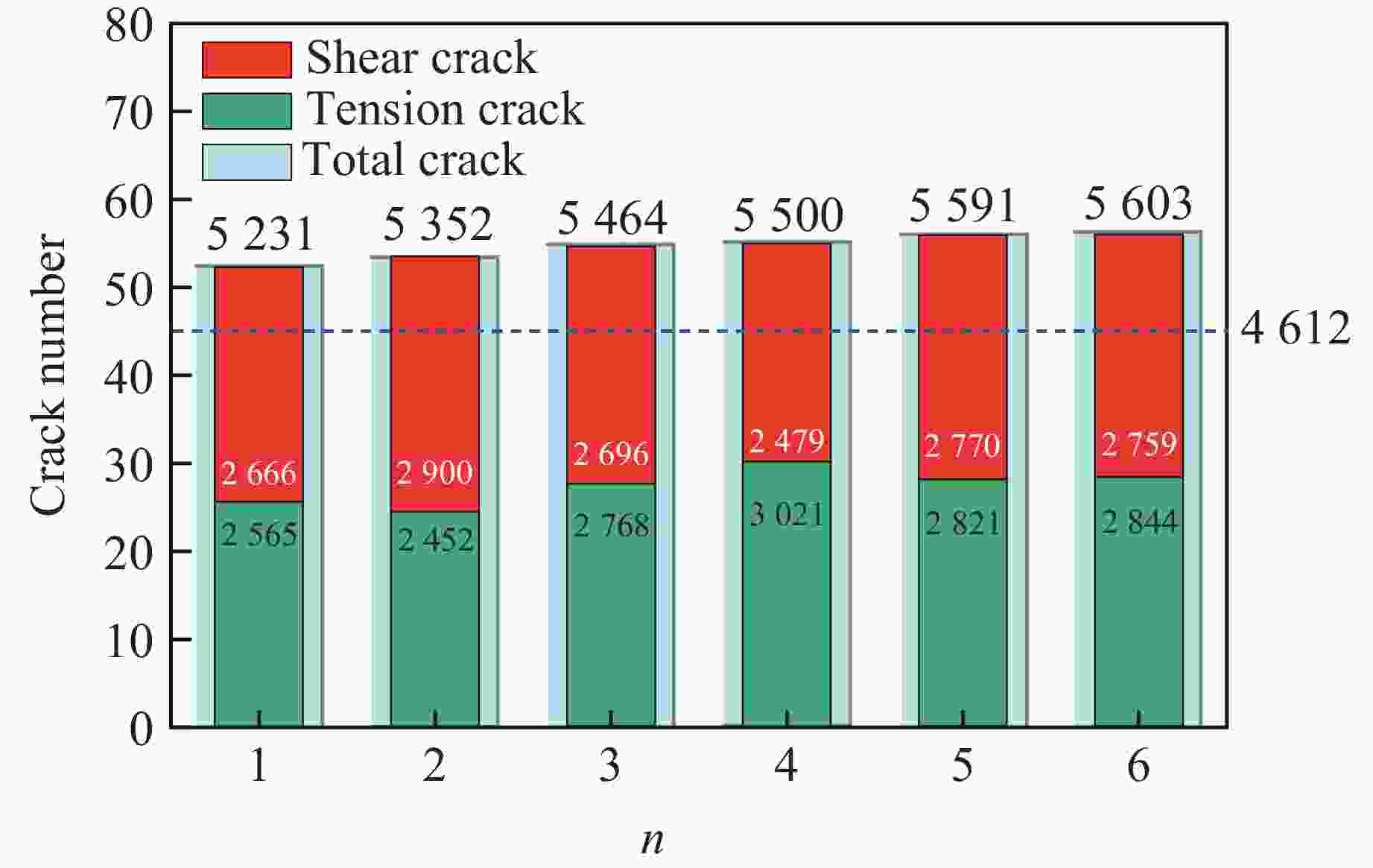
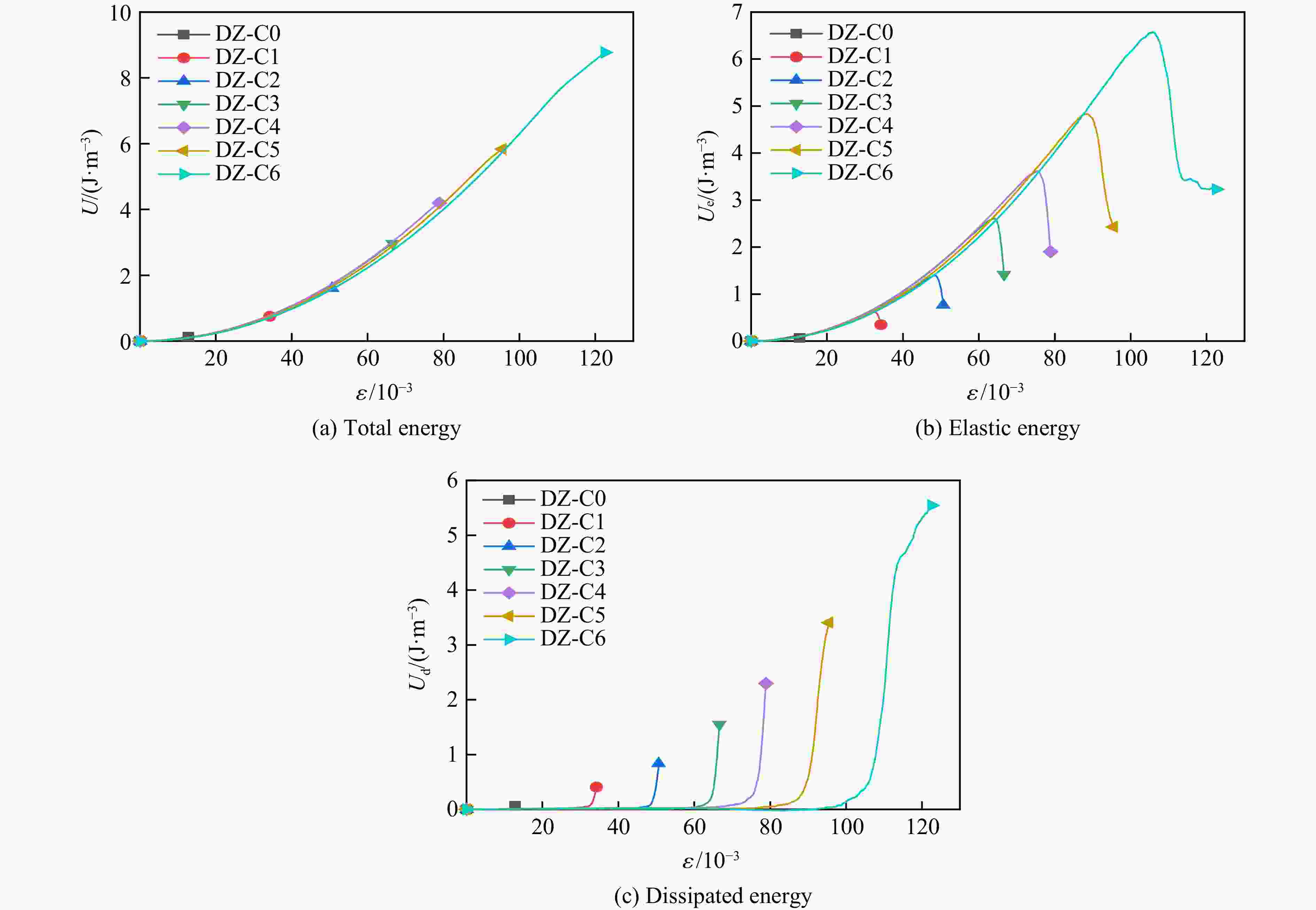
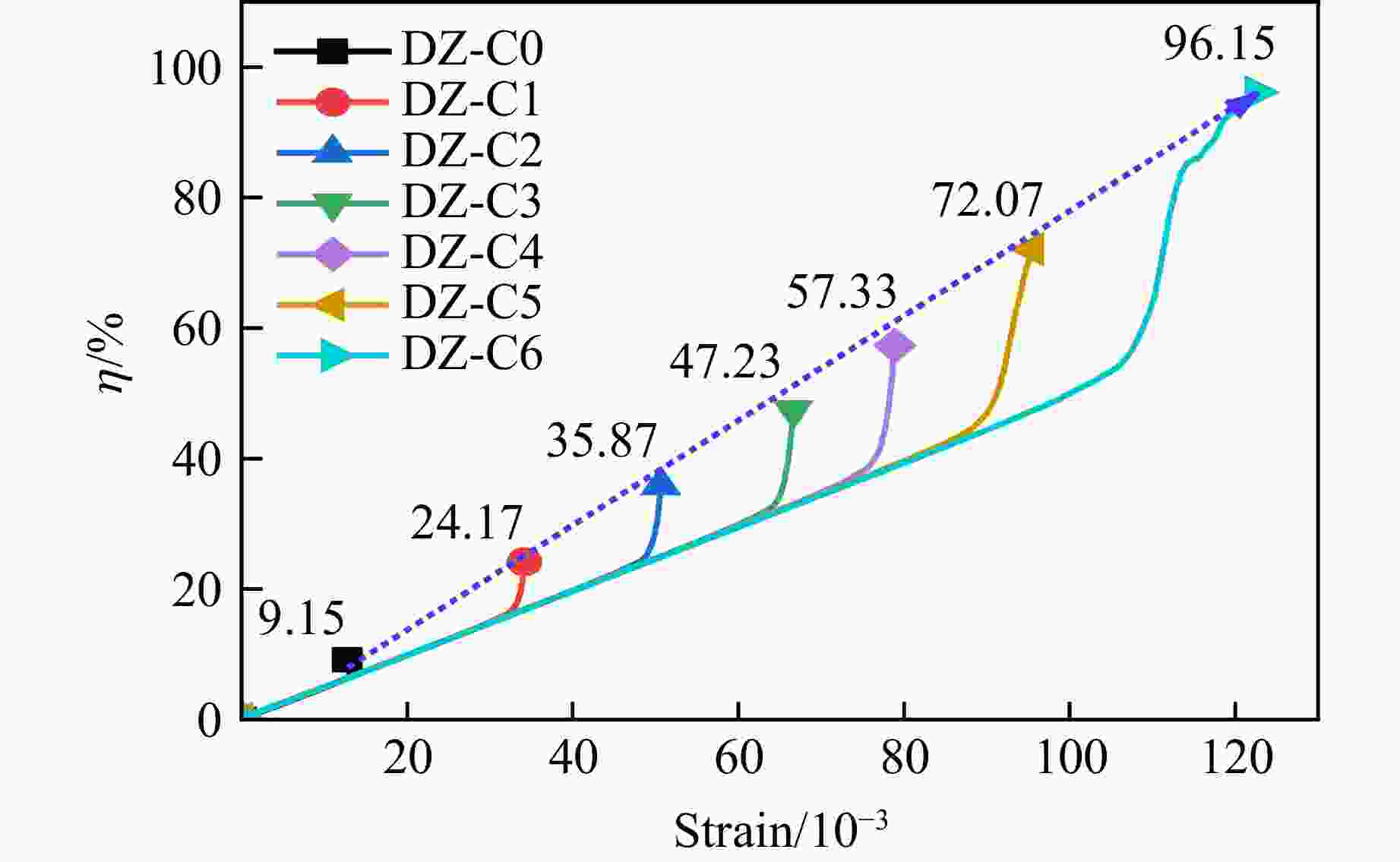
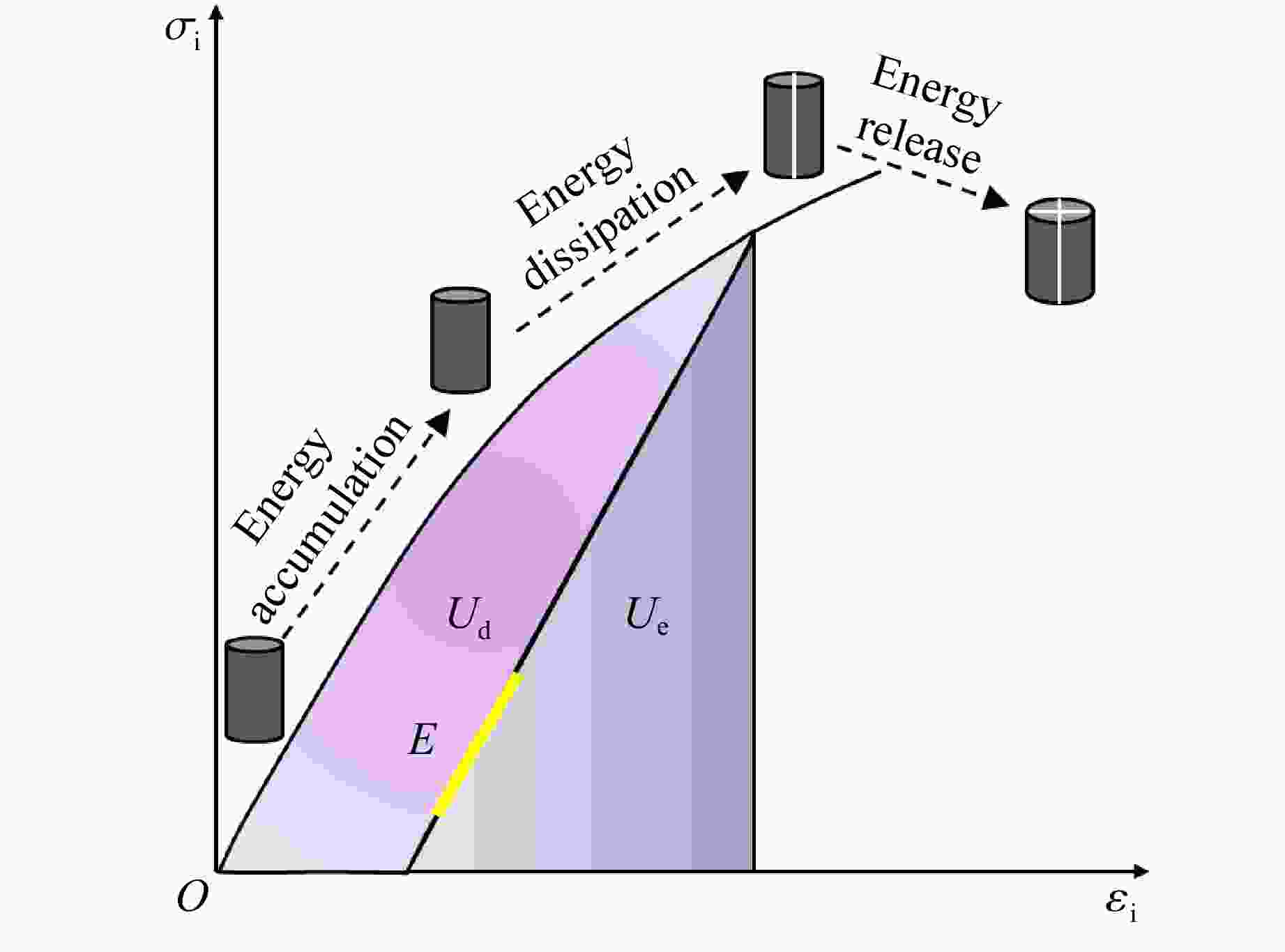
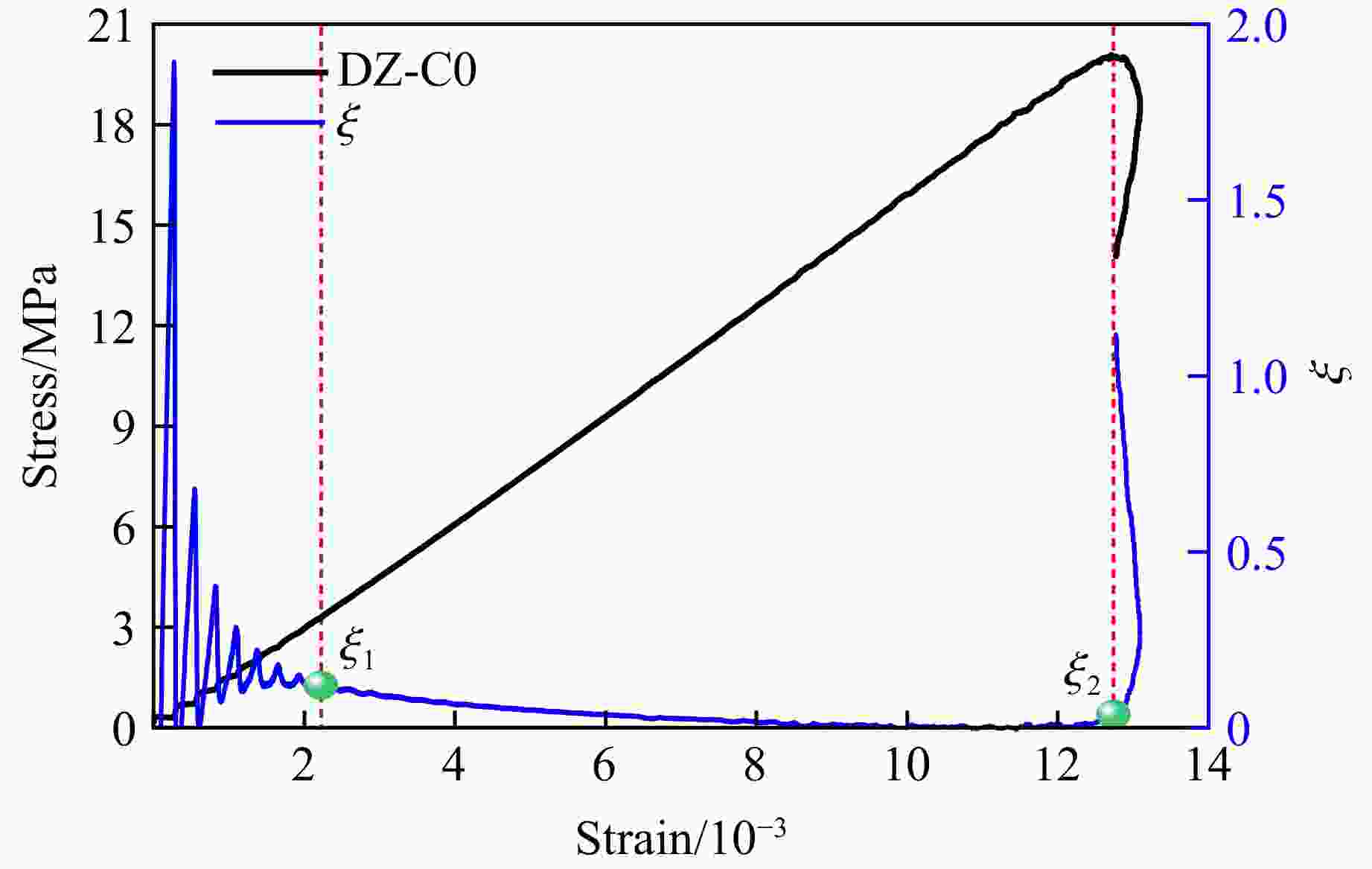
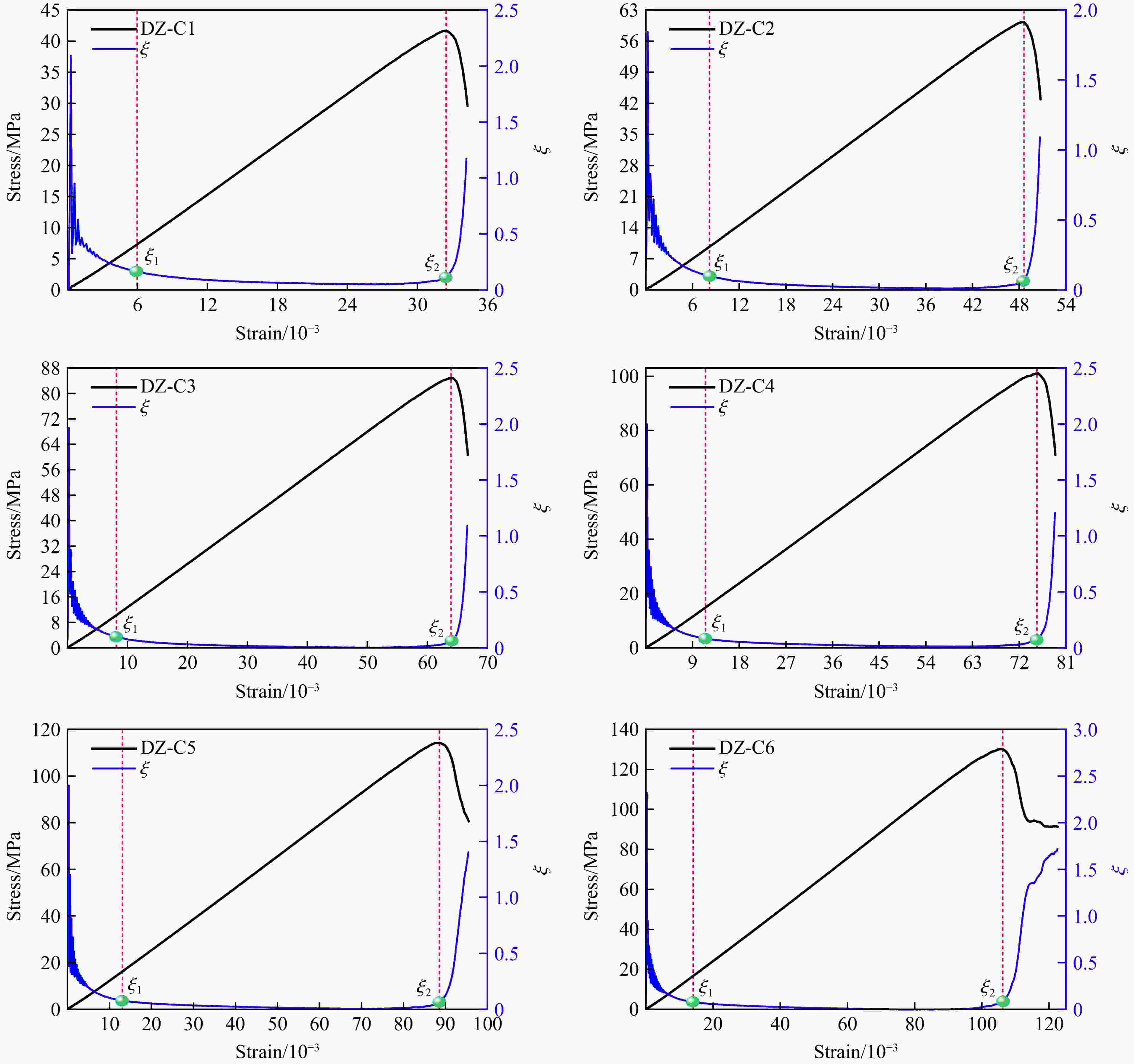
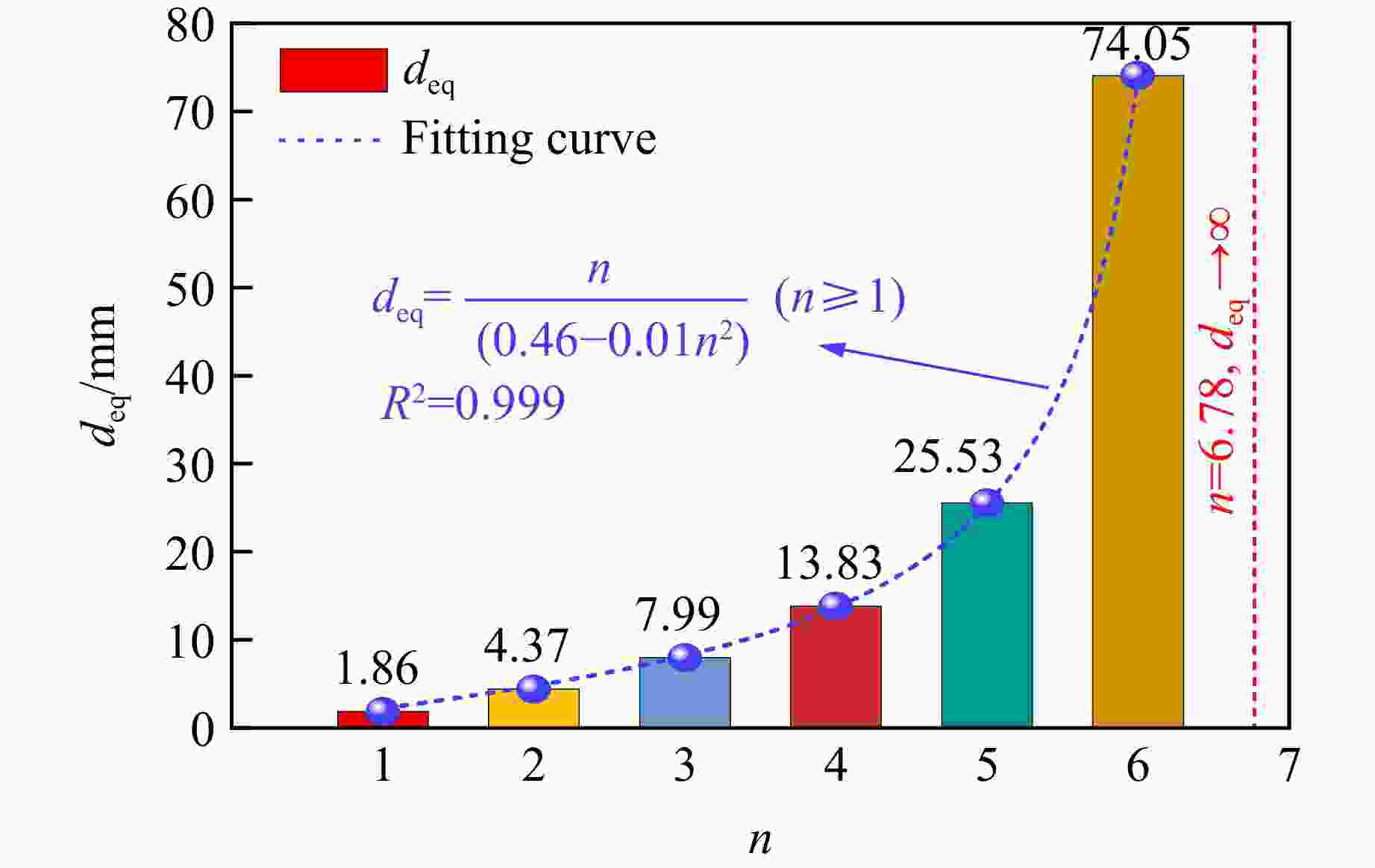
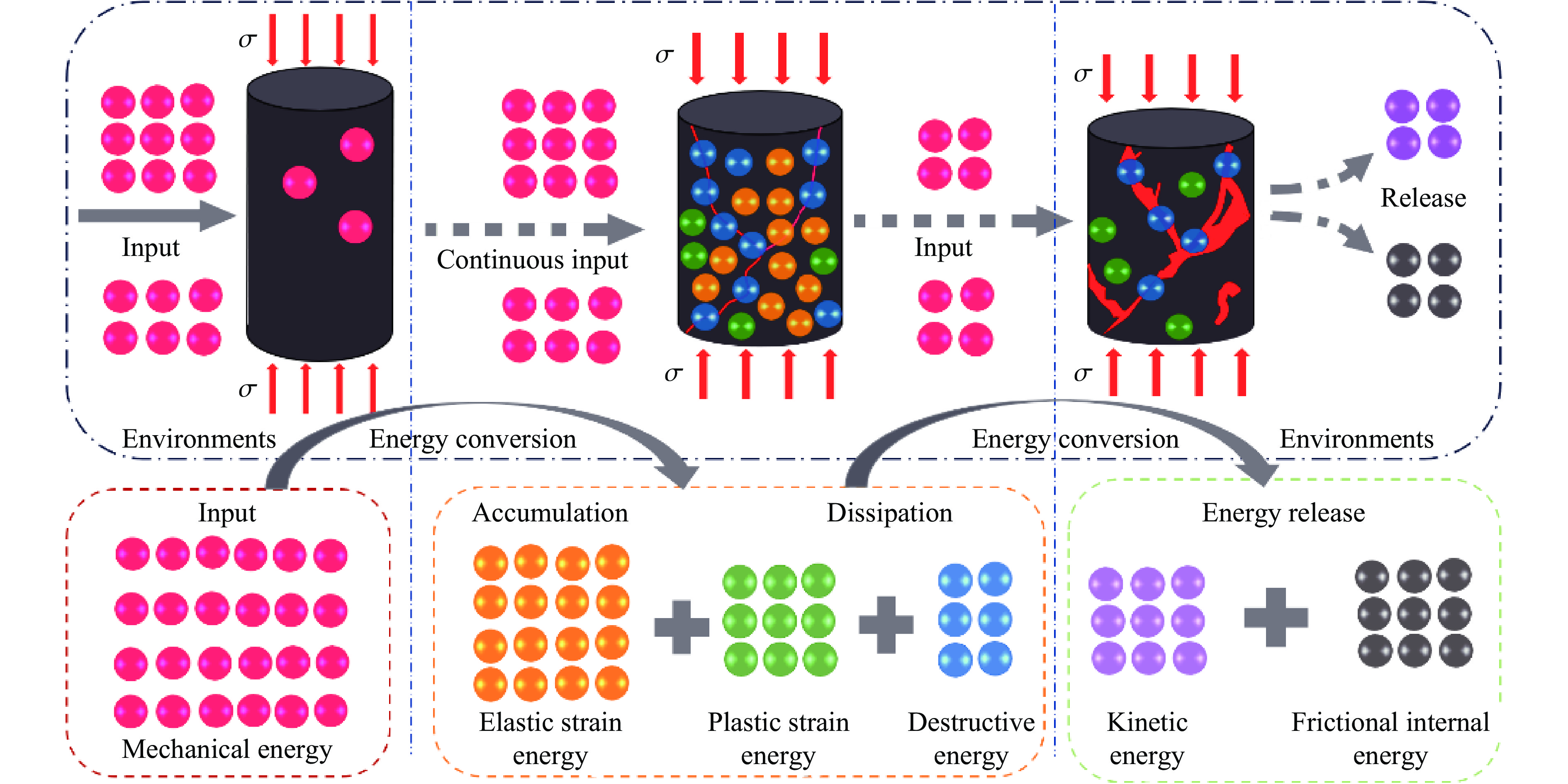
摘要: 为探究不同碳纤维增强复合材料（carbon fiber reinforced plastic，CFRP）布层数对轴压煤圆柱力学特性及能量演化的影响，结合室内单轴压缩试验，采用有限差分-离散元法（FDM-DEM）进行数值模拟。试验结果表明，无论是未约束煤圆柱，还是CFRP约束样本，应力-应变曲线均经历了压密、弹性、屈服和峰后4个阶段。CFRP布约束样本在屈服和峰后阶段表现出明显的延性破坏，其平均峰值应力、峰值应变和弹性模量分别比未约束样本高出约2、2.5和1倍。数值模拟结果显示：随着CFRP布层数增加，峰值应变和峰值应力分别提升至733%和548%；而弹性模量并未单调上升，表明在设计CFRP布层数时需平衡强度与刚度。此外，CFRP布层数的增加导致破坏机制由张拉破坏转变为剪切破坏，表明其对煤圆柱的应力分布和破坏过程影响显著。煤圆柱的总能量和耗散能随着CFRP布层数的增加显著提升，能量吸收效率最高可达10.51倍，显示其抗失稳能力显著增强。为量化CFRP布的约束效应，引入了“等效厚度”概念，发现其随着CFRP布层数增加呈非线性增长趋势，且在6.78层时，等效厚度趋近于无穷大，说明了CFRP布在提升煤圆柱结构稳定性方面的重要性，为未来研究提供了重要参考。
- 单轴压缩 /
- 碳纤维增强复合材料布 /
- 煤圆柱 /
- 有限差分-离散元法 /
- 能量演化 /
- 等效厚度
Abstract: To investigate the effects of different layers of carbon fiber reinforced plastic (CFRP) on the mechanical properties and energy evolution of axially compressed cylindrical coal samples, the finite difference method-discrete element method (FDM-DEM) coupled numerical simulation and laboratory uniaxial compression tests are combined in this paper. The test results show that both unconfined cylindrical coal samples and CFRP-confined samples undergo four stages in the stress-strain curve, namely, compression-tightness, elasticity, yielding, and post-peak. The CFRP-confined samples show obvious ductile damage in the yielding and post-peak stages, and their average peak stresses, peak strains, and elasticity modulus are about 2, 2.5 and 1 times higher than those of the unconfined samples, respectively. Numerical simulations show that the peak strain and peak stress increased to 733% and 548%, respectively, with the increase in the number of CFRP layers. The elastic modulus does not increase monotonically, indicating that a balance between strength and stiffness is required when designing the CFRP layers. In addition, the increase of CFRP layers leads to the change of the damage mechanism from tensile damage to shear damage, indicating that it has a significant effect on the stress distribution and damage process of the cylindrical coal samples. The total and dissipated energy of the cylindrical coal samples significantly increased with the increase of CFRP layers, and the energy absorption efficiency reaches up to 10.51 times, showing a significant enhancement of their destabilization resistance. To quantify the confinement effect of CFRP sheets, the concept of “equivalent thickness” is introduced. It is found that the equivalent thickness increases nonlinearly with the number of CFRP layers, and at 6.78 layers, the equivalent thickness approaches infinity, which emphasizes the importance of CFRP sheet in improving the stability of cylindrical coal sample structure, and provides an important reference for future research.
- uniaxial compression /
- carbon fiber reinforced plastic sheet /
- cylindrical coal /
- finite difference method-discrete element method /
- energy evolution /
- equivalent thickness

HTML全文

图 1 煤圆柱的能量转换过程

Figure 1. Energy conversion process of cylindrical coal samples

下载: 全尺寸图片幻灯片

图 2 CFRP条带制作

Figure 2. Preparation of CFRP strips

下载: 全尺寸图片幻灯片

图 3 CFRP条带荷载-应变曲线

Figure 3. Load-strain curves of CFRP strips

下载: 全尺寸图片幻灯片

图 4 试验设备及采集系统

Figure 4. Test equipment and acquisition systems

下载: 全尺寸图片幻灯片

图 5 单轴压缩试验的应力-应变曲线

Figure 5. Stress-strain curves of uniaxial compression tests

下载: 全尺寸图片幻灯片

图 6 PFC^3D-FLAC^3D耦合计算原理

Figure 6. Calculation principle of PFC^3D-FLAC^3D coupling

下载: 全尺寸图片幻灯片

图 7 平行黏结模型^[33–34]

Figure 7. Parallel bonding model^[33–34]

下载: 全尺寸图片幻灯片

图 8 煤圆柱模型

Figure 8. Model of cylindrical coal samples

下载: 全尺寸图片幻灯片

图 9 CFRP条带的应力-应变模拟曲线

Figure 9. Simulated stress-strain curves of CFRP strips

下载: 全尺寸图片幻灯片

图 10 试验与模拟验证

Figure 10. Verification of tests and simulations

下载: 全尺寸图片幻灯片

图 11 模拟不同CFRP层数下煤圆柱的应力-应变曲线

Figure 11. Numerical simulated stress-strain curves of cylindrical coal samples with different CFRP layers

下载: 全尺寸图片幻灯片

图 12 煤圆柱的破坏形态

Figure 12. Damage patterns of the cylindrical coal samples

下载: 全尺寸图片幻灯片

图 13 不同CFRP层数下煤圆柱的裂纹数量

Figure 13. Number of cracks in cylindrical coal samples with different CFRP layers

下载: 全尺寸图片幻灯片

图 14 不同CFRP层数下煤圆柱的能量演化规律

Figure 14. Energy evolution law of cylindrical coal samples with different CFRP layers

下载: 全尺寸图片幻灯片

图 15 不同CFRP层数下煤圆柱的能量吸收效率曲线

Figure 15. Energy absorption efficiency curves of cylindrical coal samples with different CFRP layers

下载: 全尺寸图片幻灯片

图 16 CFRP约束煤圆柱的弹性能与耗散能的关系^[20]

Figure 16. Relationship between elastic strain energy and dissipated energy of CFRP-confined cylindrical coal samples^[20]

下载: 全尺寸图片幻灯片

图 17 未约束煤圆柱的弹性能耗比曲线

Figure 17. Elastic energy consumption ratio curves of unconfined cylindrical coal sample

下载: 全尺寸图片幻灯片

图 18 不同CFRP层数下煤圆柱的弹性能耗比曲线

Figure 18. Elastic energy consumption ratio curves of cylindrical coal samples with different CFRP layers

下载: 全尺寸图片幻灯片

图 19 CFRP布约束煤圆柱的机制

Figure 19. Mechanism of CFRP-confined cylindrical coal samples

下载: 全尺寸图片幻灯片

图 20 等效厚度柱状图及拟合曲线

Figure 20. Equivalent thickness histograms and fitting curve

下载: 全尺寸图片幻灯片

表 1 CFRP布的力学参数

Table 1. Mechanical parameters of CFRP sheets

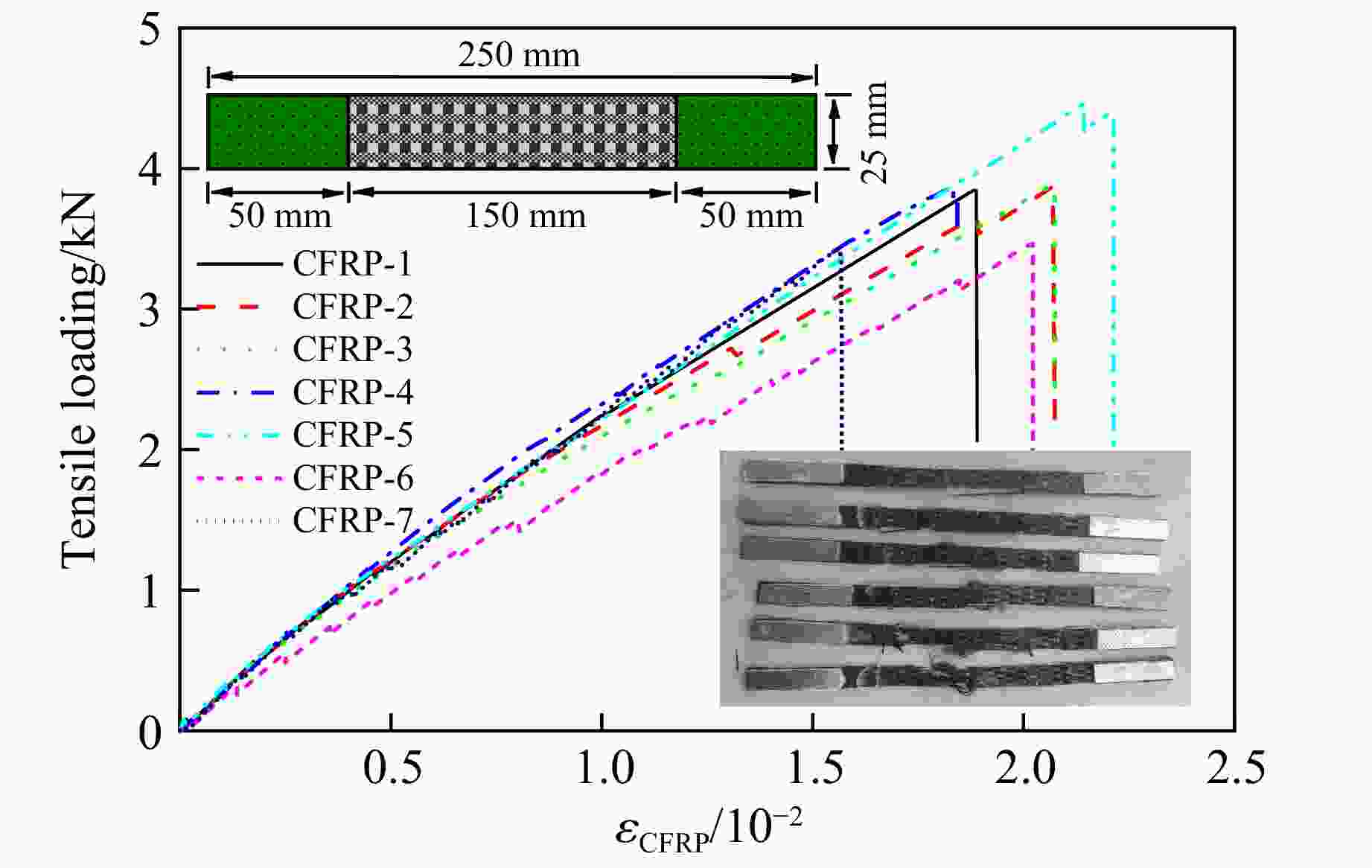
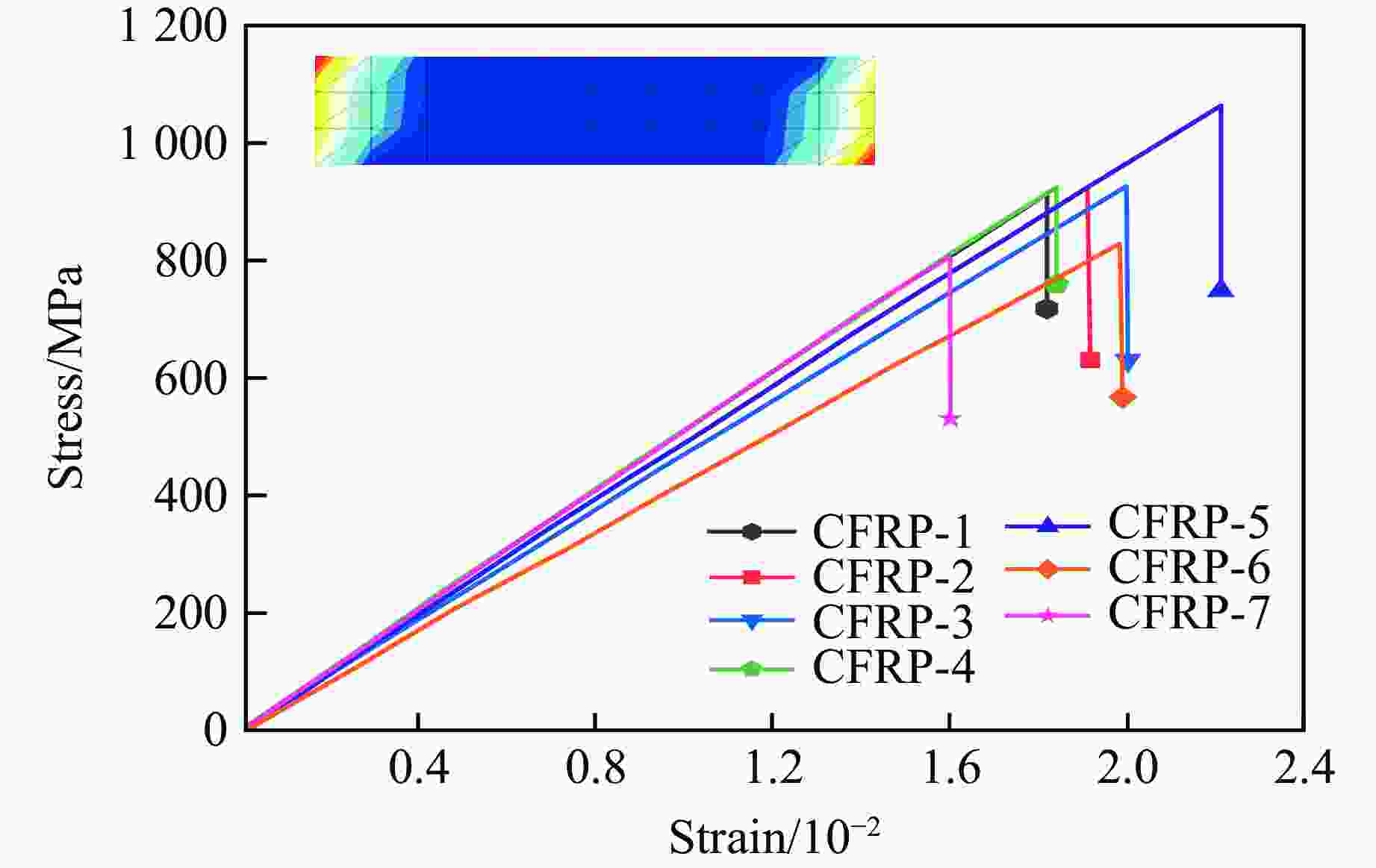
CFRP No.	F_CFRP/N	x/mm	ε_CFRP/%	T_CFRP/MPa
CFRP-1	3846.0	4.71	1.88	921.2
CFRP-2	3880.5	5.19	2.07	929.5
CFRP-3	3889.5	5.18	2.07	931.6
CFRP-4	3877.5	4.57	1.83	928.7
CFRP-5	4462.5	5.35	2.14	1068.9
CFRP-6	3466.5	5.05	2.02	830.3
CFRP-7	3408.0	3.91	1.56	816.3
Average value	3832.9	4.85	1.94	918.1

下载: 导出CSV

表 2 单轴压缩试验方案

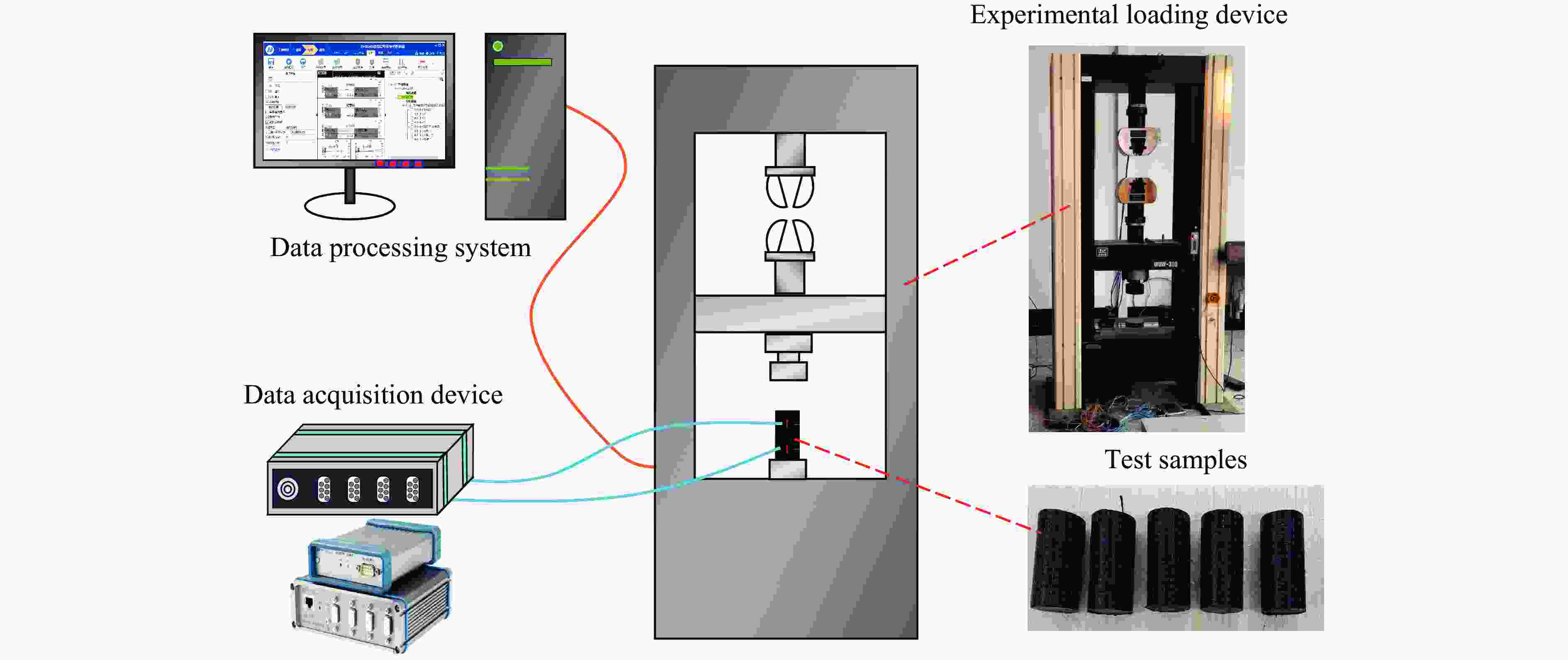
Table 2. Uniaxial compression test scheme

Specimen No.	Layer	Number of samples	Loading rate/(mm·min^–1)
C0	0	3	0.12
C1	1	3	0.12

下载: 导出CSV

表 3 煤圆柱单轴压缩试验结果

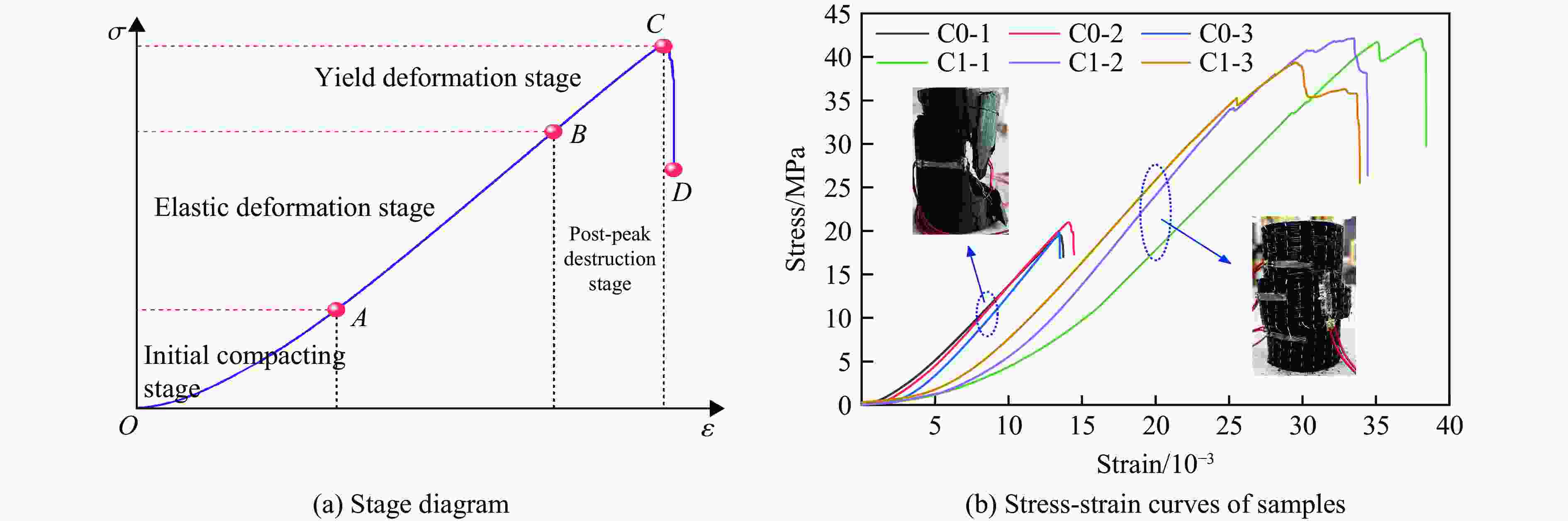
Table 3. Uniaxial compression test results of cylindrical coal specimens

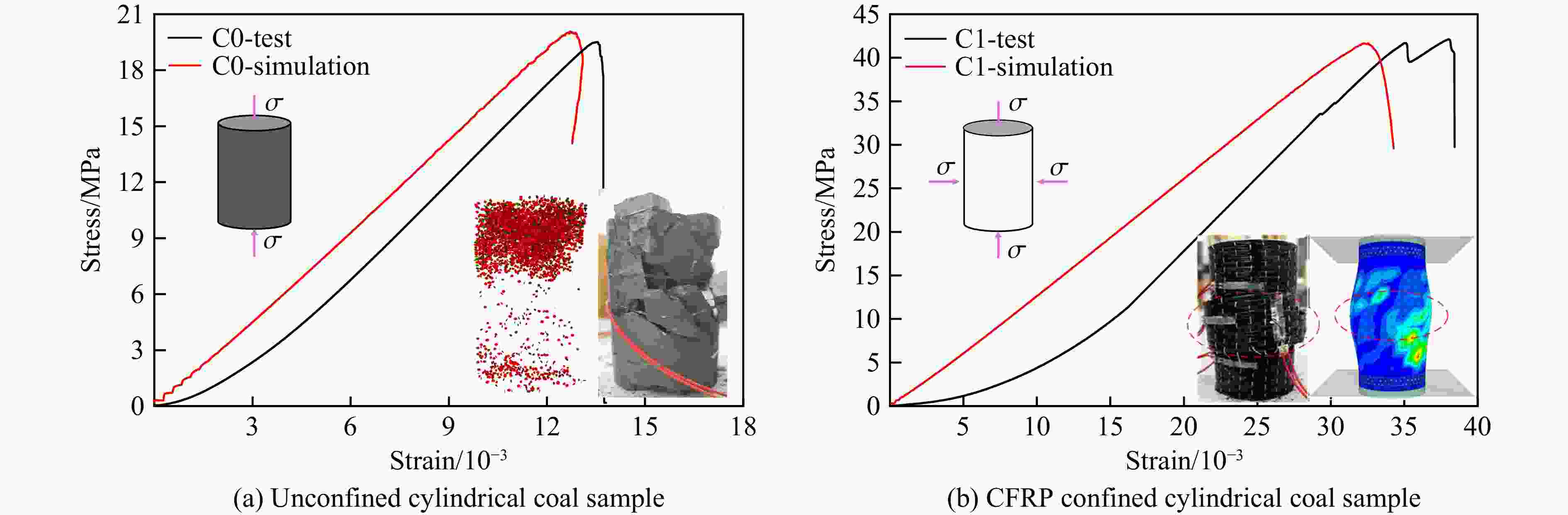
Test No.	Layer	D/mm	H/mm	σ/MPa	ε/10⁻³	E/GPa
C0-1	0	50.05	100.21	19.50	13.53	1.72
C0-2	0	49.08	100.06	21.00	14.10	1.79
C0-3	0	50.01	100.13	19.81	13.46	1.95
Average				20.10	13.70	1.82
C1-1	1	49.04	100.00	42.14	38.04	1.61
C1-2	1	49.06	100.04	42.12	33.49	1.95
C1-3	1	49.81	100.37	39.38	29.55	1.92
Average				41.21	33.69	1.83

下载: 导出CSV

表 4 试验与模拟煤圆柱样品的力学参数对比

Table 4. Comparison of mechanical parameters of cylindrical coal sample between test and simulation

Sample	σ_p			ε_p			E
Sample	Test/MPa	Sim./MPa	Error/%	Test/10⁻³	Sim./10⁻³	Error/%	Test/GPa	Sim./GPa	Error/%
Unconfined	19.50	20.08	3.0	13.53	12.71	6.1	1.72	1.63	5.2
CFRP confined	42.14	41.63	1.2	37.04	33.40	9.8	1.61	1.48	8.10

下载: 导出CSV

表 5 煤圆柱和CFRP布的细观参数

Table 5. Microscopic parameters of cylindrical coal sample and CFRP sheet

Sample	E_c/GPa	$ \overline{E}_{\mathrm{c}} $/GPa	k	σ_b/MPa	τ_b/MPa	φ/(°)	μ
Cylindrical coal	1.2	1	1	18.9	11	50	0.5

Sample	T_g/MPa	ε_g/%	E_g/GPa	d/mm	K_s/(N·m⁻³)	c_i/kPa	φ_i/(°)
CFRP sheet	918.07	1.94	47.54	0.168	3.5×10⁶	10	30

下载: 导出CSV

表 6 数值模拟方案

Table 6. Numerical simulation scheme

Sample	Size/(mm×mm)	Layer	Number of particles	Loading rate/(mm·min⁻¹)
DZ-C0–DZ-C6	50×100	0–6	8881	0.12

下载: 导出CSV

表 7 不同CFRP布层数下煤圆柱的力学参数

Table 7. Mechanical parameters of cylindrical coal samples with different CFRP sheet layers

Sample	n	ε_p/10⁻³	σ_p/MPa	E/GPa
DZ-C0	0	12.71	20.08311	1.63
DZ-C1	1	33.40	41.63361	1.48
DZ-C2	2	48.31	60.29511	1.30
DZ-C3	3	63.95	84.83669	1.38
DZ-C4	4	75.46	101.03746	1.41
DZ-C5	5	88.68	114.25265	1.35
DZ-C6	6	105.91	130.26486	1.29

下载: 导出CSV

表 8 不同CFRP层数煤圆柱的约束刚度及等效厚度

Table 8. Confinement stiffness and equivalent thickness of cylindrical coal samples with different CFRP layers

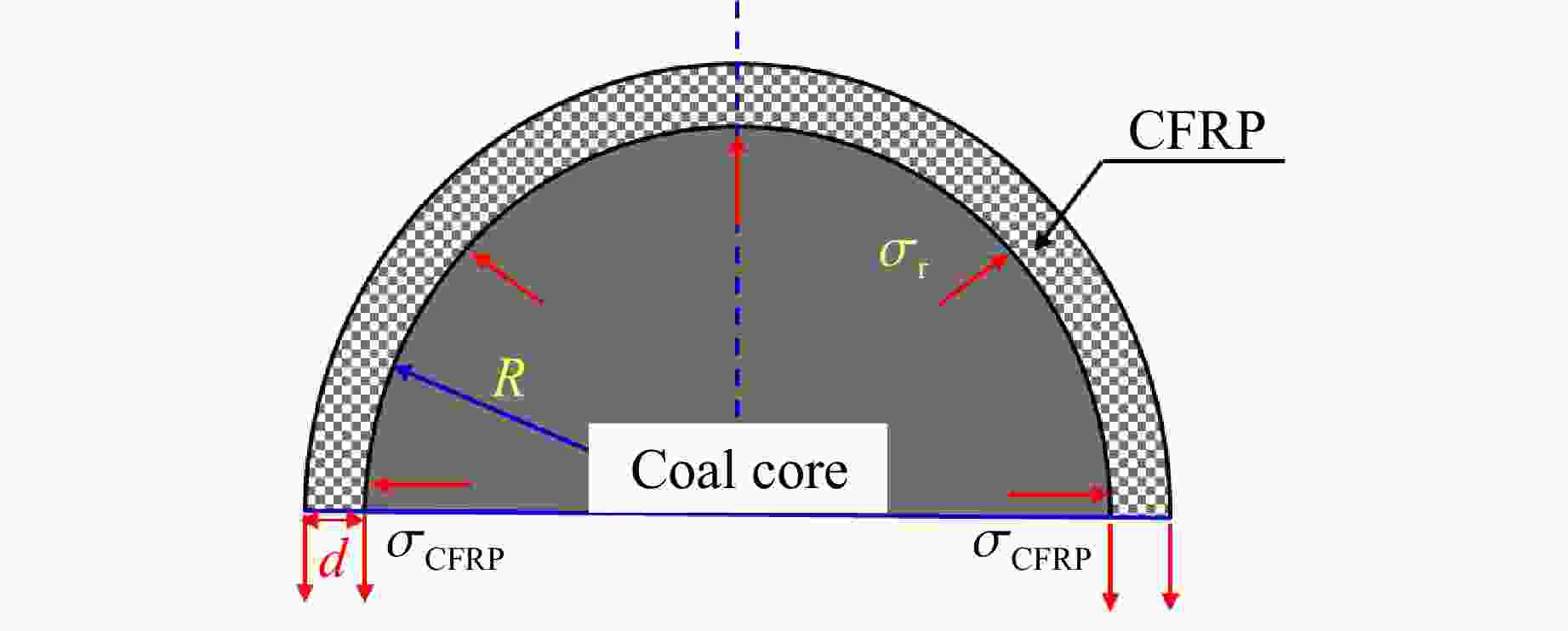
n	d/mm	E_CFRP/GPa	K_CFRP/MPa	λ	d_eq/mm
1	0.167	47.54	317.57	0.165	1.86
2	0.334	47.54	635.13	0.329	4.37
3	0.501	47.54	952.70	0.494	7.99
4	0.668	47.54	1270.27	0.658	13.83
5	0.835	47.54	1587.84	0.823	25.53
6	1.002	47.54	1905.40	0.987	74.05

下载: 导出CSV

参考文献(47)

[1]	任连伟, 宁浩, 邹友峰, 等. 采空区场地高速铁路路基变形控制研究现状与展望 [J]. 煤炭学报, 2021, 46(8): 2534–2547. doi: 10.13225/j.cnki.jccs.2020.0499 REN L W, NING H, ZOU Y F, et al. Research status and prospect on deformation control of high-speed railway subgrade in goaf site [J]. Journal of China Coal Society, 2021, 46(8): 2534–2547. doi: 10.13225/j.cnki.jccs.2020.0499
[2]	ZHANG C W, JIN Z X, FENG G R, et al. Double peaked stress-strain behavior and progressive failure mechanism of encased coal pillars under uniaxial compression [J]. Rock Mechanics and Rock Engineering, 2020, 53(7): 3253–3266. doi: 10.1007/s00603-020-02101-7
[3]	孙克国, 刘旭, 袁子义, 等. 下伏缓倾煤层开采对既有铁路隧道安全性影响分析 [J]. 中国铁道科学, 2022, 43(2): 86–95. doi: 10.3969/j.issn.1001-4632.2022.02.10 SUN K G, LIU X, YUAN Z Y, et al. Influence of excavation in underlying gently-inclined coal layer on the safety of existing railway tunnel [J]. China Railway Science, 2022, 43(2): 86–95. doi: 10.3969/j.issn.1001-4632.2022.02.10
[4]	董建军, 李昕, 梅媛, 等. 老采空区地表变电站场地稳定性的D-InSAR监测 [J]. 采矿与安全工程学报, 2022, 39(1): 62–71. doi: 10.13545/j.cnki.jmse.2020.0472 DONG J J, LI X, MEI Y, et al. D-InSAR monitoring of site stability for surface substation above old mine goaf [J]. Journal of Mining & Safety Engineering, 2022, 39(1): 62–71. doi: 10.13545/j.cnki.jmse.2020.0472
[5]	郭庆彪. 煤矿老采空区上方高速公路建设安全性评价及其关键技术研究 [J]. 测绘学报, 2019, 48(4): 532. doi: 10.11947/j.AGCS.2019.20180225 GUO Q B. Research on the safety evaluation and key technologies for the expressway construction on old goaf of coal mine [J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(4): 532. doi: 10.11947/j.AGCS.2019.20180225
[6]	PRASSETYO S H, IRNAWAN M A, SIMANGUNSONG G M, et al. New coal pillar strength formulae considering the effect of interface friction [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 123: 104102. doi: 10.1016/j.ijrmms.2019.104102
[7]	黄万朋, 赵同阳, 江东海, 等. 双巷掘进留窄小煤柱布置方式及围岩稳定性控制技术 [J]. 岩石力学与工程学报, 2023, 42(3): 617–629. doi: 10.13722/j.cnki.jrme.2022.0302 HUANG W P, ZHAO T Y, JIANG D H, et al. Arrangement of double entry driving with a narrow coal pillar in the middle and stability control technology of surrounding rock [J]. Chinese Journal of Rock Mechanics and Engineering, 2023, 42(3): 617–629. doi: 10.13722/j.cnki.jrme.2022.0302
[8]	谷长宛, 王波, 王军, 等. 基于胀锁式对穿锚索的沿空掘巷窄煤柱双向加固机理研究 [J]. 煤炭科学技术, 2022, 50(4): 106–116. doi: 10.13199/j.cnki.cst.2019-1409 GU C W, WANG B, WANG J, et al. Research on bidirectional-reinforcement mechanism of narrow coal pillar of gob-side entry driving based on inflatable lock-type anchor [J]. Coal Science and Technology, 2022, 50(4): 106–116. doi: 10.13199/j.cnki.cst.2019-1409
[9]	张洪伟, 万志军, 张源, 等. 工作面顺序接续下综放沿空掘巷窄煤柱稳定性控制 [J]. 煤炭学报, 2021, 46(4): 1211–1219. doi: 10.13225/j.cnki.jccs.2020.0028 ZHANG H W, WAN Z J, ZHANG Y, et al. Stability control of narrow coal pillars in the fully-mechanized gob-side entry during sequenced top coal caving mining [J]. Journal of China Coal Society, 2021, 46(4): 1211–1219. doi: 10.13225/j.cnki.jccs.2020.0028
[10]	张洪伟, 万志军, 张源. 非充分稳定覆岩下综放沿空掘巷窄煤柱巷旁注浆加固机理 [J]. 采矿与安全工程学报, 2018, 35(3): 489–495. doi: 10.13545/j.cnki.jmse.2018.03.006 ZHANG H W, WAN Z J, ZHANG Y. Mechanism of grouted-reinforcement in last roadway for pillar in the fully-mechanized gob-side entry [J]. Journal of Mining & Safety Engineering, 2018, 35(3): 489–495. doi: 10.13545/j.cnki.jmse.2018.03.006
[11]	冯国瑞, 马俊彪, 白锦文, 等. 关键柱柱旁双侧充填遗留煤柱链式失稳防控效果研究 [J]. 采矿与安全工程学报, 2023, 40(5): 945–956. doi: 10.13545/j.cnki.jmse.2023.0241 FENG G R, MA J B, BAI J W, et al. Study of the prevention and control effect of residual coal pillars’ chain failure after key pillar-double side backfilling [J]. Journal of Mining & Safety Engineering, 2023, 40(5): 945–956. doi: 10.13545/j.cnki.jmse.2023.0241
[12]	陈绍杰, 张俊文, 尹大伟, 等. 充填墙提升煤柱性能机理与数值模拟研究 [J]. 采矿与安全工程学报, 2017, 34(2): 268–275. doi: 10.13545/j.cnki.jmse.2017.02.010 CHEN S J, ZHANG J W, YIN D W, et al. Mechanism and numerical simulation of filling walls improving performance of coal pillar [J]. Journal of Mining & Safety Engineering, 2017, 34(2): 268–275. doi: 10.13545/j.cnki.jmse.2017.02.010
[13]	SHAYANFAR J, BARROS J A O, REZAZADEH M. Stress-strain model for FRP-confined circular concrete columns developing structural softening behavior [J]. Journal of Composites for Construction, 2024, 28(1): 04023065. doi: 10.1061/JCCOF2.CCENG-4364
[14]	WANG J Z, XIAO H Q, LU L T, et al. Axial stress-strain model for concrete in partially FRP wrapped reinforced concrete columns [J]. Construction and Building Materials, 2024, 416: 135028. doi: 10.1016/j.conbuildmat.2024.135028
[15]	LI H C, WEI Y, HU Y F, et al. Experimental and theoretical analysis of FRP-confined square lightweight aggregate concrete columns under axial compression [J]. Case Studies in Construction Materials, 2024, 20: e02982. doi: 10.1016/j.cscm.2024.e02982
[16]	DAS A J, MANDAL P K, GHOSH C N, et al. Extraction of locked-up coal by strengthening of rib pillars with FRP-a comparative study through numerical modelling [J]. International Journal of Mining Science and Technology, 2017, 27(2): 261–267. doi: 10.1016/j.ijmst.2017.01.024
[17]	白锦文, 杨欣宇, 史旭东, 等. FRP包裹对煤充结构体劈裂破坏特征的影响 [J]. 岩石力学与工程学报, 2023, 42(Suppl 1): 3541–3557. doi: 10.13722/j.cnki.jrme.2022.0517 BAI J W, YANG X Y, SHI X D, et al. Influence of FRP restricting on the splitting failure characteristics of coal-backfilling composite structures [J]. Chinese Journal of Rock Mechanics and Engineering, 2023, 42(Suppl 1): 3541–3557. doi: 10.13722/j.cnki.jrme.2022.0517
[18]	XIA Z, YAO Q L, LI X H, et al. Acoustic emission characteristics and energy mechanism of CFRP-jacketed coal specimens under uniaxial compression [J]. Construction and Building Materials, 2022, 342: 127936. doi: 10.1016/j.conbuildmat.2022.127936
[19]	李庆文, 高安梁, 禹萌萌, 等. 碳纤维布均匀约束下煤圆柱的损伤演化 [J]. 金属矿山, 2024(2): 104–113. doi: 10.19614/j.cnki.jsks.202402010 LI Q W, GAO A L, YU M M, et al. Damage evolution of coal cylinder under uniform confinement of carbon fiber sheets [J]. Metal Mine, 2024(2): 104–113. doi: 10.19614/j.cnki.jsks.202402010
[20]	李庆文, 胡露露, 曹行, 等. CFRP布均匀约束煤圆柱轴压性能 [J]. 复合材料学报, 2022, 39(11): 5611–5624. doi: 10.13801/j.cnki.fhclxb.20211201.001 LI Q W, HU L L, CAO H, et al. Axial compressive behavior of CFRP uniformly wrapped coal in circular columns [J]. Acta Materiae Compositae Sinica, 2022, 39(11): 5611–5624. doi: 10.13801/j.cnki.fhclxb.20211201.001
[21]	李庆文, 高森林, 胡露露, 等. 不同加载速率下非均质煤样能量耗散损伤本构关系 [J]. 煤炭学报, 2022, 47(Suppl 1): 90–102. doi: 10.13225/j.cnki.jccs.2022.0163 LI Q W, GAO S L, HU L L, et al. Constitutive relation of energy dissipation damage of heterogeneous coal samples under different loading rates [J]. Journal of China Coal Society, 2022, 47(Suppl 1): 90–102. doi: 10.13225/j.cnki.jccs.2022.0163
[22]	李庆文, 禹萌萌, 高森林, 等. 加载速率对碳纤维布被动约束煤能量演化的影响 [J]. 煤炭学报, 2024, 49(Suppl 1): 236–247. doi: 10.13225/j.cnki.jccs.2023.0238 LI Q W, YU M M, GAO S L, et al. Effect of loading rate on energy evolution of coal confined passively by CFRP sheets [J]. Journal of China Coal Society, 2024, 49(Suppl 1): 236–247. doi: 10.13225/j.cnki.jccs.2023.0238
[23]	LI Q W, NIE F F, PAN C C, et al. Energy dissipation damage constitutive relation of CFRP passively confined coal sample [J]. Heliyon, 2024, 10(18): e37586. doi: 10.1016/j.heliyon.2024.e37586
[24]	张亮, 王桂林, 雷瑞德, 等. 单轴压缩下不同长度单裂隙岩体能量损伤演化机制 [J]. 中国公路学报, 2021, 34(1): 24–34. doi: 10.19721/j.cnki.1001-7372.2021.01.003 ZHANG L, WANG G L, LEI R D, et al. Energy damage evolution mechanism of single jointed rock mass with different lengths under uniaxial compression [J]. China Journal of Highway and Transport, 2021, 34(1): 24–34. doi: 10.19721/j.cnki.1001-7372.2021.01.003
[25]	WANG J C, WANG Z H, YANG S L. A coupled macro- and meso-mechanical model for heterogeneous coal [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 94: 64–81. doi: 10.1016/j.ijrmms.2017.03.002
[26]	CAI W, BAI X X, SI G Y, et al. A monitoring investigation into rock burst mechanism based on the coupled theory of static and dynamic stresses [J]. Rock Mechanics and Rock Engineering, 2020, 53(12): 5451–5471. doi: 10.1007/s00603-020-02237-6
[27]	CAI W, DOU L M, SI G Y, et al. A new seismic-based strain energy methodology for coal burst forecasting in underground coal mines [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 123: 104086. doi: 10.1016/j.ijrmms.2019.104086
[28]	BIENIAWSKI Z T, HAWKES I. Suggested methods for determining tensile strength of rock materials [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1978, 15(3): 99–103. doi: 10.1016/0148-9062(78)90003-7
[29]	中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 煤和岩石物理力学性质测定方法第10部分: 煤和岩石抗拉强度测定方法: GB/T 23561.10—2010 [S]. 北京: 中国标准出版社, 2011. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, China National Standardization Administration. Methods for determining the physical and mechanical properties of coal and rock—part 10: methods for determining tensile strength of coal and rock: GB/T 23561.10—2010 [S]. Beijing: China Standard Press, 2011.
[30]	中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 定向纤维增强聚合物基复合材料拉伸性能试验方法: GB/T 3354—2014 [S]. 北京: 中国标准出版社, 2015. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, China National Standardization Administration. Test method for tensile properties of orientation fiber reinforced polymer matrix composite materials: GB/T 3354—2014 [S]. Beijing: China Standard Press, 2015.
[31]	武仁杰, 李海波. SHPB冲击作用下层状千枚岩多尺度破坏机理研究 [J]. 爆炸与冲击, 2019, 39(8): 083106. doi: 10.11883/bzycj-2019-0187 WU R J, LI H B. Multi-scale failure mechanism analysis of layered phyllite subject to impact loading [J]. Explosion and Shock Waves, 2019, 39(8): 083106. doi: 10.11883/bzycj-2019-0187
[32]	中华人民共和国住房和城乡建设部. 工程岩体试验方法标准: GB/T 50266—2013 [S]. 北京: 中国计划出版社, 2013. Ministry of Housing and Urban Rural Development of the People’s Republic of China. Standard for test methods of engineering rock mass: GB/T 50266—2013 [S]. Beijing: China Planning Press, 2013.
[33]	李庆文, 禹萌萌, 刘艺伟, 等. GFRP布被动约束标准煤矸石混凝土圆柱轴压性能细观模拟 [J]. 硅酸盐通报, 2023, 42(7): 2458–2471. doi: 10.16552/j.cnki.issn1001-1625.20230606.003 LI Q W, YU M M, LIU Y W, et al. Mesoscopic simulation on axial compression performance of standard coal gangue concrete circular-columns confined by GFRP sheet [J]. Bulletin of the Chinese Ceramic Society, 2023, 42(7): 2458–2471. doi: 10.16552/j.cnki.issn1001-1625.20230606.003
[34]	ZHANG L, REN T, LI X C, et al. Acoustic emission, damage and cracking evolution of intact coal under compressive loads: experimental and discrete element modelling [J]. Engineering Fracture Mechanics, 2021, 252: 107690. doi: 10.1016/j.engfracmech.2021.107690
[35]	XIA B W, LI Y, HU H R, et al. Effect of crack angle on mechanical behaviors and damage evolution characteristics of sandstone under uniaxial compression [J]. Rock Mechanics and Rock Engineering, 2022, 55(11): 6567–6582. doi: 10.1007/s00603-022-03016-1
[36]	李庆文, 才诗婷, 李涵静, 等. 单裂隙岩石-混凝土组合体断裂特征颗粒流模拟 [J]. 高压物理学报, 2024, 38(5): 054202. doi: 10.11858/gywlxb.20240723 LI Q W, CAI S T, LI H J, et al. Particle flow simulation of fracture characteristics of rock-concrete combination with single crack [J]. Chinese Journal of High Pressure Physics, 2024, 38(5): 054202. doi: 10.11858/gywlxb.20240723
[37]	郭润兰, 范雅琼, 王广书, 等. 基于PFC^3D的机床床身用树脂矿物复合材料损伤性能细观研究 [J]. 复合材料学报, 2022, 39(2): 834–844. doi: 10.13801/j.cnki.fhclxb.20210420.004 GUO R L, FAN Y Q, WANG G S, et al. Meso-scale study on damage performance of resin mineral composite material for machine tool bed based on PFC^3D [J]. Acta Materiae Compositae Sinica, 2022, 39(2): 834–844. doi: 10.13801/j.cnki.fhclxb.20210420.004
[38]	谭鑫, 曹明, 冯龙健, 等. 土工织物包裹碎石桩力学特性的数值模拟研究 [J]. 中国公路学报, 2020, 33(9): 136–145. doi: 10.3969/j.issn.1001-7372.2020.09.014 TAN X, CAO M, FENG L J, et al. Numerical study on mechanical behaviors of geotextile-wrapped stone column [J]. Chinese Journal of Highways, 2020, 33(9): 136–145. doi: 10.3969/j.issn.1001-7372.2020.09.014
[39]	周宏元, 于鸿鑫, 王小娟, 等. 玄武岩纤维平纹织物约束建筑固体废弃物颗粒力学性能及吸能特性 [J]. 复合材料学报, 2022, 39(2): 695–706. doi: 10.13801/j.cnki.fhclxb.20210420.003 ZHOU H Y, YU H X, WANG X J, et al. Mechanical properties and energy absorption characteristics of basalt fiber plain woven fabric constrained building solid waste particles [J]. Acta Materiae Compositae Sinica, 2022, 39(2): 695–706. doi: 10.13801/j.cnki.fhclxb.20210420.003
[40]	郭璐, 刘志芳, 李世强, 等. 改进型FCC晶格材料设计与吸能特性 [J]. 高压物理学报, 2022, 36(1): 014206. doi: 10.11858/gywlxb.20210853 GUO L, LIU Z F, LI S Q, et al. Design and energy absorption characteristic of improved FCC lattice materials [J]. Chinese Journal of High Pressure Physics, 2022, 36(1): 014206. doi: 10.11858/gywlxb.20210853
[41]	王小娟, 崔浩儒, 周宏元, 等. 玄武岩纤维增强泡沫混凝土的单轴拉伸及准静态压缩性能 [J]. 复合材料学报, 2023, 40(3): 1569–1585. doi: 10.13801/j.cnki.fhclxb.20220422.001 WANG X J, CUI H R, ZHOU H Y, et al. Mechanical performance of basalt fiber reinforced foam concrete subjected to quasi-static tensile and compressive tests [J]. Acta Materiae Compositae Sinica, 2023, 40(3): 1569–1585. doi: 10.13801/j.cnki.fhclxb.20220422.001
[42]	LI P, CAI M F. Energy evolution mechanism and failure criteria of jointed surrounding rock under uniaxial compression [J]. Journal of Central South University, 2021, 28(6): 1857–1874. doi: 10.1007/s11771-021-4735-5
[43]	MA Q, TAN Y L, LIU X S, et al. Experimental and numerical simulation of loading rate effects on failure and strain energy characteristics of coal-rock composite samples [J]. Journal of Central South University, 2021, 28(10): 3207–3222. doi: 10.1007/s11771-021-4831-6
[44]	李子运, 吴光, 黄天柱, 等. 三轴循环荷载作用下页岩能量演化规律及强度失效判据研究 [J]. 岩石力学与工程学报, 2018, 37(3): 662–670. doi: 10.13722/j.cnki.jrme.2017.0927 LI Z Y, WU G, HUANG T Z, et al. Variation of energy and criteria for strength failure of shale under traixial cyclic loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(3): 662–670. doi: 10.13722/j.cnki.jrme.2017.0927
[45]	ZHANG B W, FANG K, WANG C, et al. Energy evolution characteristics of rock under different confining conditions [J]. Frontiers in Earth Science, 2022, 10: 886134. doi: 10.3389/feart.2022.886134
[46]	周华飞, 洪恒达, 谢子令, 等. CFRP约束地质聚合物混凝土轴向应力-应变关系 [J]. 复合材料学报, 2024, 41(1): 414–425. doi: 10.13801/j.cnki.fhclxb.20230522.001 ZHOU H F, HONG H D, XIE Z L, et al. Axial stress-strain behavior of CFRP-confined geopolymer concrete [J]. Acta Materiae Compositae Sinica, 2024, 41(1): 414–425. doi: 10.13801/j.cnki.fhclxb.20230522.001
[47]	何满潮, 钱七虎. 深部岩体力学基础研究与应用 [M]. 北京: 科学出版社, 2010. HE M C, QIAN Q H. Research and application of deep rock mechanics [M]. Beijing: Science Press, 2010.