圆柱形装药爆炸驱动球形破片的飞散特性

申仕良; 李金柱; 马峰; 姚志彦

doi:10.11858/gywlxb.20240865

圆柱形装药爆炸驱动球形破片的飞散特性

doi: 10.11858/gywlxb.20240865

北京理工大学爆炸科学与安全防护全国重点实验室, 北京　100081

详细信息

作者简介:
申仕良（1999－），男，硕士研究生，主要从事爆炸与冲击动力学研究. E-mail：shen_shiliang@126.com

通讯作者:
李金柱（1972－），男，博士，副教授，主要从事爆炸与冲击动力学研究. E-mail：lijinzhu@bit.edu.cn

中图分类号: O389; O521.3
计量
- 文章访问数: 22
- HTML全文浏览量: 12
- PDF下载量: 2
出版历程
- 收稿日期: 2024-08-05
- 修回日期: 2024-08-28
- 网络出版日期: 2024-10-31

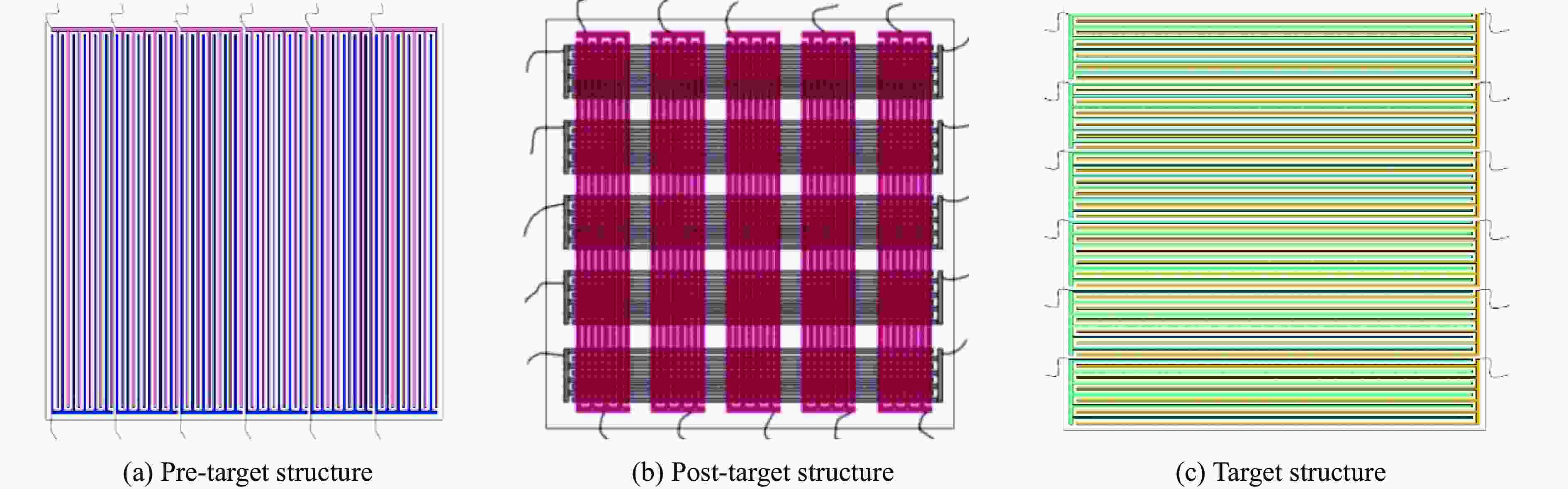
Dispersion Characteristics of Spherical Fragments Driven by Cylindrical Charge

State Key Laboratory of Explosion Science and Safety Protection, Beijing Institute of Technology, Beijing 100081, China

摘要

摘要: 为了研究球形预制钨破片在圆柱形装药驱动下的飞散规律，开展了预制破片战斗部飞散试验。针对传统梳状靶无法测量破片群速度分布的问题，设计并制作了一种全新的交叉梳状靶，成功测得了多个破片穿靶产生的脉冲信号和着靶位置。采用LS-DYNA模拟研究了圆柱形装药爆炸驱动球形破片的飞散特性。结果表明：数值模拟结果与试验结果吻合良好，交叉梳状测速靶能够较为准确地测量多个破片的飞散速度；增加装药长径比可以削弱装药两端稀疏波对破片速度的影响，但效果随长径比增加而逐渐减弱。
- 交叉梳状靶 /
- 测速装置 /
- 预制破片 /
- 飞散速度 /
- 长径比
Abstract: To investigate the dispersion characteristics of spherical tungsten fragments driven by a cylindrical charge, dispersion tests were conducted on a warhead with spherical prefabricated fragments. Considering the limitation of traditional comb targets, which can only measure the maximum velocity instead of the velocity distribution of the fragment group, a novel crossed-comb target was designed and fabricated. This velocity measurement device successfully recorded the pulse signals generated by multiple fragments penetrating the target and the impact positions. Numerical simulations were conducted using LS-DYNA to calculate the dispersion characteristics of spherical fragments driven by cylindrical charges. The results indicate that the numerical simulation results agree well with the test data. The designed crossed-comb shaped target can accurately measure the scattering velocities of multiple fragments. Increasing the length-to-diameter ratio can mitigate the effect of rarefaction waves at both ends of the charge on the fragment velocities; however, this mitigating effect diminishes as the length-to-diameter ratio continues to increase.
- cross-comb target /
- velocity measurement device /
- prefabricated fragments /
- dispersion velocity /
- length-to-diameter ratio

HTML全文

图 1 试验用弹丸照片

Figure 1. Photo of projectile in the test

下载: 全尺寸图片幻灯片

图 2 球形破片交错紧密排布方式

Figure 2. Staggered tight arrangement of spherical fragments

下载: 全尺寸图片幻灯片

图 3 交叉梳状靶结构示意图

Figure 3. Schematic diagram of cross-combed target structure

下载: 全尺寸图片幻灯片

图 4 试验所用交叉梳状靶照片

Figure 4. Cross-combed targets used in the test

下载: 全尺寸图片幻灯片

图 5 预制破片测速装置

Figure 5. Velocity measurement system of preformed fragment

下载: 全尺寸图片幻灯片

图 6 爆炸试验布局

Figure 6. Layout of explosion test

下载: 全尺寸图片幻灯片

图 7 理论着靶破片列数示意图

Figure 7. Schematic diagram of the theoretical number of fragment penetration rows

下载: 全尺寸图片幻灯片

图 8 由Shapiro公式得到的飞散角沿装药轴线方向的分布

Figure 8. Distribution of dispersion angles along the charge axis direction obtained by Shapiro’s equation

下载: 全尺寸图片幻灯片

图 9 不同测速靶上的破片穿孔情况

Figure 9. Fragment perforations on different velocity measurement targets

下载: 全尺寸图片幻灯片

图 10 破片穿透梳状靶的局部状态

Figure 10. Localized condition of fragment penetrations through the comb-shaped target

下载: 全尺寸图片幻灯片

图 11 测速靶3的前靶和后靶穿孔分布

Figure 11. Fragment perforation distribution on the front and rear targets of the velocity measurement target 3

下载: 全尺寸图片幻灯片

图 12 破片穿靶后产生的典型脉冲信号

Figure 12. Typical pulse signal generated after fragment penetration of the target

下载: 全尺寸图片幻灯片

图 13 有限元模型

Figure 13. Finite element model

下载: 全尺寸图片幻灯片

图 14 破片速度沿装药轴线的分布

Figure 14. Distribution of fragments velocity along the axis of charge

下载: 全尺寸图片幻灯片

图 15 破片飞散角沿装药轴线的分布

Figure 15. Distribution of dispersion angle along the axis of charge

下载: 全尺寸图片幻灯片

图 16 不同长径比装药结构的破片速度沿轴线的分布

Figure 16. Distribution of fragments velocity along the axis of charges with different length-to-diameter ratios

下载: 全尺寸图片幻灯片

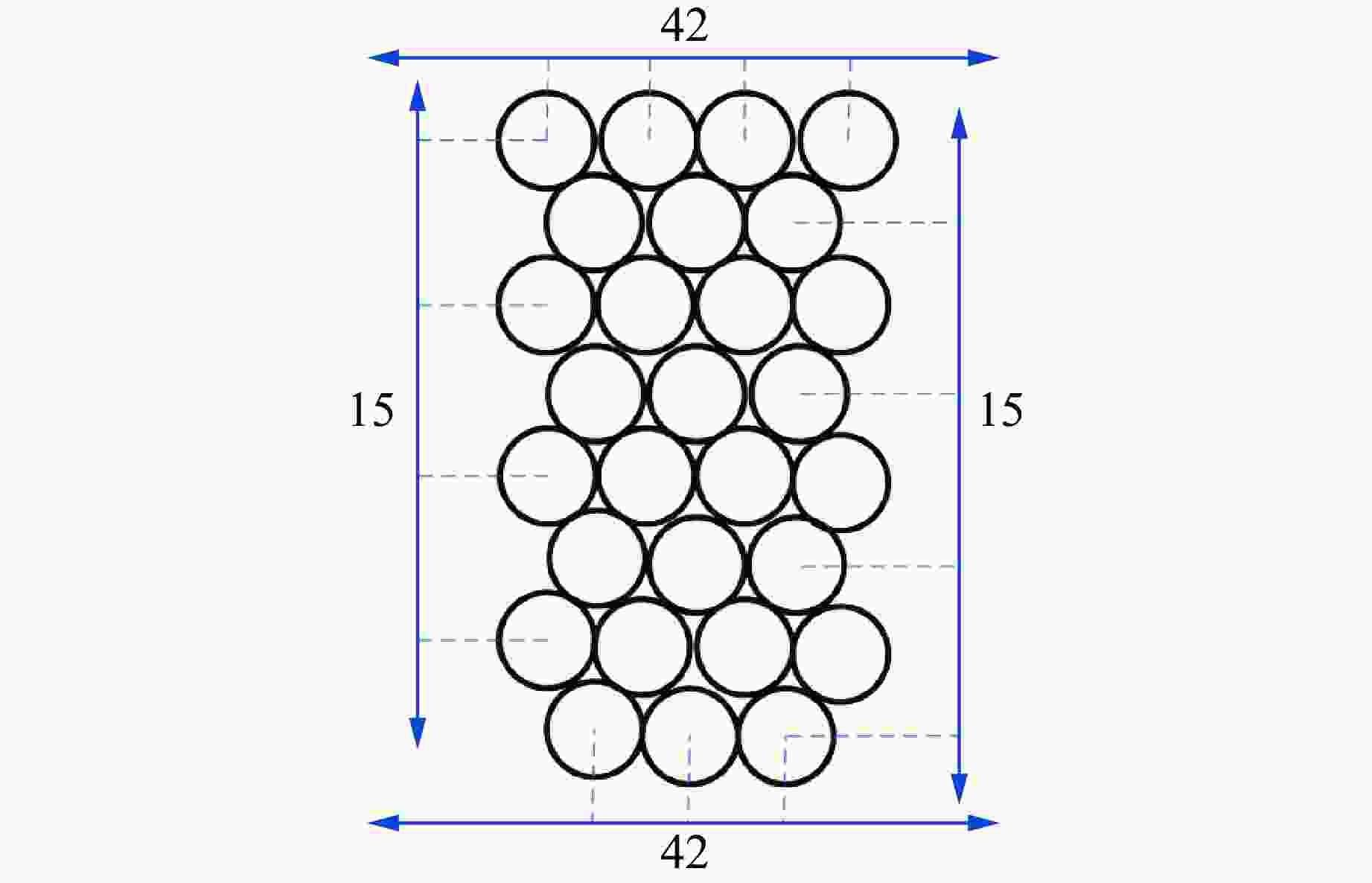
表 1 速度测量中靶板设置

Table 1. Target plate setting for velocity measurement

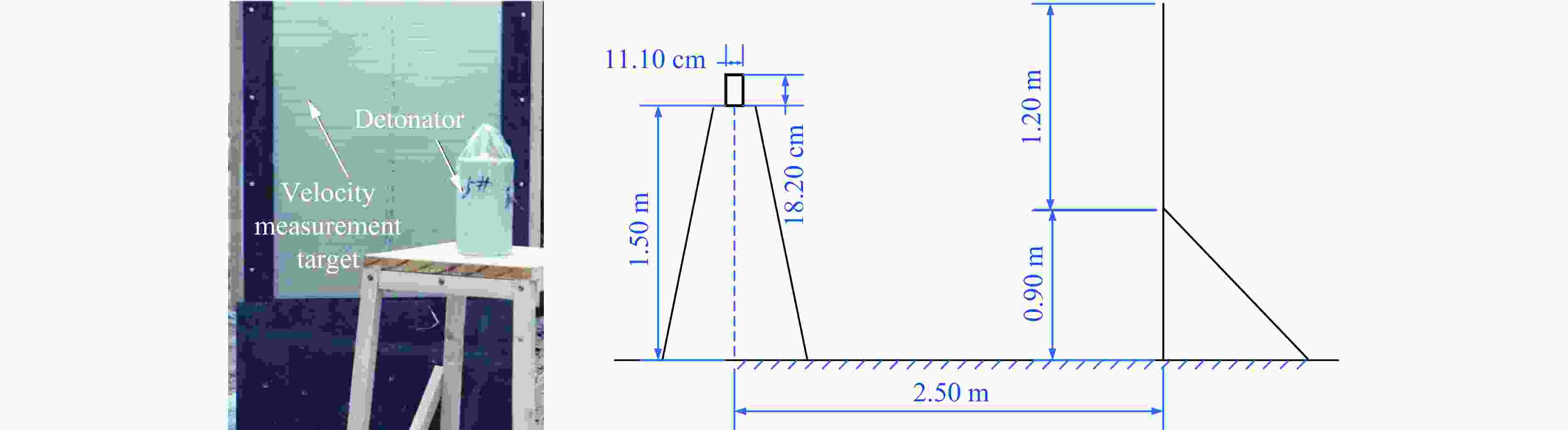
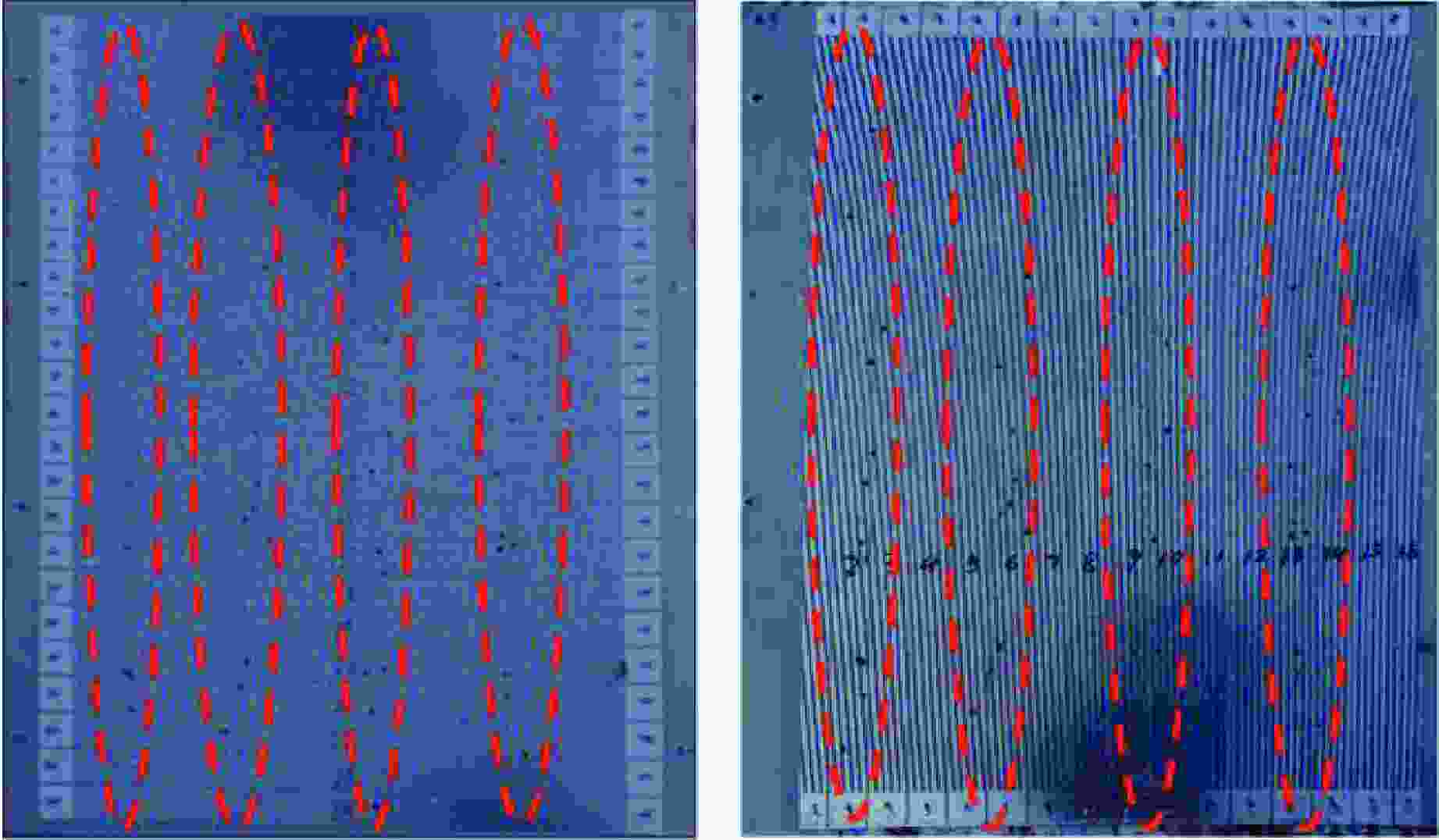
Test No.	Target No.	l/m
1	1	2.40
2	2	2.50
3	3	2.53
4	4	2.53

下载: 导出CSV

表 2 各交叉梳状靶上破片穿孔数统计

Table 2. Statistics of the number of fragment perforations on each cross-combed target

Target No.	Number of perforations
Target No.	1st column	2nd column	3rd column	4th column	Total
1	12	11	12	12	47
2	12	11	11	13	47
3	12	11	12	12	47
4	12	14	12	12	50

下载: 导出CSV

表 3 测速靶3上着靶破片的飞散角

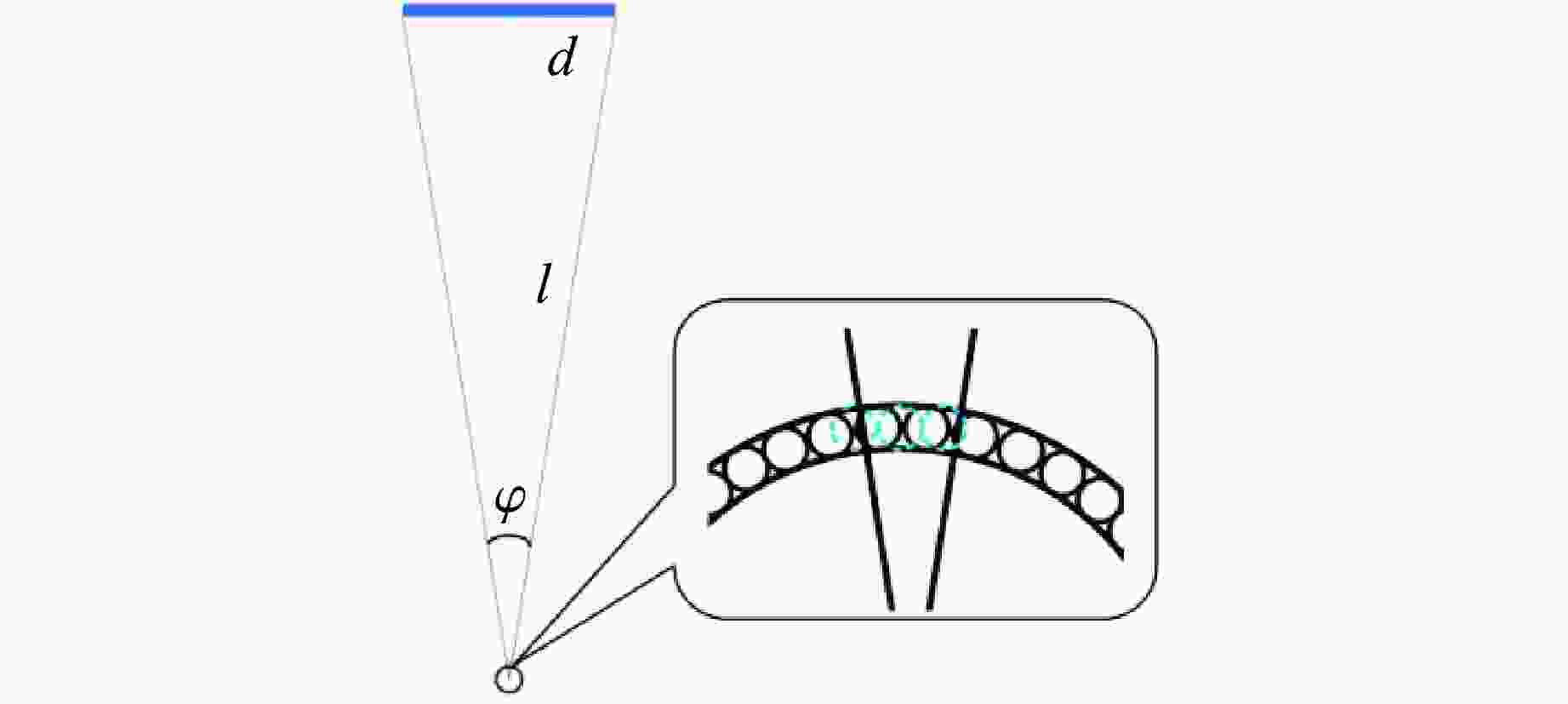
Table 3. Dispersion angles of the fragments on the velocity measurement target 3

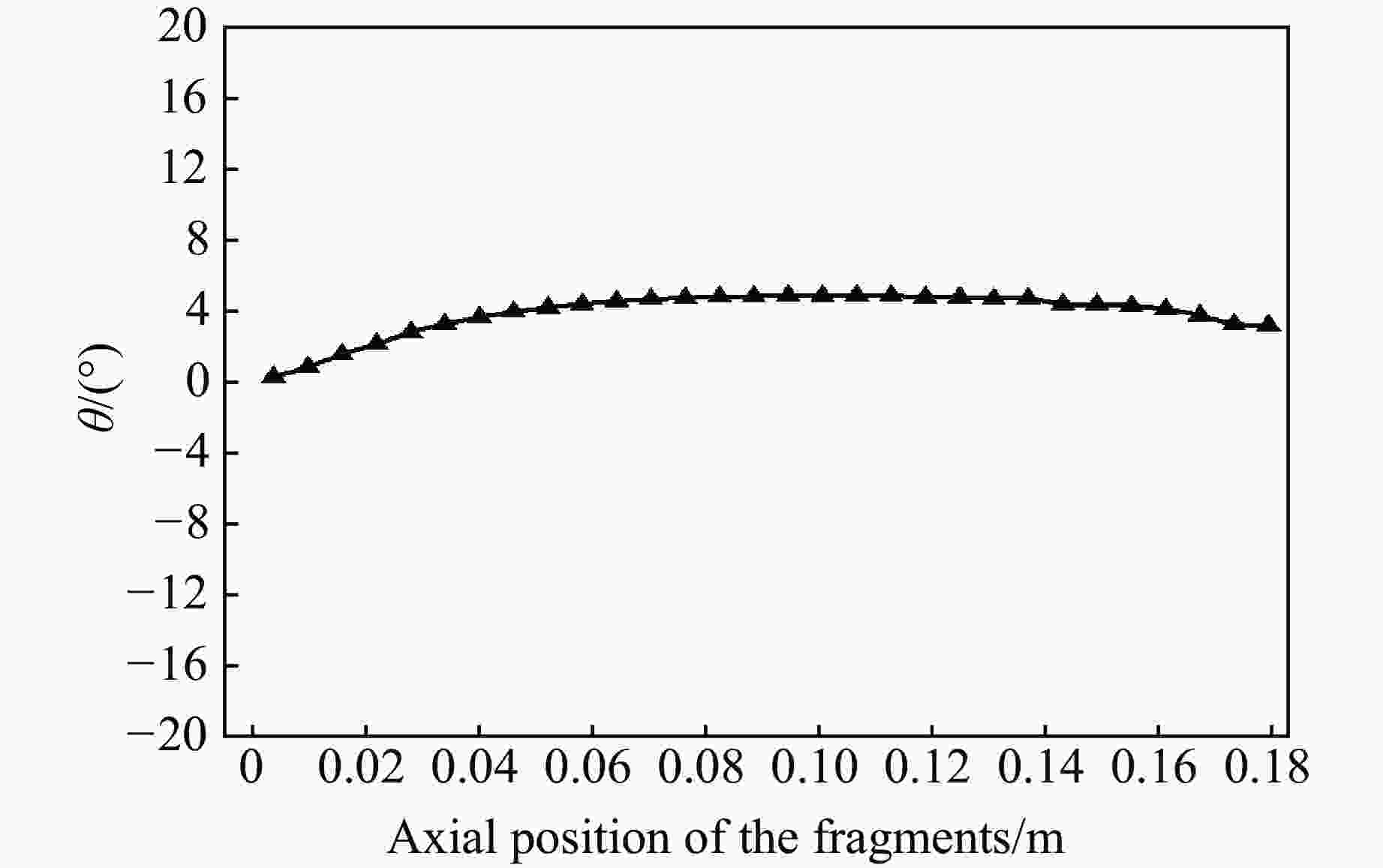
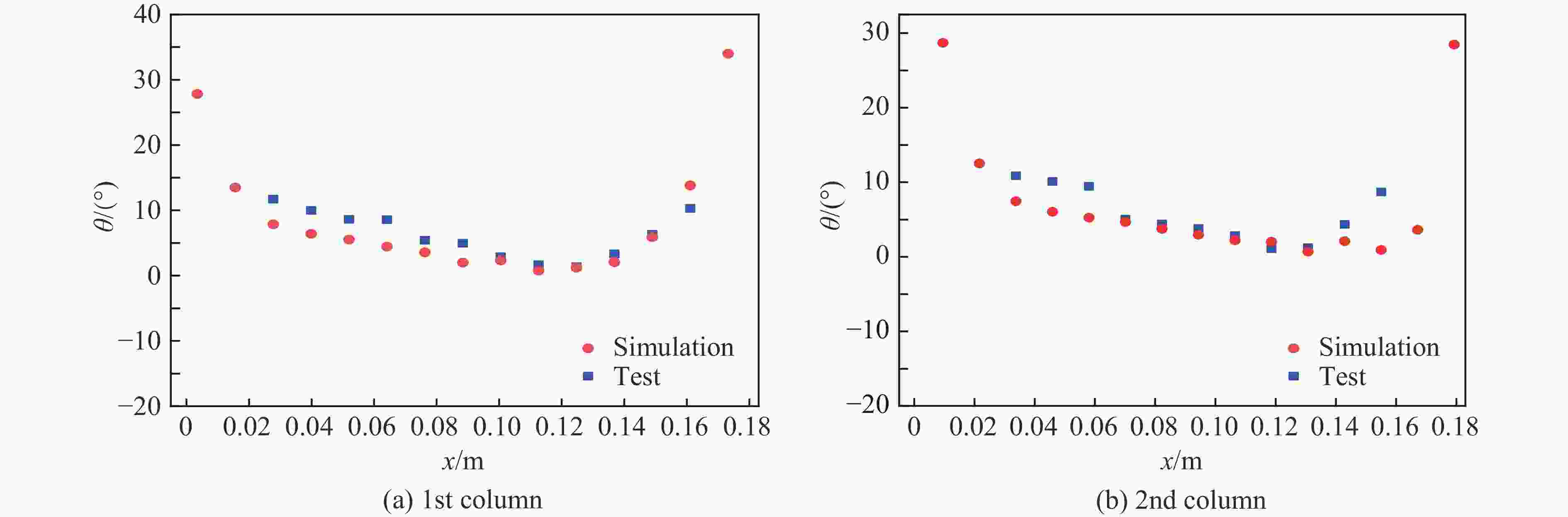
Serial No.	$ \theta $/(°)
Serial No.	1st column	2nd column	3rd column	4th column
1	10.30	8.70	10.72	9.07
2	6.32	4.34	5.85	3.66
3	3.34	1.22	2.85	1.18
4	1.36	1.08	1.90	0.85
5	1.69	2.85	1.04	1.10
6	2.90	3.80	2.67	2.71
7	4.97	4.40	4.99	4.44
8	5.42	5.04	5.47	4.95
9	8.59	9.45	8.72	5.06
10	8.61	10.10	8.90	8.46
11	9.99	10.87	9.95	9.48
12	11.70		10.66	11.13

下载: 导出CSV

表 4 试验测得的破片飞散速度

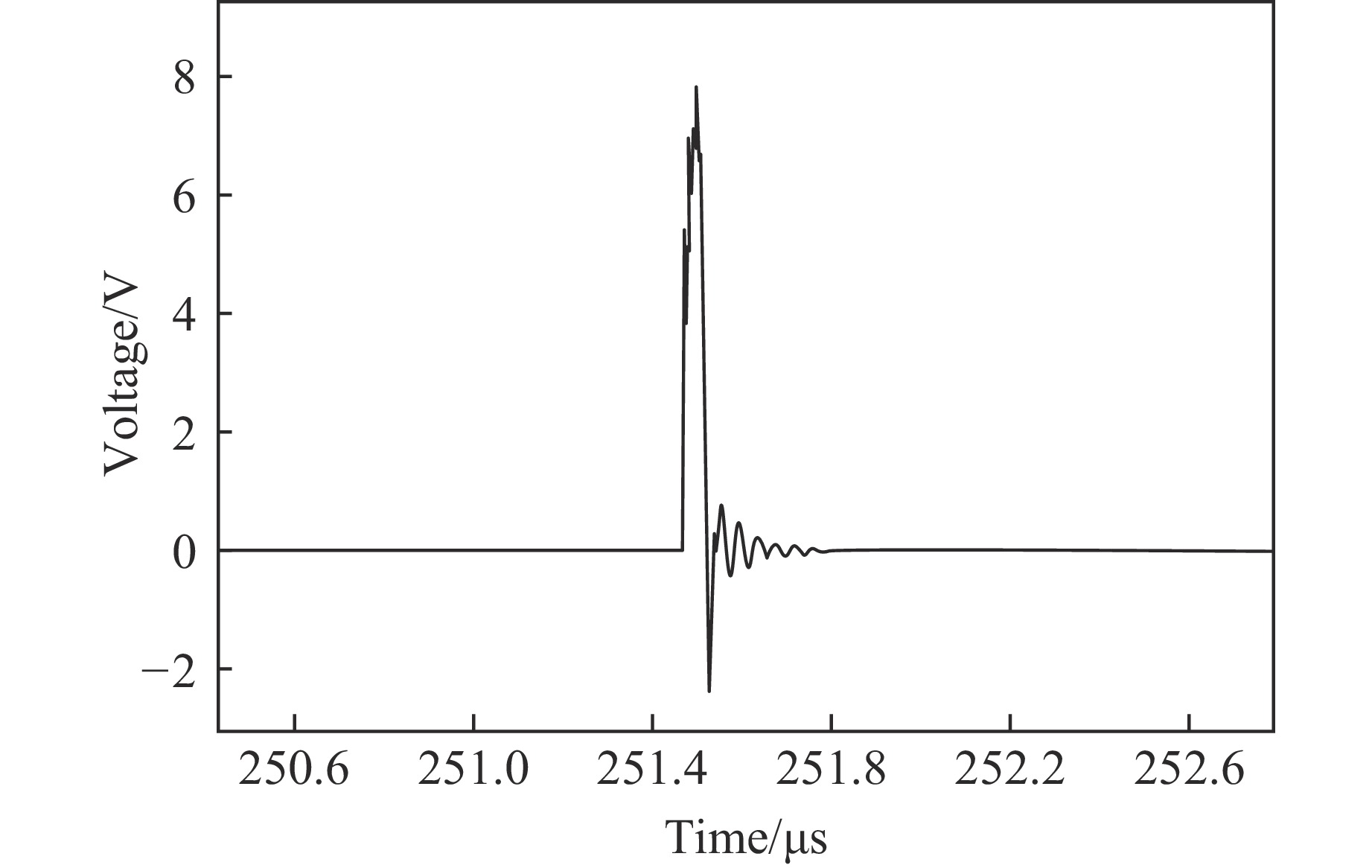
Table 4. Measured fragment dispersion velocities from the test

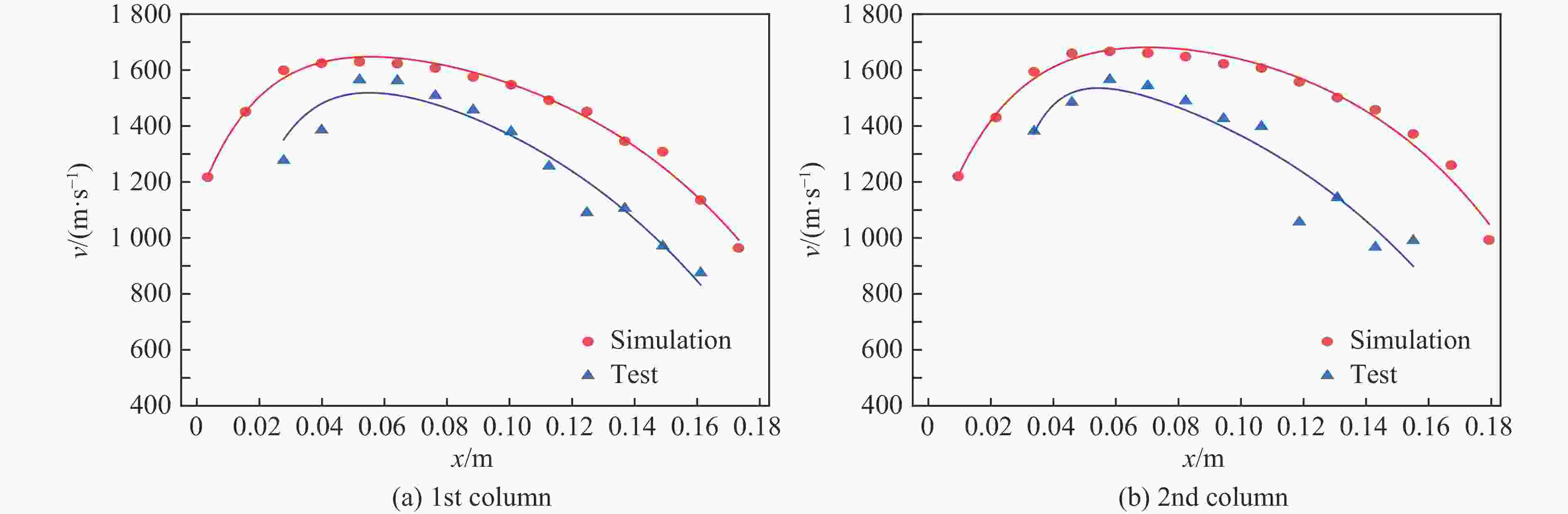
Serial No.	v/(m·s⁻¹)		Serial No.	v/(m·s⁻¹)
Serial No.	1st column	2nd column	Serial No.	1st column	2nd column
1	874.96	988.41	7	1457.39	1489.04
2	970.88	964.78	8	1508.74	1543.37
3	1105.71	1142.22	9	1562.08	1564.86
4	1090.10	1055.14	10	1564.89	1483.69
5	1256.42	1396.95	11	1385.48	1380.44
6	1380.11	1425.48	12	1276.79

下载: 导出CSV

表 5 93钨球形破片的材料参数

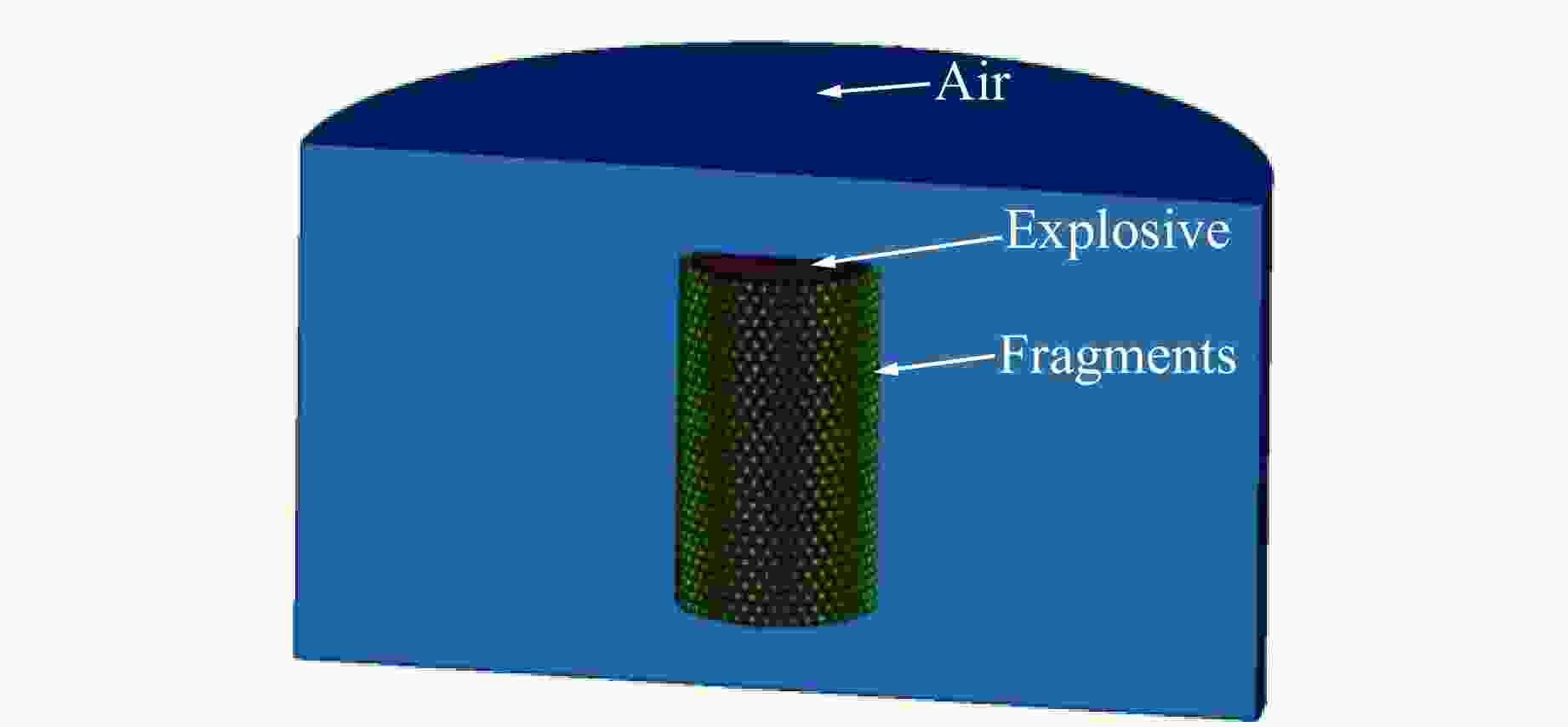
Table 5. Material parameters of 93 tungsten spherical fragments

ρ/(g·cm⁻³)	σ_s/GPa	E/GPa	G/GPa	μ
17.6	1.506	300	137	0.22

下载: 导出CSV

表 6 8701炸药性能参数

Table 6. 8701 explosive performance parameters

ρ/(g·cm⁻³)	v_D/(km·s⁻¹)	p_CJ/GPa	A/GPa	B/GPa	R₁	R₂
1.7	8.3	30	581.4	9.8016	4.1	1.4

下载: 导出CSV

表 7 不同长径比下的破片速度

Table 7. Fragments velocities under varying length-to-diameter ratios

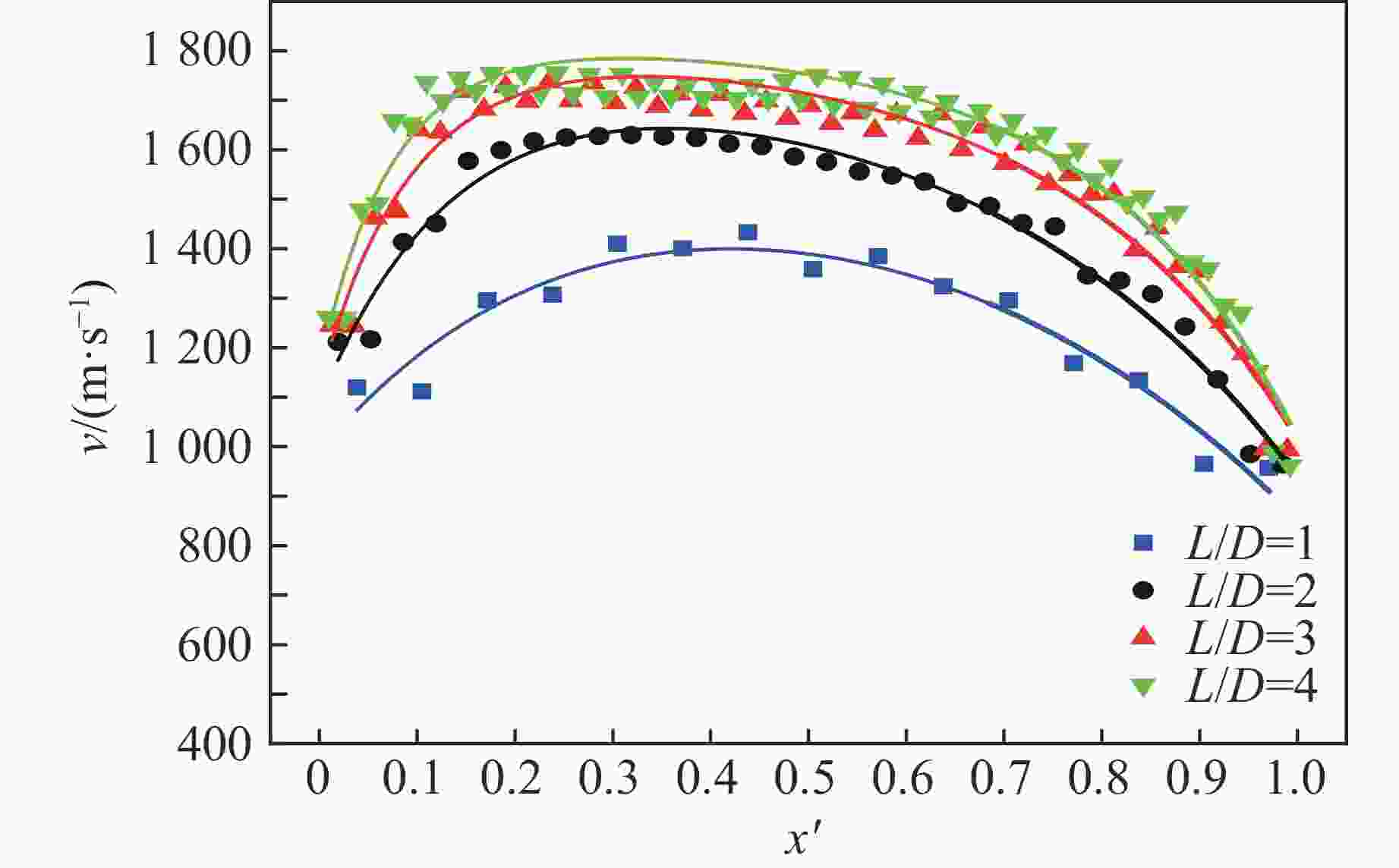
L/D	v_max/(m·s⁻¹)	v_min/(m·s⁻¹)	v_ave/(m·s⁻¹)
1	1432.98	956.72	1244.25
2	1629.43	963.78	1447.54
3	1737.14	993.59	1557.48
4	1755.82	961.62	1600.81

下载: 导出CSV

参考文献(25)

[1]	洪豆, 郑宇, 李文彬, 等. 破片战斗部杀伤面积影响规律研究 [J]. 兵器装备工程学报, 2021, 42(5): 37–42. doi: 10.11809/bqzbgcxb2021.05.007 HONG D, ZHENG Y, LI W B, et al. Research on influence law of fragment warhead’s killing area [J]. Journal of Ordnance Equipment Engineering, 2021, 42(5): 37–42. doi: 10.11809/bqzbgcxb2021.05.007
[2]	GURNEY R W. The initial velocities of fragments from bombs, shells and grenades: BRL 405 [R]. Maryland: Army Ballistic Research Laboratory, 1943.
[3]	ZULKOSKI T. Development of optimum theoretical warhead design criteria: B015617 [R]. China Lake, California: Naval Weapons Center, 1976: 39–44.
[4]	CHARRON Y J. Estimation of velocity distribution of fragmenting warheads using a modified Gurney method [D]. Wright Patterson: Air Force Institute of Technology, 1979.
[5]	HENNEQUIN E. Influence of the edge effects on the initial velocities of fragments from a warhead [C]//Proceedings of the 9th International Symposium on Ballistics. Shrivenham, 1986.
[6]	POOLE C J, OCKENDON J, CURTIS J. Gas leakage from fragmentation warheads [C]//Proceedings of the 20th International Symposium on Ballistics. Florida, 2002.
[7]	蒋浩征. 杀伤战斗部破片飞散初速V0的计算 [J]. 兵工学报, 1980(1): 68–79. JIANG H Z. Calculation of initial velocity V0 of fragments of a lethal warhead [J]. Acta Armamentarii, 1980(1): 68–79.
[8]	BACKOFEN J E. The effects of cylinder geometry and material on Gurney velocities and gas-push Gurney velocities measured during cylinder test experiments [R]. Oak Hill: BRIGS, 2002.
[9]	宋锋, 蒋建伟. 杀爆战斗部设计专家系统研究 [J]. 弹箭与制导学报, 2007, 27(4): 119–122. doi: 10.3969/j.issn.1673-9728.2007.04.035 SONG F, JIANG J W. Research on the expert design system of blast and fragmentation warhead [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(4): 119–122. doi: 10.3969/j.issn.1673-9728.2007.04.035
[10]	TAYLOR G I. The fragmentation of tubular bombs [J]. Scientific Papers of GI Taylor, 1963, 3(44): 387–390.
[11]	LI Y, CHEN D, JIANG M, et al. Research on the characteristic of projectile fragments dispersion based on fragment warhead design [J]. IOP Conference Series: Materials Science and Engineering, 2019, 573: 012104. doi: 10.1088/1757-899X/573/1/012104
[12]	冯顺山, 崔秉贵. 战斗部破片初速轴向分布规律的实验研究 [J]. 兵工学报, 1987(4): 60–63. FENG S S, CUI B G. An experimental investigation for the axial distribution of initial velocity of shells [J]. Acta Armamentarii, 1987(4): 60–63.
[13]	HUANG G Y, LI W, FENG S S. Axial distribution of fragment velocities from cylindrical casing under explosive loading [J]. International Journal of Impact Engineering, 2015, 76: 20–27. doi: 10.1016/j.ijimpeng.2014.08.007
[14]	王高, 尹国鑫, 李仰军, 等. 电阻网靶破片群速度测量方法 [J]. 探测与控制学报, 2011, 33(3): 47–50, 55. doi: 10.3969/j.issn.1008-1194.2011.03.011 WANG G, YIN G X, LI Y J, et al. Fragments velocity measuring based on resistor net target [J]. Journal of Detection & Control, 2011, 33(3): 47–50, 55. doi: 10.3969/j.issn.1008-1194.2011.03.011
[15]	田会, 金朋刚, 田亚男, 等. 一种用于破片测速的环形光幕装置 [J]. 测试技术学报, 2018, 32(4): 353–357. doi: 10.3969/j.issn.1671-7449.2018.04.014 TIAN H, JIN P G, TIAN Y N, et al. Study on the circular ring light screen device for measuring velocity of flying fragments [J]. Journal of Test and Measurement Technology, 2018, 32(4): 353–357. doi: 10.3969/j.issn.1671-7449.2018.04.014
[16]	马竹新, 王代华, 张瑞刚, 等. 基于可变阻抗靶网的多通道破片测速系统 [J]. 现代电子技术, 2022, 45(11): 83–87. doi: 10.16652/j.issn.1004⁃373x.2022.11.016 MA Z X, WANG D H, ZHANG R G, et al. Burst fragment’s multi-channel speed measuring system based on variable impedance target [J]. Modern Electronics Technique, 2022, 45(11): 83–87. doi: 10.16652/j.issn.1004⁃373x.2022.11.016
[17]	戴志远, 闫克丁. 基于高速相机的破片速度计算方法 [J]. 计算机与数字工程, 2021, 49(8): 1647–1650. doi: 10.3969/j.issn.1672-9722.2021.08.028 DAI Z Y, YAN K D. Fragment velocity calculation method based on high speed camera [J]. Computer & Digital Engineering, 2021, 49(8): 1647–1650. doi: 10.3969/j.issn.1672-9722.2021.08.028
[18]	史志鑫, 尹建平. 起爆方式对预制破片飞散性能影响的数值模拟研究 [J]. 兵器装备工程学报, 2018, 39(12): 84–88. doi: 10.11809/bqzbgcxb2018.12.017 SHI Z X, YIN J P. Numerical simulation study on effect of detonation method on the dispersion performance of prefabricated fragments [J]. Journal of Ordnance Equipment Engineering, 2018, 39(12): 84–88. doi: 10.11809/bqzbgcxb2018.12.017
[19]	邓吉平, 胡毅亭, 贾宪振, 等. 爆炸驱动球形破片飞散的数值模拟 [J]. 弹道学报, 2008, 20(4): 96–99. DENG J P, HU Y T, JIA X Z, et al. Numerical simulation of scattering characteristics of spherical fragment under blasting [J]. Journal of Ballistics, 2008, 20(4): 96–99.
[20]	刘荣琦. 预制破片爆轰过程模拟与仿真 [D]. 沈阳: 沈阳理工大学, 2023. LIU R Q. Simulation and simulation of detonation process of prefabricated fragments [D]. Shenyang: Shenyang Ligong University, 2023.
[21]	李明星, 王志军, 黄阳洋, 等. 不同形状轴向预制破片的飞散特性研究 [J]. 兵器装备工程学报, 2017, 38(12): 65–69. doi: 10.11809/scbgxb2017.12.016 LI M X, WANG Z J, HUANG Y Y, et al. Study on the scattering characteristics of different shape axial prefabricated fragment [J]. Journal of Ordnance Equipment Engineering, 2017, 38(12): 65–69. doi: 10.11809/scbgxb2017.12.016
[22]	李明静. 破片和冲击波对典型飞机机翼联合毁伤效应的研究 [D]. 北京: 北京理工大学, 2020. LI M J. Research on combined effects of fragment and blast loading on the wing of typical aircraft [D]. Beijing: Beijing Institute of Technology, 2020.
[23]	马宏伟, 王珂, 李艳, 等. 基于数字图像处理的破片速度参数测量 [J]. 测试技术学报, 2004, 18(4): 355–358. doi: 10.3969/j.issn.1671-7449.2004.04.017 MA H W, WANG K, LI Y, et al. Fragment velocity measurement based on digital image processing [J]. Journal of Test and Measurement Technology, 2004, 18(4): 355–358. doi: 10.3969/j.issn.1671-7449.2004.04.017
[24]	李丽萍, 孔德仁, 易春林, 等. 战斗部破片速度测量方法综述 [J]. 测控技术, 2014, 33(11): 5–7, 13. doi: 10.3969/j.issn.1000-8829.2014.11.002 LI L P, KONG D R, YI C L, et al. Review of method to measure the velocity of warhead fragments [J]. Measurement & Control Technology, 2014, 33(11): 5–7, 13. doi: 10.3969/j.issn.1000-8829.2014.11.002
[25]	谭多望, 王广军, 龚晏青, 等. 球形钨合金破片空气阻力系数实验研究 [J]. 高压物理学报, 2007, 21(3): 231–236. doi: 10.11858/gywlxb.2007.03.002 TAN D W, WANG G J, GONG Y Q, et al. Experimental studies on air drag coefficient of spherical tungsten fragments [J]. Chinese Journal of High Pressure Physics, 2007, 21(3): 231–236. doi: 10.11858/gywlxb.2007.03.002