First-Principles Investigation of the High-Pressure Phase Transition in Representative Alkali Metal Halides
-
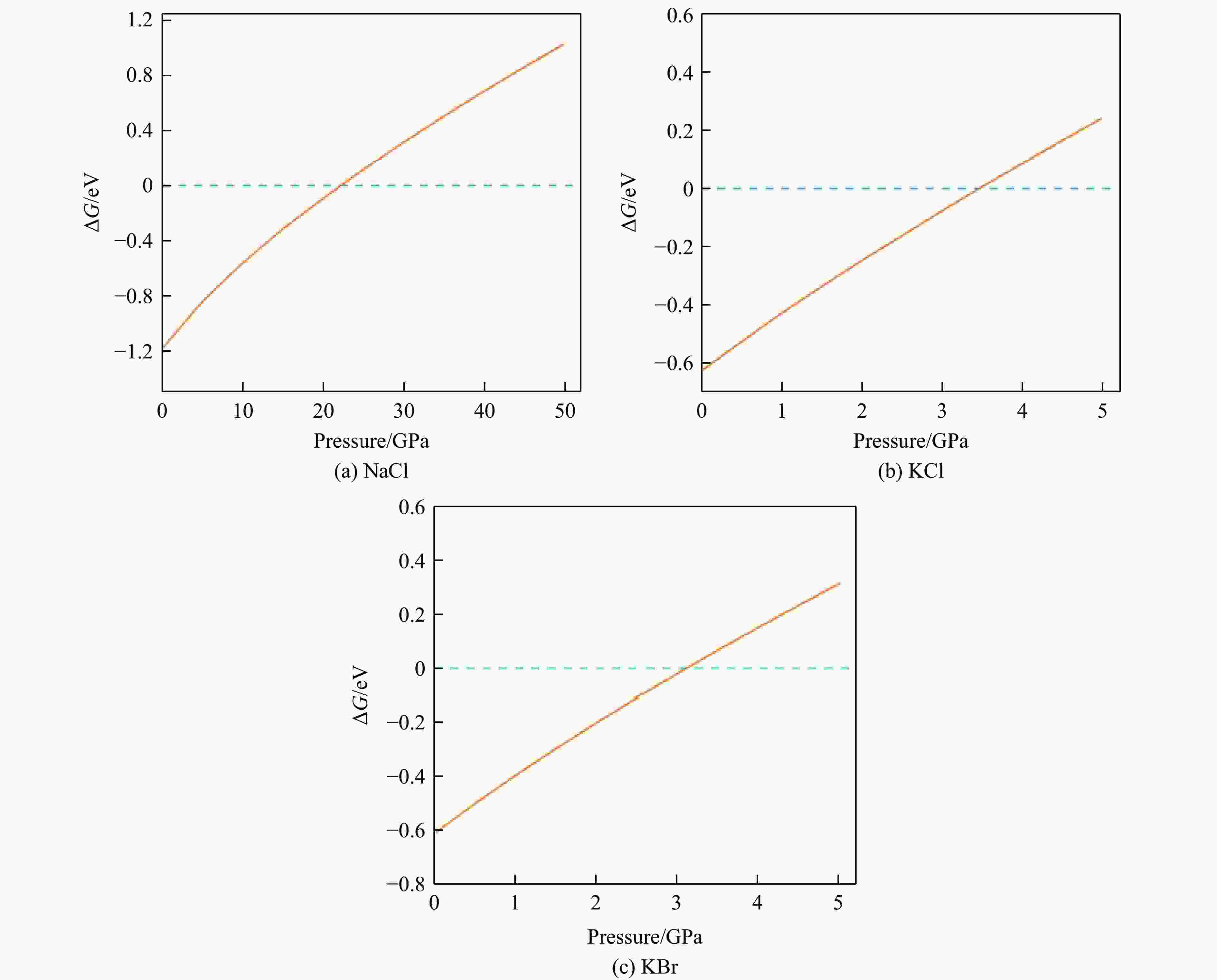
摘要: 基于密度泛函理论的第一性原理计算方法，研究了NaCl、KCl和KBr晶体在不同压力下相Ⅰ和相Ⅱ构型的几何、电子和力学性质，探讨了这些性质与相变点之间的关系，利用吉布斯自由能法对NaCl、KCl与KBr晶体的相变点进行判断。结果显示，对于NaCl的相Ⅰ结构，在0～30 GPa压力范围内，随着压力的升高，带隙不断增大；在30～50 GPa压力范围内，带隙随着压力的升高而下降，30 GPa正位于NaCl相Ⅰ结构的相变点。这表明根据电子结构判断金属卤化物在压力作用下的相变点具有一定的可行性。由高压下的晶体结构、声子谱以及力学稳定性无法对碱金属卤化物的相变点进行判断。通过吉布斯自由能法计算出了NaCl、KCl和KBr的相变点，分别为22.26、3.47和3.11 GPa。Abstract: Utilizing first-principles calculations based on density functional theory, this study investigates the geometric, electronic, and mechanical properties of NaCl, KCl, and KBr crystals in phase Ⅰ and phase Ⅱ structures under varying pressures. The relationships between these properties and the phase transition points are explored. Additionally, the Gibbs free energy method was employed to judge the phase transition points of NaCl, KCl, and KBr crystals. The results show that in the phase Ⅰ structure of NaCl, the band gap value increases with pressure from 0 to 30 GPa. However, in the range of 30−50 GPa, the band gap value decreases, indicating that 30 GPa is the phase transition point for NaCl phase Ⅰ. This suggests that pressure-induced changes in electronic structure can be indicative of metal halide phase transition points to some extent. However, pressure-induced alterations in crystal structure, phonon spectrum, and mechanical stability cannot reliably indicate alkali metal halide phase transition points. Furthermore, the phase transition points for NaCl, KCl and KBr calculated by Gibbs free energy method are 22.26, 3.47 and 3.11 GPa, respectively.
-
Key words:
- alkali halide /
- phase transition /
- first-principles /
- high pressure /
- band gap /
- Gibbs free energy
-
图 1 (a) NaCl型结构，(b) CsCl型结构
Figure 1. (a) NaCl-type structure; (b) CsCl-type structure
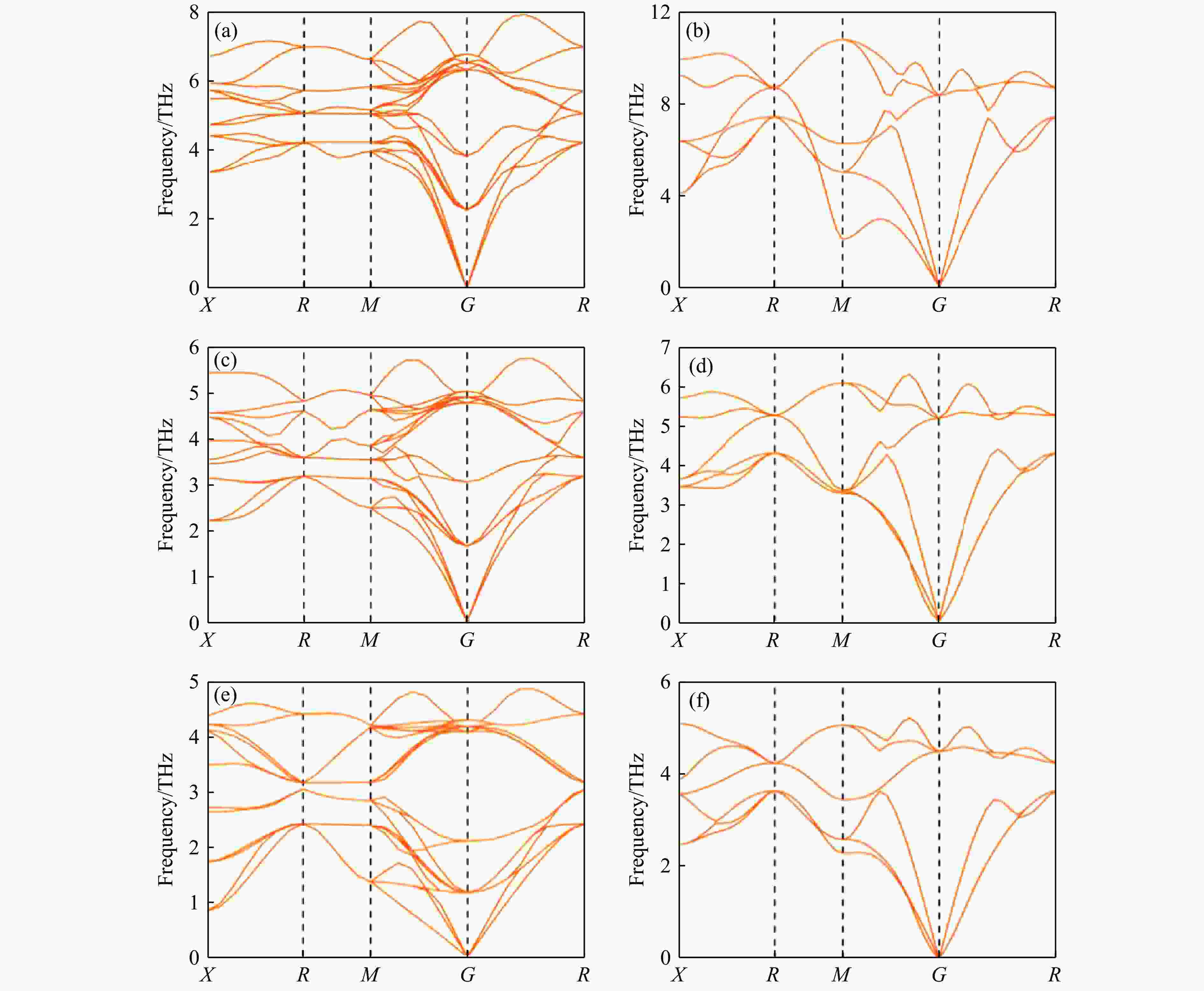
图 2 6种结构在稳定压力区间的声子谱：(a) 零压下NaCl相Ⅰ，(b) 30.6 GPa下NaCl相Ⅱ，(c) 零压下KCl相Ⅰ，(d) 2.12 GPa下KCl相Ⅱ，(e) 零压下KBr相Ⅰ，(f) 2.20 GPa下KBr相Ⅱ
Figure 2. Phonon spectra for six structures in the stable pressure range: (a) NaCl phase Ⅰ at zero pressure; (b) NaCl phase Ⅱ at 30.6 GPa; (c) KCl phase Ⅰ at zero pressure; (d) KCl phase Ⅱ at 2.12 GPa; (e) KBr phase Ⅰ at zero pressure; (f) KBr phase Ⅱ at 2.20 GPa
图 3 压力下6种结构的晶格常数a的变化：(a) 0～50 GPa下NaCl的相Ⅰ，(b) 0～50 GPa下NaCl的相Ⅱ，(c) 0～5 GPa下KCl的相Ⅰ，(d) 0～5 GPa下KCl的相Ⅱ，(e) 0～5 GPa下KBr的相Ⅰ，(f) 0～5 GPa下KBr的相Ⅱ
Figure 3. Lattice parameter a changes for six structures under pressure: (a) NaCl phase Ⅰ at 0−50 GPa; (b) NaCl phase Ⅱ at 0−50 GPa; (c) KCl phase Ⅰ at 0−5 GPa; (d) KCl phase Ⅱ at 0−5 GPa; (e) KBr phase Ⅰ at 0−5 GPa; (f) KBr phase Ⅱ at 0−5 GPa
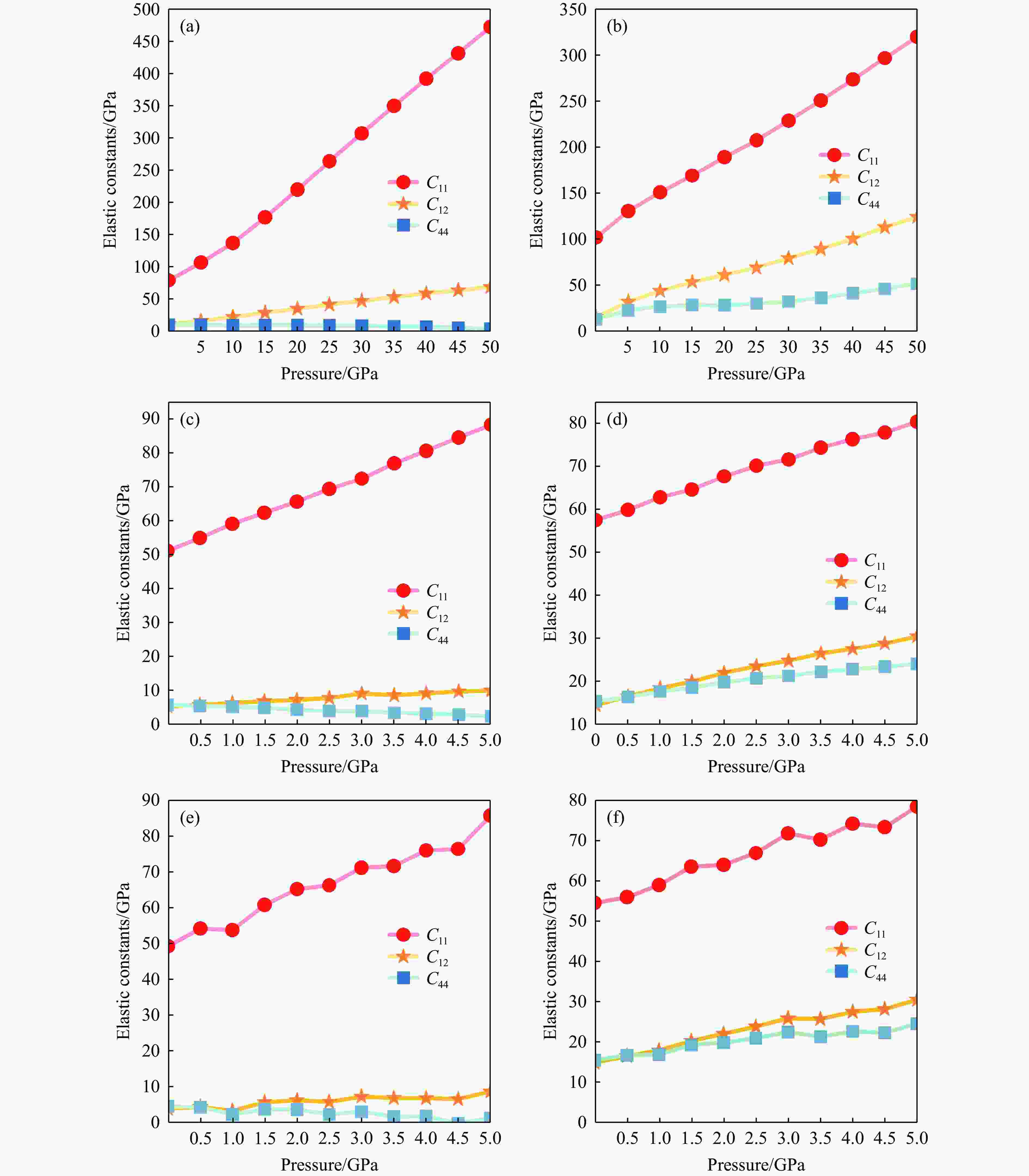
图 4 压力下6种结构的独立弹性常数：(a) 0～50 GPa下NaCl的相Ⅰ，(b) 0～50 GPa下NaCl的相Ⅱ，(c) 0～5 GPa下KCl的相Ⅰ，(d) 0～5 GPa下KCl的相Ⅱ，(e) 0～5 GPa下KBr的相Ⅰ，(f) 0～5 GPa下KBr的相Ⅱ
Figure 4. Independent elastic constants for six structures under pressure: (a) NaCl phase Ⅰ at 0−50 GPa; (b) NaCl phase Ⅱ at 0−50 GPa; (c) KCl phase Ⅰ at 0−5 GPa; (d) KCl phase Ⅱ at 0−5 GPa; (e) KBr phase Ⅰ at 0−5 GPa; (f) KBr phase Ⅱ at 0−5 GPa
图 5 压力下6种结构的能带带隙：(a) NaCl相Ⅰ，(b) NaCl相Ⅱ，(c) KCl相Ⅰ，(d) KCl相Ⅱ，(e) KBr相Ⅰ，(f) KBr相Ⅱ
Figure 5. Band gaps of six structures under pressure: (a) NaCl phase Ⅰ; (b) NaCl phase Ⅱ; (c) KCl phase Ⅰ; (d) KCl phase Ⅱ; (e) KBr phase Ⅰ; (f) KBr phase Ⅱ
图 6 NaCl、KCl和KBr的相Ⅰ与相Ⅱ的吉布斯自由能之差随压力的变化
Figure 6. Variations of Gibbs free energy difference of phase Ⅰ and phase Ⅱ structures of NaCl, KCl and KBr with pressure
表 1 NaCl、KCl、KBr的相Ⅰ和相Ⅱ结构的晶格常数和原胞体积
Table 1. Lattice constant and cell volumes for phase Ⅰ and phase Ⅱ structures of NaCl, KCl and KBr
Material Phase Space group p/GPa a/Å V0/Å3 Method NaCl Ⅰ $Fm\overline 3 m $ 0 5.672 45.637 This work 0 5.640 44.830 Experiment[18] NaCl Ⅱ $Pm\overline 3 m $ 30.6 3.043 28.186 This work 30.6 3.010 27.271 Experiment[15] KCl Ⅰ $Fm\overline 3 m $ 0 6.325 63.274 This work 0 6.294 62.333 Experiment[19] KCl Ⅱ $Pm\overline 3 m $ 2.12 3.681 49.864 This work 2.12 3.670 49.431 Experiment[20] KBr Ⅰ $Fm\overline 3 m $ 0 6.598 71.826 This work 0 6.586 71.418 Experiment[21] KBr Ⅱ $Pm\overline 3 m $ 2.20 3.833 56.293 This work 2.20 3.740 52.314 Experiment[22] 
下载: 导出CSV
表 2 NaCl、KCl、KBr的相Ⅰ（零压）和相Ⅱ（稳定压力）结构的独立弹性常数
Table 2. Independent elastic constants for phase Ⅰ (at zero pressure) and phase Ⅱ (at steady pressure) of NaCl, KCl and KBr
Material Phase C11/GPa C12/GPa C44/GPa NaCl Ⅰ 78.642 9.548 10.509 Ⅱ 230.431 79.373 31.849 KCl Ⅰ 51.087 5.107 5.587 Ⅱ 67.763 21.993 19.573 KBr Ⅰ 49.338 3.959 4.636 Ⅱ 65.451 22.265 19.708
下载: 导出CSV
表 3 NaCl、KCl、KBr的相Ⅰ和相Ⅱ结构的声子谱虚频统计
Table 3. Statistics of imaginary frequencies in the phase Ⅰ and phase Ⅱ phonon spectra for NaCl, KCl and KBr
Pressrue/GPa Imaginary frequency NaCl
(Phase Ⅰ）NaCl
(Phase Ⅱ)KCl
(Phase Ⅰ)KCl
(Phase Ⅱ)KBr
(Phase Ⅰ)KBr
(Phase Ⅱ)0 F F F F F F 0.5 F F F F F F 1.0 T F F F F F 1.5 T F F F F F 2.0 T F F F F F 2.5 T F F F F F 3.0 T F F F F F 3.5 T F F F F F 4.0 T F F F F F 4.5 T F F F F F 5.0 T F F F F F Note: “T” is imaginary frequency, while “F” is not imaginary frequency.
下载: 导出CSV
-
[1] NATTLAND D, HEYER H, FREYLAND W. Metal-nonmetal transition in liquid alkali metal-alkalihalide melts: electrical conductivity and optical reflectivity study [J]. Zeitschrift für Physikalische Chemie, 1986, 149(1): 1–15. doi: 10.1524/zpch.1986.149.1.001 [2] 张程祥, 吴绍曾, 吴姝妍, 等. NaCl、KCl和NaF晶体高压结构相变点的计算 [J]. 高压物理学报, 1993, 7(3): 233–237. doi: 10.11858/gywlxb.1993.03.011ZHANG C X, WU S Z, WU S Y, et al. Calculations of the high pressure phase transition point of NaCl, KCl and NaF crystals [J]. Chinese Journal of High Pressure Physics, 1993, 7(3): 233–237. doi: 10.11858/gywlxb.1993.03.011 [3] 孙力, 王永生, 何志谊, 等. 电子俘获材料KCl: Eu2+的光存储特性研究 [J]. 激光与红外, 2000, 30(2): 117–118, 120. doi: 10.3969/j.issn.1001-5078.2000.02.016SUN L, WANG Y S, HE Z Y, et al. Optical storage properties of electron trapping material KCl: Eu2+ [J]. Laser & Infrared, 2000, 30(2): 117–118, 120. doi: 10.3969/j.issn.1001-5078.2000.02.016 [4] 崔守鑫, 蔡灵仓, 胡海泉, 等. 氯化钠晶体在高温高压下热物理参数的分子动力学计算 [J]. 物理学报, 2005, 54(6): 2826–2831. doi: 10.7498/aps.54.2826CUI S X, CAI L C, HU H Q, et al. Molecular dynamics simulation for thermophysical parameters of sodium chloride solids at high temperature and high pressure [J]. Acta Physica Sinica, 2005, 54(6): 2826–2831. doi: 10.7498/aps.54.2826 [5] 郑东阳, 刘贺, 李春, 等. 大截面溴化钾晶体生长工艺研究 [J]. 硅酸盐学报, 2015, 43(1): 60–64. doi: 10.14062/j.issn.0454-5648.2015.01.09ZHENG D Y, LIU H, LI C, et al. Growth process of large section crystal of potassium bromide [J]. Journal of the Chinese Ceramic Society, 2015, 43(1): 60–64. doi: 10.14062/j.issn.0454-5648.2015.01.09 [6] JIANG W, YIN L, CHEN H M, et al. NaCl nanoparticles as a cancer therapeutic [J]. Advanced Materials, 2019, 31(46): 1904058. doi: 10.1002/adma.201904058 [7] BANGARU S, MURALIDHARAN G, BRAHMANANDHAN G M. Thermoluminescence and optical studies on X-irradiated terbium-doped potassium bromide crystals [J]. Journal of Luminescence, 2010, 130(4): 618–622. doi: 10.1016/j.jlumin.2009.11.005 [8] BANGARU S, RAVI D, SARADHA K. Comparison of luminescence property of gamma-ray irradiated Tb3+-doped and Ce3+ Co-doped potassium halide single crystals [J]. Luminescence, 2017, 32(3): 358–363. doi: 10.1002/bio.3187 [9] BANGARU S, SARADHA K, MURALIDHARAN G. Thermoluminescence and photoluminescence studies on γ-ray-irradiated Ce3+, Tb3+-doped potassium chloride single crystals [J]. Luminescence, 2016, 31(3): 649–653. doi: 10.1002/bio.3005 [10] OKADA G, FUJIMOTO Y, TANAKA H, et al. Dynamics of radio-photoluminescence and thermally-stimulated luminescence in KBr: Sm [J]. Journal of Materials Science: Materials in Electronics, 2017, 28(21): 15980–15986. doi: 10.1007/s10854-017-7496-z [11] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865–3868. doi: 10.1103/PhysRevLett.77.3865 [12] PERDEW J P, CHEVARY J A, VOSKO S H, et al. Erratum: atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation [J]. Physical Review B, 1993, 48(7): 4978. doi: 10.1103/PhysRevB.48.4978.2 [13] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [Phys. Rev. Lett. 77, 3865 (1996)] [J]. Physical Review Letters, 1997, 78(7): 1396. doi: 10.1103/PhysRevLett.78.1396 [14] GRIMME S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction [J]. Journal of Computational Chemistry, 2006, 27(15): 1787–1799. doi: 10.1002/jcc.20495 [15] LIU L G, BASSETT W A. Compression of Ag and phase transformation of NaCl [J]. Journal of Applied Physics, 1973, 44(4): 1475–1479. doi: 10.1063/1.1662396 [16] PRABHAKAR N V K, SINGH R K, GAUR N K, et al. High-pressure phase transitions in some alkali halides [J]. Journal of Physics: Condensed Matter, 1990, 2(15): 3445–3449. doi: 10.1088/0953-8984/2/15/002 [17] RAMOLA Y, LOUIS C N, AMALRAJ A. Electronic band structure, density of states, phase transitions, metallization and superconducting transition of KBr under high pressure [J]. Orbital: the Electronic Journal of Chemistry, 2020, 12(2): 69–75. doi: 10.17807/orbital.v12i2.1401 [18] BASSETT W A, TAKAHASHI T, MAO H K, et al. Pressure-induced phase transformation in NaCl [J]. Journal of Applied Physics, 1968, 39(1): 319–325. doi: 10.1063/1.1655752 [19] COHEN A J, GORDON R G. Theory of the lattice energy, equilibrium structure, elastic constants, and pressure-induced phase transitions in alkali-halide crystals [J]. Physical Review B, 1975, 12(8): 3228–3241. doi: 10.1103/PhysRevB.12.3228 [20] LIVSHITS L D, RYABININ Y N, LARIONOV L V. Phase transitions of potassium chloride and its alloys with rubidium chloride at high pressures [J]. Soviet Physics Technical Physics, 1969, 14: 837. [21] LEIBSSLE H. Die piezooptischen eigenschaften einiger alkalihalogenide des steinsalz-typus [J]. Zeitschrift für Kristallographie: Crystalline Materials, 1960, 114(1): 457–467. doi: 10.1524/zkri.1960.114.16.457 [22] WEIR C E, PIERMARINI G J. Lattice parameters and lattice energies of high-pressure polymorphs of some alkali halides [J]. Journal of Research of the National Bureau of Standards A, 1964, 68A(1): 105–111. doi: 10.6028/jres.068A.009 [23] 高娟, 刘其军, 蒋城露, 等. 7大晶系的力学稳定性判据及其应用: 以SiO2为例 [J]. 高压物理学报, 2022, 36(5): 051101. doi: 10.11858/gywlxb.20220575GAO J, LIU Q J, JIANG C L, et al. Criteria of mechanical stability of seven crystal systems and its application: taking silica as an example [J]. Chinese Journal of High Pressure Physics, 2022, 36(5): 051101. doi: 10.11858/gywlxb.20220575 [24] GAO J, LIU Q J, TANG B. Elastic stability criteria of seven crystal systems and their application under pressure: taking carbon as an example [J]. Journal of Applied Physics, 2023, 133(13): 135901. doi: 10.1063/5.0139232 -
下载:
点击查看大图
计量
- 文章访问数: 43
- HTML全文浏览量: 21
- PDF下载量: 1
