高温高压条件下聚合物的状态方程和相变

苏琪琦; 李蕾; 李俊; 胡建波; 耿华运; 柳雷

doi:10.11858/gywlxb.20240863

高温高压条件下聚合物的状态方程和相变

doi: 10.11858/gywlxb.20240863

中国工程物理研究院流体物理研究所冲击波物理与爆轰物理全国重点实验室, 四川绵阳　621999

基金项目: 国家自然科学基金（12174356）；中国工程物理研究院院长基金（YZJJZQ202203）；冲击波物理与爆轰物理全国重点实验室基金（JCKYS2021212002）

详细信息

作者简介:
苏琪琦（2001－），女，硕士研究生，主要从事高压材料科学与化学研究. E-mail：suqiqi22@gscaep.ac.cn

通讯作者:
柳　雷（1982－），男，博士，副研究员，主要从事高压材料结构和物性研究. E-mail：lei.liu@caep.cn

耿华运（1976－），男，博士，研究员，主要从事凝聚态物理研究. E-mail：s102genghy@caep.cn

中图分类号: O63; O521.2
计量
- 文章访问数: 251
- HTML全文浏览量: 83
- PDF下载量: 48
出版历程
- 收稿日期: 2024-07-26
- 修回日期: 2024-09-03
- 录用日期: 2024-09-03
- 网络出版日期: 2025-01-13
- 刊出日期: 2025-04-03

Polymers at High Pressures and High Temperatures: Advances in Equation of State and Phase Transition Investigations

SU Qiqi,
LI Lei^{*
, ,},
LI Jun,
HU Jianbo,
GENG Huayun^{*
, ,},
LIU Lei

National Key Laboratory of Shock Wave and Detonation Physics, Institute of Fluid Physics, CAEP, Mianyang 621999, Sichuan, China

摘要

摘要: 聚合物是现代社会最实用的材料之一，也是含能材料领域的研究热点之一。随着应用范围的不断拓展，聚合物材料的服役环境日益极端。然而，到目前为止，人们对聚合物在高温高压极端条件下的状态方程和结构相变等重要物性还知之甚少，一定程度上限制了聚合物在更广阔领域的应用。聚合物自身的混合相态和多尺度分级结构给其在极端条件下的结构和物性研究带来了巨大的挑战。本文概述了近年来高温高压条件下聚合物状态方程和相变研究领域的进展，指出了目前聚合物状态方程和相变研究所面临的问题，以及现有实验技术的局限性，最后，从实验上提出了相关问题的潜在解决方法，希望对今后高温高压极端条件下聚合物状态方程和相变研究有所裨益。
- 聚合物 /
- 高温高压 /
- 状态方程 /
- 相变
Abstract: Polymers are one of the most widely used materials in modern society. The interest of applying polymers under extreme conditions (high pressure and high temperature) is ever increasing. However, our knowledge of the equation of state (EOS) and phase transition of polymers at high pressures and high temperatures is extremely limited, which prevents their applications in broad fields. Because of their mixed phases and their hierarchical structures, investigation on the structures and properties of polymers at extreme conditions is a big challenge to date. In this short review, we summarize the recently published studies on the EOS and phase transition of polymers at extreme conditions. We point out the challenges faced and the limitations of the experimental techniques used, which is expected to be useful for the investigations of the EOS and phase transition of polymers in the future.
- polymer /
- high pressure and high temperature /
- equation of state /
- phase transition

HTML全文

盐类矿物是指以矿石或岩石形式存在于自然界的碱金属/碱土金属的卤化物、硫酸盐、碳酸盐、硝酸盐等，被广泛应用于工业和农业领域^[1]。该类矿物在高温高压下的结构相变在物理与地球科学领域备受关注，例如：2013 年理论与实验研究发现，典型离子晶体 NaCl 在高压下转变为 Na₃Cl和NaCl₃^[2]；Santos等^[3]发现，作为地球深部碳循环重要载体的碳酸盐在高温高压下具有10余种结构。硝酸根离子（ $\rm NO_3^-$ ）和碳酸根离子（ $\rm CO_3^{2-}$ ）具有等电子结构，形成的盐类矿物均为离子晶体。离子晶体中的离子键易受外部温度和压强调控而发生结构相变，鉴于 $\rm NO_3^-$ 和 $\rm CO_3^{2-}$ 在结构和电子性质上具有相似之处，高温高压下碱金属硝酸盐是否具有丰富的结构相变是值得深入探讨的问题。

碱金属硝酸盐被广泛用于多个领域，如作为传热、储热介质等运用于工业炸药、冶金淬火硬化、太阳能和核能领域^[4–6]。碱金属硝酸盐在较低压强下已经展现出丰富的相变行为^[7]，引起了许多关注。研究发现，在常压下硝酸铷（RbNO₃）从熔融态退火至常温的过程中历经了4个不同的结构，即Ⅰ、Ⅱ、Ⅲ、Ⅳ相。Ⅰ相在熔点至564 K的区间内稳定，为NaCl型的立方无序结构（空间群Fm $\overline 3$ m）^[8]；Ⅱ相在564～492 K区间稳定，具有菱方结构（空间群R $\overline 3$ m）^[7]；Ⅲ相在492～437 K区间稳定，一般认为是CsCl型立方结构（空间群Pm $\overline 3$ m）^[8]；Ⅳ相在常温下稳定，为菱方结构（空间群P3₁）^[7]。2001年，Liu等^[9]利用分子动力学模拟方法从理论上发现了RbNO₃在Ⅳ→Ⅲ相变过程中 $\rm NO_3^-$ 基团从定向有序变为无序。在高压实验研究方面，1984年Dean等^[10]通过原位X射线衍射研究发现了RbNO₃的Ⅳ→Ⅴ结构相变，其相变压强约为1.2 GPa，高压Ⅴ相为正交结构（空间群Pmmn）。

与RbNO₃的高温研究相比，RbNO₃的高压研究并不丰富。本研究将基于第一性原理计算，结合CALYPSO晶体结构预测软件，系统地探索零温下RbNO₃在0～100 GPa区间的结构与物理性质。

1. 计算方法

在0 K和0、20、40、60、80和100 GPa的压强条件下，使用CALYPSO软件^[11–12]进行RbNO₃的结构搜索。结构预测过程中演化代数为20，模拟采用2倍胞和4倍胞，每个分子式的体积在32～70 Å³区间，体积随压强的升高而减小。基于第一性原理计算，交换关联泛函采用广义梯度近似（generalized gradient approximation，GGA）^[13]的Perdew-Burke-Ernzerhof（PBE）泛函^[13]、Original vdW-DF泛函^[14]、Revised PBE for solids（PBEsol）泛函^[15]以及Revised PBE Hammer et al.（RPBE）泛函^[16]，数值模拟在VASP^[17]软件包中实现，采用投影缀加波（projected augmented wave，PAW）^[18]方法，Rb、N、O的价电子分别选为4s²4p⁶5s¹、2s²2p³和2s²2p⁴，平面波截断能取520 eV，对于R3m、Pnma和Pmmn相，布里渊区采样的网格尺寸分别为10×10×10、6×8×6和10×8×10，总能量收敛至小于1×10⁻⁵ eV/atom。采用有限位移法结合PHONOPY软件^[19]计算声子谱，扩胞数分别为3×3×2、2×3×2和3×3×3。弹性模量计算采用Voigt-Reuss-Hill（VRH）平均法^[20–21]，晶体结构和声子模式的原子位移可视化通过VESTA软件^[22]和V_Sim软件^[23]实现。

2. 结果与讨论

RbNO₃的常温常压结构为RbNO₃-Ⅳ相，空间群为P3₁。采用4种不同交换关联泛函优化0 GPa下RbNO₃-Ⅳ相的平衡体积与晶胞参数，结果列于表1。对比实验结果可以发现，4种交换关联泛函的准确性从低到高依次为RPBE、vdW-DF、 PBE、 PBEsol。因此，后续研究将主要基于PBE和PBEsol泛函展开。

表 1 RbNO₃-Ⅳ相的晶格常数的理论值与实验值的比较

Table 1. Comparison between experimental and calculated lattice parameters of RbNO₃-Ⅳ phase

Method	Condition	a/Å	c/Å	Volume/Å³
Simulation	PBE	10.68(+1.62%)	7.60(+1.88%)	867.56(+5.29%)
	vdW-DF	10.72(+2.00%)	7.62(+2.14%)	876.29(+6.35%)
	PBEsol	10.39(−1.14%)	7.39(−0.94%)	797.69(−3.19%)
	RPBE	11.14(+5.99%)	7.91(+6.03%)	982.63(+19.26%)
Experiment	T=296 K^[24]	10.47	7.44	815.58
	T=298 K^[25]	10.55	7.47	831.43
	Average	10.51	7.46	823.96

下载: 导出CSV

| 显示表格

采用PBE和PBEsol泛函在0～100 GPa压强范围内对能量较低的备选结构进行精细优化后发现，R3m、Pnma、P3₁、Pmmn相在不同的压强区间内具有热力学稳定性，其焓差随压强变化曲线如图1所示。在0 GPa下，2种泛函的预测结果均表明R3m相的能量最稳定；随压强的升高，R3m相均转变为Pnma相。继续加压，PBE泛函与PBEsol泛函预测的相变序列不同：PBE泛函预测结果表明，Pnma相先相变至Ⅳ相（即P3₁结构），再相变至Ⅴ相（即Pmmn结构）；PBEsol泛函预测结果表明，Pnma相直接转变为Ⅴ相。压强-体积关系如图2所示，其中，ΔV/V为体积坍塌率。除PBE泛函预测的Pnma→Ⅳ相变中不能看到明显的体积坍缩以外，PBE泛函所预测的其余2个相变和PBEsol预测的2个相变均存在明显的体积坍塌，这种体积不连续表明它们均为一级相变。

图 1 R3m、P3₁和Pmmn相相对于Pnma相的热力学焓差曲线

Figure 1. Calculated enthalpy difference of R3m, P3₁ and Pmmn phases relative to Pnma as a function of pressure

下载: 全尺寸图片幻灯片

图 2 R3m、Pnma、P3₁和Pmmn相的体积随压强的变化

Figure 2. Calculated volume of R3m, Pnma, P3₁ and Pmmn phases as a function of pressure

下载: 全尺寸图片幻灯片

考虑到PBEsol泛函对实验Ⅳ相的平衡体积与晶胞参数的描述更为准确，后续研究将主要采用PBEsol泛函预测零温下RbNO₃的相变序列（R3m→Pnma→Pmmn）。该序列所对应的2个相变点的压强分别为1.7和8.2 GPa，相应的体积坍塌率分别为3.73%和2.54%。由于碳酸钙的结构与碱金属硝酸盐的结构相似，两者具有等电子结构，因此，对比了它们的高压相变序列。碳酸钙的相变序列为：R $\overline 3$ c→Pnma→Pmmn→P2₁/c，相变压强分别为1、40和67 GPa^[26]。可以发现，RbNO₃的Pnma→Pmmn的相变压强远低于CaCO₃发生相同相变时的压强，其可能的原因如下：一方面，Rb⁺与 $\rm NO_3^{-}$ 之间的离子相互作用比Ca²⁺与 $\rm CO_3^{2-}$ 之间的离子作用更弱；另一方面，Rb⁺的半径大于Ca²⁺的半径，Rb⁺产生的“化学预压缩”更强。上述零温理论预测出了能量比常温常压下的Ⅳ相更小的2个低压新相（R3m相和Pnma相），表明低压下RbNO₃可能存在不同于实验给出的常温常压下Ⅳ相的低温新相。

预测获得的0 GPa下的R3m相、4 GPa下的Pnma相和12 GPa下的Pmmn相的平衡态晶格常数、原子位置列于表2，相应的晶体结构见图3。3个结构存在明显差异，三方相的单胞包含3个RbNO₃分子式，而正交相的单胞则分别包含4和2个RbNO₃分子式。3个相在0、4、12 GPa压强下的弹性常数列于表3，可以发现，三方相和正交相分别有7和9个独立的弹性常数。在R3m相中，C₄₄随压强的升高先减小后增大，其余的弹性常数均与压强呈正相关。3个相的弹性模量，即体积模量B、剪切模量G以及杨氏模量E也列于表3中，分别表示抵抗脆性变形、抵抗塑性变形和抵抗张力的能力。同一压强下Pmmn相的弹性模量最大，表明Pmmn相的抗变形能力比另2个相更强。此外，根据“伯恩-黄昆”弹性稳定性判据^[27–28]分析3个相的机械稳定性，判别条件见式(1)和式(2)。力稳定性分析显示：12 GPa时，Pnma相的C₅₅ < 0，不满足弹性稳定性判据，因而Pnma相不是弹性稳定结构；除此之外，各相在相应压强下的弹性常数均满足弹性稳定判据。

表 2 高压下R3m、Pnma和Pmmn相的晶格参数和原子位置

Table 2. Lattice parameters and atomic coordinates of R3m, Pnma and Pmmn phases at different pressures

Phase	Pressure/GPa	Lattice parameters	Wyckoff positions
R3m	0	a=b=5.64 Å, c=9.48 Å, α=β=90°, γ=120°	Rb1: 3a(0.3333, 0.6667, 0.1699) N1: 3a(0.3333, 0.6667, 0.7275) O1: 9b(0.5373, 0.0746, 0.3953)
Pnma	4	a=7.18 Å, b=5.61 Å, c=6.77 Å, α=β=γ=90°	Rb1: 4c(0.483, 0.250, 0.686) N1: 4c(0.350, 0.250, 0.122) O1: 4c(0.448, 0.250, 0.275) O5: 8d(0.302, 0.444, 0.043)
Pmmn	12	a=4.67 Å, b=5.34 Å, c=4.63 Å, α=β=γ=90°	Rb1: 2b(0.500, 0, 0.400) N1: 2a(0, 0, 0.992) O1: 2a(0, 0, 0.721) O3: 4e(0, 0.204, 0.128)

下载: 导出CSV

| 显示表格

图 3 R3m、Pnma和Pmmn相的晶体结构

Figure 3. Crystal structures of R3m, Pnma, and Pmmn phase

下载: 全尺寸图片幻灯片

表 3 高压下R3m、Pnma和Pmmn相的弹性常数和弹性模量

Table 3. Elastic constant and elastic moduli of R3m, Pnma and Pmmn phase at high pressure GPa

Phase	Pressure	C₁₁	C₁₂	C₁₃	C₁₄	C₂₂	C₂₃	C₃₃	C₄₄	C₅₅	C₆₆	B	G	E
R3m	0	37	14	11	−4			13	7		12	15	7	19
	4	75	28	21	−8			39	6		23	35	11	29
	12	124	46	42	−15			94	12		39	66	19	52
Pnma	0	22	7	9		41	9	32	7	10	9	16	10	24
	4	50	19	30		73	19	69	12	17	19	36	17	44
	12	96	43	59		129	35	119	19	−5	34	69	−57	−236
Pmmn	0	26	9	9		50	16	54	15	5	5	21	10	26
	4	60	16	25		84	32	83	33	20	9	40	21	53
	12	113	25	53		143	59	129	60	37	16	72	35	91

下载: 导出CSV

| 显示表格

$\begin{aligned} &{C_{11}} > \left| {{C_{{\text{12}}}}} \right|,\;\;\;\;{C_{44}} > 0, \\ & C_{13}^2 < \dfrac{1}{2}{C_{33}}(C_{11}+C_{12}), \\ &C_{14}^2 < \dfrac{1}{2}{C_{44}}({C_{11}} - {C_{12}}) \end{aligned}$

(1)

$\begin{aligned} &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{C_{11}} > 0,\;\;\;\;{C_{11}}{C_{22}} > C_{12}^2, \\ &{C_{11}}{C_{22}}{C_{33}}+2{C_{12}}{C_{13}}{C_{23}} - {C_{11}}C_{23}^2 - {C_{22}}C_{13}^2 - {C_{33}}C_{12}^2 > 0 \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;{C_{44}} > 0,\;\;\;\;{C_{55}} > 0,\;\;\;\;{C_{66}} > 0 \\ \end{aligned}$

(2)

为了确定RbNO₃的3个相的动力学稳定性，采用有限位移法计算了它们的声子谱。若声子谱具有负频率，则意味着动力学不稳定^[29]。在简谐近似下，分别计算了R3m、Pnma和Pmmn相在不同压强下的声子色散曲线以及声子分波态密度（phonon density of states, PHDOS），结果如图4所示。可以看出，声子谱均未出现负频率，表明3个相在相应压强下均具有动力学稳定性。

图 4 R3m、Pnma和Pmmn相的声子色散曲线以及声子态密度

Figure 4. Phonon-dispersion curves and the PHDOS of R3m, Pnma and Pmmn phase

下载: 全尺寸图片幻灯片

声子态密度分析研究表明，RbNO₃的3个相的声子态密度分布趋势皆与常压下的CaCO₃^[30]十分相似，例如：当RbNO₃（CaCO₃）的振动频率低于10 THz（12 THz）时，声子态密度的贡献主要来自于O原子与金属阳离子Rb⁺（Ca²⁺）；在振动频率32 THz附近，声子态密度的贡献主要来自于O原子；在振动频率大于40 THz的高频区，声子态密度的贡献来自于N―O键或者C―O键。采用V_Sim软件对Γ点处声子的振动模式进行可视化分析，结果表明：当频率小于10 THz时，N原子与O原子之间的距离不变，Rb和 $\rm NO_3^-$ 协同振动；在32 THz附近，R3m和Pnma相的N―O振动和C―O振动均为对称伸缩振动，与方解石和文石的特性类似；在21 THz附近，N―O振动和C―O振动均为平面内弯曲振动；在RbNO₃（CaCO₃）的振动频率约为24 THz（25 THz）时，N―O振动（C―O振动）均为平面外弯曲振动；在大于40 THz的范围内，N―O振动和C―O振动均为反对称弯曲振动。相对于0 GPa的R3m相和4 GPa的Pnma相而言，12 GPa的Pmmn相的声子振动频率整体升高，但不同模式的频率分布范围大致相同。

为了研究R3m、Pnma和Pmmn相中原子间的成键行为，计算了0 GPa的R3m相、4 GPa的Pnma相和12 GPa的Pmmn相的电子局域函数（electron localization functionm, ELF），计算结果如图5所示。三维ELF图中等值面的取值为0.8，二维ELF图的晶格切面分别为(1.000 14.005 31.363)、(20.145 2.048 −1.000)和(4.542 1.000 −1.516)。可以看出，N原子与O原子间的ELE值趋近于1，表明N―O之间存在强共价键。

图 5 R3m、Pnma和Pmmn相的电子局域函数

Figure 5. Electron localization function of R3m, Pnma and Pmmn phase

下载: 全尺寸图片幻灯片

此外，计算了0 GPa的R3m相、4 GPa的Pnma相和12 GPa的Pmmn相的晶体轨道哈密顿布居(crystal orbital Hamiton population, COHP)，计算结果如图6所示。COHP为负表示成键态。相对于O―O键和N―O键而言，Rb―O键对COHP的贡献非常小，几乎可以忽略不计，符合Rb⁺与 $\rm NO_3^-$ 之间为离子相互作用的事实。在−1.5～0 eV范围内，O―O键的COHP为正值，表明其主要来源为反键轨道，包含 $\rm NO_3^-$ 从Rb⁺处获取的1个价电子的贡献。在0 eV以下，N―O键的COHP几乎全部为负值，表明 $\rm NO_3^-$ 中的N―O键是极为稳定的强共价键，与ELF的分析结果一致。在0 GPa的R3m相、4 GPa的Pnma相和12 GPa的Pmmn相中，N原子与O原子的键长分别为1.26、1.25和1.26 Å。计算Bader电荷转移以确定Rb原子、N原子和O原子之间的电子转移情况，计算结果如表4所示。这3个结构中，硝酸根离子分别从Rb⁺获得了0.90e、0.87e和0.86e的电荷，表明压强抑制Rb⁺的电荷向 $\rm NO_3^-$ 离子转移。

图 6 R3m、Pnma和Pmmn相的COHP

Figure 6. Crystal orbital Hamilton populations of R3m, Pnma and Pmmn phase

下载: 全尺寸图片幻灯片

表 4 高压下R3m、Pnma和Pmmn相的元胞内的Bader电荷转移

Table 4. Calculated Bader charges within R3m, Pnma and Pmmn phases primitive cells at different pressures

Phase	Pressure/GPa	Atoms	Number	Charge/e	Charge transfer/e
R3m	0	Rb	1	8.10	0.90
		N	1	4.16	0.84
		O	3	6.58	−0.58
Pnma	4	Rb	4	8.13	0.87
		N	4	4.13	0.87
		O1	4	6.57	−0.57
		O2	4	6.58	−0.58
		O3	4	6.59	−0.59
Pmmn	12	Rb	2	8.14	0.86
		N	2	4.07	0.93
		O1	2	6.58	−0.58
		O2	2	6.59	−0.59
		O3	2	6.62	−0.62

下载: 导出CSV

| 显示表格

图7给出了0 GPa的R3m相、4 GPa的Pnma相和12 GPa的Pmmn相的电子能带结构和电子态密度( density of states, DOS)。电子态密度结果表明，价带主要来自O的p轨道，导带主要来自N-p与O-p的杂化。3个结构在相应压强下的带隙分别为3.06、3.40和3.10 eV。带隙的存在说明它们均为半导体材料，然而3个结构的带隙类型不同，其中，R3m结构具有直接带隙，Pnma和Pmmn结构具有间接带隙。此外，还可以发现，在结构相变过程中，带隙随压强的增加呈现非单调变化的规律，即第1次相变带隙增大，而第2次相变带隙减小。

图 7 R3m、Pnma和Pmmn相的能带结构和电子态密度

Figure 7. Band structures and partial densities of states of R3m, Pnma and Pmmn phases

下载: 全尺寸图片幻灯片

3. 结　论

采用第一性原理计算与CALYPSO结构预测相结合的方法系统地研究了RbNO₃在0～100 GPa压强范围内的高压结构与物理性质。以RbNO₃常温常压结构的实验数据为参照，测试了PBE、vdW-DF、RPBE、PBEsol泛函对结构描述的准确性，发现PBEsol泛函给出的结果最准确。基于PBEsol泛函预测出零温下RbNO₃的高压相变序列为R3m→Pnma→Pmmn，相变压强分别约为1.7 和8.2 GPa；2次相变均为一级结构相变，相应的体积坍塌率分别为3.73%和2.54%。预测零温下RbNO₃存在2个低压新相，即R3m相和Pnma相，它们在能量上均优于早期实验在常温常压下给出的P3₁结构，表明降温可能会诱导RbNO₃发生结构相变。0 GPa的R3m相、4 GPa的Pnma相和12 GPa的Pmmn相均具有力学稳定性和动力学稳定性，其带隙分别为3.06、3.40和3.10 eV，对比分析发现，压强会抑制Rb⁺的电荷向 $\rm NO_3^-$ 转移。本研究获得的硝酸铷结构与电子性质随压强的变化规律可以为其他碱金属硝酸盐的理论与实验研究提供参考。

图 1 简化的晶态聚合物多尺度分级结构模型^[19]

Figure 1. Simplified model of hierarchical structures of the crystalline polymer^[19]

下载: 全尺寸图片幻灯片

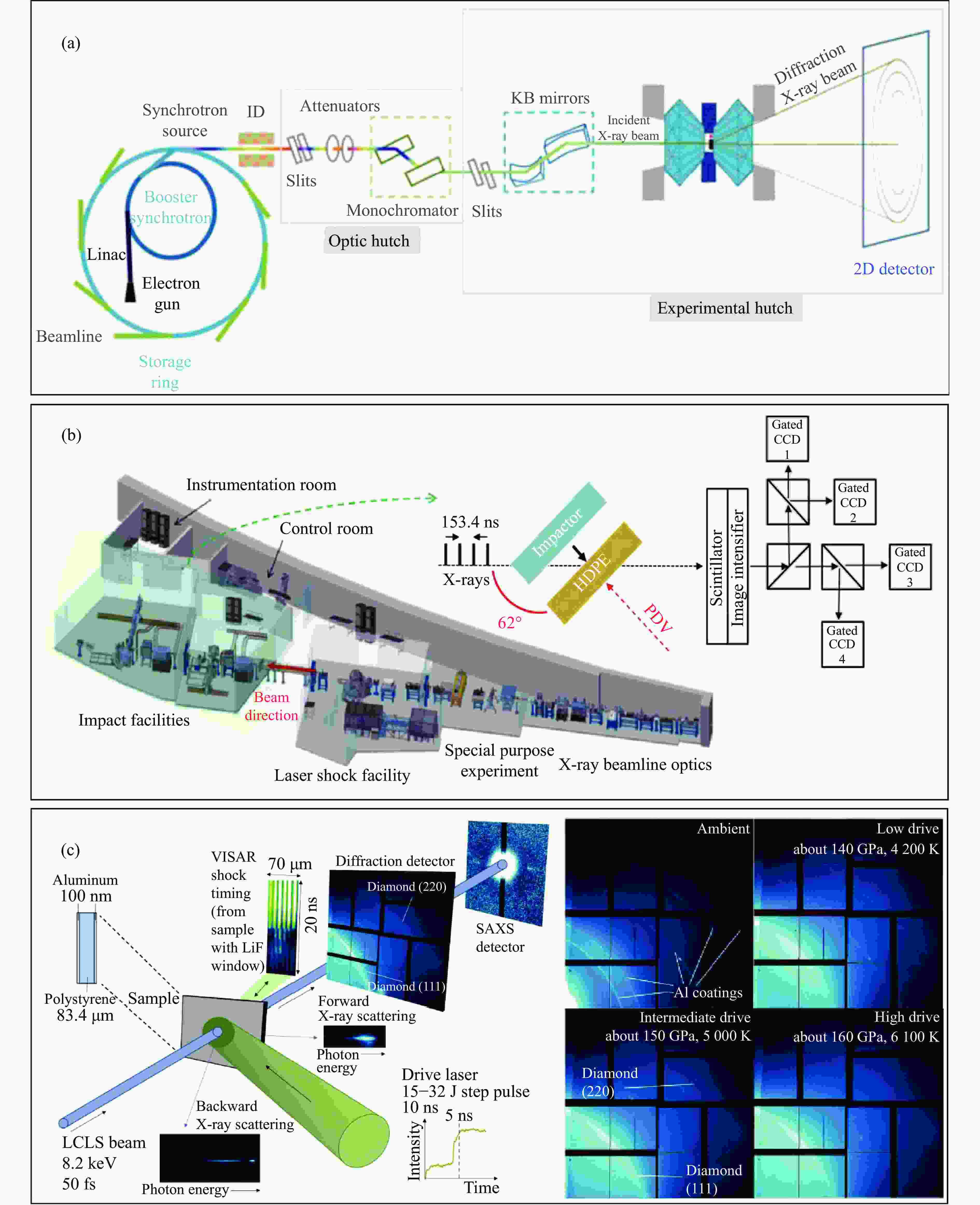
图 2 高温高压条件下聚合物的状态方程和结构研究采用的实验技术：(a) DAC加载的基于同步辐射光源的X射线衍射实验的实验系统^[22]，其中，ID为插入件（insertion device），包括扭摆器（wiggler）和波荡器（undulator），(b) 美国阿贡国家实验室APS光源的DCS实验站（该实验站建有基于轻气炮加载的同步辐射X射线衍射实验系统^[29]，其中，HDPE为高密度聚乙烯（high-density polyethylene），PDV（photon Doppler velocimetry）为光子多普勒测速），(c) 基于激光冲击加载和XFEL的聚合物结构测量实验光路（包括X射线广角衍射和小角散射等^[16]，其中，LCLS（Linac Coherent Light Source）是位于斯坦福的XFEL装置，VISAR为任意面反射激光干涉测速系统（velocity interferometer system for any reflector））

Figure 2. Experimental techniques for research of equation of state and phase transition of polymers at high pressures and high temperatures: (a) schematic of synchrotron-based X-ray diffraction beamline with diamond anvil cell, which generates high pressure and high temperature conditions^[22], in which ID is insertion device, including wigglers and undulators; (b) synchrotron-based X-ray diffraction beamline combined with gas-gun driven compression at Dynamic Compression Sector of Advanced Photon Source, Argonne National Laboratory^[29], in which HDPE is high-density polyethylene, and PDV is photon Doppler velocimetry; (c) structure determination of laser-shocked polymer using X-ray free electron laser, including X-ray wide-angle diffraction and small angle scattering techniques^[16], in which LCLS is linac coherent light source

下载: 全尺寸图片幻灯片

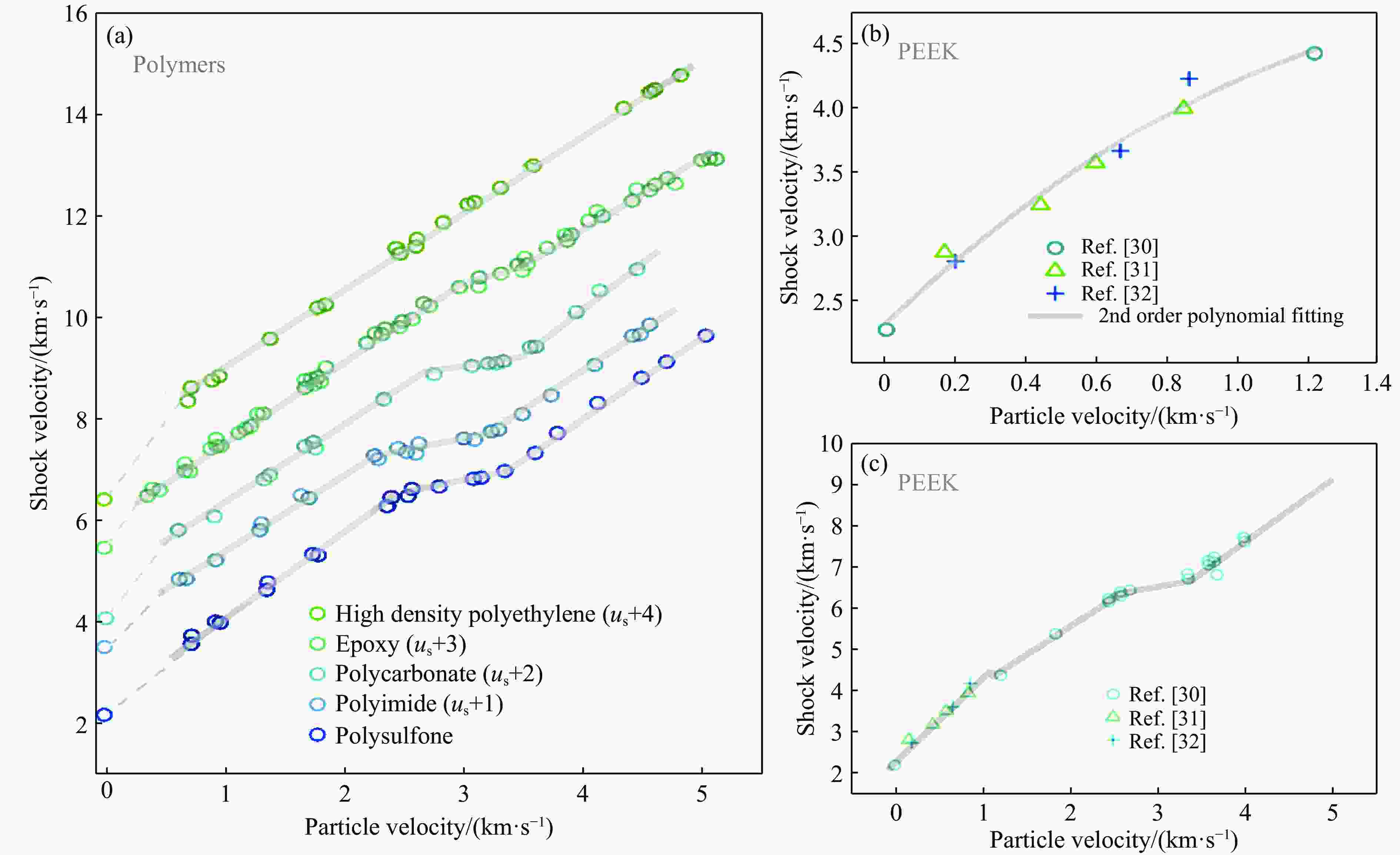
图 3 (a) 聚合物的Hugoniot状态方程^[8]，(b) PEEK的Hugoniot状态方程在低压段的数据，图中的实线是采用二次函数的拟合结果：u_s = c₀+s₁u_p+ $s_2 u_{\mathrm{p}}^2$ ，(c) PEEK的Hugoniot状态方程^[30–32]（图中的实线是一次函数拟合结果，u_s-u_p关系需分4段进行拟合）

Figure 3. (a) Hugoniot equation of states of polymers^[8]; (b) Hugoniot equation of states of PEEK at low pressures (Solid line show the quadratic fitting result: u_s = c₀+s₁u_p+ $s_2 u_{\mathrm{p}}^2$ ); (c) Hugoniot equation of states of PEEK^[30–32] (Solid lines show the linear fitting results, which are made up of four distinct lines in different regimes. )

下载: 全尺寸图片幻灯片

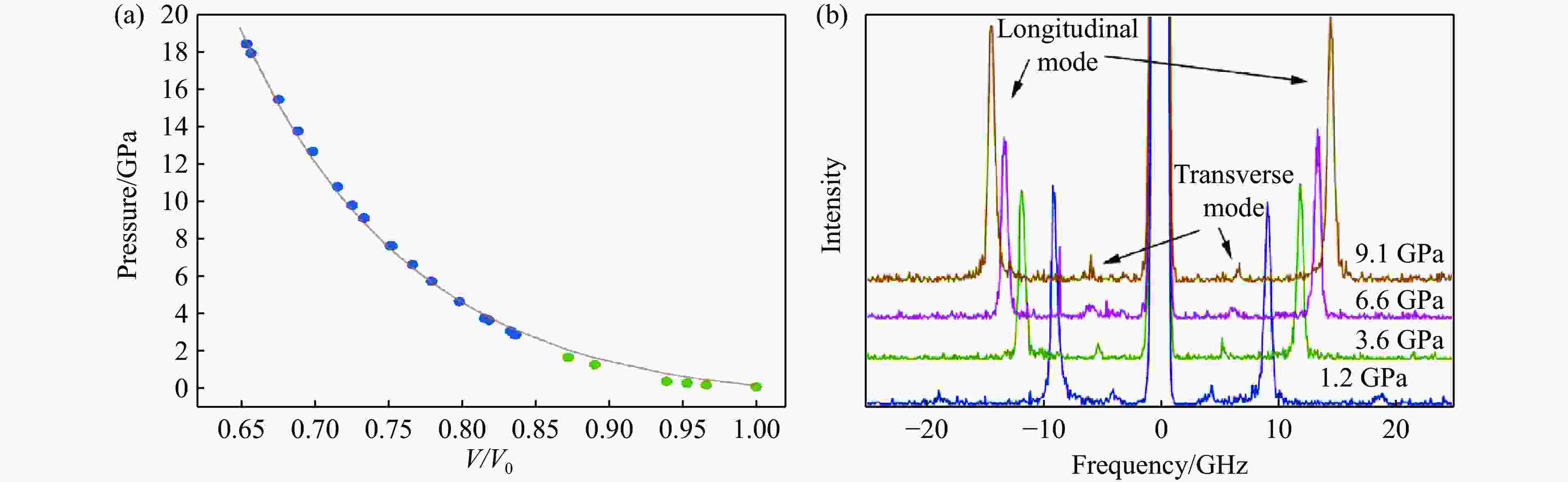
图 4 (a) Kel-F800（chlorotrifluoroethylene-co-vinylidene fluoride）在0～18.5 GPa压力范围内的状态方程^[39]（Kel-F800在低压段的压缩趋势（绿色数据点）与高压段（蓝色数据点）明显不同，实线为采用三阶Birch-Murnaghan状态方程拟合整个压力范围内的数据的结果)，(b) Kel-F800在高压下的典型布里渊散射谱

Figure 4. (a) Equation of state of Kel-F800 up to 18.5 GPa^[39], which indicates the different compressive behaviors of Kel-F800 at low pressures (green points) and high pressures (blue points) (Solid line is the fitting result of all the experimental data points using 3rd order Birch-Murnaghan equation of state); (b) the typical Brillouin spectra of Kel-F800 at high pressures

下载: 全尺寸图片幻灯片

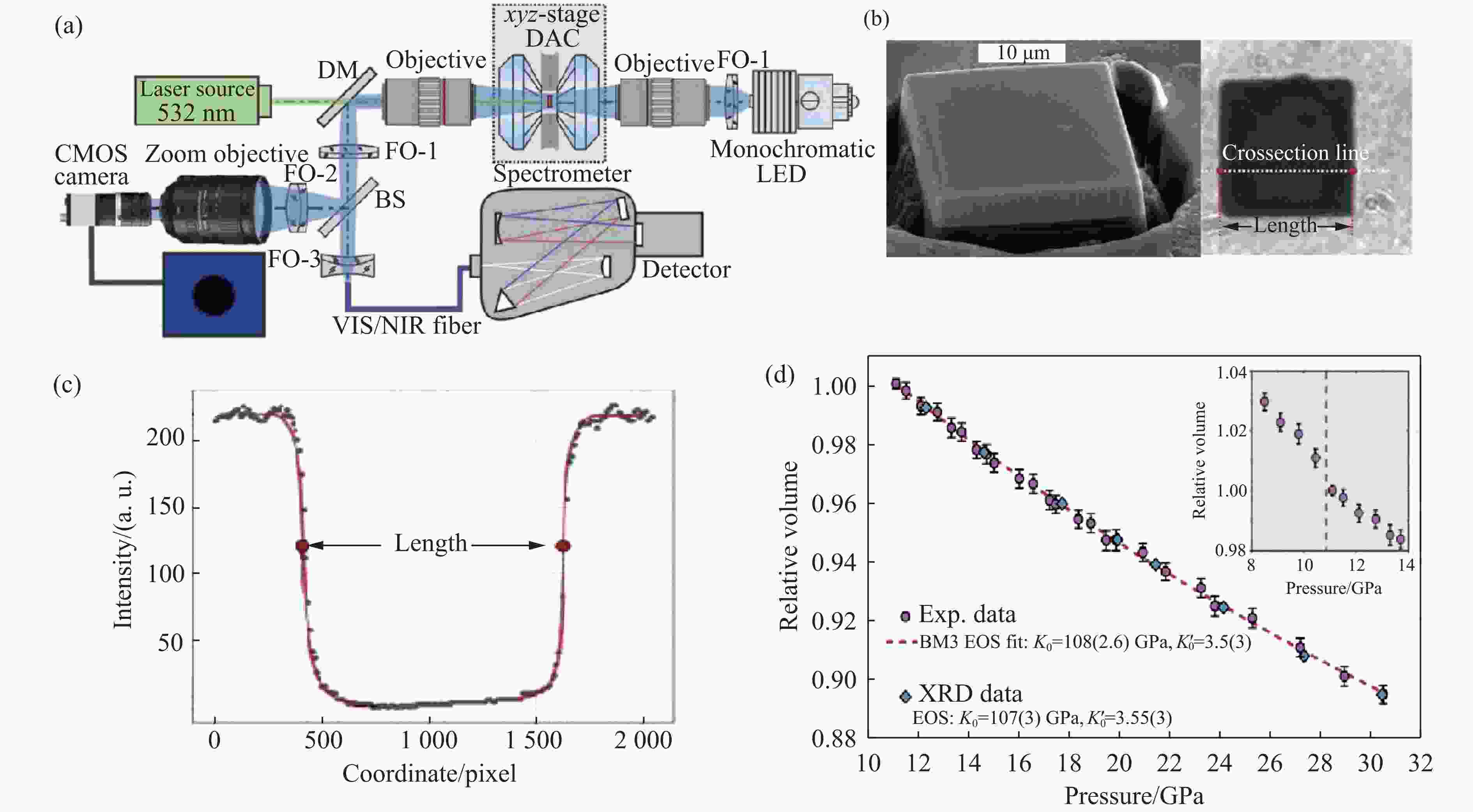
Fedotenko等^[45]发展改进的可见光成像状态方程测量方法：(a) 可见光成像状态方程测量系统（DM（dichroic mirror）为二色镜，FO （focusing optics）为聚焦光学器件，BS为50/50分光镜，CMOS是用于图像观察的相机，VIS（visible）表示可见光，NIR（near-infrared）表示近红外光），(b) 利用FIB聚焦离子束切割的规则形状的样品，(c) 样品尺寸的判读方法，(d) 可见光成像测量获得的金属Ti的状态方程与X射线衍射实验测量结果的对比，其中， ${K_0}$ 和 ${{{K}}_0 '}$ 分别为体积模量及体积模量在环境压力下的压力导数

Figure 5. Optical equation of state measurement method developed by Fedotenko et al.^[45]: (a) optical equation of state measurement system, in which DM is the long-pass dichroic mirror, FOs are the focusing optics, BS is the 50/50 beam splitter, and CMOS is the camera for image observation, VIS is visible light, NIR is near-infrared light; (b) the sample with sharp edges manufactured by focused ion beam technique; (c) linear size measurement; (d) comparison of the equation of states of metallic Ti measured by the optical method and X-ray diffraction technique, in which ${K_0}$ and ${{{K}}_0 '}$ are the bulk modulus and its pressure derivative at ambient pressure, respectively

下载: 全尺寸图片幻灯片

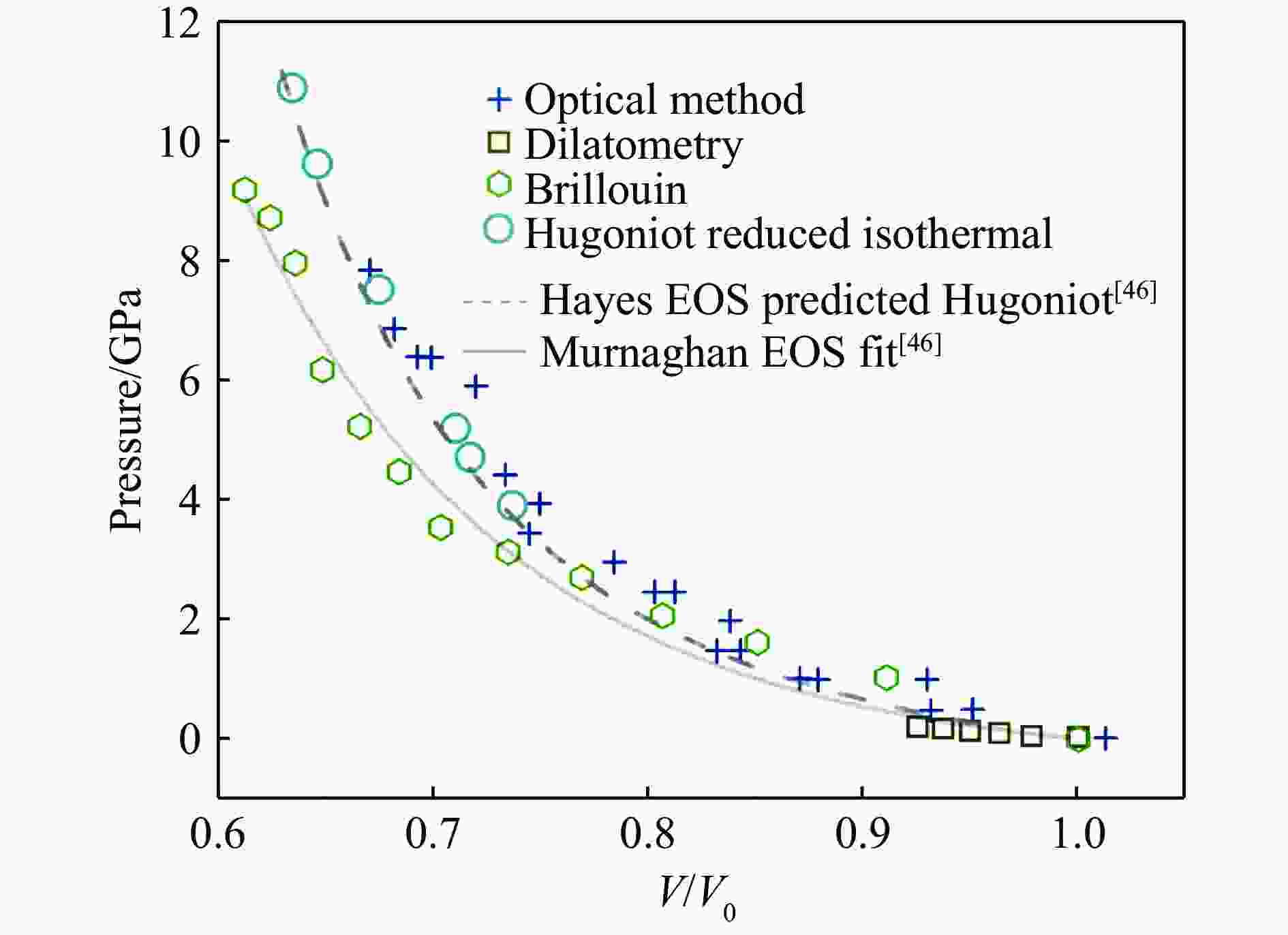
图 6 不同方法测量的VCE的状态方程^[46]（即使在12 GPa较低的压力范围内，不同方法测量的VCE的状态方程表现出很大的差异，实验数据的分散性很大）

Figure 6. Equation of states of VCE measured by different techniques^[46] (The results measured by different techniques present large discrepancy even in the very low pressure condition of 12 GPa. Furthermore, the experimental data pointes are quite scattered.)

下载: 全尺寸图片幻灯片

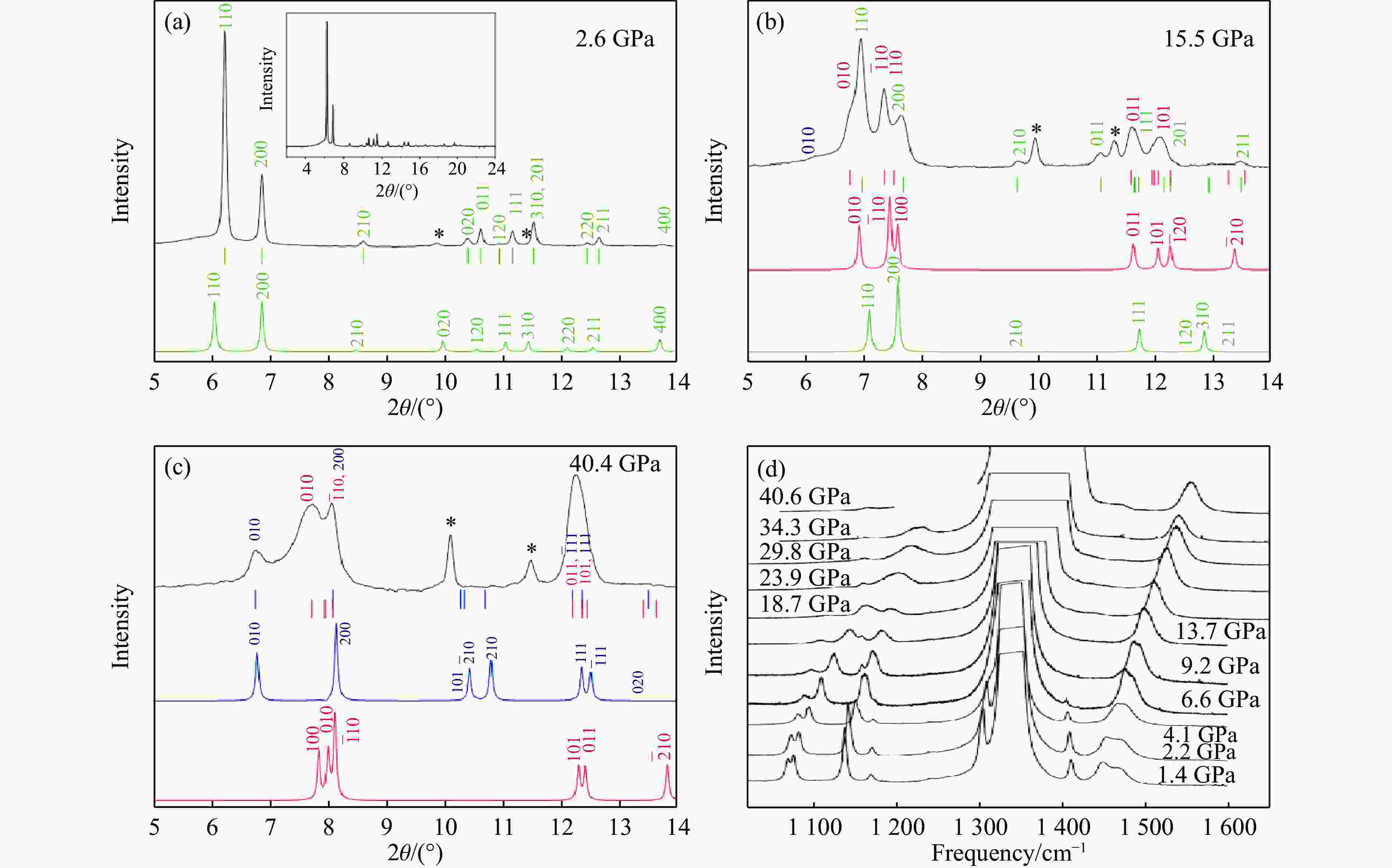
图 7 (a)～(c)不同压力下PE的典型衍射谱^[47]（绿色为理论模拟的正交的Pnma结构的衍射谱，红色为单斜的P2₁/m结构的衍射谱，蓝色为单斜的A2/m结构的衍射谱），（d）不同压力下PE的拉曼谱^[48]（1340 cm⁻¹附近的强峰是金刚石的拉曼峰）

Figure 7. (a)–(c) Typical X-ray diffraction spectra of PE at high pressures^[47] (The green, red and blue spectra are the ab initio simulated patterns of the orthorhombic Pnma, monoclinic P2₁/m, and the monoclinic A2/m structures, respectively.); (d) Raman spectra of PE at selected pressures^[48] (The broad and strong peak at about 1340 cm⁻¹ is the Raman peak from diamond anvils.)

下载: 全尺寸图片幻灯片

表 1 聚合物状态方程的测量方法比较

Table 1. Comparison of different techniques for equation of state measurement of polymers

Measurement method	Measurement information	Pressure range/GPa	Potential issues
Shock Hugoniot	Compressibility of bulk materials	>1000	Temperature effect: if the shock temperature is higher than T_g, then the measured properties are those of the glassy polymer. Strain rate dependency.
Brillouin scattering	Compressibility of bulk materials	about 1–85	Pressure limitations: for materials with a low T_g, v_T can’t be measured at low pressure (1 GPa), and at high pressure (85 GPa), the Brillouin signal of the diamond obscures the v_L signal of the polymer, which limit the pressure range for sound velocity measurements. Frequency effect: the frequency of Brillouin scattering experiments is 10⁹ Hz, which results in an overestimation of the first derivative of the bulk modulus of the polymer with respect to pressure. Numerical errors introduced by γ
Visible light imaging	Compressibility of bulk materials	>80	Small molecules of the pressure-transmitting medium enter the “free volume” of the polymer. Non-hydrostatic conditions at high pressures lead to the failure of the isotropy assumption. Low accuracy
Dilatometor	Compressibility of bulk materials	about 0.2	Pressure range too small
X-ray diffraction	Compressibility of crystalline phases	>200	Only reflects the information of the crystalline part, lacking of the information about amorphous parts, and not reflecting the compressibility of bulk materials

下载: 导出CSV

参考文献(59)

[1]	MISHRA M. Encyclopedia of polymer applications: 3 volume set [M]. Boca Raton: CRC Press, 2019.
[2]	COLCLOUGH M E, DESAI H, MILLAR R W, et al. Energetic polymers as binders in composite propellants and explosives [J]. Polymers for Advanced Technologies, 1994, 5(9): 554–560. doi: 10.1002/pat.1994.220050914
[3]	XIAO Y C, XIAO X D, XIONG Y Y, et al. Mechanical behavior of a typical polymer bonded explosive under compressive loads [J]. Journal of Energetic Materials, 2023, 41(3): 378–410. doi: 10.1080/07370652.2021.1980151
[4]	WOODS H, BODDORFF A, EWALDZ E, et al. Rheological considerations for binder development in direct ink writing of energetic materials [J]. Propellants, Explosives, Pyrotechnics, 2020, 45(1): 26–35. doi: 10.1002/prep.201900159
[5]	HUANG B B, XUE Z H, FU X L, et al. Advanced crystalline energetic materials modified by coating/intercalation techniques [J]. Chemical Engineering Journal, 2021, 417: 128044. doi: 10.1016/j.cej.2020.128044
[6]	AGRAWAL J P, DODKE V S. Some novel high energy materials for improved performance [J]. Zeitschrift für Anorganische und Allgemeine Chemie, 2021, 647(19): 1856–1882.
[7]	ABBOTT A, BRANCH B, BROWN E N, et al. The dynamic response of polymers interrogated by 3rd generation X-ray light source: LA-UR-19-29436 [R]. Los Alamos: Los Alamos National Laboratory, 2019.
[8]	CARTER W J, MARSH S P. Hugoniot equation of state of polymers: LA-13006-MS [R]. Los Alamos: Los Alamos National Laboratory, 1995.
[9]	COE J D, BROWN E, CADY C M, et al. Equation of state and damage in polyethylene: LA-UR-17-29234 [R]. Los Alamos: Los Alamos National Laboratory, 2019.
[10]	DATTELBAUM D M, SHEFFIELD S, MCGRANE S D, et al. First reactions: understanding chemistry behind the shock front: LA-UR-12-25050 [R]. Los Alamos: Los Alamos National Laboratory, 2012.
[11]	国家自然科学基金委员会, 中国科学院. 中国学科发展战略(上): 软凝聚态物理学 [M]. 北京: 科学出版社, 2020.
[12]	BRIDGMAN P W. Linear compressions to 30 000 kg/cm², including relatively incompressible substances [J]. Proceedings of the American Academy of Arts and Sciences, 1949, 77(6): 189–234. doi: 10.2307/20023541
[13]	WUNDERLICH B, ARAKAWA T. Polyethylene crystallized from the melt under elevated pressure [J]. Journal of Polymer Science: Part A: General Papers, 1964, 2(8): 3697–3706. doi: 10.1002/pol.1964.100020828
[14]	WARD I M. Mechanical properties of solid polymers [M]. 2nd ed. New York: John Wiley, 1983: 135-166.
[15]	KRAUS D, VORBERGER J, PAK A, et al. Formation of diamonds in laser-compressed hydrocarbons at planetary interior conditions [J]. Nature Astronomy, 2017, 1(9): 606–611. doi: 10.1038/s41550-017-0219-9
[16]	KRAUS D, HARTLEY N J, FRYDRYCH S, et al. High-pressure chemistry of hydrocarbons relevant to planetary interiors and inertial confinement fusion [J]. Physics of Plasmas, 2018, 25(5): 056313. doi: 10.1063/1.5017908
[17]	HE Z Y, RÖDEL M, LÜTGERT J, et al. Diamond formation kinetics in shock-compressed C-H-O samples recorded by small-angle X-ray scattering and X-ray diffraction [J]. Science Advances, 2022, 8(35): eabo0617. doi: 10.1126/sciadv.abo0617
[18]	朱诚身. 聚合物结构分析 [M]. 2版. 北京: 科学出版社, 2010.
[19]	GUO Q P. Polymer morphology: principles, characterization, and processing [M]. Hoboken: John Wiley & Son, 2016.
[20]	ALS-NIELSEN J, MCMORROW D. Elements of modern X-ray physics [M]. 2nd ed. Chichester: John Wiley & Sons, 2011.
[21]	KAO C C. Challenges and opportunities for the next decade of XFELs [J]. Nature Reviews Physics, 2020, 2(7): 340–341. doi: 10.1038/s42254-020-0196-2
[22]	LIU L. Synthesis and tuning of multifunctional materials at high pressure [D]. Uppsala: Acta Universitatis Upsaliensis, 2020.
[23]	DREWITT J W E. Liquid structure under extreme conditions: high-pressure X-ray diffraction studies [J]. Journal of Physics: Condensed Matter, 2021, 33(50): 503004. doi: 10.1088/1361-648X/ac2865
[24]	DUBROVINSKY L, KHANDARKHAEVA S, FEDOTENKO T, et al. Materials synthesis at terapascal static pressures [J]. Nature, 2022, 605(7909): 274–278. doi: 10.1038/s41586-022-04550-2
[25]	TATENO S, HIROSE K, OHISHI Y, et al. The structure of iron in Earth's inner core [J]. Science, 2010, 330(6002): 359–361. doi: 10.1126/science.1194662
[26]	SHEN G Y, MAO H K. High-pressure studies with X-rays using diamond anvil cells [J]. Reports on Progress in Physics, 2017, 80(1): 016101. doi: 10.1088/1361-6633/80/1/016101
[27]	SINCLAIR N W, TURNEAURE S J, WANG Y, et al. The fast multi-frame X-ray diffraction detector at the dynamic compression sector [J]. Journal of Synchrotron Radiation, 2021, 28(4): 1216–1228. doi: 10.1107/S1600577521003775
[28]	BROEGE D, FOCHS S, BRENT G, et al. The dynamic compression sector laser: a 100-J UV laser for dynamic compression research [J]. Review of Scientific Instruments, 2019, 90(5): 053001. doi: 10.1063/1.5088049
[29]	HUBER R C, WATKINS E B, DATTELBAUM D M, et al. In situ X-ray diffraction of high density polyethylene during dynamic drive: polymer chain compression and decomposition [J]. Journal of Applied Physics, 2021, 130(17): 175901. doi: 10.1063/5.0057439
[30]	BOETTGER J C, JOHNSON J D. SESAME equation of state number 8020: polyetheretherketone (PEEK): LA-12684-MS [R]. Los Alamos: Los Alamos National Laboratory, 1993.
[31]	MILLETT J C F, BOURNE N K, GRAY III G T. The response of polyether ether ketone to one-dimensional shock loading [J]. Journal of Physics D: Applied Physics, 2004, 37(6): 942–947. doi: 10.1088/0022-3727/37/6/021
[32]	ROBERTS A, APPLEBY-THOMAS G J, HAZELL P. Experimental determination of Grüneisen gamma for polyether ether ketone (PEEK) using the shock-reverberation technique [J]. AIP Conference Proceeding, 2012, 1426(1): 824–827.
[33]	MAERZKE K A, COE J D, TICKNOR C, et al. Equations of state for polyethylene and its shock-driven decomposition products [J]. Journal of Applied Physics, 2019, 126(4): 045902. doi: 10.1063/1.5099371
[34]	HUBER R C, PETERSON J, COE J D, et al. Polysulfone shock compressed above the decomposition threshold: velocimetry and modeling of two-wave structures [J]. Journal of Applied Physics, 2020, 127(10): 105902. doi: 10.1063/1.5124252
[35]	BARRIOS M A, HICKS D G, BOEHLY T R, et al. High-precision measurements of the equation of state of hydrocarbons at 1–10 Mbar using laser-driven shock waves [J]. Physics of Plasmas, 2010, 17(5): 056307. doi: 10.1063/1.3358144
[36]	LÜTGERT J, VORBERGER J, HARTLEY N J, et al. Measuring the structure and equation of state of polyethylene terephthalate at megabar pressures [J]. Scientific Reports, 2021, 11(1): 12883. doi: 10.1038/s41598-021-91769-0
[37]	ROOT S, MATTSSON T R, COCHRANE K, et al. Shock compression response of poly(4-methyl-1-pentene) plastic to 985 GPa [J]. Journal of Applied Physics, 2015, 118(20): 205901. doi: 10.1063/1.4936168
[38]	STEVENS L L, ORLER E B, DATTELBAUM D M, et al. Brillouin-scattering determination of the acoustic properties and their pressure dependence for three polymeric elastomers [J]. The Journal of Chemical Physics, 2007, 127(10): 104906. doi: 10.1063/1.2757173
[39]	STEVENS L L, DATTELBAUM D M, AHART M, et al. High-pressure elastic properties of a fluorinated copolymer: poly(chlorotrifluoroethylene-co-vinylidene fluoride) (Kel-F800) [J]. Journal of Applied Physics, 2012, 112(2): 023523. doi: 10.1063/1.4737590
[40]	BENJAMIN A S, AHART M, GRAMSCH S A, et al. Acoustic properties of Kel F-800 copolymer up to 85 GPa [J]. The Journal of Chemical Physics, 2012, 137(1): 014514. doi: 10.1063/1.4731706
[41]	ZHA C S, MAO H K, HEMLEY R J. Elasticity of MgO and a primary pressure scale to 55 GPa [J]. Proceedings of the National Academy of Sciences of the United States of America, 2000, 97(25): 13494–13499.
[42]	DATTELBAUM D M, JENSEN J D, SCHWENDT A M, et al. A novel method for static equation-of state-development: equation of state of a cross-linked poly(dimethylsiloxane) (PDMS) network to 10 GPa [J]. The Journal of Chemical Physics, 2005, 122(14): 144903. doi: 10.1063/1.1879872
[43]	SHEN G Y, MEI Q, PRAKAPENKA V B, et al. Effect of helium on structure and compression behavior of SiO₂ glass [J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(15): 6004–6007.
[44]	ZENG Z D, WEN J G, LOU H B, et al. Preservation of high-pressure volatiles in nanostructured diamond capsules [J]. Nature, 2022, 608(7923): 513–517. doi: 10.1038/s41586-022-04955-z
[45]	FEDOTENKO T, SOUZA D S, KHANDARKHAEVA S, et al. Isothermal equation of state of crystalline and glassy materials from optical measurements in diamond anvil cells [J]. Review of Scientific Instruments, 2021, 92(6): 063907. doi: 10.1063/5.0050190
[46]	DATTELBAUM D M, STEVENS L L. Equations of state of binders and related polymers [M]//PEIRIS S M, PIERMARINI G J. Static Compression of Energetic Materials. Berlin Heidelberg: Springer, 2008: 127–202.
[47]	FONTANA L, VINH D Q, SANTORO M, et al. High-pressure crystalline polyethylene studied by X-ray diffraction and ab initio simulations [J]. Physical Review B, 2007, 75(17): 174112. doi: 10.1103/PhysRevB.75.174112
[48]	FONTANA L, SANTORO M, BINI R, et al. High-pressure vibrational properties of polyethylene [J]. The Journal of Chemical Physics, 2010, 133(20): 204502. doi: 10.1063/1.3507251
[49]	CAPATINA D, D’AMICO K, NUDELL J, et al. DCS—a high flux beamline for time resolved dynamic compression science—design highlights [J]. AIP Conference Proceedings, 2016, 1741(1): 030036.
[50]	ROSS M. The ice layer in Uranus and Neptune-diamonds in the sky? [J]. Nature, 1981, 292(5822): 435–436. doi: 10.1038/292435a0
[51]	HARTLEY N J, BROWN S, COWAN T E, et al. Evidence for crystalline structure in dynamically-compressed polyethylene up to 200 GPa [J]. Scientific Reports, 2019, 9(1): 4196. doi: 10.1038/s41598-019-40782-5
[52]	FULLER W, OATES C R, GREENALL R J, et al. X-ray and neutron diffraction studies of the structure of PEEK [J]. Conference Series-Institute of Physics, 1990: 213−224.
[53]	WU W, WIGNALL G D, MANDELKERN L. A SANS study of the plastic deformation mechanism in polyethylene [J]. Polymer, 1992, 33(19): 4137–4140. doi: 10.1016/0032-3861(92)90617-6
[54]	RAI D K, GILLILAN R E, HUANG Q Q, et al. High-pressure small-angle X-ray scattering cell for biological solutions and soft materials [J]. Journal of Applied Crystallography, 2021, 54(1): 111–122. doi: 10.1107/S1600576720014752
[55]	GEORGIEV G, DAI P S, OYEBODE E, et al. Real-time small angle X-ray scattering study of two-stage melt crystallization of PEEK [J]. Journal of Materials Science, 2001, 36(6): 1349–1361. doi: 10.1023/A:1017595201893
[56]	杨科, 蒋升, 闫帅, 等. 上海同步辐射光源高压相关线站概述 [J]. 高压物理学报, 2020, 34(5): 050102. doi: 10.11858/gywlxb.20200584 YANG K, JIANG S, YAN S, et al. Application of shanghai synchrotron radiation source in high pressure research [J]. Chinese Journal of High Pressure Physics, 2020, 34(5): 050102. doi: 10.11858/gywlxb.20200584
[57]	程贺, 张玮, 王芳卫, 等. 中国散裂中子源的多学科应用 [J]. 物理, 2019, 48(11): 701–707. doi: 10.7693/wl20191101 CHENG H, ZHANG W, WANG F W, et al. Applications of the China spallation neutron source [J]. Physics, 2019, 48(11): 701–707. doi: 10.7693/wl20191101
[58]	李晓东, 袁清习, 徐伟, 等. 第四代高能同步辐射光源HEPS及高压相关线站建设 [J]. 高压物理学报, 2020, 34(5): 050101. doi: 10.11858/gywlxb.20200554 LI X D, YUAN Q X, XU W, et al. Introduction of fourth-generation high energy photon source HEPS and the beamlines for high-pressure research [J]. Chinese Journal of High Pressure Physics, 2020, 34(5): 050101. doi: 10.11858/gywlxb.20200554
[59]	王洪翠, 张波, 谷鸣. SHINE装置的准直器设计 [J]. 真空电子技术, 2022(1): 32–35, 47. WANG H C, ZHANG B, GU M. Design of collimators for SHINE facility [J]. Vacuum Electronics, 2022(1): 32–35, 47.