基于活跃子空间的爆压不确定度传递分析

梁霄; 范孟君; 王言金; 王瑞利

doi:10.11858/gywlxb.20240862

基于活跃子空间的爆压不确定度传递分析

doi: 10.11858/gywlxb.20240862

1.
山东科技大学数学与系统科学学院, 山东青岛　266590
2.
北京应用物理与计算数学研究所, 北京　100094
3.
河南省科学院, 河南郑州　450052

基金项目: 国家自然科学基金（12171047）；国家自然科学基金委-中国工程物理研究院NSAF联合基金（U2230208）；山东省自然科学基金（ZR2021BA056）；国家留学基金委公派访学项目（CSC202308370209）

详细信息

作者简介:
梁　霄（1984－），男，博士，副教授，主要从事爆轰不确定度量化研究. E-mail：mathlx@163.com

中图分类号: O241; O521.3
计量
- 文章访问数: 155
- HTML全文浏览量: 64
- PDF下载量: 34
出版历程
- 收稿日期: 2024-07-26
- 修回日期: 2024-08-24
- 网络出版日期: 2024-11-01
- 刊出日期: 2025-04-03

Uncertainty Propagation Analysis of Detonation Pressure Based on Active Subspace

1.
School of Mathematics and System Sciences, Shandong University of Science and Technology, Qingdao 266590, Shandong, China
2.
Institute of Applied Physics and Computational Mathematics, Beijing 100094, China
3.
Henan Academy of Sciences, Zhengzhou 450052, Henan, China

摘要

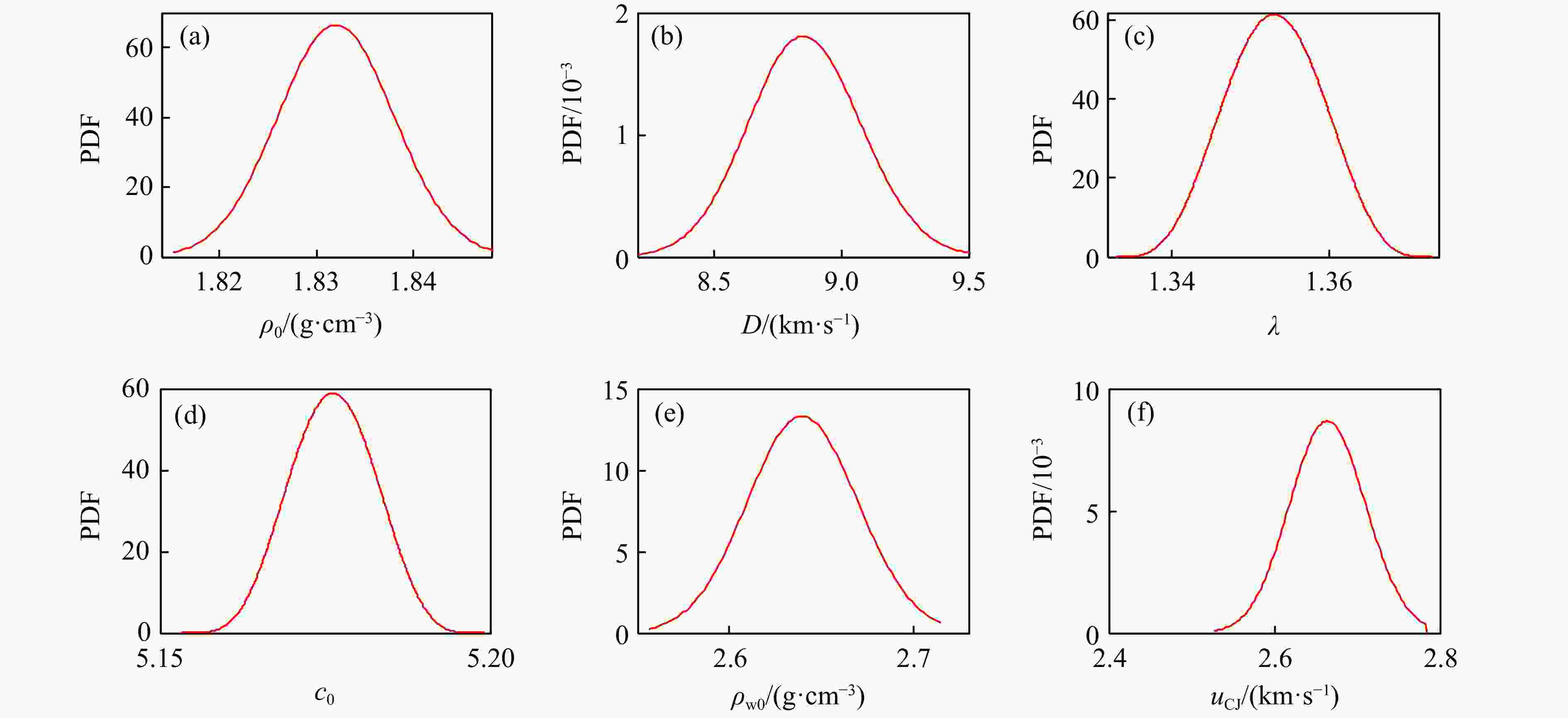
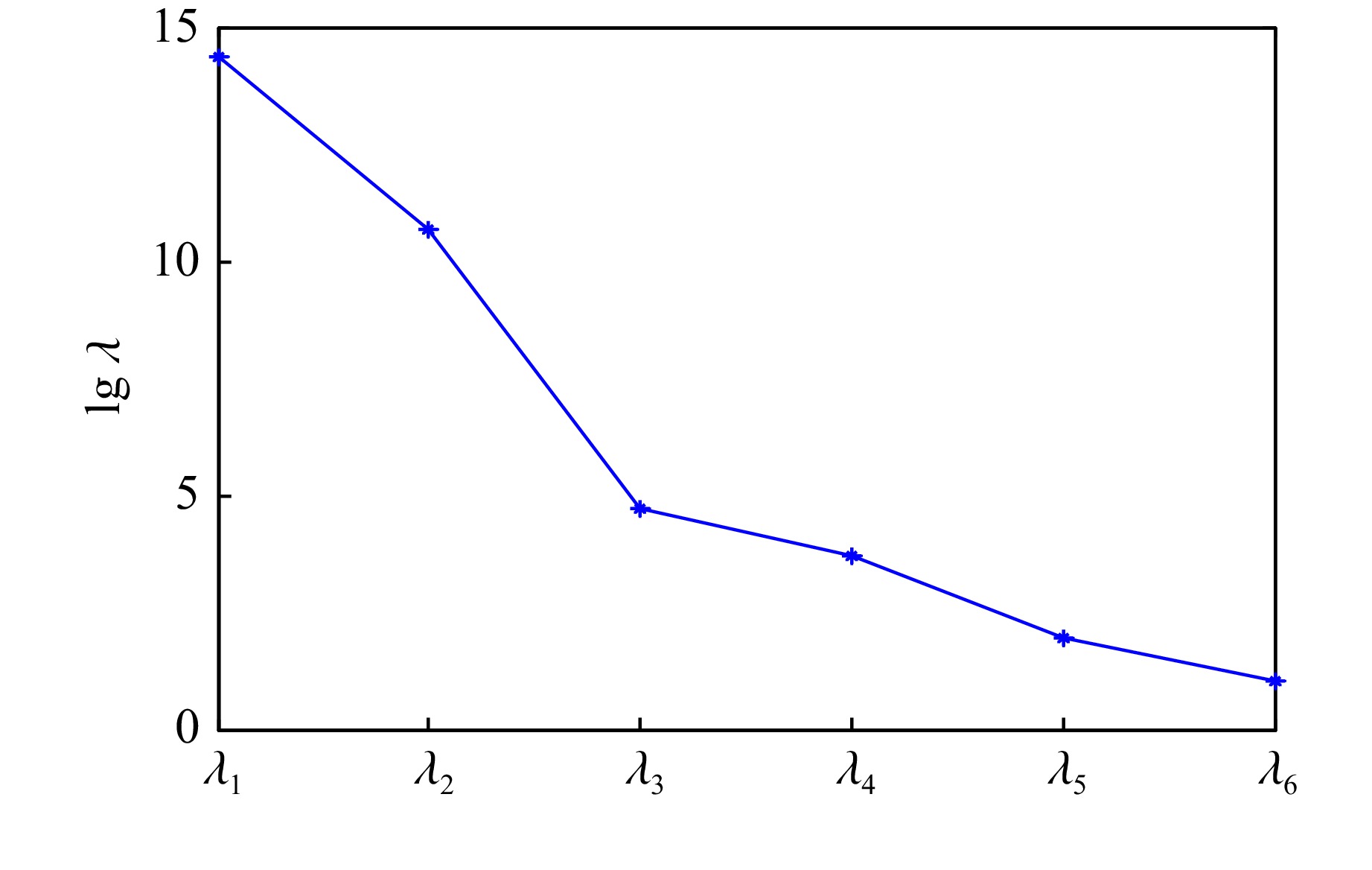
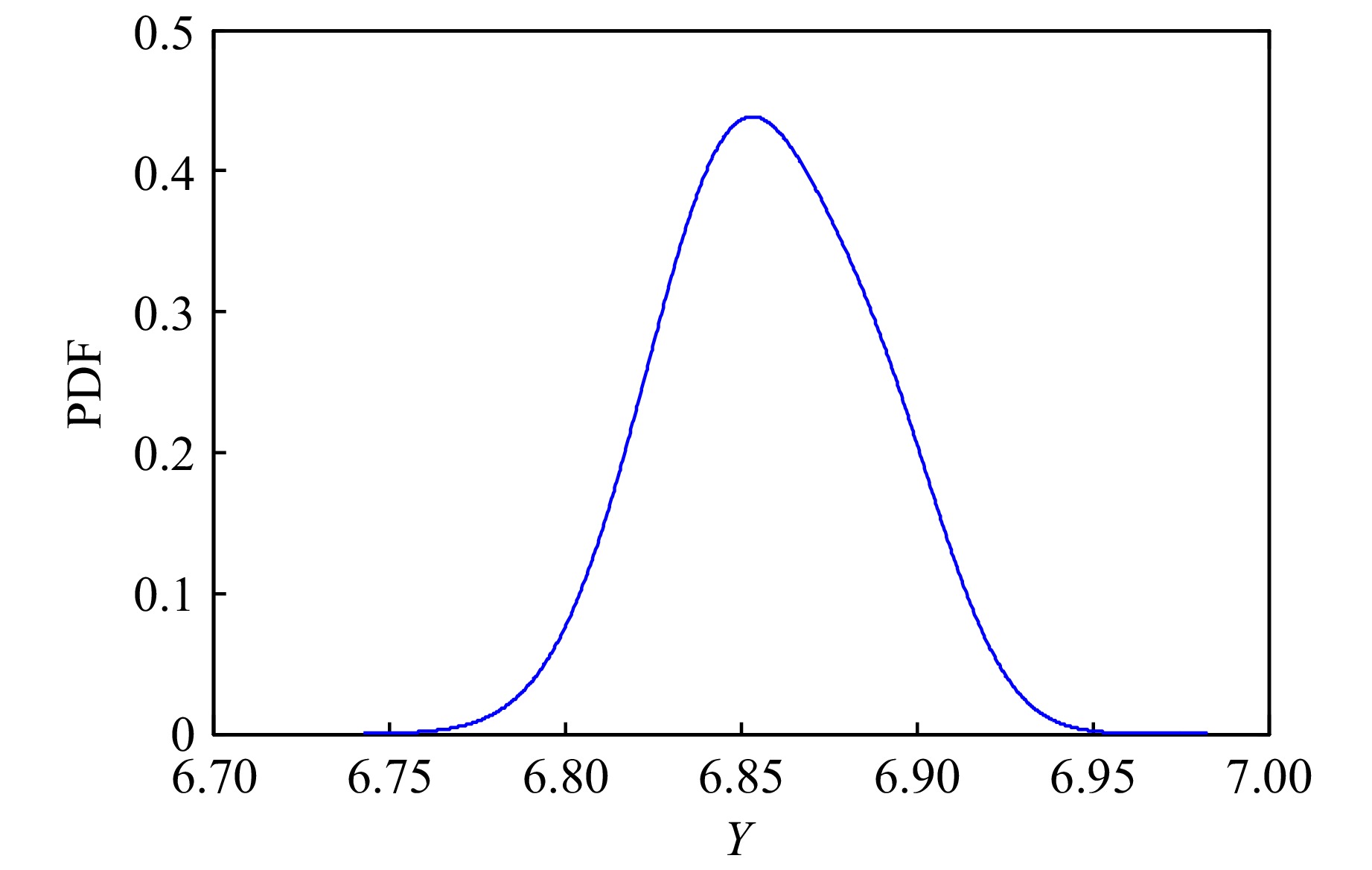
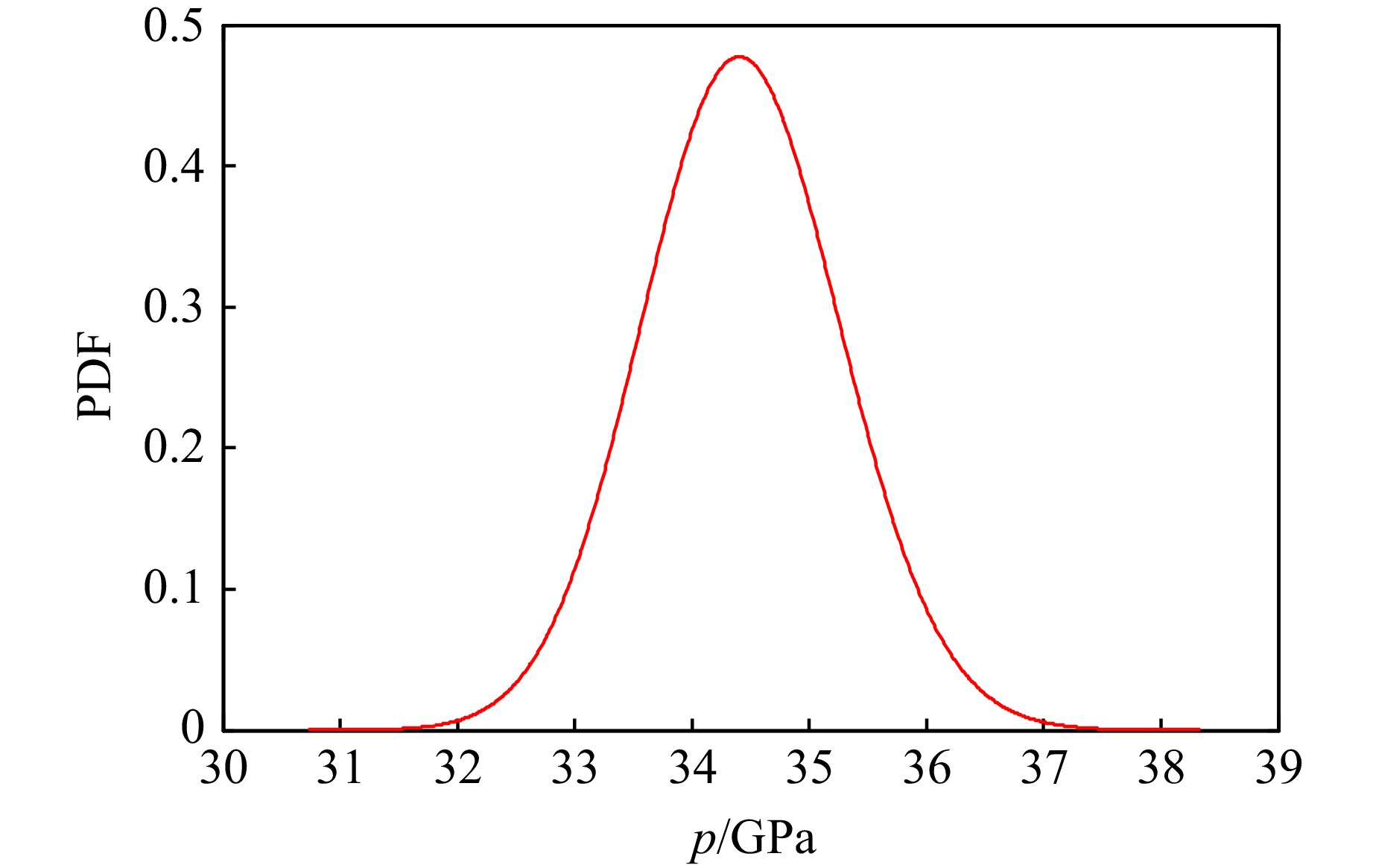
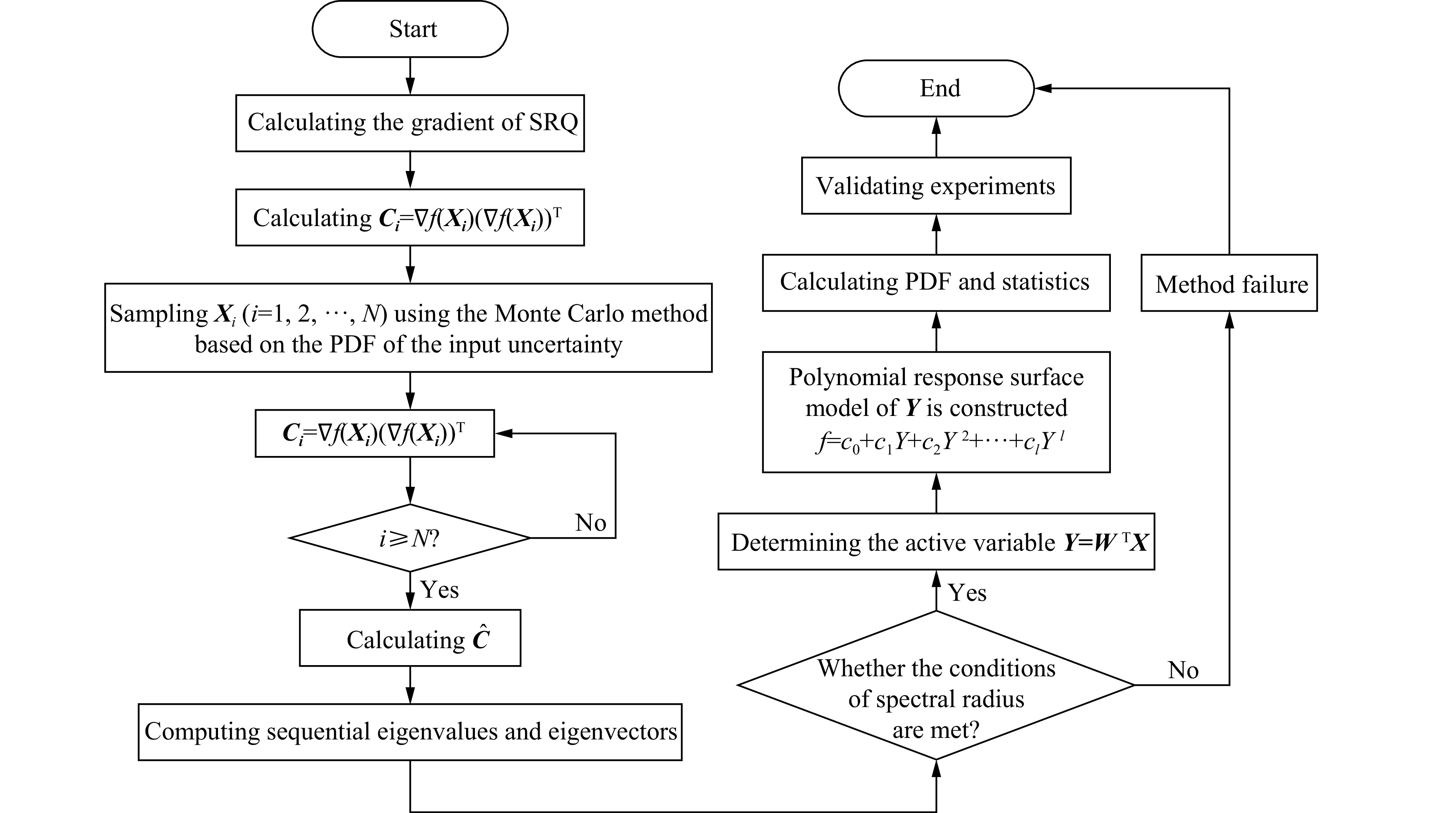
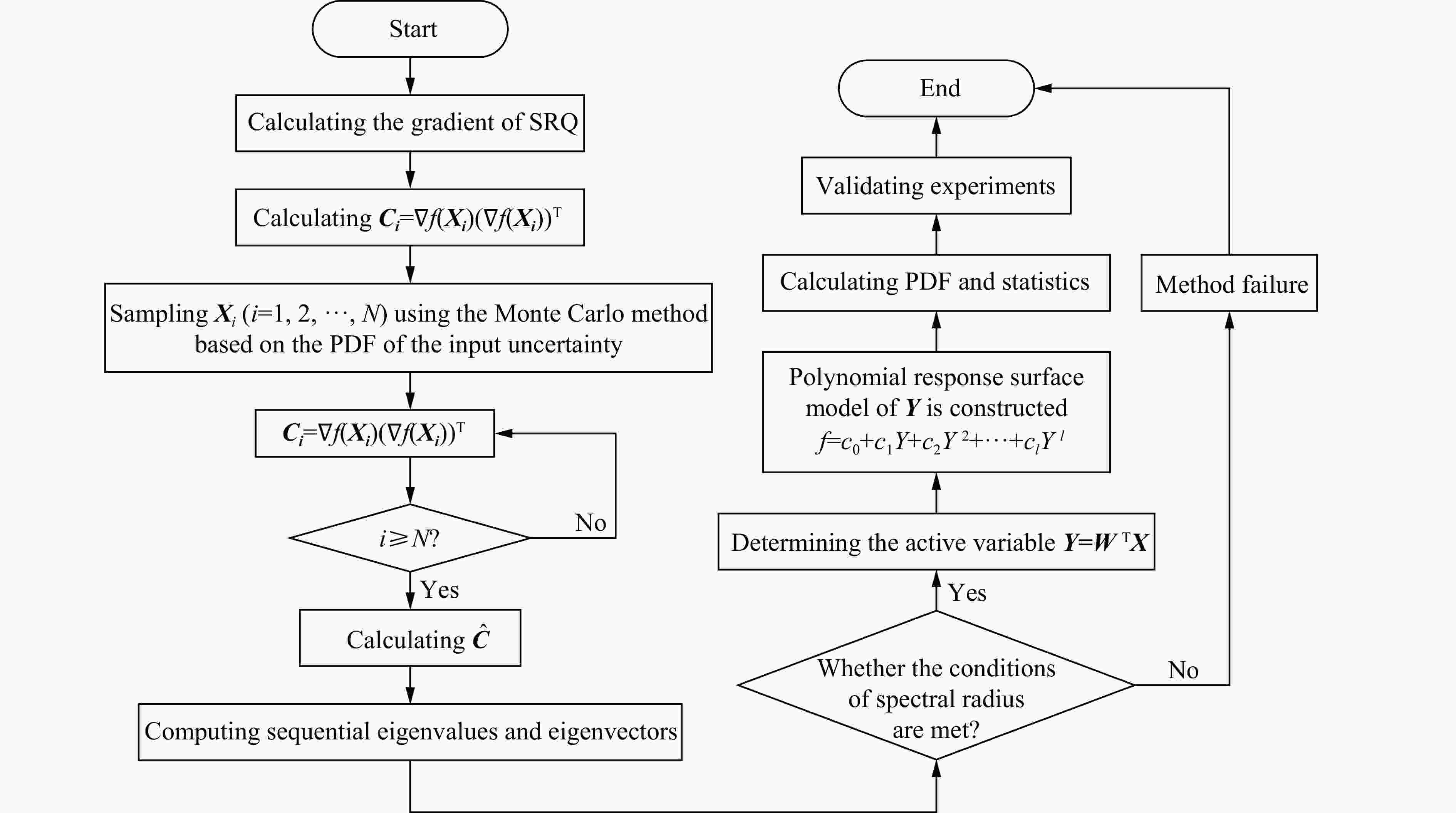
摘要: 爆压间接标定中的不确定度无法消除，不确定度量化能提高模型的可信度和预测能力。然而，爆压间接标定函数具有复杂非线性结构耦合多输入变量等特征，使得爆压不确定度传播研究遇到“维数灾难”等问题。活跃子空间是处理爆压不确定度量化的有效工具。首先，导出系统响应量（system response quantity, SRQ）的梯度协方差矩阵；然后，基于Monte Carlo方法，寻找活跃变量，即SRQ变化最快的方向；接着，将高维输入不确定度转化成一维空间处理，避免了“维数灾难”；最后，建立基于一维活跃变量的四阶多项式响应面模型。结果表明，活跃子空间方法成功刻画了输入不确定度对SRQ的影响，且试验结果落在代理模型预测值的置信区间内，确认了爆压模型的预测能力。研究还发现，爆压的离散程度较大，与孙承纬的结论吻合。此外，建立了一种新的爆压模型。该模型是仿射变换与多项式函数的复合运算，具有形式简洁、光滑性好、鲁棒能力强、运算速度快的特点，且系统输入量是随机变量而非固定值，多项式拟合系数不因输入不确定度的变化而改变。该研究方法具备体系性，可以推广到其他类型的炸药爆压预测。
- 活跃子空间 /
- 不确定度量化 /
- 爆压 /
- 响应面模型 /
- 降维
Abstract: Uncertainty cannot be eliminated in the indirect calibration of the detonation pressure, and the predictability and credibility of the model can be enhanced through uncertainty quantification of the detonation pressure. However, the indirect calibration function of the detonation pressure exhibits complex nonlinearity coupled with multiple inputs, making the study of uncertainty propagation of detonation pressure prone to issues such as the “curse of dimensionality”. Active subspace is proven to be an effective tool for handling uncertainty quantification of the detonation pressure model. The specific steps are as follows: to begin with, the covariance matrix is derived based on gradient of the system response quantity (SRQ). Then an active variable is deduced through the Monte Carlo method, which is the direction whose perturbations produce the greatest change in SRQ. A single derived active subspace is used as the input uncertainty instead of the six parameters. The “curse of dimensionality” can be relieved in this case. Finally, a fourth-order polynomial response surface model is established based on a one-dimensional active variable. The results show that the effects of input uncertainty on SRQ are successfully characterized using the means of the active subspace technique. The test data fall within the confidence interval of the predicted values from the surrogate model, and the predictive capability of the detonation pressure model is validated. The study also reveals that there is a significant degree of dispersion in detonation pressure, which is consistent with the viewpoint of Prof. Chengwei Sun. Furthermore, a new detonation pressure model is constructed in this paper. This model is a composite operation between an affine transformation and a polynomial function. It retains the characteristic of a concise form, sufficient smoothness, strong robustness, and fast computation. The input of the model is a random variable rather than a fixed value, and the polynomial coefficients remain unchangeable when it confronts the variability of input uncertainty. The research is an extension and development of previous scholars. Moreover, the research methodology is systematic, which can be applied to detonation pressure prediction for other types of explosives.
- active subspace /
- uncertainty quantification /
- detonation pressure /
- surface model /
- dimension reduction

HTML全文

爆压是刻画炸药爆轰性能的重要指标，关系到炸药的工业应用能力和爆轰数值模拟的精度和可信度。然而，爆轰是极度剧烈的瞬态（约100 ns）物理化学反应，空间尺度极小（约100 μm），爆压甚至高达100 GPa^[1–5]。爆轰的极端特征给爆压标定带来巨大挑战。直接标定爆压需要复杂的流程、昂贵的设备、精密的仪器仪表。与之相比，炸药密度的测量成本较低，爆速标定试验也相对简单。因此，先标定易于测量的物理量，再使用工程经验和物理定律间接导出爆压，成为爆压标定的常用方法。特别是研制新配方炸药时，间接标定爆压几乎成为必用的手段^[6–9]。但是，间接标定使用的数学模型具有模型结构复杂、多系统输入量（multi-input）等特征，且在一定程度上直接或间接使用最小二乘法，从而导致系统响应量（system response quantity, SRQ）对系统输入量的赋值敏感。爆压标定值伴随着系统输入量的变化而剧烈抖动。事实上，爆轰领域的专家学者已普遍达成共识，即受炸药组分的异质性和测试仪器的精度限制，系统输入量的标定值必然会在一定范围内波动^{[1–2, 10]}。爆轰的复杂性导致爆压间接测试模型中引入了数学物理假设、模型简化和近似，这是爆压标定中不确定度的又一来源。

如上所述，爆压间接标定中的输入不确定度是不可避免的^{[3–4, 9, 11]}。不确定度的存在又在一定程度上限制了间接标定的精度、效率和可靠性。遗憾的是，目前，绝大多数的爆压标定公式都是建立在确定的爆速等系统输入量的基础上^{[1–2, 6–8]}。事实上，不确定度的存在会让工程技术人员产生困惑，影响间接标定的可信度。因此，采用合理的数理工具量化输入不确定度，评估输入不确定度对爆压的影响，即实现爆压模型的不确定度量化（uncertainty quantification, UQ），对于提高爆压的间接标定可信度、拓宽模型适用范围、消除工程技术人员的顾虑至关重要。

爆压标定模型的不确定度量化研究面临的困难之一在于多输入不确定度。非线性模型耦合多输入不确定度会导致SRQ大幅偏离预测值。多输入不确定度使得不确定度传播过程中遇到“维数灾难”。因此，在保证预测精度的基础上，寻找合适的算法、降低计算维度、提高计算效率成为爆压标定领域亟待解决的问题^[9–12]。

活跃子空间（active subspace, AS）方法是处理高维不确定爆压间接标定模型的潜在有效降维工具^[10]。AS方法最早于2014年由 Constantine等^[13–14]提出，通过构造并分解类似协方差的梯度矩阵来确定输入不确定度中变化最快的方向，并以该方向为基函数，构建一个低维子空间，进而构造低维子空间上的代理模型。该方法在保留关键信息的同时，显著减少了计算量，避免了“维数灾难”。主成分分析和灵敏度分析在一定范畴内均可看作AS的特例。

AS方法自提出之后，迅速在欧美顶尖高校引起轰动，哈佛大学、麻省理工学院和剑桥大学等均多次开设AS研讨班。研究成果已经应用于燃烧冲压发动机（scramjet）、卫星导航、翼型设计、锂电池研发等重要工业领域^[15–19]。我国的AS研究虽然起步较早，但是截至目前，相关成果屈指可数。Hu等^[20–21]使用AS降维方法实现了卫星系统中的多学科优化设计，同时还进一步提出了广义AS的混合不确定性降维方法；王娜娜等^[22]将AS降维方法应用在湍流燃烧模拟中。对于爆轰领域，国内外至今未见AS方法应用的相关报道。AS方法在工业和国防领域的成功经验可以为爆压模型的不确定度传播研究提供借鉴。

综上所述，寻找鲁棒性强、模型复杂度低、容许系统输入量适度波动的爆压代理模型，是提高爆压标定准确性的目标之一。虽然AS方法在爆压不确定度量化研究中的应用尚未见报道，但是其自身的理想结构完全契合爆压不确定度传播研究，并且AS方法在其他领域取得的成功能够为爆压参数间接标定提供参考。此外，基于活跃变量的响应面模型法（response surface methodology，RSM）还可直接构造输入不确定度与SRQ之间的非线性映射。该代理模型在保留精度的同时，有望降低数标定成本，提升光滑性，从而构造一种新的、高效的爆压间接标定模型，进一步推广前人的研究成果。本研究将采用AS方法对爆压的不确定度进行分析。

1. AS基本理论

令 ${ {{\boldsymbol{X}}}} \in$ $\chi$ $\subset {\mathrm{R}}^m$ 表示输入不确定度，其中： $\chi$ 为 ${{{\boldsymbol{X}}}}$ 的支集（supporting set），R^m为m维Euclid空间。设 ${\boldsymbol{X}}$ 的联合概率密度函数（probability distribution function，PDF）为 $\rho (x)$ ，利用SRQ f的梯度向量构造类似协方差的矩阵

$\begin{aligned} {\boldsymbol{C}} = {\mathrm{E}}((\nabla f){(\nabla f)^{\mathrm{T}}}) &= \int_{{{\mathrm{R}}^m}} {(\nabla f){{(\nabla f)}^{\mathrm{T}}}\rho {\mathrm{d}}x} = {\boldsymbol{W}}{\boldsymbol{\varLambda}} {{\boldsymbol{W}}^{\mathrm{T}}} \\ \end{aligned}$

(1)

式中：E为期望算子； ${\boldsymbol{\varLambda}}$ 为C的特征值矩阵， ${\boldsymbol{\varLambda}} = {\mathrm{diag}}({\lambda _1}, \cdots ,{\lambda _m})$ ， ${\lambda _1} \geqslant \cdots \geqslant {\lambda _m} \geqslant 0$ ； ${\boldsymbol{W}}$ 为 ${\boldsymbol{\varLambda}}$ 对应的特征向量构成的矩阵。

将特征值矩阵和特征向量分块

${\boldsymbol{\varLambda}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\varLambda}} ^{n \times n}_1}}&0 \\ 0&{{{\boldsymbol{\varLambda}} _2}} \end{array}} \right] ,\;\;\;\;\;\; {\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{W}}_1}}&{{{\boldsymbol{W}}_2}} \end{array}} \right]$

(2)

式中： ${{\boldsymbol{\varLambda}} _1} = {\mathrm{diag}}({\lambda _1}, \cdots ,{\lambda _n})$ ， ${{\boldsymbol{\varLambda}} _2}$ 为后m−n个特征值构成的矩阵， ${{\boldsymbol{W}}_1}$ 为 ${\boldsymbol{W}}$ 前n个特征向量矩阵， ${{\boldsymbol{W}}_2}$ 为后m−n个特征向量构成的矩阵。若 ${\lambda _n} \geqslant {\lambda _{n+1}}$ ，则称 ${\boldsymbol{C}}$ 中存在谱间隙。此时，称输入不确定度 ${\boldsymbol{X}}$ 的旋转变换 ${\boldsymbol{Y}} = {{\boldsymbol{W}}_1}{\boldsymbol{X}}$ 为活跃变量， ${\boldsymbol{Z}} = {{\boldsymbol{W}}_2}{\boldsymbol{X}}$ 为非活跃变量。根据文献[]，f沿着 ${\boldsymbol{Y}}$ 方向上的变化比沿着 ${\boldsymbol{Z}}$ 方向的变化快得多。特别地，当 ${\lambda _{n+1}} = \cdots = {\lambda _m} = 0$ 时，f在 ${\boldsymbol{Z}}$ 方向上的变化为零。

在工程领域，很难显式计算式(1)中的m重积分，进而无法给出式(1)中矩阵 ${\boldsymbol{C}}$ 的精确值。通常使用Monte Carlo方法求解AS矩阵 ${\boldsymbol{C}}$ 及其相应的特征值和特征向量。具体而言， ${\boldsymbol{C}}$ 有如下逼近公式

${\boldsymbol{C}} \approx \hat {\boldsymbol{C}} = \frac{1}{N}\sum\limits_{j = 1}^N {(\nabla {f_j}){{(\nabla {f_j})}^{\mathrm{T}}}}$

(3)

式中： $\nabla {f_j} = \nabla f({{{\boldsymbol X}}_j})$ ， ${{{\boldsymbol X}}_j} \in \mathcal{X}$ （ $j = 1, \cdots ,N$ ），样本点X_j根据 $\rho ({{x}})$ 抽样得到。

1.1 多项式响应面模型

如上所述，沿敏感方向 ${\boldsymbol{Y}} = {{\boldsymbol{W}}_1}{\boldsymbol{X}}$ ，系统输入量的扰动能对SRQ产生最大程度的影响。接下来，将沿 ${\boldsymbol{Y}} = {{\boldsymbol{W}}_1}{\boldsymbol{X}}$ 构建代理模型，降低系统输入不确定度的维数，即构造SRQ f的近似值

$f({\boldsymbol{X}}) \approx g({\boldsymbol{Y}})$

(4)

寻找合适代理模型g关系到AS的精度，是AS研究的重要目标。按照国际惯例^[21]，g又称为桥（bridge）函数。

采用广义多项式拟合输入不确定度与SRQ之间的映射关系，进而通过回归分析标定参数，具有结构简单、运行周期短、计算成本可忽略的优势，可用作AS的桥函数。n元l阶多项式响应面模型表征如下

$g({{Y}}) = {\alpha _0}+\sum\limits_{i = 1}^n {{\alpha _i}{Y_i}+} \sum\limits_{i = 1}^n {\sum\limits_{j = i}^n {{\alpha _{ij}}{Y_i}{Y_j}} } + \cdot \cdot \cdot +\sum\limits_{{i_1} = 1}^n {\sum\limits_{{i_2} = {i_1}}^n { \cdot \cdot \cdot \sum\limits_{{i_l} = {i_{l - 1}}}^n {{\alpha _{{i_1}{i_2} \cdot \cdot {i_l}}}{Y_{{i_{\text{1}}}}}{Y_{{i_2}}} \cdot \cdot \cdot } } } {Y_{{i_l}}}$

(5)

特别地，当n=1时，多项式代理模型表征为

$g({{Y}}) = {c_0}+{c_1}Y+{c_2}{Y^2}+ \cdots +{c_l}{Y^l}$

(6)

使用最小二乘法标定式(6)的系数c₀ ～c_l，步骤如下。

选取M个样本点X_i，分别计算Y_i和f (X_i)，进而计算

$\hat {\boldsymbol{c}} = {\rm {argmin}} ({\left\| {{\boldsymbol {Ac}} - {\boldsymbol{f}}} \right\|^2})$

(7)

式中： ${\boldsymbol{A}}$ 为Vandermonde矩阵， ${\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&{{Y_1}}&{Y_1^2}& \cdots &{Y_1^l} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1&{{Y_M}}&{Y_M^2}& \cdots &{Y_M^l} \end{array}} \right]$ ； ${\boldsymbol{f}} = \left[ {\begin{array}{*{20}{c}} {f({X_1})} \\ \vdots \\ {f({X_M})} \end{array}} \right]$ ； ${\boldsymbol{c}} = \left[ {\begin{array}{*{20}{c}} {{c_0}} \\ \vdots \\ {{c_l}} \end{array}} \right]$ 。

1.2 误差分析

AS降维提高了计算效率，但也导致SRQ的真实值与预测值的差异。根据文献[]，SRQ f和代理模型 $g({\boldsymbol{Y}})$ 的误差^[20]为

${\int {(f({{\boldsymbol x}}) - g({\boldsymbol{W}}_1^{\rm T}{\boldsymbol{x}}))} ^2}\rho {\mathrm{d}}{{\boldsymbol x}} \leqslant C({\lambda _{n+1}}+{\lambda _{n+2}}+ \cdots +{\lambda _m})$

(8)

式中：常数C依赖于 $\rho ({{\boldsymbol x}})$ 。因此， ${\lambda _{n+1}}+{\lambda _{n+2}}+ \cdots +{\lambda _m}$ 越小，活跃变量 ${\boldsymbol{X}}$ 对SRQ f的影响越大。据此，确定AS存在的判据为

$\frac{{{\lambda _{n+1}}+{\lambda _{n+2}}+ \cdots +{\lambda _m}}}{{{\lambda _1}+{\lambda _2}+ \cdots +{\lambda _m}}} \leqslant \alpha$

(9)

式中： $\alpha =0.01$ 。

需要注意的是，若 ${\boldsymbol{Y}}$ 为坐标轴方向，则AS方法退化成主成分分析，因此，可以认为，AS方法是主成分分析的一种延伸。

1.3 基于AS的不确定度量化流程

按照1.1节和1.2节的理论分析，基于AS的不确定度量化流程如图1所示。

图 1 基于AS的降维流程

Figure 1. Flow chart of dimensionality reduction based on active subspace

下载: 全尺寸图片幻灯片

2. 爆压的不确定度量化和传播

2.1 爆压的不确定度量化

孙承纬等^[1]根据ZND模型，结合阻抗匹配公式，利用界面粒子速度，导出了待测炸药爆压模型，其表达式为

$p = \frac{1}{2}{u_{\mathrm{CJ}}}\left[ {{\rho _{{\mathrm{w}}0}}({c_0}+s{u_{\mathrm{CJ}}})+{\rho _0}D} \right]$

(10)

式中：ρ₀为PBX9501的初始密度，D为PBX9501的爆速，u_CJ为CJ点界面粒子速度，ρ_w0为LiF的初始密度，c₀为LiF的冲击绝热线常数，s为LiF的Hugoniot斜率。

首先，假设本研究的物理量服从对数正态分布LN(μ, σ)，然后利用具体试验数据，通过Kolmogorov-Smirnov假设检验方法验证假设的合理性。对数期望μ和对数方差σ可由物理量的期望和方差导出，具体计算公式和标定流程见文献[3]。根据文献[3]标定的数据，ρ₀≈LN(0.6206, 0.0016)为PBX9501的初始密度，密度的期望为1.860 g/cm³，标准差为0.003 g/cm³。D≈LN(9.089, 0.025)为PBX9501的爆速，期望为8860 m/s，标准差为221 m/s。根据文献[6–7]，标定u_CJ≈LN(7.8879, 0.0135)为CJ点界面粒子速度，期望为2665 m/s，标准差为36 m/s。ρ_w0≈LN(0.9708, 0.0010)为LiF的初始密度，期望为2.644 g/cm³，标准差为0.02 g/cm³。

由于唯象参数无法通过试验直接标定，因此，根据工程经验，假设唯象参数服从Beta分布。利用文献[6–7]，假设LiF的冲击绝热线常数c₀≈B(5.153, 5.199, 6, 6)，其中B(5.153, 5.199, 6, 6)为Beta分布，[5.153, 5.159]为c₀的支集，后2个参数6和6为形状参数，根据工程经验^[3]得到。LiF的Hugoniot斜率s≈B(1.343, 1.363, 6, 6)。

图2为输入不确定度的PDF图。

图 2 输入不确定度的概率密度函数

Figure 2. PDF of the input uncertainty

下载: 全尺寸图片幻灯片

根据式(10)和第1节，得到

$\begin{aligned} \nabla {\boldsymbol{p}} &= {\left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial p}}{{\partial {\rho _0}}}}&{\dfrac{{\partial p}}{{\partial D}}}&{\dfrac{{\partial p}}{{\partial s}}}&{\dfrac{{\partial p}}{{\partial {c_0}}}}&{\dfrac{{\partial p}}{{\partial {\rho _{{\mathrm{w}}0}}}}}&{\dfrac{{\partial p}}{{\partial {u_{\mathrm{CJ}}}}}} \end{array}} \right]^{\mathrm{T}}} \\ & = {\left[ {\begin{array}{*{20}{c}} {\dfrac{1}{2}{u_{\mathrm{CJ}}}D}&{\dfrac{1}{2}{u_{\mathrm{CJ}}}{\rho _0}}&{\dfrac{1}{2}{\rho _{{\mathrm{w}}0}}u_{\mathrm{CJ}}^2}&{\dfrac{1}{2}{u_{\mathrm{CJ}}}{\rho _{\rm{{w0}}}}}&{\dfrac{1}{2}{u_{\mathrm{CJ}}}{c_0}}&{\dfrac{1}{2}\left( {{\rho _{{\mathrm{w}}0}}{c_0}+{\rho _0}D} \right)} \end{array}+s{\rho _{{\mathrm{w}}0}}{u_{\mathrm{CJ}}}} \right]^{\rm {T}}} \\ \end{aligned}$

(11)

进而

${\boldsymbol{C}} = {\mathrm{E}}(\nabla {\boldsymbol{p}}{(\nabla {\boldsymbol{p}})^{\mathrm{T}}}) = \frac{1}{4}{\mathrm{E}}\left[ {\begin{array}{*{20}{c}} {u_{\mathrm{CJ}}^2{D^2}}&{u_{\mathrm{CJ}}^2D{\rho _0}}&{u_{\mathrm{CJ}}^3D{\rho _{{\mathrm{w}}0}}}&{u_{\mathrm{CJ}}^2D{\rho _{{\mathrm{w}}0}}}&{u_{\mathrm{CJ}}^2{c_0}D} &{{u_{\mathrm{CJ}}}DQ} \\ {u_{\mathrm{CJ}}^2D{\rho _0}}&{u_{\mathrm{CJ}}^2\rho _0^2}&{u_{\mathrm{CJ}}^3{\rho _0}{\rho _{{\mathrm{w}}0}}}&{u_{\mathrm{CJ}}^2{\rho _0}{\rho _{{\mathrm{w}}0}}}&{u_{\mathrm{CJ}}^2{c_0}{\rho _0}}&{{u_{\mathrm{CJ}}}{\rho _0}Q} \\ {u_{\mathrm{CJ}}^3D{\rho _{{\mathrm{w}}0}}}&{u_{\mathrm{CJ}}^3{\rho _0}{\rho _{{\mathrm{w}}0}}}&{\rho _{{\mathrm{w}}0}^2u_{\mathrm{CJ}}^4}&{\rho _{{\mathrm{w}}0}^2u_{\mathrm{CJ}}^3}&{{\rho _{{\mathrm{w}}0}}u_{\mathrm{CJ}}^3{c_0}}&{{\rho _{{\mathrm{w}}0}}u_{\mathrm{CJ}}^2Q} \\ {u_{\mathrm{CJ}}^2D{\rho _{{\mathrm{w}}0}}}&{u_{\mathrm{CJ}}^2{\rho _0}{\rho _{{\mathrm{w}}0}}}&{\rho _{{\mathrm{w}}0}^2u_{\mathrm{CJ}}^3}&{\rho _{{\mathrm{w}}0}^2u_{\mathrm{CJ}}^2}&{u_{\mathrm{CJ}}^2{c_0}{\rho _{{\mathrm{w}}0}}}&{{u_{\mathrm{CJ}}}{\rho _{{\mathrm{w}}0}}Q} \\ {u_{\mathrm{CJ}}^2{c_0}D}&{u_{\mathrm{CJ}}^2{\rho _0}{\rho _{{\mathrm{w}}0}}}&{{\rho _{{\mathrm{w}}0}}u_{\mathrm{CJ}}^3{c_0}}&{u_{\mathrm{CJ}}^2{c_0}{\rho _{{\mathrm{w}}0}}}&{c_0^2u_{\mathrm{CJ}}^2}&{{u_{\mathrm{CJ}}}{c_0}Q} \\ {{u_{\mathrm{CJ}}}DQ}&{{u_{\mathrm{CJ}}}{\rho _0}Q}&{{\rho _{{\mathrm{w}}0}}u_{\mathrm{CJ}}^2Q}&{{u_{\mathrm{CJ}}}{\rho _{{\mathrm{w}}0}}Q}&{{u_{\mathrm{CJ}}}{c_0}Q}&{{Q^2}} \end{array}} \right]$

(12)

式中： $Q = {\rho _{{\mathrm{w}}0}}{c_0}+{\rho _0}D+2s{\rho _{{\mathrm{w}}0}}{u_{\mathrm{CJ}}}$ 。

根据输入不确定度 ${\boldsymbol{X}} = {({\rho _0},D,s,{c_0},{\rho _{{\mathrm{w}}0}},{u_{\mathrm{CJ}}})^{\mathrm{T}}}$ 的联合PDF，在 ${\boldsymbol{X}}$ 的支集中随机选取 $N = {10^6}$ 个样本 $\left\{ {{{\boldsymbol{X}}_1}, \cdots ,{{\boldsymbol{X}}_N}} \right\}$ ，其中 ${{\boldsymbol{X}}_i} = {({\rho _{0i}},{D_i},{s_i},{c_{0i}},{\rho _{{\mathrm{w}}0i}},{u_{{\mathrm{CJ}}i}})^{\mathrm{T}}}$ （ $i = 1,2, \cdots ,N$ ）。利用Monte Carlo原理，式(12)近似为

${\boldsymbol{C}} \approx \hat {\boldsymbol{C}} = \frac{1}{N}\sum\limits_{i = 1}^N {\nabla {{\boldsymbol{p}}_i}{{(\nabla {{\boldsymbol{p}}_i})}^{\mathrm{T}}}}$

(13)

式中： $\nabla {{\boldsymbol{p}}_i} = \dfrac{1}{2}{\left[ {\begin{array}{*{20}{c}} {{u_{{\mathrm{CJ}}i}}{D_i}}&{{u_{{\mathrm{CJ}}i}}{\rho _{0i}}}&{{\rho _{{\mathrm{w}}0i}}u_{{\mathrm{CJ}}i}^2}&{{u_{{\mathrm{CJ}}i}}{\rho _{{\mathrm{w}}0i}}}&{{u_{{\mathrm{CJ}}i}}{c_{0i}}}&{{\rho _{{\mathrm{w}}0i}}{c_{0i}}+{\rho _{0i}}{D_i}+2{s_i}{\rho _{{\mathrm{w}}0i}}{u_{{\mathrm{CJ}}i}}} \end{array}} \right]^{\mathrm{T}}}$ ，对 $\hat {\boldsymbol{C}}$ 进行特征值分解， $\hat {\boldsymbol{C}} = \hat {\boldsymbol{W}}\hat {\boldsymbol{\varLambda}} {\hat {\boldsymbol{W}}^{\rm T}}$ ，顺序特征值为

$\hat {\boldsymbol{\varLambda}} = {\rm {diag}}({\lambda _1}, \cdot \cdot \cdot ,{\lambda _6}) = {\rm {diag}}(8.493 \times {10^{13}},\,3.305 \times {10^{10}},\,6.244 \times {10^3},\,3.323 \times {10^4},\,9.329\,9,\,1.927\,3)$

(14)

给出了对数尺度下特征值的分布示意图。可以看出，特征值的尺度逐渐递减，且递减速度很快，同时 ${\lambda _1} \approx {10^3}{\lambda _2}$ 。另外， $\dfrac{{{\lambda _2}+{\lambda _3}+{\lambda _4}+{\lambda _5}+{\lambda _6}}}{{{\lambda _1}+{\lambda _2}+{\lambda _3}+{\lambda _4}+{\lambda _5}+{\lambda _6}}} \approx 1.21 \times {10^{ - 4}} < \alpha = 0.01$ 。由式(9)可知，存在谱间隙。结合1.2节可以得到，孙承纬等^[1]提出的爆压间接标定模型即式(10)存在AS。

图 3 对数尺度下特征值的分布

Figure 3. Distribution of eigenvalues for the logarithmic scale

下载: 全尺寸图片幻灯片

此时，根据特征值大小将C的特征值矩阵和特征向量矩阵分块

$\hat {\boldsymbol{\varLambda}} = \left[ {\begin{array}{*{20}{c}} {{{\hat {\boldsymbol{\varLambda}} }_1}}&0 \\ 0&{{{\hat {\boldsymbol{\varLambda}} }_2}} \end{array}} \right] ,\;\;\;\;\;\; \hat {\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} {{{\hat {\boldsymbol{W}}}_1}}&{{{\hat {\boldsymbol{W}}}_2}} \end{array}} \right]$

(15)

式中： ${\hat {\boldsymbol{\varLambda}} _1} = {\rm {diag}}(8.49 \times {10^{13}})$ ， ${\hat {\boldsymbol{\varLambda}} _2} = {\rm {diag}}(3.30 \times {10^{10}},6.24 \times {10^3},3.32 \times {10^4},9.339,1.927\,3)$ 。最大特征值 ${\lambda _1} = 8.49 \times {10^{13}}$ 对应的特征向量为

${\hat {\boldsymbol{W}}_1} = {\left[ {\begin{array}{*{20}{c}} {0.828\,1}&{0.000\,2}&{0.560\,5}&{0.000\,3}&{0.000\,6}&{0.002\,6} \end{array}} \right]^{\mathrm{T}}}$

(16)

活跃变量定义为

${ Y} = \hat{\boldsymbol{W}}_1^{\mathrm{T}}{\boldsymbol{X}}$

(17)

此时，根据图2中的信息和式(17)，计算得到Y的PDF，如图4所示。

图 4 活跃变量Y的概率密度函数

Figure 4. PDF of the active variable Y

下载: 全尺寸图片幻灯片

利用1.2节理论，在AS式(17)中构建多项式响应面模型

$p = {d_0}+{d_1}Y+{d_2}{Y^2}+{d_3}{Y^3}+{d_4}{Y^4}$

(18)

根据所示信息，随机抽取M=10⁵个样本点，计算相应的Vandemonde矩阵，再利用1.1节的最优化理论，计算得到 $({d_0},{d_1},{d_2},{d_3},{d_4}) = (117.92,878.64,5\,820.11,28\,920.81,159.03)$ 。

利用图4和式(18)，进一步得到爆压的PDF，如图5所示。利用图5信息，得到爆压的期望为34.67 GPa，标准差为1.51 GPa，95%置信水平下的置信区间为[32.75 GPa, 36.01 GPa]，如表1所示。

图 5 基于AS的爆压的概率密度函数

Figure 5. PDF of detonation pressure deduced from active subspace

下载: 全尺寸图片幻灯片

表 1 爆压的试验和统计结果

Table 1. Test and statistical results of the detonation pressure GPa

Statistical results				Test data^[2]
Mean	Standard deviation	Upper confidence limit	Lower confidence limit	Test data^[2]
34.67	1.51	36.01	32.75	34.41

下载: 导出CSV

| 显示表格

为展示本方法的优点，图6给出了AS方法与Monte Carlo方法的收敛曲线对比，其中，Monte Carlo方法的采样次数分别取1×10⁵、5×10⁵、1×10⁶、5×10⁶、1×10⁷。从图6可以看出：当采样次数为1×10⁵时，PDF的峰值明显偏低；当采样次数为5×10⁵时，PDF曲线在峰值处出现振荡；当采样次数达到甚至超过1×10⁶后，AS导出的PDF曲线与Monte Carlo方法导出的PDF曲线吻合良好。

图 6 AS和Monte Carlo方法得到的爆压的概率密度函数

Figure 6. PDF of detonation pressure deduced from AS and Monte Carlo methods

下载: 全尺寸图片幻灯片

2.2 机理分析

AS的本质是通过线性变换得到高维空间中敏感性较高的方向，进而在此方向构造简洁实用的代理模型。使用AS成功执行了爆压不确定度传播，这种降维方法更有效，且适应性更强，能够提高爆压的间接标定效率。

从表1可以看出，采用AS方法得到的爆压均值与试验结果相差不大，且AS方法得到的置信区间包含前人试验标定的爆压结果，确认了式(18)的可信度。

从图5可以看出，虽然输入不确定度很小，但是SRQ的波动仍然很大。进一步计算发现，SRQ爆压的标准差与期望之比是1.51 GPa/34.67 GPa=4.35%，比图2中初始密度和速度等物理量的相对标准差大得多，即爆压的离散程度较大，与孙承纬等^[1]的结论吻合。出现差异的部分原因是由爆压代理模型的复杂非线性结构造成的。

Monte Carlo方法的缺点是收敛速度慢，优点是不需要任何假设，使用直接，可看作不确定意义下的精确解。将AS方法与采样次数不小于10⁶的直接Monte Carlo方法标定的PDF进行对比，发现两者得到的曲线吻合很好，具有相似的偏度和几乎相等的峰度，且峰值几乎吻合，特别是尾项几乎重合，即失效概率几乎一致。因此，代理模型保留了高分辨率系统的非线性特征，验证了计算模型的有效性。

此外，当前方法使用的样本数比经典Monte Carlo方法所需的样本数少。原因在于本研究使用Monte Carlo方法寻找变化最快的方向，标定活跃变量，并建立多项式代理模型。式(17)和式(18)的复杂程度较低，计算成本较低。

事实上，式(17)和式(18)构造了一个新的爆压预测数学模型，它是输入不确定度的多项式变换与仿射变换的复合。与式(10)相比，其形式更简洁，光滑性更强，运算速度更快，计算成本可忽略不计。

3. 结论与展望

本研究首次使用AS技术刻画了输入不确定度对SRQ的影响，展示了爆压的置信区间，实现了爆轰不确定度量化，继承和发展了文献[1]的研究成果，提高了爆压模型的可信度和可靠性。首先，探索并获得了输入不确定度变化最快的方向，将输入不确定度的维度从六维降为一维，在一定程度上缓解了“维数灾难”，进而在此方向上建立爆压的多项式响应面模型，即式(18)。该模型本质上是输入不确定度的线性变换和多项式函数的复合运算，具有形式简洁、光滑性好、运算速度快的特点。另外，式(18)中的系统输入量是一个概率分布而非固定值，允许物理量在一定范围内依靠规定的概率结构变动，而系数保持不变。换言之，式(18)建立了一种输入不确定度（随机向量）到SRQ的非线性变换，与直接构造的代理模型相比，系数不因系统输入量的改变而发生变动，具有鲁棒性强的特点。

针对爆压公式，即式(10)，将原六维输入不确定度空间映射到一维AS上，四阶多项式响应面模型只需计算5个系数，相比之下，全张量积四阶多项式响应面模型需要计算280个系数，不具备计算可行性，且提高多项式的次数愈加困难。本方法还可以进一步提高多项式次数，增加光滑程度，对于结构更加复杂的爆压模型意义重大。此外，输入不确定度维数的降低加快了计算效率，降低了计算成本，在一定程度上缓解了“维数灾难”。

本研究方法具有体系性和普适性，可以推广到其他类型的炸药和爆压公式。对于复杂的爆轰系统，爆压公式中从输入参数 ${\boldsymbol{X}}$ 到目标量映射的梯度 $\nabla {\boldsymbol{p}}$ 有时不能直接解析得到，下一步拟将AS降维方法推广到处理隐式爆轰系统的不确定度量化的降维问题。另外，确定最小样本数的阈值，进一步加快计算效率，对于复杂模型尤为重要，是一个具有挑战性的研究课题，但至今未见此方面的研究。最后，爆压还与装药厚度及配方成分密切关联，如在工程爆破中，经常在炸药中添加铝粉、玻璃微珠、珍珠岩、乳化剂和敏化剂等，如何量化这些因子的不确定因素，如何评估装药厚度和添加剂对爆压的影响，也是下一步的研究内容。

感谢合作导师Christian Soize教授的指导，感谢北京流体动力科学研究中心胡星志研究员提供的技术指导。

图 1 基于AS的降维流程

Figure 1. Flow chart of dimensionality reduction based on active subspace

下载: 全尺寸图片幻灯片

图 2 输入不确定度的概率密度函数

Figure 2. PDF of the input uncertainty

下载: 全尺寸图片幻灯片

图 3 对数尺度下特征值的分布

Figure 3. Distribution of eigenvalues for the logarithmic scale

下载: 全尺寸图片幻灯片

图 4 活跃变量Y的概率密度函数

Figure 4. PDF of the active variable Y

下载: 全尺寸图片幻灯片

图 5 基于AS的爆压的概率密度函数

Figure 5. PDF of detonation pressure deduced from active subspace

下载: 全尺寸图片幻灯片

图 6 AS和Monte Carlo方法得到的爆压的概率密度函数

Figure 6. PDF of detonation pressure deduced from AS and Monte Carlo methods

下载: 全尺寸图片幻灯片

表 1 爆压的试验和统计结果

Table 1. Test and statistical results of the detonation pressure GPa

Statistical results Test data^[2]
Mean Standard deviation Upper confidence limit Lower confidence limit

34.67 1.51 36.01 32.75 34.41

下载: 导出CSV

参考文献(22)

[1]	孙承纬, 卫玉章, 周之奎. 应用爆轰物理 [M]. 北京: 国防工业出版社, 2000: 216–239. SUN C W, WEI Y Z, ZHOU Z K. Applied detonation physics [M]. Beijing: National Defense Industry Press, 2000: 216–239.
[2]	MADER C L. Numerical modeling of explosives and propellants [M]. 3rd ed. Boca Raton: CRC Press, 2008.
[3]	LIANG X, WANG R, GHANEM R. Uncertainty quantification of detonation through adapted polynomial chaos [J]. International Journal for Uncertainty Quantification, 2020, 10(1): 83–100. doi: 10.1615/Int.J.UncertaintyQuantification.2020030630
[4]	LIANG X, WANG R L. Verification and validation of detonation modeling [J]. Defence Technology, 2019, 15(3): 398–408. doi: 10.1016/j.dt.2018.11.005
[5]	梁霄, 王瑞利, 胡星志, 等. 基于多项式混沌方法对C-J爆轰参数不确定度的分析 [J]. 爆炸与冲击, 2023, 43(10): 104202. doi: 10.11883/bzycj-2023-0030 LIANG X, WANG R L, HU X Z, et al. Uncertainty analysis of C-J detonation parameters based on polynomial chaos theory [J]. Explosion and Shock Waves, 2023, 43(10): 104202. doi: 10.11883/bzycj-2023-0030
[6]	舒俊翔, 裴红波, 黄文斌, 等. 几种常用炸药的爆压与爆轰反应区精密测量 [J]. 爆炸与冲击, 2022, 42(5): 052301. doi: 10.11883/bzycj-2021-0305 SHU J X, PEI H B, HUANG W B, et al. Accurate measurements of detonation pressure and detonation reaction zones of several commonly-used explosives [J]. Explosion and Shock Waves, 2022, 42(5): 052301. doi: 10.11883/bzycj-2021-0305
[7]	赵万广, 周显明, 李加波, 等. LiF单晶的高压折射率及窗口速度的修正 [J]. 高压物理学报, 2014, 28(5): 571–576. doi: 10.11858/gywlxb.2014.05.010 ZHAO W G, ZHOU X M, LI J B, et al. Refractive index of LiF single crystal at high pressure and its window correction [J]. Chinese Journal of High Pressure Physics, 2014, 28(5): 571–576. doi: 10.11858/gywlxb.2014.05.010
[8]	戴诚达, 王翔, 谭华. Hugoniot实验的粒子速度测量不确定度分析 [J]. 高压物理学报, 2005, 19(2): 113–119. doi: 10.11858/gywlxb.2005.02.003 DAI C D, WANG X, TAN H. Evaluation for uncertainty of particle velocity in Hugoniot measurements [J]. Chinese Journal of High Pressure Physics, 2005, 19(2): 113–119. doi: 10.11858/gywlxb.2005.02.003
[9]	梁霄, 王瑞利. 基于冲击Hugoniot关系的爆压性质和不确定度量化 [J]. 兵工学报, 2024, 45(5): 1673–1680. doi: 10.12382/bgxb.2022.1207 LIANG X, WANG R L. Property and uncertainty quantification of detonation pressure based on shock Hugoniot relationship [J]. Acta Armamentarii, 2024, 45(5): 1673–1680. doi: 10.12382/bgxb.2022.1207
[10]	WILKINS M L. Computer simulation of dynamic phenomena [M]. Berlin: Springer, 1999.
[11]	BENNER P, MEHRMANN V, SORENSEN D C. Dimension reduction of large-scale systems [M]. Berlin: Springer, 2005.
[12]	HUGHES K T, CHARONKO J J, PRESTRIDGE K P, et al. Proton radiography of explosively dispersed metal particles with varying volume fraction and varying carrier phase [J]. Shock Waves, 2021, 31(1): 75–88. doi: 10.1007/s00193-020-00983-8
[13]	CONSTANTINE P G, DOW E, WANG Q Q. Active subspace methods in theory and practice: applications to kriging surfaces [J]. SIAM Journal on Scientific Computing, 2014, 36(4): A1500–A1524. doi: 10.1137/130916138
[14]	CONSTANTINE P G. Active subspaces: emerging ideas for dimension reduction in parameter studies [M]. Philadelphia: Society for Industrial and Applied Mathematics, 2015: 21–88.
[15]	CONSTANTINE P G, EMORY M, LARSSON J, et al. Exploiting active subspaces to quantify uncertainty in the numerical simulation of the HyShot Ⅱ scramjet [J]. Journal of Computational Physics, 2015, 302: 1–20. doi: 10.1016/j.jcp.2015.09.001
[16]	WEI J L, AN J, ZHANG Q, et al. Exploiting active subspaces for geometric optimization of cavity-stabilized supersonic flames [J]. AIAA Journal, 2023, 61(8): 3353–3364. doi: 10.2514/1.J062748
[17]	CORTESI A F, CONSTANTINE P G, MAGIN T E, et al. Forward and backward uncertainty quantification with active subspaces: application to hypersonic flows around a cylinder [J]. Journal of Computational Physics, 2020, 407: 109079. doi: 10.1016/j.jcp.2019.109079
[18]	KIM J, WANG Z Q, SONG J. Adaptive active subspace-based metamodeling for high-dimensional reliability analysis [J]. Structural Safety, 2024, 106: 102404. doi: 10.1016/j.strusafe.2023.102404
[19]	GREY Z J, CONSTANTINE P G. Active subspaces of airfoil shape parameterizations [J]. AIAA Journal, 2018, 56(5): 2003–2017. doi: 10.2514/1.J056054
[20]	HU X Z, CHEN X Q, LATTARULO V, et al. Multidisciplinary optimization under high-dimensional uncertainty for small satellite system design [J]. AIAA Journal, 2016, 54(5): 1732–1741. doi: 10.2514/1.J054627
[21]	胡星志. 活跃子空间降维不确定性设计优化方法及其航天应用 [M]. 北京: 中国宇航出版社, 2023. HU X Z. Uncertainty-based design optimization approach and aerospace application with active subspace dimension reduction [M]. Beijing: China Astronautic Publishing House, 2023.
[22]	王娜娜, 解青, 苏星宇, 等. 湍流燃烧机理和调控的活性子空间分析方法 [J]. 航空学报, 2021, 42(12): 625228. doi: 10.7527/S1000-6893.2021.25228 WANG N N, XIE Q, SU X Y, et al. Active subspace methods for analysis and optimization of turbulent combustion [J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(12): 625228. doi: 10.7527/S1000-6893.2021.25228