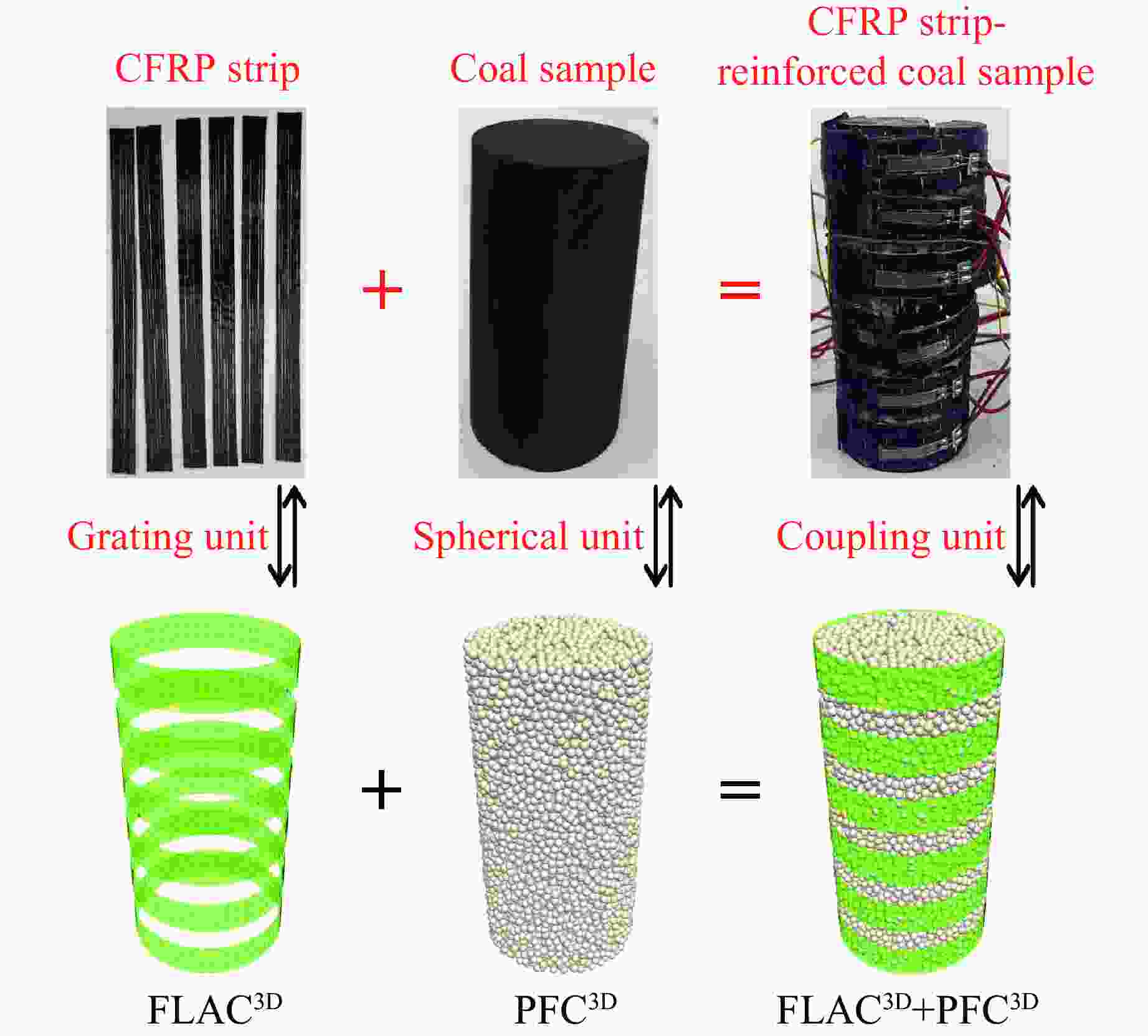
Microscopic Simulation Study on Uniaxial Compressive Creep Characteristics of Coal Samples Constrained by Different Numbers of Carbon Fiber Reinforced Polymer Strips
-
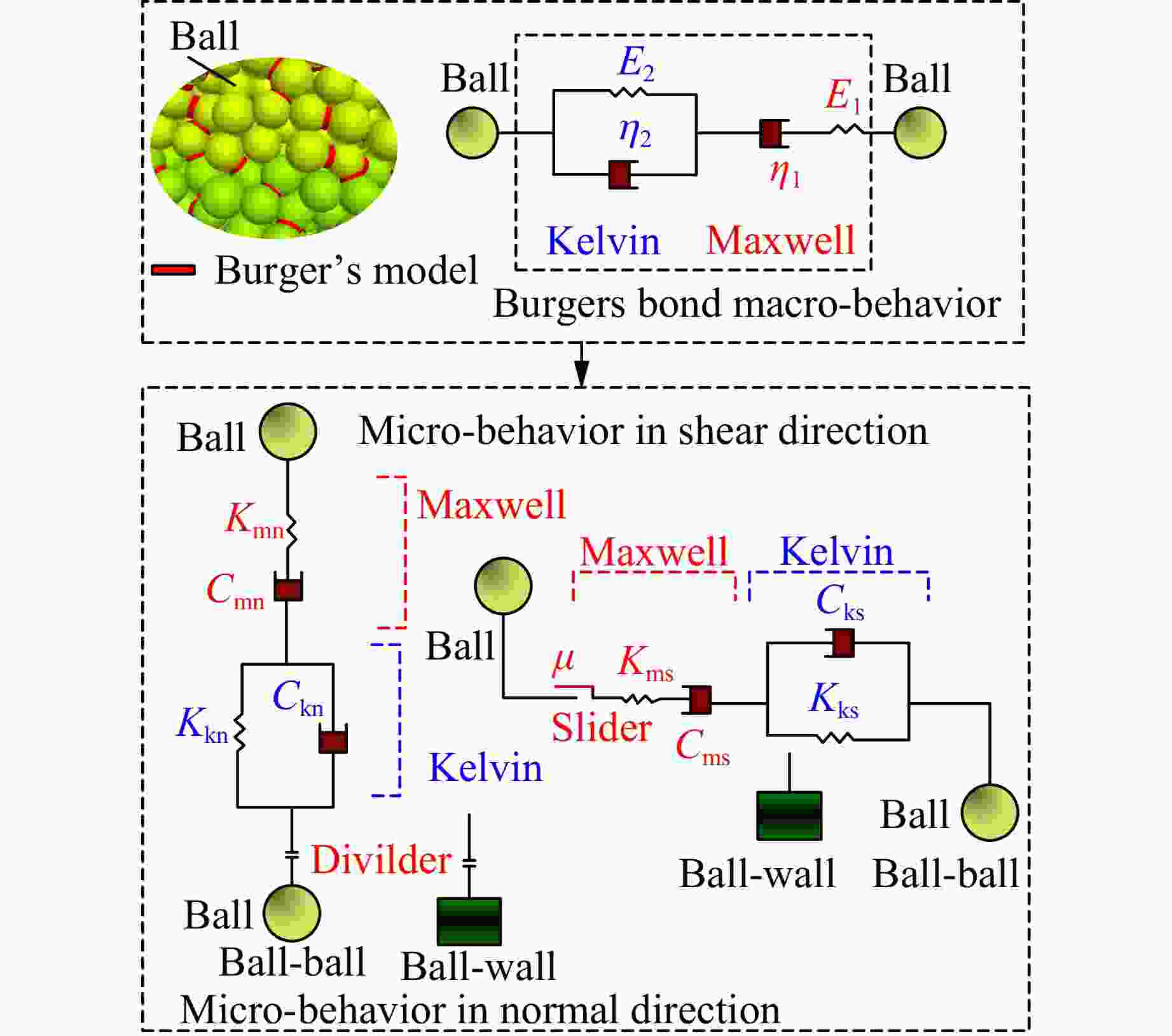
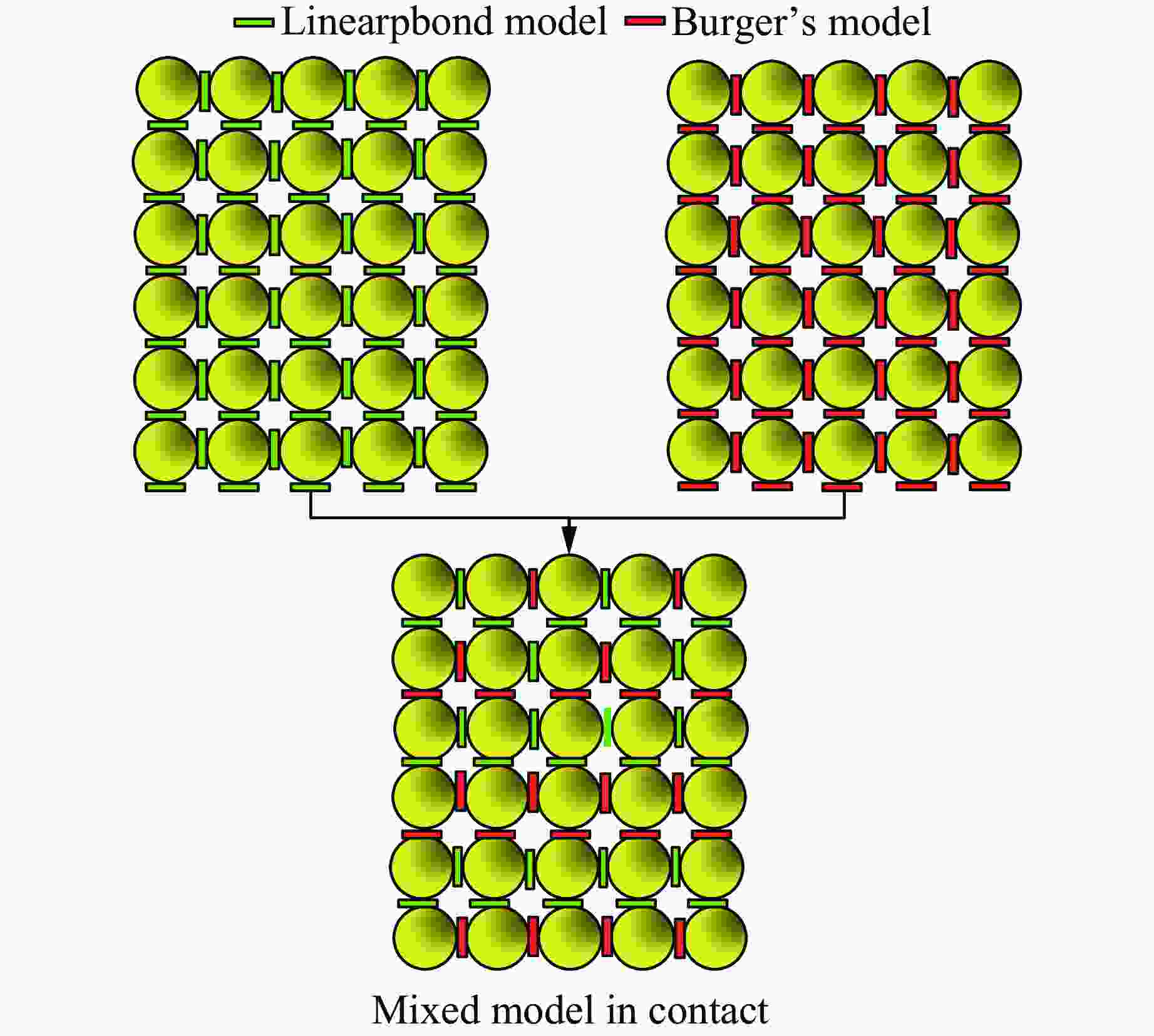
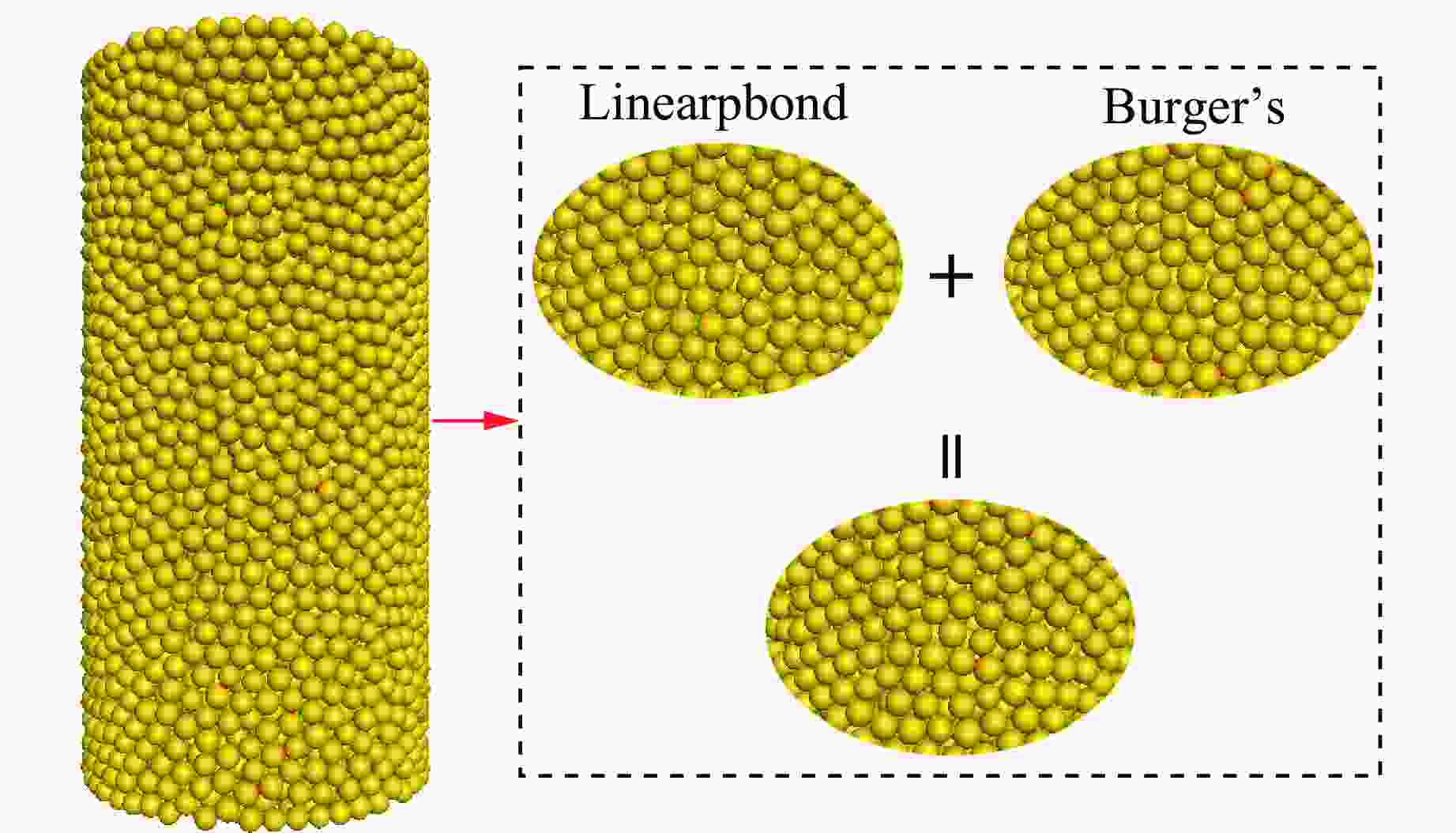
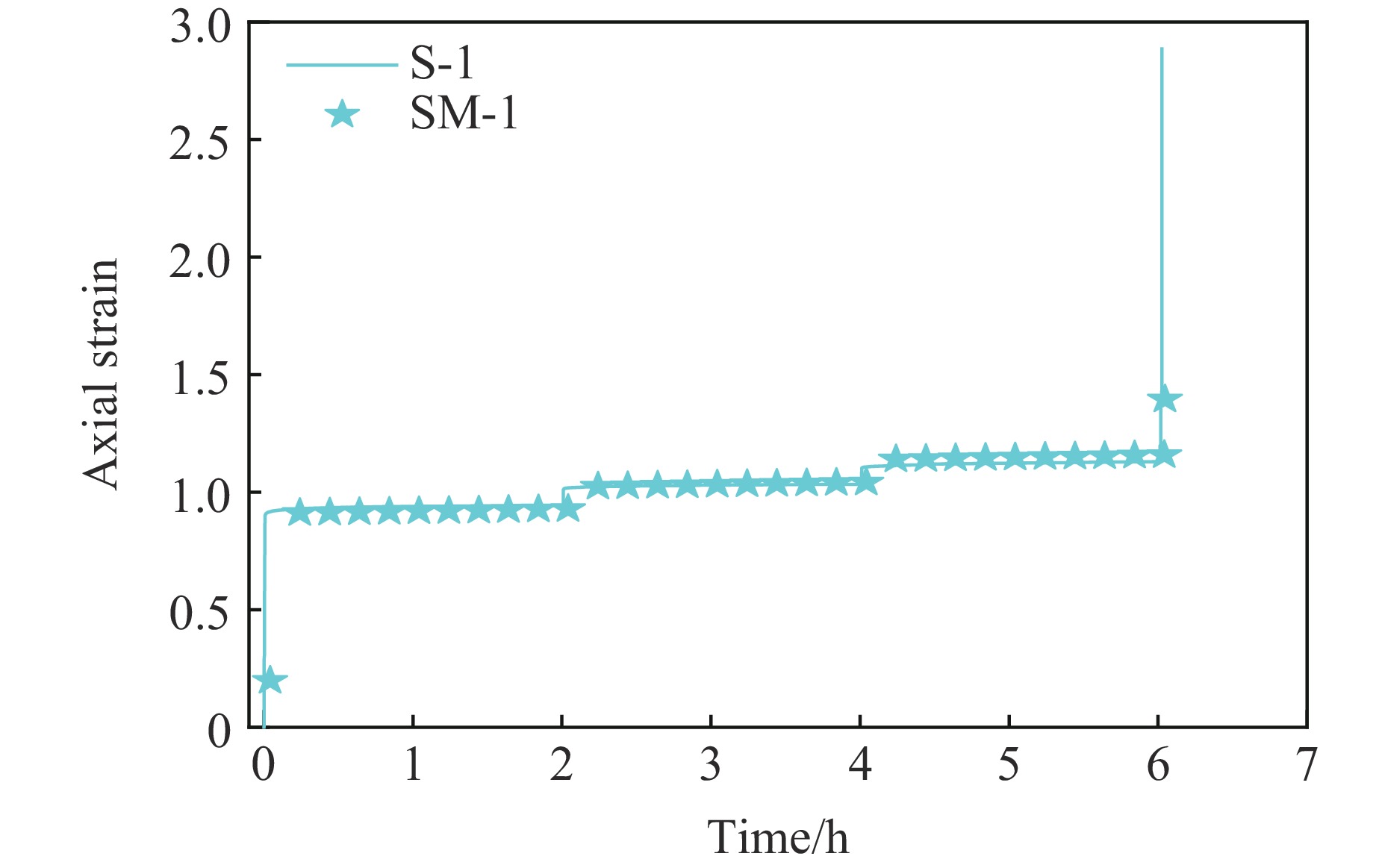
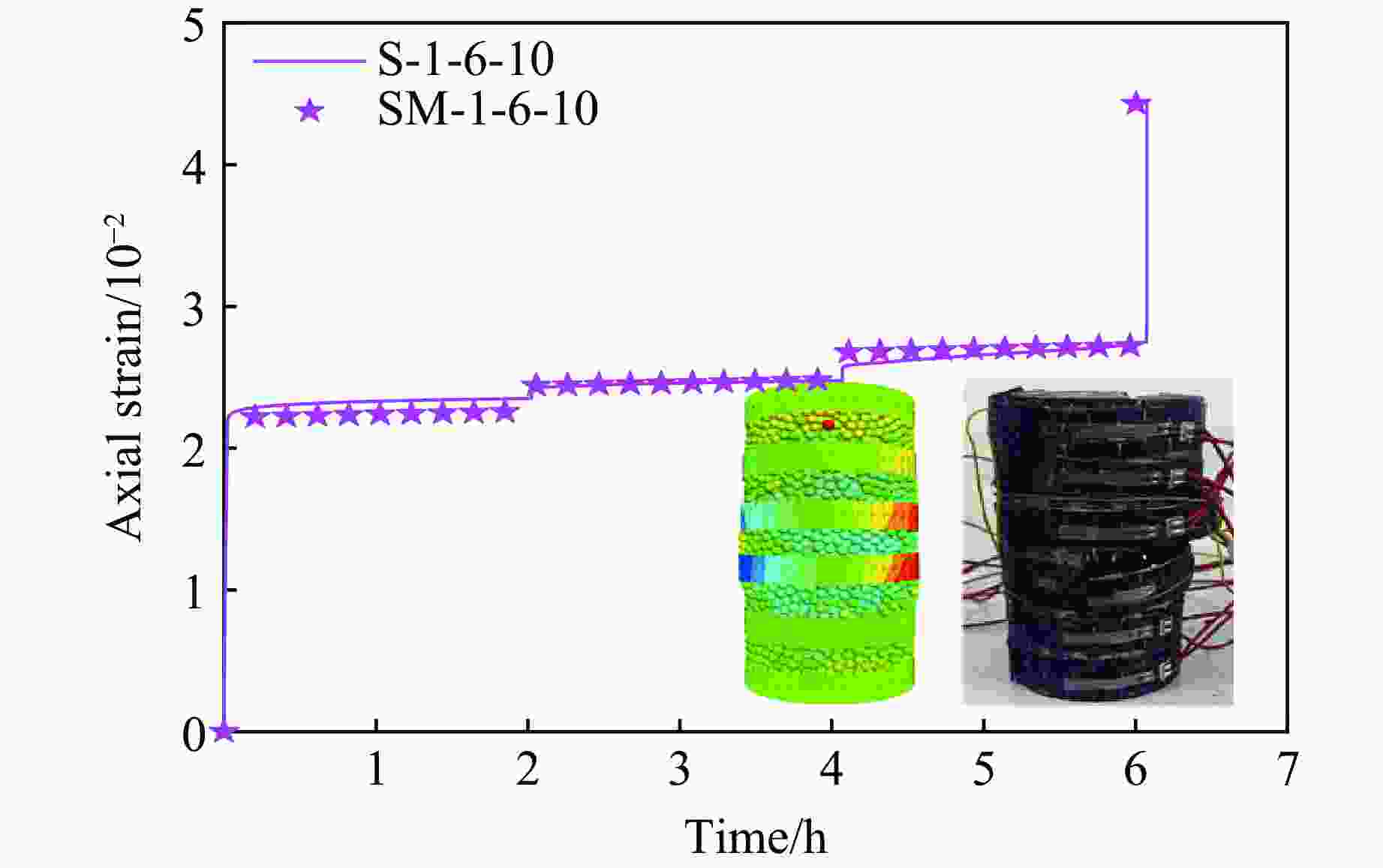
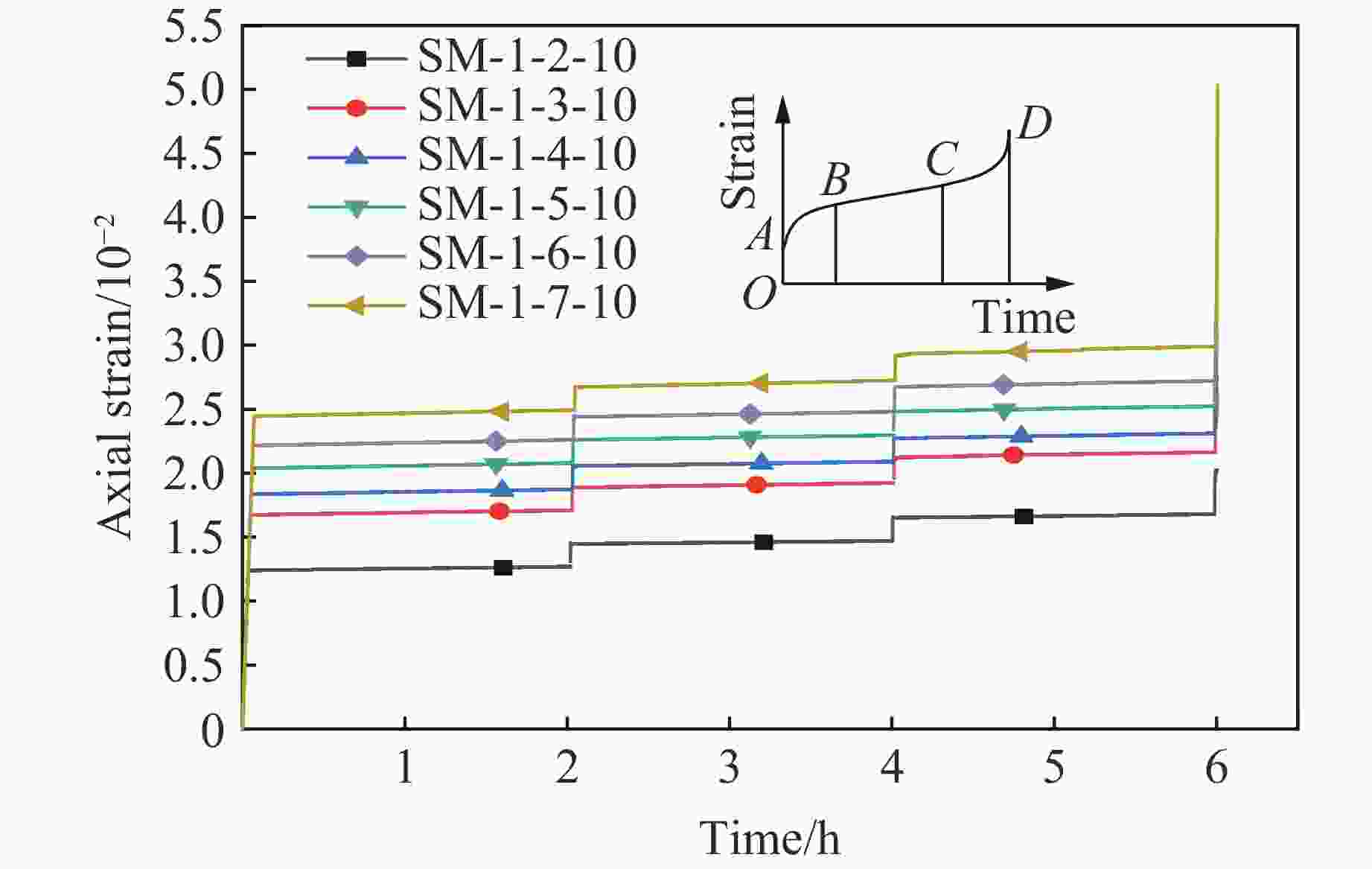
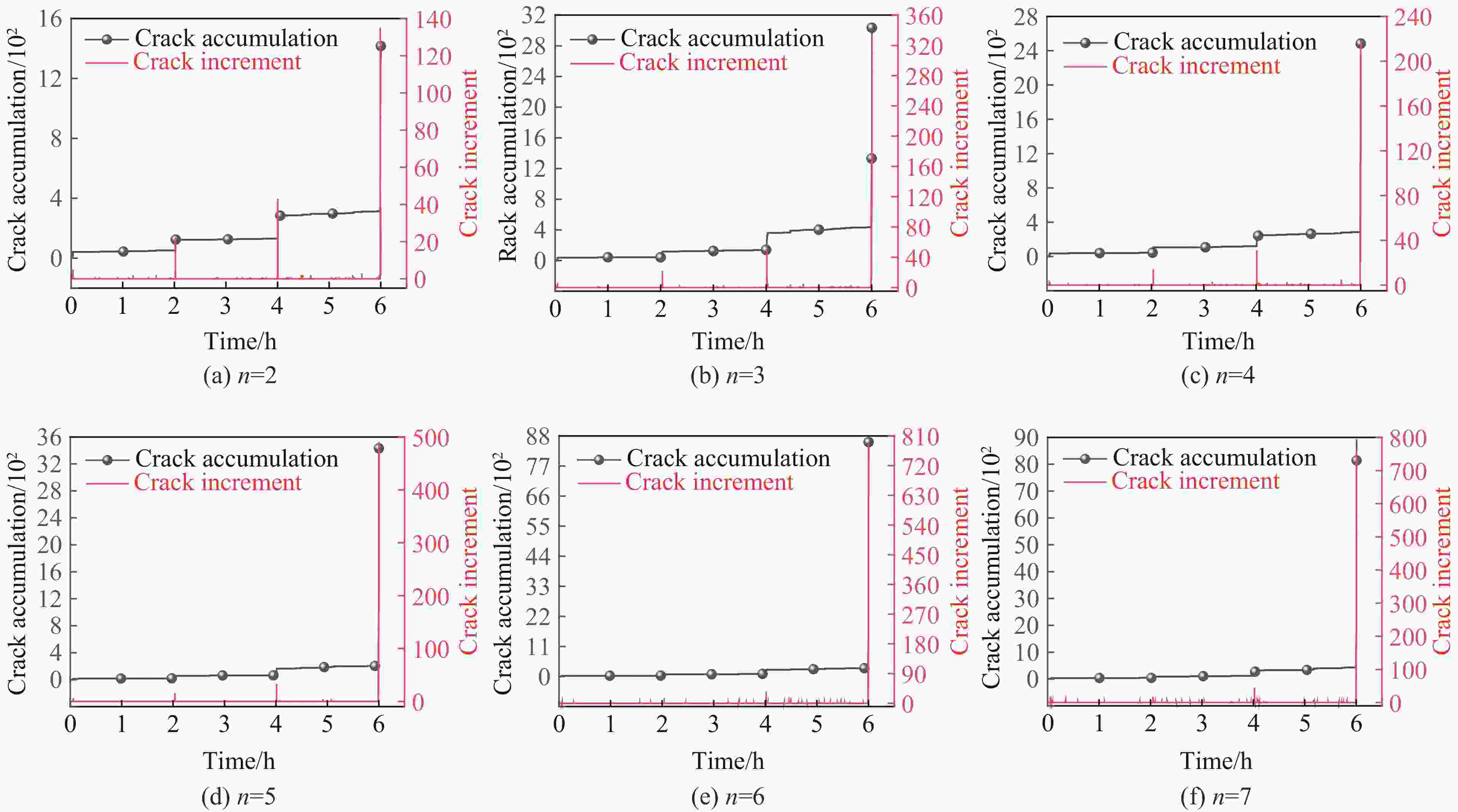
摘要: 为探究不同数量碳纤维增强复合材料(carbon fiber reinforced polymer, CFRP)条带对轴压煤样蠕变力学特性的影响,耦合PFC3D软件与FLAC3D软件,结合伯格斯(Burger’s)模型与平行黏结(Linearpbond)模型,建立混合接触的细观数值模型。根据未约束煤与6条带CFRP约束煤样单轴压缩蠕变室内试验,验证了数值模型的可靠性。研究了2~7条带CFRP约束煤样在单轴压缩蠕变下的力学特性及能量演化。研究表明:随着条带数的增加,煤样在初始阶段的轴向应变整体呈现增大趋势,加速蠕变阶段轴向应变明显增大;混合接触模型内部接触的最大力整体呈现增大趋势;伯格斯模型接触数量与平行黏结模型接触数量的比值约为1∶9时,数值模拟模型能够反映出煤样蠕变的力学特性;增加CFRP条带数,煤样的径向变形受到限制,产生的剪切微裂纹增多,煤样内部的剪切破坏更加严重,煤样的破坏形态由张拉破坏逐渐向剪切破坏转变;随着碳纤维布条带数量的增加,煤样的总能量、弹性能、耗散能均增加,在煤样发生蠕变失稳前,弹性能的变化与总能量的变化较为相似。
-
关键词:
- 碳纤维增强复合材料 /
- 条带数 /
- 单轴压缩蠕变 /
- 伯格斯模型 /
- PFC3D-FLAC3D耦合
Abstract: To investigate the influence of carbon fiber reinforced polymer (CFRP) strip with different number on the creep mechanical properties of coal samples under axial compression, a coupled numerical simulation using PFC3D and FLAC3D software was conducted, and a hybrid contact model combining the Burger’s model and the Linearpbond model was established. The reliability of the numerical model was validated based on laboratory uniaxial compressive creep tests of unconstrained coal and coal samples constrained with 6 strips of CFRP sheet. The mechanical properties and energy evolution of coal samples constrained with 2 to 7 strips of CFRP sheet under uniaxial compression were studied by numerical simulations. The results show that as the number of strips increases, the initial axial strain of the coal sample tends to increase overall, with a significant increase in axial strain during the accelerated creep stage, and the maximum internal contact force in the hybrid contact model tends to increase overall. The ratio of the contact quantity of Burger’s model to that of Linearpbond model is about 1∶9, and this ratio in the numerical simulation model could reflect the creep mechanical properties of coal samples. Increasing the number of CFRP strips restricts radial deformation, increases the number of shear micro-cracks, causes more severe shear damage within the coal sample, and the failure mode of the coal sample changes from tensile failure to shear failure. As the number of strips increases, the total energy, elastic energy, and dissipated energy all increase, and the change in elastic energy is similar to the change in total energy before the coal sample experiencing creep instability. -
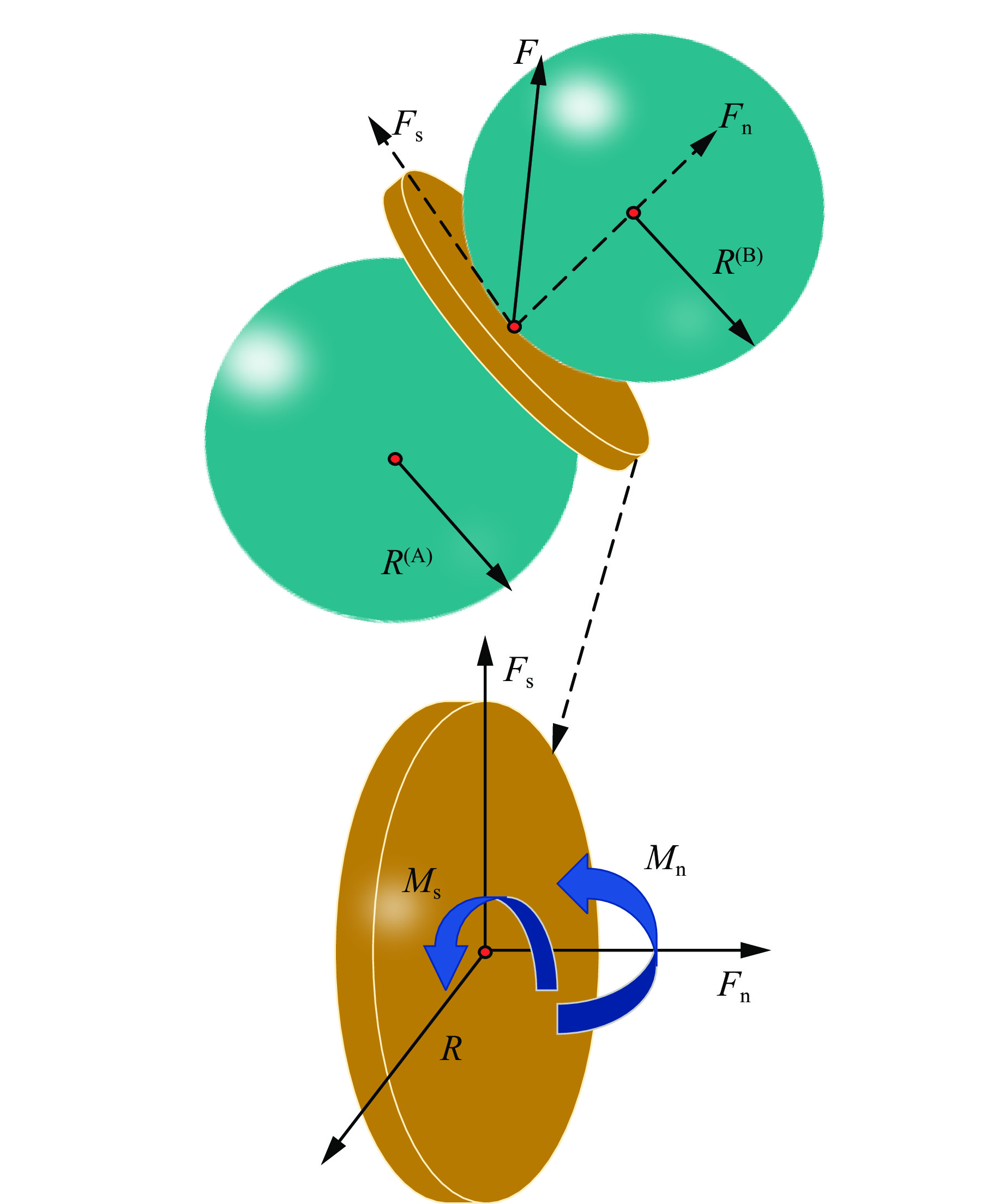
表 1 接触模型的细观参数
Table 1. Microscopic parameters of contact model
Linearpbond model Linearpbond effective modulus/GPa Linearpbond
stiffness ratioNormal bond strength/MPa Tangential bond strength/MPa Coefficient of friction Angle of friction/(°) 1 1.4 10 10 1.5 50 Burger’s model Maxwell bulk modulus/MPa Maxwell viscosity coefficient/(MPa·s) Kelvin bulk modulus/MPa Kelvin viscosity coefficient/(MPa·s) Coefficient of
friction1 90 10 1 1.5 表 2 CFRP条带模型参数
Table 2. Model parameters of CFRP sheets
Tg/MPa Eg/GPa t/(mm·ply−1) φi/(°) 918.07 47.54 0.167 30 表 3 不同数量CFRP条带约束煤样破坏时的力链
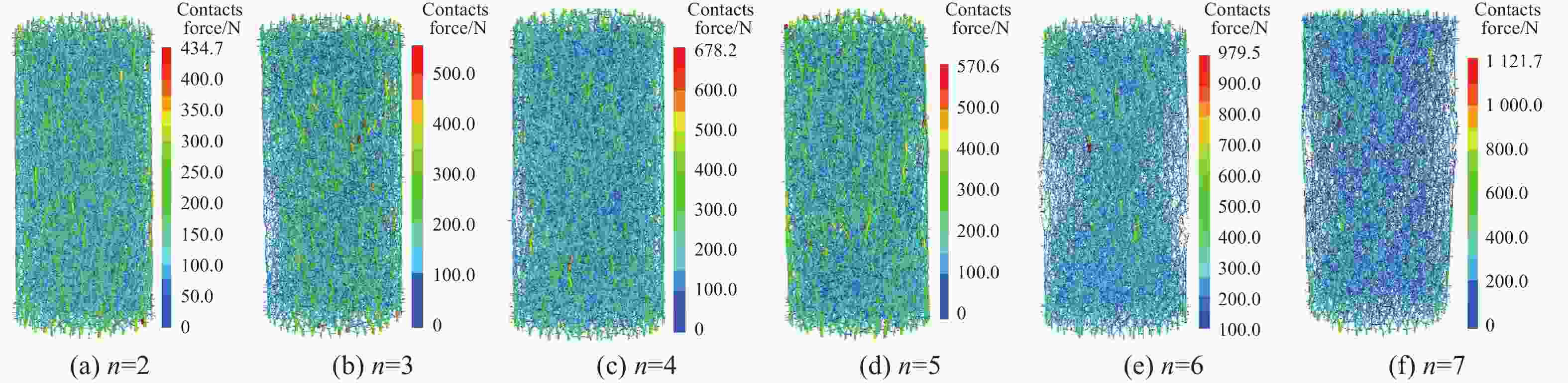
Table 3. Force chains in coal samples at failure constrained by different numbers of CFRP strips
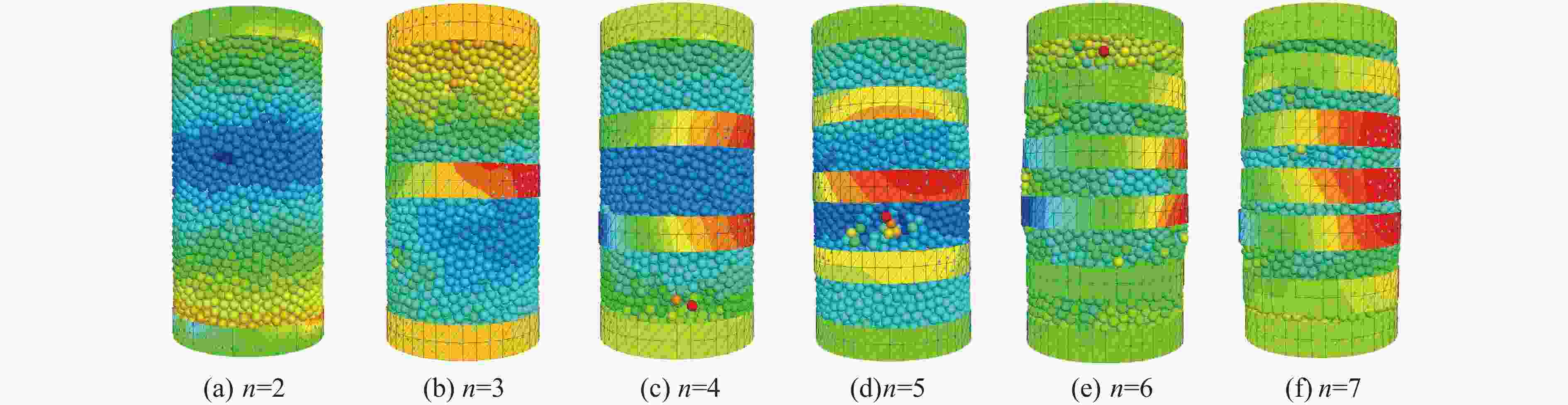
Number of strips Number of contacts Maximum contact force/N 2 30511 434.7 3 28852 534.9 4 29378 678.2 5 28609 570.7 6 25655 979.5 7 25747 1121.7 表 4 不同数量CFRP条带约束煤样破坏时的裂隙数量
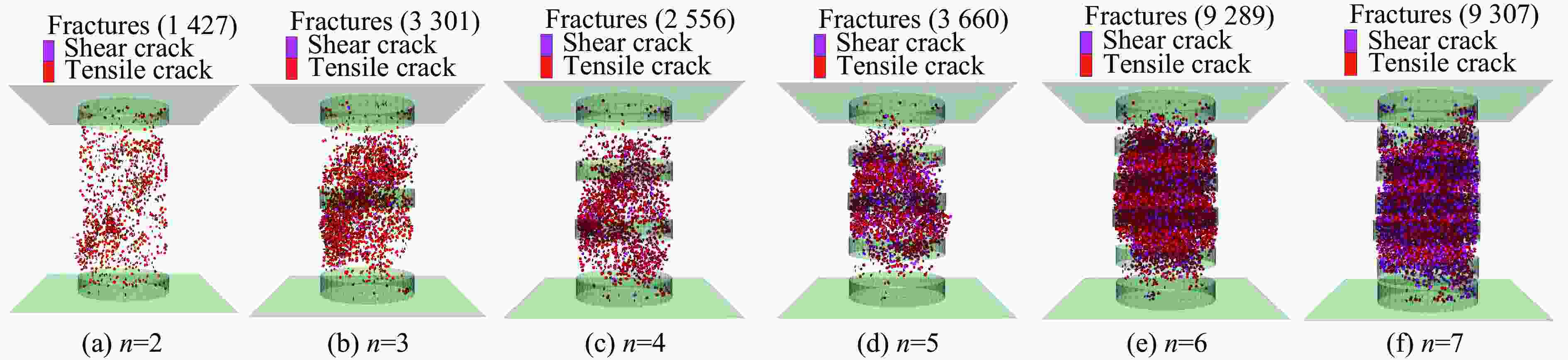
Table 4. Number of cracks in the failure of coal samples constrained by different numbers of CFRP strips
Number of strips Number of tension cracks Number of shear cracks Total number of cracks 2 1420 7 1427 3 3014 287 3301 4 2167 389 2556 5 2553 1107 3660 6 6832 2457 9289 7 4295 5012 9307 -
[1] 蒋威. 厚硬基本顶综放开采沿空巷道变形破坏机制及控制 [D]. 北京: 中国矿业大学(北京), 2021.JIANG W. Deformation mechanism and stability control of roadway along goaf in fully mechanized top coal caving face with thick and hard roof [D]. Beijing: China University of Mining & Technology-Beijing, 2021. [2] ZHAO T B, GUO W Y, TAN Y L, et al. Case studies of rock bursts under complicated geological conditions during multi-seam mining at a depth of 800 m [J]. Rock Mechanics and Rock Engineering, 2018, 51(5): 1539–1564. doi: 10.1007/s00603-018-1411-7 [3] ZHU W B, CHEN L, ZHOU Z L, et al. Failure propagation of pillars and roof in a room and pillar mine induced by longwall mining in the lower seam [J]. Rock Mechanics and Rock Engineering, 2019, 52(4): 1193–1209. doi: 10.1007/s00603-018-1630-y [4] JIANG S Y, FAN G W, LI Q Z, et al. Effect of mining parameters on surface deformation and coal pillar stability under customized shortwall mining of deep extra-thick coal seams [J]. Energy Reports, 2021, 7: 2138–2154. doi: 10.1016/J.EGYR.2021.04.008 [5] CAO Y, XU J H, CHEN L, et al. Experimental study on granite acoustic emission and micro-fracture behavior with combined compression and shear loading: phenomenon and mechanism [J]. Scientific Reports, 2020, 10(1): 22051. doi: 10.1038/s41598-020-78137-0 [6] YANG Y J, DUAN H Q, XING L Y, et al. Fatigue characteristics of coal specimens under cyclic uniaxial loading [J]. Geotechnical Testing Journal, 2019, 42(2): 331–346. doi: 10.1520/GTJ20170263 [7] 王波, 谷长宛, 王军, 等. 对穿锚索加固作用下沿空掘巷留设煤柱承压性能试验研究 [J]. 中国矿业大学学报, 2020, 49(2): 262–270. doi: 10.13247/j.cnki.jcumt.001125WANG B, GU C W, WANG J, et al. Bearing capacity experimental study of coal pillar in the gob-side entry driving under the reinforcement of inflatable lock-type anchor [J]. Journal of China University of Mining & Technology, 2020, 49(2): 262–270. doi: 10.13247/j.cnki.jcumt.001125 [8] 赵国贞, 马占国, 孙凯, 等. 小煤柱沿空掘巷围岩变形控制机理研究 [J]. 采矿与安全工程学报, 2010, 27(4): 517–521. doi: 10.3969/j.issn.1673-3363.2010.04.013ZHAO G Z, MA Z G, SUN K, et al. Research on deformation controlling mechanism of the narrow pillar of roadway driving along next goaf [J]. Journal of Mining & Safety Engineering, 2010, 27(4): 517–521. doi: 10.3969/j.issn.1673-3363.2010.04.013 [9] 陈绍杰, 张俊文, 尹大伟, 等. 充填墙提升煤柱性能机理与数值模拟研究 [J]. 采矿与安全工程学报, 2017, 34(2): 268–275. doi: 10.13545/j.cnki.jmse.2017.02.010CHEN S J, ZHANG J W, YIN D W, et al. Mechanism and numerical simulation of filling walls improving performance of coal pillar [J]. Journal of Mining & Safety Engineering, 2017, 34(2): 268–275. doi: 10.13545/j.cnki.jmse.2017.02.010 [10] 张洪伟, 万志军, 张源, 等. 工作面顺序接续下综放沿空掘巷窄煤柱稳定性控制 [J]. 煤炭学报, 2021, 46(4): 1211–1219. doi: 10.13225/j.cnki.jccs.2020.0028ZHANG H W, WAN Z J, ZHANG Y, et al. Stability control of narrow coal pillars in the fully-mechanized gob-side entry during sequenced top coal caving mining [J]. Journal of China Coal Society, 2021, 46(4): 1211–1219. doi: 10.13225/j.cnki.jccs.2020.0028 [11] WANG Z Y, FENG P, ZHAO Y, et al. FRP-confined concrete core-encased rebar for RC columns: concept and axial compressive behavior [J]. Composite Structures, 2019, 222: 110915. doi: 10.1016/j.compstruct.2019.110915 [12] SIWOWSKI T, RAJCHEL M. Structural performance of a hybrid FRP composite-lightweight concrete bridge girder [J]. Composites Part B: Engineering, 2019, 174: 107055. doi: 10.1016/j.compositesb.2019.107055 [13] AL-SAADI N T K, MOHAMMED A, AL-MAHAIDI R, et al. A state-of-the-art review: near-surface mounted FRP composites for reinforced concrete structures [J]. Construction and Building Materials, 2019, 209: 748–769. doi: 10.1016/j.conbuildmat.2019.03.121 [14] JYOTI D A, KUMAR M P, NATH G C, et al. Extraction of locked-up coal by strengthening of rib pillars with FRP-A comparative study through numerical modelling [J]. International Journal of Mining Science and Technology, 2017, 27(2): 261–267. doi: 10.1016/j.ijmst.2017.01.024 [15] ZOU X X, D’ANTINO T, SNEED L H. Investigation of the bond behavior of the fiber reinforced composite-concrete interface using the finite difference method (FDM) [J]. Composite Structures, 2021, 278: 114643. doi: 10.1016/j.compstruct.2021.114643 [16] XU C X, WU Y A, LIU X Q, et al. Experimental research on seismic behavior of seismic-damaged double-deck viaduct frame pier strengthened with CFRP and enveloped steel [J]. Materials, 2022, 15(23): 8668. doi: 10.3390/ma15238668 [17] 马超, 王作虎, 路德春, 等. CFRP加固地铁车站结构中柱地震损伤评价研究 [J]. 岩土工程学报, 2020, 42(12): 2249–2256. doi: 10.11779/CJGE202012011MA C, WANG Z H, LU D C, et al. Seismic damage evaluation of CFRP-strengthened columns in subway stations [J]. Chinese Journal of Geotechnical Engineering, 2020, 42(12): 2249–2256. doi: 10.11779/CJGE202012011 [18] GRIGGS D. Creep of rocks [J]. The Journal of Geology, 1939, 47(3): 225–251. doi: 10.1086/624775 [19] ZHAO Z, WU P, WANG L, et al. Influence of moisture content on creep mechanical characteristic and mic-fracture behavior of water-bearing coal specimen [J]. Geofluids, 2022, 2022: 4014462. doi: 10.1155/2022/4014462 [20] WANG D B, ZLOTNIK S, DÍEZ P, et al. A numerical study on hydraulic fracturing problems via the proper generalized decomposition method [J]. Computer Modeling in Engineering & Sciences, 2020, 122(2): 703–720. doi: 10.32604/cmes.2020.08033 [21] XIA C, LIU Z, ZHOU C Y. Burger’s bonded model for distinct element simulation of the multi-factor full creep process of soft rock [J]. Journal of Marine Science and Engineering, 2021, 9(9): 945. doi: 10.3390/jmse9090945 [22] 袁海平, 曹平, 许万忠, 等. 岩石粘弹塑性本构关系及改进的Burgers蠕变模型 [J]. 岩土工程学报, 2006, 28(6): 796–799. doi: 10.3321/j.issn:1000-4548.2006.06.024YUAN H P, CAO P, XU W Z, et al. Visco-elastop-lastic constitutive relationship of rock and modified Burgers creep model [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 796–799. doi: 10.3321/j.issn:1000-4548.2006.06.024 [23] HE P F, KULATILAKE P H S W, YANG X X, et al. Detailed comparison of nine intact rock failure criteria using polyaxial intact coal strength data obtained through PFC3D simulations [J]. Acta Geotechnica, 2018, 13(2): 419–445. doi: 10.1007/s11440-017-0566-9 [24] ZHANG L, REN T, LI X C, et al. Acoustic emission, damage and cracking evolution of intact coal under compressive loads: experimental and discrete element modelling [J]. Engineering Fracture Mechanics, 2021, 252: 107690. doi: 10.1016/j.engfracmech.2021.107690 [25] 王刚, 王锐, 武猛猛, 等. 渗透压-应力耦合作用下煤体常规三轴试验的颗粒流模拟 [J]. 岩土力学, 2016, 37(Suppl 1): 537–546. doi: 10.16285/j.rsm.2016.S1.070WANG G, WANG R, WU M M, et al. Simulation of conventional triaxial test on coal under hydro-mechanical coupling by particle flow code [J]. Rock and Soil Mechanics, 2016, 37(Suppl 1): 537–546. doi: 10.16285/j.rsm.2016.S1.070 [26] LI W J, HAN Y H, WANG T, et al. DEM micromechanical modeling and laboratory experiment on creep behavior of salt rock [J]. Journal of Natural Gas Science and Engineering, 2017, 46: 38–46. doi: 10.1016/j.jngse.2017.07.013 [27] 谭鑫, 曹明, 冯龙健, 等. 土工织物包裹碎石桩力学特性的数值模拟研究 [J]. 中国公路学报, 2020, 33(9): 136–145. doi: 10.3969/j.issn.1001-7372.2020.09.014TAN X, CAO M, FENG L J, et al. Numerical study on mechanical behaviors of geotextile-wrapped stone column [J]. China Journal of Highway and Transport, 2020, 33(9): 136–145. doi: 10.3969/j.issn.1001-7372.2020.09.014 [28] 郭润兰, 范雅琼, 王广书, 等. 基于PFC3D的机床床身用树脂矿物复合材料损伤性能细观研究 [J]. 复合材料学报, 2022, 39(2): 834–844. doi: 10.13801/j.cnki.fhclxb.20210420.004GUO R L, FAN Y Q, WANG G S, et al. Meso-scale study on damage performance of resin mineral composite material for machine tool bed based on PFC3D [J]. Acta Materiae Compositae Sinica, 2022, 39(2): 834–844. doi: 10.13801/j.cnki.fhclxb.20210420.004 [29] 石崇, 张强, 王盛年. 颗粒流(PFC5.0)数值模拟技术及应用 [M]. 北京: 中国建筑工业出版社, 2018.SHI C, ZHANG Q, WANG S N. Numerical simulation technology and application with particle flow code (PFC 5.0) [M]. Beijing: China Architecture & Building Press, 2018. [30] 李庆文, 胡露露, 曹行, 等. CFRP布均匀约束煤圆柱轴压性能 [J]. 复合材料学报, 2022, 39(11): 5611–5624. doi: 10.13801/j.cnki.fhclxb.20211201.001LI Q W, HU L L, CAO H, et al. Axial compressive behavior of CFRP uniformly wrapped coal in circular columns [J]. Acta Materiae Compositae Sinica, 2022, 39(11): 5611–5624. doi: 10.13801/j.cnki.fhclxb.20211201.001 [31] 胡光辉, 徐涛, 陈崇枫, 等. 基于离散元法的脆性岩石细观蠕变失稳研究 [J]. 工程力学, 2018, 35(9): 26–36. doi: 10.6052/j.issn.1000-4750.2017.05.0356HU G H, XU T, CHEN C F, et al. A microscopic study of creep and fracturing of brittle rocks based on discrete element method [J]. Engineering Mechanics, 2018, 35(9): 26–36. doi: 10.6052/j.issn.1000-4750.2017.05.0356 [32] 李庆文, 高森林, 胡露露, 等. 不同加载速率下非均质煤样能量耗散损伤本构关系 [J]. 煤炭学报, 2022, 47(Suppl 1): 90–102. doi: 10.13225/j.cnki.jccs.2022.0163LI Q W, GAO S L, HU L L, et al. Constitutive relation of energy dissipation damage of heterogeneous coal samples under different loading rates [J]. Journal of China Coal Society, 2022, 47(Suppl 1): 90–102. doi: 10.13225/j.cnki.jccs.2022.0163 [33] 李庆文, 禹萌萌, 高森林, 等. 加载速率对碳纤维布被动约束煤能量演化的影响 [J]. 煤炭学报, 2024, 49(Suppl 1): 236–247. doi: 10.13225/j.cnki.jccs.2023.0238LI Q W, YU M M, GAO S L, et al. Effect of loading rate on energy evolution of coal confined passively by CFRP sheets [J]. Journal of China Coal Society, 2024, 49(Suppl 1): 236–247. doi: 10.13225/j.cnki.jccs.2023.0238 [34] 岳少飞, 王开, 张小强, 等. 不同加载速率无烟煤蠕变特性及能量演化规律 [J]. 煤炭学报, 2023, 48(8): 3060–3075. doi: 10.13225/j.cnki.jccs.2023.0120YUE S F, WANG K, ZHANG X Q, et al. Creep properties and energy evolution of anthracite coal with different loading rates [J]. Journal of China Coal Society, 2023, 48(8): 3060–3075. doi: 10.13225/j.cnki.jccs.2023.0120 [35] 杨磊, 王晓卿, 李建忠. 不同冲击倾向性煤单轴压缩下能量演化与损伤特征 [J]. 煤炭科学技术, 2021, 49(6): 111–118. doi: 10.13199/j.cnki.cst.2021.06.013YANG L, WANG X Q, LI J Z. Energy evolution and damage characteristics of coal with different bursting liability under uniaxial compression [J]. Coal Science and Technology, 2021, 49(6): 111–118. doi: 10.13199/j.cnki.cst.2021.06.013 -






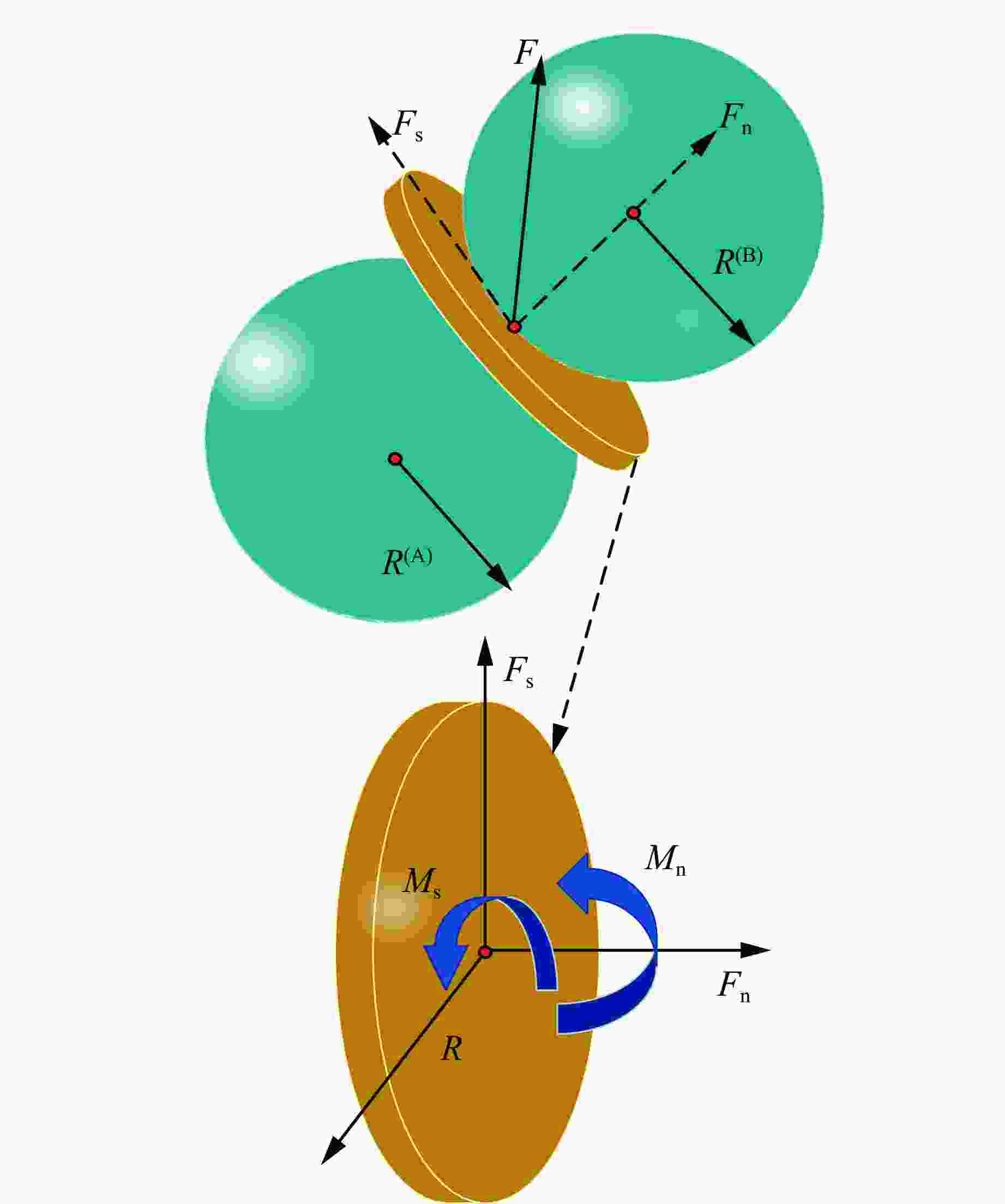
 下载:
下载: