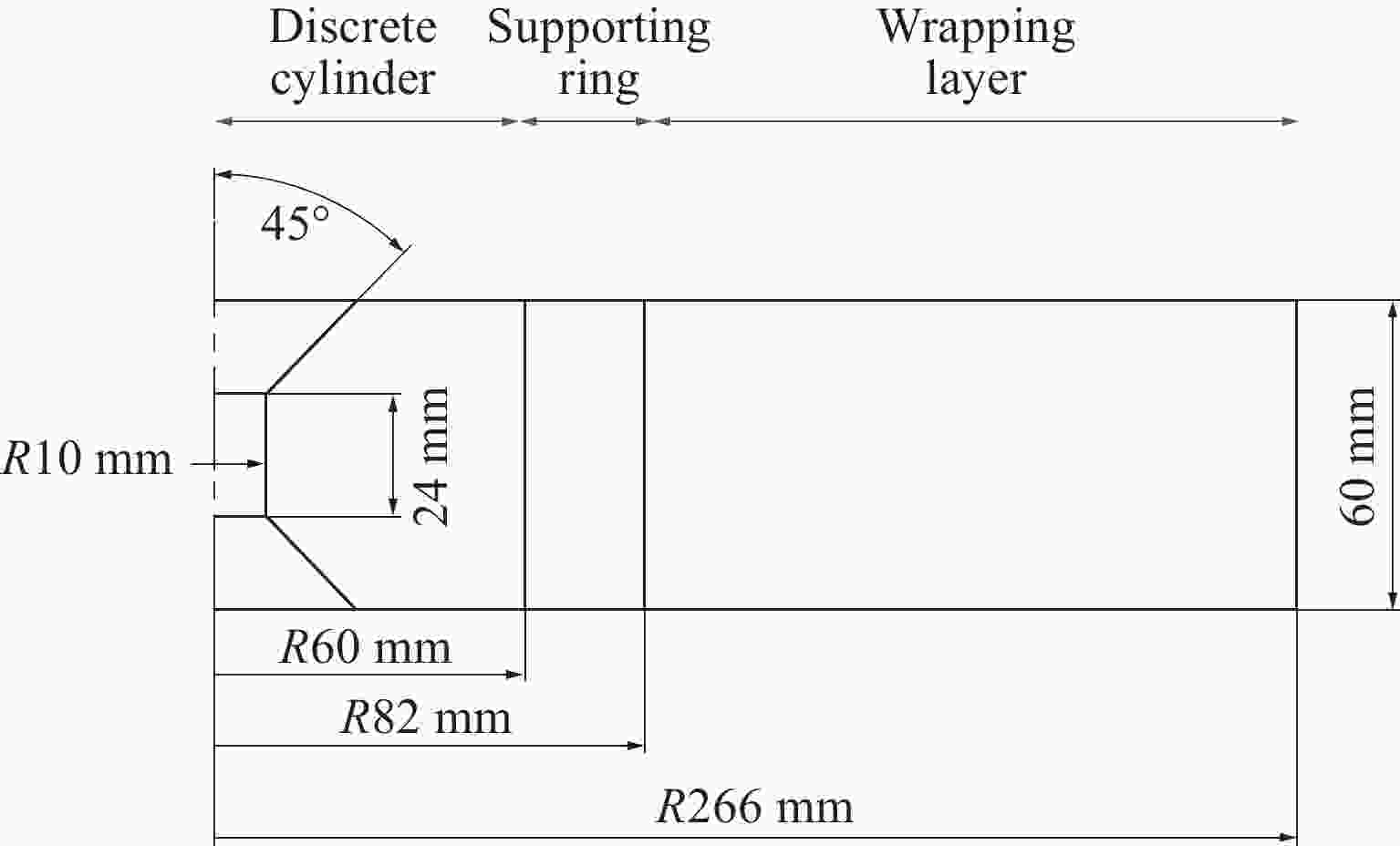
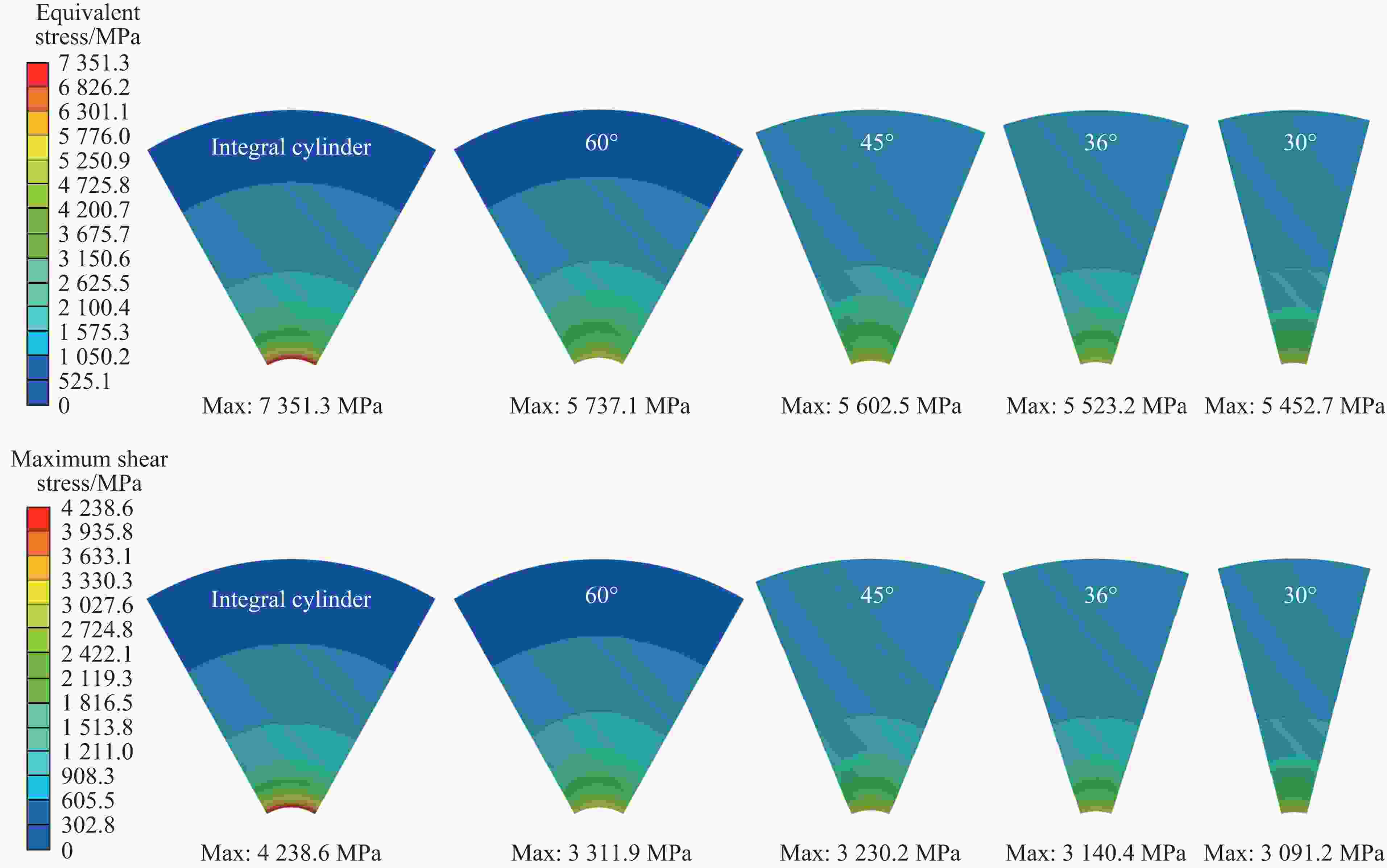
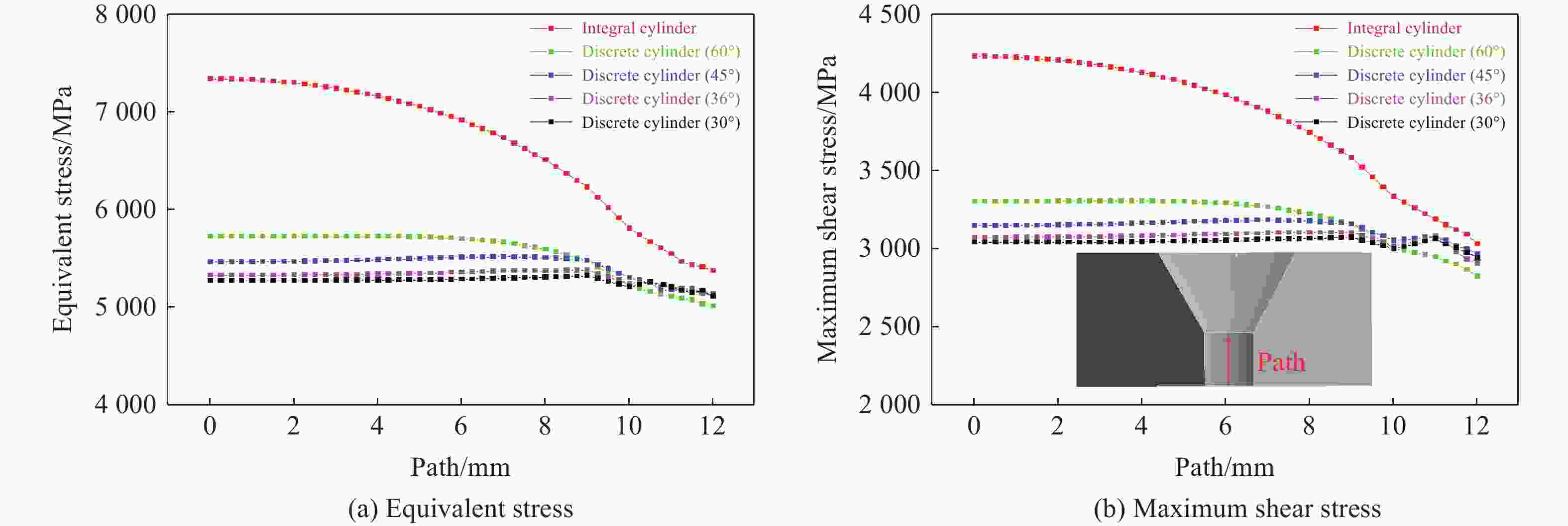
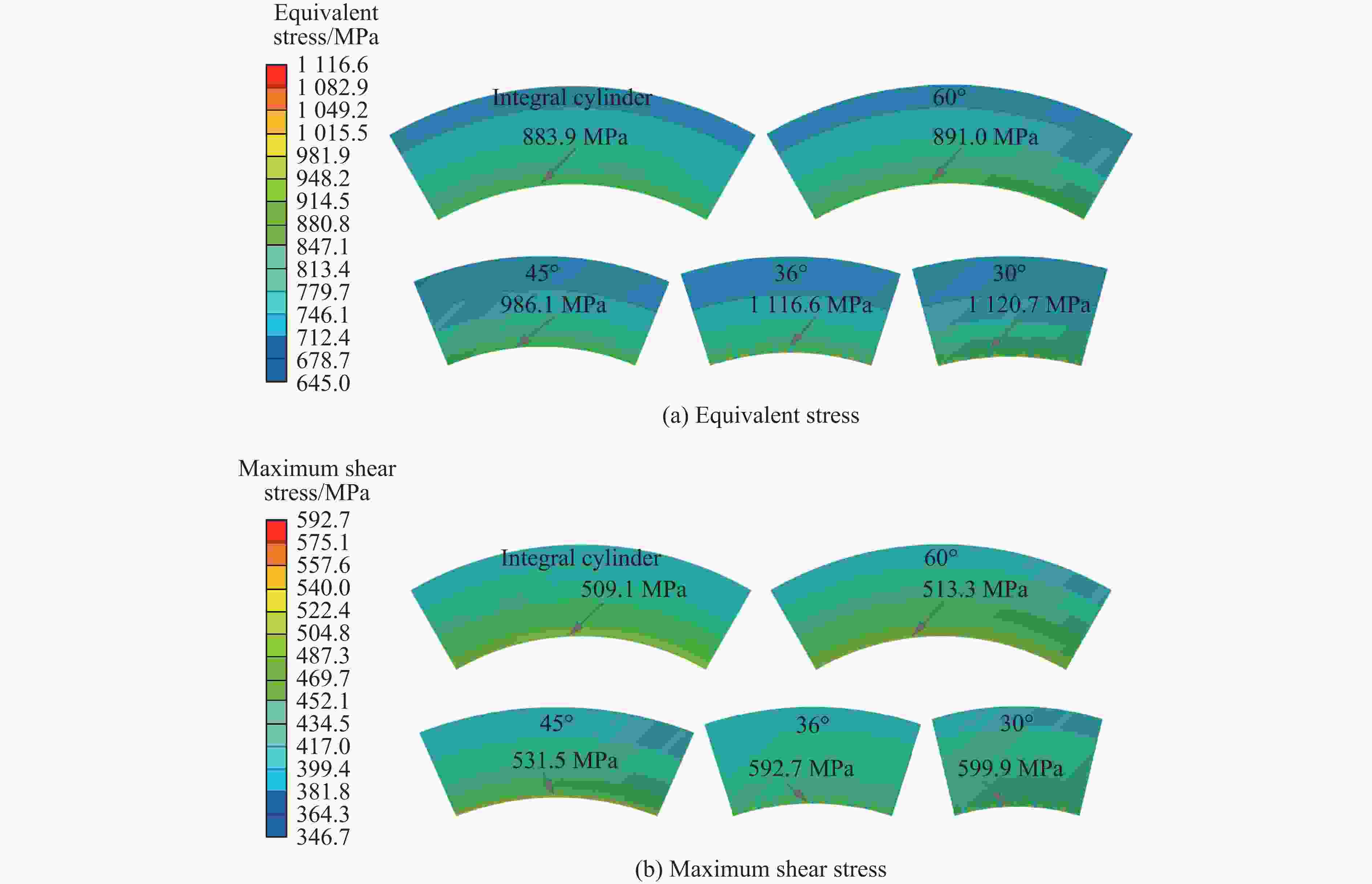
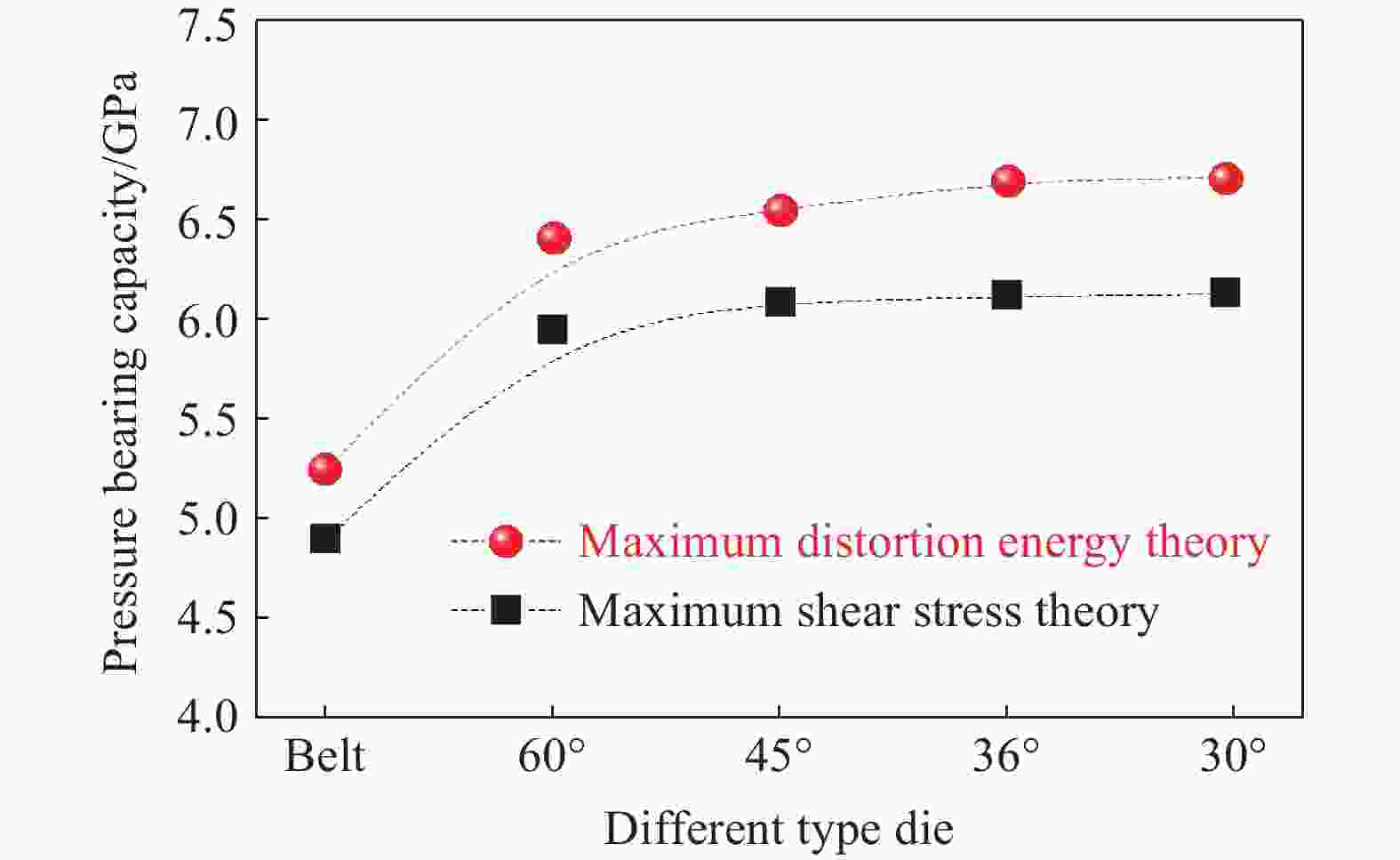
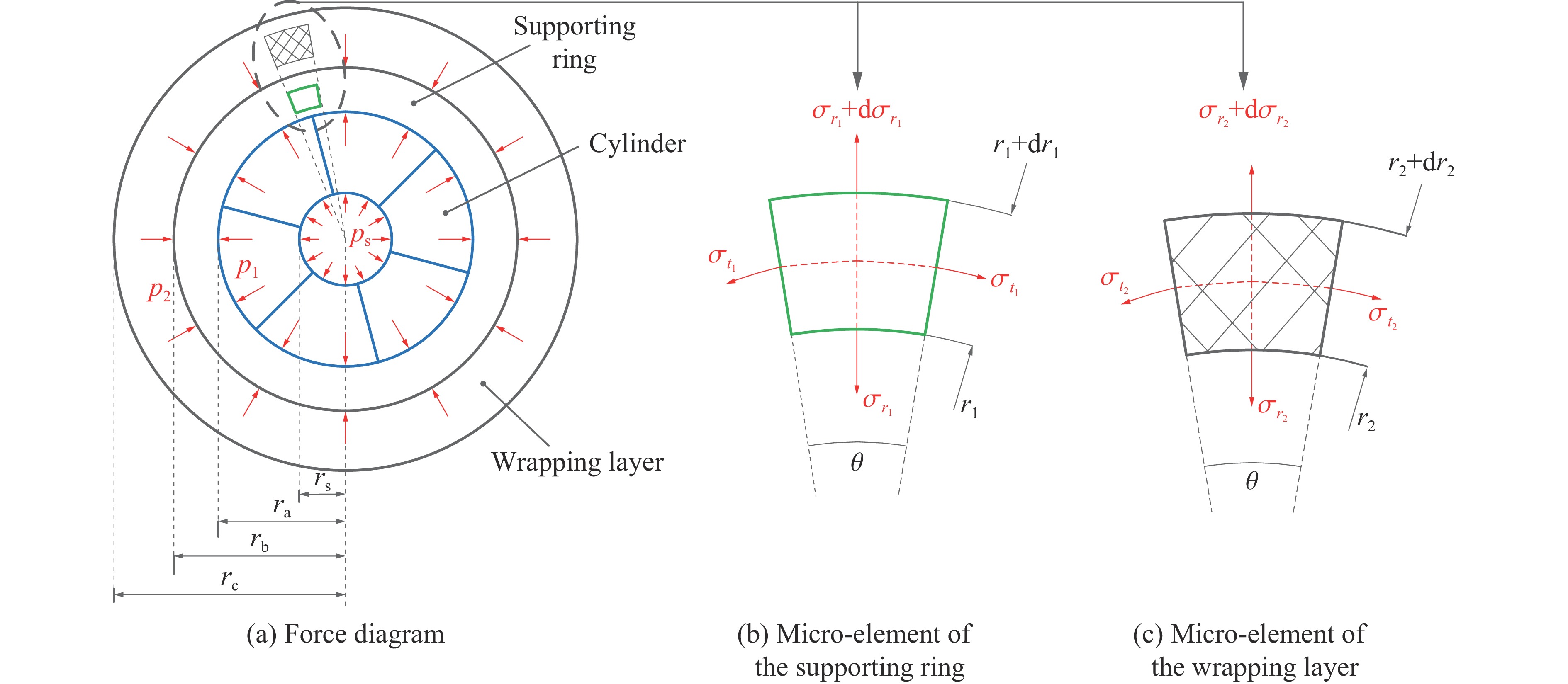
| [1] |
ITO E, KATSURA T, YAMAZAKI D, et al. A new 6-axis apparatus to squeeze the Kawai-cell of sintered diamond cubes [J]. Physics of the Earth and Planetary Interiors, 2009, 174(1): 264–269.
|
| [2] |
YANG Y F, LI M Z, WANG B L. Study on stress distribution of tangent split high pressure apparatus and its pressure bearing capacity [J]. Diamond and Related Materials, 2015, 58: 180–184. doi: 10.1016/j.diamond.2015.07.010
|
| [3] |
王伯龙, 李明哲, 刘志卫, 等. 新型切向分块式两面顶超高压模具 [J]. 高压物理学报, 2019, 33(1): 013102. doi: 10.11858/gywlxb.20180595WANG B L, LI M Z, LIU Z W, et al. A novel tangential split-belt ultrahigh pressure apparatus [J]. Chinese Journal of High Pressure Physics, 2019, 33(1): 013102. doi: 10.11858/gywlxb.20180595
|
| [4] |
YANG Y F, LI M Z, LIU Z W, et al. Numerical simulation and experiment on split tungsten carbide cylinder of high pressure apparatus [J]. Review of Scientific Instruments, 2015, 86(12): 125113. doi: 10.1063/1.4939033
|
| [5] |
李胜华, 李金良. 球弧式纵向剖分超高压模具 [J]. 高压物理学报, 2020, 34(6): 063302. doi: 10.11858/gywlxb.20200538LI S H, LI J L. Spherical arc longitudinal split ultra-high pressure mold [J]. Chinese Journal of High Pressure Physics, 2020, 34(6): 063302. doi: 10.11858/gywlxb.20200538
|
| [6] |
刘志卫, 吴承伟, 童明俊, 等. 钢丝缠绕剖分式超高压模具等张力预紧分析 [J]. 高压物理学报, 2021, 35(1): 013302. doi: 10.11858/gywlxb.20200591LIU Z W, WU C W, TONG M J, et al. Analysis of equal tension pre-tightening of steel wire winding split ultra-high pressure die [J]. Chinese Journal of High Pressure Physics, 2021, 35(1): 013302. doi: 10.11858/gywlxb.20200591
|
| [7] |
KHVOSTANTSEV L G, SLESAREV V N. Large-volume high-pressure devices for physical investigations [J]. Physics-Uspekhi, 2008, 51(10): 1099–1104.
|
| [8] |
LIU Z W, LI M Z, YANG Y F, et al. Study on pressure capacity of multilayer stagger-split die, using simulation-based optimization [J]. High Pressure Research, 2013, 33(4): 787–794. doi: 10.1080/08957959.2013.825793
|
| [9] |
朱瑞林. 圆筒形压力容器自增强若干问题研究 [J]. 机械工程学报, 2010, 46(6): 126–133. doi: 10.3901/JME.2010.06.126ZHU R L. Study on autofrettage of cylindrical pressure vessels [J]. Journal of Mechanical Engineering, 2010, 46(6): 126–133. doi: 10.3901/JME.2010.06.126
|
| [10] |
ZHAO L, LI M Z, LI R, et al. Stress analysis of the multi-layer stagger-split die for synthesizing gem quality large single crystal diamond [J]. Diamond and Related Materials, 2018, 83(3): 57–59.
|
| [11] |
YI Z, FU W Z. Numerical study on stress distribution of double-layered split ultrahigh pressure die [J]. Journal of Nanoelectronics and Optoelectronics, 2018, 13(8): 1134–1140. doi: 10.1166/jno.2018.2381
|
| [12] |
王伯龙, 李明哲, 刘志卫, 等. 新型多层交错剖分超高压模具的数值模拟及其试验验证 [J]. 高压物理学报, 2018, 32(6): 27–32. doi: 10.11858/gywlxb.20180560WANG B L, LI M Z, LIU Z W, et al. Numerical simulation and experiment on new multilayer stagger-split die of ultra-high pressure apparatus [J]. Chinese Journal of High Pressure Physics, 2018, 32(6): 27–32. doi: 10.11858/gywlxb.20180560
|
| [13] |
姚裕成. 人造金刚石和超高压高温技术 [M]. 北京: 化学工业出版社, 1996: 35−36.YAO Y C. Artificial diamond and ultra-high pressure and high temperature technology [M]. Beijing: Chemical Industry Press, 1996: 35−36.
|
| [14] |
杨云飞, 李明哲, 刘志卫, 等. 缠绕式挤压筒结构及缠绕层预应力分析 [J]. 机械工程学报, 2015, 51(12): 89–94. doi: 10.3901/JME.2015.12.089YANG Y F, LI M Z, LIU Z W, et al. Structure of wire winded extrusion container and the analysis of the pre-stressed winding layer [J]. Journal of Mechanical Engineering, 2015, 51(12): 89–94. doi: 10.3901/JME.2015.12.089
|
| [15] |
GETTING I C, CHEN G, BROWN J A. The strength and rheology of commercial tungsten carbide cermets used in high-pressure apparatus [J]. Pure and Applied Geophysics, 1993, 141(2): 545–577.
|






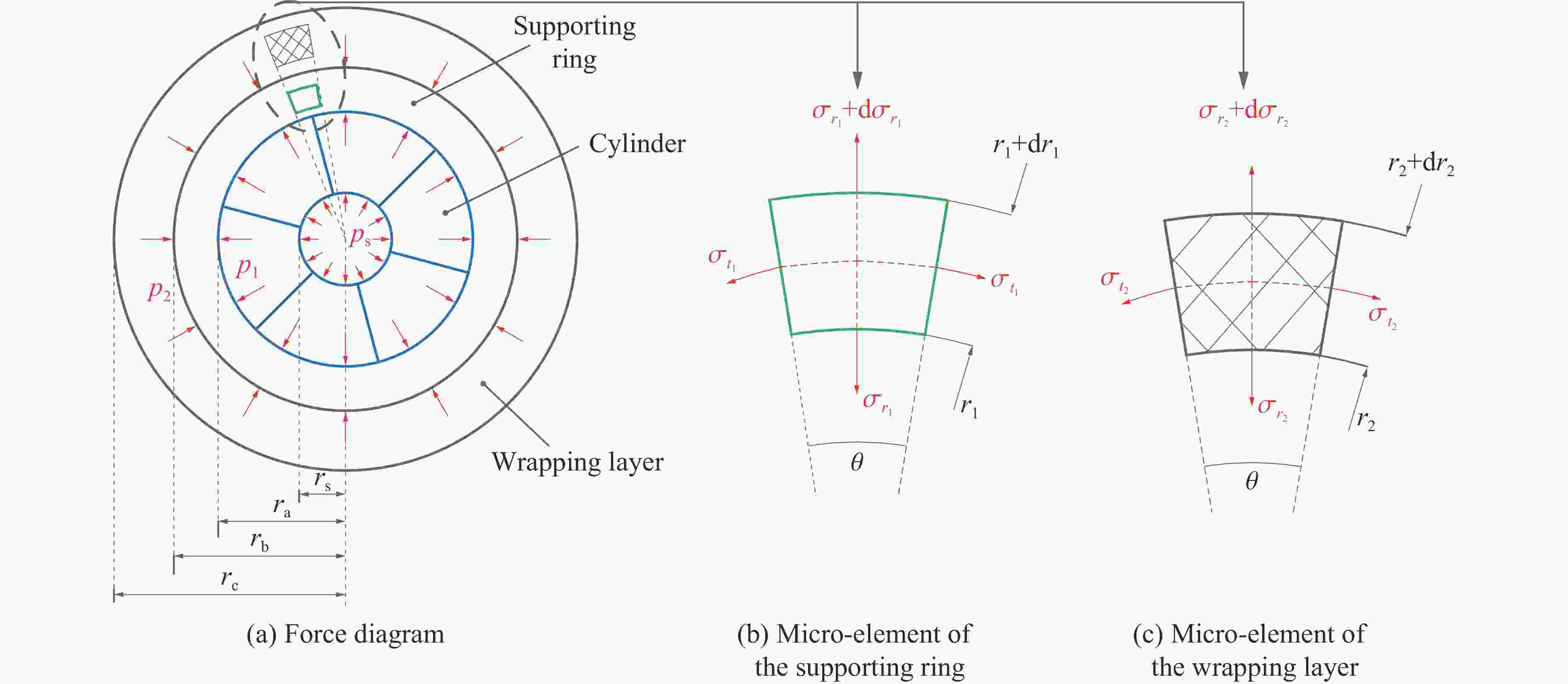
 下载:
下载: