Current Coefficient Law in Simulation of Magnetically Driven Solid Liner Experiment
-
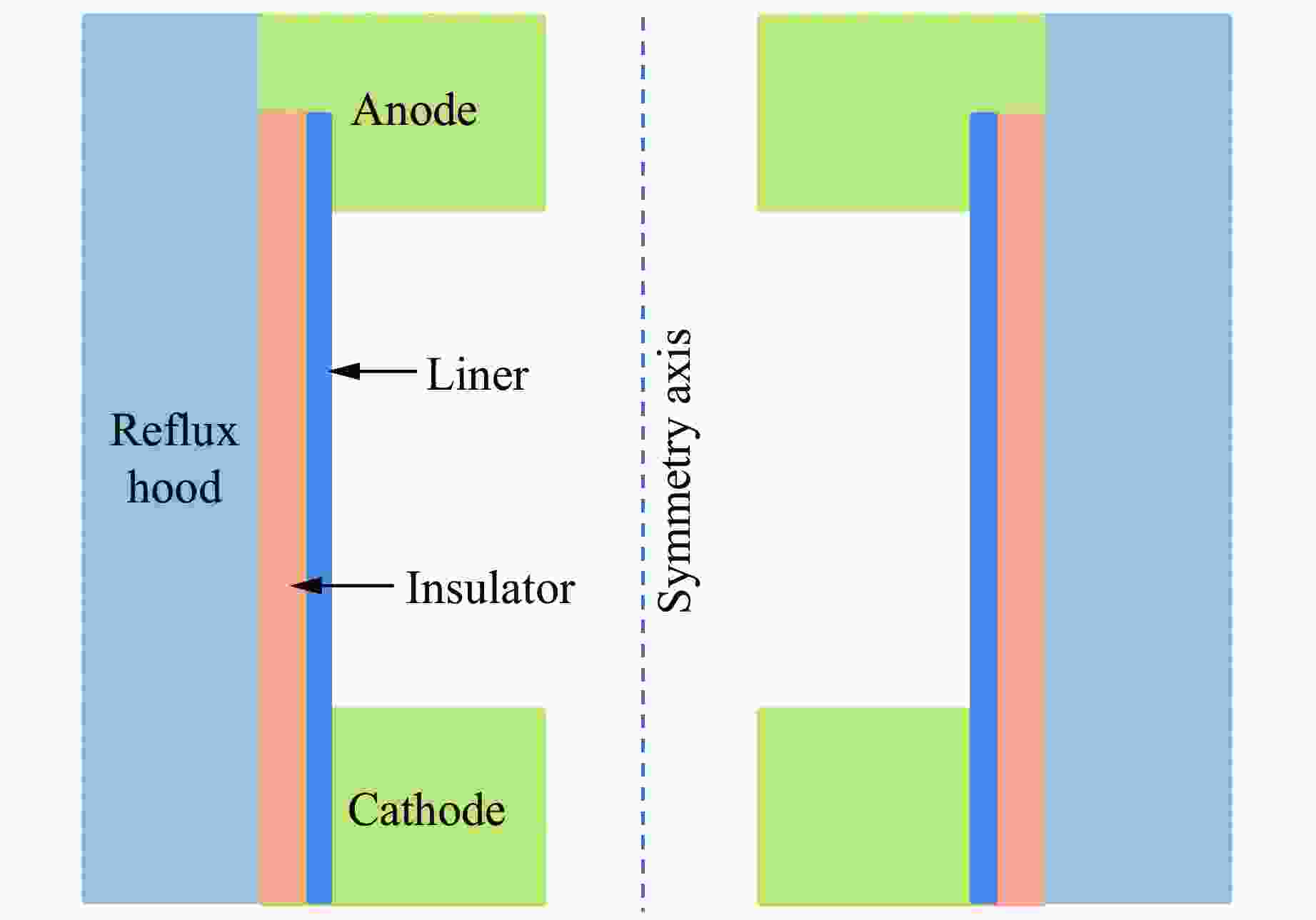
摘要: 采用不可压缩理论模型，对FP-2装置上开展的磁驱动固体套筒实验进行了模拟分析。模拟结果表明，无论是二维磁流体力学理论模型，还是其他不可压缩理论模型，回流罩结构磁驱动固体套筒的边界磁感应强度公式中都包含一个小于1的套筒电流系数。对不同套筒厚度、不同套筒半径条件下磁驱动固体套筒实验的电流系数进行了模拟，发现电流系数不仅与套筒内半径有关，还与套筒厚度有关；套筒内半径越大，套筒电流系数越小；套筒厚度越大，套筒电流系数越小。准确掌握磁驱动固体套筒电流系数的变化规律，可使磁流体程序从磁驱动固体套筒实验的后验模拟发展为精确预测，使磁流体力学模型真正具备正确设计和指导磁驱动固体套筒相关实验的理论能力。
-
关键词:
- 磁驱动固体套筒实验 /
- 二维磁驱动数值模拟程序 /
- 磁流体力学 /
- 电流系数 /
- 回流罩结构
Abstract: The magnetically driven solid liner experiments on the FP-2 device were simulated and analyzed based on the incompressible theoretical model. The simulation results show that the boundary magnetic induction strength formula for the magnetically driven solid liner of the reflux hood structure contains a liner current coefficient of less than 1, regardless of whether it is a two-dimensional magnetohydrodynamic (MHD) theoretical model or other incompressibility theoretical models. The current coefficient law of the magnetically driven solid liner experiment on the FP-2 was studied by simulating the magnetically driven solid liner experiment with different thickness and radii. The current coefficient of magnetically driven solid liner experiment is not only related to the liner’s inner radius, but also to the liner’s thickness. The larger the inner radius of the liner, the smaller the current coefficient, and the larger the thickness of the liner, the smaller the current coefficient. Exploring the current coefficient law in magnetically driven solid liner experiment with reflux hood structure can make the MHD code develop from post-simulation to accurate prediction. And the MHD theoretical model can be employed to design correctly and guide the related experiments of magnetically driven solid liner with a reflux hood structure. -
近年来随着液化天然气(LNG，Liquefied Natural Gas)产业在全球迅速发展，天然气的液化技术和设备也在不断发展完善、日渐成熟。我国LNG领域内的相关研究起步较晚，许多技术远远落后发达国家水平，在天然气液化工艺及装置的生产等方面缺乏自主产权。因此，开展天然气液化工艺及装置的研究，对于实现液化装置的国产化、高效化有十分重要的意义[1-3]。
超声速旋流分离技术是一种新兴的天然气加工处理技术，被较为广泛地用于天然气脱水、脱重烃、脱酸等方面，近年来开始逐渐应用于天然气液化方面[4-7]。天然气超声速液化的原理是：高压天然气混合物在Laval喷管内达到一定的温度、压力条件，开始凝结成核，最终凝结成液滴，在后续工艺中进行进一步气液分离。与传统的天然气液化技术相比，具有结构工艺简单、支持无人操作(适用于海底天然气处理)、对水合物抑制剂依赖性小、投资和运行成本低等优势[8-9]。
为了探究入口复杂多变的压力条件对天然气超声速液化特性的影响，对甲烷-乙烷气体混合物的超声速凝结流动特性进行研究，在凝结成核与生长理论的基础上建立了适用于甲烷-乙烷双可凝气体混合物的凝结流动数学模型，重点研究了入口压力对天然气混合物在Laval喷管内主要流动与凝结参数的影响规律。
1. Laval喷管结构设计
Laval喷管结构主要包括入口段、渐缩段、喉部及扩张段4部分[10-11]。各部分参数如表 1所示，L0为入口长度，r1为渐缩段入口半径，L1为渐缩段长度，rcr为喉部截面半径，L2为渐扩段长度，r2为渐扩段出口半径。为尽量减小流场涡流的影响，渐缩段采用双三次曲线设计，喉部采用一段平缓光滑的圆弧作为过渡曲线，渐扩段采用等膨胀率设计，膨胀率取为10 000 s-1。考虑到实验加工方便，保证曲面的精度，且能够更加直观地观察Laval喷管内部的流场分布情况，所设计Laval喷管截面采用矩形截面，三维结构如图 1所示。
表 1 Laval喷管各部分参数Table 1. Parameters of Laval nozzleL0/mm r1/mm L1/mm rcr/mm L2/mm r2/mm 50.00 20.00 56.01 2.50 71.28 6.15 2. 超声速凝结流动数学模型及计算方法
2.1 数学模型
采用欧拉双流体模型开展数值计算，控制方程主要包括气相流动方程和液相流动方程。在无滑移假设及欧拉双流体模型的前提下分别建立气相及液相流动控制方程组，液滴数目守恒方程及液滴半径、数目、湿度关系式分别添加到对应源相方程中[12-14]。
气相流动控制方程组
∂ρv∂t+∂∂xj(ρvuj)=Sm (1) ∂ρc2∂t+∂∂xj(ρc2uj)=Sm,c2 (2) ∂∂t(ρvui)+∂∂xj(ρvujui)=−∂pv∂xi+∂∂xj[μ(∂uj∂xi+∂ui∂xj−23δij∂uj∂xj)]+∂∂xj(−ρv¯u′iu′j)+Su (3) ∂∂t(ρvE)+∂∂xj(ρvujE+ujpv)=∂∂xj(keff∂T∂xj+uiτeff)+Sh (4) 液相流动控制方程组
∂∂t(ρY)+∂∂xj(ρujY)=SY (5) ∂ρN∂t+∂∂xj(ρNuj)=J (6) rd=3√3Y/(4πρLN) (7) 式中:ui、uj为时均速度分量，m/s；ρv为气相密度，kg/m3；ρ为气液混合相密度，kg/m3；pv为时均压力，Pa；μ为黏度，kg/(m·s)；δij为Kronecker delta数；E为总能量，J/kg；keff为有效导热系数，W/(m·K)；τeff为有效应力张量，无量纲；Y为液相质量分数，无量纲；rd为液滴半径，m；drd/dt为液滴生长速率，m/s；N为液滴数目，kg-1。
成核模型采用文献[15-16]中提出的双组分气体自发凝结成核模型修正方法。液滴生长过程采用Gyarmathy液滴生长模型，模型中液滴与气体间的传热系数[17-18]为
kr=λvrd11+2√8π1.5Pvγ1+γKn (8) 依据传热、传质过程，可推导得到液滴生长速率计算模型
drddt=λvρLhLV(Ts−T)(1−rcrd)rd(1+2√8π1.5Pvγ1+γKn) (9) 式中:λv为气体导热系数，W/(m·K)；Pv为气体Prandtl数；γ为气体比热比；hLV为凝结潜热，J/kg；Ts为气体压力对应的饱和温度，K；Kn表示Kundsen数。由于双组分气体不存在压力对应的饱和温度Ts这一概念，将双组分相图中露点线类比于单组分中饱和曲线。
针对气体状态方程的选择，由于低温气体已偏离理想气体假设，本研究采用了NIST真实气体模型进行计算。
2.2 湍流模型
湍流发生时会导致流体之间相互交换动量、能量，也会造成浓度的改变。本研究建模时忽略相间速度的滑移，即液滴产生不影响湍流，因此只考虑气相的湍流方程。FLUENT中提供了以下几种湍流模型：S-A模型、标准k-ε模型、RNG k-ε模型、Realizable k-ε模型、k-ω模型以及雷诺应力模型。S-A模型主要应用流动分离区附近模拟，标准k-ε模型、RNG k-ε模型一般用于各向同性的均匀湍流，k-ω模型可用于带压梯度的流动模拟和跨声速激波模拟，雷诺应力模型主要用于龙卷风、燃烧室等强烈旋转流动的模拟。对Laval喷管内跨声速流动，采用k-ω模型可以获得较为理想的计算精度和计算速度，故本研究采用该模型进行数值计算。
2.3 计算方法
气体在Laval喷管中的流动属于高速可压缩流动，采用密度基进行求解，流动控制方程组、湍流动能方程、湍流耗散率方程均采用二阶迎风格式进行离散。
根据双组分气体在Laval喷管内的高速可压缩的流动特性，入口和出口边界设置为压力入口边界和压力出口边界条件，对于气体在Laval喷管内的超声速流动，由于所有的流动参数都可从Laval喷管内部外推得到，故在出口处不进行相应设置，固体壁面边界设置为无滑移、无渗流、绝热边界条件。
在数学模型中，由于气相方程添加了源相方程，液相方程定义了标量以及引入的真实气体方程，这些仅靠在FLUENT自带的模型和材料物性无法满足要求，需要编写相应的用户自定义函数(UDF)。本研究编写UDF时，分别定义DEFINE AJUST、DEFINE SOURCE和DEFINE PROPERTY 3个宏函数。DEFINE AJUST宏用来定义过饱和度、过冷度、成核速率、液滴生长率、液滴半径、液滴质量以及液滴表面张力等参数，DEFINE SOURCE宏用来定义控制方程中的质量、动量和能量源相，DEFINE PROPERTY用来定义数值计算中用到的真实气体的热力学参数如黏度系数、导热系数等。
3. 实验验证
为验证所建立的双组分气体凝结数学模型及数值计算方法的准确性，采用本研究所设计的Laval喷管结构，在中国石油大学(华东)超声速气体凝结流动实验系统开展了水-乙醇双可凝组分气体凝结相变实验研究。实验条件为：Laval喷管入口压力0.586 MPa，入口温度288.05 K，气体湿度98.1%，水与乙醇摩尔体积比84:16，气体流量为323.78标方每小时，实验测得的Laval喷管沿程压力分布如图 2所示，可以看出，压力分布实验结果与数值计算结果吻合较好，说明本研究所建立的双组分气体超声速凝结流动特性数学模型及数值计算方法具有一定的准确性和可靠性。
图 2 Laval喷管沿程压力分布数据对比Figure 2. Comparison of pressure distribution data in Laval nozzle4. 不同压力条件下天然气超声速液化特性
保持入口温度及组成(甲烷体积分数90%、乙烷体积分数10%)不变，研究不同的入口压力对Laval喷管内部甲烷-乙烷双组分气体凝结过程中压力、温度、成核率、液滴生长率、液滴半径、液相质量分数的影响。在数值计算中设定的入口温度为270 K，设定入口压力分别为5.5、6.0和6.5 MPa。Laval喷管内双组分气体凝结参数的变化趋势及对比如图 3~图 8所示。
从压力与温度分布可以看出，气体进入Laval喷管后压力、温度不断降低，当达到一定过冷度时，气体发生凝结并释放潜热，但凝结突跃现象对压力造成的影响并不显著，压力在Laval喷管渐扩段减小到了一个比较稳定状态，温度在减小到最小值后又略微上升，这主要是由于液滴凝结释放潜热引起的。随着入口压力的增大，出口压力略微升高，温升位置有所提前，出口温度也越高，这是因为，随着入口压力的增大，液滴成核与凝结量也随之增多，释放的潜热也就越多。
从成核率分布可以看出，保持其他条件一致，当压力发生变化时，成核速率的变化趋势几乎相同，在刚进入Laval喷管的一段距离内为零，在某一位置处开始，成核率从零开始突跃一直增大到峰值后迅速减小至零。随着入口压力从5.5 MPa增大到6.5 MPa，成核的发生位置(Wilson点)不断向前移动，逐渐向Laval喷管喉部靠拢，且成核率的最值逐渐增大。当压力为5.5 MPa时，成核发生位置为x=0.120 6 m，且在x=0.147 5 m处达到极限成核，为4.044×1020 m-3·s-1；当压力为6 MPa时，成核发生位置较5.5 MPa时向前移动，为x=0.119 9 m，极限成核位置也随压力的增大而前移，在x=0.139 3 m处达到8.062×1020 m-3·s-1；当压力继续增大为6.5 MPa时，成核发生位置较6 MPa时更加靠近喉部，为x=0.118 2 m，极限成核位置在x=0.132 8 m处，为9.015×1020 m-3·s-1。
从液滴半径分布可以看出，随着入口压力的增大，Laval喷管内平均液滴半径越大，出口液滴半径也随之增大，当压力为5.5、6.0、6.5 MPa时，对应最大液滴半径尺寸分别为415.86、447.88和477.44 nm。由此可知，压力的升高有利于液滴的生长。
从液滴生长率分布可以看出，液滴生长率在气体刚进入Laval喷管时一直为零，当液滴开始发生成核凝结时液滴生长率开始突增，变化到最大值后又迅速减小，最终减小为零。综合图 6和图 7还可以看出，随着入口压力的升高，在成核开始时液滴生长率较大，液滴半径增长速度较快，但一段距离后液滴生长率下降更大，液滴半径增长速度也明显放缓。
从液相质量分数分布可以看出，伴随着混合气体的凝结成核，液相质量分数也不断增大，且随着入口压力的升高，Laval喷管出口处的湿度值随之增大，当压力为5.5 MPa时，湿度的最大值为3.989 2%，当压力增大到6.5 MPa时湿度最终增大到7.382 0%。
5. 结论
(1) 建立了三维双组分天然气混合物超声速凝结流动数学模型，对Laval喷管内双组分混合物凝结流动进行了数值模拟，得出沿Laval喷管轴向的参数分布，通过开展双可凝组分气体凝结相变实验，对比发现数值模拟与实验结果基本一致，说明了所建立数学模型及计算方法的正确性。
(2) 利用数值模型研究了入口参数对天然气混合物超声速液化特性的影响，结果表明，保持Laval喷管入口温度及组成不变，增大入口压力，混合气体成核位置前移，成核率、平均液滴半径、液相质量分数均随之增大，即入口压力越大，混合气体在Laval喷管内越易发生凝结。在实际生产中，可以通过调节入口压力来促进天然气的凝结，提高Laval喷管的液化效率。
-
图 1 回流罩固体套筒实验装置的初始结构剖面
Figure 1. Cross section of magnetically driven solid liner experiment setup with a reflux hood
图 2 磁驱动固体套筒实验测得的电流
Figure 2. Measured currents for magnetically driven solid liner experiments
图 3 不可压缩模型模拟得到的套筒内界面速度
Figure 3. Liner interface velocity simulated by incompressible model
图 4 实验 1～实验4的套筒内界面速度
Figure 4. Interface velocities of the experimental liners for Exp. 1−Exp. 4
表 1 磁驱动固体套筒实验的套筒参数
Table 1. Liner parameters of the magnetically driven solid liner experiments
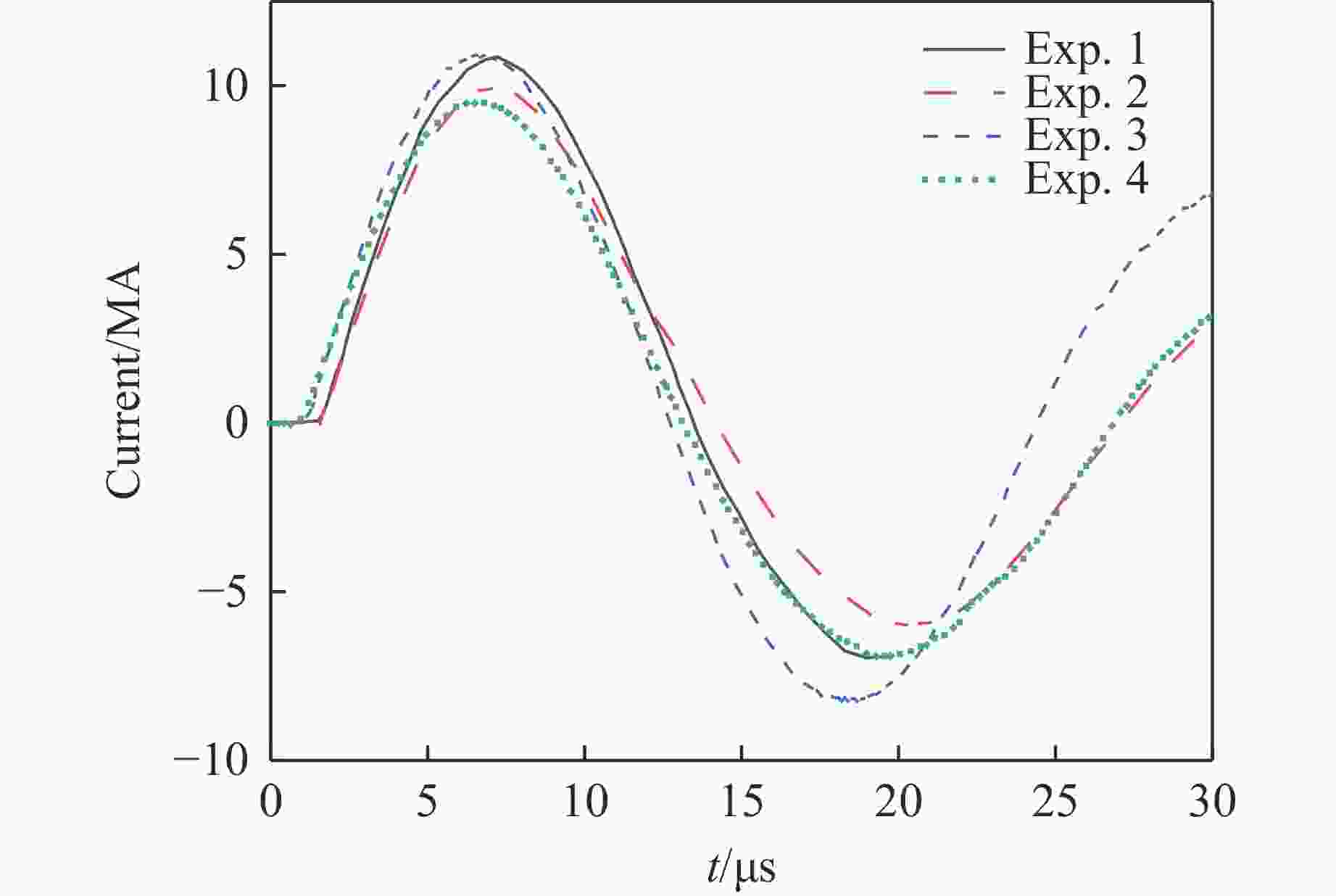
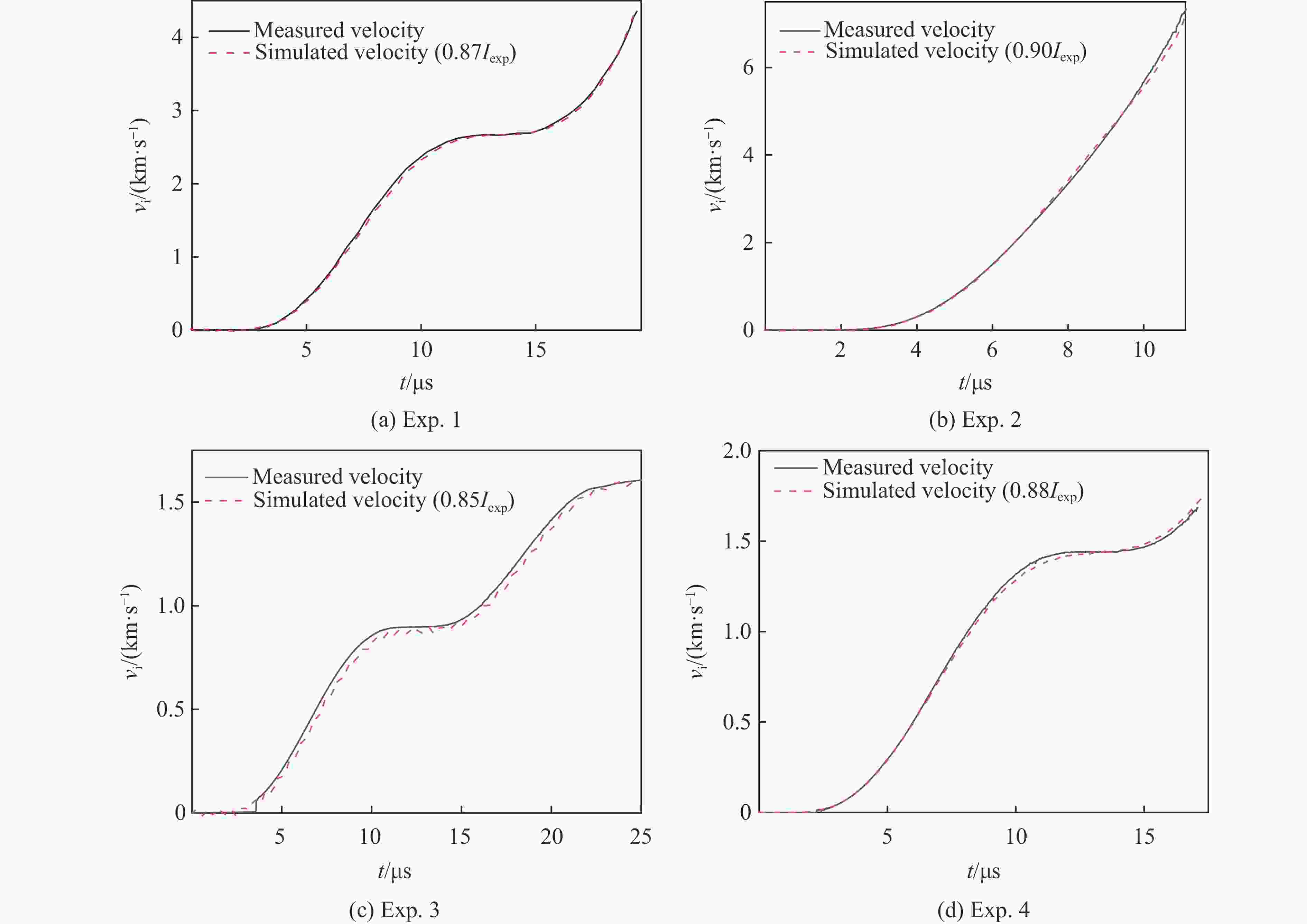
Exp. No. Liner material Liner’s inner radius/mm Liner’s thickness/mm 1 Al 45 0.6 2 Al 30 0.6 3 Al 45 1.6 4 Al 30 1.9 
下载: 导出CSV
表 2 磁驱动固体套筒实验的电流系数
Table 2. Current coefficients of the magnetically driven solid liner experiments
Exp. No. Liner’s inner radius/mm Liner’s thickness/mm fc 1 45 0.6 0.87 2 30 0.6 0.90 3 45 1.6 0.85 4 30 1.9 0.88
下载: 导出CSV
-
[1] TURCHI P J, BAKER W L. Generation of high-energy plasmas by electromagnetic implosion [J]. Journal of Applied Physics, 1973, 44(11): 4936–4945. doi: 10.1063/1.1662066 [2] MARTIN M R, LEMKE R W, MCBRIDE R D, et al. Solid liner implosions on Z for producing multi-megabar, shockless compressions [J]. Physics of Plasmas, 2012, 19(5): 056310. doi: 10.1063/1.3694519 [3] BUYKO A M, ZMUSHKO V V, ATCHISION W L, et al. Results and prospects of material strength studies on electrophysical facilities based on perturbation growth in liner systems [J]. IEEE Transactions on Plasma Science, 2008, 36(1): 104–111. doi: 10.1109/TPS.2007.914072 [4] KAUL A M, IVANOVSKY A V, ATCHISON W L, et al. Damage growth and recollection in aluminum under axisymmetric convergence using a helical flux compression generator [J]. Journal of Applied Physics, 2014, 115(2): 023516. doi: 10.1063/1.4861411 [5] REINOVSKY R E, ANDERSON W E, ATCHISO W L, et al. Instability growth in magnetically imploded high-conductivity cylindrical liners with material strength [J]. IEEE Transactions on Plasma Science, 2002, 30(5): 1764–1776. doi: 10.1109/TPS.2002.805418 [6] REINOVSKY R E, ATCHISO W L, DIMONTE G, et al. Pulsed-power hydrodynamics: an application of pulsed-power and high magnetic fields to the exploration of material properties and problems in experimental hydrodynamics [J]. IEEE Transactions on Plasma Science, 2008, 36(1): 112–124. doi: 10.1109/TPS.2007.914708 [7] ZHANG S L, LIU W, WANG G L, et al. Investigation of convergent Richtmyer-Meshkov instability at tin/xenon interface with pulsed magnetic driven imploding [J]. Chinese Physics B, 2019, 28(4): 044702. doi: 10.1088/1674-1056/28/4/044702 [8] RYUTOV D D, DERZON M S, MATZEN M K. The physics of fast Z pinches [J]. Reviews of Modern Physics, 2000, 72(1): 167–223. doi: 10.1103/RevModPhys.72.167 [9] 丁宁, 杨震华, 宁成. Z箍缩等离子体内爆实验金属丝阵负载优化设计分析 [J]. 物理学报, 2004, 53(3): 808–817. doi: 10.7498/aps.53.808DING N, YANG Z H, NING C. Optimization design of a wire array load for Z-pinch plasma implosion experiments [J]. Acta Physica Sinica, 2004, 53(3): 808–817. doi: 10.7498/aps.53.808 [10] 丁宁, 张扬, 宁成, 等. PTS装置Z箍缩负载设计分析 [J]. 物理学报, 2008, 57(5): 3027–3037. doi: 10.7498/aps.57.3027DING N, ZHANG Y, NING C, et al. Design and analysis of the Z-pinch loads on the PTS facility [J]. Acta Physica Sinica, 2008, 57(5): 3027–3037. doi: 10.7498/aps.57.3027 [11] 章征伟, 魏懿, 孙奇志, 等. 材料强度对电磁驱动固体套筒内爆过程的影响 [J]. 强激光与粒子束, 2016, 28(4): 045017. doi: 10.11884/HPLPB201628.125017ZHANG Z W, WEI Y, SUN Q Z, et al. Effect of material strength on electromagnetic driven solid liner implosion [J]. High Power Laser and Particle Beams, 2016, 28(4): 045017. doi: 10.11884/HPLPB201628.125017 [12] 张绍龙, 章征伟, 孙奇志, 等. 电流脉冲前沿对电磁驱动固体套筒内爆的影响 [J]. 强激光与粒子束, 2017, 29(10): 105002. doi: 10.11884/HPLPB201729.170161ZHANG S L, ZHANG Z W, SUN Q Z, et al. Effect of current rise time on electromagnetic driven solid liner implosion [J]. High Power Laser and Particle Beams, 2017, 29(10): 105002. doi: 10.11884/HPLPB201729.170161 [13] 章征伟, 王贵林, 张绍龙, 等. 电作用量在磁驱动固体套筒内爆设计分析中的应用 [J]. 物理学报, 2020, 69(5): 050701. doi: 10.7498/aps.69.20191690ZHANG Z W, WANG G L, ZHANG S L, et al. Application of electrical action to design and analysis of magnetically driven solid liner implosion [J]. Acta Physica Sinica, 2020, 69(5): 050701. doi: 10.7498/aps.69.20191690 [14] TUCKER T J, TOTH R P. EBW1: a computer code for the prediction of the behavior of electrical circuits containing exploding wire elements: SAND-75-0041 [R]. Albuquerque: Sandia National Laboratory, 1975. [15] 章征伟. 磁驱动固体套筒内爆理论与实验研究 [D]. 绵阳: 中国工程物理研究院, 2020: 49−59.ZHANG Z W. Theoretic and experimental study on magnetically driven solid liner implosion [D]. Mianyang: China Academy of Engineering Physics, 2020: 49−59. [16] 张扬, 戴自换, 孙奇志, 等. FP-1装置铝套筒内爆动力学过程的一维磁流体力学模拟 [J]. 物理学报, 2018, 67(8): 080701. doi: 10.7498/aps.67.20172300ZHANG Y, DAI Z H, SUN Q Z, et al. One-dimensional magneto-hydrodynamics simulation of magnetically driven solid liner implosions on FP-1 facility [J]. Acta Physica Sinica, 2018, 67(8): 080701. doi: 10.7498/aps.67.20172300 [17] 阚明先, 贾月松, 张南川, 等. 回流罩结构Z-箍缩实验的数值模拟 [J]. 强激光与粒子束, 2023, 35(2): 025003. doi: 10.11884/HPLPB202335.220271KAN M X, JIA Y S, ZHANG N C, et al. Simulation of Z-pinch experiments with a reflux hood structure [J]. High Power Laser and Particle Beams, 2023, 35(2): 025003. doi: 10.11884/HPLPB202335.220271 [18] ROUSCULP C L, ORO D M, GRIEGO J R, et al. Investigation of surface phenomena in shocked tin in converging geometry: LA-UR-16-21901 [R]. Los Alamos: Los Alamos National Laboratory, 2016. [19] SUN Q Z, JIA Y S, ZHANG Z W, et al. Cylindrical metal liner implosion at extremes of pressure and material velocity on an intense pulsed power facility-FP-2 [J]. Review of Scientific Instruments, 2022, 93(1): 013904. doi: 10.1063/5.0064238 [20] 阚明先, 王刚华, 赵海龙, 等. 磁驱动飞片二维磁流体力学数值模拟 [J]. 强激光与离子束, 2013, 25(8): 2137–2141. doi: 10.3788/HPLPB20132508.2137KAN M X, WANG G H, ZHAO H L, et al. Two-dimensional magneto-hydrodynamic simulations of magnetically accelerated flyer plates [J]. High Power Laser and Particle Beams, 2013, 25(8): 2137–2141. doi: 10.3788/HPLPB20132508.2137 [21] 阚明先, 蒋吉昊, 王刚华, 等. 衬套内爆ALE方法二维MHD数值模拟 [J]. 四川大学学报(自然科学版), 2007, 44(1): 91–96. doi: 10.3969/j.issn.0490-6756.2007.01.020KAN M X, JIANG J H, WANG G H, et al. ALE simulation of 2D MHD for liner [J]. Journal of Sichuan University (Natural Science Edition), 2007, 44(1): 91–96. doi: 10.3969/j.issn.0490-6756.2007.01.020 [22] KAN M X, ZHANG Z H, XIAO B, et al. Simulation of magnetically driven flyer plate experiments with an improved magnetic field boundary formula [J]. High Energy Density Physics, 2018, 26: 38–43. doi: 10.1016/j.hedp.2017.12.002 [23] 阚明先, 段书超, 王刚华, 等. 自由面被烧蚀磁驱动飞片的数值模拟 [J]. 强激光与粒子束, 2017, 29(4): 045003. doi: 10.11884/HPLPB201729.160482KAN M X, DUAN S C, WANG G H, et al. Numerical simulation of magnetically driven flyer plate of ablated free surface [J]. High Power Laser and Particle Beams, 2017, 29(4): 045003. doi: 10.11884/HPLPB201729.160482 [24] 阚明先, 段书超, 王刚华, 等. 磁驱动飞片发射实验结构系数初步研究 [J]. 强激光与粒子束, 2020, 32(8): 085002. doi: 10.11884/HPLPB202032.200072KAN M X, DUAN S C, WANG G H, et al. Structure coefficient in magnetically driven flyer plate experiment [J]. High Power Laser and Particle Beams, 2020, 32(8): 085002. doi: 10.11884/HPLPB202032.200072 [25] 阚明先, 刘利新, 南小龙, 等. 磁驱动样品实验数值模拟研究 [J]. 高压物理学报, 2023, 37(6): 062301. doi: 10.11858/gywlxb.20230683KAN M X, LIU L X, NAN X L, et al. Numerical simulation of magnetically driven sample experiment [J]. Chinese Journal of High Pressure Physics, 2023, 37(6): 062301. doi: 10.11858/gywlxb.20230683 [26] 阚明先, 段书超, 张朝辉, 等. 二维磁驱动数值模拟程序MDSC2的验证与确认 [J]. 强激光与粒子束, 2019, 31(6): 065001. doi: 10.11884/HPLPB201931.180300KAN M X, DUAN S C, ZHANG Z H, et al. Verification and validation of two dimensional magnetically driven simulation code MDSC2 [J]. High Power Laser and Particle Beams, 2019, 31(6): 065001. doi: 10.11884/HPLPB201931.180300 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 153
- HTML全文浏览量: 62
- PDF下载量: 29
