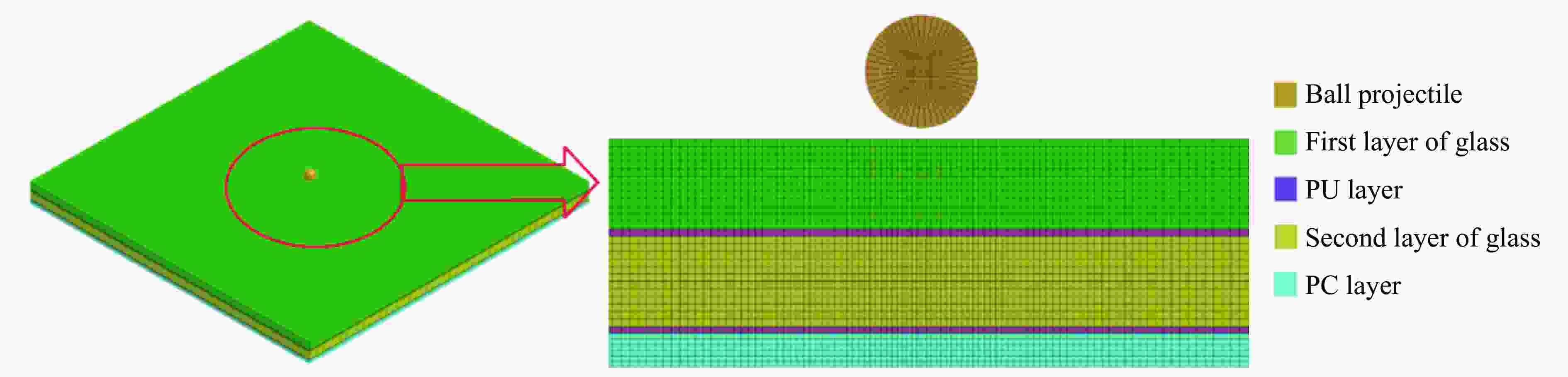
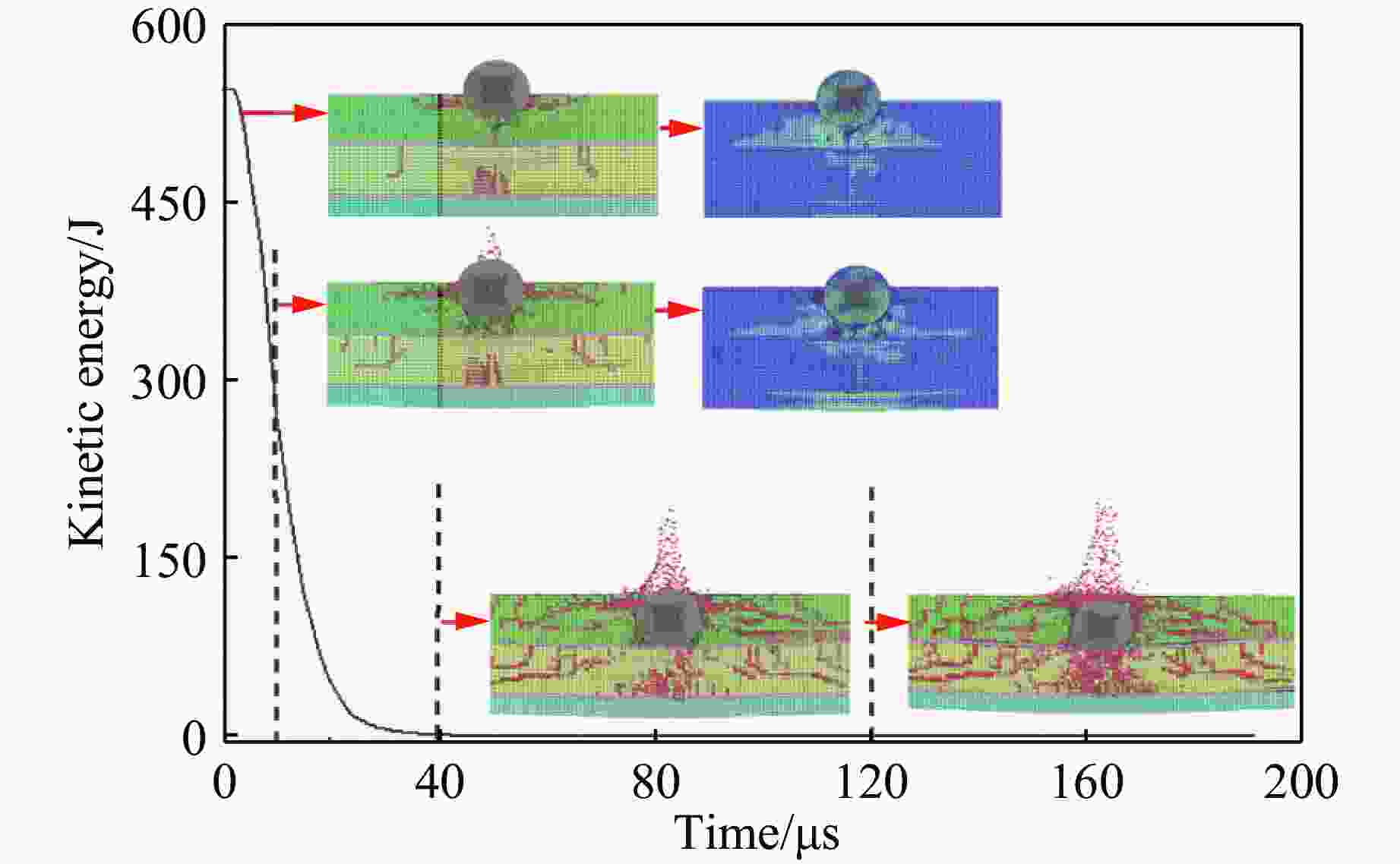
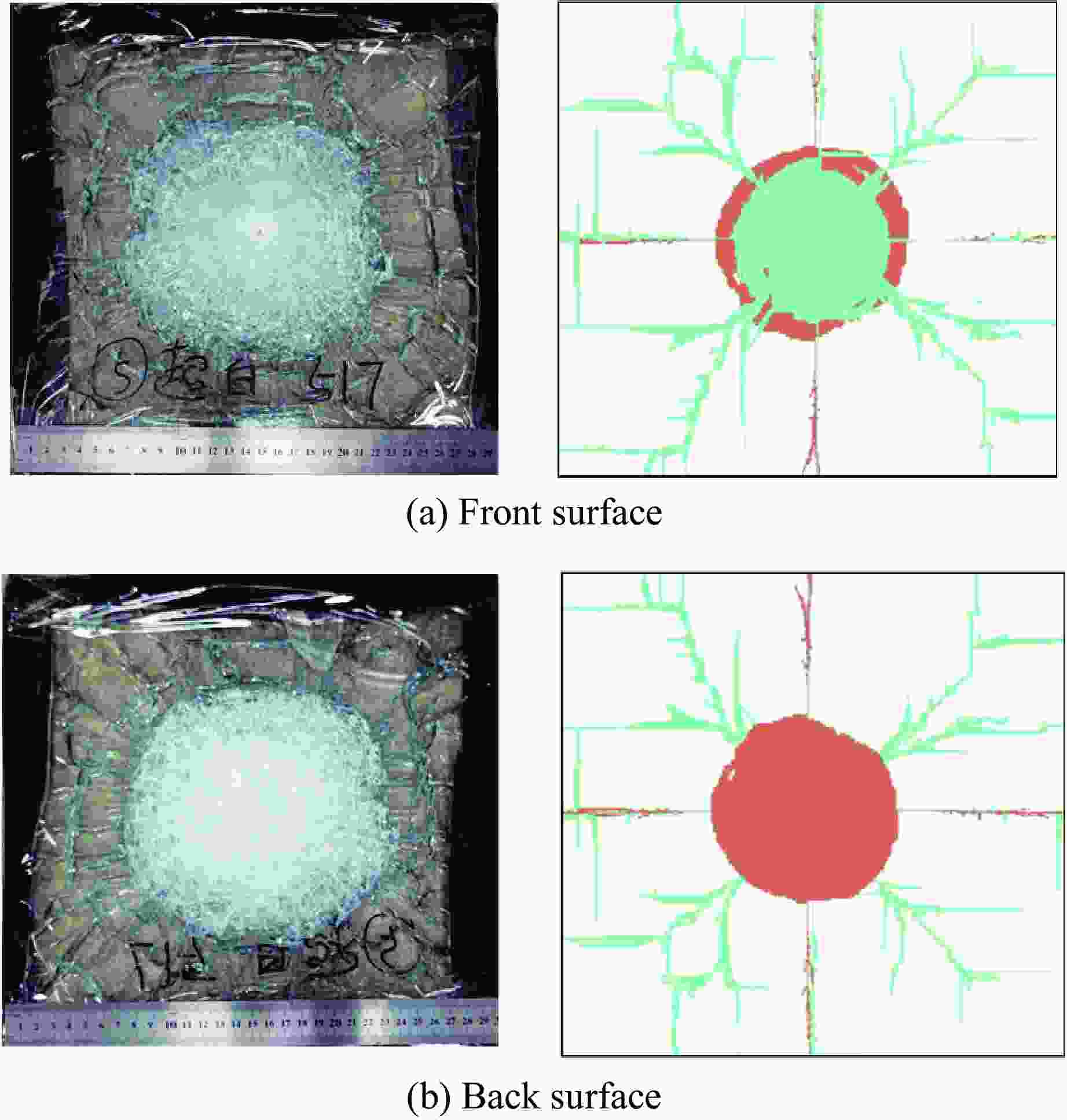
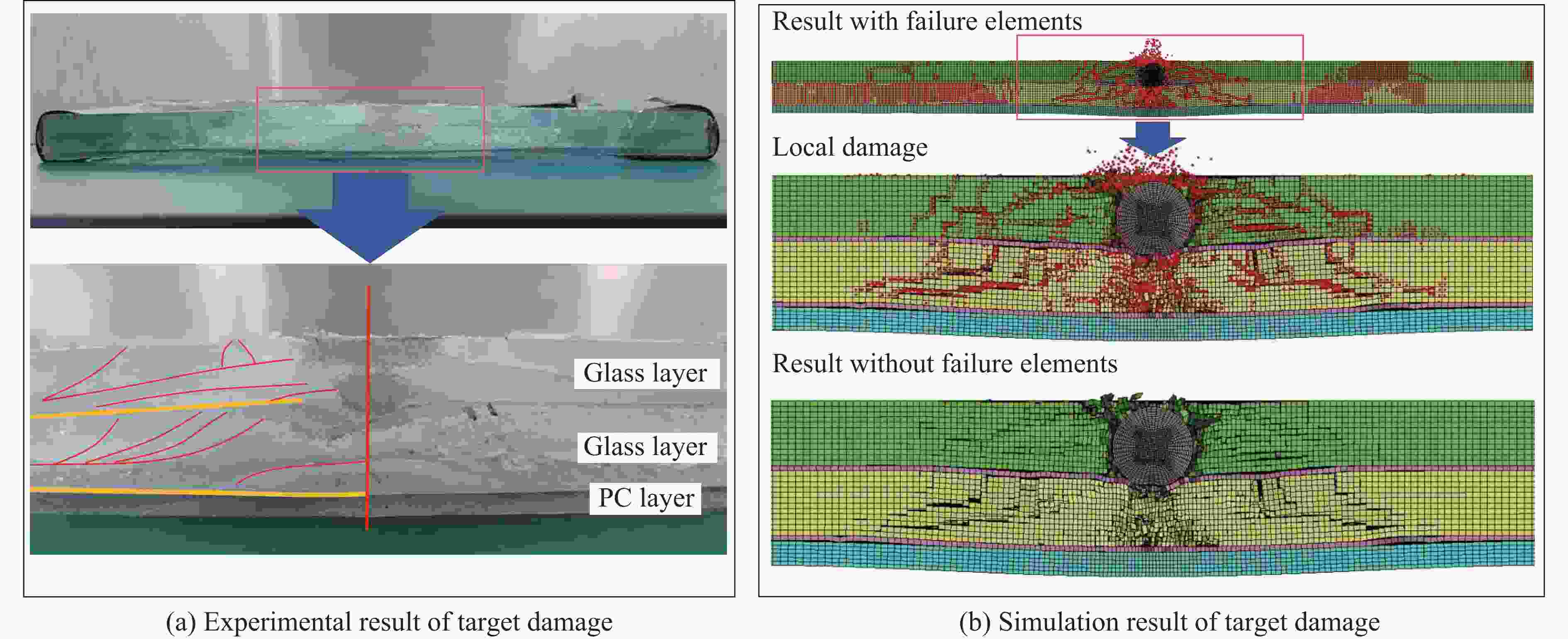
Damage Mechanism of Glass Composite Armor Subjected to Projectile at High Impact Velocity
-
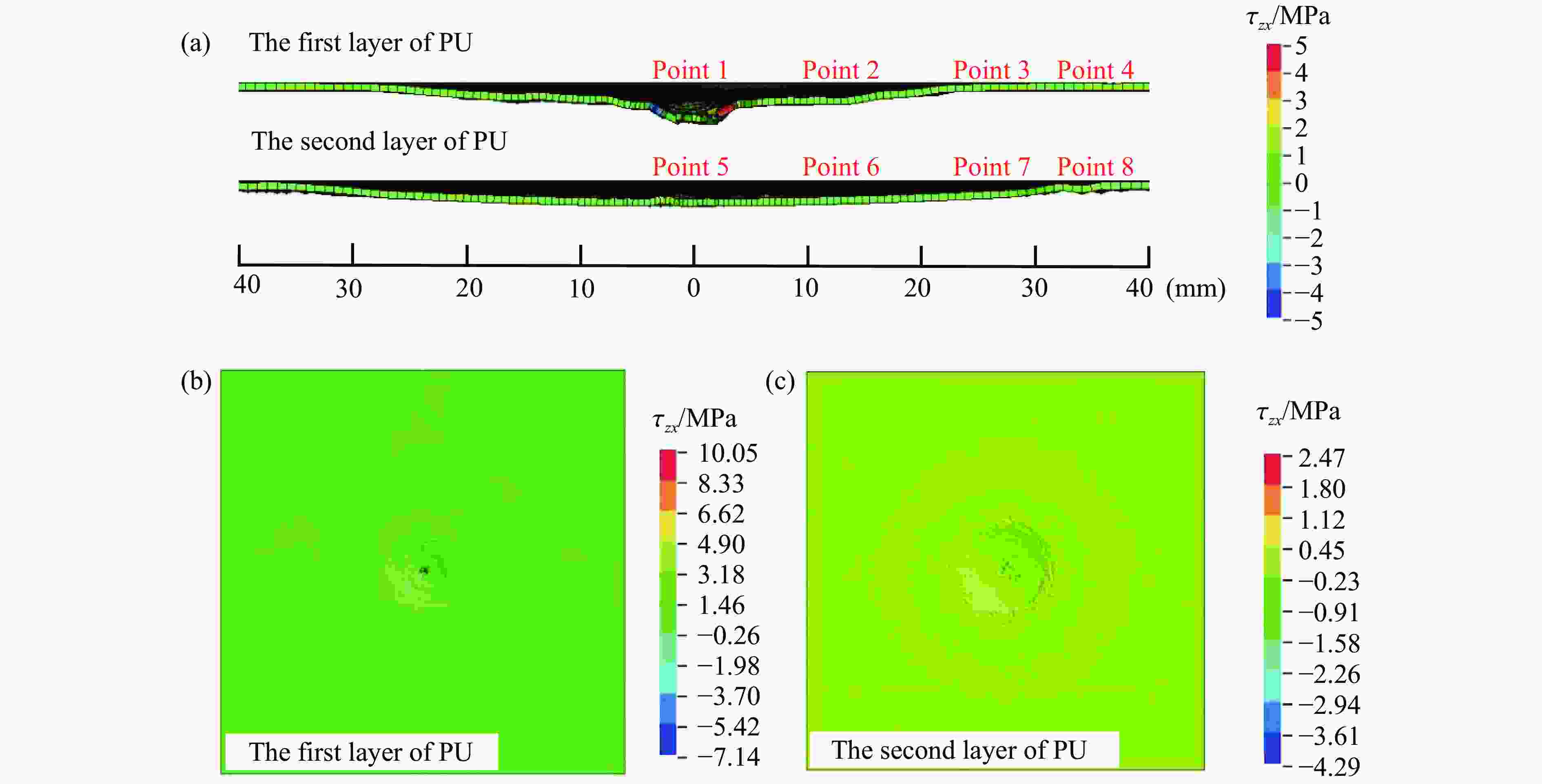
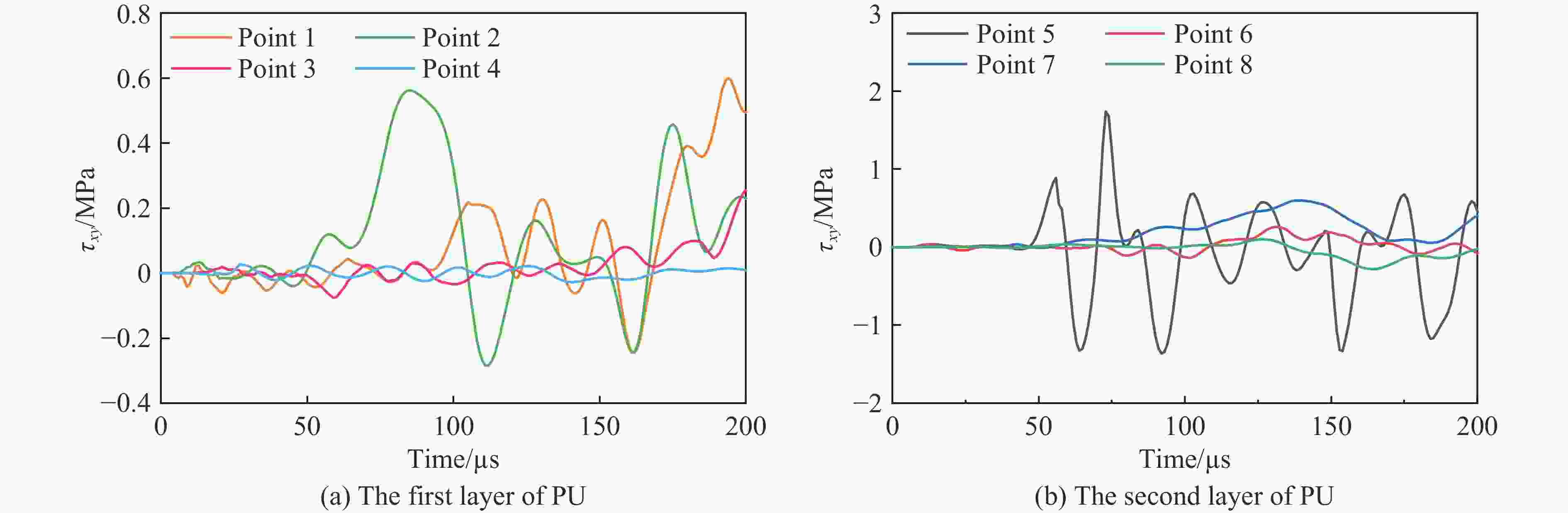
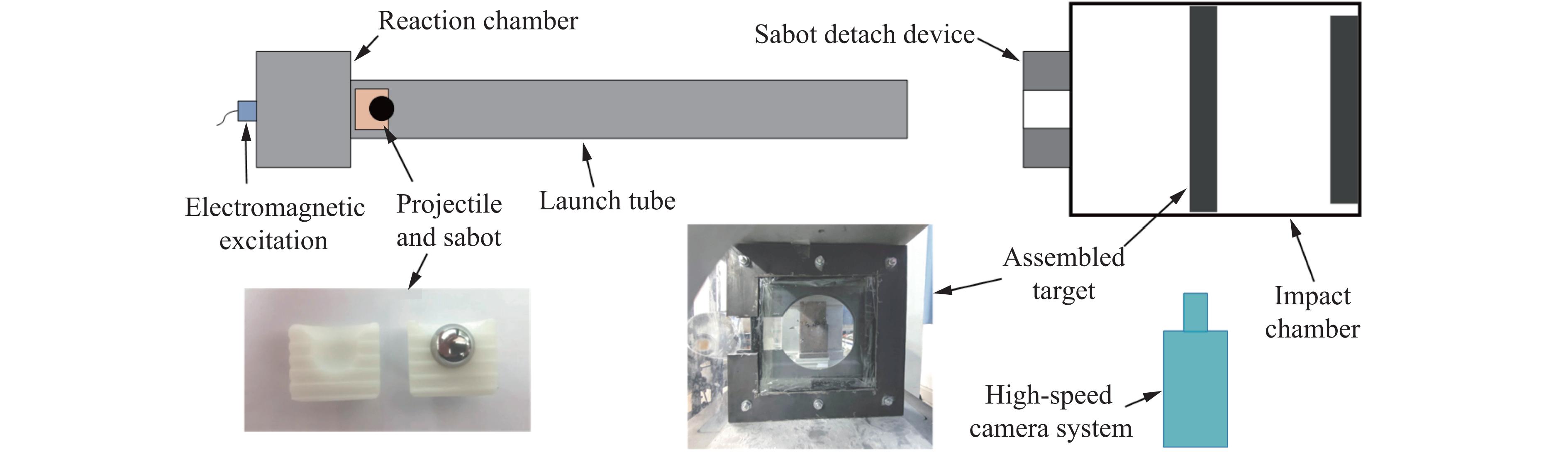
摘要: 玻璃叠层复合装甲具有良好的透光性和抗冲击性能,广泛应用于军事和民用防护领域。由于玻璃容易发生失效或破碎,为了获得靶板的冲击损伤机制,开展了钢球高速撞击下的试验和数值模拟研究。结果表明,在第1层玻璃破碎锥和应力波传播的作用下,第2层玻璃破碎锥体积和整体损伤面积显著大于第1层玻璃。弹丸高速撞击下,玻璃层形成了大量径向和环向裂纹,其中,在Rayleigh波作用下形成的环向裂纹可以阻止径向裂纹传播造成的次生裂纹扩展。根据损伤程度不同,玻璃层分为粉末区、小尺寸碎片区、大尺寸碎片区和径向裂纹区。受应力波传播、靶板弯曲变形以及破碎玻璃的体积膨胀共同作用,玻璃层沿厚度方向出现了竖向裂纹和平行破碎锥面的斜向裂纹。玻璃之间聚氨酯黏结层可造成竖向裂纹偏转,在一定程度上阻碍了裂纹沿厚度方向传播。玻璃/聚氨酯/聚碳酸酯之间,受介质波阻抗不同,导致界面的剪切波作用,胶层出现了局部分层现象。聚碳酸酯依靠自身的塑性变形聚集了破碎装玻璃颗粒,形成了局部高应力状态区域,完成了对弹丸的持续阻碍作用。因此,聚氨酯胶层的变形主要为破碎锥对其直接剪切作用所致。Abstract: The glass laminated composite armor exhibits good light transmission and impact resistance, making it widely used in military and civil protection fields. However, due to the susceptibility of glass to failure and breakage, the experiments and numerical simulations were carried out to investigate the impact damage mechanism of the target plate under high-speed impact of the steel ball projectile. Results show that under the action of breaking cone of first glass layer and stress wave propagation, the volume of breaking cone in the second layer of glass and the overall damage area are significantly larger than those in the first layer. During high-speed impact, many radial and circumferential cracks form in the glass layer. The circumferential cracks, resulting from Rayleigh waves, can prevent the propagation of secondary cracks caused by the radial crack propagation. The glass layer can be divided into the powder region, small fragment region, large fragment region and radial crack region according to different damage degrees. Along the thickness direction, the combined action of stress wave propagation, bending deformation of the target plate and volume expansion of the broken glass result in vertical and oblique cracks along the breaking cone in the glass layer. The PU bonding layer between the glass layer can deflect vertical cracks and hinder the propagation of the cracks along the thickness direction. At the interfaces between the glass/PU/PC layers, shear wave action arises due to the differences in dielectric wave impedance, leading to localized stratification within the adhesive layer. The deformation of PC layer gathers broken glass particles, forming a local high-stress area and complets the continuous obstruction of the projectile. Finally, the deformation of the PU adhesive layer is primarily induced by the shear stress caused from the breaking cone of the glass layer.
-
表 1 玻璃材料的JH2本构模型参数
Table 1. Parameters of JH2 constitutive model for glass material
ρ/(kg·m–3) G/GPa K1/GPa K2/GPa K3/GPa T/GPa σHEL/GPa pHEL/GPa 2488 29.6 40.8 −136.6 239.8 0.078 6 2.75 A B C M N D1 D2 1.679 1.783 0.0144 0.637 0.982 0.005 0.8 表 2 PU材料的Mooney-Rivlin本构模型参数
Table 2. Parameters of Mooney-Rivlin constitutive model for PU material
ρ/(kg·m–3) ν C10/MPa C01/MPa 1100 0.495 1.6 0.06 表 3 PC材料的简化JC本构模型参数
Table 3. Parameters of simplified JC constitutive model for PC material
ρ/(kg·m–3) ν E/GPa A1/MPa B1/MPa N1 C1 1200 0.38 2.34 56 176 2.67 0.09 表 4 试验与数值模拟的侵彻深度对比
Table 4. Comparison of depth of penetration between experiment and simulation
No. Impact velocity/(m·s–1) Depth of penetration Exp./mm Sim./mm Error/% 1 336 4.9 4.1 16.30 2 413 5.8 6.1 5.20 3 517 11.3 10.2 9.70 4 634 13.4 15.3 14.20 -
[1] 韩国庆, 张先锋, 谈梦婷, 等. 透明陶瓷材料冲击响应特性及损伤演化规律研究 [J]. 力学进展, 2023, 53(3): 497–560. doi: 10.6052/1000-0992-23-007HAN G Q, ZHANG X F, TAN M T, et al. Research on impact response characteristics and damage evolution law of transparent ceramics [J]. Advances in Mechanics, 2023, 53(3): 497–560. doi: 10.6052/1000-0992-23-007 [2] KLEMENT R, ROLC S, MIKULIKOVA R, et al. Transparent armour materials [J]. Journal of the European Ceramic Society, 2008, 28(5): 1091–1095. doi: 10.1016/j.jeurceramsoc.2007.09.036 [3] 牛欢欢, 张英杰, 李志强. 爆炸载荷下中空钢化夹层玻璃的动态响应 [J]. 高压物理学报, 2021, 35(6): 064102. doi: 10.11858/gywlxb.20210764NIU H H, ZHANG Y J, LI Z Q. Dynamic response of hollow tempered laminated glass under explosive load [J]. Chinese Journal of High Pressure Physics, 2021, 35(6): 064102. doi: 10.11858/gywlxb.20210764 [4] GRUJICIC M, BELL W C, PANDURANGAN B. Design and material selection guidelines and strategies for transparent armor systems [J]. Materials & Design, 2012, 34: 808–819. doi: 10.1016/j.matdes.2011.07.007 [5] XU J, LI Y B, LIU B H, et al. Experimental study on mechanical behavior of PVB laminated glass under quasi-static and dynamic loadings [J]. Composites Part B: Engineering, 2011, 42(2): 302–308. doi: 10.1016/j.compositesb.2010.10.009 [6] LI D, ZHANG H Y, LEI X W, et al. Three-stage breakage model for laminated glass plate under low-velocity impact [J]. Ceramics International, 2023, 49(2): 2648–2662. doi: 10.1016/j.ceramint.2022.09.245 [7] CHEN J J, XU J, YAO X F, et al. Experimental investigation on the radial and circular crack propagation of PVB laminated glass subject to dynamic out-of-plane loading [J]. Engineering Fracture Mechanics, 2013, 112/113: 26–40. doi: 10.1016/j.engfracmech.2013.09.010 [8] WANG X E, YANG J, LIU Q, et al. Experimental investigations into SGP laminated glass under low velocity impact [J]. International Journal of Impact Engineering, 2018, 122: 91–108. doi: 10.1016/j.ijimpeng.2018.06.010 [9] CAI L, ZHANG Y Q, WEI X R, et al. Study on the effect of different sandwich materials on the impact resistance of laminated glass [J]. Construction and Building Materials, 2022, 360: 129603. doi: 10.1016/j.conbuildmat.2022.129603 [10] 邓佳杰, 章健, 张先锋, 等. YAG透明陶瓷复合靶抗弹机理研究 [J]. 北京理工大学学报, 2022, 42(6): 620–628. doi: 10.15918/j.tbit1001-0645.2021.230DENG J J, ZHANG J, ZHANG X F, et al. Investigation on bullet proof mechanism of YAG transparent ceramic composite targets [J]. Transactions of Beijing Institute of Technology, 2022, 42(6): 620–628. doi: 10.15918/j.tbit1001-0645.2021.230 [11] 刘滢, 黄君伟, 郭新涛, 等. MgAl2O4透明陶瓷复合结构抗弹性能的数值模拟研究 [J]. 稀有金属, 2023, 47(4): 529–537. doi: 10.13373/j.cnki.cjrm.XY20110010LIU Y, HUANG J W, GUO X T, et al. Numerical simulation of ballistic resistance of MgAl2O4 transparent laminate structure [J]. Chinese Journal of Rare Metals, 2023, 47(4): 529–537. doi: 10.13373/j.cnki.cjrm.XY20110010 [12] WANG X E, MENG Y R, YANG J, et al. Optimal kernel extreme learning machine model for predicting the fracture state and impact response of laminated glass panels [J]. Thin-Walled Structures, 2021, 162: 107541. doi: 10.1016/j.tws.2021.107541 [13] VEDRTNAM A, PAWAR S J. Experimental and simulation studies on fracture and adhesion test of laminated glass [J]. Engineering Fracture Mechanics, 2018, 190: 461–470. doi: 10.1016/j.engfracmech.2017.12.044 [14] OSNES K, HOLMEN J K, GRUE T, et al. Perforation of laminated glass: an experimental and numerical study [J]. International Journal of Impact Engineering, 2021, 156: 103922. doi: 10.1016/j.ijimpeng.2021.103922 [15] STRASSBURGER E, BAUER S, POPKO G. Damage visualization and deformation measurement in glass laminates during projectile penetration [J]. Defence Technology, 2014, 10(2): 226–238. doi: 10.1016/j.dt.2014.05.008 [16] GAO Y B, LI D C, ZHANG W, et al. Constitutive modelling of the TiB2-B4C composite by experiments, simulation and neutral network [J]. International Journal of Impact Engineering, 2019, 132: 103310. doi: 10.1016/j.ijimpeng.2019.05.024 [17] 贾哲. 弹道冲击下防弹玻璃的损伤机理和抗侵彻性能研究 [D]. 太原: 中北大学, 2023: 21–33.JIA Z. Study on damage mechanism and anti-penetration performance of bulletproof glass under ballistic impact [D]. Taiyuan: North University of China, 2023: 21–33. [18] SPATHIS G D. Polyurethane elastomers studied by the Mooney-Rivlin equation for rubbers [J]. Journal of Applied Polymer Science, 1991, 43(3): 613–620. doi: 10.1002/app.1991.070430323 [19] SARIKAYA M, GÜDEN M, KAMBUR Ç, et al. Development of the Johnson-Cook flow stress and damage parameters for the impact response of polycarbonate: experimental and numerical approach [J]. International Journal of Impact Engineering, 2023, 179: 104674. doi: 10.1016/j.ijimpeng.2023.104674 [20] 刘赛, 张伟贵, 吕振华. 穿甲燃烧弹侵彻陶瓷复合装甲和玻璃复合装甲的FEM-SPH耦合计算模型 [J]. 爆炸与冲击, 2021, 41(1): 014201. doi: 10.11883/bzycj-2020-0069LIU S, ZHANG W G, LU Z H. An FEM-SPH coupled model for simulating penetration of armor-piercing bullets into ceramic composite armors and glass composite armors [J]. Explosion and Shock Waves, 2021, 41(1): 014201. doi: 10.11883/bzycj-2020-0069 [21] MOHAGHEGHIAN I, CHARALAMBIDES M N, WANG Y, et al. Effect of the polymer interlayer on the high-velocity soft impact response of laminated glass plates [J]. International Journal of Impact Engineering, 2018, 120: 150–170. doi: 10.1016/j.ijimpeng.2018.06.002 -







 下载:
下载: