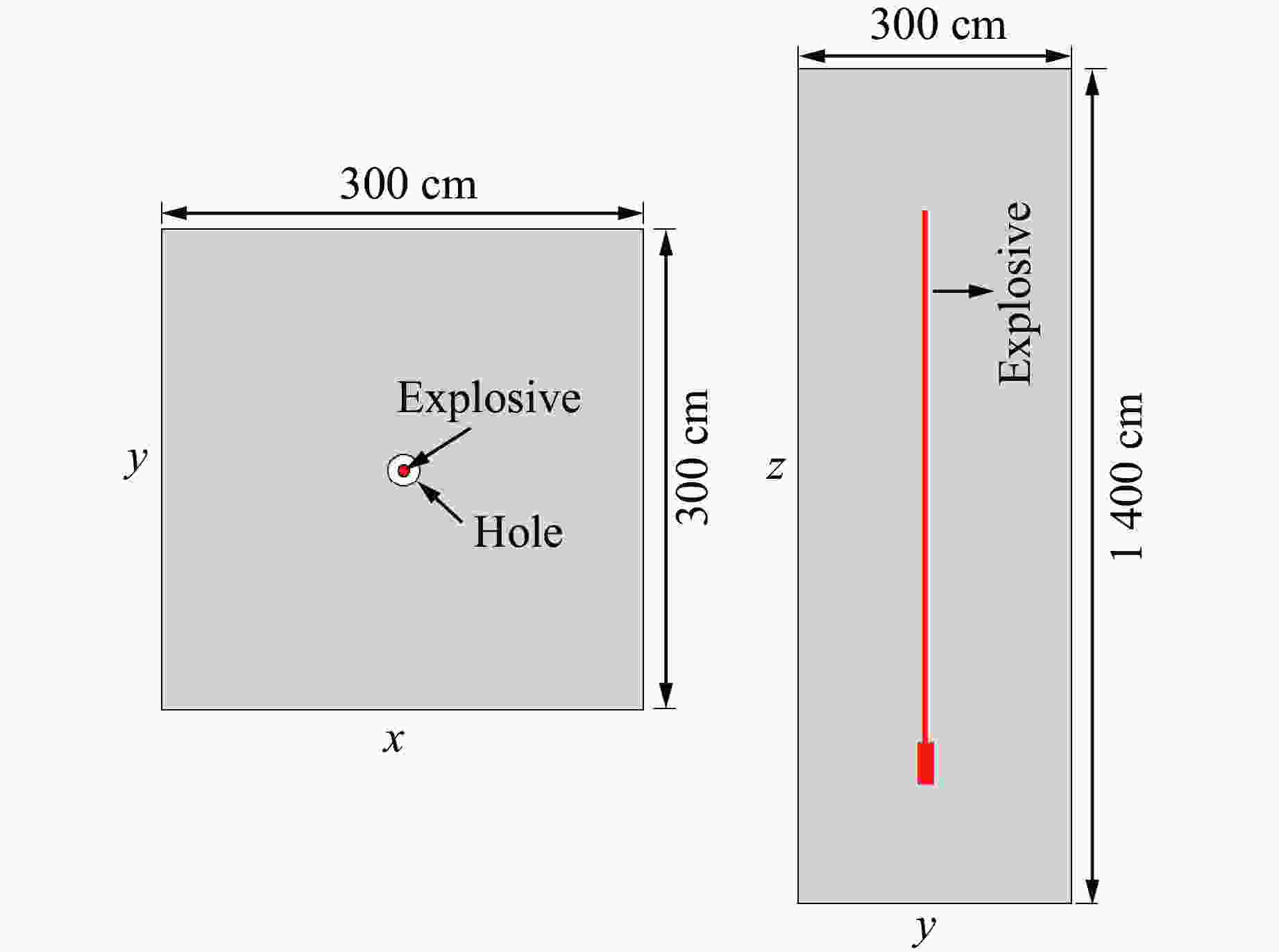
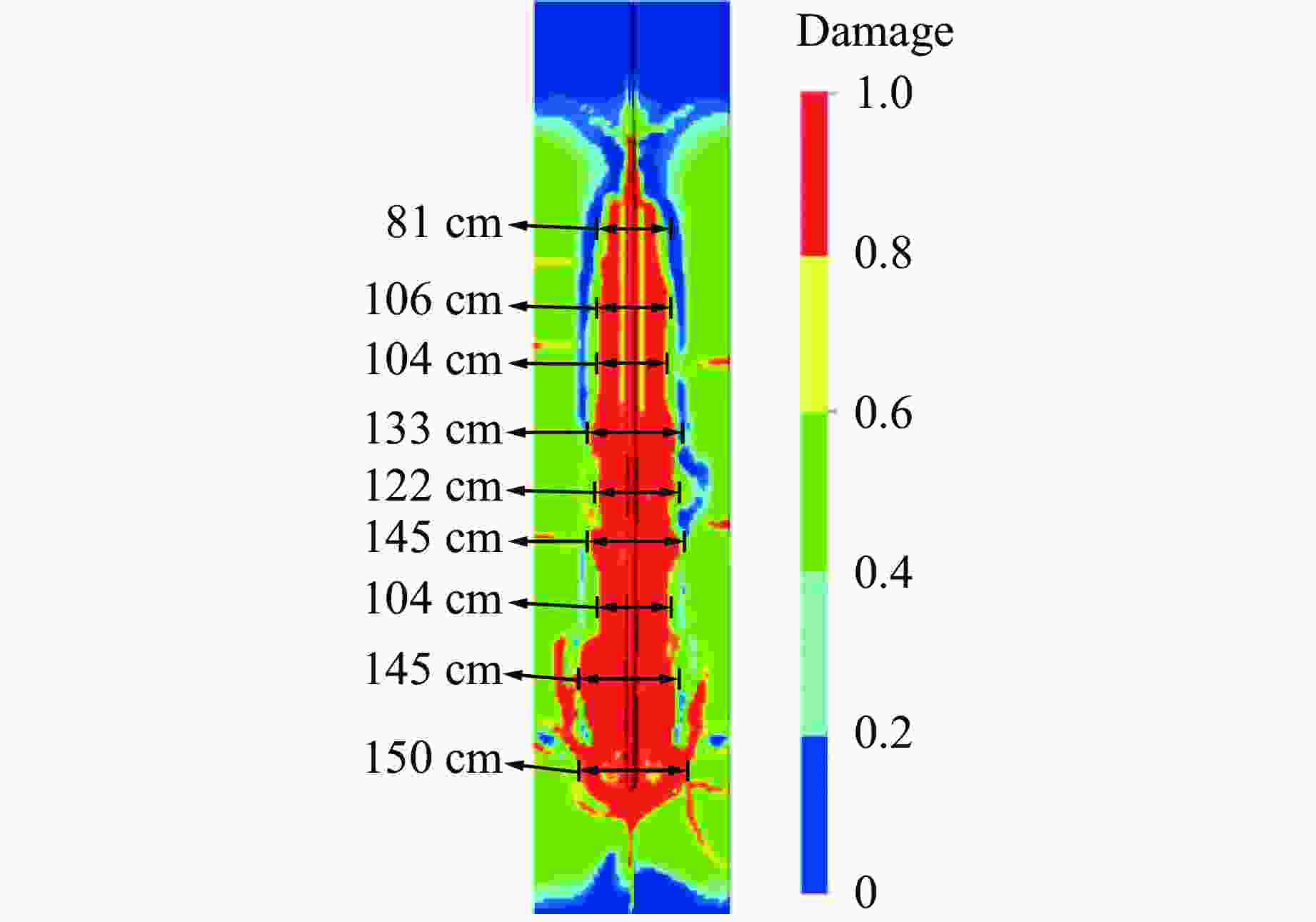
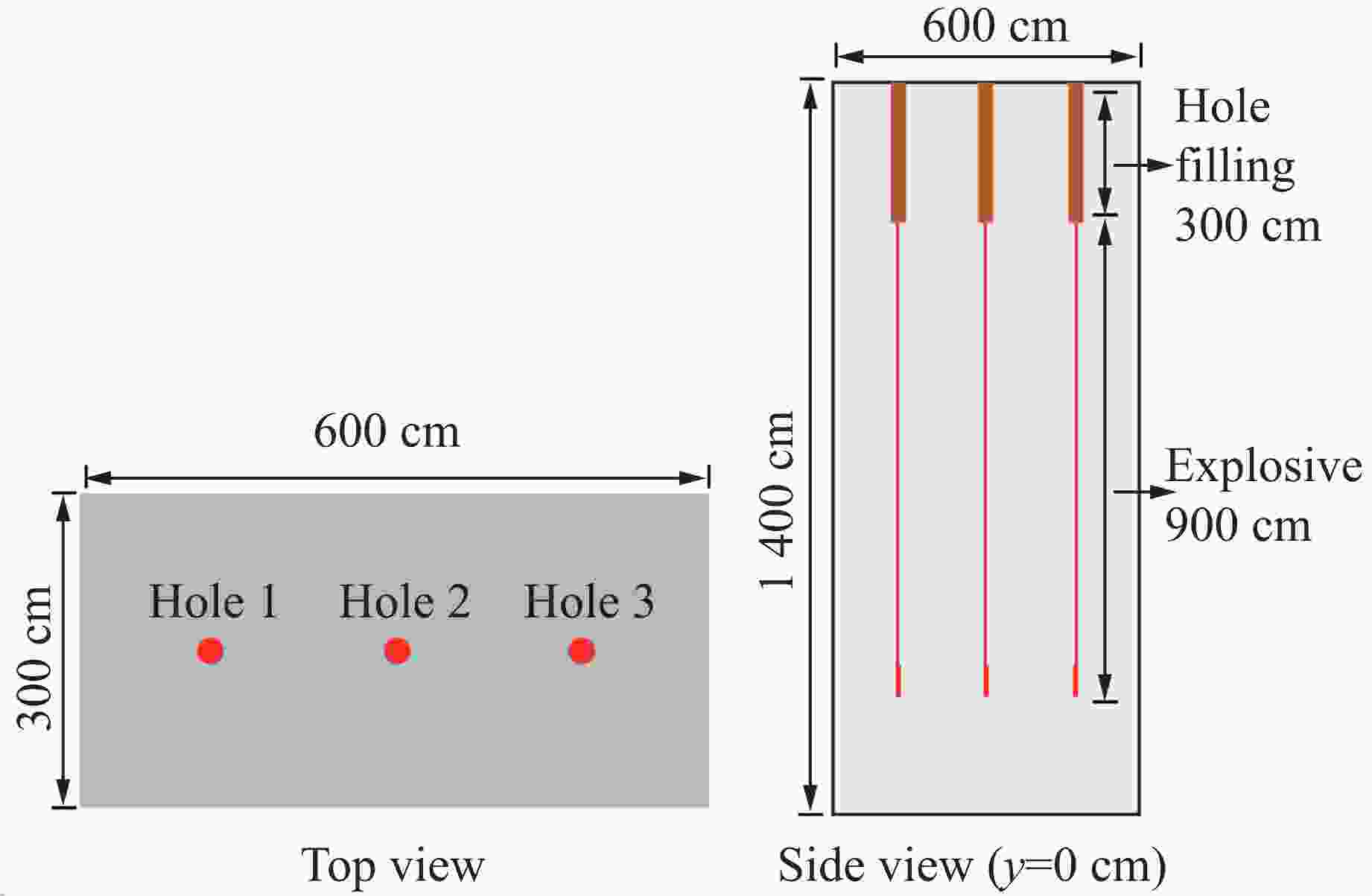
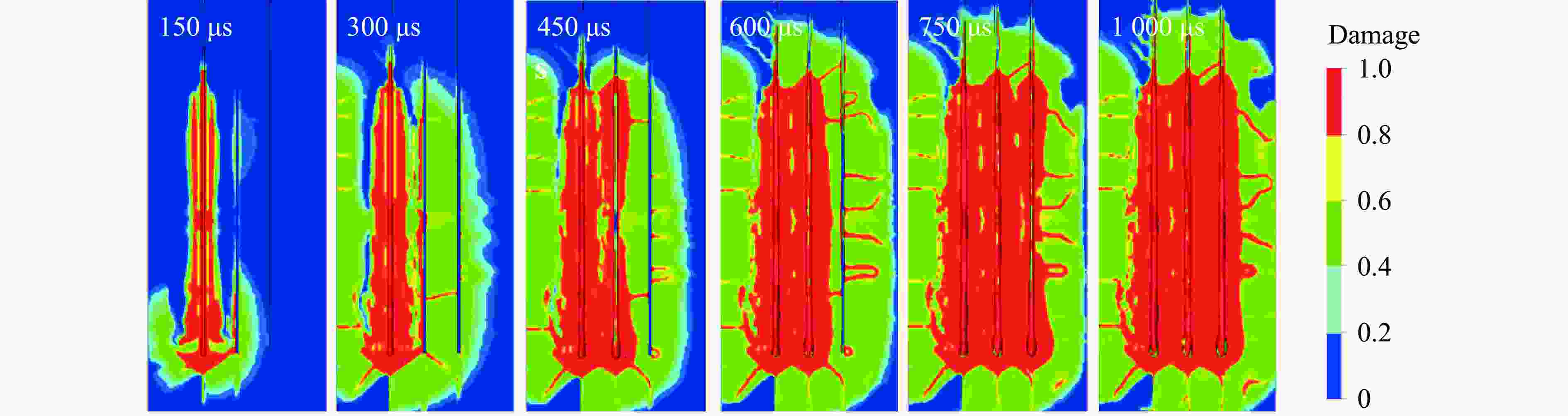
Optimization Study of Pre-Splitting Hole Spacing for Continuous Charging Based on RHT Constitutive Model
-
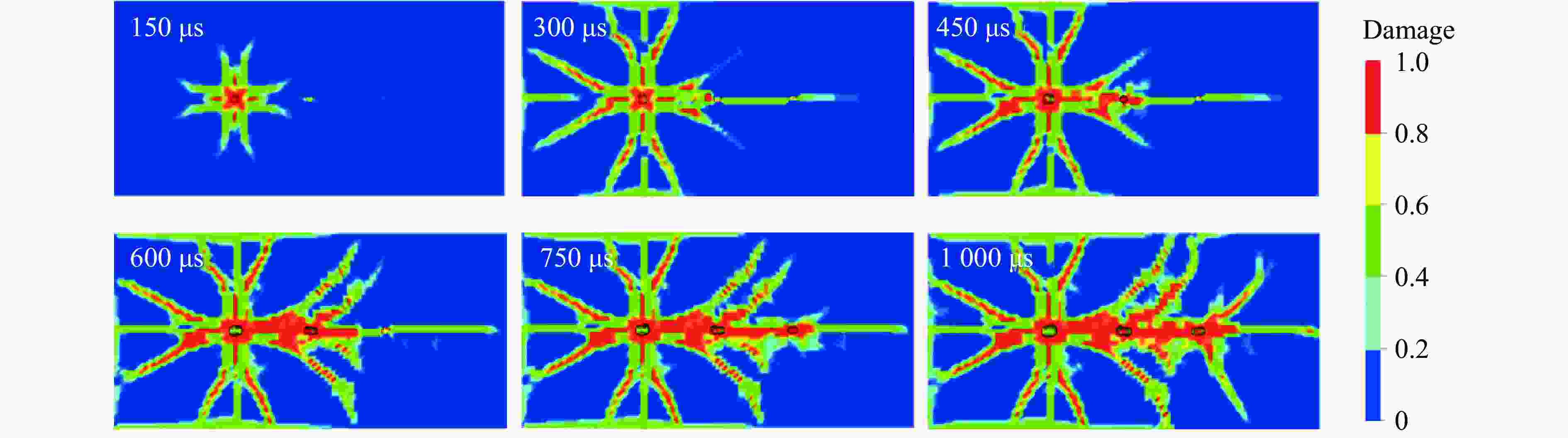
摘要: 为解决北衙金矿在使用预裂爆破技术时整体爆破效果不佳的问题，基于RHT损伤本构模型，利用ANSYS/LS-DYNA数值模拟软件，开展了不同孔距下预裂爆破的数值模拟研究。结果表明：当预裂孔炮孔间距为120 cm时，孔间裂纹存在较为明显的分叉，且裂纹扩展范围较大；当炮孔间距为130 cm时，裂纹向四周扩展的范围减小，且炮孔周围岩石的损伤程度明显降低；当炮孔间距增加至140 cm时，相邻预裂孔连线上的裂纹仅在局部连通，无法实现孔间贯穿。上述结果说明，130 cm的炮孔间距在降低预裂爆破自身对岩体的扰动与实现有效爆破成缝之间达到了平衡。基于数值模拟试验结果开展了现场试验，爆破效果良好。研究结果可为矿山的预裂爆破设计和施工提供参考。Abstract: In order to solve the problem of poor overall blasting effect when using pre-splitting blasting technology in Beiya gold mine, based on RHT damage constitutive model, numerical simulation research on pre-splitting blasting under different hole spacings was carried out by using ANSYS/LS-DYNA numerical simulation software. The results show that when the hole spacing of pre-splitting hole is set to 120 cm, the crack between holes has obvious bifurcation and the crack propagation range is large. When the hole spacing is set to 130 cm, the crack propagation range decreases within the surrounding area, and the rock damage around the blast hole is obviously reduced. When the hole spacing is further increased to 140 cm, it is found that the cracks on the connecting line of adjacent pre-splitting holes are only locally connected and cannot penetrate through holes. It shows that the 130 cm hole spacing has reached an ideal balance between reducing the disturbance of the pre-splitting blasting itself to the rock mass and achieving effective blasting. Based on the results of numerical simulation, the site test has achieved good blasting effect. The research results can provide reference for the design and construction of pre-splitting blasting in similar mines.
-
图 7 调整优化后的应力-应变曲线对比图
Figure 7. Comparison of stress-strain curves after adjustment and optimization
图 9 单孔爆破近区损伤结果（y=0）
Figure 9. Near-field damage results of single-hole blasting (y = 0)
图 11 炮孔间距为120 cm时预裂面的损伤情况
Figure 11. Pre-splitting surface damage at hole spacing of 120 cm
图 12 炮孔间距为120 cm时孔间裂纹的扩展情况
Figure 12. Inter-hole crack propagation at hole spacing of 120 cm
表 1 灰岩的静力学参数
Table 1. Limestone’s statics parameters
$ {\rho }_{0} $/(g∙cm−3) $ f\mathrm{_c} $/MPa $ f\mathrm{_t} $/MPa $ E $/GPa ν c0/(m·s−1) 2.68 51.95 2.62 5.08 0.28 3605 
下载: 导出CSV
表 2 不同围压下岩石的力学参数
Table 2. Mechanic parameters of rock under different confining pressures
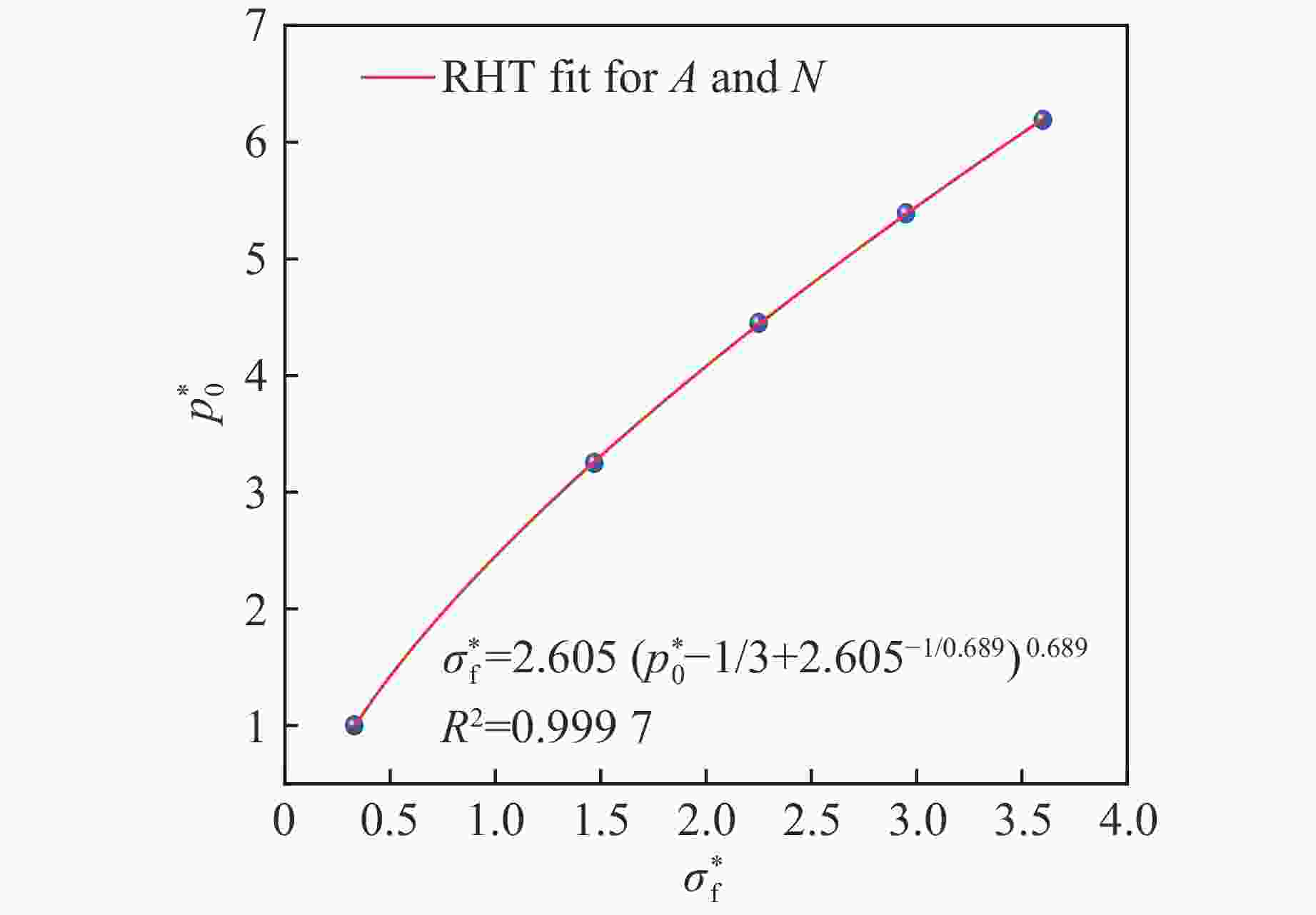
$ {\sigma }_{1} $/MPa $ {\sigma }_{2}/\mathrm{M}\mathrm{P}\mathrm{a} $ $ {\sigma }_{3} $/MPa $ {P}_{0}^{*} $ $ \sigma_{\mathrm{f}}^* $ 51.95 0 0 0.33 1.00 188.84 20 20 1.47 3.25 271.18 40 40 2.25 4.45 340.01 60 60 2.95 5.39 401.57 80 80 3.60 6.19
下载: 导出CSV
表 3 灰岩的RHT本构参数
Table 3. RHT constitutive parameters of limestone
$ f\mathrm{_c} $/MPa $ f_{\mathrm{\;t}}^{\mathrm{*}} $ D1 G $ \varepsilon_{\mathrm{p}}^{\mathrm{m}} $ $ {p}_{\mathrm{e}\mathrm{l}} $/MPa XI A N Q0 51.95 0.05 0.04 1.98 0.01 39.93 0.5 2.605 0.689 0.68 B $ \beta\mathrm{_c} $ $ \beta\mathrm{_t} $ B1 B0 $ n_{\mathrm{p}} $ $ g_{\mathrm{t}}^{\mathrm{*}} $ Af $ f_{\mathrm{s}}^{\mathrm{*}} $ T1/GPa 0.05 0.02 0.025 1.6 1.6 3 0.7 0.27 0.17 34.83 A1/GPa A2/GPa A3/GPa $ g_{\mathrm{c}}^{\mathrm{*}} $ Nf $ {p}_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}} $/MPa T2 34.83 55.73 30.3 0.8 0.63 0.06 0
下载: 导出CSV
表 4 2#岩石乳化炸药物理力学参数
Table 4. Physical and mechanical parameters of 2# rock emulsion explosive
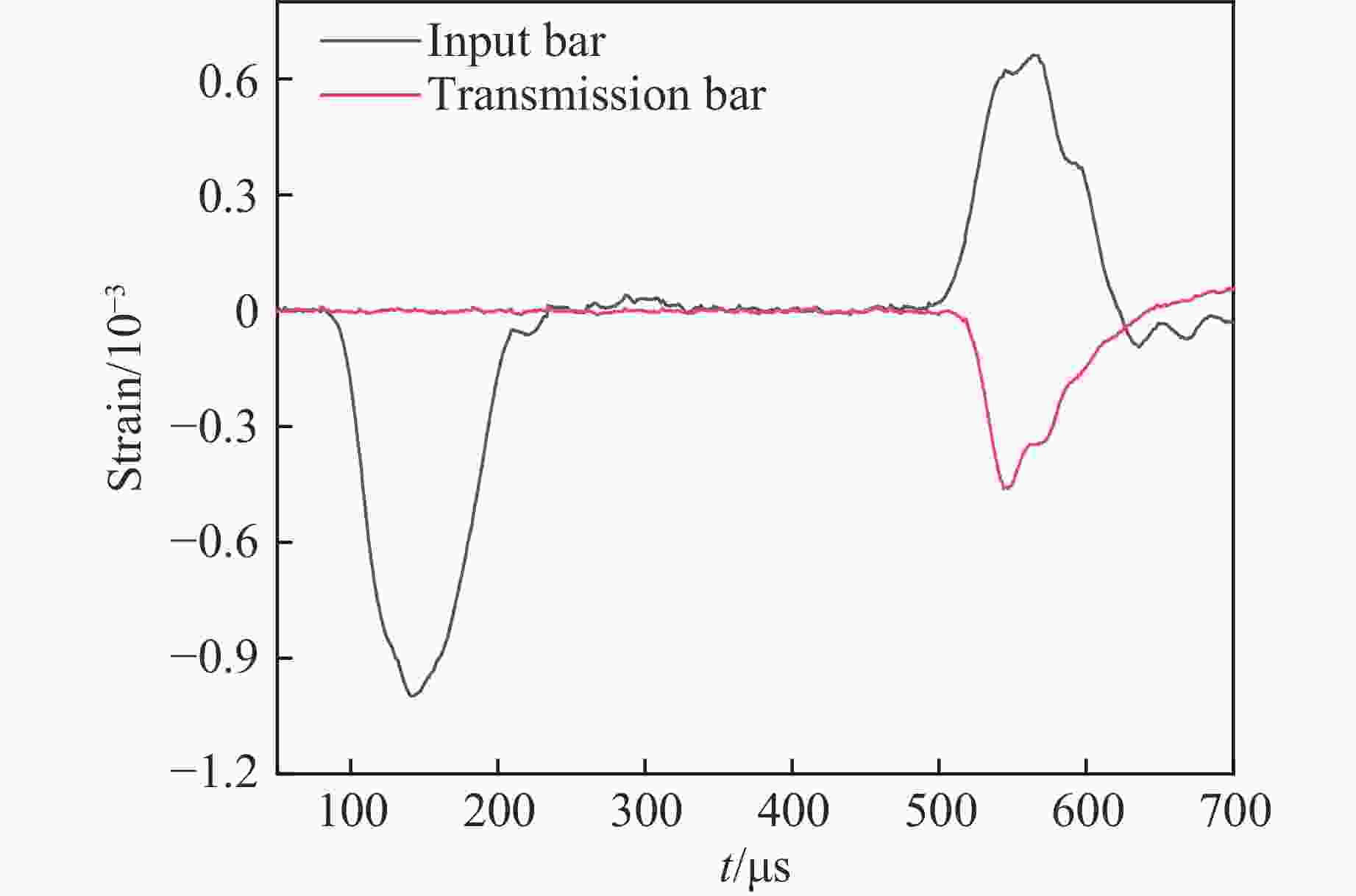
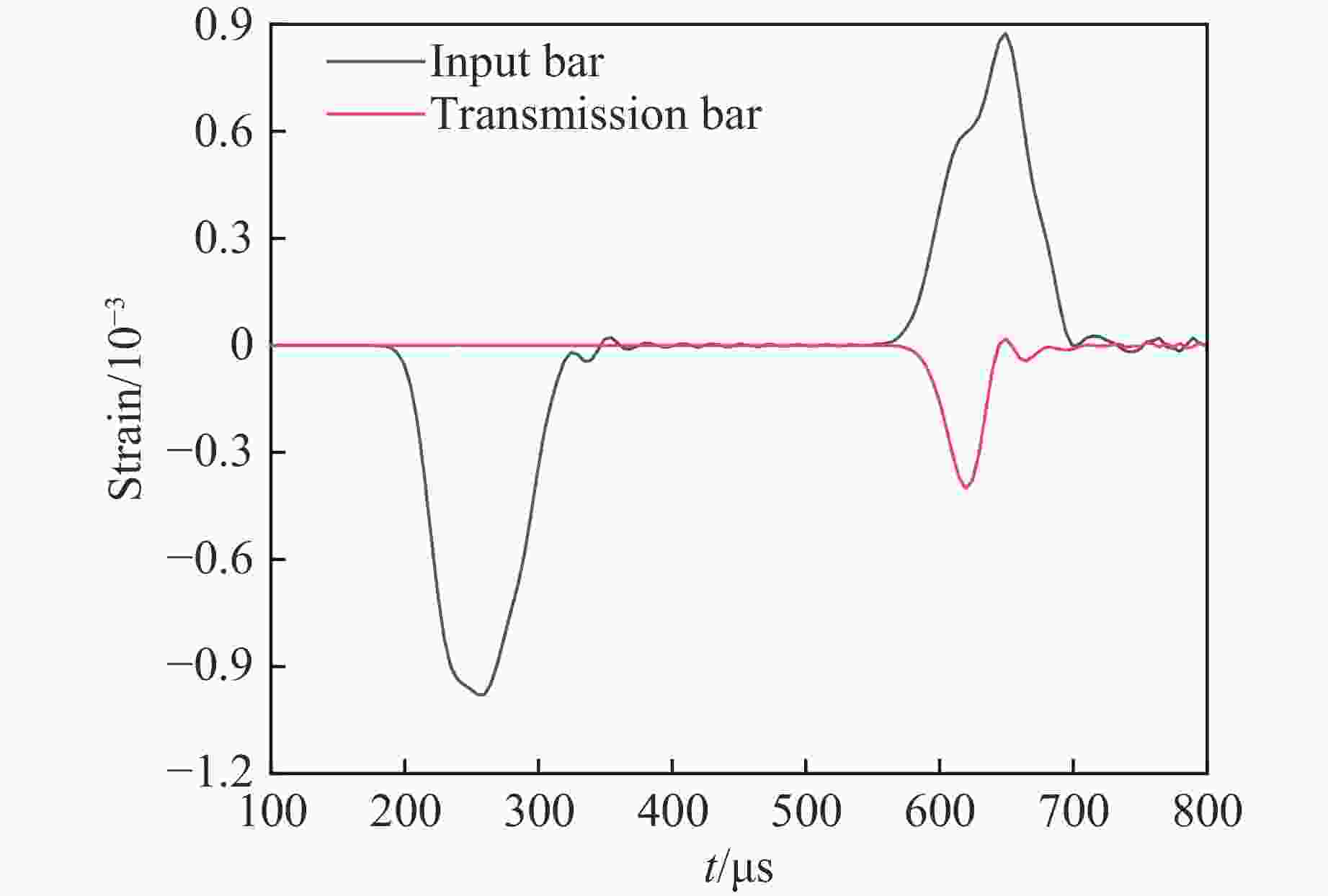
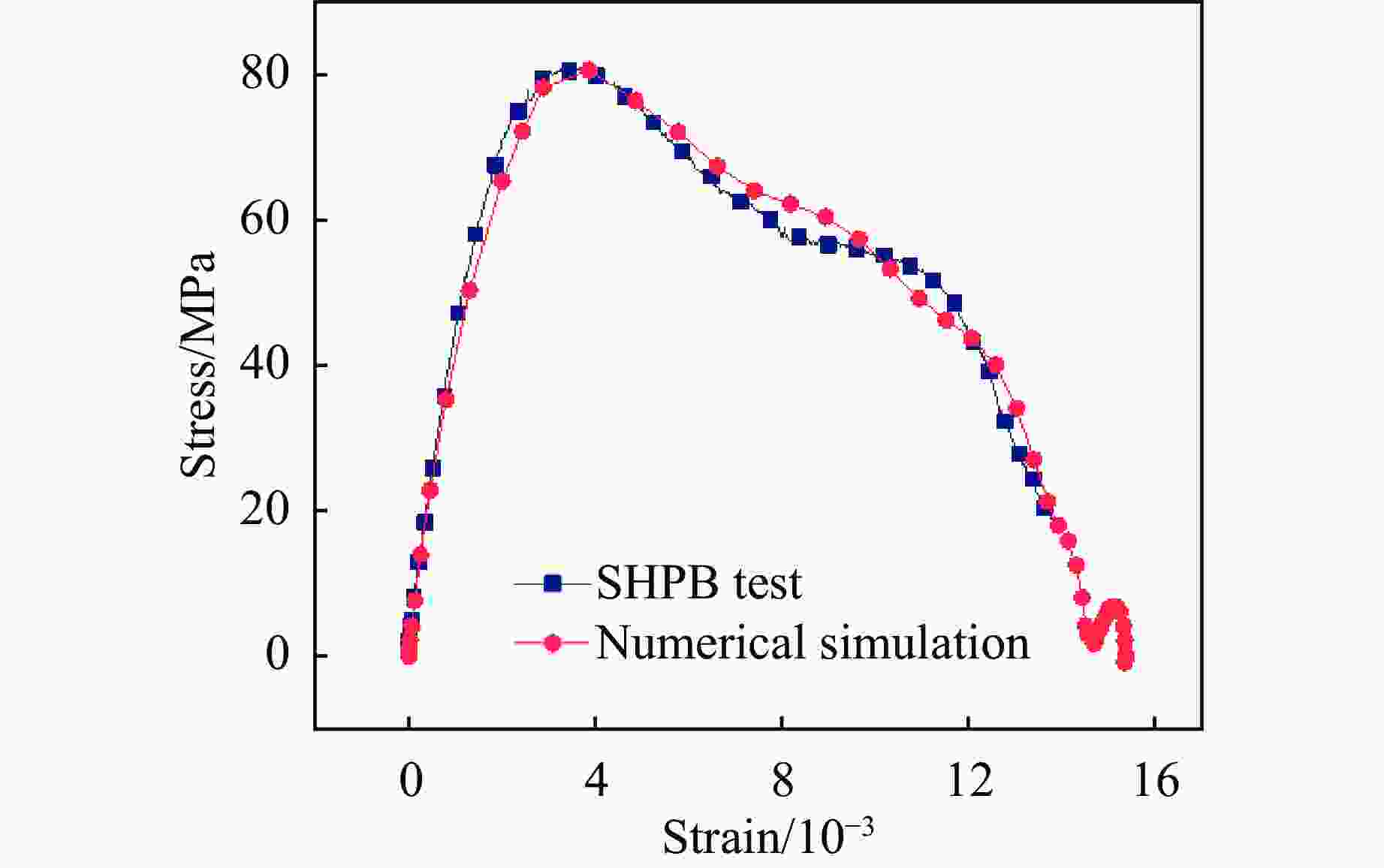
$ {\rho }_{0}/ $(g·cm−3) $ D/ $(m·s−1) $ p\mathrm{_J}/\text{GPa} $ $ A\mathrm{_{e_{ }}}/\text{GPa} $ $ B\mathrm{_e}/\text{GPa} $ $ {R}_{1} $ $ {R}_{2} $ $ \omega $ $ {e}_{0}/\text{GPa} $ 1.25 3200 9.53 276.2 8.44 5.2 2.1 0.57 3.87
下载: 导出CSV
表 5 预裂爆破的爆破参数
Table 5. The blasting parameters of pre-splitting blasting
d/mm Dhole/cm H/m L/m l/m 115 130 12 9 3
下载: 导出CSV
-
[1] 唐海, 李海波, 周青春, 等. 预裂爆破震动效应试验研究 [J]. 岩石力学与工程学报, 2010, 29(11): 2277–2284.TANG H, LI H B, ZHOU Q C, et al. Experimental study of vibration effect of presplit blasting [J]. Journal of Rock Mechanics and Engineering, 2010, 29(11): 2277–2284. [2] 许守信, 黄绍威, 李二宝, 等. 复杂破碎岩体矩形聚能药包预裂爆破试验研究 [J]. 金属矿山, 2021(11): 55–63. doi: 10.19614/j.cnki.jsks.202111008XU S X, HUANG S W, LI E B, et al. Experimental study on pre-splitting blasting of rectangular shaped charge in complex fractured rock mass [J]. Metal Mine, 2021(11): 55–63. doi: 10.19614/j.cnki.jsks.202111008 [3] ZHANG Z X, HOSSEINI S, MONJEZI M, et al. Extension of reliability information of z-numbers and fuzzy cognitive map: development of causality-weighted rock engineering system to predict and risk assessment of blast-induced rock size distribution [J]. International Journal of Rock Mechanics and Mining Sciences, 2024, 178: 105779. doi: 10.1016/j.ijrmms.2024.105779 [4] 王卫华, 刘洋, 张理维, 等. 基于RHT模型双孔同时爆破均质岩体损伤的数值模拟 [J]. 黄金科学技术, 2022, 30(3): 414–426. doi: 10.11872/j.issn.1005-2518.2022.03.130WANG W H, LIU Y, ZHANG L W, et al. Numerical simulation of homogeneous rock mass damage caused by two-hole simultaneous blasting based on RHT model [J]. Gold Science and Technology, 2022, 30(3): 414–426. doi: 10.11872/j.issn.1005-2518.2022.03.130 [5] 王子琛, 李祥龙, 王惠芬, 等. 基于正交设计模拟实验的预裂爆破参数优化方法研究 [J]. 有色金属工程, 2021, 11(5): 96–101. doi: 10.3969/j.issn.2095-1744.2021.05.015WANG Z C, LI X L, WANG H F, et al. Study on optimization method of pre-splitting blasting parameters based on orthogonal design simulation experiment [J]. Nonferrous Metals Engineering, 2021, 11(5): 96–101. doi: 10.3969/j.issn.2095-1744.2021.05.015 [6] MA J, LI X L, WANG J G, et al. Experimental study on vibration reduction technology of hole-by-hole presplitting blasting [J]. Geofluids, 2021, 2021(1): 5403969. doi: 10.1155/2021/5403969 [7] 陈啸林, 张智宇, 王凯, 等. 某露天矿山预裂爆破参数优选与试验研究 [J]. 高压物理学报, 2023, 37(6): 065301.CHEN X L, ZHANG Z Y, WANG K, et al. Optimization and experimental study of pre-splitting blasting parameters in a certain open-pit mine [J]. Chinese Journal of High Pressure Physics, 2023, 37(6): 0653011. [8] 李祥龙, 杨长辉, 王建国, 等. 基于模型试验的预裂孔爆破参数优选 [J]. 高压物理学报, 2022, 36(2): 025301. doi: 10.11858/gywlxb.20210830LI X L, YANG C H, WANG J G, et al. Parameter optimization of presplitting blasting based on model test [J]. Chinese Journal of High Pressure Physics, 2022, 36(2): 025301. doi: 10.11858/gywlxb.20210830 [9] 崔年生. 不耦合装药系数对预裂爆破效果影响的数值模拟研究 [J]. 矿业研究与开发, 2018, 38(4): 10–13. doi: 10.13827/j.cnki.kyyk.2018.04.003CUI N S. Numerical simulation of the influence of uncoupled charge coefficients on presplitting blasting effect [J]. Mining Research and Development, 2018, 38(4): 10–13. doi: 10.13827/j.cnki.kyyk.2018.04.003 [10] ZHANG C, CHEN Y H, WANG Y L, et al. Discrete element method simulation of granular materials considering particle breakage in geotechnical and mining engineering: a short review [J]. Green and Smart Mining Engineering, 2024, 1(2): 190–207. doi: 10.1016/j.gsme.2024.06.003 [11] ZUO T, LI X L, WANG J G, et al. Insights into natural tuff as a building material: effects of natural joints on fracture fractal characteristics and energy evolution of rocks under impact load [J]. Engineering Failure Analysis, 2024, 163: 108584. doi: 10.1016/J.ENGFAILANAL.2024.108584 [12] 张若棋, 丁育青, 汤文辉, 等. 混凝土HJC、RHT本构模型的失效强度参数 [J]. 高压物理学报, 2011, 25(1): 15–22. doi: 10.11858/gywlxb.2011.01.003ZHANG R Q, DING Y Q, TANG W H, et al. The failure strength parameters of HJC and RHT concrete constitutive models [J]. Chinese Journal of High Pressure Physics, 2011, 25(1): 15–22. doi: 10.11858/gywlxb.2011.01.003 [13] 黄永辉, 孙博, 张智宇, 等. 岩石RHT本构的爆破碎裂判定方法优化及验证 [J]. 北京理工大学学报, 2023, 43(6): 565–574. doi: 10.15918/j.tbit1001-0645.2022.157HUANG Y H, SUN B, ZHANG Z Y, et al. Optimization and verification of blasting fragmentation judgment method for RHT constitutive model of rock [J]. Transactions of Beijing Institute of Technology, 2023, 43(6): 565–574. doi: 10.15918/j.tbit1001-0645.2022.157 [14] 李洪超, 陈勇, 刘殿书, 等. 岩石RHT模型主要参数敏感性及确定方法研究 [J]. 北京理工大学学报, 2018, 38(8): 779–785. doi: 10.15918/j.tbit1001-0645.2018.08.002LI H C, CHEN Y, LIU D S, et al. Sensitivity analysis determination and optimization of rock RHT parameters [J]. Transactions of Beijing Institute of Technology, 2018, 38(8): 779–785. doi: 10.15918/j.tbit1001-0645.2018.08.002 [15] 杨宝俊. 弹性波理论 [M]. 北京: 科学出版社, 1990.YANG B J. Elastic wave theory [M]. Beijing: Science Press, 1990. [16] 王宇涛. 基于RHT本构的岩体爆破破碎模型研究 [D]. 北京: 中国矿业大学(北京), 2015.WANG Y T. The study of the broken model for rock mass blasting based on RHT constitutive equations [D]. Beijing: China University of Mining and Technology (Beijing), 2015. [17] THOMAS B. The RHT concrete model in LS-DYNA [C]//Proceedings of the 8th European LS-DYNA Users Conference. Strasbourg, 2011. [18] BROWN E T, HOEK E. Underground excavations in rock [M]. London: CRC Press, 1980. [19] DEHGHAN BANADAKI M M, MOHANTY B. Numerical simulation of stress wave induced fractures in rock [J]. International Journal of Impact Engineering, 2012, 40/41: 16–25. doi: 10.1016/j.ijimpeng.2011.08.010 [20] XIE L X, LU W B, ZHANG Q B, et al. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses [J]. Tunnelling and Underground Space Technology, 2017, 66: 19–33. doi: 10.1016/j.tust.2017.03.009 -
下载:
点击查看大图
图(15) / 表(5)
计量
- 文章访问数: 10
- HTML全文浏览量: 0
- PDF下载量: 0
