G54钢的动高压性能实验研究

王波; 裴红波; 李绪海; 高齐; 何雨; 陈咏龙; 桂毓林

doi:10.11858/gywlxb.20240833

G54钢的动高压性能实验研究

doi: 10.11858/gywlxb.20240833

王波^1,,
裴红波¹,
李绪海¹,
高齐²,
何雨^1,*, ,,
陈咏龙¹,
桂毓林¹

1.
中国工程物理研究院流体物理研究所, 四川绵阳　621999
2.
钢铁研究总院有限公司特殊钢研究院, 北京　100081

详细信息

作者简介:
王　波（1988－），男，博士，工程师，主要从事冲击动力学研究. E-mail：bowang_my@163.com

通讯作者:
何　雨（1987－），男，博士，高级工程师，主要从事冲击动力学研究. E-mail：hexiaoyu@mail.ustc.edu.cn

中图分类号: O346.4
计量
- 文章访问数: 51
- HTML全文浏览量: 18
- PDF下载量: 7
出版历程
- 收稿日期: 2024-06-25
- 修回日期: 2024-07-22
- 录用日期: 2024-08-19
- 网络出版日期: 2024-09-11

Experimental Study on Dynamic High Pressure Properties of G54 Steel

WANG Bo^1
,,
PEI Hongbo¹,
LI Xuhai¹,
GAO Qi²,
HE Yu^{1,*
, ,},
CHEN Yonglong¹,
GUI Yulin¹

1.
Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621999, Sichuan, China
2.
Institute for Special Steels, Central Iron and Steel Research Institute Co., Ltd., Beijing 100081, China

摘要

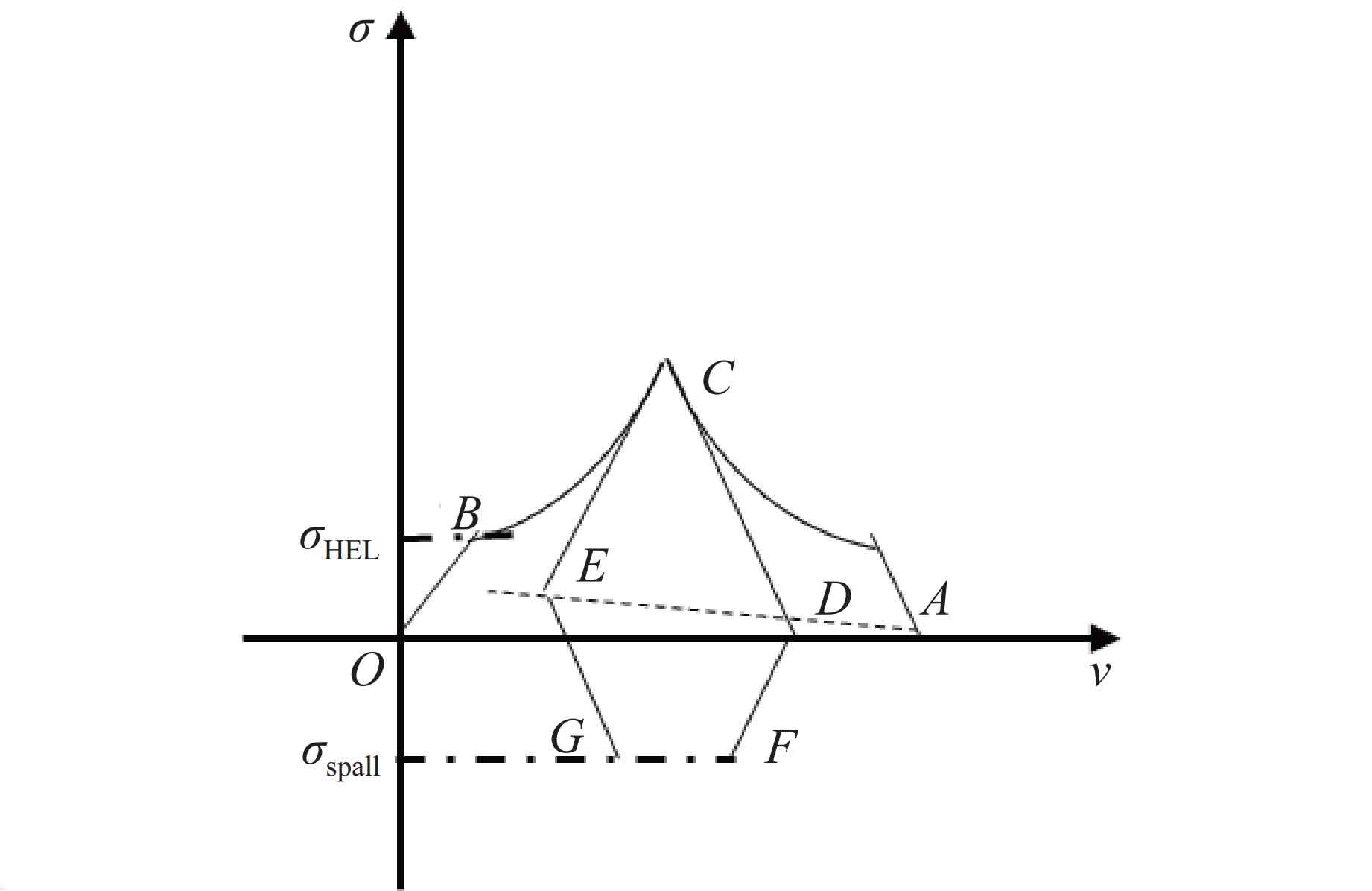
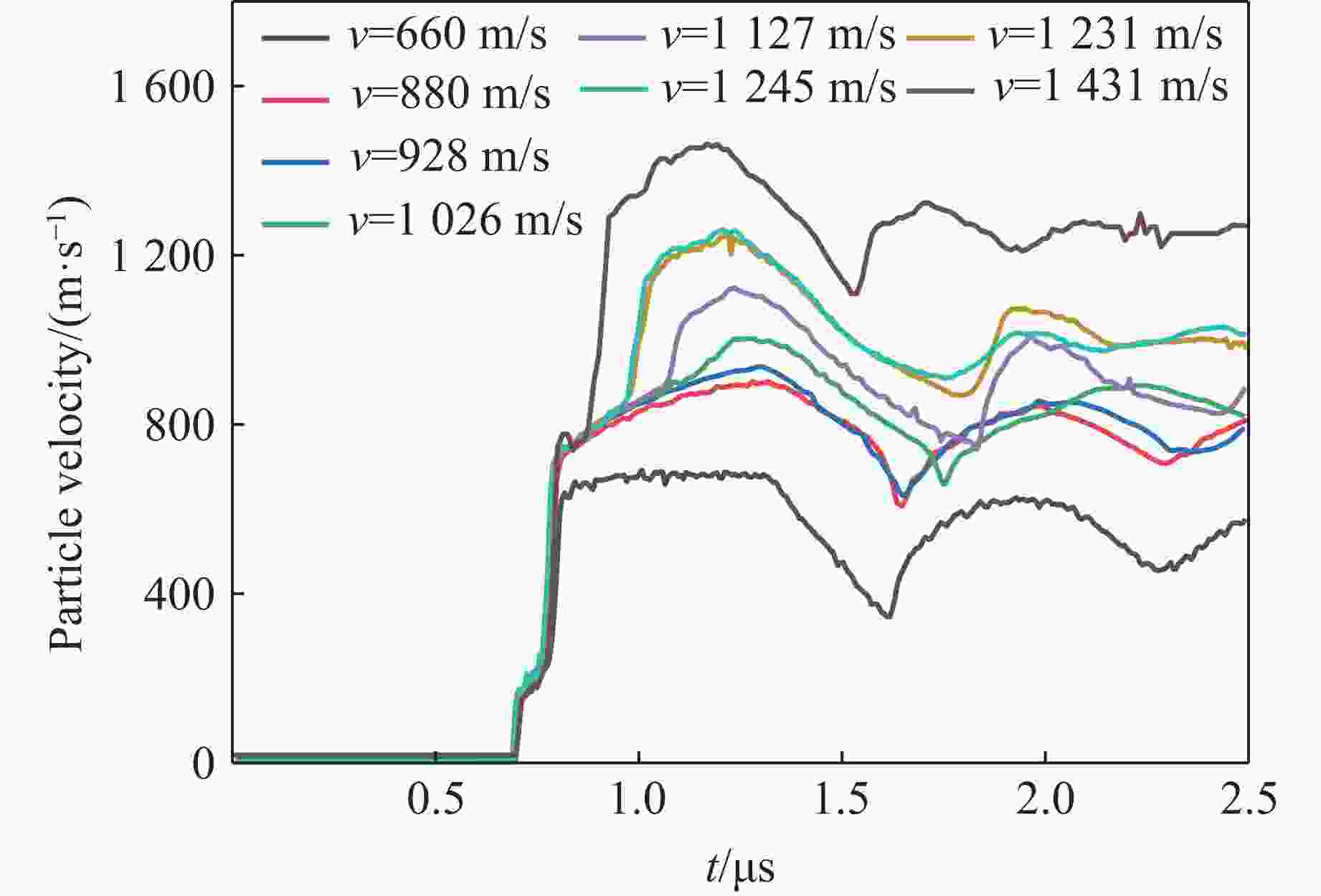
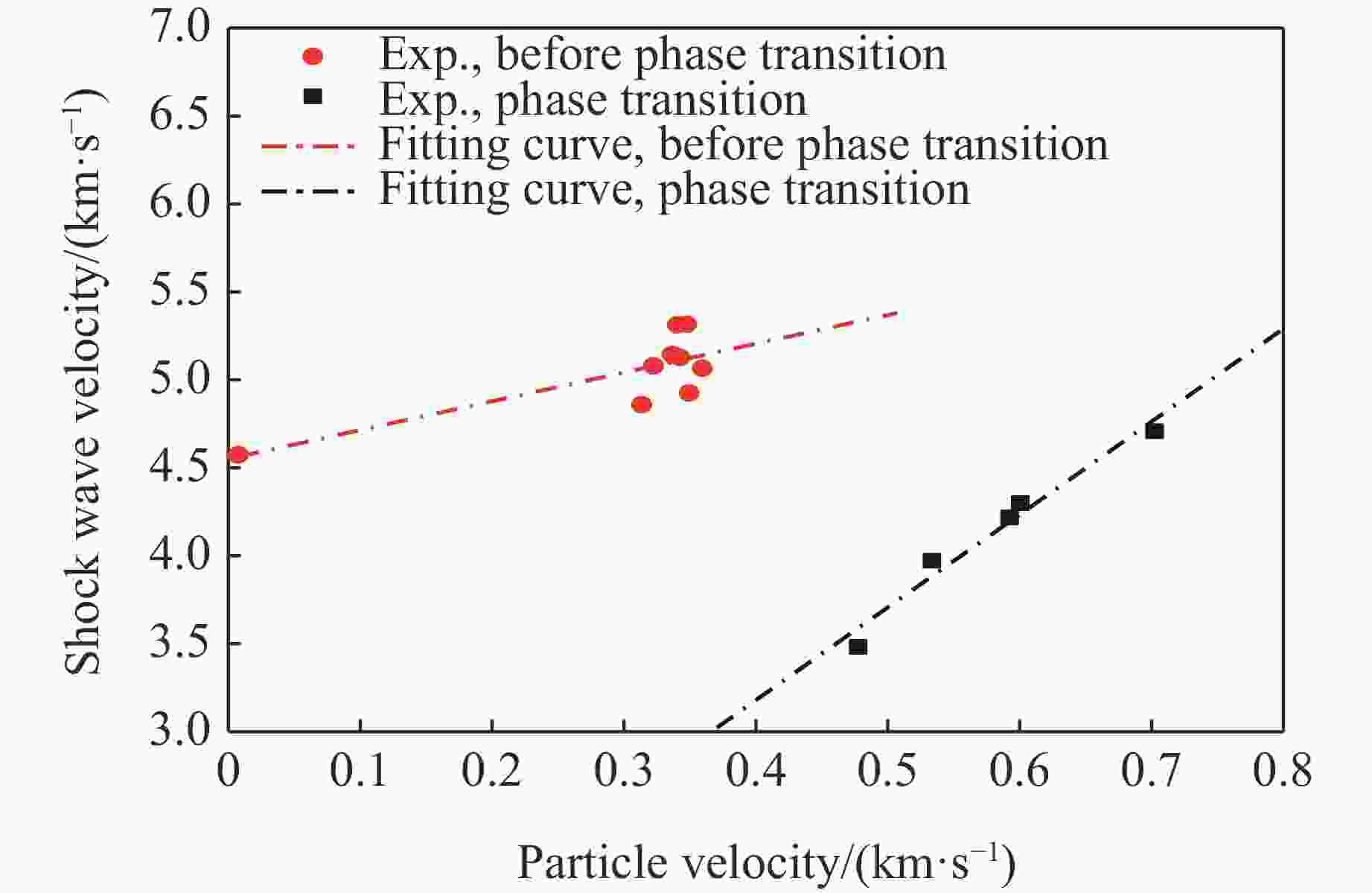
摘要: G54钢是我国自主研制的一种新型超高强度钢，具有较高的潜在应用价值。为了研究该材料的动高压性能，为应用推广提供数据支撑，采用火炮作为加载手段，开展了G54钢的飞片对称碰撞实验。实验飞片速度为600～1400 m/s，通过测量G54钢样品的背表面粒子速度-时间历史，获得了典型的冲击相变及层裂信号。通过对粒子速度进行分析，结合材料密度及声速测试结果，获得了冲击压力为13～23 GPa下G54钢的Hugoniot弹性极限、层裂强度、冲击波速度-粒子速度（D-u）关系以及冲击相变点等动高压性能参数。对实验样品进行回收及金相分析发现，随着飞片速度的增加，材料层裂面的损伤机制逐渐从微孔洞聚合主导的韧性断裂向绝热剪切主导的韧性断裂转变。
- G54钢 /
- 对称碰撞实验 /
- Hugoniot弹性极限 /
- 冲击波速度-粒子速度关系 /
- 层裂强度
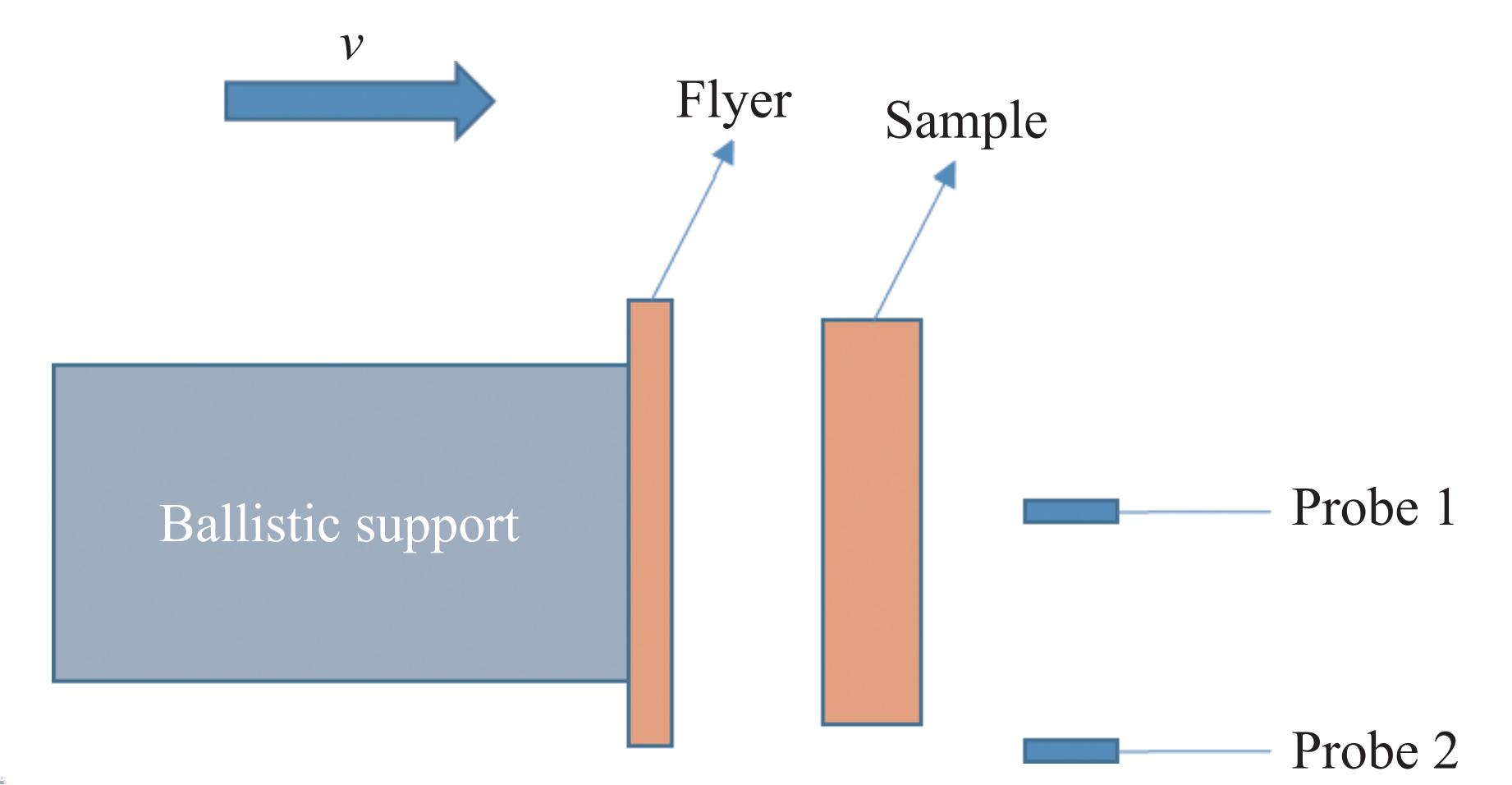
Abstract: G54 steel is a new type of ultra-high strength steel independently developed in China, which has strong potential application value. In order to study the dynamic high-pressure performance of the material and provide data support for its application and popularization, the flyer symmetric impact experiments of G54 steel were conducted by using artillery as loading means. The experimental flyer velocities ranged from 600 m/s to 1400 m/s. By measuring the velocity-time history of particles on the back surface of G54 steel samples, the typical impact transformation and spallation signals were obtained. By analyzing particle velocities, material density and sound velocity measurements, the Hugoniot elastic limit, spallation strength, shock wave velocity-particle velocity (D-u) relationship and impact transformation point of G54 steel under impact pressure of 13–23 GPa were obtained. The metallographic analysis results of the recovered sample show that the damage mechanism of the spallation surface changes from ductile fracture dominated by micropore polymerization to ductile fracture dominated by adiabatic shear with the increase of flyer velocity.
- G54 steel /
- symmetric collision experiment /
- Hugoniot elastic limit /
- shock wave velocity-particle velocity relation /
- spall strength

HTML全文

图 1 飞片撞击靶板发生破坏的过程

Figure 1. Failure process of target plate under flyer impact

下载: 全尺寸图片幻灯片

图 2 碰靶过程的σ-v曲线

Figure 2. σ-v curve for impact target process

下载: 全尺寸图片幻灯片

图 3 实验装置示意图

Figure 3. Schematic diagram of the experimental device

下载: 全尺寸图片幻灯片

图 4 实验装置实物

Figure 4. Photograph of the experimental device

下载: 全尺寸图片幻灯片

图 5 自由面粒子速度波形汇总

Figure 5. Summary for free surface particle velocity

下载: 全尺寸图片幻灯片

图 6 典型波形及物理量含义

Figure 6. Typical waveforms and meanings of physical quantities

下载: 全尺寸图片幻灯片

图 7 冲击波速度-粒子速度关系

Figure 7. Shock wave velocity versus particle velocity

下载: 全尺寸图片幻灯片

图 8 回收飞片及样品形貌

Figure 8. Morphology of the recovered flyer and samples

下载: 全尺寸图片幻灯片

图 9 回收样品的金相照片

Figure 9. Metallographic photograph of recovered sample

下载: 全尺寸图片幻灯片

表 1 常温常压下G54钢的材料参数

Table 1. Parameters of G54 steel at room temperature and pressure

$ \rho /(\mathrm{k}\mathrm{g}\cdot{\mathrm{m}}^{-3}) $	$ {C}_{\mathrm{L}0}/(\mathrm{k}\mathrm{m}\cdot{\mathrm{s}}^{-1}) $	$ {C}_{0}/(\mathrm{k}\mathrm{m}\cdot{\mathrm{s}}^{-1}) $	E/GPa	$ {C}_{\mathrm{T}0}/(\mathrm{k}\mathrm{m}\cdot{\mathrm{s}}^{-1}) $	$ \nu $
7 970	5.777	4.555	194.77	3.077	0.302

下载: 导出CSV

表 2 数据处理结果

Table 2. Results of data processing

No.	v/($ \mathrm{m}\cdot{\mathrm{s}}^{-1}) $	$ {\sigma }_{\mathrm{H}\mathrm{E}\mathrm{L}}/ \mathrm{G}\mathrm{P}\mathrm{a}$	$ {\sigma }_{\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e}}/\mathrm{G}\mathrm{P}\mathrm{a} $	$ {\sigma }_{\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{l}\mathrm{l}}/\mathrm{G}\mathrm{P}\mathrm{a} $	$ D/ (\mathrm{k}\mathrm{m}\cdot{\mathrm{s}}^{-1})$	$ u/(\mathrm{k}\mathrm{m}\cdot{\mathrm{s}}^{-1}) $	$ {D}_{\mathrm{P}\mathrm{T}}/(\mathrm{k}\mathrm{m}\cdot{\mathrm{s}}^{-1}) $	$ u_{\mathrm{p}2}/ (\mathrm{k}\mathrm{m}\cdot{\mathrm{s}}^{-1})$
1	660	3.147 5		5.824 7	4.820	0.306
2	880	3.058 6		5.067 9	5.041	0.315
3	928	3.357 4		6.540 7	5.088	0.335
4	1 026	3.339 8	13.50	7.394 6	4.886	0.342	3.447	0.474
5	1 127	3.591 1	14.55	8.198 5	5.277	0.340	3.938	0.530
6	1 231	3.443 5	14.22	8.175 8	5.274	0.333	4.182	0.589
7	1 245	3.374 9	13.79	6.075 5	5.106	0.329	4.264	0.597
8	1 431	3.155 5	14.54	6.266 5	5.028	0.352	4.673	0.699

下载: 导出CSV

参考文献(12)

[1]	李先雨. M54钢的静动态力学行为及毁伤效应研究 [D]. 北京: 北京理工大学, 2022: 1−17. LI X Y. Investigation on static and dynamic mechanical behaviors and damage effect of the M54 steel [D]. Beijing: Beijing Institute of Technology, 2022: 1−17.
[2]	秦玉荣, 苏杰, 杨卓越, 等. 三种超高强度钢的动态力学性能 [J]. 金属热处理, 2014, 39(12): 83–86. QIN Y R, SU J, YANG Z Y, et al. Dynamic mechanical properties of three kinds of ultrahigh strength steel [J]. Heat Treatment of Metals, 2014, 39(12): 83–86.
[3]	冯九胜. 四类高强钢的冲击韧性和平面应变断裂韧性研究 [J]. 中国材料进展, 2018, 37(4): 313–316. doi: 10.7502/j.issn.1674-3962.2018.04.10 FENG J S. Study on impact toughness and plane strain fracture toughness of four kinds of high-strength steels [J]. Materials China, 2018, 37(4): 313–316. doi: 10.7502/j.issn.1674-3962.2018.04.10
[4]	谭华. 实验冲击波物理 [M]. 北京: 国防工业出版社, 2018. TAN H. Experimental shock wave physics [M]. Beijing: National Defense Industry Press, 2018.
[5]	谭叶, 俞宇颖, 戴诚达, 等. 反向碰撞法测量Bi的低压Hugoniot数据 [J]. 物理学报, 2011, 60(10): 106401. doi: 10.7498/aps.60.106401 TAN Y, YU Y Y, DAI C D, et al. Measurement of low-pressure Hugoniot data for bismuth with reverse-impact geometry [J]. Acta Physica Sinica, 2011, 60(10): 106401. doi: 10.7498/aps.60.106401
[6]	董石, 孟川民, 肖元陆, 等. 反应气体驱动二级轻气炮技术的初步研究 [J]. 高压物理学报, 2017, 31(2): 182–186. doi: 10.11858/gywlxb.2017.02.011 DONG S, MENG C M, XIAO Y L, et al. Preliminary study of two-stage light gas gun using reactive gas as driving energy [J]. Chinese Journal of High Pressure Physics, 2017, 31(2): 182–186. doi: 10.11858/gywlxb.2017.02.011
[7]	曹落霞, 胡海波, 陈永涛, 等. 磁驱动飞片加载下纯铁的冲击相变和层裂特性 [J]. 高压物理学报, 2015, 29(4): 248–254. doi: 10.11858/gywlxb.2015.04.002 CAO L X, HU H B, CHEN Y T, et al. Shock-induced phase transition and spallation in pure iron under magnetically driven flyer plate loading [J]. Chinese Journal of High Pressure Physics, 2015, 29(4): 248–254. doi: 10.11858/gywlxb.2015.04.002
[8]	张万甲, 杨中正. 93钨合金断裂特性研究 [J]. 高压物理学报, 1995, 9(4): 279–288. doi: 10.11858/gywlxb.1995.04.007 ZHANG W J, YANG Z Z. Studies on the fracture behaviour for 93 tungsten alloy [J]. Chinese Journal of High Pressure Physics, 1995, 9(4): 279–288. doi: 10.11858/gywlxb.1995.04.007
[9]	KINSLOW R. High-velocity impact phenomena [M]. New York: Academic Press, 1970.
[10]	裴晓阳, 彭辉, 贺红亮, 等. 延性金属层裂自由面速度曲线物理涵义解读 [J]. 物理学报, 2015, 64(3): 034601. doi: 10.7498/aps.64.034601 PEI X Y, PENG H, HE H L, et al. Discussion on the physical meaning of free surface velocity curve in ductile spallation [J]. Acta Physica Sinica, 2015, 64(3): 034601. doi: 10.7498/aps.64.034601
[11]	桂毓林, 王彦平, 刘仓理, 等. 无钴合金钢的冲击响应实验研究 [J]. 高压物理学报, 2005, 19(2): 127–131. doi: 10.3969/j.issn.1000-5773.2005.02.005 GUI Y L, WANG Y P, LIU C L, et al. An experimental study on shock response of no-Co steel [J]. Chinese Journal of High Pressure Physics, 2005, 19(2): 127–131. doi: 10.3969/j.issn.1000-5773.2005.02.005
[12]	桂毓林, 刘仓理, 王彦平, 等. AF1410钢的层裂断裂特性研究 [J]. 高压物理学报, 2006, 20(1): 34–38. doi: 10.3969/j.issn.1000-5773.2006.01.008 GUI Y L, LIU C L, WANG Y P, et al. Spall fracture properties of AF1410 steel [J]. Chinese Journal of High Pressure Physics, 2006, 20(1): 34–38. doi: 10.3969/j.issn.1000-5773.2006.01.008