弹体侵彻混凝土的优化模型及可视化仿真研究

苏永超; 宁建国; 许香照

doi:10.11858/gywlxb.20240811

弹体侵彻混凝土的优化模型及可视化仿真研究

doi: 10.11858/gywlxb.20240811

北京理工大学爆炸科学与安全防护全国重点实验室, 北京　100081

基金项目: 国家自然科学基金（12372350）

详细信息

作者简介:
苏永超（1999－），男，硕士研究生，主要从事侵彻力学及可视化研究. E-mail：s15802440892@163.com

通讯作者:
许香照（1989－），男，博士，特别副研究员，主要从事冲击动力学研究. E-mail：xzxu@bit.edu.cn

中图分类号: O346.5; O521.9
计量
- 文章访问数: 319
- HTML全文浏览量: 80
- PDF下载量: 40
出版历程
- 收稿日期: 2024-05-13
- 修回日期: 2024-05-31
- 录用日期: 2024-09-18
- 网络出版日期: 2024-12-02
- 刊出日期: 2025-04-03

Optimization Model and Visualization Simulation of Projectile Penetration into Concrete

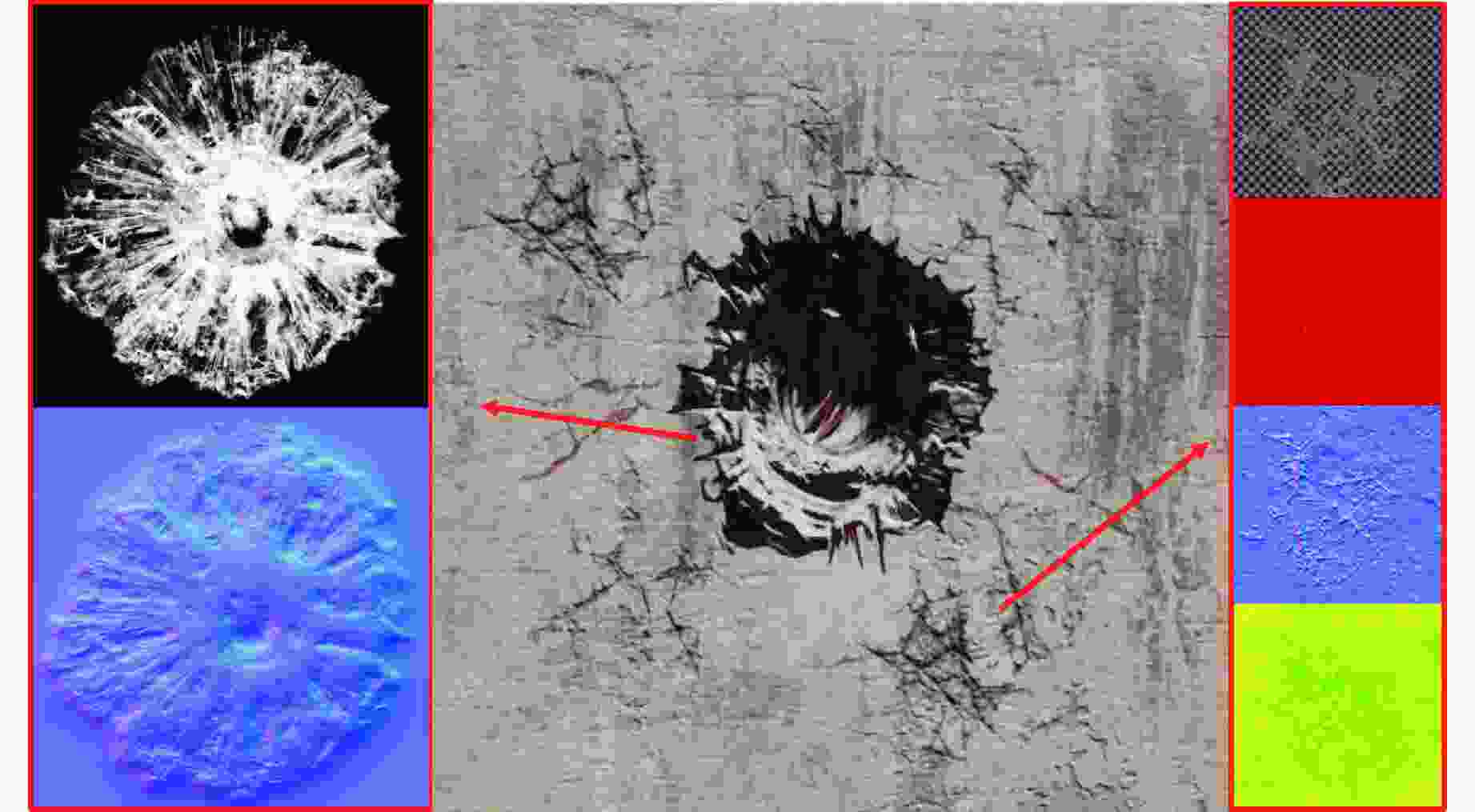
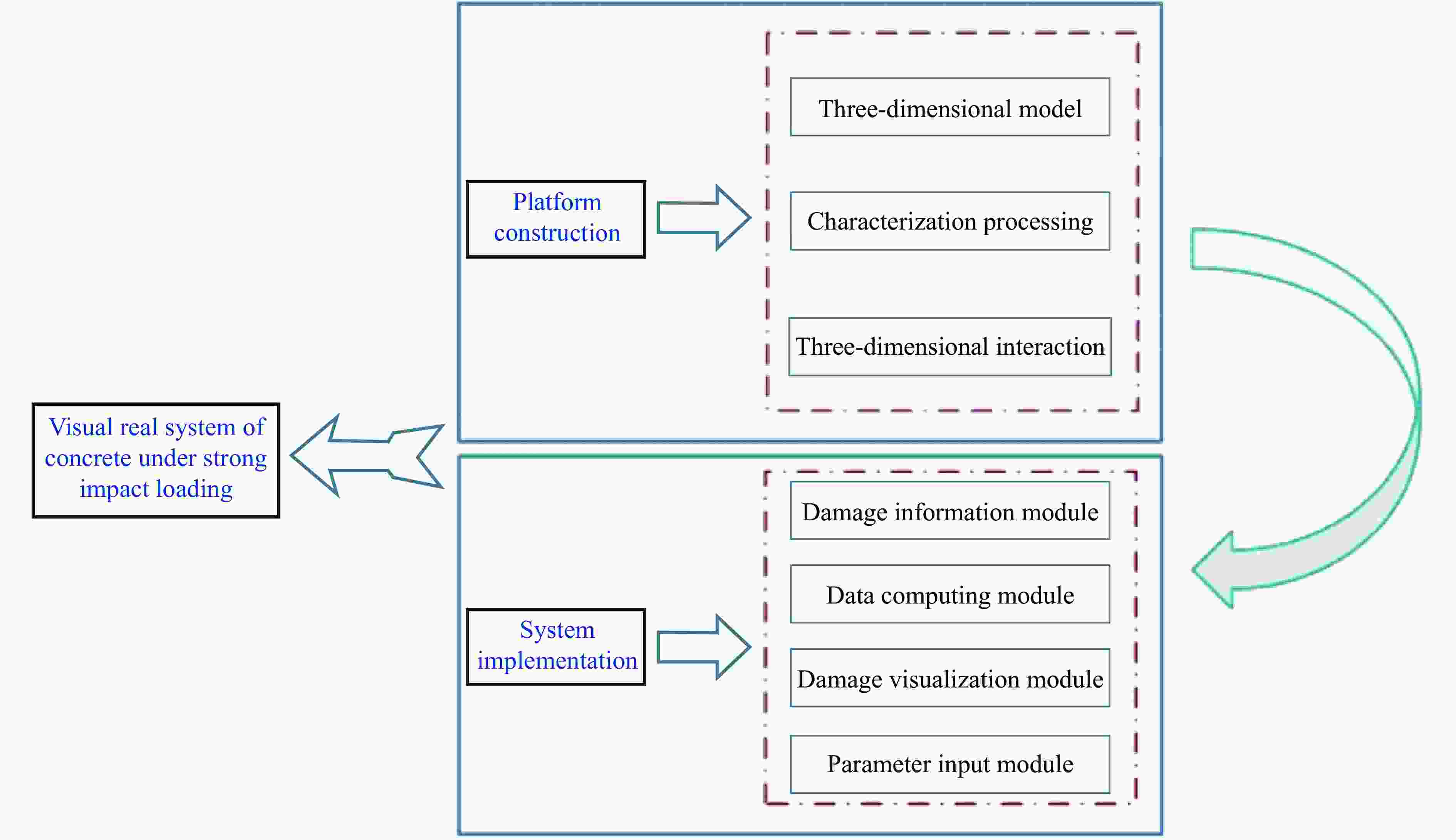
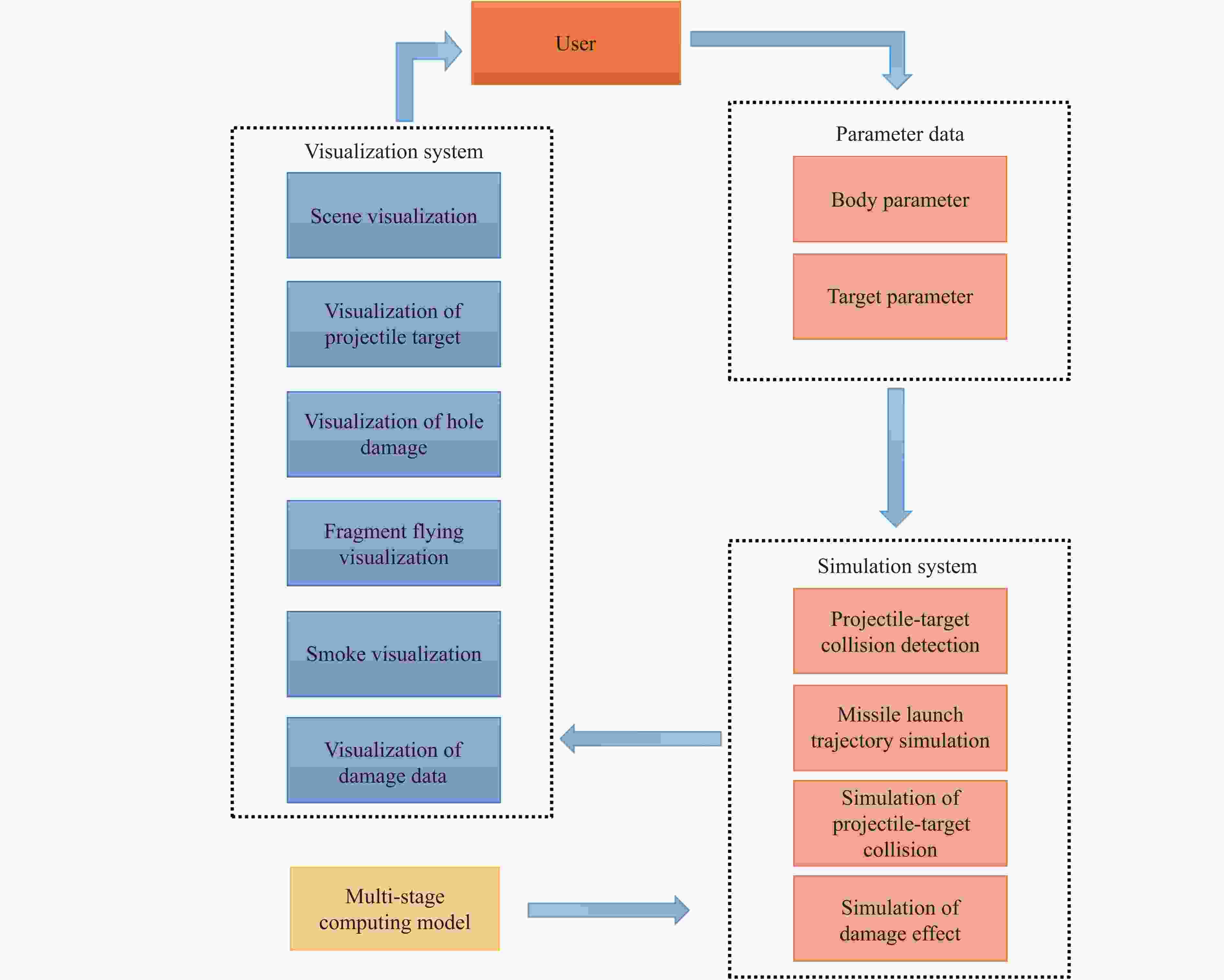
State Key Laboratory of Explosion Science and Safety Protection, Beijing Institute of Technology, Beijing 100081, China

摘要

摘要: 利用可视化仿真技术研究弹体侵彻混凝土的毁伤机理和靶板响应是爆炸冲击领域的重要课题。混凝土作为常见的建筑材料，在遭受爆炸冲击或高速弹体侵彻时，其毁伤行为复杂多变。介绍了一种理论研究与可视化技术相结合的可视化仿真方法。基于空腔膨胀理论建立了优化的侵彻计算模型，可以预测弹体侵彻混凝土的侵彻深度特征。利用可视化物理引擎，对弹体运动轨迹、开坑孔径、靶板损伤、碎石飞溅等进行了细致的表征处理和仿真，增强了场景的真实性和可靠性。开发的可视化仿真系统不仅能够从多角度观察弹体侵彻混凝土的过程，而且能够高效、准确地分析和预测弹体侵彻混凝土靶的损伤行为和动力响应，在建筑工程设计和安全评估中具有重要的应用前景，为理解和探索混凝土侵彻机理提供了新的视角。
- 弹体侵彻 /
- 混凝土 /
- 可视化仿真 /
- 物理引擎
Abstract: Using visual simulation technology to investigate the damage mechanism and target response of projectile penetration into concrete is an important research topic in the field of explosive impact. Concrete, as a common building material, has complex and varied damage behavior when subjected to explosive impact or high-speed projectile penetration. Herein, a visual simulation method is introduced, which is based on the combination of theoretical research and visualization technology. An optimized model of penetration calculation is established based on the theory of cavity expansion, which can predict the characteristics of the penetration depth of concrete penetrated by the projectile. Using a visualization physics engine, the trajectory of the projectile, the aperture of the open pit, the damage of the target slab, and the debris splash are carefully characterized and simulated, which enhances to the realism and reliability of the scene. The developed visual simulation system can not only observe the process of projectile penetration into concrete from multiple perspectives, but also efficiently and accurately analyze and predict the damage behavior and dynamic response of projectile penetration into concrete targets. It has important application prospects in the design and safety assessment of construction projects, providing a novel perspectives for understanding and exploring the mechanism of concrete penetration.
- projectile penetration /
- concrete /
- visual simulation /
- physics engine

HTML全文

图 1 13.5～36.2 MPa评价指标

Figure 1. 13.5–36.2 MPa regression evaluation indicator

下载: 全尺寸图片幻灯片

图 2 51.0～62.8 MPa评价指标

Figure 2. 51.0–62.8 MPa regression evaluation indicator

下载: 全尺寸图片幻灯片

图 3 优化模型预测结果的误差对比

Figure 3. Comparison of errors in the prediction results of the optimisation model

下载: 全尺寸图片幻灯片

图 4 孔洞与裂缝纹理

Figure 4. Hole and crack texture

下载: 全尺寸图片幻灯片

图 5 孔洞计算函数

Figure 5. Hole calculation function

下载: 全尺寸图片幻灯片

图 6 碎石材质纹理

Figure 6. Gravel material texture

下载: 全尺寸图片幻灯片

图 7 烟雾材质纹理

Figure 7. Smoke material texture

下载: 全尺寸图片幻灯片

图 8 毁伤效果

Figure 8. Destruction effect

下载: 全尺寸图片幻灯片

图 9 可视化系统结构

Figure 9. Structure of the visualization system

下载: 全尺寸图片幻灯片

图 10 仿真模块之间的关系

Figure 10. Relationship of simulation modules

下载: 全尺寸图片幻灯片

图 11 弹体参数输入

Figure 11. Input of projectile parameters

下载: 全尺寸图片幻灯片

图 12 靶体参数输入

Figure 12. Input of target parameters

下载: 全尺寸图片幻灯片

图 13 数据传递接收

Figure 13. Data transmission reception

下载: 全尺寸图片幻灯片

图 14 数据对比

Figure 14. Comparison of data

下载: 全尺寸图片幻灯片

图 15 侵彻过程对比

Figure 15. Comparison of penetration processes

下载: 全尺寸图片幻灯片

图 16 毁伤对比

Figure 16. Comparison of destruction

下载: 全尺寸图片幻灯片

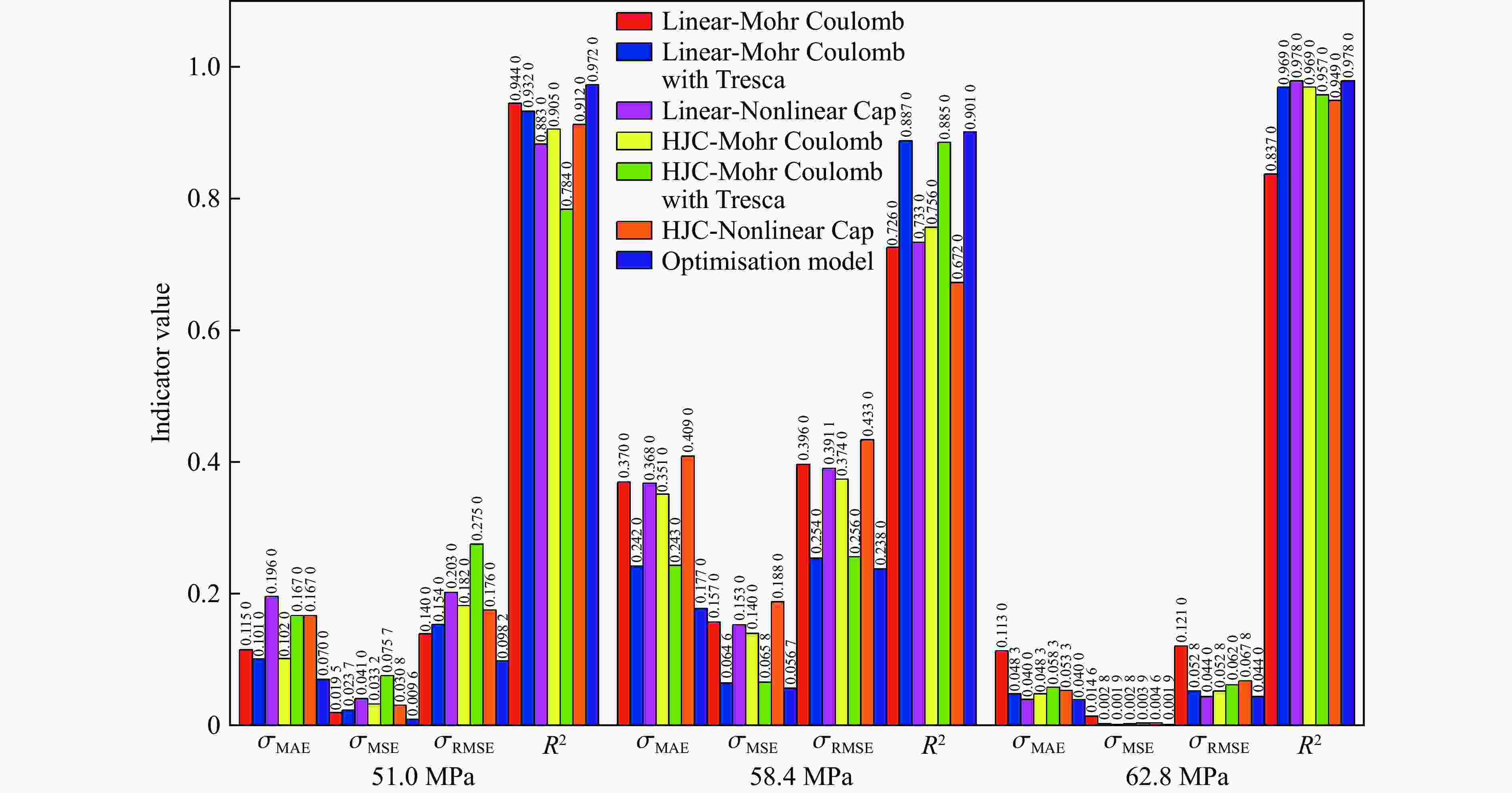
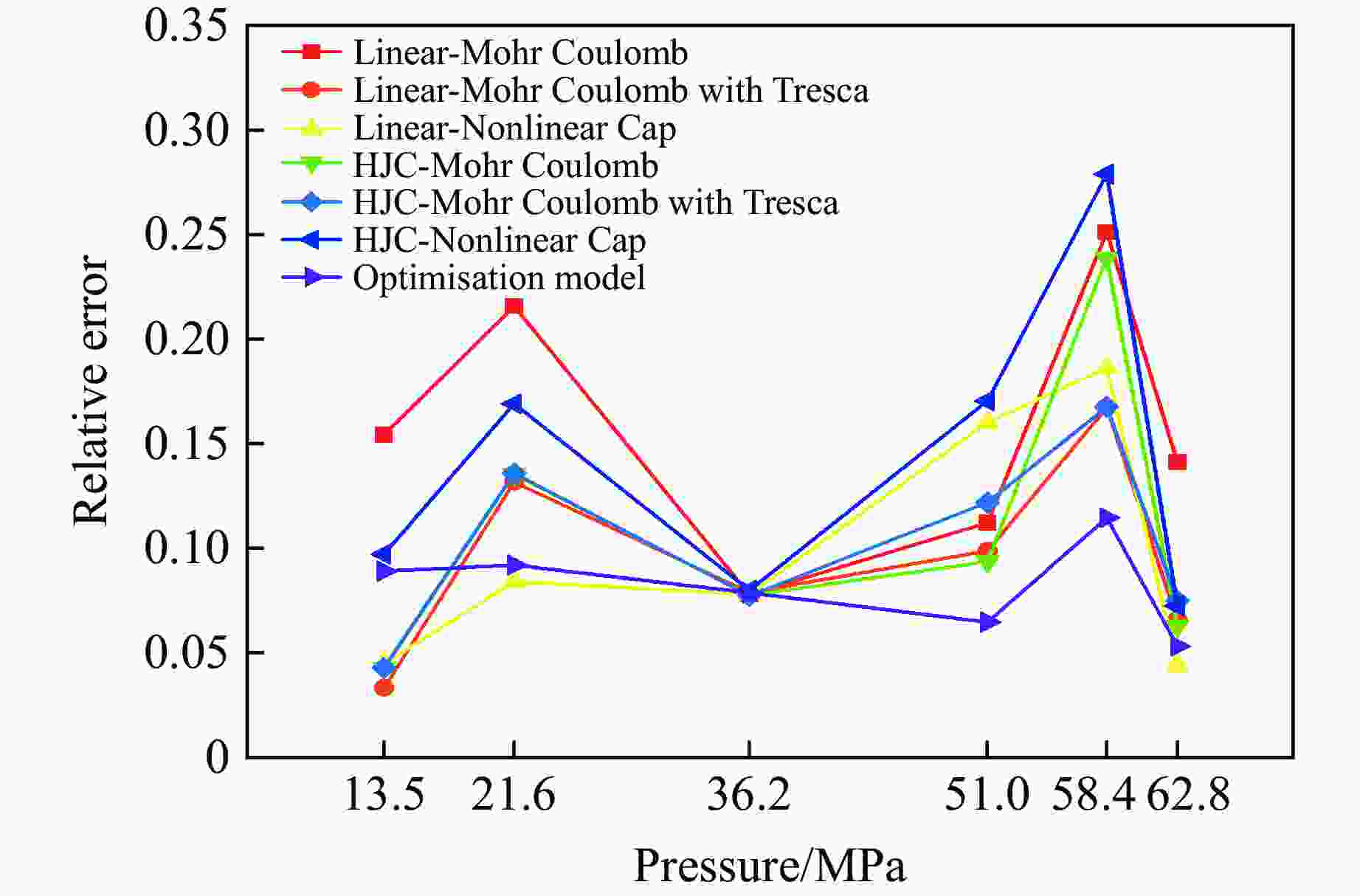
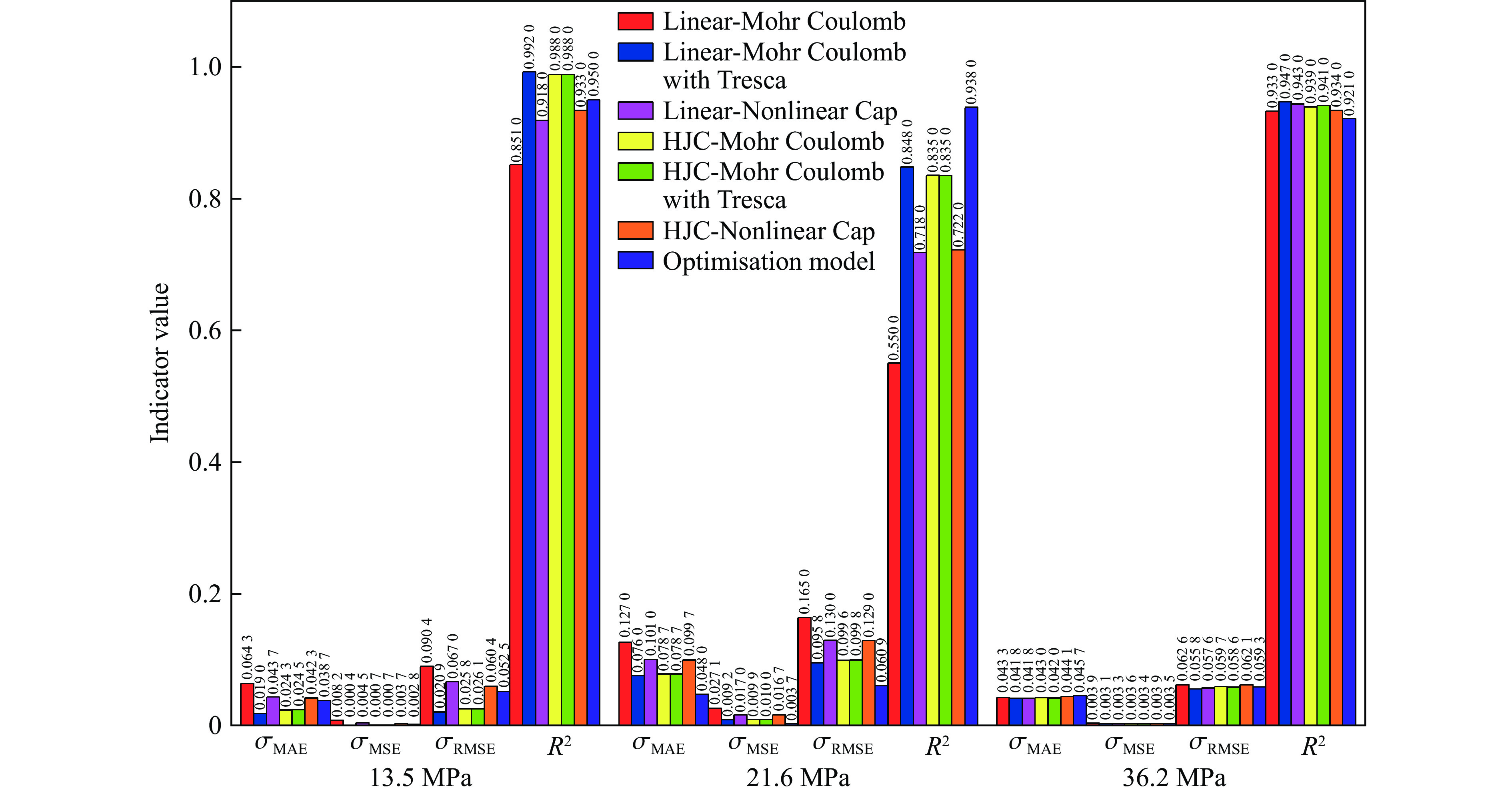
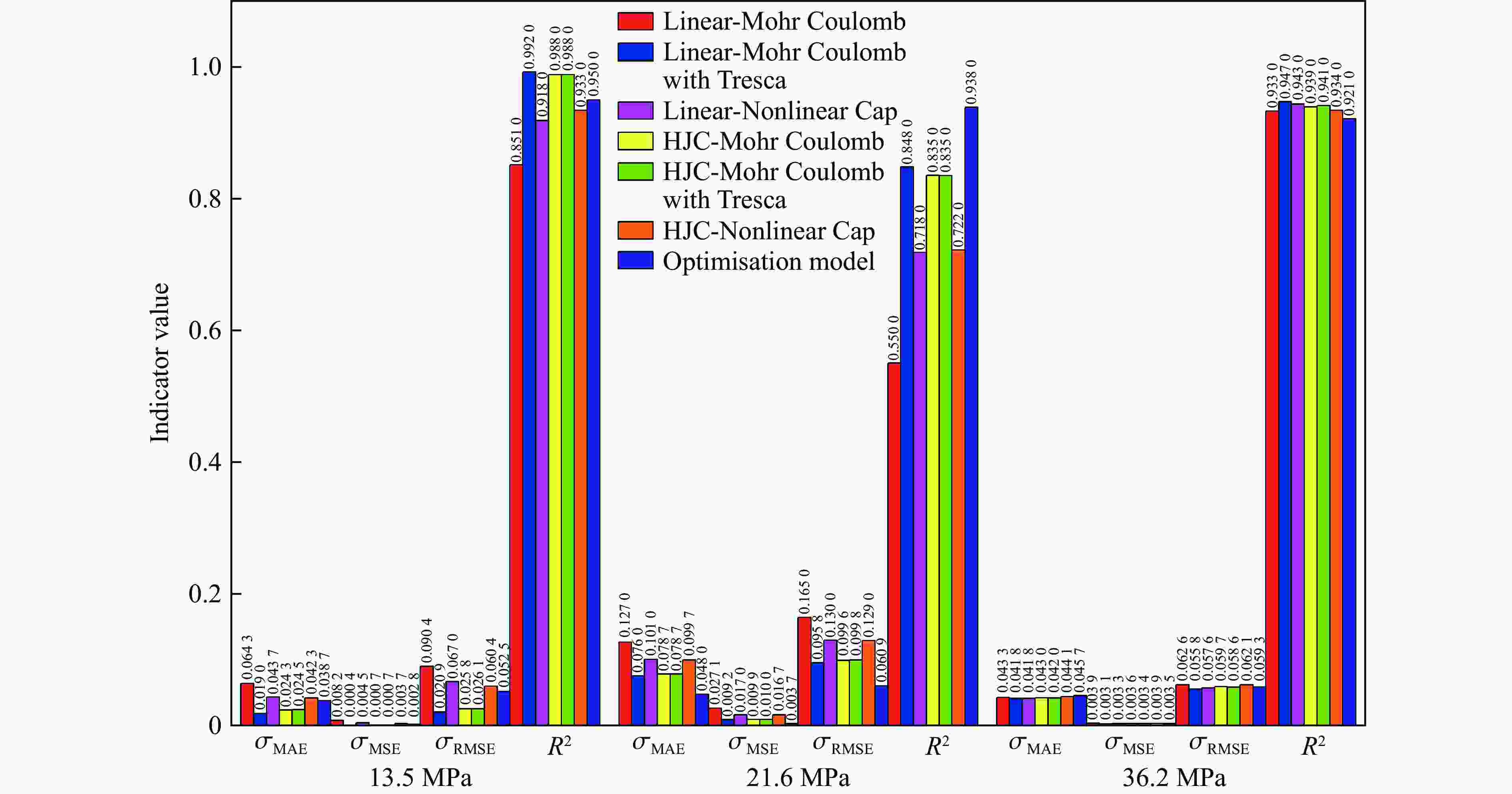
表 1 30.5 mm口径弹体侵彻51.0 MPa靶板（ρ=2300 kg/m³）深度实验数据

Table 1. Experimental data on the depth of penetration of a 30.5 mm projectile into a 51.0 MPa target slab (ρ=2300 kg/m³)

m/kg	v/(m·s⁻¹)	H_exp/m	H_LMC/m	$\delta_{\rm{LMC}}$ /%	H_MCT/m	$\delta_{\rm{MCT}}$ /%	H_LNC/m	$\delta_{\rm{LNC}}$ /%
1.60	405	0.37	0.28	25.02	0.28	23.87	0.23	37.79
	446	0.42	0.33	20.53	0.34	19.19	0.28	33.66
	545	0.56	0.49	12.69	0.50	10.90	0.41	26.04
	651	0.78	0.69	12.14	0.70	9.99	0.59	24.42
	804	1.05	1.04	1.10	1.07	1.94	0.91	12.93
	821	1.23	1.08	11.96	1.12	9.18	0.96	22.28
	900	1.41	1.30	7.53	1.35	4.30	1.17	17.37
	1 009	1.75	1.65	5.91	1.71	2.15	1.50	14.50
	1 069	1.96	1.85	5.39	1.93	1.36	1.70	13.24
	1 201	2.03	2.36	16.20	2.47	21.87	2.21	8.70

m/kg	v/(m·s⁻¹)	H_exp/m	H_HMC/m	$\delta_{\rm{HMC}}$ /%	H_HMCT/m	$\delta_{\rm{HMCT}}$ /%	H_HNC/m	$\delta_{\rm{HNC}}$ /%
1.60	405	0.37	0.29	21.88	0.32	13.51	0.24	34.55
	446	0.42	0.35	16.85	0.39	8.14	0.29	30.19
	545	0.56	0.52	7.79	0.57	1.40	0.44	22.17
	651	0.78	0.73	6.41	0.80	2.51	0.62	20.47
	804	1.05	1.12	6.48	1.22	16.13	0.96	8.40
	821	1.23	1.17	5.11	1.27	3.45	1.01	18.25
	900	1.41	1.41	0.10	1.54	8.99	1.23	13.11
	1 009	1.75	1.79	2.37	1.95	11.34	1.57	10.14
	1 069	1.96	2.02	3.15	2.20	12.18	1.79	8.85
	1 201	2.03	2.58	27.13	2.81	38.34	2.32	14.10

下载: 导出CSV

表 2 实验验证数据

Table 2. Experimental validation data

Case	Projectile			Target slab		v/(m·s⁻¹)	H/m
Case	m/kg	d/mm	$\delta_{\rm{CRH}}$	f_c/MPa	ρ/(kg·m⁻³)	v/(m·s⁻¹)	H/m
1	1.600	30.5	3	51.0	2300	545	0.560
2	1.600	30.5	3	51.0	2300	1 201	2.030
3	0.478	20.3	3	58.4	2320	610	0.491
4	0.478	20.3	3	58.4	2320	1 009	1.300
5	1.620	30.5	3	58.4	2320	445	0.460
6	1.620	30.5	3	58.4	2320	980	1.950
7	0.480	20.3	3	62.8	2300	821	0.760

下载: 导出CSV

表 3 系统测试数据对比

Table 3. Comparison of system test data

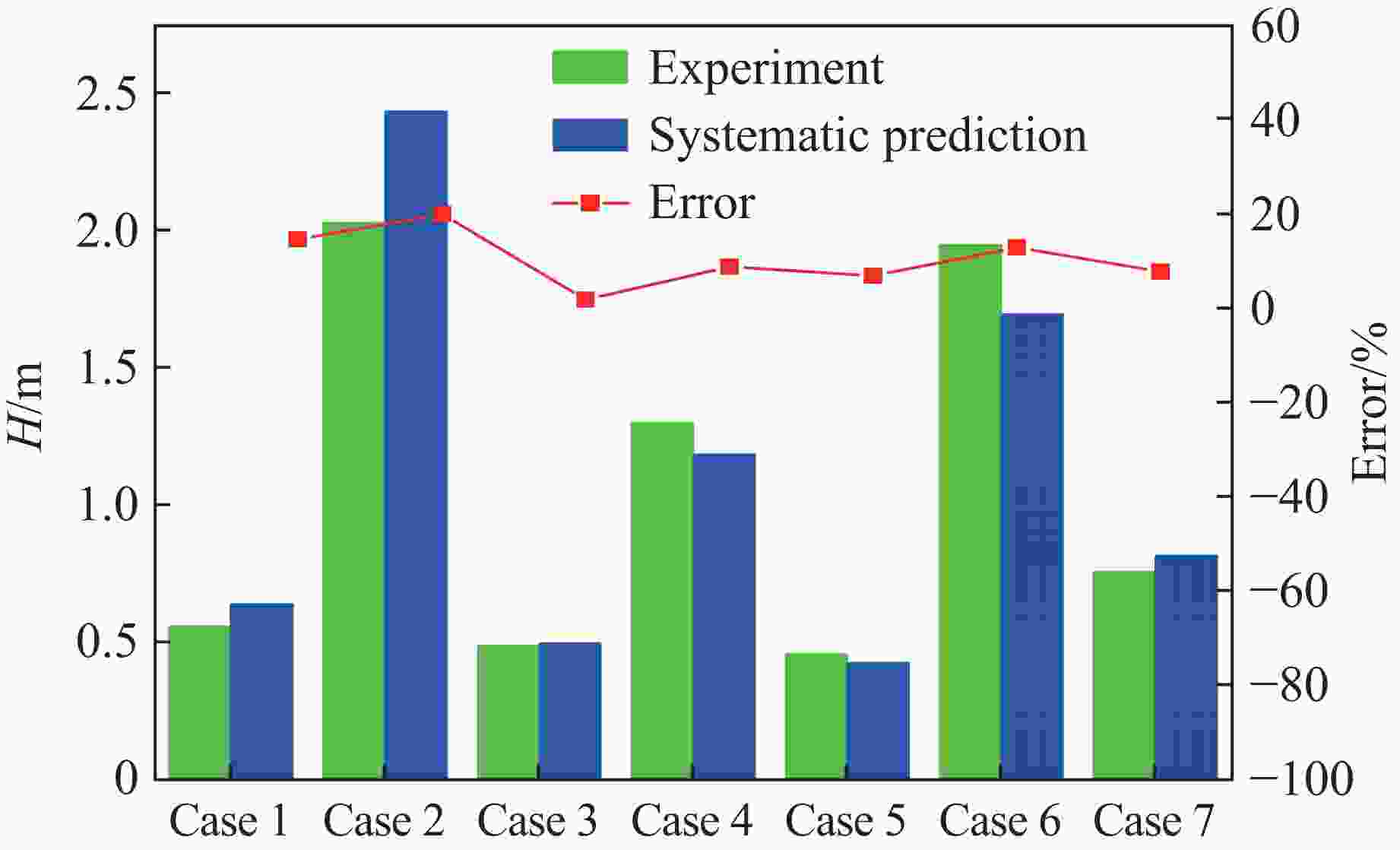
Case	H/m		Error/%
Case	Experiment	Systematic prediction	Error/%
1	0.560	0.642	14.6
2	2.030	2.434	19.9
3	0.491	0.500	1.8
4	1.300	1.185	8.8
5	0.460	0.428	6.9
6	1.950	1.697	12.9
7	0.760	0.819	7.7

下载: 导出CSV

参考文献(38)

[1]	金丰年, 刘黎, 张丽萍, 等. 深钻地武器的发展及其侵彻 [J]. 解放军理工大学学报(自然科学版), 2002, 3(2): 34–40. JIN F N, LIU L, ZHANG L P, et al. Development of projectiles and their penetration [J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2002, 3(2): 34–40.
[2]	王涛, 余文力, 王少龙, 等. 国外钻地武器的现状与发展趋势 [J]. 导弹与航天运载技术, 2005(5): 51–56. WANG T, YU W L, WANG S L, et al. Development of deep-drilling weapons and their penetration [J]. Missiles and Space Vechicles, 2005(5): 51–56.
[3]	NING J G, REN H L, LI Z, et al. A mass abrasion model with the melting and cutting mechanisms during high-speed projectile penetration into concrete slabs [J]. Acta Mechanica Sinica, 2022, 38(10): 121597. doi: 10.1007/s10409-022-21597-x
[4]	YANKELEVSKY D, FELDGUN V. The embedment of a high velocity rigid ogive nose projectile into a concrete target [J]. International Journal of Impact Engineering, 2020, 144: 103631. doi: 10.1016/j.ijimpeng.2020.103631
[5]	NING J G, MENG F L, MA T B, et al. Failure analysis of reinforced concrete slab under impact loading using a novel numerical method [J]. International Journal of Impact Engineering, 2020, 144: 103647. doi: 10.1016/j.ijimpeng.2020.103647
[6]	CHEN X G, LU F Y, ZHANG D. Penetration trajectory of concrete targets by ogived steel projectiles experiments and simulations [J]. International Journal of Impact Engineering, 2018, 120: 202–213. doi: 10.1016/j.ijimpeng.2018.06.004
[7]	焦登伟. 混凝土/钢筋混凝土高速侵彻贯穿问题的数值模拟与实验研究 [D]. 北京: 北京理工大学, 2018. JIAO D W. Numerical simulation and experimental research on high-speed penetration of concrete/reinforced concrete [D]. Beijing: Beijing Institute of Technology, 2018.
[8]	CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics [J]. International Journal of Impact Engineering, 2002, 27(6): 619–637. doi: 10.1016/S0734-743X(02)00005-2
[9]	ROSENBERG Z, DEKEL E. Analytical solution of the spherical cavity expansion process [J]. International Journal of Impact Engineering, 2009, 36(2): 193–198. doi: 10.1016/j.ijimpeng.2007.12.014
[10]	WU H, HEN X W, HE L L, et al. Stability analyses of the mass abrasive projectile high-speed penetrating into concrete target. Part Ⅰ: engineering model for the mass loss and nose-blunting of ogive nosed projectiles [J]. Acta Mechanica Sinica, 2014, 30(6): 933–942. doi: 10.1007/s10409-014-0090-1
[11]	XU X Z, SU Y C, FENG Y B. Optimization analysis of state equation and failure criterion for concrete slab subjected to impact loading [J]. International Journal of Impact Engineering, 2024, 186: 104872. doi: 10.1016/j.ijimpeng.2023.104872
[12]	WANG M, WANG K L, ZHAO Q C et al. LQR control and optimization for trajectory tracking of biomimetic robotic fish based on unreal engine [J]. Biomimetics, 2023, 8(2): 236. doi: 10.3390/biomimetics8020236
[13]	丁钱. 基于模型驱动的复杂系统装备互操作可视化仿真与验证平台设计与实现 [D]. 南京: 南京邮电大学, 2018. DING Q. Design and implementation of a visual simulation and verification platform for equipment interoperability of complex system based on model driven [D]. Nanjing: Nanjing University of Posts and Telecommunications, 2018.
[14]	CHEN R C, AKKUS I E, FRANCIS P. SplitX: high-performance private analytics [C]//Proceedings of the ACM SIGCOMM 2013 Conference on SIGCOMM. Hong Kong, China: Association for Computing Machinery, 2013: 315–326.
[15]	SHEWCHENKO N, FONRNIER E, WONNACOTT M, et al. A vulnerability/lethality model for the combat soldier, a new paradigm—basis and initial development [C]//Personal Armour Systems Symposium. Nuremberg-Fürth, Germany, 2012.
[16]	贺歆. 弹目遭遇动态可视化仿真研究 [D]. 南京: 南京理工大学, 2004. HE X. Simulation study on dynamic visualization of projectile encounters [D]. Nanjing: Nanjing University of Science and Technology, 2004.
[17]	刘云. 弹目遭遇可视化仿真关键技术研究 [D]. 南京: 南京理工大学, 2004. LIU Y. Research on the key technology of visual simulation of projectile encounter [D]. Nanjing: Nanjing University of Science and Technology, 2004.
[18]	RUSYAK I, SUFIYANOV V, KOLOLEV S, et al. Software complex for simulation of internal and external ballistics of artillery shot [C]//International Conference on Military Technologies (ICMT). Brno, Czech Republic: IEEE, 2015.
[19]	BUŻANTOWICZ W. Matlab script for 3D visualization of missile and air target trajectories [J]. International Journal of Computer and Information Technology, 2016, 5(5): 419–422.
[20]	SCHOEDER W J, MARTIN, AVILA , et al. The visualization toolkit user’s guide [M]. New York, USA: Kitware Inc., 2001.
[21]	刘建斌, 徐豫新, 高鹏, 等. 火箭杀爆弹毁伤幅员仿真 [J]. 兵工学报, 2016, 37(Suppl 2): 159–164. LIU J B, XU Y X, GAO P, et al. Simulation of the extent of damage caused by rocket explosive projectiles [J]. Acta Armamentarii, 2016, 37(Suppl 2): 159–164.
[22]	高鹏, 徐豫新, 李可, 等. 火箭杀爆弹动爆毁伤幅员计算方法与可视化仿真实现 [J]. 兵工学报, 2016, 37(Suppl 2): 216–220. GAO P, XU Y X, LI K, et al. Calculation method and visual simulation implementation of kinetic explosion damage amplitude of rocket explosive projectiles [J]. Acta Armamentarii, 2016, 37(Suppl 2): 216–220.
[23]	YANG Y B, QIAN L X, MING Q U. Lethality test simulation system for conventional warhead based on numerical results [C]//Asia Simulation Conference/6th International Conference on System Simulation and Scientific Computing. Beijing, 2005: 267–271.
[24]	杨云斌, 屈明, 钱立新. 破片战斗部威力仿真方法与仿真软件研究 [J]. 计算机仿真, 2007, 24(10): 14–19. YANG Y B, QU M, QIAN L X. Lethality simulation method & software for fragmentation warhead [J]. Computer Simulation, 2007, 24(10): 14–19.
[25]	WANG Y, ZHANG W Y, NING J G. Streamline-based visualization of 3D explosion fields [C]//International Conference on Computational Intelligence and Security. Sanya, Hainan: IEEE, 2011.
[26]	LI B X, LIANG Z G, PENG S, et al. Bullet external ballistic visualization simulation software design [C]//International Conference on Machine Learning and Computer Application. Shenyang, Liaoning: IEEE, 2021.
[27]	张进强, 蒋夏军. 外弹道可视化仿真研究与实现 [J]. 计算机工程与科学, 2015, 37(2): 372–378. ZHANG J Q, JIANG X J. Research and implementation of visualization simulation for external trajectory [J]. Computer Engineering & Science, 2015, 37(2): 372–378.
[28]	程翔, 李苑青, 王丽华. 基于OpenGL的六自由度三维弹道仿真技术研究 [J]. 电子科技, 2017, 30(6): 15–20. CHENG X, LI W Q, WANG L H. Research on six degree of freedom 3D trajectory simulation based on OpenGL [J]. Electronic Science and Technology, 2017, 30(6): 15–20.
[29]	王彪, 程鹏举, 韩卓茜, 等. 基于C#与STK的多雷达跟踪弹道导弹系统设计与实现 [J]. 计算机科学与应用, 2020, 10(6): 1185–1193. doi: 10.12677/CSA.2020.106123 WANG B, CHENG P J, HAN Z X, et al. Design and implementation of multi-radar tracking ballistic missile system based on C# and STK [J]. Computer Science and Application, 2020, 10(6): 1185–1193. doi: 10.12677/CSA.2020.106123
[30]	纪录, 吴国东, 王志军, 等. 基于STK的弹箭半实物飞行实时可视化仿真 [J]. 火力与指挥控制, 2020, 45(2): 170–174, 179. JI L, WU G D, WANG Z J, et al. Missile-rocket semi-physical flight simulation based on STK true time visualization technology [J]. Fire Control & Command Control, 2020, 45(2): 170–174, 179.
[31]	TIAN X J, TAO T J, LOU Q X, et al. Modification and application of limestone HJC constitutive model under the impact load [J]. Lithosphere, 2022, 2021: 6443087. doi: 10.2113/2022/6443087
[32]	FELDGUN V R, YANKELEVSKY D Z. Constitutive equations for reliable projectile penetration analysis into a concrete medium [J]. International Journal of Protective Structures, 2019, 11(2): 159–184.
[33]	DONG H, WU H J, LI J Z, et al. Dynamic spherical cavity expansion analysis of concrete/rock based on hoek-brown criterion [J]. Journal of Physics: Conference Series, 2020, 1507: 032012. doi: 10.1088/1742-6596/1507/3/032012
[34]	YANG H W, ZHANG J, WANG Z Y, et al. Numerical study on the resistance of rigid projectiles penetrating into semi-infinite concrete targets [J]. Acta Mechanica Sinica, 2021, 37(3): 482–493. doi: 10.1007/s10409-021-01054-6
[35]	LI Z, XU X Z. Theoretical investigation on failure behavior of ogive-nose projectile subjected to impact loading [J]. Materials, 2020, 13(23): 5372. doi: 10.3390/ma13235372
[36]	JADON A, PATIL A, JADON S. A comprehensive survey of regression based loss functions for time series forecasting [J/OL]. Arxiv, 2022: 2211.02989.
[37]	FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets [J]. International Journal of Impact Engineering, 1994, 15(4): 395–405. doi: 10.1016/0734-743X(94)80024-4
[38]	FORRESTAL M J, FREW D J, HANCHAK S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles [J]. International Journal of Impact Engineering, 1996, 18(5): 465–476. doi: 10.1016/0734-743X(95)00048-F