单轴压缩下裂隙倾角对花岗岩-混凝土力学行为及能量演化的影响

李庆文; 李涵静; 钟宇奇; 李玲; 才诗婷; 刘艺伟

doi:10.11858/gywlxb.20240803

单轴压缩下裂隙倾角对花岗岩-混凝土力学行为及能量演化的影响

doi: 10.11858/gywlxb.20240803

李庆文^1,,
李涵静^1,*, ,,
钟宇奇¹,
李玲¹,
才诗婷¹,
刘艺伟^{1, 2}

1.
辽宁工业大学土木建筑工程学院, 辽宁锦州　121001
2.
山东建筑大学土木工程学院, 山东济南　250101

基金项目: 辽宁省教育厅基本科研面上项目（JYTMS20230866）；辽宁省自然科学基金面上项目（2023-MS-298 ）；辽宁省博士科研启动基金（2019-BS-120）；辽宁省自然科学基金指导项目（20180550297）

详细信息

作者简介:
李庆文（1987－），男，博士，副教授，主要从事岩石力学、新材料与新型组合结构、离散元-有限差分跨尺度耦合数值模拟研究. E-mail：lgjzlqw@163.com

通讯作者:
李涵静（1999－），女，硕士研究生，主要从事计算颗粒力学研究. E-mail：1965213088@qq.com

中图分类号: O346.1; TU45
计量
- 文章访问数: 85
- HTML全文浏览量: 55
- PDF下载量: 13
出版历程
- 收稿日期: 2024-04-26
- 修回日期: 2024-05-23
- 网络出版日期: 2024-09-02

Influence of Crack Angles on the Mechanical Behavior and Energy Evolution of Granite-Concrete under Uniaxial Compression

LI Qingwen^1
,,
LI Hanjing^{1,*
, ,},
ZHONG Yuqi¹,
LI Ling¹,
CAI Shiting¹,
LIU Yiwei^{1, 2}

1.
School of Civil and Architectural Engineering, Liaoning University of Technology, Jinzhou 121001, Liaoning, China
2.
School of Civil Engineering, Shandong Jianzhu University, Jinan 250101, Shandong, China

摘要

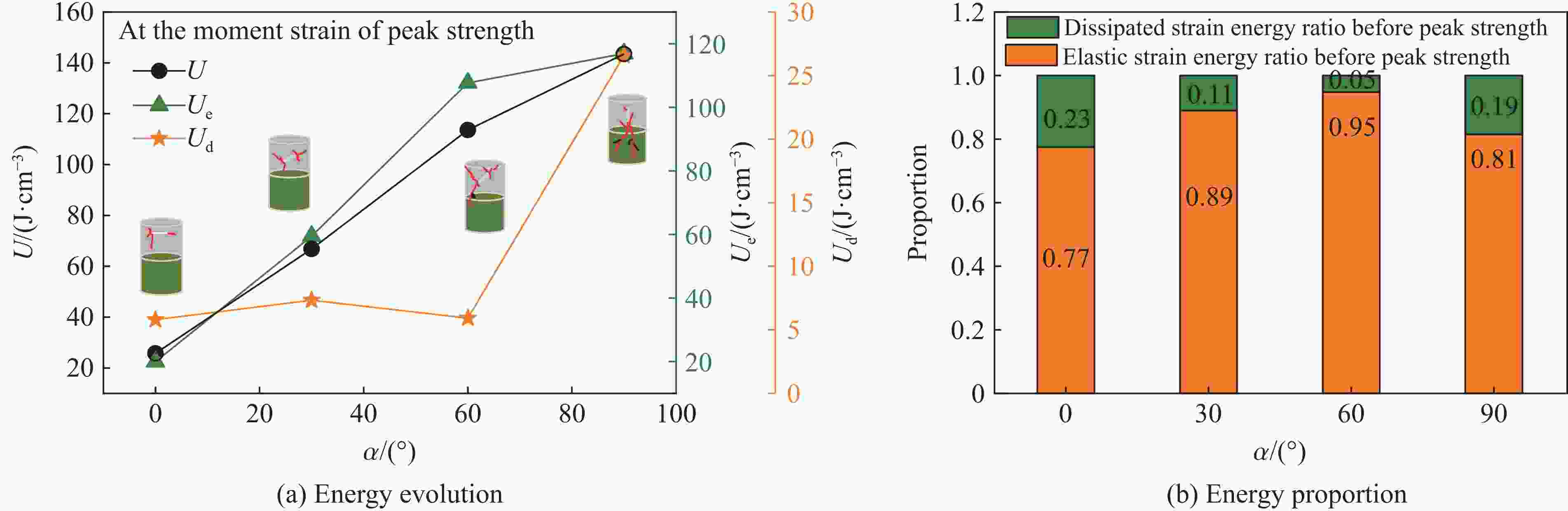
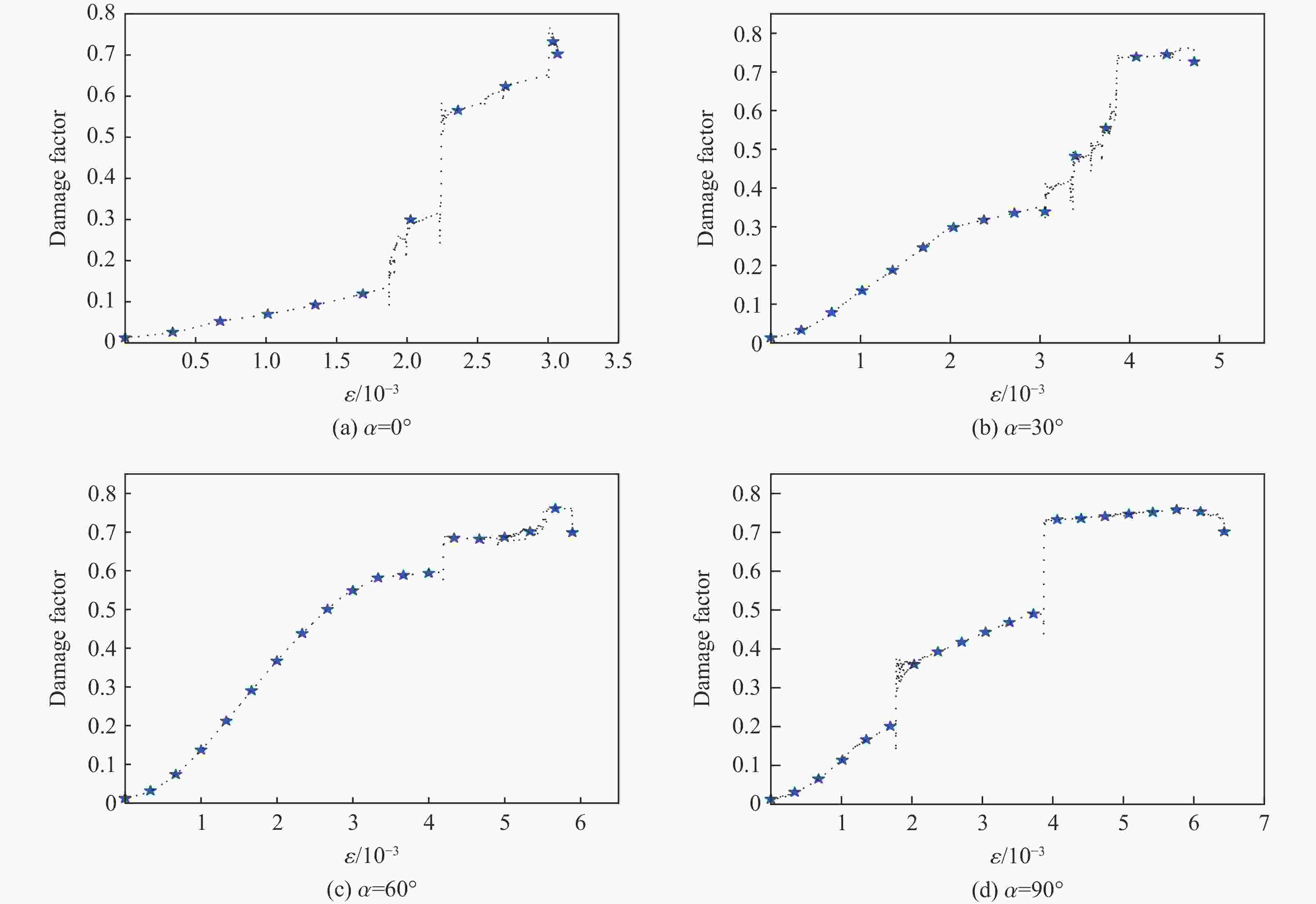
摘要: 为探究单轴压缩下不同裂隙倾角对花岗岩-混凝土组合体试件的强度及能量演化的影响，结合室内试验标定的细观参数，采用二维离散元颗粒流程序（PFC^2D）对组合体试件开展了数值模拟研究。结果表明：花岗岩-混凝土的强度和变形特征受裂隙倾角影响，其强度和变形参数随裂隙倾角的增大呈逐渐增大趋势；在单轴压缩过程中，试样内部能量转化为宏观裂纹扩展，最终的破坏模式主要以拉伸失效断裂和剪切失效断裂为主；组合体试件的总能量和耗散能随裂隙倾角的增大而增大，试件破坏时总应变能大于耗散能。基于耗散能的计算，构建了损伤本构方程，当损伤因子为0.8时，试件接近极限状态，此时的能量消耗较大，显著降低了组合体试件的强度。
- 花岗岩-混凝土组合体 /
- 单裂隙 /
- 离散元颗粒流程序 /
- 单轴压缩 /
- 能量损伤本构
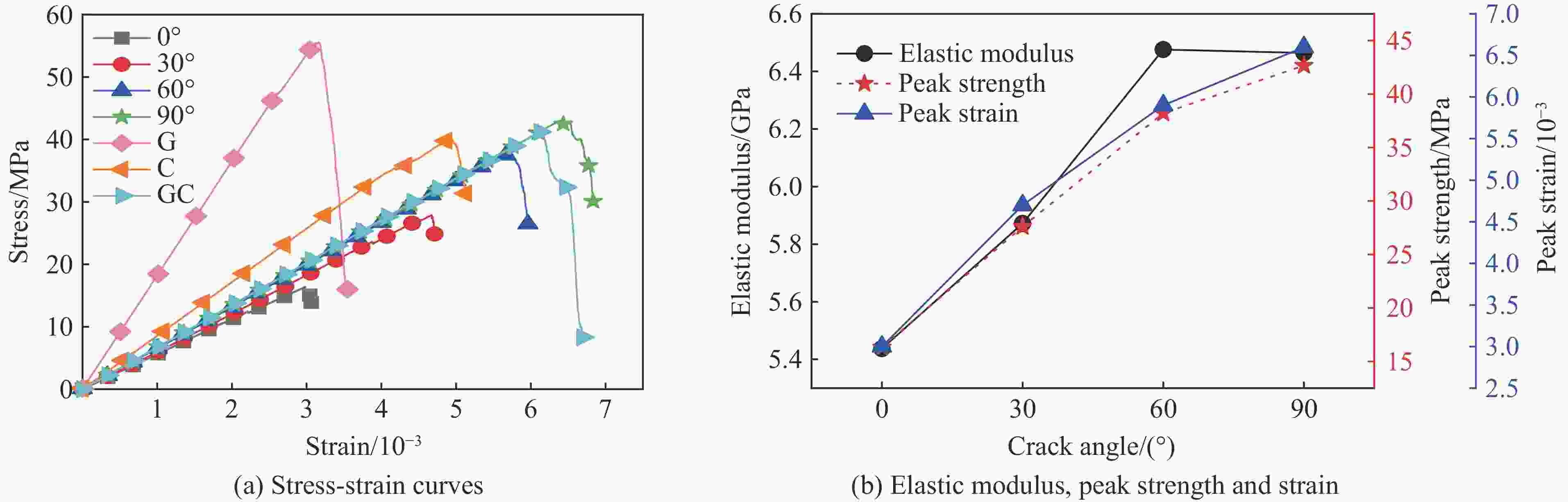
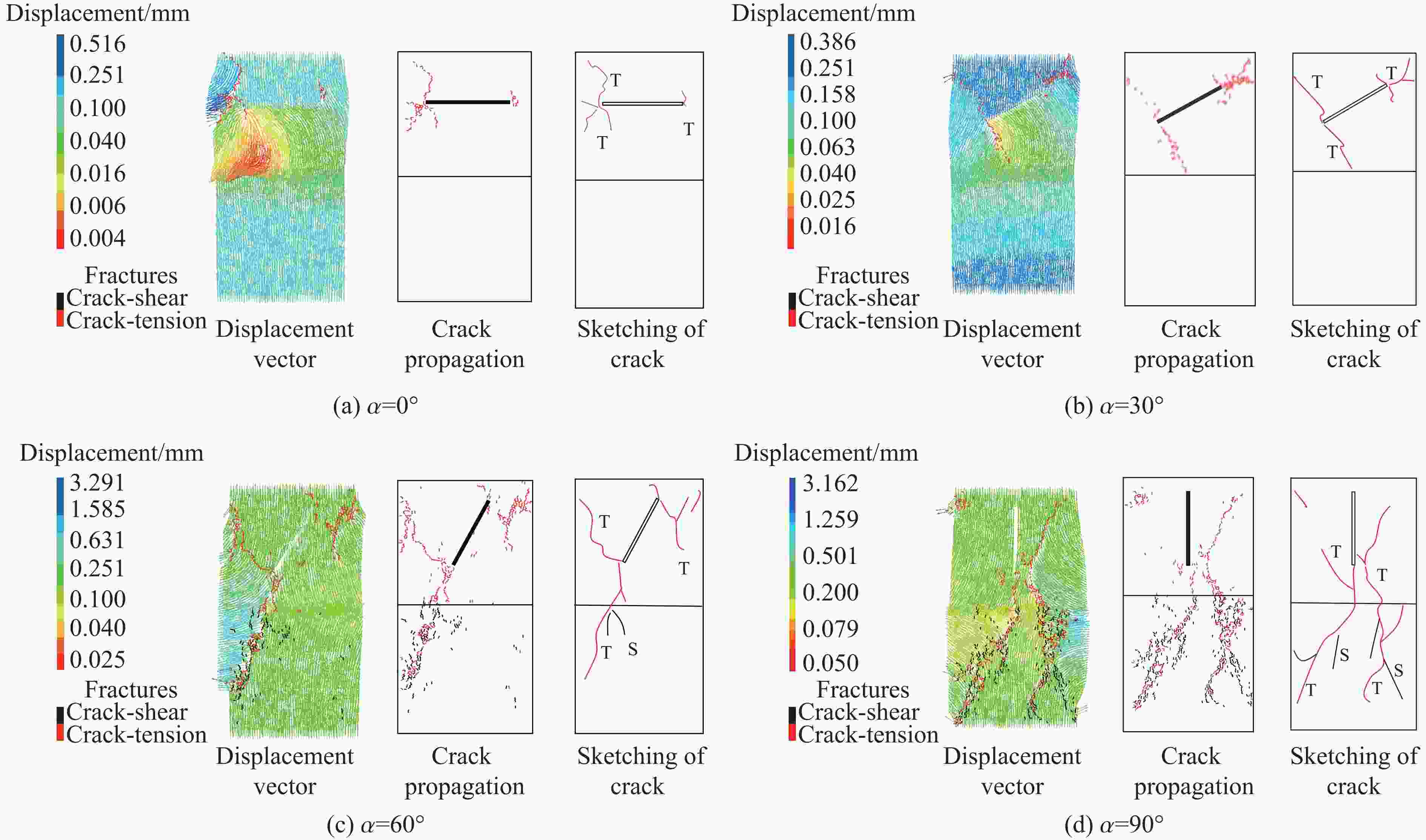
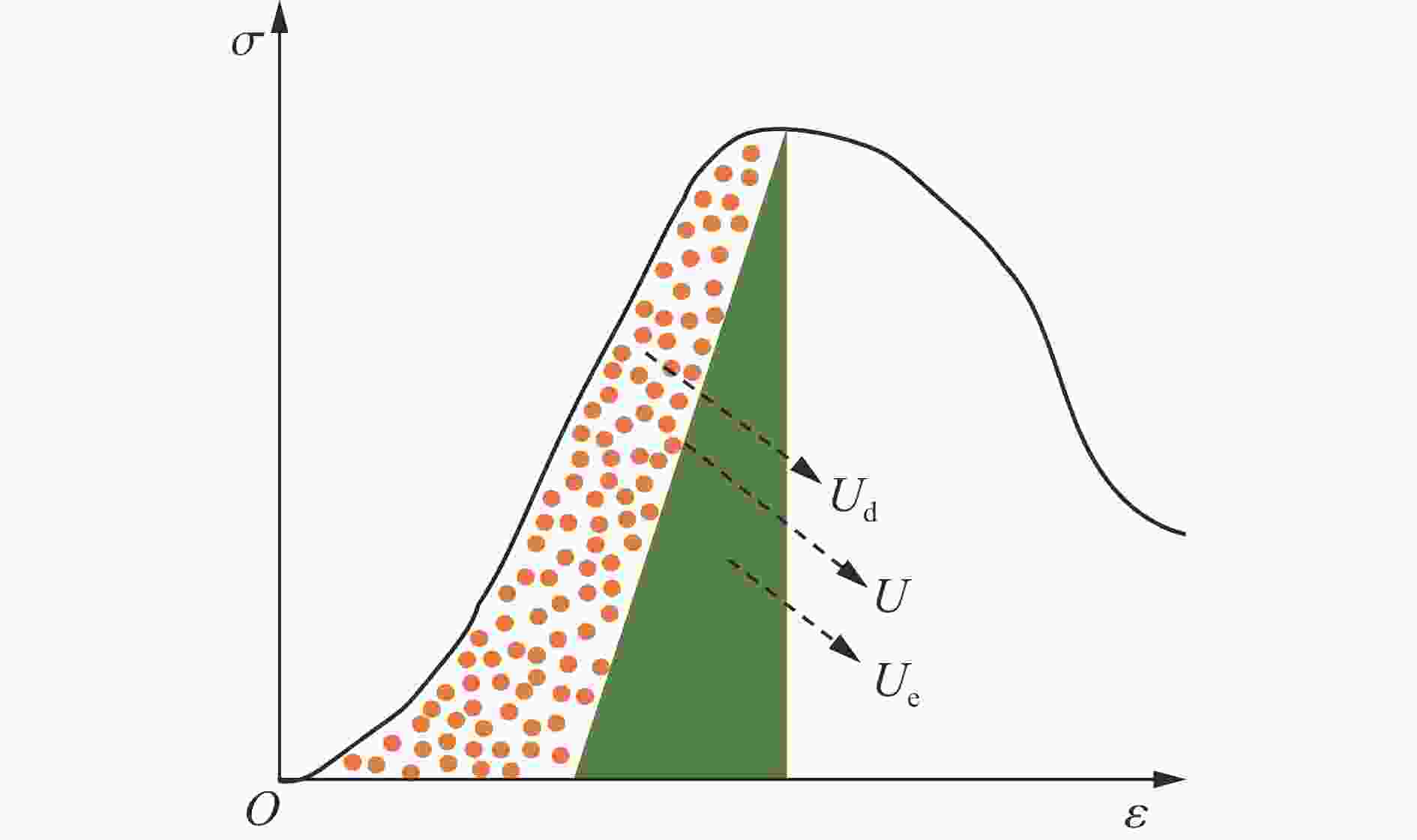
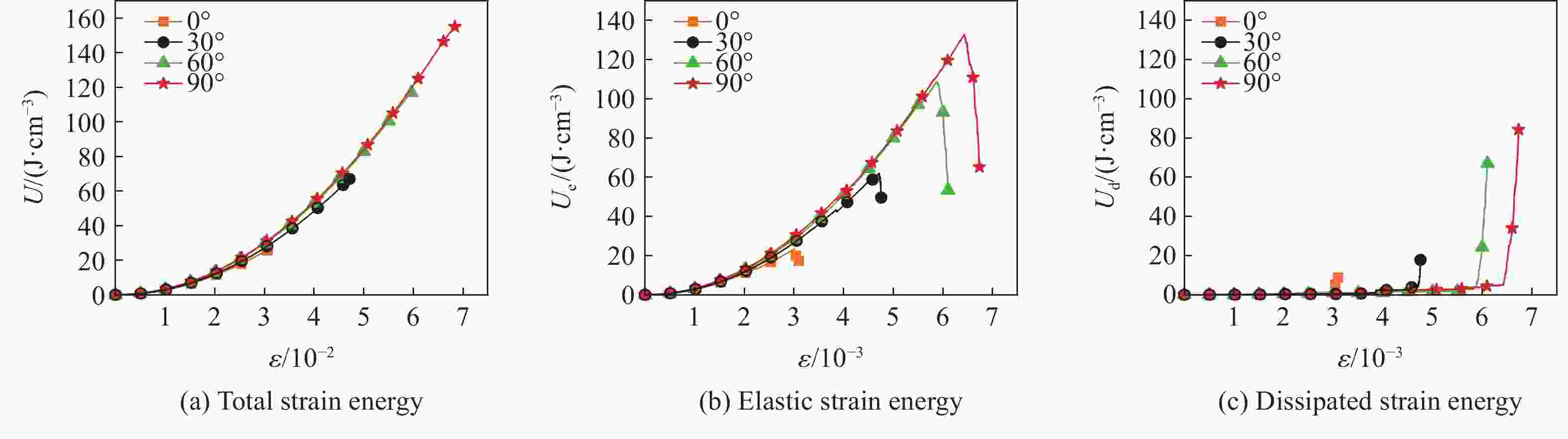
Abstract: To investigate the influence of the crack angle on the strength and energy evolution of granite-concrete composite specimens under uniaxial compression, a numerical simulation study was conducted using the two-dimensional particle flow code (PFC^2D) based on the micro-parameters calibrated through laboratory tests. The research results indicate that the strength and deformation characteristics of granite-concrete are affected by crack angles, and their strength and deformation parameters gradually increase with the increase of crack angle. During the uniaxial compression process, the internal energy of the specimens transforms into macroscopic crack propagation, and the final failure modes are mainly tensile fractures and shear fractures. The total energy and dissipated energy of the composite specimens increase with the increase of crack angle, and the total strain energy is more than the dissipated energy when the specimens are damaged. Based on the calculation of dissipated energy, a damage constitutive equation was constructed, indicating that when the damage factor reaches 0.8, the specimen is already close to its limit state, resulting in significant energy consumption and a decrease in the strength of the composite specimen.
- granite-concrete composite /
- single crack /
- particle flow code /
- uniaxial compression /
- energy damage constitutive

HTML全文

图 1 单轴压缩试验装置

Figure 1. Testing machine of the uniaxial compression

下载: 全尺寸图片幻灯片

图 2 室内单轴压缩试验得到的应力-应变曲线

Figure 2. Stress-strain curves of indoor uniaxial compression tests

下载: 全尺寸图片幻灯片

图 3 接触模型^[30]

Figure 3. Contact model^[30]

下载: 全尺寸图片幻灯片

图 4 试验与数值模拟得到的应力-应变曲线及破坏形态对比

Figure 4. Comparison of stress-strain curves and failure modes between test and numerical simulation

下载: 全尺寸图片幻灯片

图 5 单裂隙花岗岩-混凝土试样的数值模型

Figure 5. Numerical model of granite-concrete specimen with single crack

下载: 全尺寸图片幻灯片

图 6 PFC^2D的数值模拟结果

Figure 6. Numerical simulation results of PFC^2D

下载: 全尺寸图片幻灯片

图 7 裂纹扩展路径

Figure 7. Propagation path of cracks

下载: 全尺寸图片幻灯片

图 8 一般岩石的弹性能与耗散能之间的关系^[37]

Figure 8. Relationship between elastic energy and dissipated energy of general rock^[37]

下载: 全尺寸图片幻灯片

图 9 不同裂隙倾角下花岗岩-混凝土试件的能量演化

Figure 9. Energy evolution of granite-concrete specimen under different fracture angles

下载: 全尺寸图片幻灯片

图 10 不同倾角下花岗岩-混凝土试件峰值时刻的能量演化

Figure 10. Energy evolution of granite-concrete specimen under different angles at the moment of peak strength

下载: 全尺寸图片幻灯片

图 11 考虑裂隙倾角的参数修正

Figure 11. Parameter correction considering crack dip angle

下载: 全尺寸图片幻灯片

图 12 本构模型的验证

Figure 12. Verification of constitutive model

下载: 全尺寸图片幻灯片

图 13 损伤因子演化曲线

Figure 13. Evolution curves of damage factor

下载: 全尺寸图片幻灯片

表 1 C40混凝土的配合比

Table 1. Mixture ratio of C40 concrete kg/m³

Cement	Mineral filler	Fly ash	Sand	Aggregate	Admixture
270	75	45	860	880	8.5

下载: 导出CSV

表 2 试验结果分析

Table 2. Analysis of test results

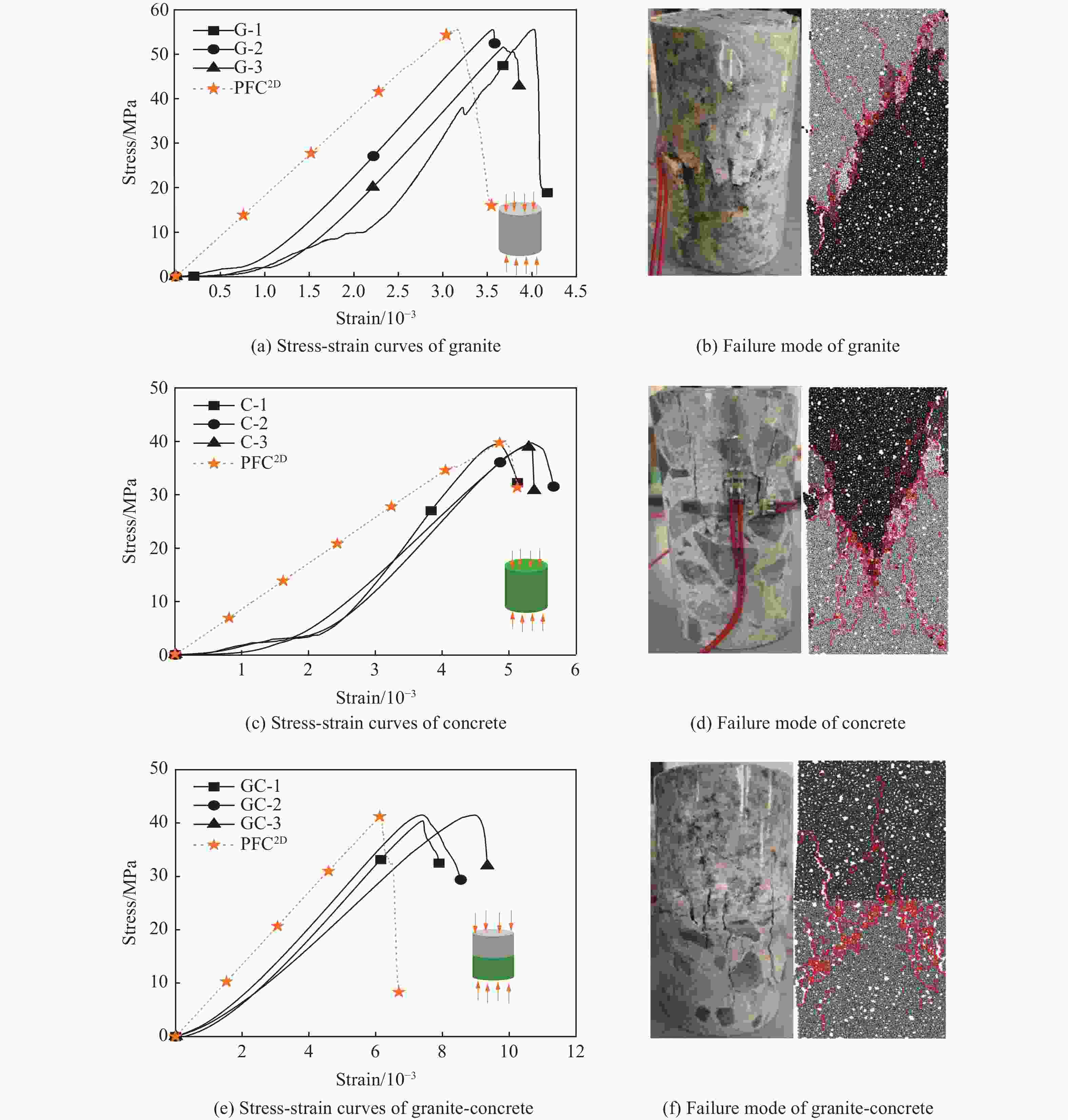
Material	Sample ID	Compressive strength/MPa		Elastic modulus/GPa
Material	Sample ID	Test data	Average value	Test data	Average value
Granite	G-1	55.5	54.2	28.0	24.3
	G-2	55.5		22.1
	G-3	51.5		22.9
Concrete	C-1	39.4	39.3	16.1	18.7
	C-2	39.7		18.2
	C-3	38.9		21.8
Granite-concrete	GC-1	40.4	41.1	7.2	6.7
	GC-2	41.5		6.7
	GC-3	41.5		6.1
Note: In sample ID, G represents the granite, C represents the concrete, GC denotes the granite-concrete, and 1, 2, 3 represents the sample number.

下载: 导出CSV

表 3 试验值与模拟值的比较

Table 3. Comparison between test and simulated value

Material	Effective modulus			Peak stress
Material	Test/GPa	Simulation/GPa	Error/%	Test/MPa	Simulation/MPa	Error/%
Granite	24.3	24.3	0	54.2	55.3	2.0
Concrete	18.7	18.7	0	39.3	40.1	2.0
Granite-concrete	6.7	6.7	0	41.1	41.1	0

下载: 导出CSV

表 4 材料细观参数

Table 4. Microscopic parameters of materials

Material	Density/ (kg·m⁻³)	Tensile strength/MPa	Cohesive strength/MPa	Effective modulus/GPa	Particle friction coefficient	Stiffness ratio	Friction angle/(°)
Granite	2790	50	150	17.5	0.3	2.53	30
Concrete	2360	51	50	8.0	0.2	1.33	70

下载: 导出CSV

表 5 界面细观参数

Table 5. Microscopic parameters of interfaces

Normal stiffness/ (N·m⁻¹)	Shear stiffness/ (N·m⁻¹)	Cohesion/GPa	Joint friction angle/(°)	Frictional coefficient
9×10⁷	4.5×10⁸	20	20	0.6

下载: 导出CSV

表 6 数值模拟方案

Table 6. Scheme of numerical simulation

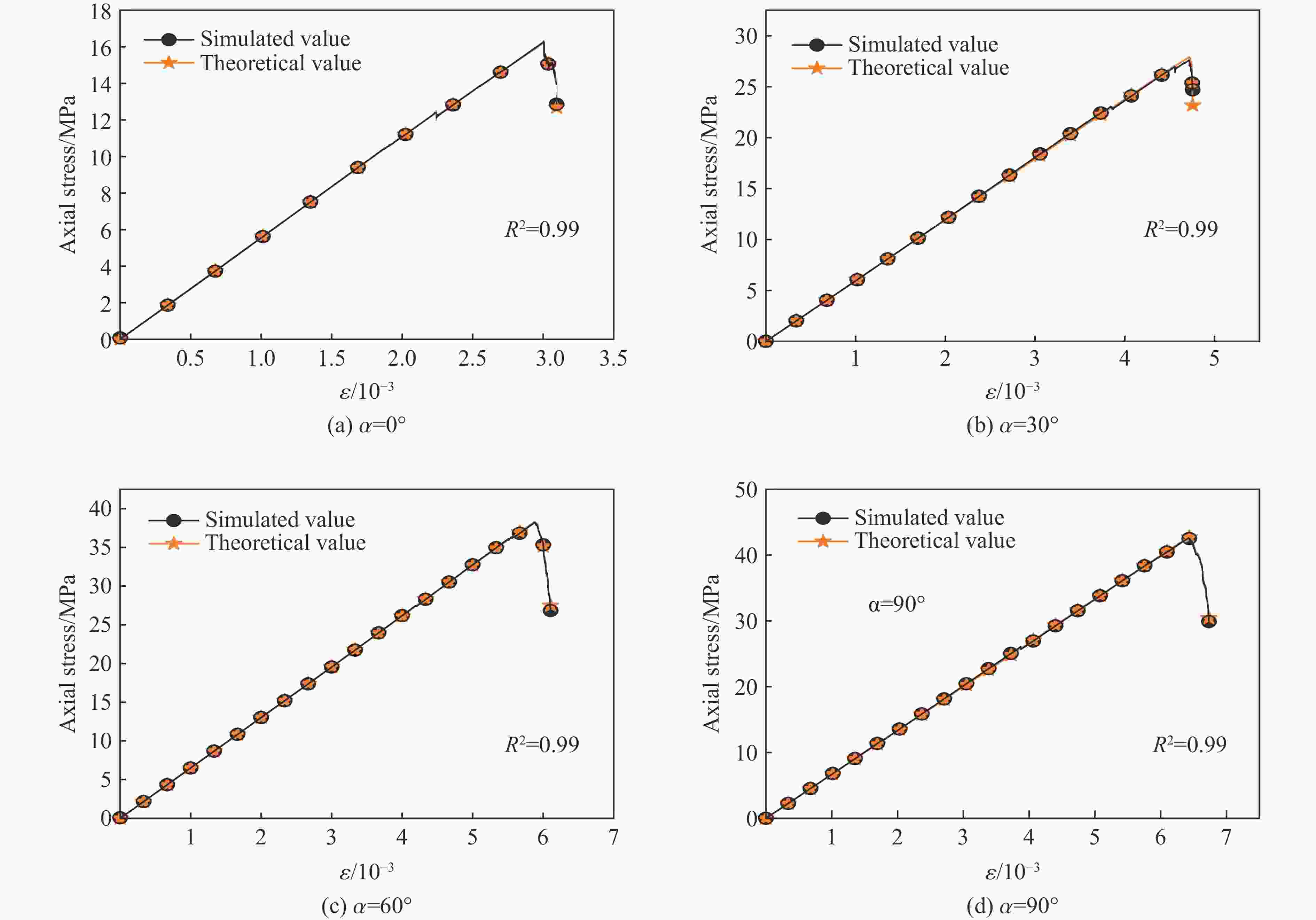
α/(°)	Model	L/mm	H/mm	v₀/(mm·s⁻¹)	E/GPa	σ_max/MPa	ε_i/10⁻³
0		30	1	0.01	5.437	16.31	0.30
30		30	1	0.01	5.872	27.60	0.47
60		30	1	0.01	6.476	38.21	0.59
90		30	1	0.01	6.464	42.66	0.66

下载: 导出CSV

参考文献(47)

[1]	FU J W, HAERI H, SARFARAZI V, et al. The shear behaviors of concrete-gypsum specimens containing double edge cracks under four-point loading conditions [J]. Theoretical and Applied Fracture Mechanics, 2022, 119: 103361. doi: 10.1016/j.tafmec.2022.103361
[2]	LI D J, SHI C, RUAN H N, et al. Study on shear behavior of coral reef limestone-concrete interface [J]. Marine Georesources & Geotechnology, 2022, 40(4): 438–447. doi: 10.1080/1064119X.2021.1906365
[3]	DONG W, WU Z M, ZHANG B S, et al. Study on shear-softening constitutive law of rock-concrete interface [J]. Rock Mechanics and Rock Engineering, 2021, 54(9): 4677–4694. doi: 10.1007/s00603-021-02536-6
[4]	ZHANG D C, SHE H C, XIAO T L. Influence of coplanar double fissures on failure characteristics of sandstone and fracture mechanics analysis [J]. Frontiers in Earth Science, 2023, 11: 1180636. doi: 10.3389/feart.2023.1180636
[5]	BISTA D, SAS G, JOHANSSON F, et al. Influence of location of large-scale asperity on shear strength of concrete-rock interface under eccentric load [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2020, 12(3): 449–460. doi: 10.1016/j.jrmge.2020.01.001
[6]	DONG W, WU Z M, ZHOU X M, et al. An experimental study on crack propagation at rock-concrete interface using digital image correlation technique [J]. Engineering Fracture Mechanics, 2017, 171: 50–63. doi: 10.1016/j.engfracmech.2016.12.003
[7]	YANG L Y, ZHANG F, LIN C Y, et al. Experimental study on failure characteristics of rock-fiber concrete composite under compression load [J]. Structures, 2022, 44: 1863–1873. doi: 10.1016/j.istruc.2022.09.007
[8]	LI X J, LAN L J, BAI Y F, et al. Study on fracture failure mechanism and crack propagation law of granite-shotcrete composite structure [J]. Arabian Journal of Geosciences, 2022, 15(6): 464. doi: 10.1007/s12517-022-09676-1
[9]	WEI X, SHEN Y J, LI X T, et al. Influence of freeze-thaw cycles and shear rate on sandstone-concrete interfacial bond strength: experiment and degradation model [J]. Construction and Building Materials, 2022, 327: 126986. doi: 10.1016/j.conbuildmat.2022.126986
[10]	SHEN Y J, ZHANG H, ZHANG J Y, et al. Sandstone-concrete interface transition zone (ITZ) damage and debonding micromechanisms under freeze-thaw [J]. Sciences in Cold and Arid Regions, 2021, 13(2): 133–149. doi: 10.3724/SP.J.1226.2021.20056
[11]	PAN J, SHEN Y J, YANG G S, et al. Debonding behaviors and micro-mechanism of the interface transition zone in sandstone-concrete interface in response to freeze-thaw conditions [J]. Cold Regions Science and Technology, 2021, 191: 103359. doi: 10.1016/j.coldregions.2021.103359
[12]	XIA W, CUI S A, XU L L, et al. Study on the fracture performance for rock-concrete interface in the high geothermal tunnel environment [J]. Construction and Building Materials, 2022, 347: 128568. doi: 10.1016/j.conbuildmat.2022.128568
[13]	HU Y P, WANG M N, WANG Z L, et al. Mechanical behavior and constitutive model of shotcrete-rock interface subjected to heat damage and variable temperature curing conditions [J]. Construction and Building Materials, 2020, 263: 120171. doi: 10.1016/j.conbuildmat.2020.120171
[14]	陆文博, 晏鄂川, 邹浩, 等. 我国倾倒变形体发育规律研究 [J]. 长江科学院院报, 2017, 34(8): 111–119. doi: 10.11988/ckyyb.20160484 LU W B, YAN E C, ZOU H, et al. Development rules of toppling deformation slopes in China [J]. Journal of Yangtze River Scientific Research Institute, 2017, 34(8): 111–119. doi: 10.11988/ckyyb.20160484
[15]	邓鹏海, 刘泉声, 黄兴. 隧道底板渐进破裂碎胀大变形: 一种新的底鼓机制研究 [J]. 岩土力学, 2023, 44(5): 1512–1529. doi: 10.16285/j.rsm.2022.0831 DENG P H, LIU Q S, HUANG X. Progressive fracture and swelling deformation of tunnel floor: a new floor heave mechanism [J]. Rock and Soil Mechanics, 2023, 44(5): 1512–1529. doi: 10.16285/j.rsm.2022.0831
[16]	李树忱, 马腾飞, 蒋宇静, 等. 深部多裂隙岩体开挖变形破坏规律模型试验研究 [J]. 岩土工程学报, 2016, 38(6): 987–995. doi: 10.11779/CJGE201606003 LI S C, MA T F, JIANG Y J, et al. Model tests on deformation and failure laws in excavation of deep rock mass with multiple fracture sets [J]. Chinese Journal of Geotechnical Engineering, 2016, 38(6): 987–995. doi: 10.11779/CJGE201606003
[17]	CAO W G, TAN X, ZHANG C, et al. Constitutive model to simulate full deformation and failure process for rocks considering initial compression and residual strength behaviors [J]. Canadian Geotechnical Journal, 2019, 56(5): 649–661. doi: 10.1139/cgj-2018-0178
[18]	李庆文, 禹萌萌, 高森林, 等. 加载速率对碳纤维布被动约束煤能量演化影响研究 [J/OL]. 煤炭学报(2023-06-08)[2024-04-26]. https://doi.org/10.13225/j.cnki.jccs.2023.0238. LI Q W, YU M M, GAO S L, et al. The effect of loading rate on energy evolution of coal confined passively by CFRP sheets [J/OL]. Journal of China Coal Society (2023-06-08)[2024-04-26]. https://doi.org/10.13225/j.cnki.jccs.2023.0238.
[19]	周辉, 李震, 杨艳霜, 等. 岩石统一能量屈服准则 [J]. 岩石力学与工程学报, 2013, 32(11): 2170–2184. ZHOU H, LI Z, YANG Y S, et al. Unified energy yield criterion of rock [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(11): 2170–2184.
[20]	ZHAO Y Q, LI Q S, ZHANG K, et al. Effect of fissure angle on energy evolution and failure characteristics of fractured rock under uniaxial cyclic loading [J]. Scientific Reports, 2023, 13(1): 2678. doi: 10.1038/s41598-022-26091-4
[21]	HU J, WANG H K, XIA Z G, et al. Mechanical properties and acoustic emission characteristics of two dissimilar layers of rock-like specimens with prefabricated parallel fissures [J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources, 2024, 10(1): 19. doi: 10.1007/s40948-024-00755-z
[22]	武世岩, 黄彦华. 含弧形裂隙花岗岩裂纹扩展特征PFC模拟 [J]. 中南大学学报(自然科学版), 2023, 54(1): 169–182. doi: 10.11817/j.issn.1672-7207.2023.01.016 WU S Y, HUANG Y H. PFC simulation on crack coalescence behavior of granite specimens containing an arc fissure [J]. Journal of Central South University (Science and Technology), 2023, 54(1): 169–182. doi: 10.11817/j.issn.1672-7207.2023.01.016
[23]	中华人民共和国水利部. 水利水电工程岩石试验规程: SL/T 264—2020 [S]. 北京: 中国水利水电出版社, 2020. Ministry of Water Resources of the People’s Republic of China. Code for rock tests in water and hydropower projects: SL/T 264—2020 [S]. Beijing: China Water & Power Press, 2020.
[24]	SONG L B, WANG G, WANG X K, et al. The influence of joint inclination and opening width on fracture characteristics of granite under triaxial compression [J]. International Journal of Geomechanics, 2022, 22(5): 04022031. doi: 10.1061/(ASCE)GM.1943-5622.0002372
[25]	李琦. 单轴压缩过程中岩石-混凝土一体两介质体声发射特性研究 [D]. 邯郸: 河北工程大学, 2018. LI Q. Research on acoustic emission characteristics of rock and concrete monolithic body in uniaxial compression [D]. Handan: Hebei University of Engineering, 2018.
[26]	SU C, WU Z, XU H, et al. Analysis of influencing factors of pneumatic flow enhancement of pumped concrete based on discrete element method [J]. Frontiers in Earth Science, 2022, 10: 968085. doi: 10.3389/FEART.2022.968085
[27]	陆建友. 岩石-混凝土圆盘径向压缩条件下力学性能研究 [D]. 焦作: 河南理工大学, 2018. LU J Y. Study on mechanical properties of rock-concrete disc under radial compression [D]. Jiaozuo: Henan Polytechnic University, 2018.
[28]	YUE Z F, MENG F Z, ZHOU X, et al. Influence of non-persistent joint aperture and inclination angle on the shear behavior and fracture mode of solid rock and concrete material [J]. Construction and Building Materials, 2022, 316: 125892. doi: 10.1016/j.conbuildmat.2021.125892
[29]	SHANG Y H, XU L R, LI Y W. Unloading response characteristics of cross fault caverns: effect of fault angles [J]. Geotechnical and Geological Engineering, 2022, 40(3): 1061–1073. doi: 10.1007/s10706-021-01942-5
[30]	石崇, 张强, 王盛年. 颗粒流(PFC5.0)数值模拟技术及应用 [M]. 北京: 中国建筑工业出版社, 2018. SHI C, ZHANG Q, WANG S N. Numerical simulation technology and application with particle flow code (PFC5.0) [M]. Beijing: China Architecture & Building Press, 2018.
[31]	陈鹏宇, 孔莹, 余宏明. 岩石单轴压缩PFC^2D模型细观参数标定研究 [J]. 地下空间与工程学报, 2018, 14(5): 1240–1249. CHEN P Y, KONG Y, YU H M. Research on the calibration method of microparameters of a uniaxial compression PFC^2D model for rock [J]. Chinese Journal of Underground Space and Engineering, 2018, 14(5): 1240–1249.
[32]	许尚杰, 尹小涛, 马双科, 等. 基于颗粒流的混凝土材料数值实验研究 [J]. 实验力学, 2009, 24(3): 251–258. XU S J, YIN X T, MA S K, et al. Numerical test study of concrete material based on particle flow [J]. Journal of Experimental Mechanics, 2009, 24(3): 251–258.
[33]	冯一. 基于岩石细观力学的裂缝闭合机理研究 [D]. 成都: 西南石油大学, 2016. FENG Y. Fracture closure mechanism based on rock meso-mechanics [D]. Chengdu: Southwest Petroleum University, 2016.
[34]	易婷, 唐建新, 王艳磊. 裂隙倾角及数目对岩体强度和破坏模式的影响 [J]. 地下空间与工程学报, 2021, 17(1): 98–106, 134. YI T, TANG J X, WANG Y L. Effect of fracture dip angle and number on mechanical properties and failure modes of rock mass [J]. Chinese Journal of Underground Space and Engineering, 2021, 17(1): 98–106, 134.
[35]	王国艳, 于广明, 李刚, 等. 初始裂隙倾角对岩石破坏模式及峰值强度的影响 [J]. 中国矿业, 2017, 26(10): 173–176. WANG G Y, YU G M, LI G, et al. Influence of initial crack dip angle on failure mode and peak strength of rock [J]. China Mining Magazine, 2017, 26(10): 173–176.
[36]	李庆文, 才诗婷, 李涵静, 等. 单裂隙岩石-混凝土组合体断裂特征颗粒流模拟 [J]. 高压物理学报, 2024, 38(5): 054202. LI Q W, CAI S T, LI H J, et al. Particle flow simulation of fracture characteristics of rock-concrete combination with single crack [J]. Chinese Journal of High Pressure Physics, 2024, 38(5): 054202.
[37]	王桂林, 张亮, 许明, 等. 单轴压缩下非贯通节理岩体损伤破坏能量演化机制研究 [J]. 岩土工程学报, 2019, 41(4): 639–647. doi: 10.11779/CJGE201904006 WANG G L, ZHANG L, XU M, et al. Energy damage evolution mechanism of non-across jointed rock mass under uniaxial compression [J]. Chinese Journal of Geotechnical Engineering, 2019, 41(4): 639–647. doi: 10.11779/CJGE201904006
[38]	李庆文, 曾杏钢, 张向东, 等. 碳纤维布层数对煤圆柱力学特性影响的细观研究 [J]. 煤炭科学技术, 2023, 51(8): 73–85. doi: 10.13199/j.cnki.cst.2022-0976 LI Q W, ZENG X G, ZHANG X D, et al. Mesoscopic study on the effect of CFRP layers on the mechanical properties of coal circular-columns [J]. Coal Science and Technology, 2023, 51(8): 73–85. doi: 10.13199/j.cnki.cst.2022-0976
[39]	李庆文, 高安梁, 禹萌萌, 等. 碳纤维布均匀约束下煤圆柱的损伤演化 [J]. 金属矿山, 2024(2): 104–113. doi: 10.19614/j.cnki.jsks.202402010 LI Q W, GAO A L, YU M M, et al. Damage evolution of coal cylinder under uniform confinement of carbon fiber sheets [J]. Metal Mine, 2024(2): 104–113. doi: 10.19614/j.cnki.jsks.202402010
[40]	尹升华, 侯永强, 杨世兴, 等. 单轴压缩下混合集料胶结充填体变形破坏及能耗特征分析 [J]. 中南大学学报(自然科学版), 2021, 52(3): 936–947. doi: 10.11817/j.issn.1672-7207.2021.03.025 YIN S H, HOU Y Q, YANG S X, et al. Analysis of deformation failure and energy dissipation of mixed aggregate cemented backfill during uniaxial compression [J]. Journal of Central South University (Science and Technology), 2021, 52(3): 936–947. doi: 10.11817/j.issn.1672-7207.2021.03.025
[41]	XIA B W, LI Y, HU H R, et al. Effect of crack angle on mechanical behaviors and damage evolution characteristics of sandstone under uniaxial compression [J]. Rock Mechanics and Rock Engineering, 2022, 55(11): 6567–6582. doi: 10.1007/s00603-022-03016-1
[42]	马秋峰, 刘志河, 秦跃平, 等. 基于能量耗散理论的岩石塑性-损伤本构模型 [J]. 岩土力学, 2021, 42(5): 1210–1220. doi: 10.16285/j.rsm.2020.1091 MA Q F, LIU Z H, QIN Y P. Rock plastic-damage constitutive model based on energy dissipation [J]. Rock and Soil Mechanics, 2021, 42(5): 1210–1220. doi: 10.16285/j.rsm.2020.1091
[43]	张琪, 李祥春, 李彪, 等. 单轴压缩条件下煤体的宏-微观损伤破坏特征研究 [J/OL]. 采矿与安全工程学报(2023-11-03)[2024-04-26]. https://www.chinacaj.net/i,92,489849,0.html. ZHANG Q, LI X C, LI B, et al. Research on the damage characteristics of macro and microscopic scales of a loaded coal under uniaxial compression [J/OL]. Journal of Mining & Safety Engineering (2023-11-03)[2024-04-26]. https://www.chinacaj.net/i,92,489849,0.html.
[44]	张慧梅, 谢祥妙, 张蒙军, 等. 真三轴应力状态下岩石损伤本构模型 [J]. 力学与实践, 2015, 37(1): 75–78. doi: 10.6052/1000-0879-13-517 ZHANG H M, XIE X M, ZHANG M J, et al. Damage constitutive model of rock under the true triaxial confinement state [J]. Mechanics in Engineering, 2015, 37(1): 75–78. doi: 10.6052/1000-0879-13-517
[45]	宋浩然, 李守宇, 张庆文, 等. 含水泥砂岩声发射阶段特征与损伤演化研究 [J]. 地下空间与工程学报, 2024, 20(1): 72–81. SONG H R, LI S Y, ZHANG Q W, et al. The acoustic emission stage characteristics and damage evolution of argillaceous siltstone [J]. Chinese Journal of Underground Space and Engineering, 2024, 20(1): 72–81.
[46]	李庆文, 高森林, 胡露露, 等. 不同加载速率下非均质煤样能量耗散损伤本构关系 [J]. 煤炭学报, 2022, 47(Suppl 1): 90–102. LI Q W, GAO S L, HU L L, et al. Constitutive relation of energy dissipation damage of heterogeneous coal samples under different loading rates [J]. Journal of China Coal Society, 2022, 47(Suppl 1): 90–102.
[47]	张超, 杨楚卿, 白允. 岩石类脆性材料损伤演化分析及其模型方法研究 [J]. 岩土力学, 2021, 42(9): 2344–2354. doi: 10.16285/j.rsm.2021.0278 ZHANG C, YANG C Q, BAI Y. Investigation of damage evolution and its model of rock-like brittle materials [J]. Rock and Soil Mechanics, 2021, 42(9): 2344–2354. doi: 10.16285/j.rsm.2021.0278