Study on the Behavior of Blasting Crack Propagation under Different Crack Widths
-
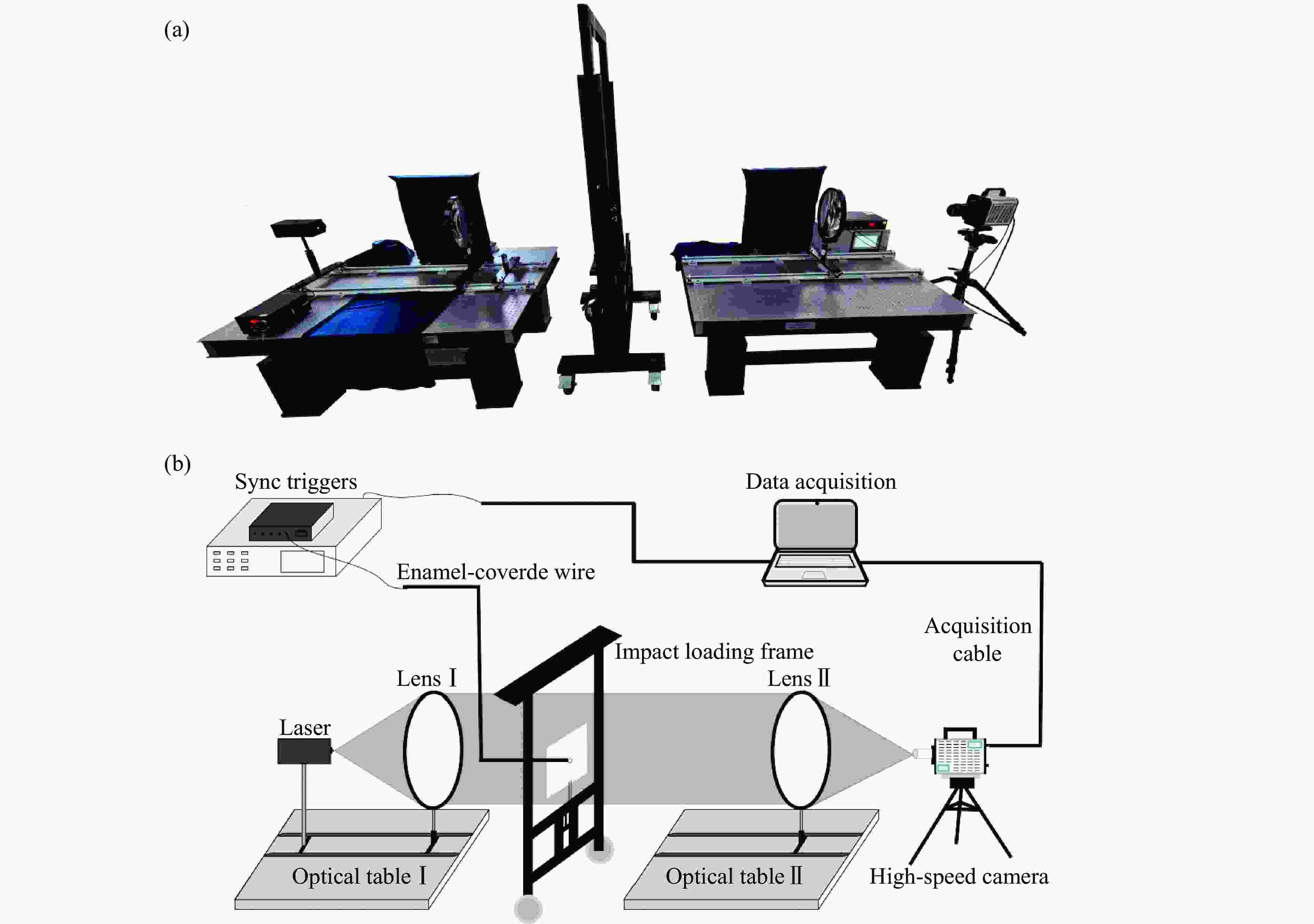
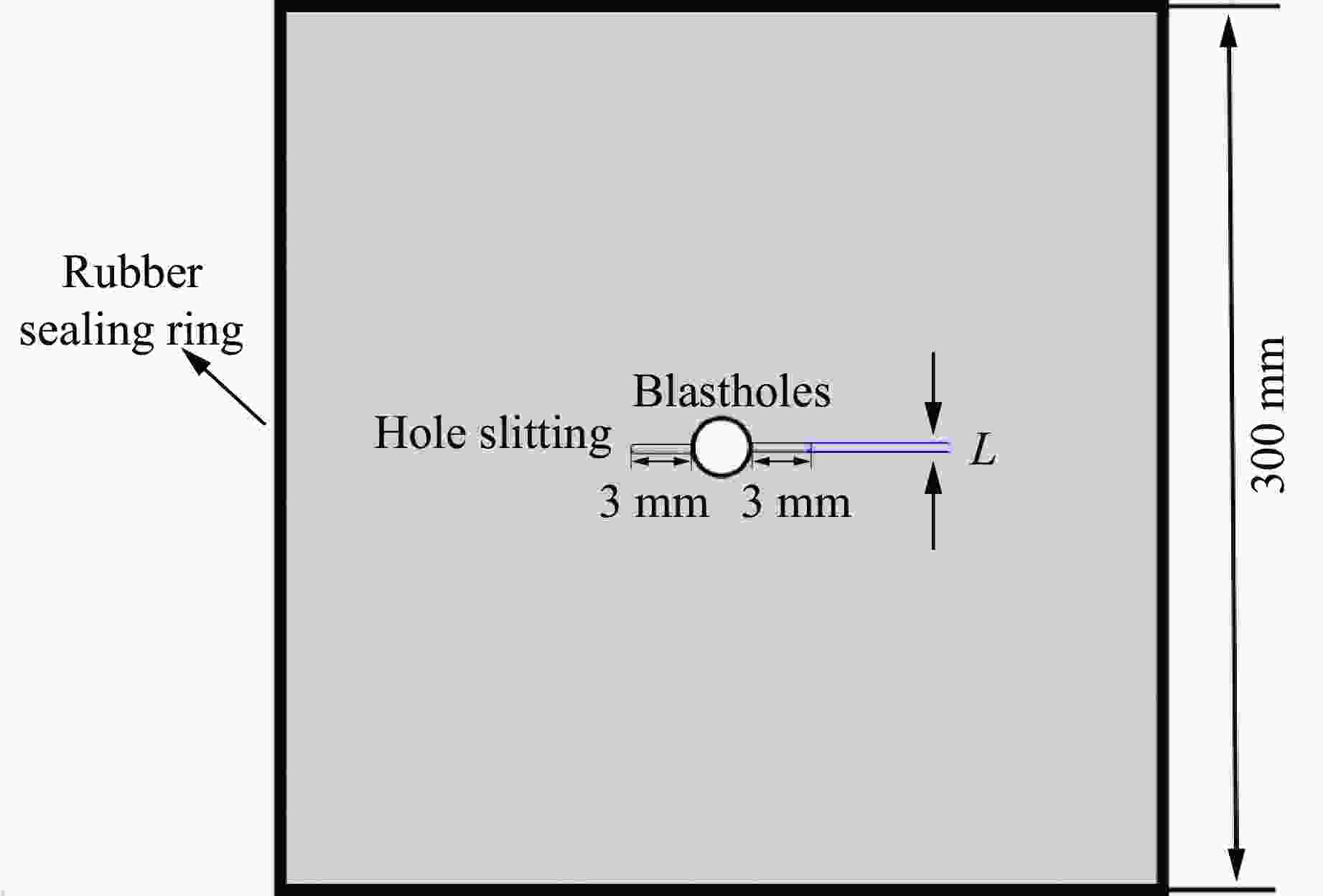
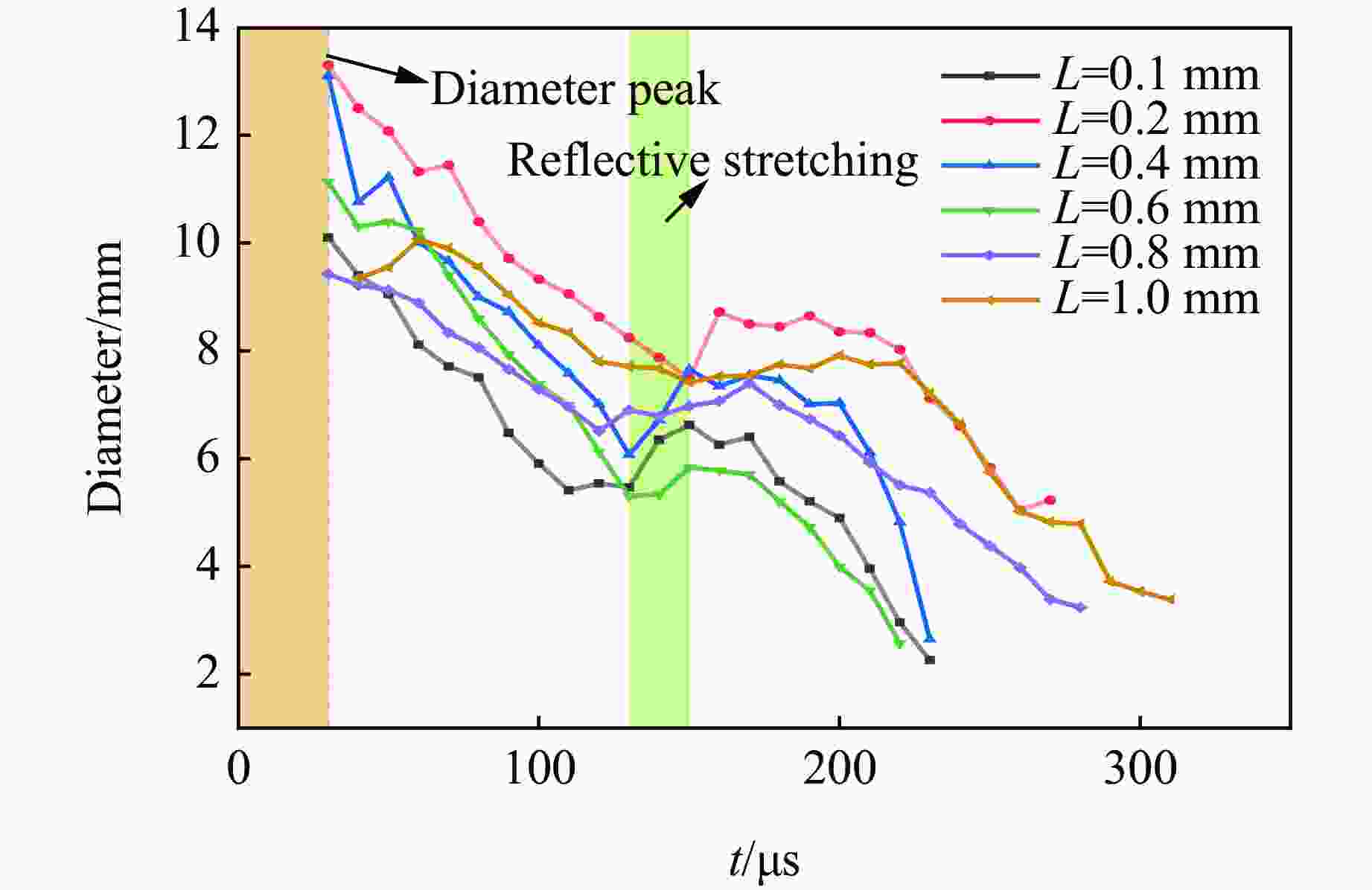
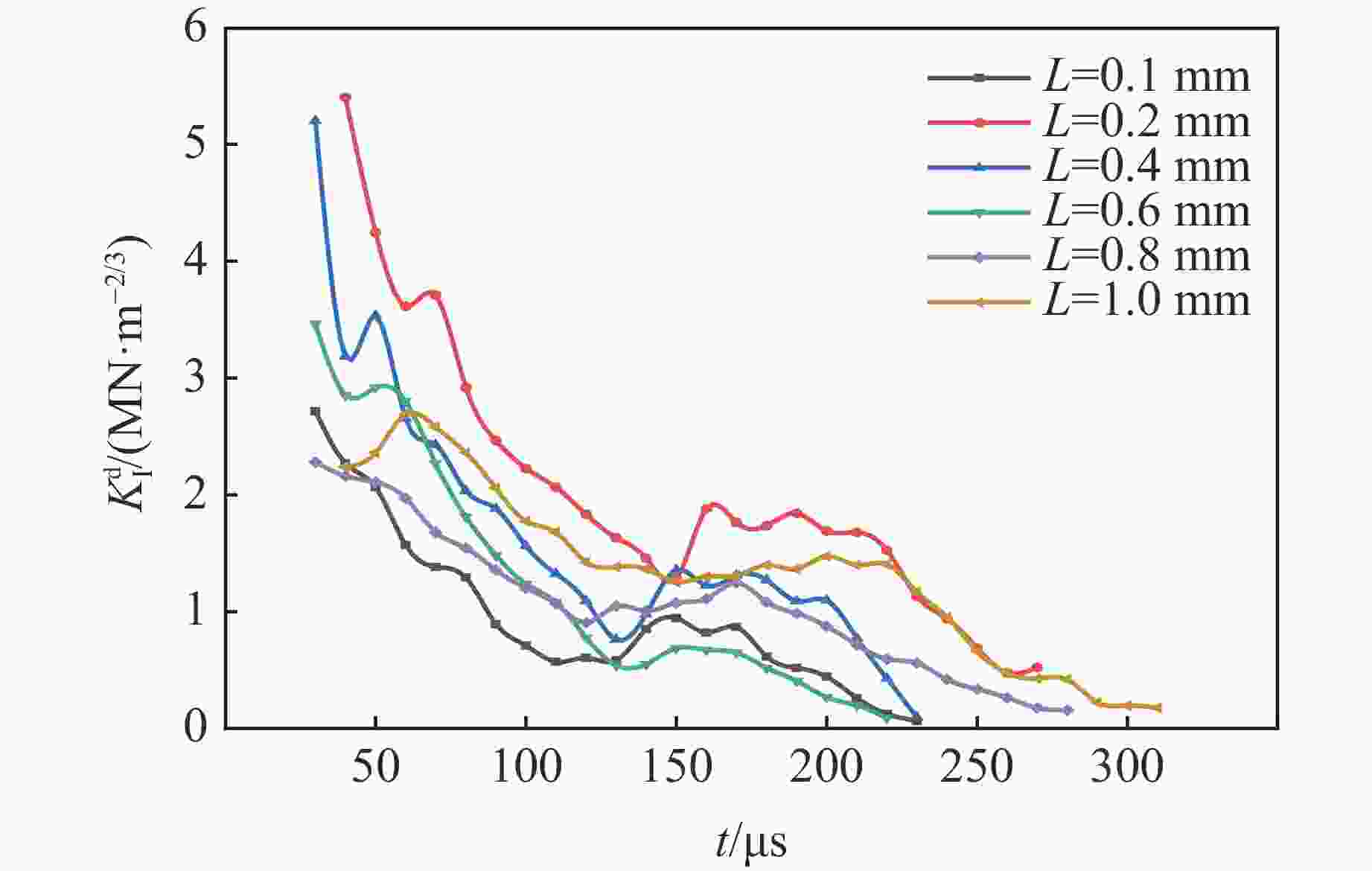
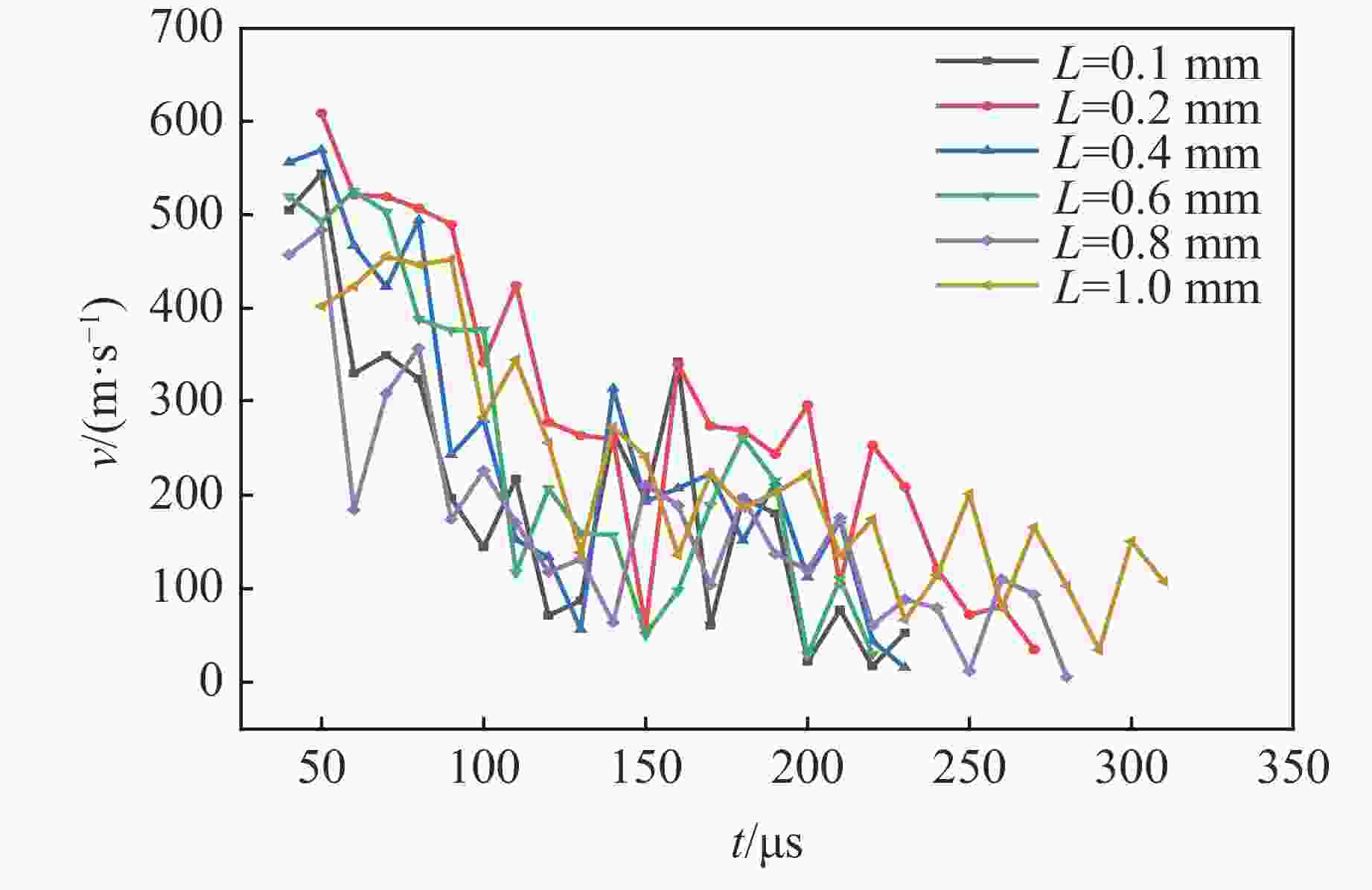
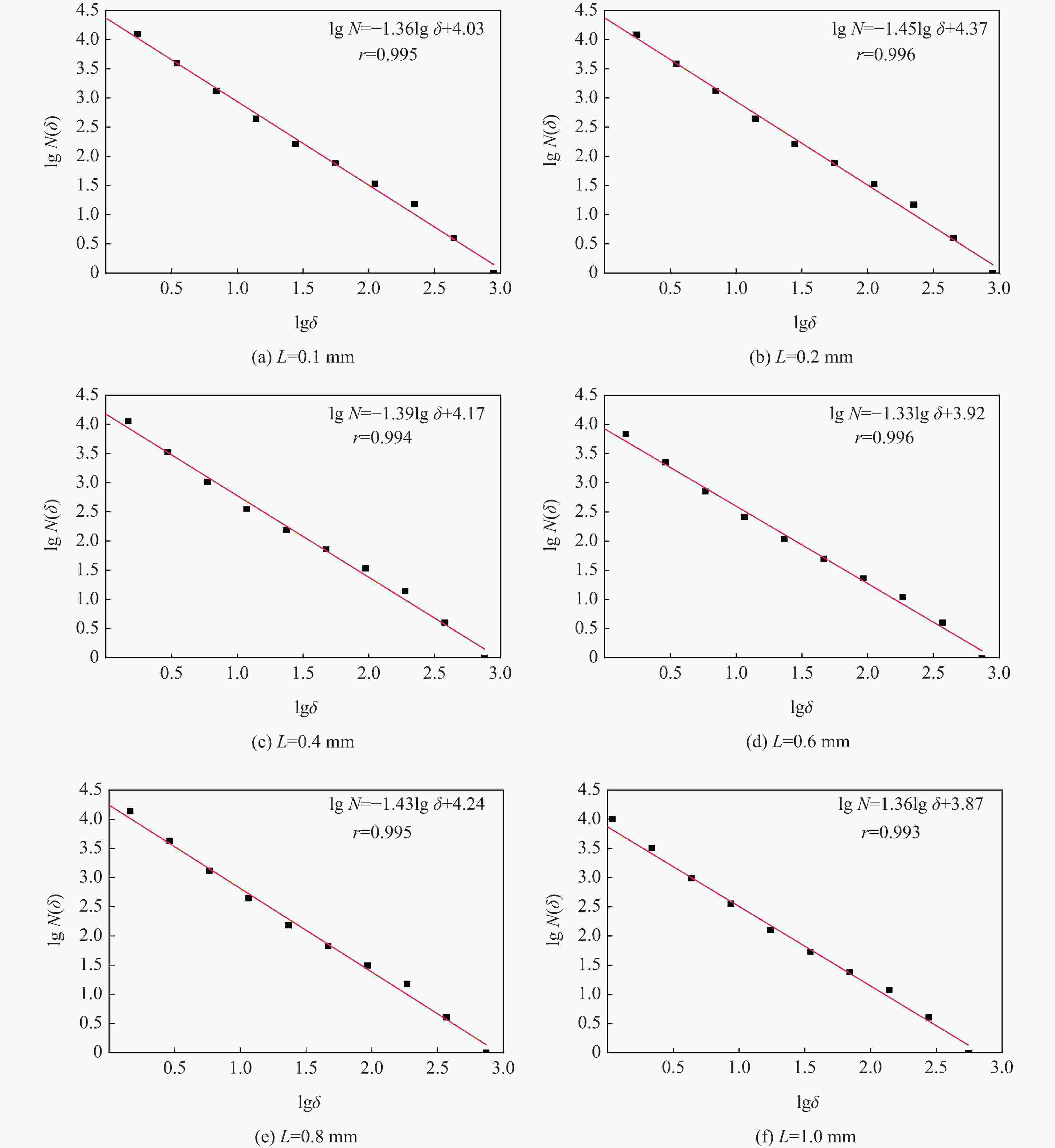
摘要: 为探讨炮孔不同割缝宽度对爆生裂纹动态扩展行为的影响，采用数字激光动态焦散线实验系统和分形理论，研究了6种不同割缝宽度时爆生裂纹的扩展规律。结果表明：割缝方向的爆生裂纹长度均大于非割缝方向的爆生裂纹长度；随着割缝宽度的增加，爆生裂纹扩展长度呈现先增大后减小的变化趋势；当割缝宽度增加到0.4 mm时，主裂纹扩展长度最大，割缝宽度继续增加后，主裂纹扩展长度减小。当割缝宽度为0.2 和0.4 mm时，分形维数较其他割缝宽度更大，爆生主裂纹的扩展长度较其他宽度下的扩展长度更长，试件定向断裂效果更优。随着割缝宽度的增加，割缝主裂纹的扩展应力强度因子和速度峰值呈现先快速降低再增加至二次峰值，最后振荡下降的变化趋势。割缝宽度为0.2和0.4 mm时，主裂纹应力强度因子的峰值和扩展速度峰值较其他割缝宽度更大。研究成果可为实际爆破工程中的割缝参数选择提供依据。Abstract: To study the influence of slit width on the dynamic propagation behavior of blast cracks, the digital laser dynamic caustic line experimental system and fractal theory were used to study the propagation laws of blast cracks at six different crack widths. The results show that the length of burst cracks in the cut direction is greater than that in the non-cut direction. With the increase of the slit width, the propagation length of burst crack increases first and then decreases. When the slit width increases to 0.4 mm, the main crack propagation length is the largest, and when the slit width continues to increase, the main crack propagation length decreases. When the slit width is 0.2 and 0.4 mm, the fractal dimension is larger than that of other slit widths, the expansion length of the main crack is longer than that of other widths, and the directional fracture effect of the specimen is better. With the increase of the slit width, the stress intensity factor and velocity peak value of the main crack propagation of the slot shows a trend of first decreasing rapidly, then increasing to the secondary peak, and finally oscillating and decreasing. When the crack width is 0.2 and 0.4 mm, the peak value of the stress intensity factor and the expansion velocity of the main crack are larger than those of other crack widths. The research results provide a certain basis for the selection of slit parameters in actual blasting engineering.
-
Key words:
- dynamic caustic lines /
- crack propagation /
- stress intensity factor /
- box dimension
-
图 2 动焦散实验系统实物照片和原理示意图
Figure 2. Photo and schematic diagram of the dynamic caustic experimental system
图 4 不同割缝宽度（0.1、0.2、0.4、0.6、0.8、1.0 mm）试件的爆后裂纹分布
Figure 4. Crack distribution of specimens with different slit widths (0.1, 0.2, 0.4, 0.6, 0.8, 1.0 mm) after blasting
图 6 割缝左侧焦散斑直径-时间演化曲线
Figure 6. Diameter-time evolution curves of caustic speckle on the left side of slit
图 7 试件左侧裂纹尖端的应力强度因子
Figure 7. Stress intensity factor at the crack tip on the left side of the specimen
图 9 不同割缝宽度下左侧裂纹的扩展速度-时间曲线
Figure 9. Velocity-time curves of left crack propagation under different slit widths
$ {E}_{\mathrm{d}} $/GPa $ \mu_{\mathrm{ }} $ |$ c $|/(m2·N−1) $ c_{\mathrm{p}} $/(m·s−1) $ {c}_{\mathrm{s}} $/(m·s−1) 6.10 0.31 0.88×10−10 2320 1260 
下载: 导出CSV
表 2 裂纹的扩展长度
Table 2. Propagation lengths of the crack
L/mm Crack length/mm Left Right 0.1 41.4 41.3 0.2 63.5 64.0 0.4 69.0 73.0 0.6 57.2 46.2 0.8 38.4 40.0 1.0 39.7 37.4
下载: 导出CSV
-
[1] LI X D, LIU K W, QIU T, et al. Study of presplit blasting under high in-situ stress [J]. Engineering Fracture Mechanics, 2023, 288: 109360. doi: 10.1016/j.engfracmech.2023.109360 [2] 杨仁树, 苏洪. 爆炸荷载下含预裂缝的裂纹扩展实验研究 [J]. 煤炭学报, 2019, 44(2): 482–489. doi: 10.13225/j.cnki.jccs.2018.0110YANG R S, SU H. Experimental study on crack propagation with pre-crack under explosion load [J]. Journal of China Coal Society, 2019, 44(2): 482–489. doi: 10.13225/j.cnki.jccs.2018.0110 [3] 苏洪, 龚悦, 杨仁树, 等. 爆炸荷载作用下预裂缝宽度对裂纹扩展的影响 [J]. 中国矿业大学学报, 2021, 50(3): 579–586. doi: 10.13247/j.cnki.jcumt.001253SU H, GONG Y, YANG R S, et al. Influence of pre-splitting crack width on crack propagation under blast loading [J]. Journal of China University of Mining & Technology, 2021, 50(3): 579–586. doi: 10.13247/j.cnki.jcumt.001253 [4] 韩磊, 侯水云, 贾湛永. 深孔预裂爆破弱化坚硬陷落柱技术研究 [J]. 煤炭工程, 2018, 50(6): 81–84. doi: 10.11799/ce201806023HAN L, HOU S Y, JIA Z Y. Technology research of deep hole presplit blasting for hard collapse column weakening [J]. Coal Engineering, 2018, 50(6): 81–84. doi: 10.11799/ce201806023 [5] PAN C, XIE L X, LI X, et al. Numerical investigation of effect of eccentric decoupled charge structure on blasting-induced rock damage [J]. Journal of Central South University, 2022, 29(2): 663–679. doi: 10.1007/s11771-022-4947-3 [6] 韦丹, 黄海华, 彭四佑, 等. 断层破碎带光面爆破技术研究与应用 [J]. 爆破, 2023, 40(1): 85–91. doi: 10.3963/j.issn.1001-487X.2023.01.012WEI D, HUANG H H, PENG S Y, et al. Research and application of smooth blasting technology in fault fracture zone [J]. Blasting, 2023, 40(1): 85–91. doi: 10.3963/j.issn.1001-487X.2023.01.012 [7] 李龙福, 方建国, 汪禹, 等. 分次分段掘进爆破技术在复杂破碎岩体中的应用 [J]. 金属矿山, 2022(4): 79–83. doi: 10.19614/j.cnki.jsks.202204011LI L F, FANG J G, WANG Y, et al. Application of staged excavation blasting technology in complex broken rock mass [J]. Metal Mine, 2022(4): 79–83. doi: 10.19614/j.cnki.jsks.202204011 [8] 岳中文, 王煦. 不同切槽孔方向爆生裂纹扩展行为试验与分析 [J]. 煤炭学报, 2016, 41(Suppl 2): 412–418. doi: 10.13225/j.cnki.jccs.2015.1043YUE Z W, WANG X. Experimental analysis on behaviors of blast-induced crack propagation in different notched borehole orientations [J]. Journal of China Coal Society, 2016, 41(Suppl 2): 412–418. doi: 10.13225/j.cnki.jccs.2015.1043 [9] 岳中文, 邱鹏, 杨仁树, 等. 切槽炮孔偏心装药爆源近区裂纹动态力学特征实验研究 [J]. 岩石力学与工程学报, 2017, 36(Suppl 2): 3792–3798. doi: 10.13722/j.cnki.jrme.2016.0575YUE Z W, QIU P, YANG R S, et al. Experimental study on crack dynamic mechanical characteristic near blasting source of grooved borehole with eccentric decouple charge [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(Suppl 2): 3792–3798. doi: 10.13722/j.cnki.jrme.2016.0575 [10] DING C X, YANG R S, XIAO C L, et al. Directional fracture behavior and stress evolution process of the multi-slit charge blasting [J]. Soil Dynamics and Earthquake Engineering, 2022, 152: 107037. doi: 10.1016/j.soildyn.2021.107037 [11] MENG N K, CHEN Y, BAI J B, et al. Numerical simulation of directional fracturing by shaped charge blasting [J]. Energy Science & Engineering, 2020, 8(5): 1824–1839. doi: 10.1002/ese3.635 [12] 罗勇, 沈兆武. 切缝药包岩石定向断裂爆破的研究 [J]. 振动与冲击, 2006, 25(4): 155–158. doi: 10.3969/j.issn.1000-3835.2006.04.042LUO Y, SHEN Z W. Study on the directional fracture controlled blasting with slit-charge in rock [J]. Journal of Vibration and Shock, 2006, 25(4): 155–158. doi: 10.3969/j.issn.1000-3835.2006.04.042 [13] 段宝福, 柴明星, 魏玉冠, 等. 切缝药包参数对切缝效果的影响研究[J]. 煤炭技术, 2024, 43(5): 29−33.DUAN B F, CHAI M X, WEI Y G, et al. Study on the influence of slit charge parameters on slit effect [J]. Coal Technology, 2024, 43(5): 29−33. [14] YIN Y, SUN Q, ZOU B P, et al. Numerical study on an innovative shaped charge approach of rock blasting and the timing sequence effect in microsecond magnitude [J]. Rock Mechanics and Rock Engineering, 2021, 54(9): 4523–4542. doi: 10.1007/s00603-021-02516-w [15] 黄寅洪, 张庆彬, 颜天成, 等. 环向切缝药包爆破块度分布特征及其机理研究 [J]. 工程爆破, 2023, 29(6): 122–132. doi: 10.19931/j.EB.20230001HUANG Y H, ZHANG Q B, YAN T C, et al. Study on blasting fragmentation and characteristics of circumferential slit charge [J]. Engineering Blasting, 2023, 29(6): 122–132. doi: 10.19931/j.EB.20230001 [16] LIU C W, LU Y Y, XIA B W, et al. Directional fracturing by slotting-blasting-caused stress wave form changes [J]. International Journal of Impact Engineering, 2019, 129: 141–151. doi: 10.1016/j.ijimpeng.2019.02.002 [17] LANGEFORS U, KIHLSTRÖM B. The modern technique of rock blasting [M]. 3rd ed. New York: John Wiley and Sons, 1978: 296−321. [18] 乔国栋, 高魁, 郑明亮, 等. 含控制孔切槽爆破的裂隙扩展机制研究 [J]. 工程爆破, 2020, 26(2): 24–31. doi: 10.3969/j.issn.1006-7051.2020.02.004QIAO G D, GAO K, ZHENG M L, et al. Study on crack propagation mechanism of grooving blasting with controlled hole [J]. Engineering Blasting, 2020, 26(2): 24–31. doi: 10.3969/j.issn.1006-7051.2020.02.004 [19] 李清, 郭洋, 刘航, 等. 切槽定向断裂控制爆破的数值模拟研究 [J]. 矿业研究与开发, 2015, 35(12): 79–83. doi: 10.13827/j.cnki.kyyk.2015.12.018LI Q, GUO Y, LIU H, et al. Numerical simulation on pre-notched directional fracture blast [J]. Mining Research and Development, 2015, 35(12): 79–83. doi: 10.13827/j.cnki.kyyk.2015.12.018 [20] 岳中文, 杨仁树, 郭东明, 等. 爆炸应力波作用下缺陷介质裂纹扩展的动态分析 [J]. 岩土力学, 2009, 30(4): 949–954. doi: 10.3969/j.issn.1000-7598.2009.04.015YUE Z W, YANG R S, GUO D M, et al. Dynamic analysis of crack propagation in media containing flaws under the explosive stress wave [J]. Rock and Soil Mechanics, 2009, 30(4): 949–954. doi: 10.3969/j.issn.1000-7598.2009.04.015 [21] THEOCARIS P S, GDOUTOS E E. The modified Dugdale-Barenblatt model adapted to various fracture configurations in metals [J]. International Journal of Fracture, 1974, 10(4): 549–564. doi: 10.1007/BF00155258 [22] PAPADOPOULOS G A. Dynamic caustics and its applications [J]. Optics and Lasers in Engineering, 1990, 13(3/4): 211–249. doi: 10.1016/0143-8166(90)90047-D [23] KALTHOFF J F. The shadow optical method of caustics [M]//LAGARDE A. Static and Dynamic Photoelasticity and Caustics: Recent Developments. Vienna: Springer, 1987: 407–522. [24] NAKAGAWA K, SAKAMOTO T, YOSHIKAI R. Model study of the guide hole effect on the smooth blasting [J]. Journal of the Physical Society of Japan, 1982, 43: 75–82. [25] KUTTER H K, FAIRHURST C. On the fracture process in blasting [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1971, 8(3): 181–202. doi: 10.1016/0148-9062(71)90018-0 [26] ROSSMANITH H P, DAEHNKE A, NASMILLNER R E K, et al. Fracture mechanics applications to drilling and blasting [J]. Fatigue & Fracture of Engineering Materials & Structures, 1997, 20(11): 1617–1636. doi: 10.1111/j.1460-2695.1997.tb01515.x [27] 谢和平, 陈至达. 分形(fractal)几何与岩石断裂 [J]. 力学学报, 1988, 20(3): 264–271.XIE H P, CHEN Z D. Fractal geometry and fracture of rock [J]. Acta Mechanica Sinica, 1988, 20(3): 264–271. -
下载:
点击查看大图
图(10) / 表(2)
计量
- 文章访问数: 60
- HTML全文浏览量: 11
- PDF下载量: 15
