花岗岩板双基火药切槽爆破破坏过程研究

王多良; 李洪伟; 梁昊; 李世影; 吴延梦; 赵静; 李纯志; 肖忠良

doi:10.11858/gywlxb.20240711

花岗岩板双基火药切槽爆破破坏过程研究

doi: 10.11858/gywlxb.20240711

1.
安徽理工大学化工与爆破学院, 安徽淮南　232001
2.
南京理工大学化学与化工学院, 江苏南京　210094
3.
泸州北方化学工业有限公司, 四川泸州　646003

基金项目: 安徽高校自然科学研究项目（2022yjrc17）

详细信息

作者简介:
王多良（2000－），男，硕士研究生，主要从发射药及装药研究. E-mail：wangduoliang0720@163.com

通讯作者:
李洪伟（1979－），男，硕士，教授，主要从事爆炸技术及应用研究. E-mail：lihw@aust.edu.cn

中图分类号: O346.1; TJ562
计量
- 文章访问数: 93
- HTML全文浏览量: 37
- PDF下载量: 22
出版历程
- 收稿日期: 2024-01-16
- 修回日期: 2024-03-13
- 录用日期: 2024-03-27
- 刊出日期: 2024-07-25

Damage Process of Double Base Propellant Grooved Blasting on Granite Slab

1.
School of Chemical and Blasting Engineering, Anhui University of Science and Technology, Huainan 232001, Anhui, China
2.
School of Chemistry and Chemical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
3.
Luzhou North Chemical Industries Co., Ltd., Luzhou 646003, Sichuan, China

摘要

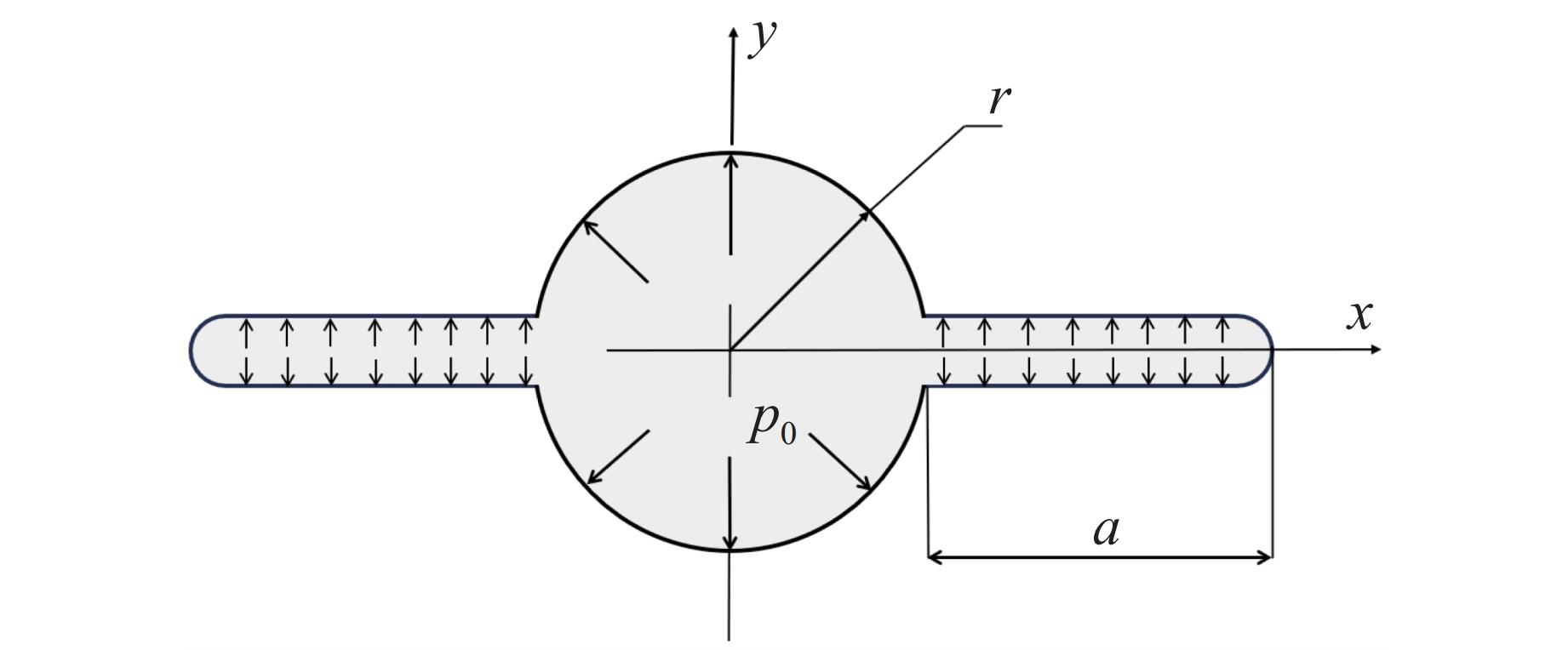
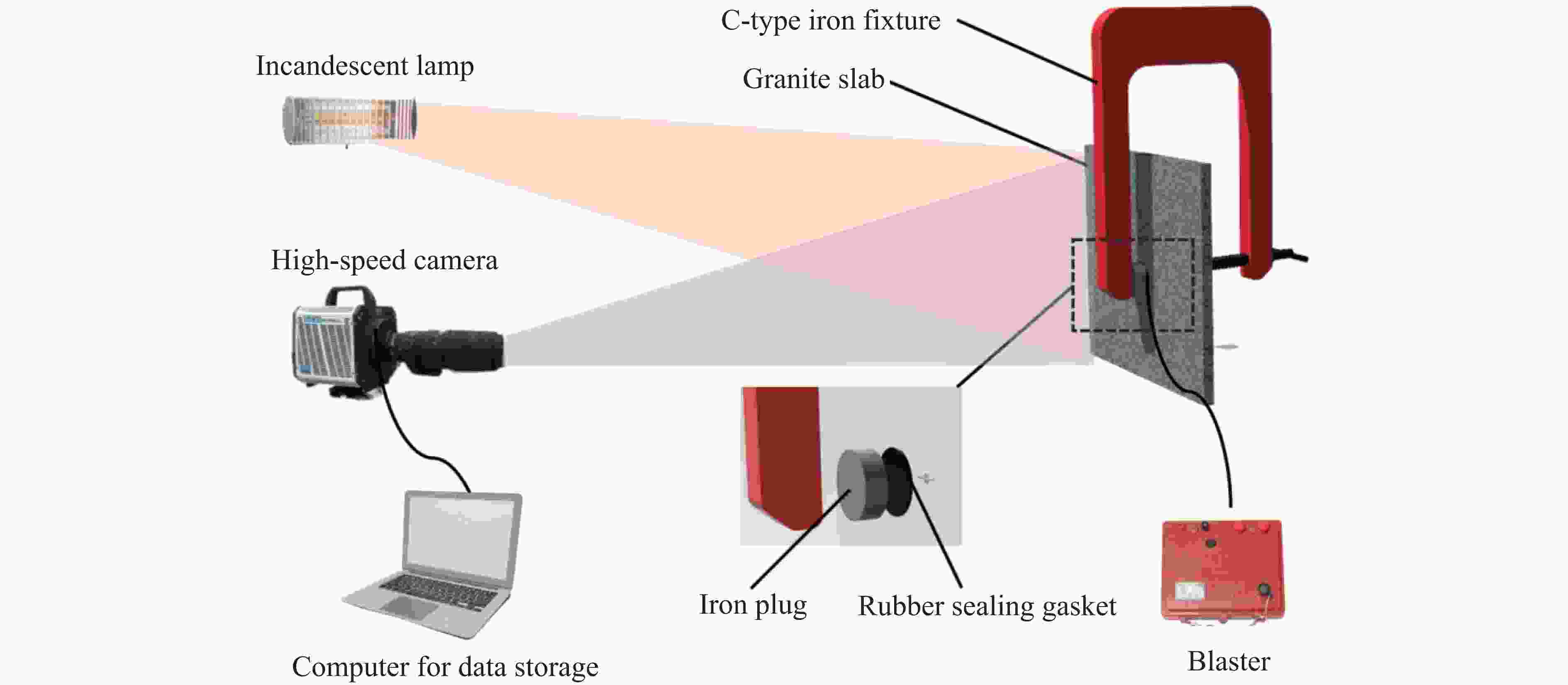
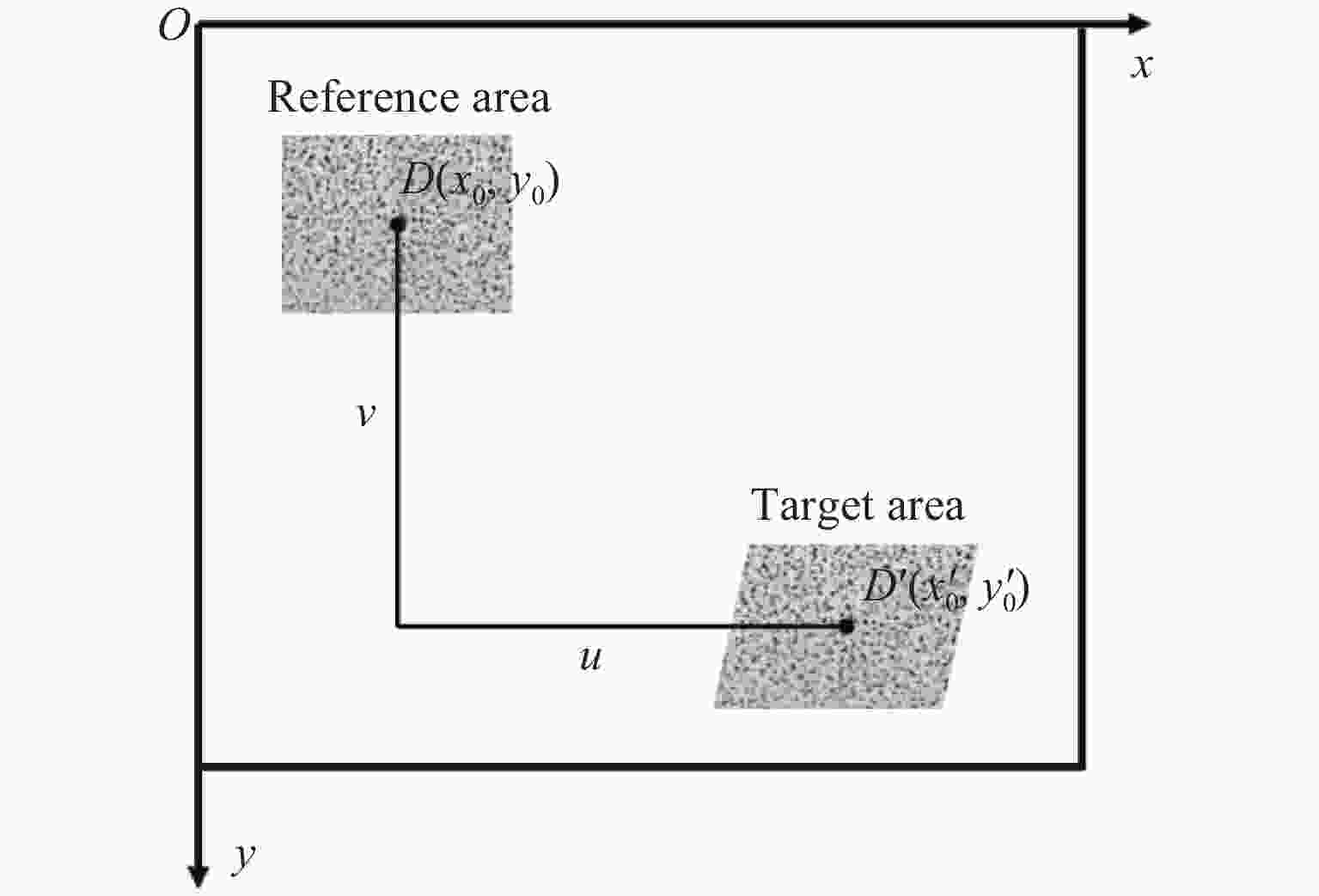
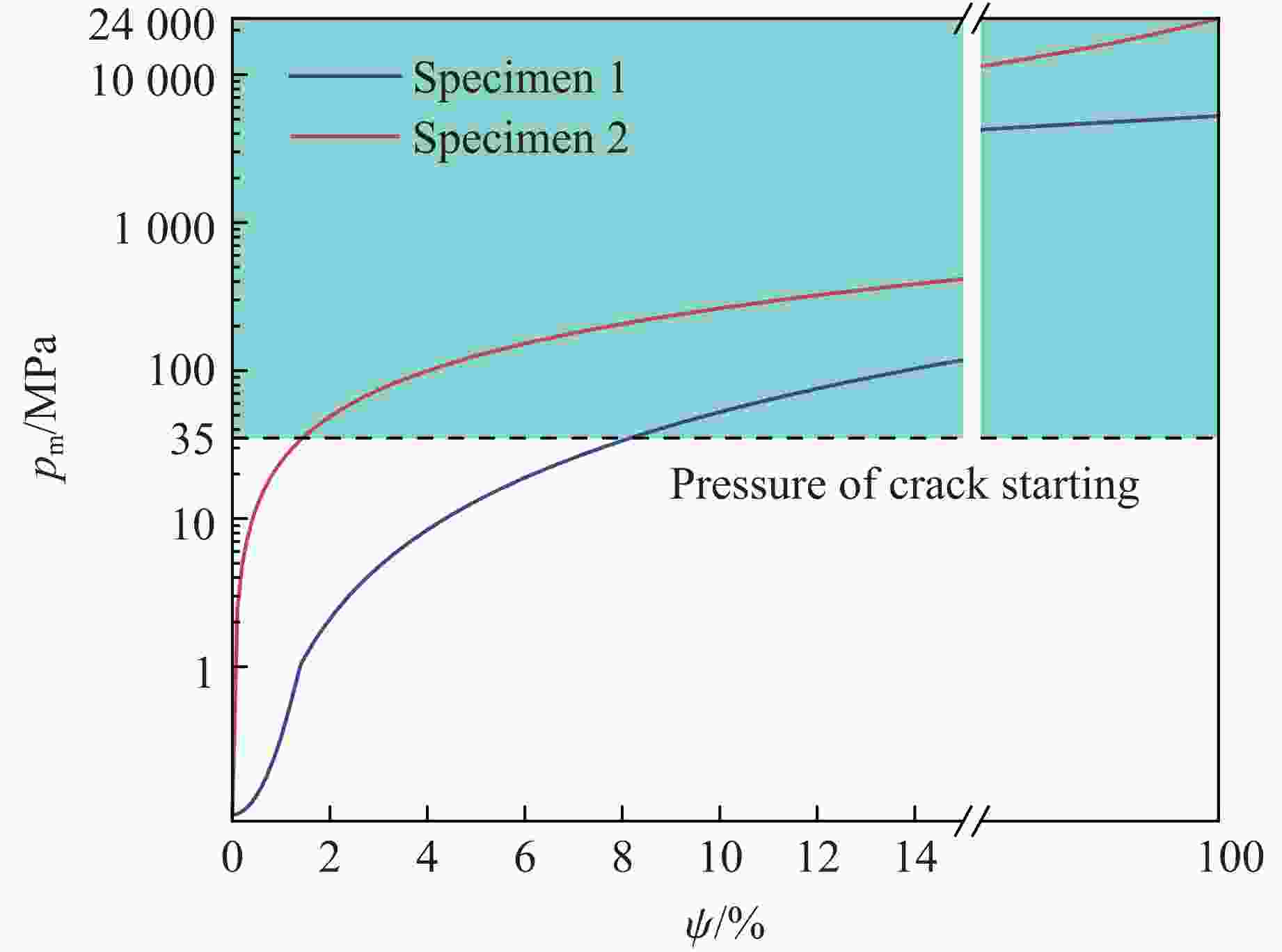
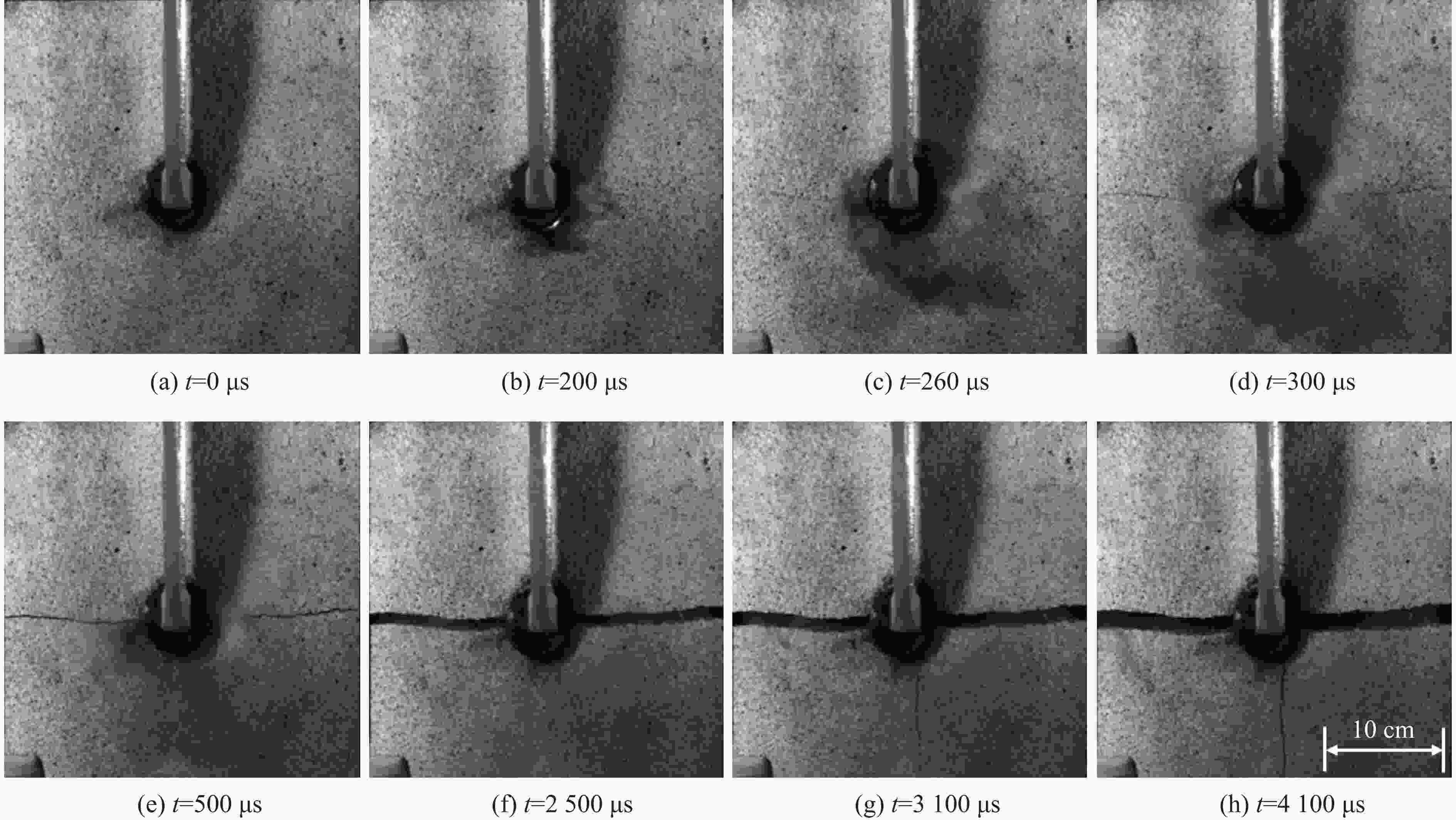
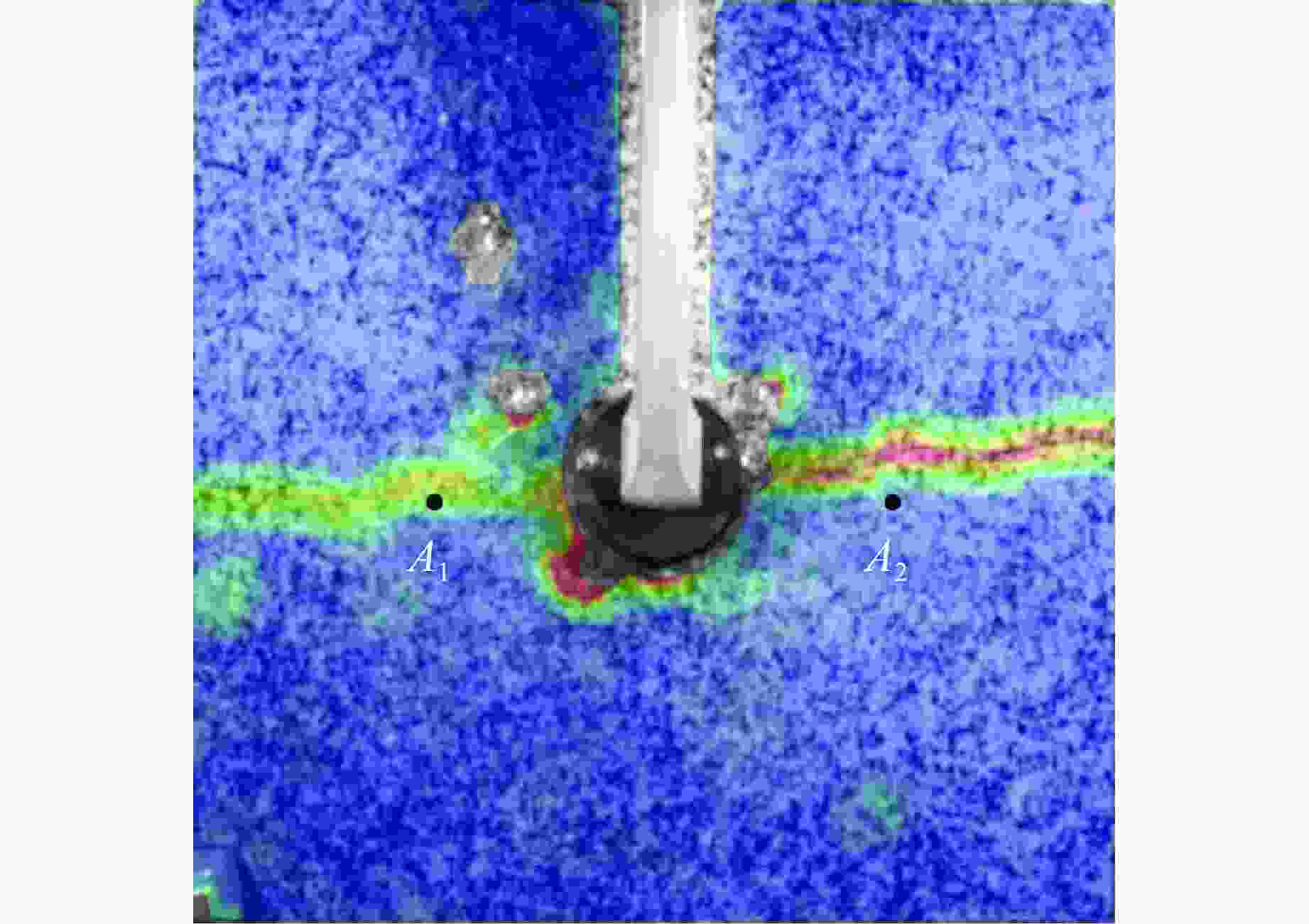
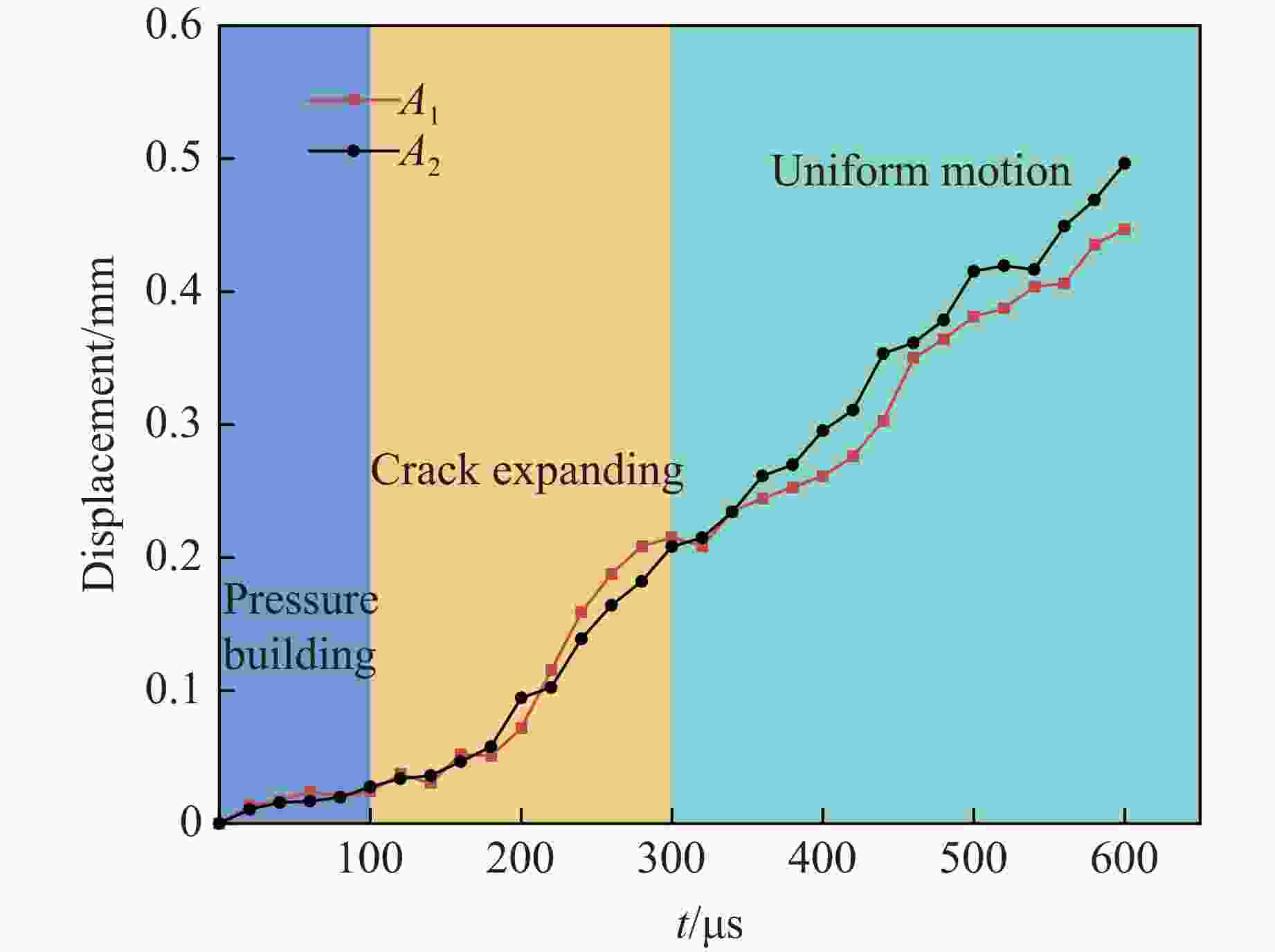
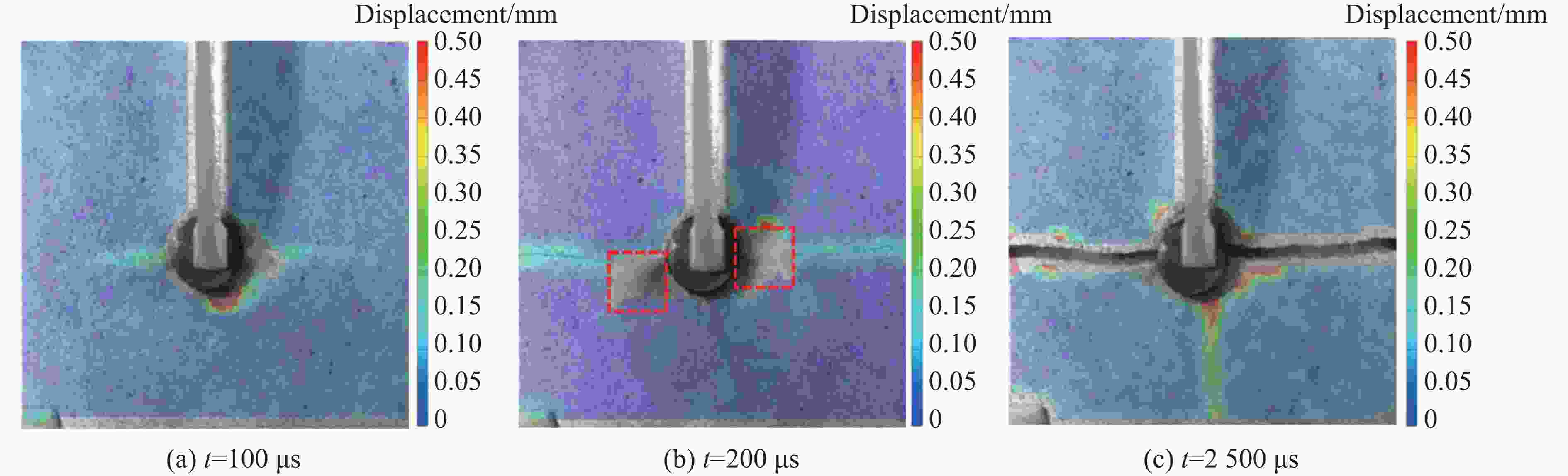
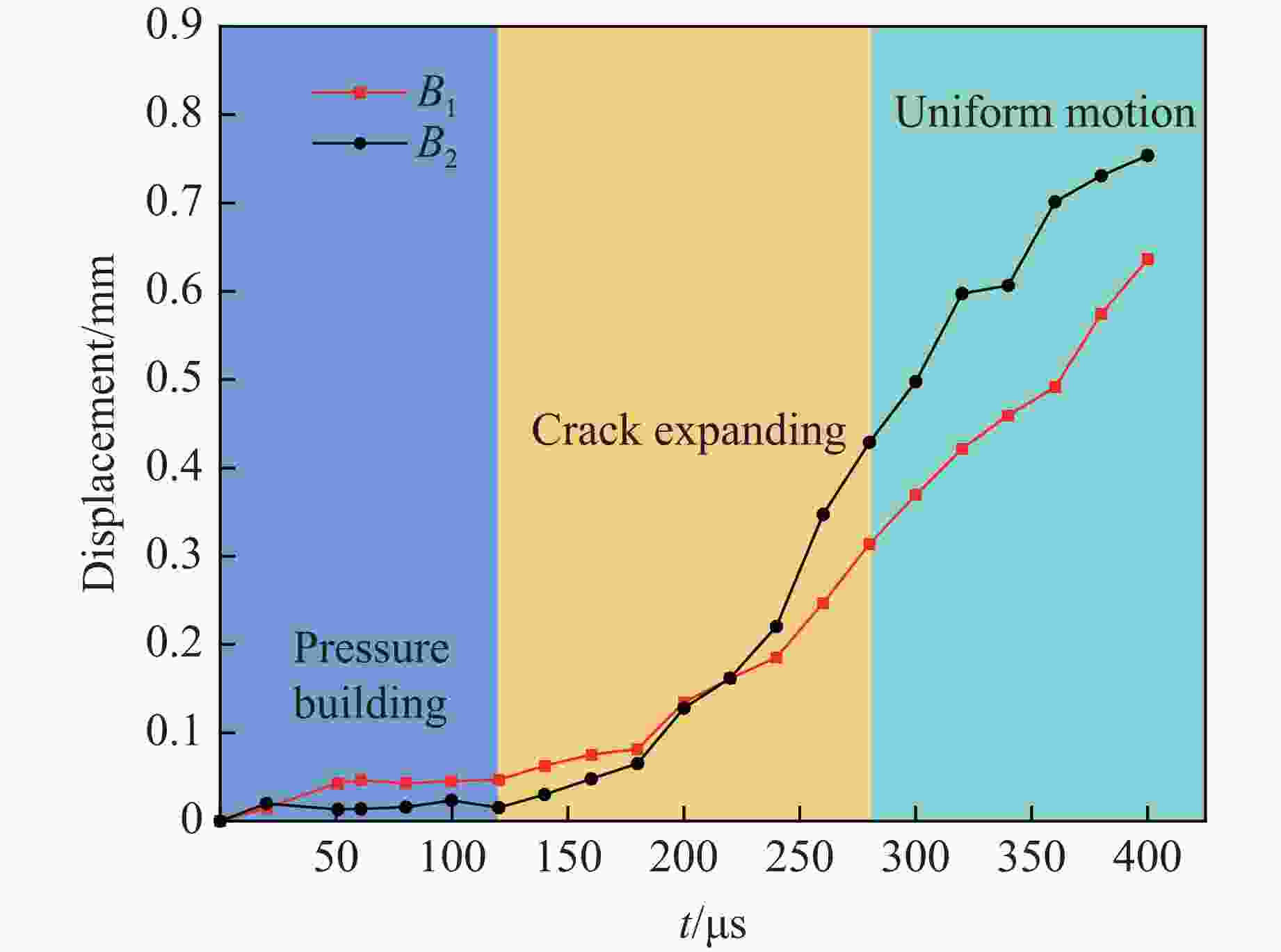
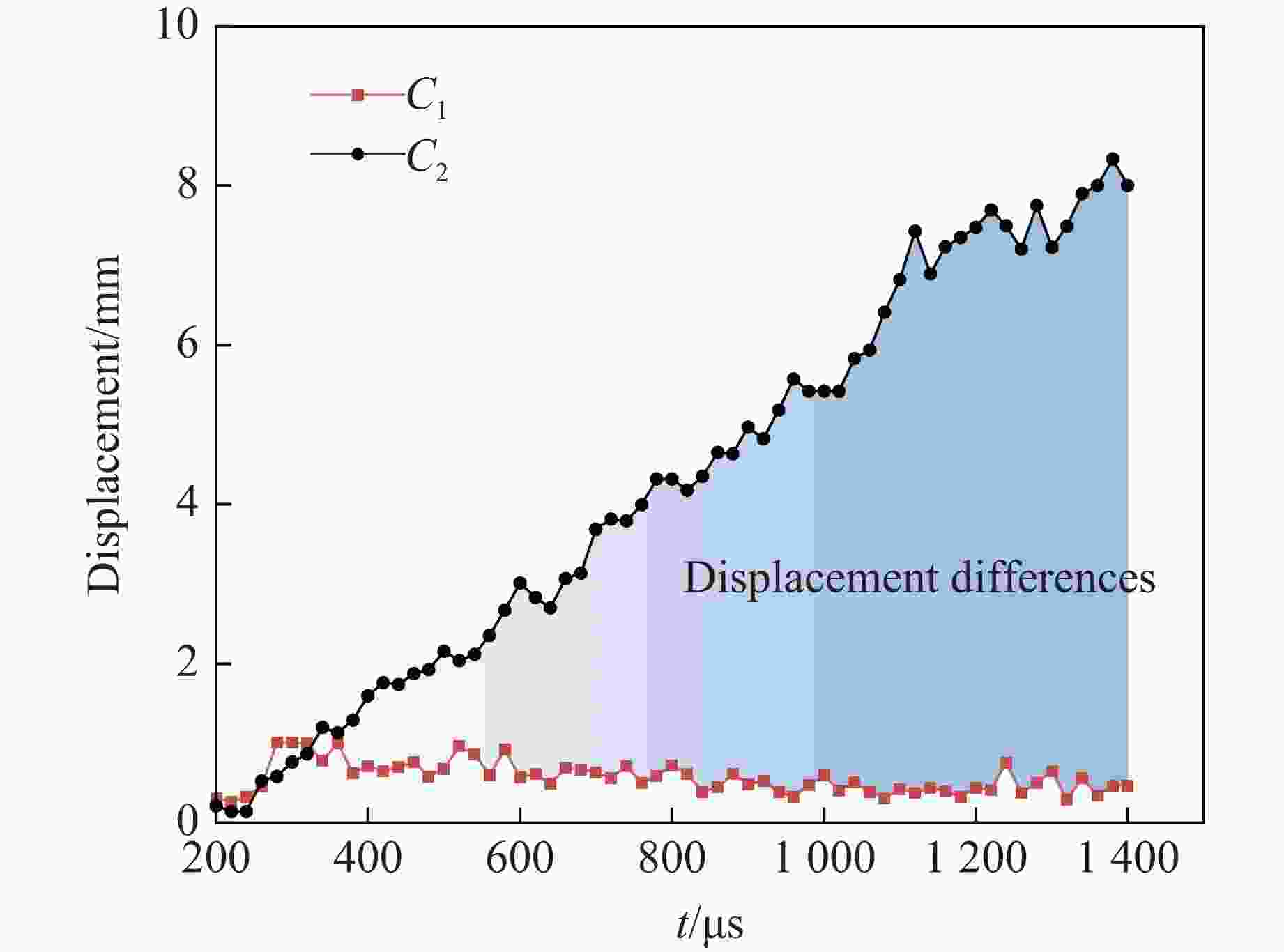
摘要: 针对目前炸药切槽爆破存在非切槽方向上岩石破坏的问题，研究了双基火药切槽爆破特性。基于火药燃气释放规律，计算了双基火药被激发后密闭炮孔内的压力变化情况。结合高速摄影和数字图像相关（digital image correlation, DIC）方法，开展了炮孔的火药装填密度分别为0.84和0.96 g/cm³的2组实验，探究了火药作用下花岗岩板的动态破坏过程。结果表明：火药点火后，2组实验中花岗岩板均在100 μs时沿切槽方向起裂，200 μs时裂纹贯穿石板；当装填密度为0.96 g/cm³时，试件在断裂后上下石板分离速度较大，在封堵橡胶的摩擦力和试件惯性的共同作用下，2500 μs时上下石板被横向拉裂，裂纹沿垂直方向。炮孔预制切槽为火药燃气的气楔作用提供了空间，很好地引导裂纹的扩展，孔壁周围没有形成压碎区。双基火药燃烧产生的准静态压力是裂纹起裂、扩展的主要动力。研究结果为双基火药在岩体定向爆破上的应用提供了参考。
- 切槽爆破 /
- 岩石断裂 /
- 双基火药 /
- 动态破坏过程 /
- 数字图像相关法
Abstract: Aiming at the current groove blasting problems of additional damage, the feasibility of double base propellant for groove blasting was explored. Based on the propellant gas release behavior, the pressure change of the double base propellant in the closed hole was calculated. Combined with high-speed photography and digital image correlation (DIC) method, two groups of experiments were carried out with propellant loading density of 0.84 and 0.96 g/cm³ to investigate the dynmic destruction process of granite slabs under the action of propellant. The results show that the granite slabs in the two groups of experiments were cracked along the groove direction at 100 μs after ignition, and the cracks penetrated through the slabs at 200 μs; the specimen with a charge density of 0.96 g/cm³ had a larger separation speed between the upper and lower slabs after fracture, and the upper and lower slabs were cracked by the friction of the blocking rubber and the inertia of the specimen, and the cracks were in the vertical direction at 2 500 μs. The grooves around the blast hole provide space for the effect of the propellant gas, and the grooves can effectively guide the direction of crack propagation, no crushing zone formed around the hole wall. The quasi-static pressure generated by the combustion of double-base propellant is the main driving force for crack initiation and propagation. The experimental results have some implications for the use of double base propellant in controlled rock blasting projects.
- grooved blasting /
- rock fracture /
- double base propellant /
- dynamic destructive process /
- digital image correlation

HTML全文

图 1 应力强度因子的修正系数

Figure 1. Correction factor for stress intensity factor

下载: 全尺寸图片幻灯片

图 2 切槽爆破的断裂力学模型

Figure 2. Fracture mechanics model of groove blasting

下载: 全尺寸图片幻灯片

图 3 水射流加工后的花岗岩板

Figure 3. Granite specimens processed by water jetting

下载: 全尺寸图片幻灯片

图 4 高速摄影实验平台

Figure 4. High-speed photography experiment platform

下载: 全尺寸图片幻灯片

图 5 DIC原理示意图

Figure 5. Schematic diagram of the principle of DIC method

下载: 全尺寸图片幻灯片

图 6 破坏后的试件

Figure 6. Specimens after destruction

下载: 全尺寸图片幻灯片

图 7 2个试件的压力-已燃质量百分比曲线

Figure 7. Pressure-percentage of burned mass curves of two specimens

下载: 全尺寸图片幻灯片

图 8 试件1的高速摄影结果

Figure 8. High-speed photographic results of specimen 1

下载: 全尺寸图片幻灯片

图 9 试件2的高速摄影结果

Figure 9. High-speed photographic results of specimen 2

下载: 全尺寸图片幻灯片

图 10 试件1的DIC分析结果

Figure 10. DIC analysis results of specimen 1

下载: 全尺寸图片幻灯片

图 11 试件1测点的位置

Figure 11. Measurement points locations of specimen 1

下载: 全尺寸图片幻灯片

图 12 测点A₁和A₂的位移-时间曲线

Figure 12. Displacement-time curves of points A₁ and A₂

下载: 全尺寸图片幻灯片

图 13 试件2的DIC分析结果

Figure 13. DIC analysis results of specimen 2

下载: 全尺寸图片幻灯片

图 14 试件2中测点的位置

Figure 14. Measurement points’ locations of specimen 2

下载: 全尺寸图片幻灯片

图 15 测点B₁、B₂的位移-时间曲线

Figure 15. Displacement-time curves of points B₁ and B₂

下载: 全尺寸图片幻灯片

图 16 测点C₁、C₂的位移-时间曲线

Figure 16. Displacement-time curves of points C₁ and C₂

下载: 全尺寸图片幻灯片

表 1 几种岩石的断裂韧度

Table 1. Fracture toughness for several rock types

Type of rock	$ {K_{{\rm I}{{\mathrm{C}}} }} $/(MPa·m^1/2）	Type of rock	K_IC/(MPa·m^1/2）
Siltstone	0.35–2.56	Dolostones	1.70–2.57
Limestone	0.95–2.17	Granite	1.12–2.80
Shale	0.42–1.10	Marble	0.82–2.67

下载: 导出CSV

表 2 实验用花岗岩板的力学参数

Table 2. Mechanical parameters of experimental granite specimens

Density/(g·cm⁻³)	Elastic modulus/GPa	Poisson’s ratio	Compressive strength/MPa	Tensile strength/MPa	Dynamic tensile strength/MPa
2.72	41	0.23	200	20	32

下载: 导出CSV

参考文献(22)

[1]	汪旭光. 爆破设计与施工 [M]. 北京: 冶金工业出版社, 2011: 28–33.
[2]	范勇, 孙金山, 贾永胜, 等. 高地应力硐室光面爆破孔间应力相互作用与成缝机制 [J]. 岩石力学与工程学报, 2023, 42(6): 1352–1365. FAN Y, SUN J S, JIA Y S, et al. Stress interaction and crack penetration mechanism between smooth blasting holes for tunnel excavation under high in-situ stress [J]. Chinese Journal of Rock Mechanics and Engineering, 2023, 42(6): 1352–1365.
[3]	XU J C, WANG Z L, RUI G R. Tunnel slotting-blasting numerical modeling using rock tension-compression coupling damage algorithm [J]. Applied Sciences, 2022, 12(13): 6714. doi: 10.3390/app12136714
[4]	WANG Z L, WANG H C, WANG J G, et al. Finite element analyses of constitutive models performance in the simulation of blast-induced rock cracks [J]. Computers and Geotechnics, 2021, 135: 104172. doi: 10.1016/j.compgeo.2021.104172
[5]	HOLLOWAY D C, BJARRNHOLT G, WILSON W H. A field study of fracture control techniques for smooth wall blasting [C]//The 27th U. S. Symposium on Rock Mechanics (USRMS). Tuscaloosa, Alabama: ARMA, 1986: 456−463.
[6]	宗琦. 岩石炮孔预切槽爆破断裂成缝机理研究 [J]. 岩土工程学报, 1998, 20(1): 30–33. doi: 10.3321/j.issn:1000-4548.1998.01.008 ZONG Q. Investigations into mechanism of crack formation for grooved hole-well blasting [J]. Chinese Journal of Geotechnical Engineering, 1998, 20(1): 30–33. doi: 10.3321/j.issn:1000-4548.1998.01.008
[7]	岳中文, 郭洋, 王煦. 切槽孔爆炸载荷下裂纹扩展行为的实验研究 [J]. 岩石力学与工程学报, 2015, 34(10): 2018–2026. YUE Z W, GUO Y, WANG X. Experimental study of crack propagation under blasting load in notched boreholes [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(10): 2018–2026.
[8]	杨立云, 董鹏翔, 王启睿, 等. 爆生气体驱动双共线Ⅰ型裂纹的扩展行为 [J]. 矿业科学学报, 2023, 8(4): 538–547. YANG L Y, DONG P X, WANG Q R, et al. Propagation behavior of two collinear mode Ⅰ cracks driven by explosive gas [J]. Journal of Mining Science and Technology, 2023, 8(4): 538–547.
[9]	DAEHNKE A, ROSSMANITH H P, NAPIER J A L. Gas pressurisation of blast-induced conical cracks [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(3/4): 626.
[10]	王树仁, 朱振海, 魏有志. 爆生气体对破岩作用的动光弹研究 [J]. 煤炭学报, 1986(1): 11–22. WANG S R, ZHU Z H, WEI Y Z. Dynamic photoelastic investigation of rock fragmentation by explosive gas [J]. Journal of China Coal Society, 1986(1): 11–22.
[11]	杨仁树, 苏洪. 爆炸荷载下含预裂缝的裂纹扩展实验研究 [J]. 煤炭学报, 2019, 44(2): 482–489. YANG R S, SU H. Experimental study on crack propagation with pre-crack under explosion load [J]. Journal of China Coal Society, 2019, 44(2): 482–489.
[12]	肖川, 宋浦, 张默贺. 含能材料发展的若干思考 [J]. 火炸药学报, 2022, 45(4): Ⅰ–Ⅳ. doi: 10.14077/j.issn.1007-7812.202206026
[13]	李世影, 肖忠良, 李宇, 等. 某中小口径武器用梯度硝基发射装药效应 [J]. 含能材料, 2023, 31(11): 1134–1140. doi: 10.11943/CJEM2022243 LI S Y, XIAO Z L, LI Y, et al. Study on the effect of nitro gradiently distributed propellant charge for a small and medium caliber weapon [J]. Chinese Journal of Energetic Materials, 2023, 31(11): 1134–1140. doi: 10.11943/CJEM2022243
[14]	薛冰, 凌静, 陈华东, 等. 单基发射药与乳化炸药爆破振动特性对比研究 [J]. 爆破, 2022, 39(3): 145–150, 208. doi: 10.3963/j.issn.1001-487X.2022.03.022 XUE B, LING J, CHEN H D, et al. Comparative study on blasting vibration characteristics of single-base gun propellant and emulsion explosive [J]. Blasting, 2022, 39(3): 145–150, 208. doi: 10.3963/j.issn.1001-487X.2022.03.022
[15]	薛冰, 唐运彬, 赵静, 等. 单基发射药孤石爆破特性实验研究 [J]. 爆破, 2022, 39(2): 140–146. doi: 10.3963/j.issn.1001-487X.2022.02.021 XUE B, TANG Y B, ZHAO J, et al. Experimental study on boulder blasting characteristics of single-base gun propellant [J]. Blasting, 2022, 39(2): 140–146. doi: 10.3963/j.issn.1001-487X.2022.02.021
[16]	张小兵. 枪炮内弹道学 [M]. 北京: 北京理工大学出版社, 2014: 98–108. ZHANG X B. Interior ballistics of guns [M]. Beijing: Beijing Institute of Technology Press, 2014: 98–108.
[17]	宗琦. 爆生气体的准静态破岩特性 [J]. 岩土力学, 1997, 18(2): 73–78. doi: 10.16285/j.rsm.1997.02.014 ZONG Q. Investigation on features of rock quasi-static fragmentation by gaseous explosion product [J]. Rock and Soil Mechanics, 1997, 18(2): 73–78. doi: 10.16285/j.rsm.1997.02.014
[18]	王铎. 断裂力学 [M]. 哈尔滨: 哈尔滨工业大学出版社, 1989: 52−59.
[19]	秦虎. 边界元法在断裂控制机理研究中的应用 [J]. 矿冶, 1994, 3(4): 13–16, 6. QIN H. Application of boundary element method to a study of fracture control mechanism [J]. Mining and Metallurgy, 1994, 3(4): 13–16, 6.
[20]	LIN Q, YUAN H N, BIOLZI L, et al. Opening and mixed mode fracture processes in a quasi-brittle material via digital imaging [J]. Engineering Fracture Mechanics, 2014, 131: 176–193. doi: 10.1016/j.engfracmech.2014.07.028
[21]	YAMAGUCHI I. A laser-speckle strain gauge [J]. Journal of Physics E: Scientific Instruments, 1981, 14(11): 1270–1273. doi: 10.1088/0022-3735/14/11/012
[22]	赵宏立, 刘来东, 靳建伟, 等. 压力下降条件下一种双基发射药的瞬态燃烧特性 [J]. 火炸药学报, 2012, 35(1): 64–68. doi: 10.3969/j.issn.1007-7812.2012.01.015 ZHAO H L, LIU L D, JIN J W, et al. Transient combustion performance of gun propellant under depressurization condition [J]. Chinese Journal of Explosives & Propellants, 2012, 35(1): 64–68. doi: 10.3969/j.issn.1007-7812.2012.01.015