中等应变率下纸蜂窝结构的力学性能研究

马昊; 陈美多; 袁良柱; 王鹏飞; 徐松林

doi:10.11858/gywlxb.20240701

中等应变率下纸蜂窝结构的力学性能研究

doi: 10.11858/gywlxb.20240701

马昊^1,,
陈美多¹,
袁良柱¹,
王鹏飞¹,
徐松林^{1, 2,*, ,}

1.
中国科学技术大学, 中国科学院材料力学行为和设计重点实验室, 安徽合肥　230027
2.
中国地震局地震预测研究所高压物理与地震科技联合实验室, 北京　100036

基金项目: 国家自然科学基金（11672286，11872361）；高压物理与地震科技联合实验室开放基金（2019HPPES01）；中央高校基本科研业务费专项资金（WK2480000008）

详细信息

作者简介:
马　昊（2000－），男，硕士研究生，主要从事冲击动力学研究. E-mail：haoma@mail.ustc.edu.cn

通讯作者:
徐松林（1971－），男，博士，研究员，主要从事冲击作用下材料的动态响应研究. E-mail：slxu99@ustc.edu.cn

中图分类号: O341
计量
- 文章访问数: 92
- HTML全文浏览量: 29
- PDF下载量: 24
出版历程
- 收稿日期: 2024-01-02
- 修回日期: 2024-01-13
- 刊出日期: 2024-07-25

Study on Mechanical Properties of Paper Honeycomb Structure at Medium Strain Rates

MA Hao^1
,,
CHEN Meiduo¹,
YUAN Liangzhu¹,
WANG Pengfei¹,
XU Songlin^{1, 2,*
, ,}

1.
CAS Key Laboratory for Mechanical Behavior and Design of Materials, University of Science and Technology of China, Hefei 230027, Anhui, China
2.
The United Laboratory of High-Pressure Physics and Earthquake Science, Institute of Earthquake Science, China Earthquake Administration, Beijing 100036, China

摘要

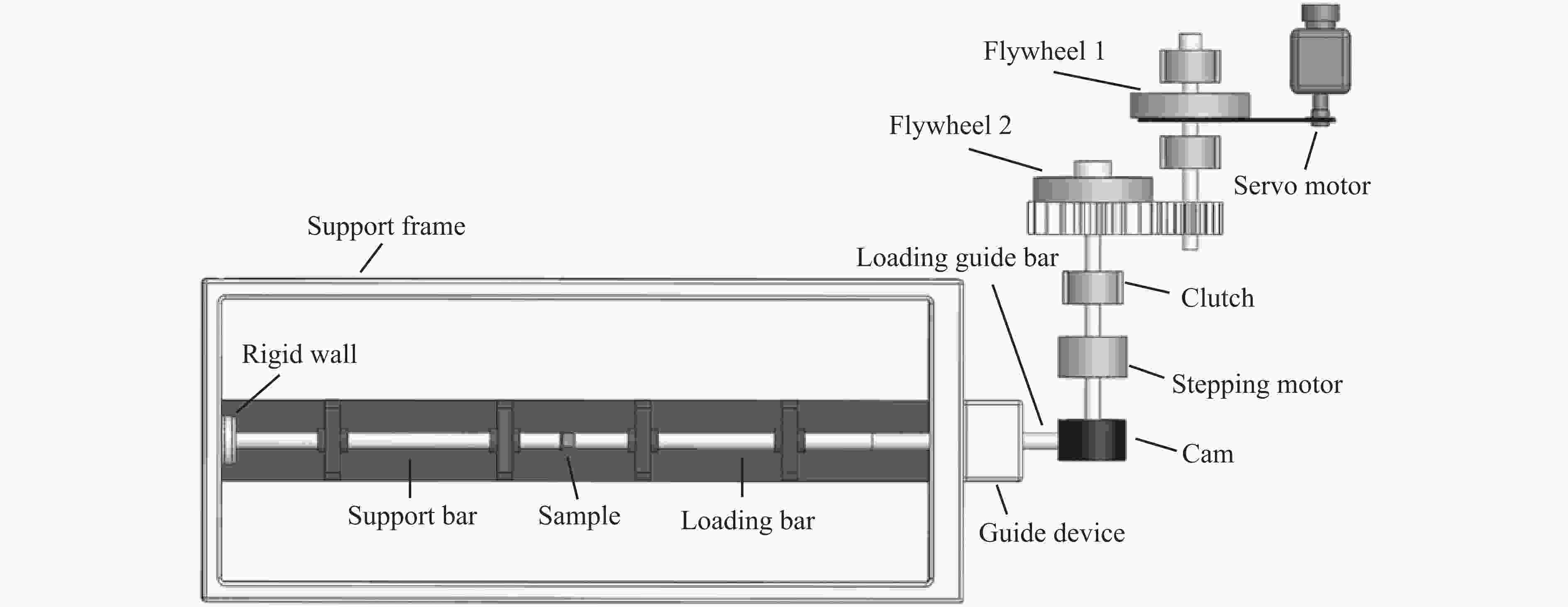
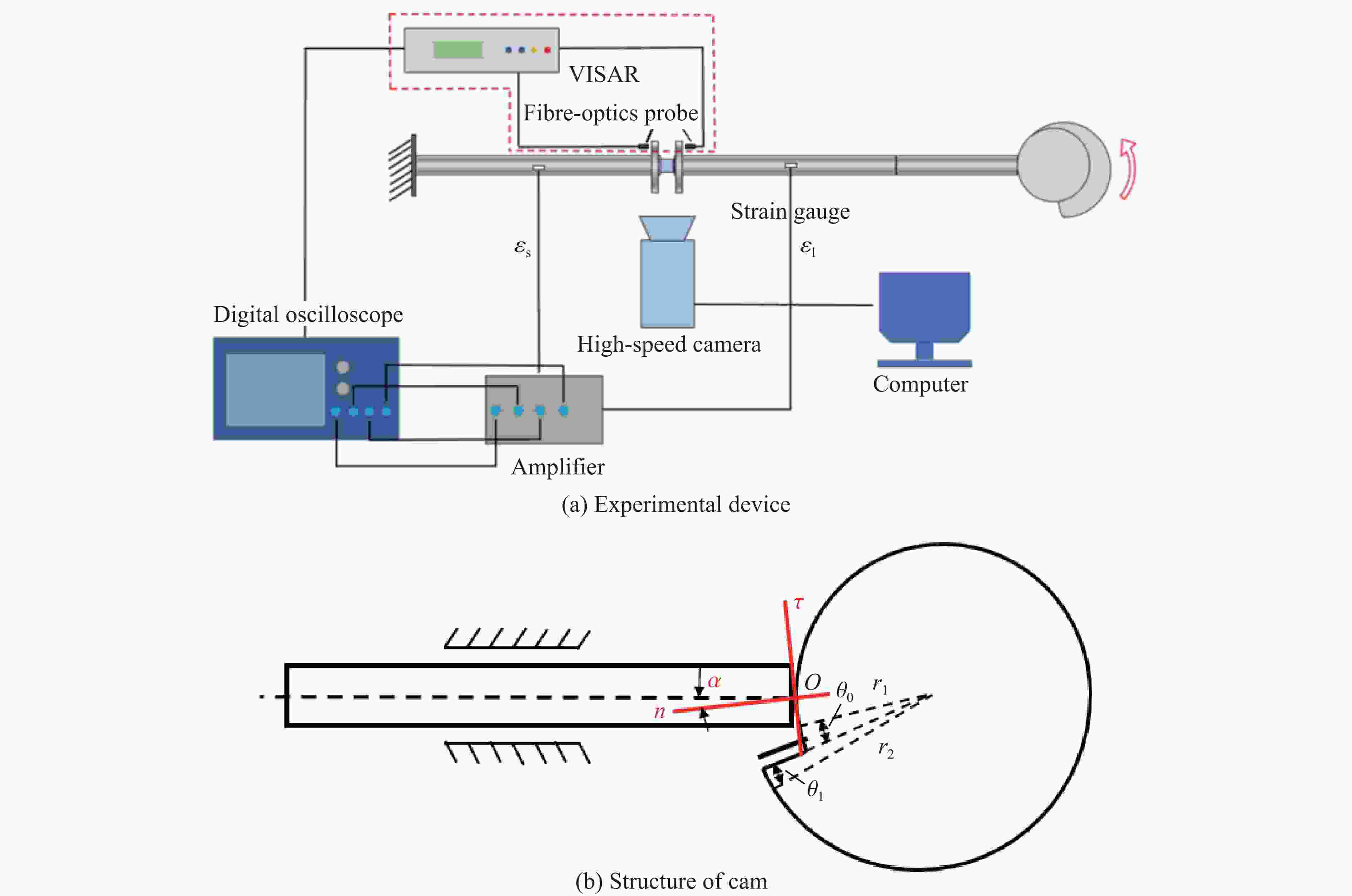
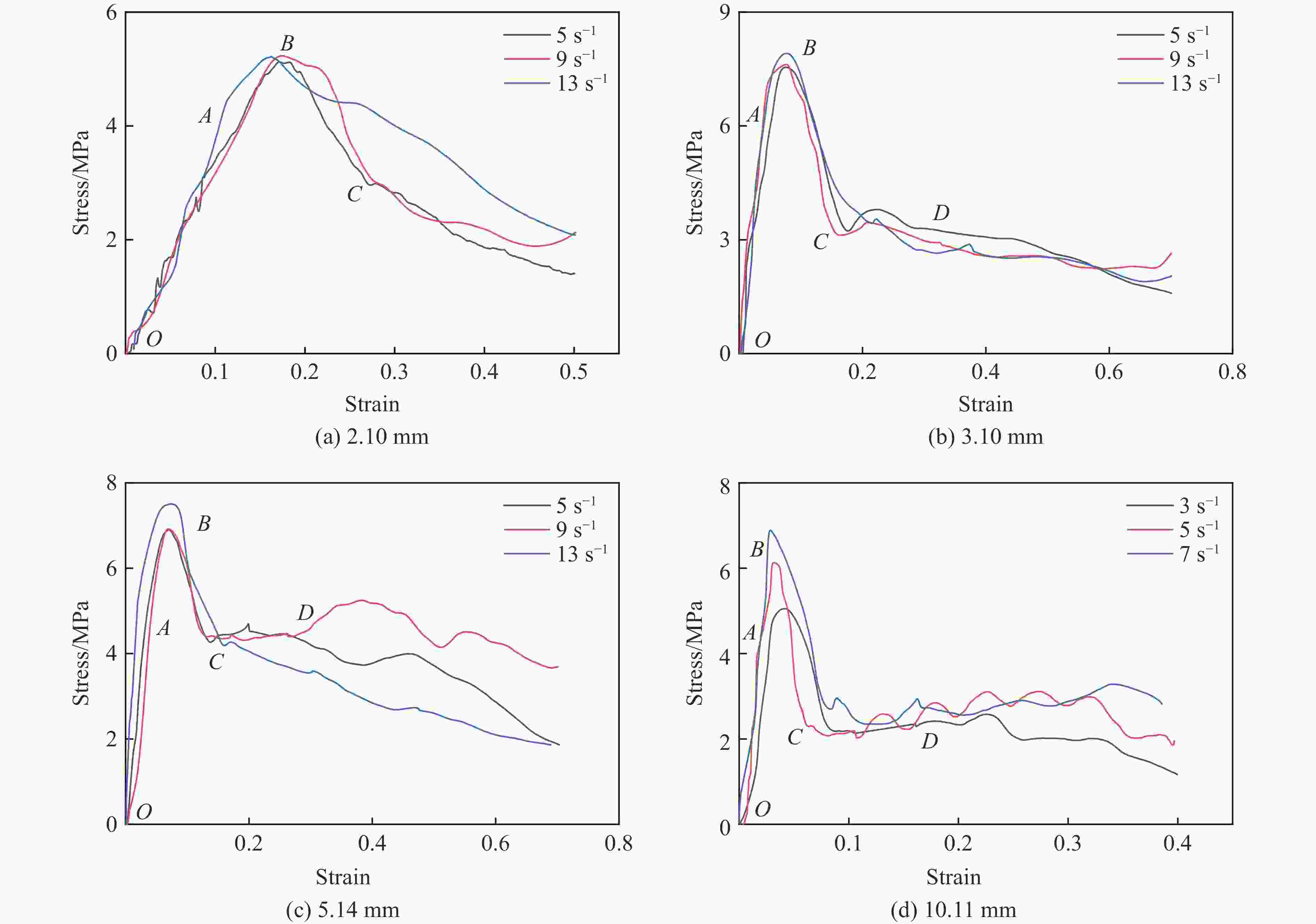
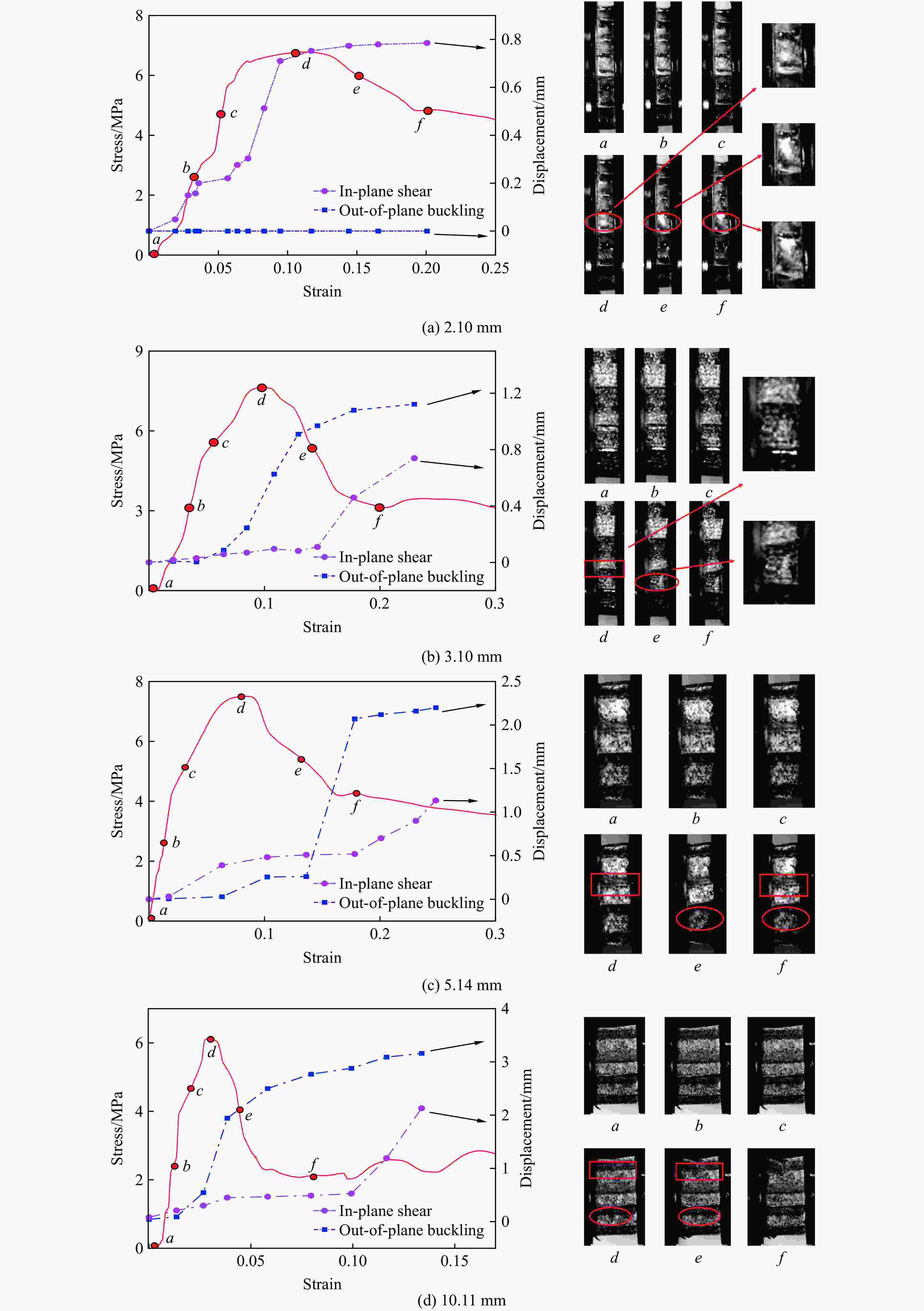
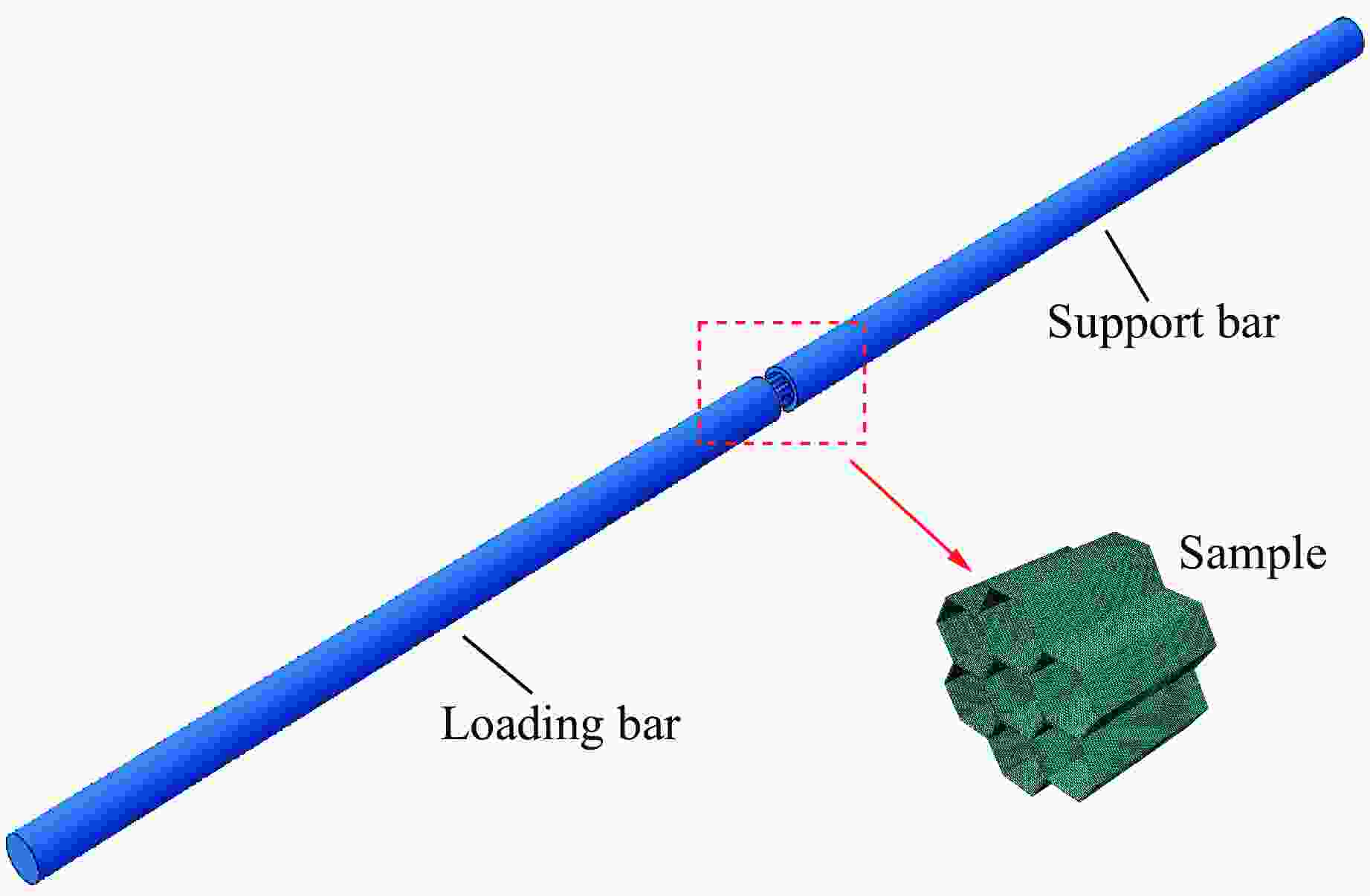
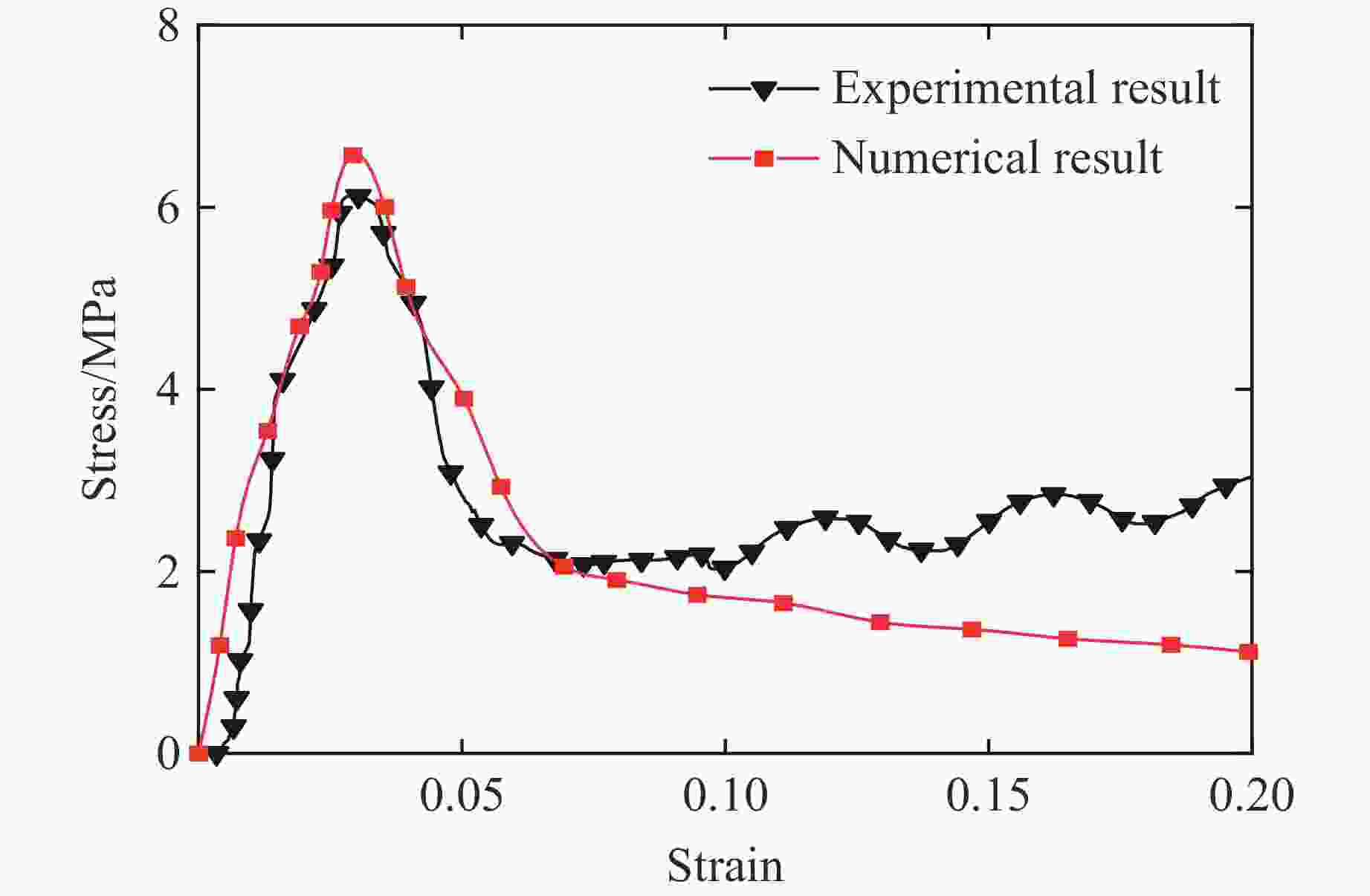
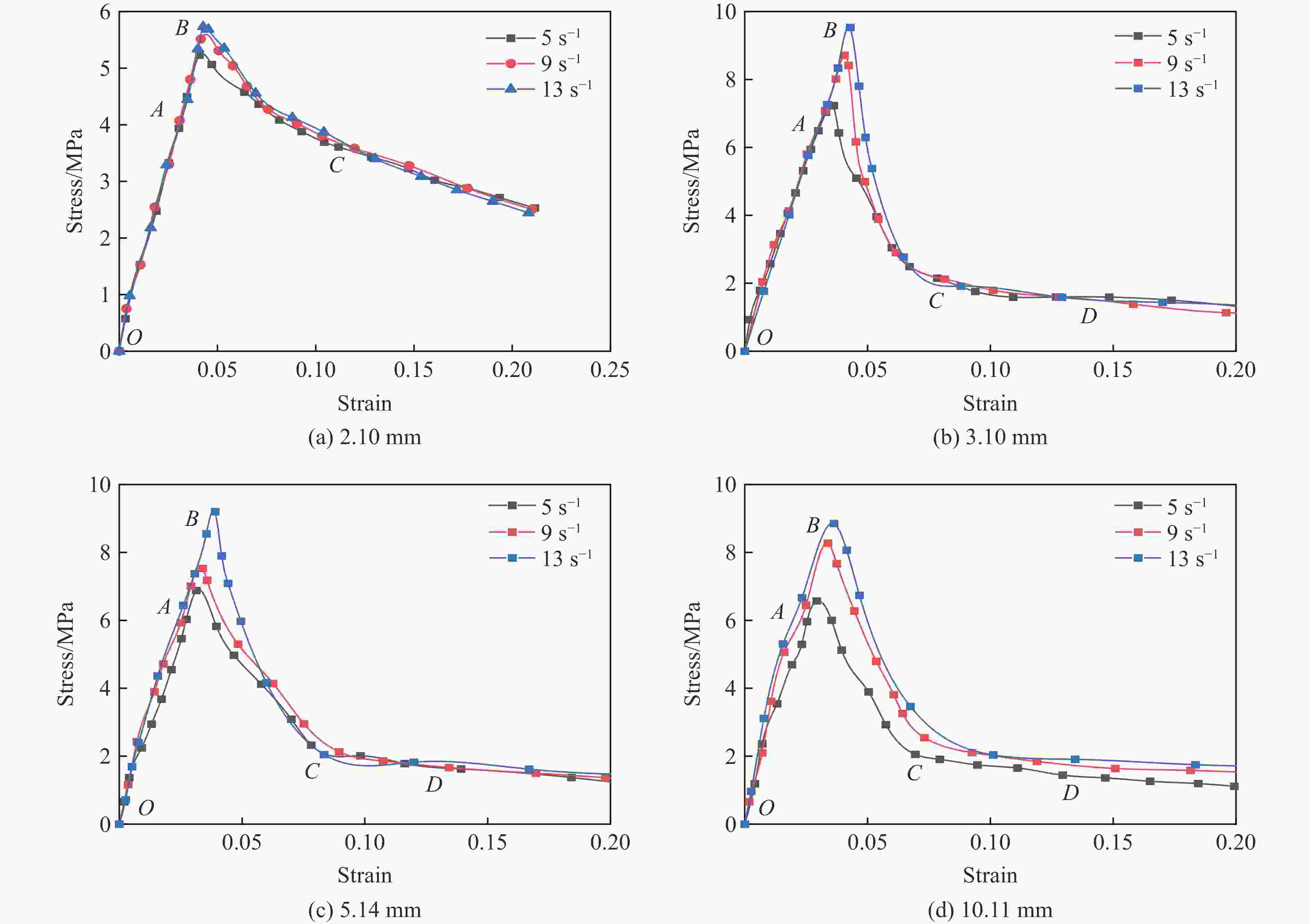
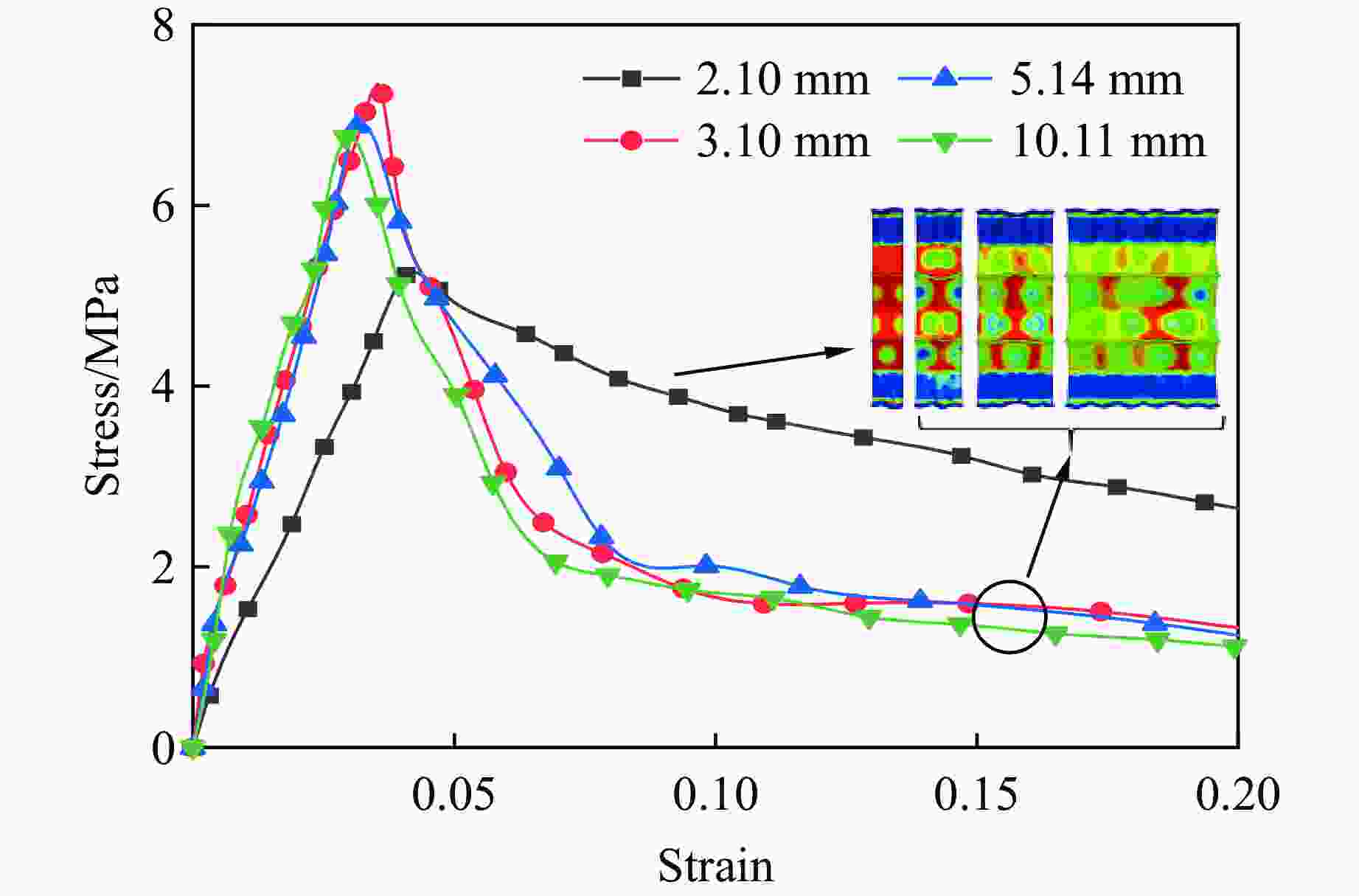
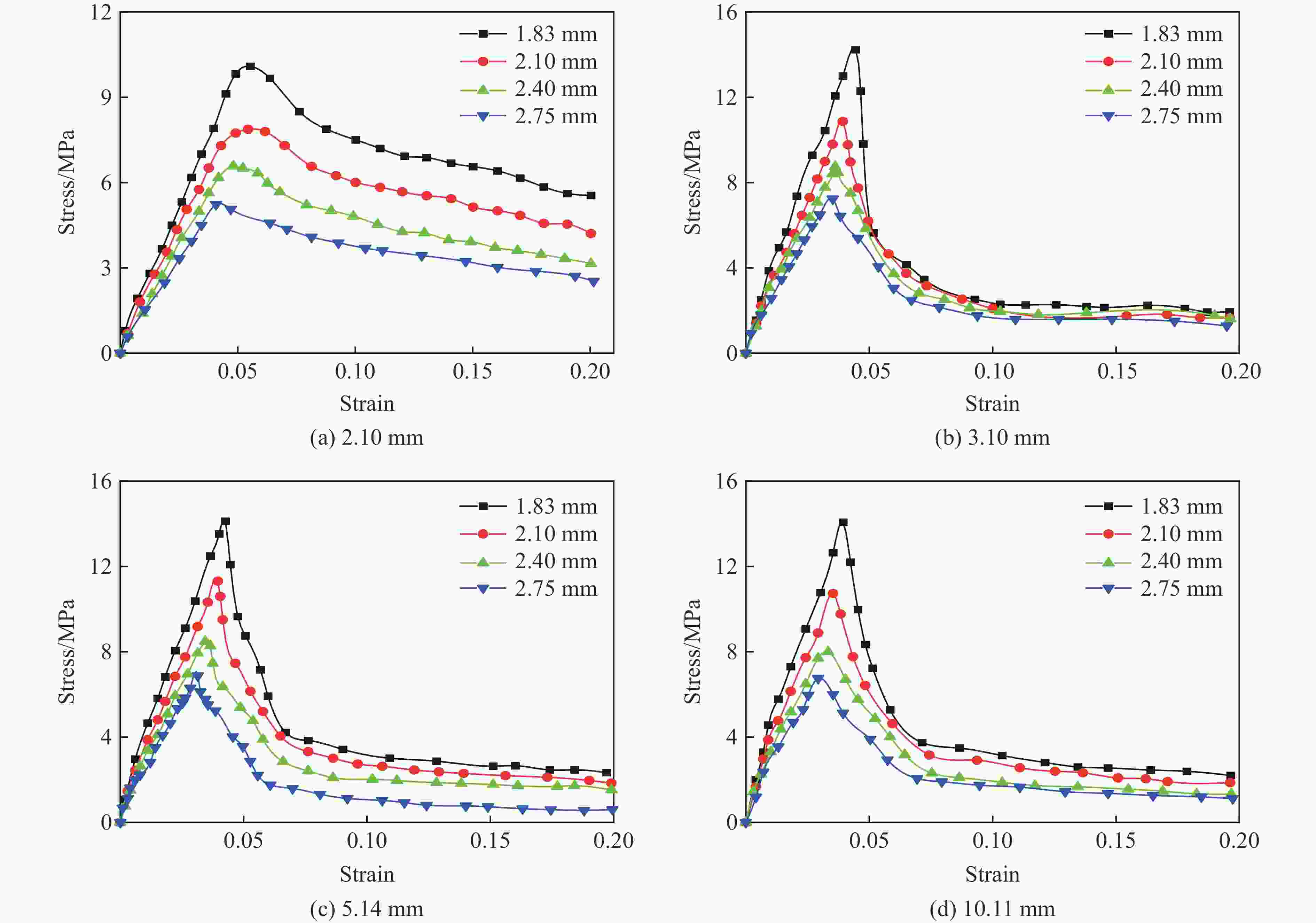
摘要: 应用新研制的中应变率实验装置结合激光干涉测速系统完成了纸蜂窝结构的动态加载实验，研究纸蜂窝结构在中应变率下的力学性能；结合高速摄影和数字图像相关方法，得到纸蜂窝结构的变形过程和动态失效机制，并采用数值方法进一步探究其动态失效机制。结果表明：纸蜂窝结构表现出明显的应变率效应；厚度为2.10 mm的纸蜂窝屈服强度明显低于其他3种尺寸，表现出异常尺寸效应，应力-应变曲线下降段也有较大差异。产生异常尺寸效应的主要原因是，随着试样尺寸的增大，纸蜂窝结构的破坏模式发生了变化。中应变率加载过程中，纸蜂窝结构的失效机制为破坏模式的转变—由面外壁屈曲破坏转变为面内剪切破坏。本研究还利用数值模型分析了胞元宽度的变化对结构力学性能的影响，该研究结果对于薄壁结构的优化设计具有很好的参考意义。
- 中等应变率 /
- 纸蜂窝 /
- 失效机制 /
- 面外屈曲 /
- 动态响应
Abstract: Combining the laser interferometry system, using the newly developed experimental device at medium strain rates to conduct the dynamic loading experiment of paper honeycomb structure. The purpose is to study the mechanical properties of paper honeycomb structure at medium strain rates. The deformation process and dynamic failure mechanism of paper honeycomb structure were obtained by high-speed photography and digital image correlation method. Numerical methods were used to further explore the dynamic failure mechanism. The results show that the paper honeycomb structure exhibits obvious strain rate effect. The yield strength of 2.10 mm thick paper honeycomb is obviously lower than the other three sizes, showing abnormal size effect. The descending section of stress-strain curve of 2.10 mm thick paper honeycomb is also different. The main reason for it is that the failure mode of paper honeycomb structure changes with the increase of sample size. The failure mechanism of paper honeycomb structure during the loading process at medium strain rates is the change of two failure modes, namely from out-of-plane buckling to in-plane shear. The effect of cell width on mechanical properties of the structure was analyzed by numerical model. This study is a good reference significance for the optimal design of thin-walled structures.
- medium strain rate /
- paper honeycomb /
- failure mechanism /
- out-of-plane buckling /
- dynamic response

HTML全文

图 1 纸蜂窝样品

Figure 1. Paper honeycomb samples

下载: 全尺寸图片幻灯片

图 2 递进式凸轮加载的中应变率实验装置

Figure 2. Mediate strain rate experimental device with progressive cam loading

下载: 全尺寸图片幻灯片

图 3 递进式凸轮加载的中应变率实验系统

Figure 3. A mediate strain rate experimental system with progressive cam loading

下载: 全尺寸图片幻灯片

图 4 中应变率下不同厚度样品的应力-应变曲线

Figure 4. Stress-strain curves of samples with different thicknesses at medium strain rate

下载: 全尺寸图片幻灯片

图 5 不同尺寸纸蜂窝试样的应力-应变曲线对比

Figure 5. Comparison of stress-strain curves of paper honeycomb samples of different sizes

下载: 全尺寸图片幻灯片

图 6 中应变率下纸蜂窝的变形过程

Figure 6. Deformation process of paper honeycomb at medium strain rate

下载: 全尺寸图片幻灯片

图 7 中应变率下的有限元模型

Figure 7. Finite element model with medium strain rate

下载: 全尺寸图片幻灯片

图 8 模型可靠性验证

Figure 8. Model reliability verification

下载: 全尺寸图片幻灯片

图 9 数值模拟结果

Figure 9. Numerical simulation result

下载: 全尺寸图片幻灯片

图 10 不同尺寸纸蜂窝试样的应力-应变曲线对比

Figure 10. Comparison of stress-strain curves of paper honeycomb samples of different sizes

下载: 全尺寸图片幻灯片

图 11 纸蜂窝的变形过程

Figure 11. Paper honeycomb deformation process

下载: 全尺寸图片幻灯片

图 12 胞宽对蜂窝结构的影响

Figure 12. Effect of cell width on cellular structure

下载: 全尺寸图片幻灯片

表 1 纸蜂窝结构的实验结果

Table 1. Experimental results of paper honeycomb structure

Sample size/mm	Strain rate/s⁻¹	The peak state		Stress-drop/MPa
Sample size/mm	Strain rate/s⁻¹	Stress/MPa	Strain	Stress-drop/MPa
2.10	5	5.11	0.174
	9	5.21	0.173
	13	5.22	0.162
3.10	5	7.54	0.077	4.30
	9	7.60	0.076	4.48
	13	7.92	0.076	4.49
5.14	5	6.90	0.070	2.53
	9	6.92	0.069	2.54
	13	7.49	0.069	3.29
10.11	3	5.04	0.040	2.84
	5	6.13	0.039	3.83
	7	6.88	0.028	4.18

下载: 导出CSV

表 2 纸蜂窝基体的材料参数

Table 2. Paper honeycomb matrix’s material parameters

Poisson’s ratio	Elastic modulus/GPa	Compression strength/MPa	Density/(kg·m^–3)
0.2	4	180	1100

下载: 导出CSV

参考文献(28)

[1]	MIAO C H, XU S L, SONG Y P, et al. Influence of stress state on dynamic breakage of quartz glass spheres subjected to lower velocity impacting [J]. Powder Technology, 2022, 397: 117081. doi: 10.1016/j.powtec.2021.117081
[2]	CHEN M D, XU S L, YUAN L Z, et al. Influence of stress state on dynamic behaviors of concrete under true triaxial confinements [J]. International Journal of Mechanical Sciences, 2023, 253: 108399. doi: 10.1016/j.ijmecsci.2023.108399
[3]	卜乐虎, 王鹏飞, 武杨帆, 等. 基于卷积神经网络的两相复合结构动态力学性能研究 [J]. 高压物理学报, 2023, 37(3): 034201. doi: 10.11858/gywlxb.20230601 BU L H, WANG P F, WU Y F, et al. Research on dynamic mechanical properties of two-phase composites based on convolutional neural network [J]. Chinese Journal of High Pressure Physics, 2023, 37(3): 034201. doi: 10.11858/gywlxb.20230601
[4]	薛晓, 乔禹, 王鹏飞, 等. 碳纳米管纤维的动态拉伸力学性能研究 [J]. 实验力学, 2020, 35(5): 811–819. doi: 10.7520/1001-4888-19-213 XUE X, QIAO Y, WANG P F, et al. Dynamic tensile mechanical properties of carbon nanotube fiber [J]. Journal of Experimental Mechanics, 2020, 35(5): 811–819. doi: 10.7520/1001-4888-19-213
[5]	HUANG J, XU S, YI H, et al. Size effect on the compression breakage strengths of glass particles [J]. Powder Technology, 2014, 268: 86–94. doi: 10.1016/j.powtec.2014.08.037
[6]	SUN J B, FANG H. The analysis of crashworthiness and dissipation mechanism of novel floating composite honeycomb structure against ship-OWT collision [J]. Ocean Engineering, 2023, 287: 115819. doi: 10.1016/j.oceaneng.2023.115819
[7]	HOU W B, SHEN Y X, JIANG K, et al. Study on mechanical properties of carbon fiber honeycomb curved sandwich structure and its application in engine hood [J]. Composite Structures, 2022, 286: 115302. doi: 10.1016/j.compstruct.2022.115302
[8]	WANG J F, SHI C Y, YANG N, et al. Strength, stiffness, and panel peeling strength of carbon fiber-reinforced composite sandwich structures with aluminum honeycomb cores for vehicle body [J]. Composite Structures, 2018, 184: 1189–1196. doi: 10.1016/j.compstruct.2017.10.038
[9]	CLARKE D J, IMEDIEGWU C, MOAT R, et al. A systematic numerical and experimental study into the mechanical properties of five honeycombs [J]. Composites Part B: Engineering, 2023, 264: 110895. doi: 10.1016/j.compositesb.2023.110895
[10]	XU M C, ZHAO Z A, WANG P D, et al. Mechanical performance of bio-inspired hierarchical honeycomb metamaterials [J]. International Journal of Solids and Structures, 2022, 254/255: 111866. doi: 10.1016/j.ijsolstr.2022.111866
[11]	WANG Z G, LI Z D, XIONG W. Numerical study on three-point bending behavior of honeycomb sandwich with ceramic tile [J]. Composites Part B: Engineering, 2019, 167: 63–70. doi: 10.1016/j.compositesb.2018.11.108
[12]	ZHOU H, XU P, XIE S C, et al. Mechanical performance and energy absorption properties of structures combining two Nomex honeycombs [J]. Composite Structures, 2018, 185: 524–536. doi: 10.1016/j.compstruct.2017.11.059
[13]	HEIMBS S, SCHMEER S, MIDDENDORF P, et al. Strain rate effects in phenolic composites and phenolic-impregnated honeycomb structures [J]. Composites Science and Technology, 2007, 67(13): 2827–2837. doi: 10.1016/j.compscitech.2007.01.027
[14]	KAMAN M O, SOLMAZ M Y, TURAN K. Experimental and numerical analysis of critical buckling load of honeycomb sandwich panels [J]. Journal of Composite Materials, 2010, 44(24): 2819–2831. doi: 10.1177/0021998310371541
[15]	WANG D M. Impact behavior and energy absorption of paper honeycomb sandwich panels [J]. International Journal of Impact Engineering, 2009, 36(1): 110–114. doi: 10.1016/j.ijimpeng.2008.03.002
[16]	LIU L Q, WANG H, GUAN Z W. Experimental and numerical study on the mechanical response of Nomex honeycomb core under transverse loading [J]. Composite Structures, 2015, 121: 304–314. doi: 10.1016/j.compstruct.2014.11.034
[17]	YANG W C, ZHANG X F, YANG K J, et al. Shear property characterization of aramid paper and its application to the prediction of honeycomb behaviors [J]. Composite Structures, 2020, 254: 112800. doi: 10.1016/j.compstruct.2020.112800
[18]	JANG W Y, KYRIAKIDES S. On the buckling and crushing of expanded honeycomb [J]. International Journal of Mechanical Sciences, 2015, 91: 81–90. doi: 10.1016/j.ijmecsci.2014.02.008
[19]	SHAN J F, XU S L, ZHOU L J, et al. Dynamic fracture of aramid paper honeycomb subjected to impact loading [J]. Composite Structures, 2019, 223: 110962. doi: 10.1016/j.compstruct.2019.110962
[20]	PETRAS A, SUTCLIFFE M P F. Failure mode maps for honeycomb sandwich panels [J]. Composite Structures, 1999, 44(4): 237–252. doi: 10.1016/S0263-8223(98)00123-8
[21]	CASTANIÉ B, BOUVET C, AMINANDA Y, et al. Modelling of low-energy/low-velocity impact on Nomex honeycomb sandwich structures with metallic skins [J]. International Journal of Impact Engineering, 2008, 35(7): 620–634. doi: 10.1016/j.ijimpeng.2007.02.008
[22]	WU X R, YU H J, GUO L C, et al. Experimental and numerical investigation of static and fatigue behaviors of composites honeycomb sandwich structure [J]. Composite Structures, 2019, 213: 165–172. doi: 10.1016/j.compstruct.2019.01.081
[23]	苗春贺, 徐松林, 马昊, 等. 递进式凸轮加载的中等应变率实验技术 [J]. 爆炸与冲击, 2023, 43(3): 034101. doi: 10.11883/bzycj-2022-0344 MIAO C H, XU S L, MA H, et al. An experimental technique for medium strain-rate loading by a progressive cam [J]. Explosion and Shock Waves, 2023, 43(3): 034101. doi: 10.11883/bzycj-2022-0344
[24]	KESHAVANARAYANA S, THOTAKURI M V. Off-axis compression behaviour of honeycomb core in WT-plane [J]. International Journal of Crashworthiness, 2009, 14(2): 173–181. doi: 10.1080/13588260802614373
[25]	徐小村. GFRP/纸蜂窝复合材料的制备及力学性能研究 [D]. 南京: 南京航空航天大学, 2020. XU X C. Preparation and mechanical properties of GFRP/paper honeycomb composites [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2020.
[26]	KADIR N A, AMINANDA Y, DAWOOD M S I S, et al. Numerical analysis of kraft paper honeycomb subjected to uniform compression loading [J]. Journal of Physics: Conference Series, 2017, 914: 012004. doi: 10.1088/1742-6596/914/1/012004
[27]	KILCHERT S V. Nonlinear finite element modelling of degradation and failure in folded core composite sandwich structures [D]. Stuttgart: University of Stuttgart, 2013.
[28]	ZHANG J, ASHBY M F. The out-of-plane properties of honeycombs [J]. International Journal of Mechanical Sciences, 1992, 34(6): 475–489. doi: 10.1016/0020-7403(92)90013-7