高压下硝酸肼结构演化的中远红外光谱和第一性原理计算研究

曾阳阳; 朱刚贝; 王文涛; 白莎; 郑朝阳; 于国洋; 杨延强

doi:10.11858/gywlxb.20230804

高压下硝酸肼结构演化的中远红外光谱和第一性原理计算研究

doi: 10.11858/gywlxb.20230804

1.
中国工程物理研究院流体物理研究所, 四川绵阳　621999
2.
中国科学院大连化学物理研究所, 辽宁大连　116023
3.
西北大学化学与材料学院, 陕西西安　710127

基金项目: 国家自然科学基金（U2030113）；冲击波物理与爆轰物理重点实验室基金（2021JCJQLB05712）；中国科学院重点实验室基金（CXJJ-22S034）

详细信息

作者简介:
曾阳阳（1983－），男，博士，助理研究员，主要从事含能材料高温高压理论与实验研究. E-mail：caep2012@163.com

通讯作者:
于国洋（1982－），男，博士，副研究员，主要从事含能材料超快光谱实验研究. E-mail：yuguoyang@caep.cn

中图分类号: O521.2
计量
- 文章访问数: 13
- HTML全文浏览量: 6
- PDF下载量: 5
出版历程
- 收稿日期: 2023-12-06
- 修回日期: 2023-12-22
- 网络出版日期: 2024-03-14

Mid- and Far-Infrared Spectroscopic and First-Principles Computational Study of the Structural Evolution of Hydrazine Nitrate under High Pressure

1.
Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621999, Sichuan, China
2.
Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, Liaoning, China
3.
College of Chemistry and Materials Science, Northwest University, Xi’an 710127, Shaanxi, China

摘要

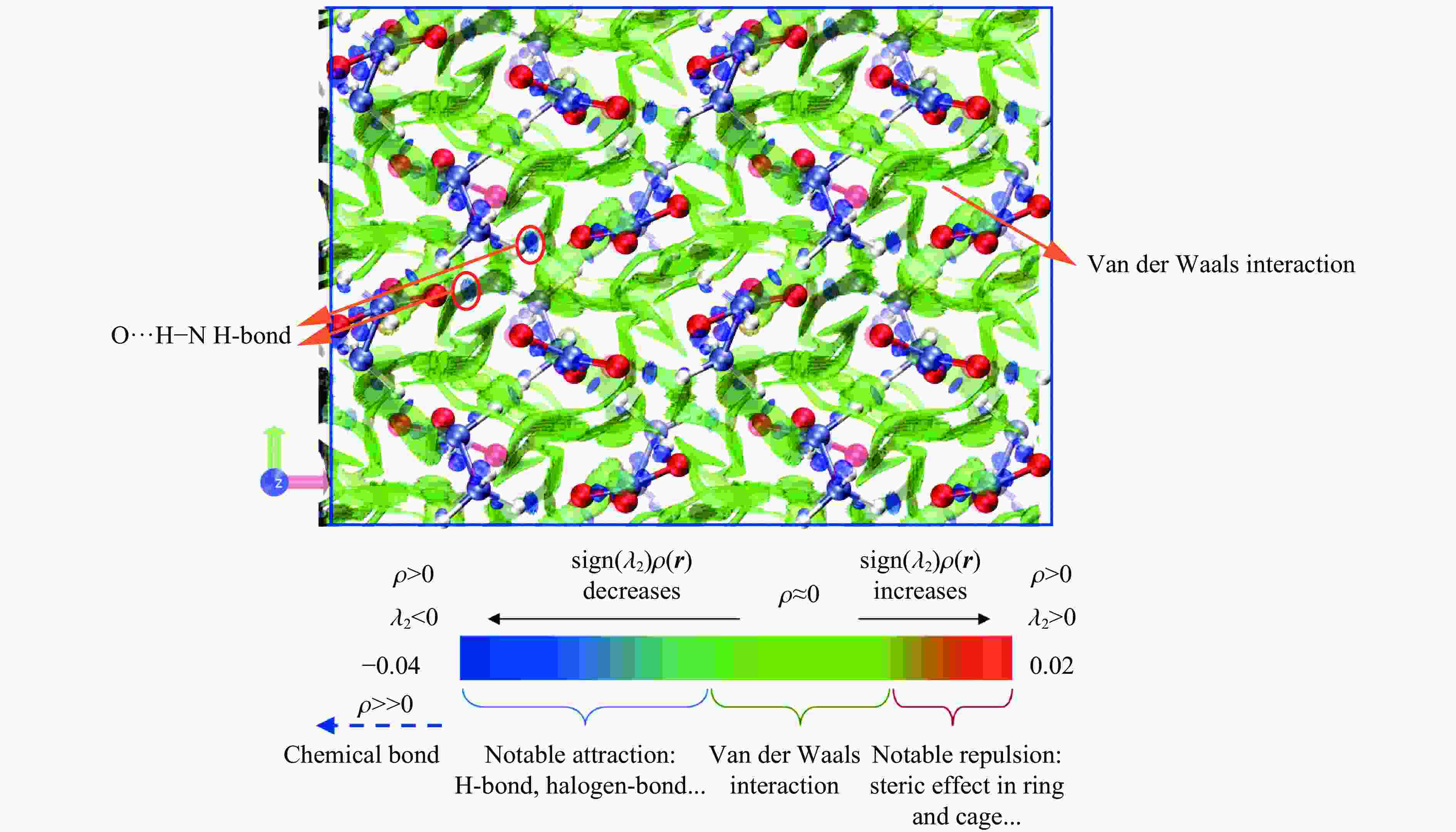
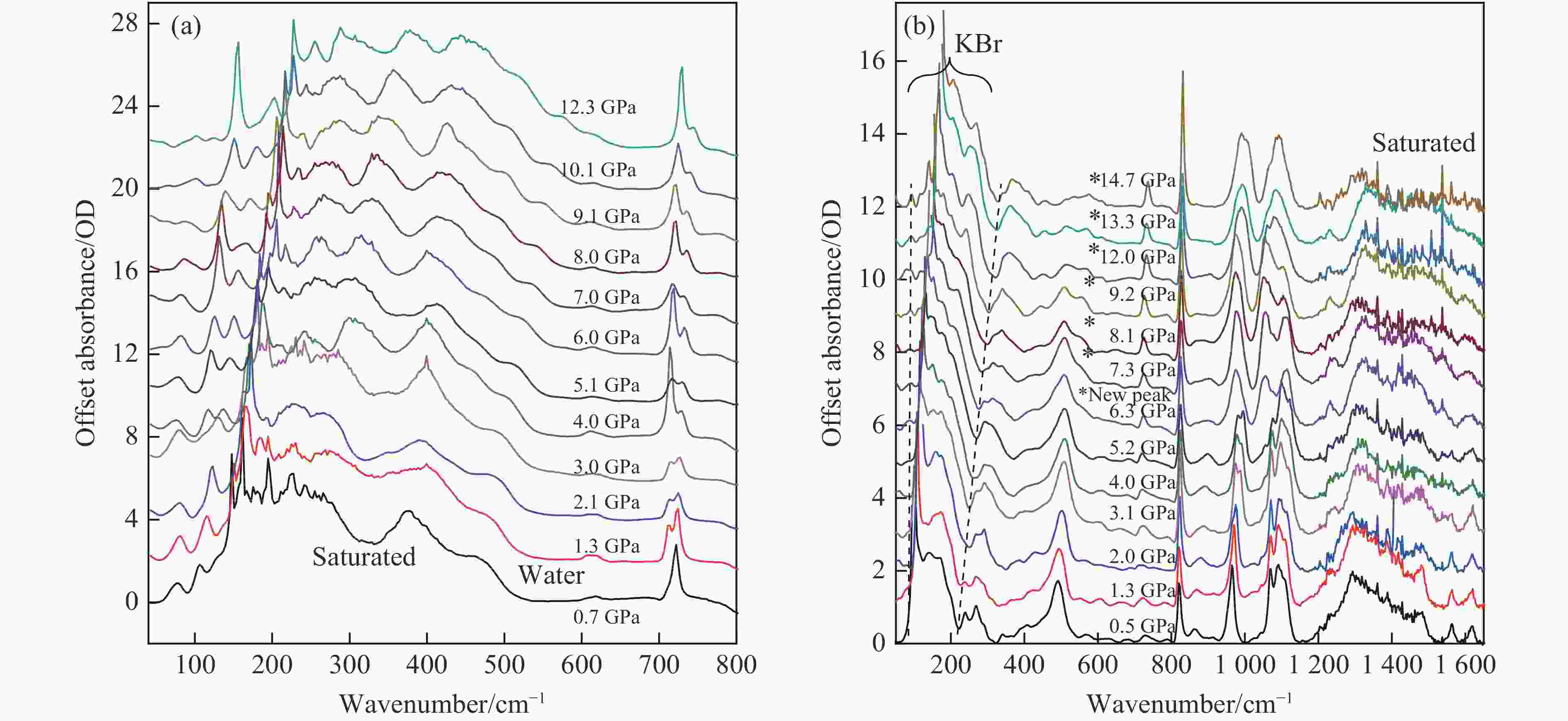
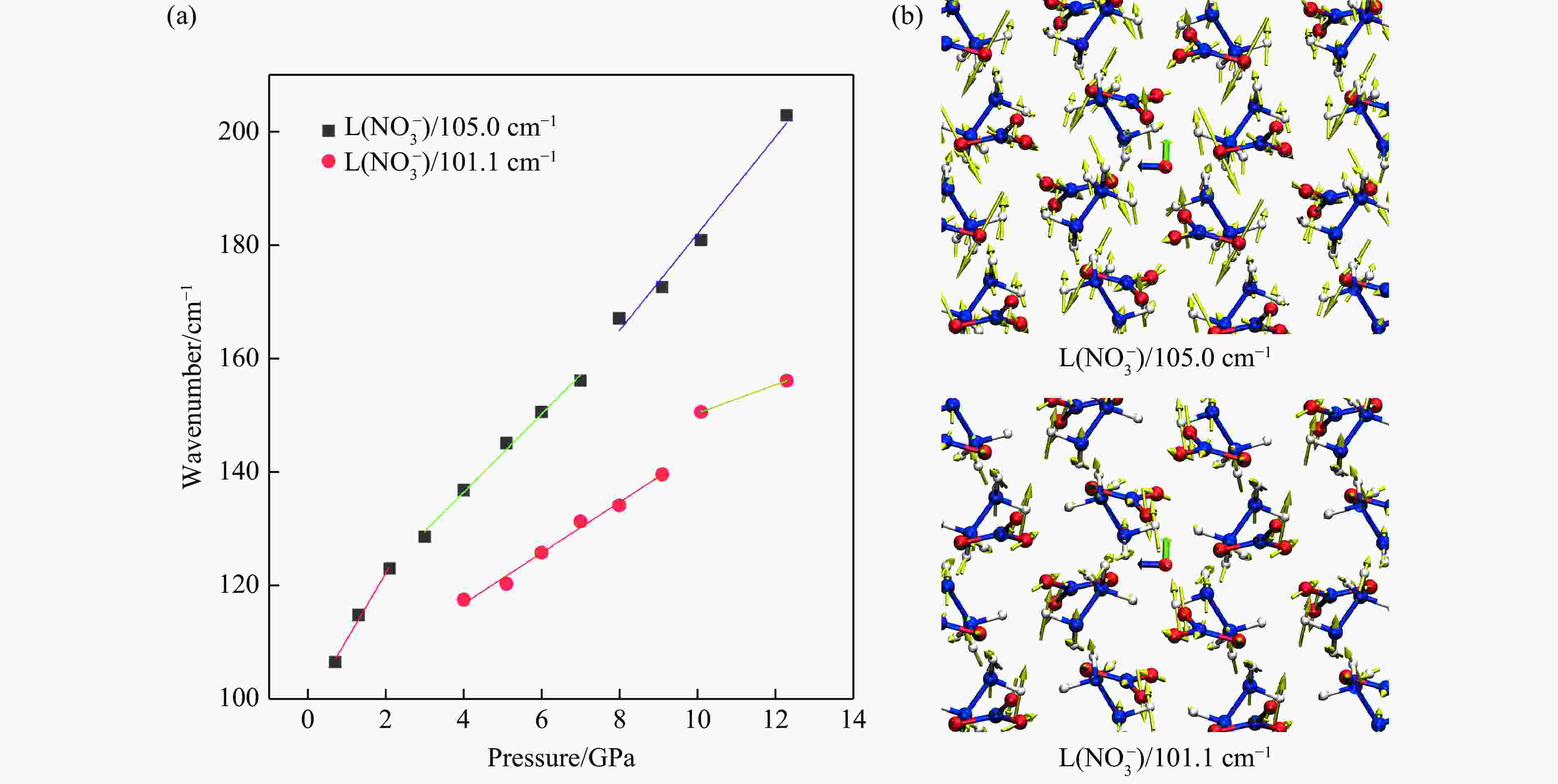
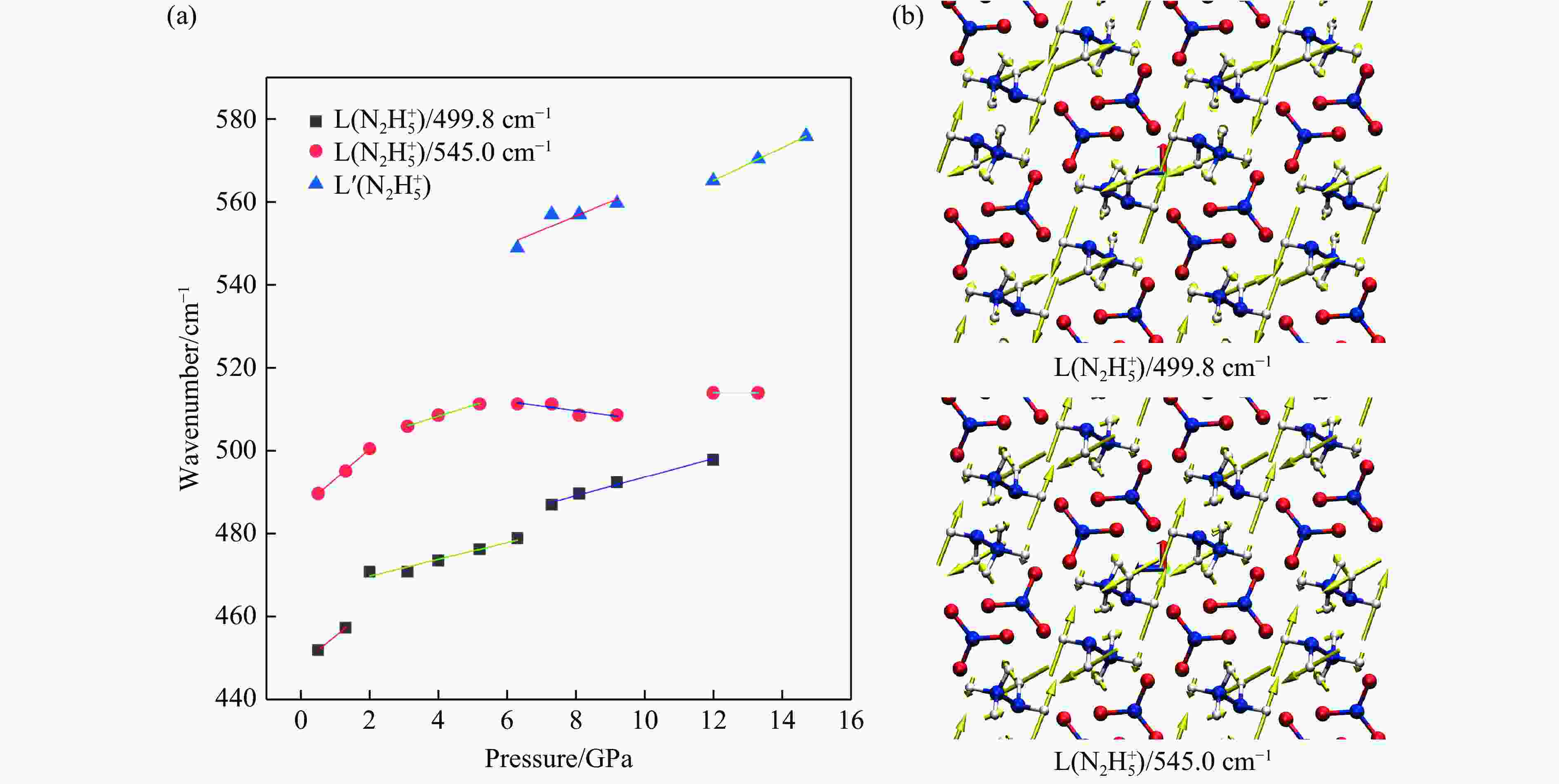
摘要: 对于含能材料，6 THz（200 cm⁻¹）以内的晶格振动模式对外部压力变化引起的结构变化非常敏感，因此，中远红外振动光谱可作为研究含能材料高压相变的有力手段。利用基于空气等离子体产生的中远红外超宽带光谱技术，结合金刚石对顶砧，获得了含能材料硝酸肼的高压振动光谱。同时，采用第一性原理方法，计算了硝酸肼的晶体结构和红外光谱，在此基础上对分子间的相互作用进行了分析。综合实验和计算结果，揭示了压力作用下分子间氢键和范德瓦尔斯相互作用对材料中分子结构和堆垛变化的影响，获得了硝酸肼的相变过程。
- 硝酸肼 /
- 中远红外光谱 /
- 第一性原理计算 /
- 高压 /
- 相变
Abstract: For energetic materials, the lattice vibration modes in the 6 THz (200 cm⁻¹) range are very sensitive to structural changes caused by external temperature and pressure changes. Therefore, mid- and far-infrared vibrational spectroscopy can be used as a powerful tool to study high-pressure phase transitions in these materials. We have obtained high-pressure vibrational spectra of hydrazine nitrate, using mid- and far-infrared ultra-broadband spectroscopy, whose broadband was generated by air plasma, combined with a diamond anvil cell (DAC). The crystal structure of hydrazine nitrate, as well as the infrared spectrum, were calculated by using the first principle method. Based on the calculation, the intermolecular interactions were analyzed. Combined with the experimental results, it was revealed that the structural changes under pressure alter the strength of intermolecular hydrogen bonds and van der Waals interactions, which in turn affects the low-frequency vibrational modes. And by analyzing the vibrational spectra, we observed the phase transition process of hydrazine nitrate.
- hydrazine nitrate /
- mid- and far- infrared spectra /
- first principle computation /
- high pressure /
- phase transition

HTML全文

图 1 α相HN晶胞结构^[8]（灰色球为氢原子，红色球为氧原子，蓝色球为氮原子，绿色虚线表示分子间氢键）

Figure 1. Crystal cell structure of α-HN^[8] (The gray balls represent H atoms, the red balls represent O atoms, the blue balls represent N atoms, and the green dashed lines represent intermolecular hydrogen bonds.)

下载: 全尺寸图片幻灯片

图 2 α-HN 2×2×2超胞结构中弱相互作用的IRI图示（灰色球为氢原子，红色球为氧原子，蓝色球为氮原子）

Figure 2. IRI representation of weak interactions of α-HN 2×2×2 supercell (The gray balls represent H atoms, the red balls represent O atoms, and the blue balls represent N atoms.)

下载: 全尺寸图片幻灯片

图 3 HN的高压红外吸收光谱：(a) 纯HN的远红外谱，(b) HN与KBr混合的中红外谱

Figure 3. High pressure infrared absorption spectra of HN: (a) far-infrared spectra of pure HN; (b) mid-infrared spectra of HN mixed with KBr

下载: 全尺寸图片幻灯片

图 4 硝酸基团平动振动模式的吸收峰随压力的变化规律

Figure 4. Effect of pressure on infrared absorption spectra shifts of nitrate libration modes

下载: 全尺寸图片幻灯片

图 5 肼离子平动振动模式对应的吸收峰随压力的变化规律

Figure 5. Effect of pressure on infrared absorption spectra shifts of hydrazine libration modes

下载: 全尺寸图片幻灯片

表 1 HN晶格参数的计算结果与实验结果比较

Table 1. Calculated crystal lattice parameters of HN compared with experimental data

Method	a/Å	b/Å	c/Å	β/(°)	V/Å³
Expt.^[7]	11.23	11.73	5.17	90.00	681.03
Expt.^[8]	7.9649	5.6569	8.1221	91.34	365.85
Expt.^[9]	8.0150	5.7250	8.1560	92.30	374.00
Calc. (this work)	7.9041	5.7271	8.1447	89.17	368.65
δ(Expt.^[8])/%	−0.8	1.2	0.3	−2.4	0.8
δ(Expt.^[9])/%	−1.4	0.04	−0.1	−3.4	−1.4

下载: 导出CSV

参考文献(33)

[1]	LIU J P. Liquid explosives [M]. Berlin: Springer, 2015: 330–337.
[2]	丁黎, 赵凤起, 高茵. 硝酸肼及硝酸肼基推进剂的研究进展 [J]. 飞航导弹, 2007(2): 51–55. doi: 10.3969/j.issn.1009-1319.2007.02.013 DING L, ZHAO F Q, GAO Y. Research progress of hydrazine nitrate and hydrazine nitrate-based propellants [J]. Aerospace Technology, 2007(2): 51–55. doi: 10.3969/j.issn.1009-1319.2007.02.013
[3]	UTKIN A V, MOCHALOVA V M. Shock wave and detonation properties of pressed hydrazine nitrate [J]. Propellants, Explosives, Pyrotechnics, 2018, 43(6): 552–558. doi: 10.1002/prep.201800047
[4]	UTKIN A V, MOCHALOVA V M, TORUNOV S I, et al. Detonation properties of hydrazine nitrate [J]. Journal of Physics: Conference Series, 2019, 1147: 012034. doi: 10.1088/1742-6596/1147/1/012034
[5]	邹展, 赵许群, 史海. 核废水中硝酸肼、硝酸羟胺的分析方法 [J]. 工业用水与废水, 2019, 50(1): 83–87. doi: 10.3969/j.issn.1009-2455.2019.01.020 ZOU Z, ZHAO X Q, SHI H. Analysis method of hydrazine nitrate and hydroxylamine nitrate in nuclear wastewater [J]. Industrial Water & Wastewater, 2019, 50(1): 83–87. doi: 10.3969/j.issn.1009-2455.2019.01.020
[6]	KLAPOTKE T M. Energetic materials encyclopedia [M]. 2nd ed. Berlin: De Gruyter, 2021: 944–948.
[7]	ROBINSON R J, MCCRONE W C. Crystallographic data 169: hydrazine nitrate (l) [J]. Analytical Chemistry, 1958, 30(5): 1014–1015. doi: 10.1021/ac60137a623
[8]	GRIGORIEV M S, MOISY P, DEN AUWER C, et al. Hydrazinium nitrate [J]. Acta Crystallographica Section E, 2005, E61: i216–i217. doi: 10.1107/S1600536805029211
[9]	夏云霞, 孙杰, 毛治华, 等. 硝酸肼晶体结构研究 [J]. 含能材料, 2008, 16(1): 73–76. doi: 10.3969/j.issn.1006-9941.2008.01.021 XIA Y X, SUN J, MAO Z H, et al. Crystal structure of hydrazine nitrate [J]. Chinese Journal of Energetic Materials, 2008, 16(1): 73–76. doi: 10.3969/j.issn.1006-9941.2008.01.021
[10]	MACRAE C F, SOVAGO I, COTTRELL S J, et al. Mercury 4.0: from visualization to analysis, design and prediction [J]. Journal of Applied Crystallography, 2020, 53: 226–235. doi: 10.1107/S1600576719014092
[11]	CHELLAPPA R S, DATTELBAUM D M, VELISAVLJEVIC N, et al. The phase diagram of ammonium nitrate [J]. The Journal of Chemical Physics, 2012, 137(6): 064504. doi: 10.1063/1.4733330
[12]	DUNUWILLE M, YOO C S. Phase diagram of ammonium nitrate [J]. The Journal of Chemical Physics, 2013, 139(21): 214503. doi: 10.1063/1.4837715
[13]	孙晓宇, 梁文韬, 李相东, 等. 高温高压下高能钝感炸药TATB物性及相关实验技术研究进展 [J]. 高压物理学报, 2022, 36(3): 030101. doi: 10.11858/gywlxb.20220520 SUN X Y, LIANG W T, LI X D, et al. Advances of high-temperature and high-pressure physical properties and experimental technology on high-energy insensitive explosive TATB [J]. Chinese Journal of High Pressure Physics, 2022, 36(3): 030101. doi: 10.11858/gywlxb.20220520
[14]	CIEZAK J A. The high-pressure characterization of energetic materials: 1,4-dimethyl-5-aminotetrazolium 5-nitrotetrazolate [J]. Propellants, Explosives, Pyrotechnics, 2011, 36(5): 446–450. doi: 10.1002/prep.201100031
[15]	PRAVICA M, YULGA B, LIU Z X, et al. Infrared study of 1,3,5-triamino-2,4,6-trinitrobenzene under high pressure [J]. Physical Review B, 2007, 76(6): 064102. doi: 10.1103/PhysRevB.76.064102
[16]	ZHU G B, YANG Y Q. High-pressure ultrafast time-resolved far-infrared full-spectrum spectroscopy with air-based upconversion [J]. Light: Science & Applications, 2024 (submitted).
[17]	LU T, CHEN Q X. Interaction region indicator: a simple real space function clearly revealing both chemical bonds and weak interactions [J]. Chemistry: Methods, 2021, 1(5): 231–239. doi: 10.1002/cmtd.202100007
[18]	WANG Y P, WANG F, ZHU G B, et al. Deconvoluting the energy transport mechanisms in all-inorganic CsPb₂Br₅/CsPbBr₃ perovskite composite systems [J]. APL Materials, 2022, 10(3): 031101. doi: 10.1063/5.0083022
[19]	CHANG X, LI J, MU J, et al. Impact of the uniaxial strain on terahertz modulation characteristics in flexible epitaxial VO₂ film across the phase transition [J]. Optics Express, 2023, 31(8): 13243–13254. doi: 10.1364/OE.488947
[20]	MAO H K, XU J, BELL P M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions [J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B5): 4673–4676. doi: 10.1029/JB091iB05p04673
[21]	BADRO J. James Badro’s homepage [EB/OL]. (2013-05-06)[2023-12-22]. http://james.badro.org/.
[22]	KÜHNE T D, IANNUZZI M, DEL BEN M, et al. CP2K: an electronic structure and molecular dynamics software package-quickstep: efficient and accurate electronic structure calculations [J]. The Journal of Chemical Physics, 2020, 152(19): 194103. doi: 10.1063/5.0007045
[23]	LIPPERT G, HUTTER J, PARRINELLO M. The Gaussian and augmented-plane-wave density functional method for ab initio molecular dynamics simulations [J]. Theoretical Chemistry Accounts, 1999, 103(2): 124–140. doi: 10.1007/s002140050523
[24]	OLIVEIRA D V, LAUN J, PEINTINGER M F, et al. BSSE-correction scheme for consistent Gaussian basis sets of double- and triple-zeta valence with polarization quality for solid-state calculations [J]. Journal of Computational Chemistry, 2019, 40(27): 2364–2376. doi: 10.1002/jcc.26013
[25]	PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1999, 77(18): 3865–3868.
[26]	GRIMME S, ANTONY J, EHRLICH S, et al. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu [J]. The Journal of Chemical Physics, 2010, 132(15): 154104. doi: 10.1063/1.3382344
[27]	GRIMME S, EHRLICH S, GOERIGK L. Effect of the damping function in dispersion corrected density functional theory [J]. Journal of Computational Chemistry, 2011, 32(7): 1456–1465. doi: 10.1002/jcc.21759
[28]	LU T. MfakeG program [EB/OL]. (2023-01-22) [2023-12-22]. http://sobereva.com/soft/MfakeG.
[29]	HUMPHREY W, DALKE A, SCHULTEN K. VMD: visual molecular dynamics [J]. Journal of Molecular Graphics, 1996, 14(1): 33–38. doi: 10.1016/0263-7855(96)00018-5
[30]	LU T, CHEN F W. Multiwfn: a multifunctional wavefunction analyzer [J]. Journal of Computational Chemistry, 2012, 33(5): 580–592. doi: 10.1002/jcc.22885
[31]	郑海飞. 金刚石压腔高温高压实验技术及其应用 [M]. 北京: 科学出版社, 2014: 179–185.
[32]	刘志国, 千正男. 高压技术 [M]. 哈尔滨: 哈尔滨工业大学出版社, 2012: 255–263.
[33]	STEELE B A, OLEYNIK I L. New phase of ammonium nitrate: a monoclinic distortion of AN-Ⅳ [J]. The Journal of Chemical Physics, 2015, 143(23): 234705. doi: 10.1063/1.4937420