Prediction of Synthesis Condition and Magnetic Property of Screened Metallic Double-Perovskite Antiferromagnet Mn2FeOsO6
doi: 10.11858/gywlxb.20230783
-
摘要: 提出了一种理论方法,用于预测复杂磁性双钙钛矿化合物的电子构型、多晶体形态、合成条件和物理性质。该方法对于双钙钛矿化合物的预测准确且高效。确定了一种反铁磁金属材料Mn2FeOsO6,它具有极高的反铁磁Néel相变温度(TN)。大量分析表明Mn2FeOsO6在费米能级附近具有很高的态密度和反铁磁构型,总磁矩为零。本研究结果表明,Mn2FeOsO6的TN高达680 K,代表自旋电子学领域的一个潜在突破。构建了Mn2FeOsO6的TN的复杂磁性模型,获得了相对可靠的磁激发谱,可与潜在的中子散射谱进行比较。这一理论方法得到的合成条件符合许多已合成的双钙钛矿化合物的实验合成条件,且该方法具有预测其他复杂磁性构型的潜力。研究成果有望在新型双钙钛矿材料的大数据预测中发挥关键作用。Abstract: We present a theoretical approach for predicting the electron configuration, polymorph, synthesis condition, and physical properties of complex magnetic double perovskite compounds. Our method is reasonable and computationally efficient, allowing us to identify an antiferromagnetic (AFM) metallic material, namely Mn2FeOsO6, with a high AFM Néel transition temperature (TN). Through extensive analysis, we demonstrate that Mn2FeOsO6 possesses a high density of states near the Fermi level and an AFM configuration, resulting in a zero total magnetic moment. Our findings suggest that the expectedTN of Mn2FeOsO6 is as high as 680 K, representing a potential breakthrough in the field of spintronics. We have also constructed a sophisticated magnetic model for this material, and obtained a reasonably reliable magnetic excitation spectrum potentially comparable with neutron scattering spectra. This theoretical approach provides synthesis conditions that are consistent with many synthesized double perovskite compounds in experiments, and it holds promise for the prediction of other complex magnetic configurations. Our study may play a key role in the big data prediction of novel double perovskite materials.
-
Key words:
- double-perovskite /
- antiferromagnet /
- Mn2FeOsO6
-
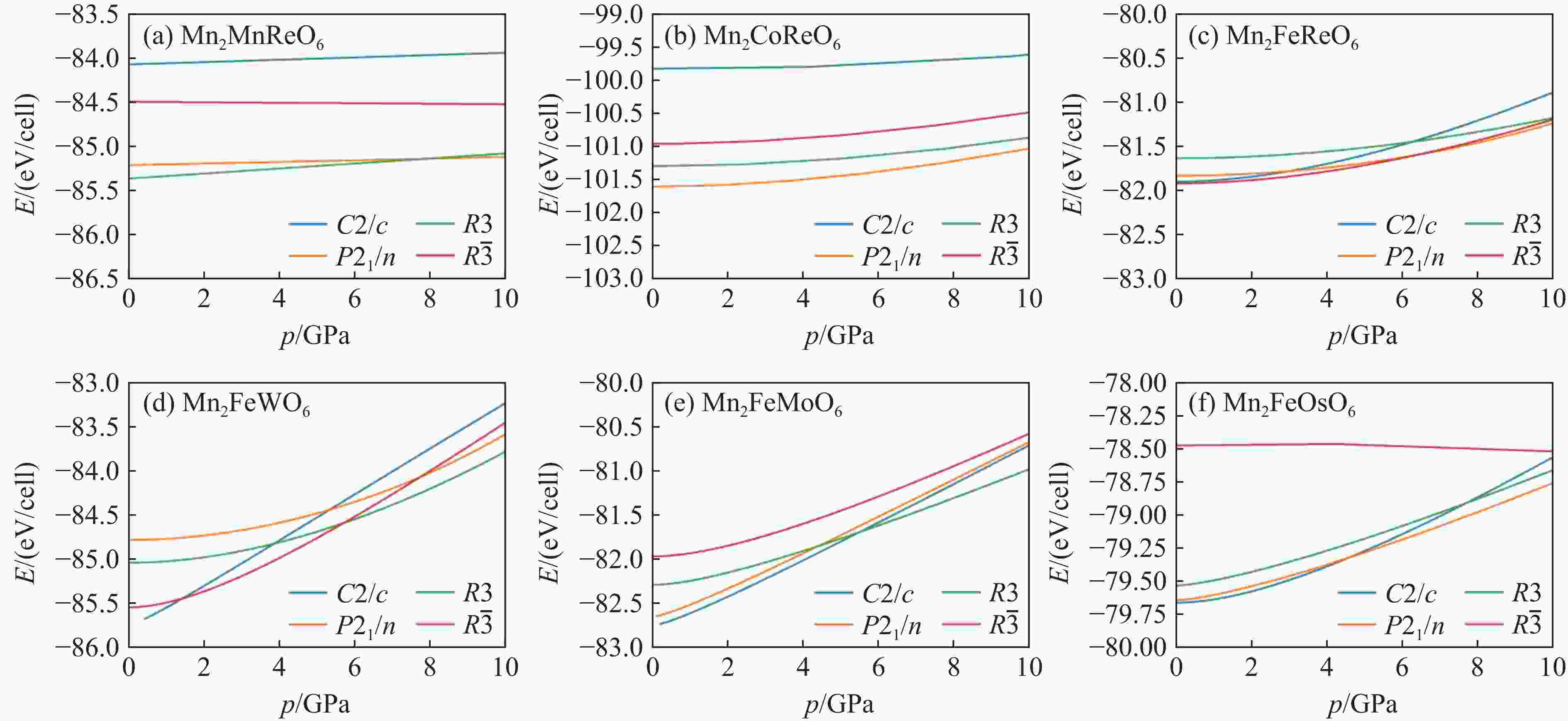
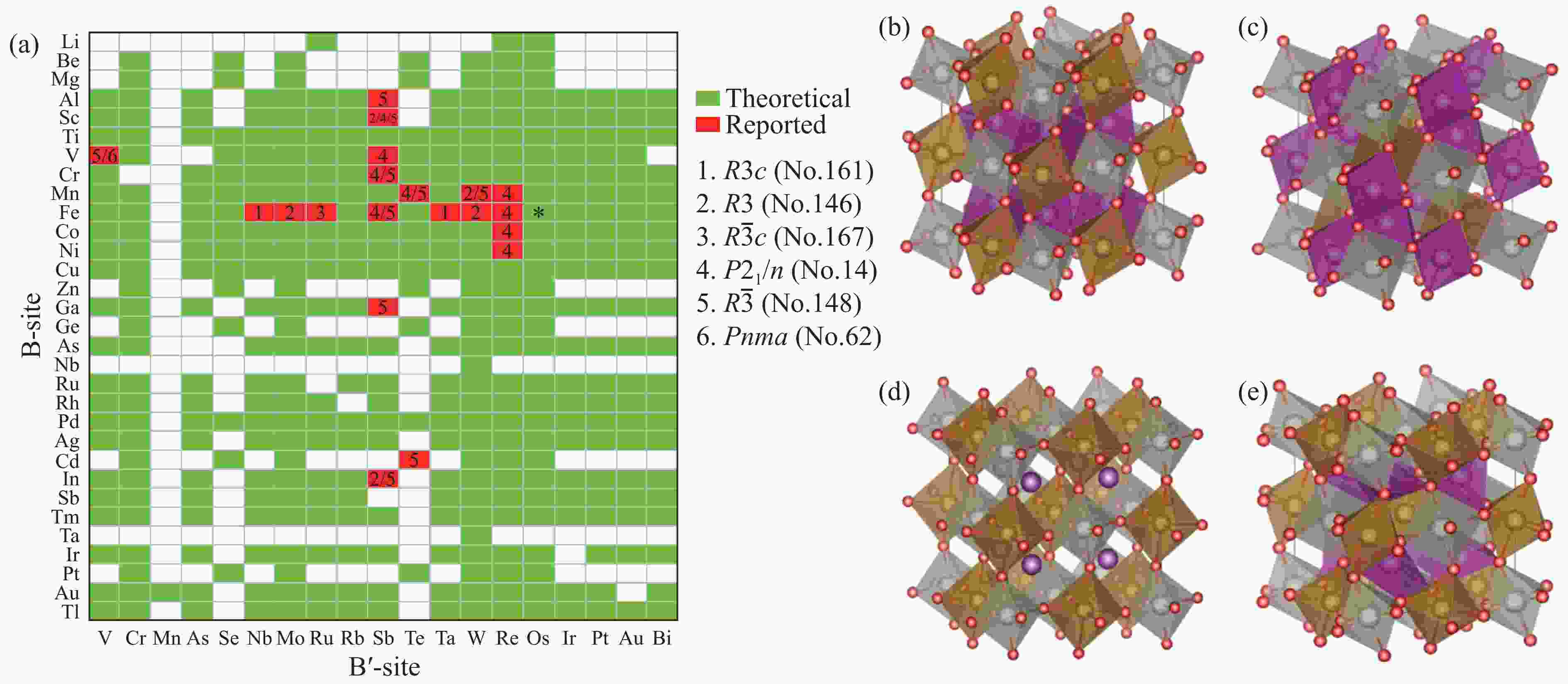
Figure 1. (a) Possible combinations of Mn2BB′O6 in the chemical space of B and B′ cations under charge balance (The possible, reported, and inexistent compounds are displayed in green, red, and blank, respectively. The numbers marked for the 20 known compounds denote the space group types listed on the right side.); (b)–(e) the crystal structures of some of the known compounds, including Mg3TeO6-type (R
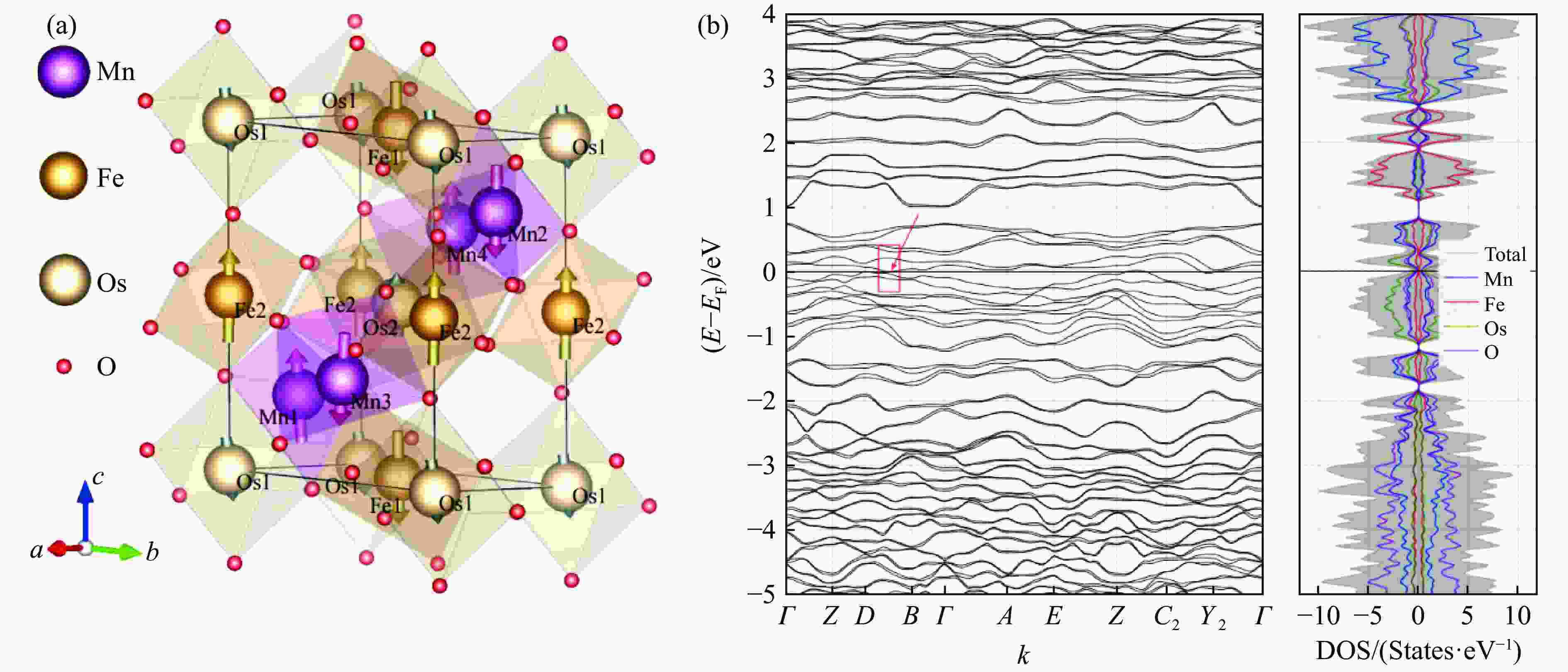
$ \overline{3} $ )[36–37], Ni3TeO6-type (R3)[38–39], β-Li3VF6-type (C2/c)[40–42], and GdFeO3-type (P21/n)[43–44](To ensure that our calculations are compatible with different magnetic configurations and atomic distortions, we have useda 40-atom super-cell, which can be considered as a (2, 2, 2) multiple of the ideal single perovskite structure alongthe three axes of Cartesian coordinates[50–51]. (b)–(e) also show the examples of collinear magnetic structure thatwe considered structure optimization with (b) FM, (c) Type Ⅰ AFM, (d) Type Ⅱ AFM and (e) Type Ⅲ AFM.)Figure 3. DFT results of Mn2FeOsO6 in consideration of SOC, DFT+U (UFe = 4.6 eV, UMn = 4 eV, UOs = 2.0 eV) and non-collinear magnetism: (a) the predicted atomic and magnetic structures, with a distorted GdFeO3-type monoclinic structure (P21/n) as for Mn2FeReO6[16, 29–30] (The arrow on each atom represents the spin orientation and the size of spin value. Every spin is almostlaying at <001> direction, forming a relatively ideal AFM configuration.); (b) energy band structure near Fermi level andspin-resolved density of states (DOS) (Mn2FeOsO6 has no bandgap, forming as conductor. There is a suspectedformation of Dirac points between wavevectors B-D, marked by red rectangle and arrow. The DOS of spin-upand spin-down are basically the same, verifying the AFM configuration of Mn2FeOsO6.)
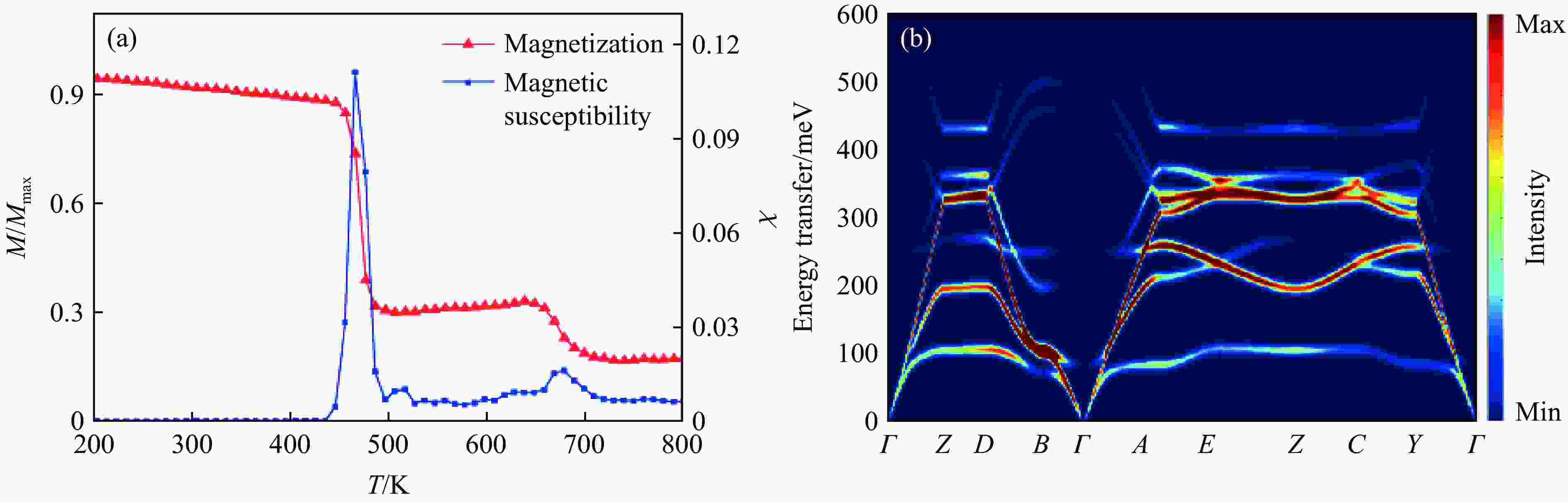
Figure 4. Magnetism of Mn2FeOsO6: (a) calculated magnetization and magnetic susceptibility via classical Monte Carlo simulation (The red line represents the theoretical total magnetic moment M divided by saturation magnetic moment Mmax, while the blue line represents the relative magnetic susceptibility χ, both indicating the phase transition positions around temparature T about 480 K.); (b) simulated excitation spectrum using SpinW package (The vertical axis represents the energy of the excitation spectrum,and the colors correspond to the intensity of the excitation spectrum.)
Table 1. Structural and electronic properties of the 7 experimentally realized TMO double perovskite-related compounds, along with the predicted Mn2FeOsO6. Here
$n_{\mathrm{d}} $ ≥14 provide certain displacement and deformation due to the influence of strong magnetism, resulting in low symmetry (R3 and P21/n)Compound Space group nd Synthesis conditions Physical properties Magnetic structure Ref. Mn2FeMoO6 R3 16 1350 ℃, 8 GPa Multiferroic,
TC = 337 KType-Ⅱ AFM [17] Mn2FeWO6 R3 14 1400 ℃, 8 GPa Second-Harmonic generation,
TN = 70 KType-Ⅰ AFM [24] Mn2MnWO6 R3 15 1400 ℃, 8 GPa TN = 58 K Type-Ⅰ AFM [15] Mn2CoReO6 P21/n 14 1300 ℃, 8 GPa Semiconductor, TN = 94 K Type-Ⅱ AFM [26] Mn2FeReO6 P21/n 17 1350 ℃, 5/11 GPa Half-metal, TC = 520 K Type-Ⅲ AFM [16, 29–30] Mn2MnReO6 P21/n 17 1400 ℃, 5/8 GPa Semiconductor, TN = 50 K Type-Ⅱ AFM [29, 31] Mn2NiReO6 P21/n 17 1573 ℃, 8 GPa Semiconductor, TN = 80 K Type-Ⅱ AFM [73] Mn2FeOsO6 P21/n 18 5 GPa Metal, TN = 680 K Type-Ⅲ AFM This work Table 2. Magnetic exchange
$J_{i j}$ between magnetic ions within a magnetic unit cell of Mn2FeOsO6i j Jij/meV i j Jij/meV i j Jij/meV i j Jij/meV Mn1 Mn2 0.97 Mn2 Mn3 −19.20 Mn3 Fe1 1.01 Mn4 Os2 −15.77 Mn1 Mn3 40.48 Mn2 Mn4 39.88 Mn3 Fe2 13.49 Fe1 Fe2 −12.01 Mn1 Mn4 −20.07 Mn2 Fe1 15.06 Mn3 Os1 −16.74 Fe1 Os1 35.37 Mn1 Fe1 −14.33 Mn2 Fe2 18.32 Mn3 Os2 15.65 Fe1 Os2 35.37 Mn1 Fe2 −16.58 Mn2 Os1 12.26 Mn4 Fe1 −1.26 Fe2 Os1 9.14 Mn1 Os1 −12.72 Mn2 Os2 25.43 Mn4 Fe2 −13.27 Fe2 Os2 −33.49 Mn1 Os2 −27.35 Mn3 Mn4 28.61 Mn4 Os1 17.05 Os1 Os2 −6.61 -
[1] FUSIL S, GARCIA V, BARTHÉLÉMY A, et al. Magnetoelectric devices for spintronics [J]. Annual Review of Materials Research, 2014, 44: 91–116. doi: 10.1146/annurev-matsci-070813-113315 [2] KOBAYASHI K I, KIMURA T, SAWADA H, et al. Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure [J]. Nature, 1998, 395(6703): 677–680. doi: 10.1038/27167 [3] ZHOU J P, DASS R, YIN H Q, et al. Enhancement of room temperature magnetoresistance in double perovskite ferrimagnets [J]. Journal of Applied Physics, 2000, 87(9): 5037–5039. doi: 10.1063/1.373240 [4] SERRAT D, DE TERESA J M, IBARRA M R. Double perovskites with ferromagnetism above room temperature [J]. Journal of Physics: Condensed Matter, 2007, 19(2): 023201. doi: 10.1088/0953-8984/19/2/023201 [5] MORROW R, MISHRA R, RESTREPO O D, et al. Independent ordering of two interpenetrating magnetic sublattices in the double perovskite Sr2CoOsO6 [J]. Journal of the American Chemical Society, 2013, 135(50): 18824–18830. doi: 10.1021/ja407342w [6] FENG H L, ARAI M, MATSUSHITA Y, et al. High-temperature ferrimagnetism driven by lattice distortion in double perovskite Ca2FeOsO6 [J]. Journal of the American Chemical Society, 2014, 136(9): 3326–3329. doi: 10.1021/ja411713q [7] CHEN J, WANG X, HU Z W, et al. Enhanced magnetization of the highest- TC ferrimagnetic oxide Sr2CrOsO6 [J]. Physical Review B, 2020, 102(18): 184418. doi: 10.1103/PhysRevB.102.184418 [8] KROCKENBERGER Y, MOGARE K, REEHUIS M, et al. Sr2CrOsO6: end point of a spin-polarized metal-insulator transition by 5 d band filling [J]. Physical Review B, 2007, 75(2): 020404. doi: 10.1103/PhysRevB.75.020404 [9] WAKABAYASHI Y K, KROCKENBERGER Y, TSUJIMOTO N, et al. Ferromagnetism above 1 000 K in a highly cation-ordered double-perovskite insulator Sr3OsO6 [J]. Nature Communications, 2019, 10(1): 535. [10] LI R J, ZHU X Z, FU Q F, et al. Nanosheet-based Nb12O29 hierarchical microspheres for enhanced lithium storage [J]. Chemical Communications, 2019, 55(17): 2493–2496. doi: 10.1039/C8CC09924C [11] MCCALL S, CAO G, CROW J E, et al. Metamagnetism of single crystal Ca3Ru2O7 in high magnetic fields [J]. Physica B: Condensed Matter, 1998, 246/247: 144–148. doi: 10.1016/S0921-4526(98)00042-8 [12] KOMAREK A C, STRELTSOV S V, ISOBE M, et al. CaCrO3: an anomalous antiferromagnetic metallic oxide [J]. Physical Review Letters, 2008, 101(16): 167204. doi: 10.1103/PhysRevLett.101.167204 [13] WANG B X, ROSENKRANZ S, RUI X, et al. Antiferromagnetic defect structure in LaNiO3– δ single crystals [J]. Physical Review Materials, 2018, 2(6): 064404. doi: 10.1103/PhysRevMaterials.2.064404 [14] LI M R, RETUERTO M, WALKER D, et al. Magnetic-structure-stabilized polarization in an above-room-temperature ferrimagnet [J]. Angewandte Chemie International Edition, 2014, 53(40): 10774–10778. doi: 10.1002/anie.201406180 [15] LI M R, MCCABE E E, STEPHENS P W, et al. Magnetostriction-polarization coupling in multiferroic Mn2MnWO6 [J]. Nature Communications, 2017, 8(1): 2037. doi: 10.1038/s41467-017-02003-3 [16] LI M R, RETUERTO M, DENG Z, et al. Giant magnetoresistance in the half-metallic double-perovskite ferrimagnet Mn2FeReO6 [J]. Angewandte Chemie, 2015, 127(41): 12237–12241. doi: 10.1002/ange.201506456 [17] LI M R, RETUERTO M, STEPHENS P W, et al. Low-temperature cationic rearrangement in a bulk metal oxide [J]. Angewandte Chemie International Edition, 2016, 55(34): 9862–9867. doi: 10.1002/anie.201511360 [18] MORROW R, SOLIZ J R, HAUSER A J, et al. The effect of chemical pressure on the structure and properties of A2CrOsO6 (A = Sr, Ca) ferrimagnetic double perovskite [J]. Journal of Solid State Chemistry, 2016, 238: 46–52. doi: 10.1016/j.jssc.2016.02.025 [19] HOU Y S, XIANG H J, GONG X G. Lattice-distortion induced magnetic transition from low-temperature antiferromagnetism to high-temperature ferrimagnetism in double perovskites A2FeOsO6 (A = Ca, Sr) [J]. Scientific Reports, 2015, 5(1): 13159. doi: 10.1038/srep13159 [20] NAVEEN K, REEHUIS M, ADLER P, et al. Reentrant magnetism at the borderline between long-range antiferromagnetic order and spin-glass behavior in the B-site disordered perovskite system Ca2− x Sr x FeRuO6 [J]. Physical Review B, 2018, 98(22): 224423. doi: 10.1103/PhysRevB.98.224423 [21] ANDERSON M T, GREENWOOD K B, TAYLOR G A, et al. B-cation arrangements in double perovskites [J]. Progress in Solid State Chemistry, 1993, 22(3): 197–233. doi: 10.1016/0079-6786(93)90004-B [22] GIBB T C. A study of superexchange interactions in the perovskite Sr2FeRuO6 by Monte Carlo analysis [J]. Journal of Materials Chemistry, 2005, 15(37): 4015–4019. doi: 10.1039/b506752a [23] CHANG J, LEE K, JUNG M H, et al. Emergence of room-temperature magnetic ordering in artificially fabricated ordered-double-perovskite Sr2FeRuO6 [J]. Chemistry of Materials, 2011, 23(11): 2693–2696. doi: 10.1021/cm200454z [24] LI M R, CROFT M, STEPHENS P W, et al. Mn2FeWO6: a new Ni3TeO6-type polar and magnetic oxide [J]. Advanced Materials, 2015, 27(13): 2177–2181. doi: 10.1002/adma.201405244 [25] TAN X Y, MCCABE E E, ORLANDI F, et al. MnFe0.5Ru0.5O3: an above-room-temperature antiferromagnetic semiconductor [J]. Journal of Materials Chemistry C, 2019, 7(3): 509–522. doi: 10.1039/C8TC05059G [26] FRANK C E, MCCABE E E, ORLANDI F, et al. Mn2CoReO6: a robust multisublattice antiferromagnetic perovskite with small A-site cations [J]. Chemical Communications, 2019, 55(23): 3331–3334. doi: 10.1039/C9CC00038K [27] LI M R, STEPHENS P W, CROFT M, et al. Mn2(Fe0.8Mo0.2)MoO6: a double perovskite with multiple transition metal sublattice magnetic effects [J]. Chemistry of Materials, 2018, 30(14): 4508–4514. doi: 10.1021/acs.chemmater.8b00250 [28] CAI G H, GREENBLATT M, LI M R. Polar magnets in double corundum oxides [J]. Chemistry of Materials, 2017, 29(13): 5447–5457. doi: 10.1021/acs.chemmater.7b01567 [29] LI M R, HODGES J P, RETUERTO M, et al. Mn2MnReO6: synthesis and magnetic structure determination of a new transition-metal-only double perovskite canted antiferromagnet [J]. Chemistry of Materials, 2016, 28(9): 3148–3158. doi: 10.1021/acs.chemmater.6b00755 [30] ARÉVALO-LÓPEZ A M, MCNALLY G M, ATTFIELD J P. Large magnetization and frustration switching of magnetoresistance in the double-perovskite ferrimagnet Mn2FeReO6 [J]. Angewandte Chemie International Edition, 2015, 54(41): 12074–12077. doi: 10.1002/anie.201506540 [31] ARÉVALO-LÓPEZ A M, STEGEMANN F, ATTFIELD J P. Competing antiferromagnetic orders in the double perovskite Mn2MnReO6 (Mn3ReO6) [J]. Chemical Communications, 2016, 52(32): 5558–5560. doi: 10.1039/C6CC01290F [32] VASALA S, KARPPINEN M. A2B 'B ''O6 perovskites: a review [J]. Progress in Solid State Chemistry, 2015, 43(1/2): 1–36. doi: 10.1016/j.progsolidstchem.2014.08.001 [33] GILIOLI E, EHM L. High pressure and multiferroics materials: a happy marriage [J]. IUCrJ, 2014, 1(6): 590–603. doi: 10.1107/S2052252514020569 [34] BELIK A A, YI W. High-pressure synthesis, crystal chemistry and physics of perovskites with small cations at the A site [J]. Journal of Physics: Condensed Matter, 2014, 26(16): 163201. doi: 10.1088/0953-8984/26/16/163201 [35] SHANNON R D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides [J]. Acta Crystallographica Section A: Crystal Physics, Diffraction, Theoretical and General Crystallography, 1976, 32(5): 751–767. [36] SCHULZ H, BAYER G. Structure determination of Mg3TeO6 [J]. Acta Crystallographica Section B: Structural Crystallography and Crystal Chemistry, 1971, 27(4): 815–821. doi: 10.1107/S0567740871002954 [37] SELB E, DECLARA L, BAYARJARGAL L, et al. Crystal structure and properties of a UV-transparent high-pressure polymorph of Mg3TeO6 with second harmonic generation response [J]. European Journal of Inorganic Chemistry, 2019, 2019(43): 4668–4676. doi: 10.1002/ejic.201900998 [38] GHOSH A, CHEN K H, QIU X S, et al. Anisotropy in the magnetic interaction and lattice-orbital coupling of single crystal Ni3TeO6 [J]. Scientific Reports, 2018, 8(1): 15779. doi: 10.1038/s41598-018-33976-w [39] FERNÁNDEZ-CATALÁ J, SINGH H, WANG S B, et al. Hydrothermal synthesis of Ni3TeO6 and Cu3TeO6 nanostructures for magnetic and photoconductivity applications [J]. ACS Applied Nano Materials, 2023, 6(6): 4887–4897. doi: 10.1021/acsanm.3c00630 [40] HAN Y F, ZENG Y J, HENDRICKX M, et al. Universal A-cation splitting in LiNbO3-type structure driven by intrapositional multivalent coupling [J]. Journal of the American Chemical Society, 2020, 142(15): 7168–7178. doi: 10.1021/jacs.0c01814 [41] FUJITA K, KAWAMOTO T, YAMADA I, et al. LiNbO3-type InFeO3: room-temperature polar magnet without second-order Jahn-Teller active ions [J]. Chemistry of Materials, 2016, 28(18): 6644–6655. doi: 10.1021/acs.chemmater.6b02783 [42] VARGA T, KUMAR A, VLAHOS E, et al. Coexistence of weak ferromagnetism and ferroelectricity in the high pressure LiNbO3-type phase of FeTiO3 [J]. Physical Review Letters, 2009, 103(4): 047601. doi: 10.1103/PhysRevLett.103.047601 [43] BELIK A A, STEFANOVICH S Y, LAZORYAK B I, et al. BiInO3: a polar oxide with GdFeO3-type perovskite structure [J]. Chemistry of Materials, 2006, 18(7): 1964–1968. doi: 10.1021/cm052627s [44] VASYLECHKO L, MATKOVSKII A, SAVYTSKII D, et al. Crystal structure of GdFeO3-type rare earth gallates and aluminates [J]. Journal of Alloys and Compounds, 1999, 291(1/2): 57–65. doi: 10.1016/S0925-8388(99)00247-9 [45] MALYI O I, DALPIAN G M, ZHAO X G, et al. Realization of predicted exotic materials: the burden of proof [J]. Materials Today, 2020, 32: 35–45. doi: 10.1016/j.mattod.2019.08.003 [46] LUFASO M W, WOODWARD P M. Prediction of the crystal structures of perovskites using the software program SPuDS [J]. Acta Crystallographica Section B: Structural Science, 2001, 57(6): 725–738. doi: 10.1107/S0108768101015282 [47] BARTEL C J, SUTTON C, GOLDSMITH B R, et al. New tolerance factor to predict the stability of perovskite oxides and halides [J]. Science Advances, 2019, 5(2): eaav0693. doi: 10.1126/sciadv.aav0693 [48] FILIP M R, GIUSTINO F. The geometric blueprint of perovskites [J]. Proceedings of the National Academy of Sciences of the United States of America, 2018, 115(21): 5397–5402. doi: 10.1073/pnas.1719179115 [49] SUN Q D, YIN W J. Thermodynamic stability trend of cubic perovskites [J]. Journal of the American Chemical Society, 2017, 139(42): 14905–14908. doi: 10.1021/jacs.7b09379 [50] CHEN P, LIU B G. Giant ferroelectric polarization and electric reversal of strong spontaneous magnetization in multiferroic Bi2FeMoO6 [J]. Journal of Magnetism and Magnetic Materials, 2017, 441: 497–502. doi: 10.1016/j.jmmm.2017.06.019 [51] CHEN P, GRISOLIA M N, ZHAO H J, et al. Energetics of oxygen-octahedra rotations in perovskite oxides from first principles [J]. Physical Review B, 2018, 97(2): 024113. doi: 10.1103/PhysRevB.97.024113 [52] SU H P, LI S F, HAN Y F, et al. Predicted polymorph manipulation in an exotic double perovskite oxide [J]. Journal of Materials Chemistry C, 2019, 7(39): 12306–12311. doi: 10.1039/C9TC03367J [53] HAN Y F, WU M X, GUI C R, et al. Data-driven computational prediction and experimental realization of exotic perovskite-related polar magnets [J]. NPJ Quantum Materials, 2020, 5(1): 92. doi: 10.1038/s41535-020-00294-2 [54] MURNAGHAN F D. The compressibility of media under extreme pressures [J]. Proceedings of the National Academy of Sciences of the United States of America, 1944, 30(9): 244–247. doi: 10.1073/pnas.30.9.244 [55] HALDER A, GHOSH A, DASGUPTA T S. Machine-learning-assisted prediction of magnetic double perovskites [J]. Physical Review Materials, 2019, 3(8): 084418. doi: 10.1103/PhysRevMaterials.3.084418 [56] HALDER A, NAFDAY D, SANYAL P, et al. Computer predictions on Rh-based double perovskites with unusual electronic and magnetic properties [J]. NPJ Quantum Materials, 2018, 3(1): 17. doi: 10.1038/s41535-018-0091-6 [57] ZHAO H J, ÍÑIGUEZ J, REN W, et al. Atomistic theory of hybrid improper ferroelectricity in perovskites [J]. Physical Review B, 2014, 89(17): 174101. doi: 10.1103/PhysRevB.89.174101 [58] BENEDEK N A, FENNIE C J. Why are there so few perovskite ferroelectrics [J]. The Journal of Physical Chemistry C, 2013, 117(26): 13339–13349. doi: 10.1021/jp402046t [59] HOWARD C J, KENNEDY B J, WOODWARD P M. Ordered double perovskites—a group-theoretical analysis [J]. Acta Crystallographica Section B, 2003, 59(4): 463–471. doi: 10.1107/S0108768103010073 [60] GLAZER A M. The classification of tilted octahedra in perovskites [J]. Acta Crystallographica Section B, 1972, 28(11): 3384–3392. [61] RONDINELLI J M, MAY S J, FREELAND J W. Control of octahedral connectivity in perovskite oxide heterostructures: an emerging route to multifunctional materials discovery [J]. MRS Bulletin, 2012, 37(3): 261–270. doi: 10.1557/mrs.2012.49 [62] ZHOU Q D, TAN T Y, KENNEDY B J, et al. Crystal structures and phase transitions in Sr doped Ba2InTaO6 perovskites [J]. Journal of Solid State Chemistry, 2013, 206: 122–128. doi: 10.1016/j.jssc.2013.08.007 [63] FU W T, GÖTZ R J, IJDO D J W. On the symmetry and crystal structures of Ba2LaIrO6 [J]. Journal of Solid State Chemistry, 2010, 183(2): 419–424. doi: 10.1016/j.jssc.2009.12.006 [64] GUENNOU M, BOUVIER P, CHEN G S, et al. Multiple high-pressure phase transitions in BiFeO3 [J]. Physical Review B, 2011, 84(17): 174107. doi: 10.1103/PhysRevB.84.174107 [65] XIE T, GROSSMAN J C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties [J]. Physical Review Letters, 2018, 120(14): 145301. doi: 10.1103/PhysRevLett.120.145301 [66] WANG Y C, MA Y M. Perspective: crystal structure prediction at high pressures [J]. The Journal of Chemical Physics, 2014, 140(4): 040901. doi: 10.1063/1.4861966 [67] KRESSE G, HAFNER J. Ab initio molecular dynamics for liquid metals [J]. Physical Review B, 1993, 47(1): 558–561. doi: 10.1103/PhysRevB.47.558 [68] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Physical Review B, 1999, 59(3): 1758–1775. doi: 10.1103/PhysRevB.59.1758 [69] KRESSE G, HAFNER J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium [J]. Physical Review B, 1994, 49(20): 14251–14269. doi: 10.1103/PhysRevB.49.14251 [70] BLÖCHL P E. Projector augmented-wave method [J]. Physical Review B, 1994, 50(24): 17953–17979. doi: 10.1103/PhysRevB.50.17953 [71] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865–3868. doi: 10.1103/PhysRevLett.77.3865 [72] TOTH S, LAKE B. Linear spin wave theory for single-Q incommensurate magnetic structures [J]. Journal of Physics: Condensed Matter, 2015, 27(16): 166002. doi: 10.1088/0953-8984/27/16/166002 [73] SOLANA-MADRUGA E, ALHARBI, K N, HERZ M, et al. Unconventional magnetism in the high pressure ‘all transition metal’ double perovskite Mn2NiReO6 [J]. Chemical Communications, 2020, 56(83): 12574–12577. doi: 10.1039/D0CC04756B [74] LI S D, CHEN P, LIU B G. Promising ferrimagnetic double perovskite oxides towards high spin polarization at high temperature [J]. AIP Advances, 2013, 3(1): 012107. doi: 10.1063/1.4775352 -







 下载:
下载: