Dynamic Behavior and Constitutive Relationship of Titanium Alloy Ti6Al4V under High Temperature and High Strain Rate
-
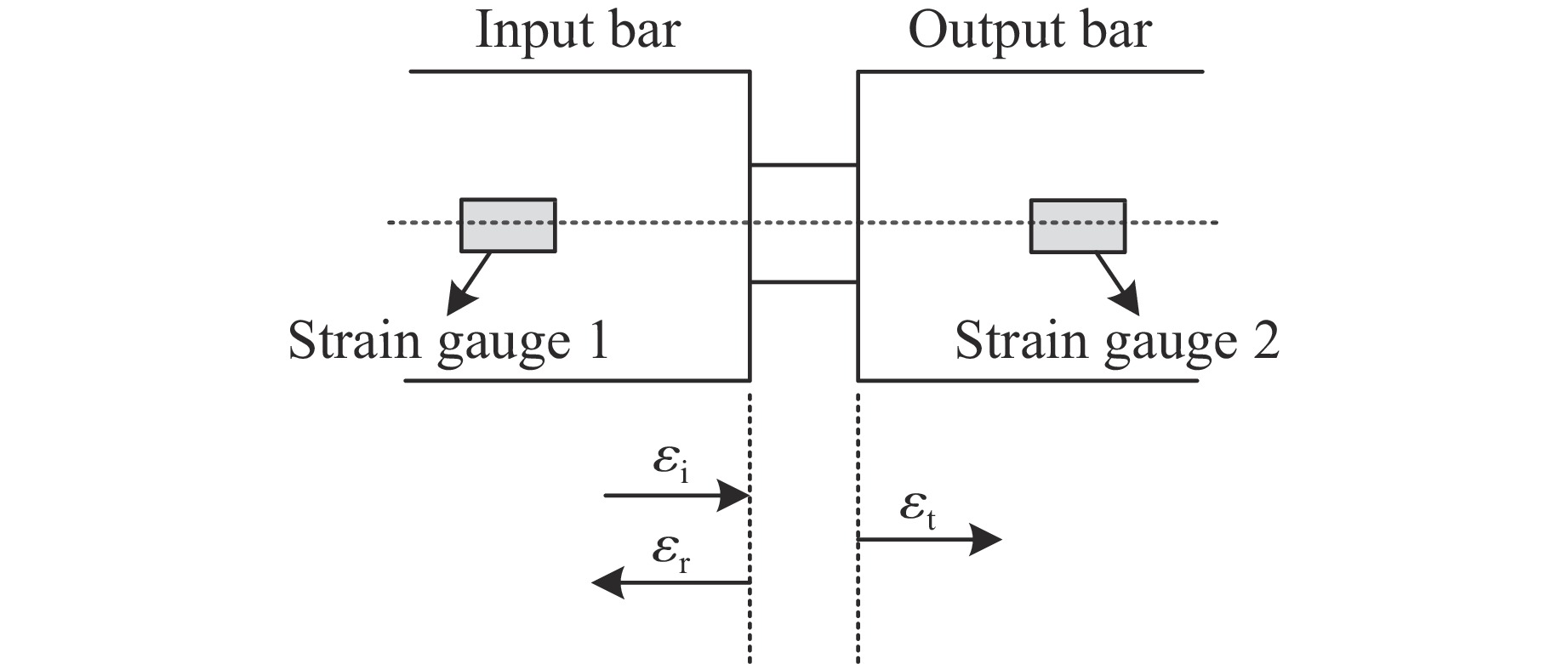
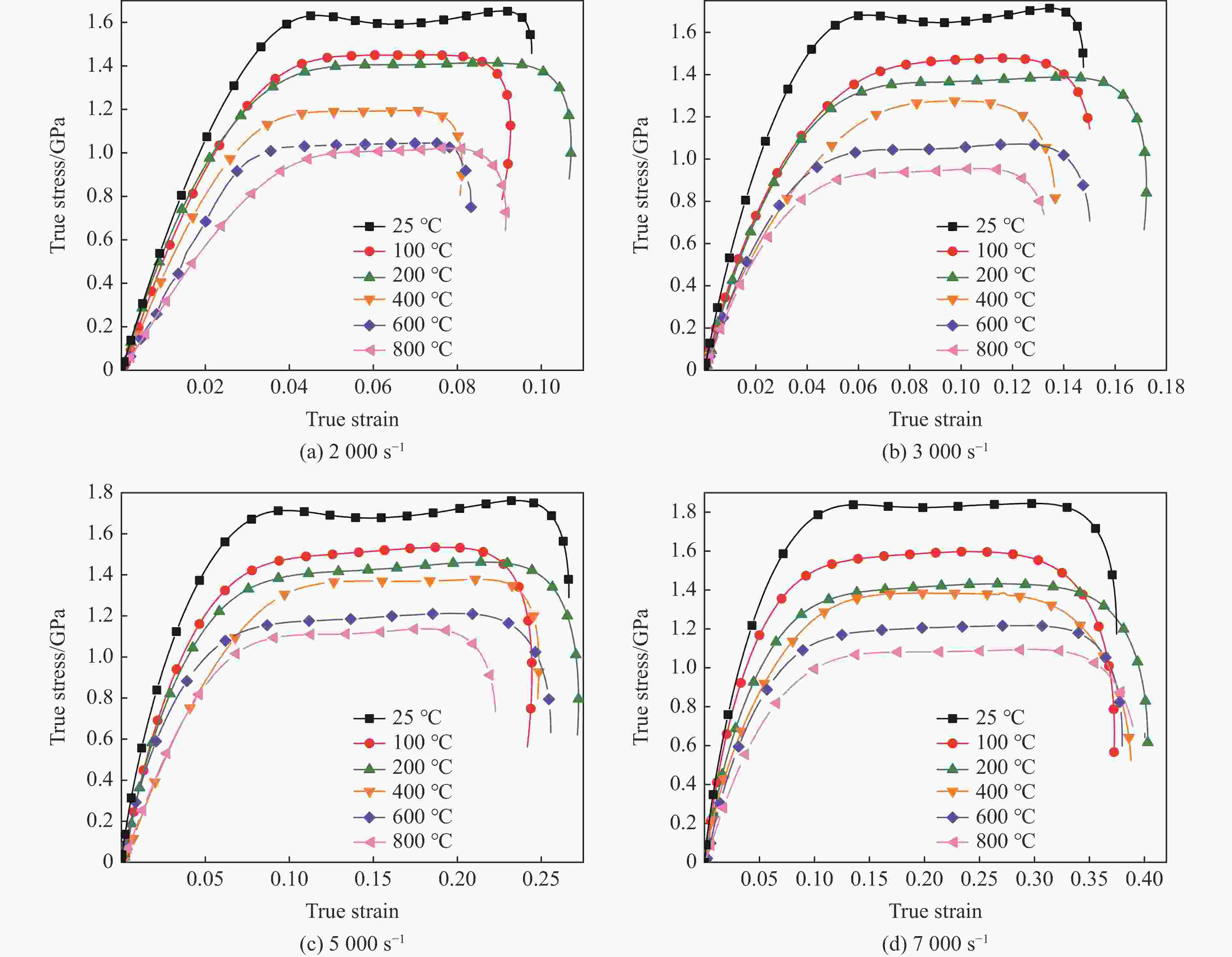
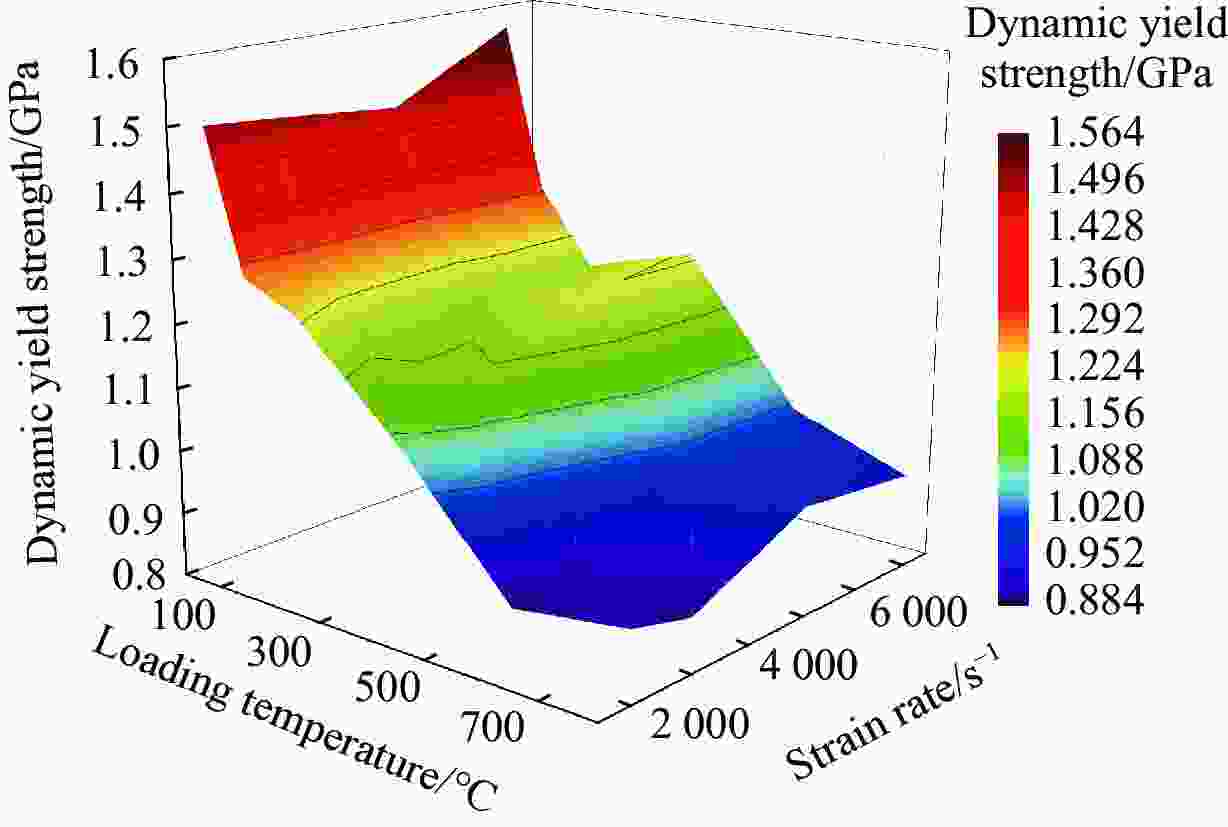
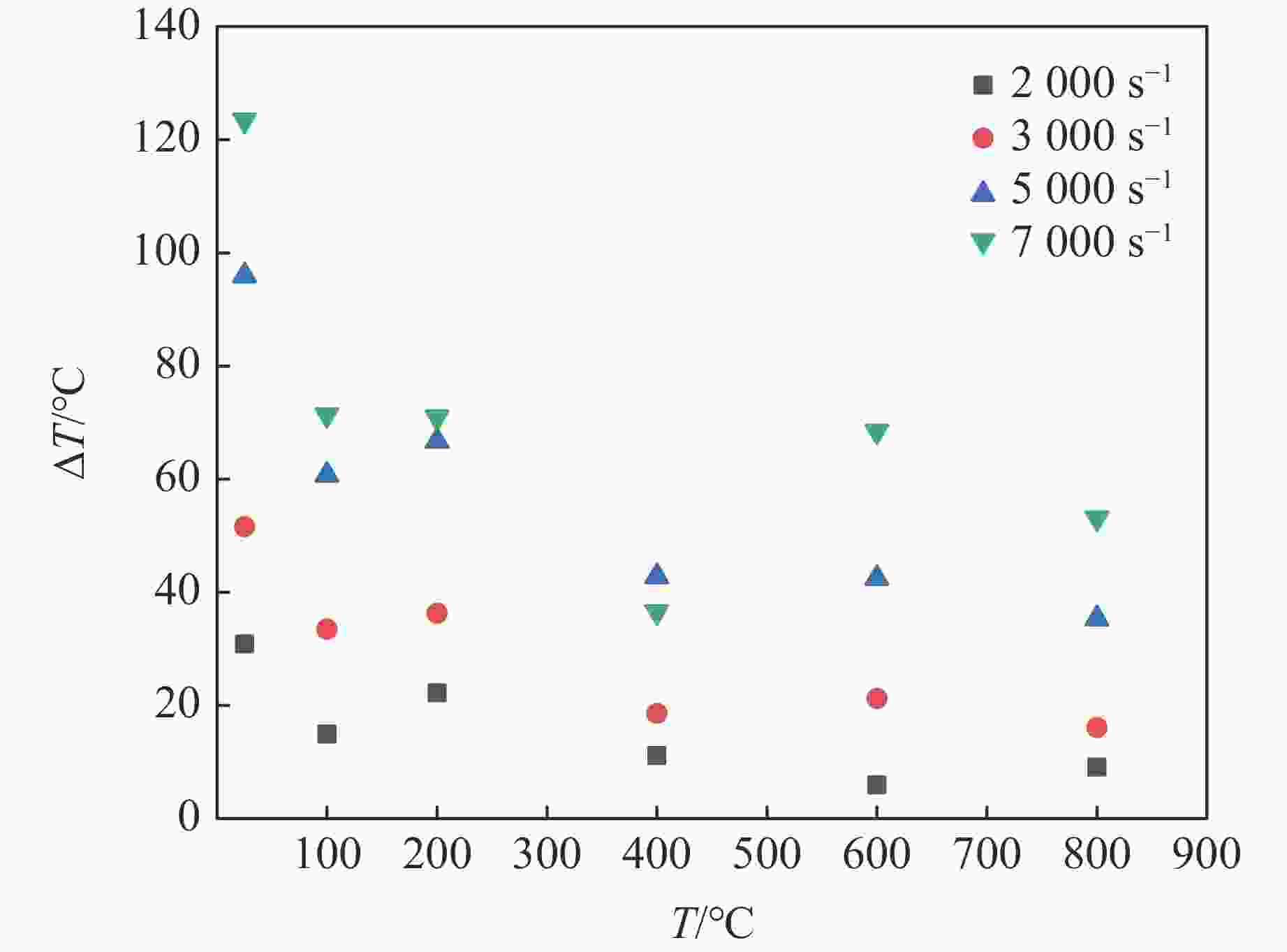
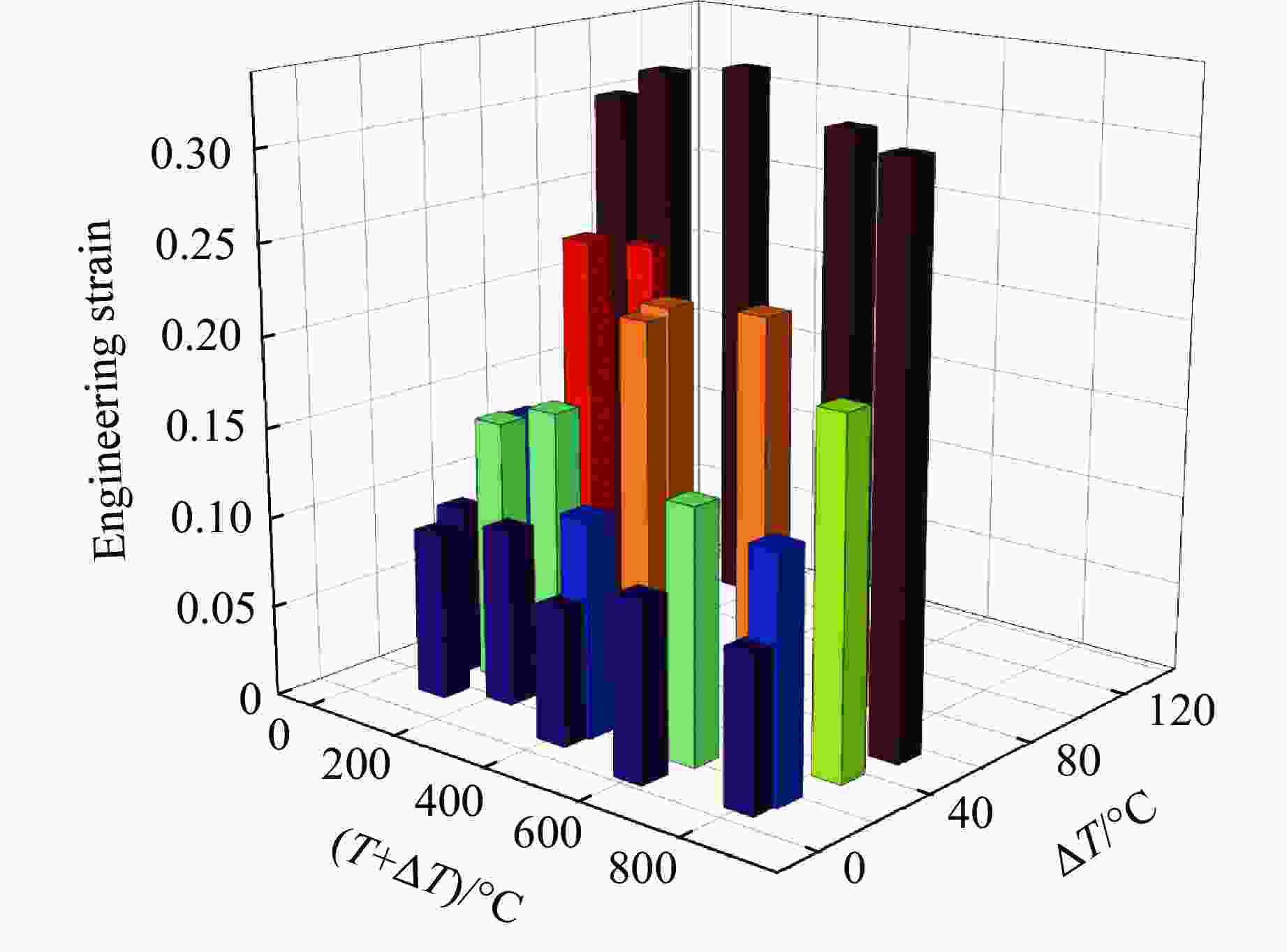
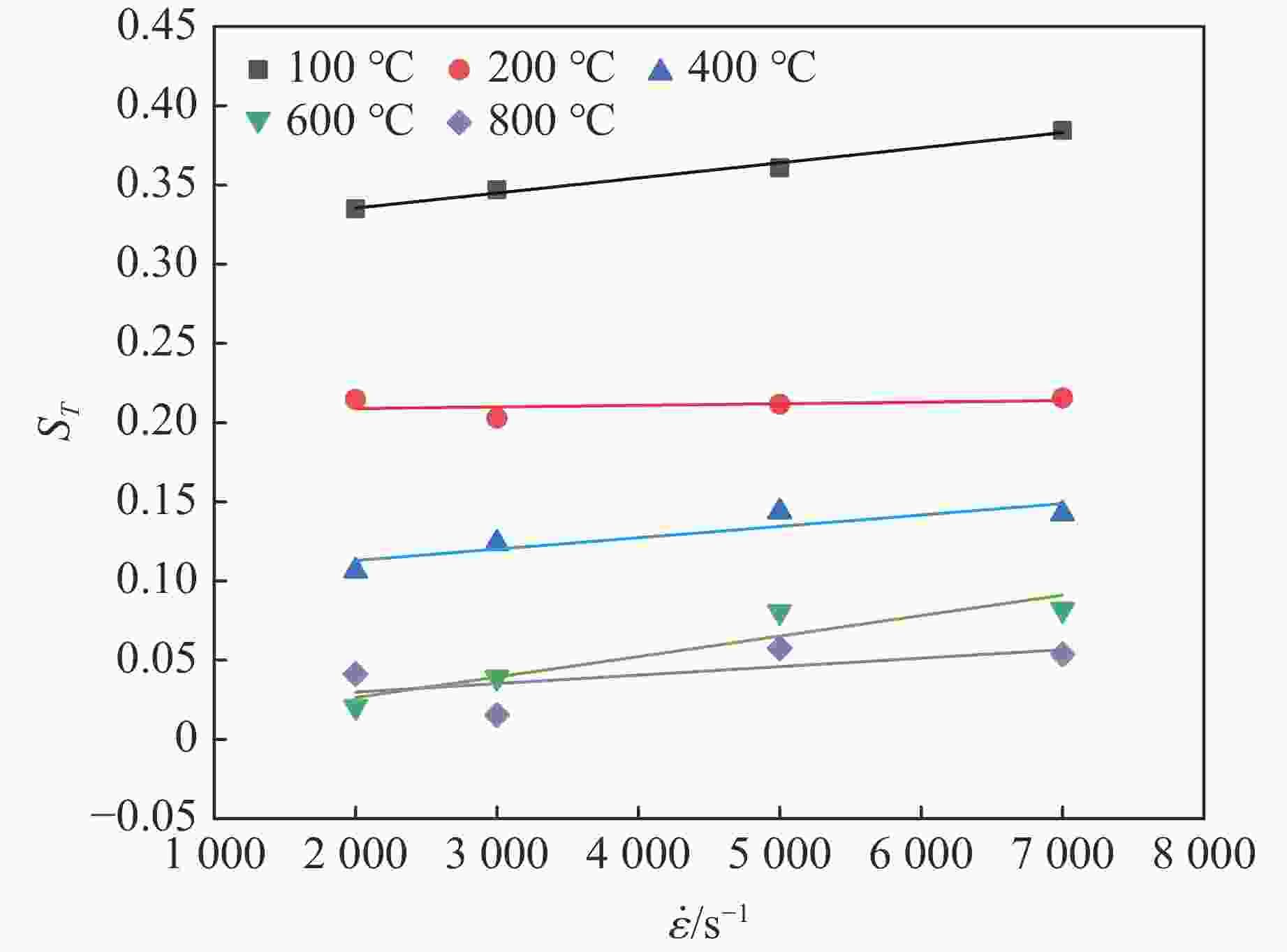
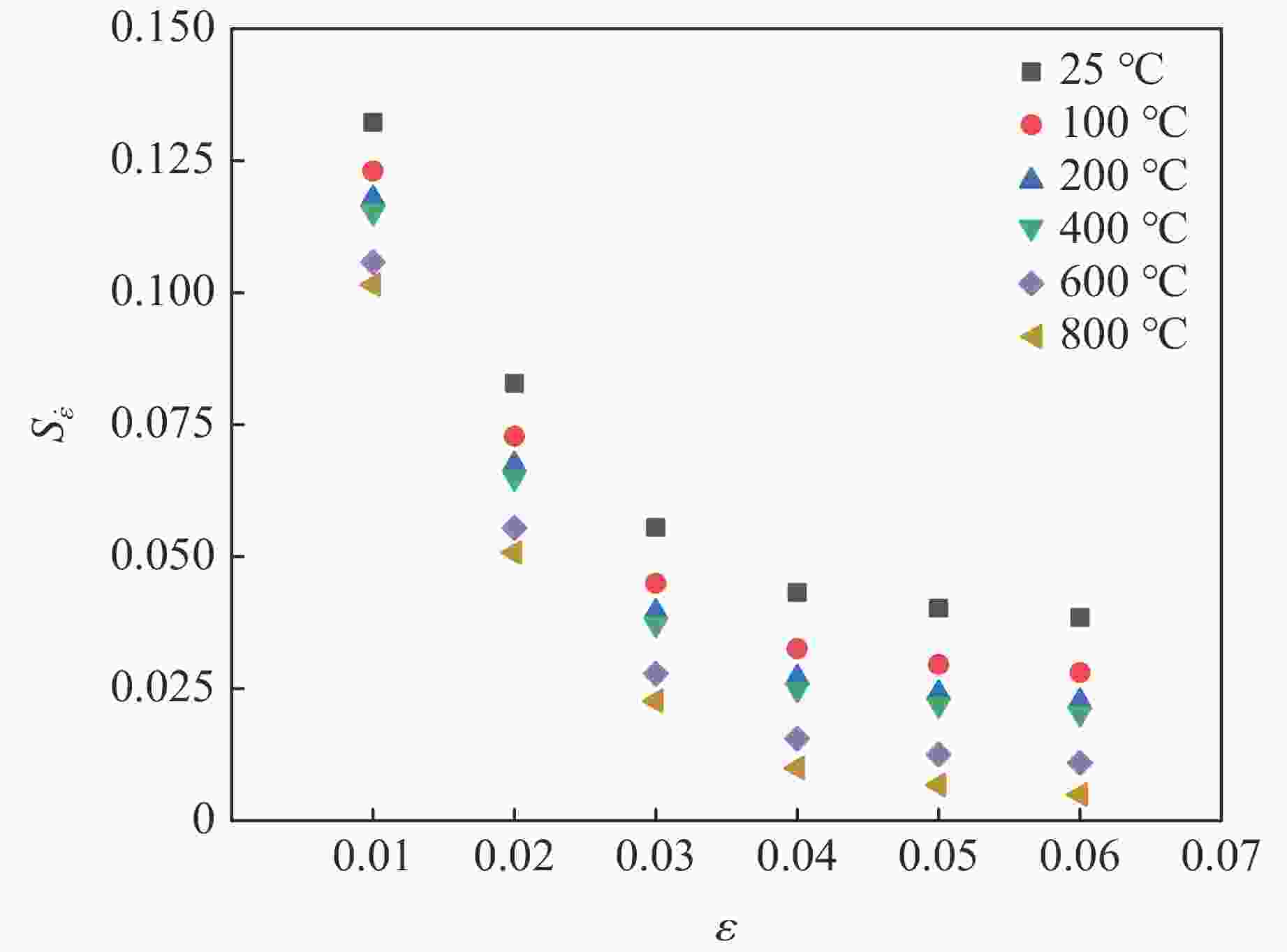
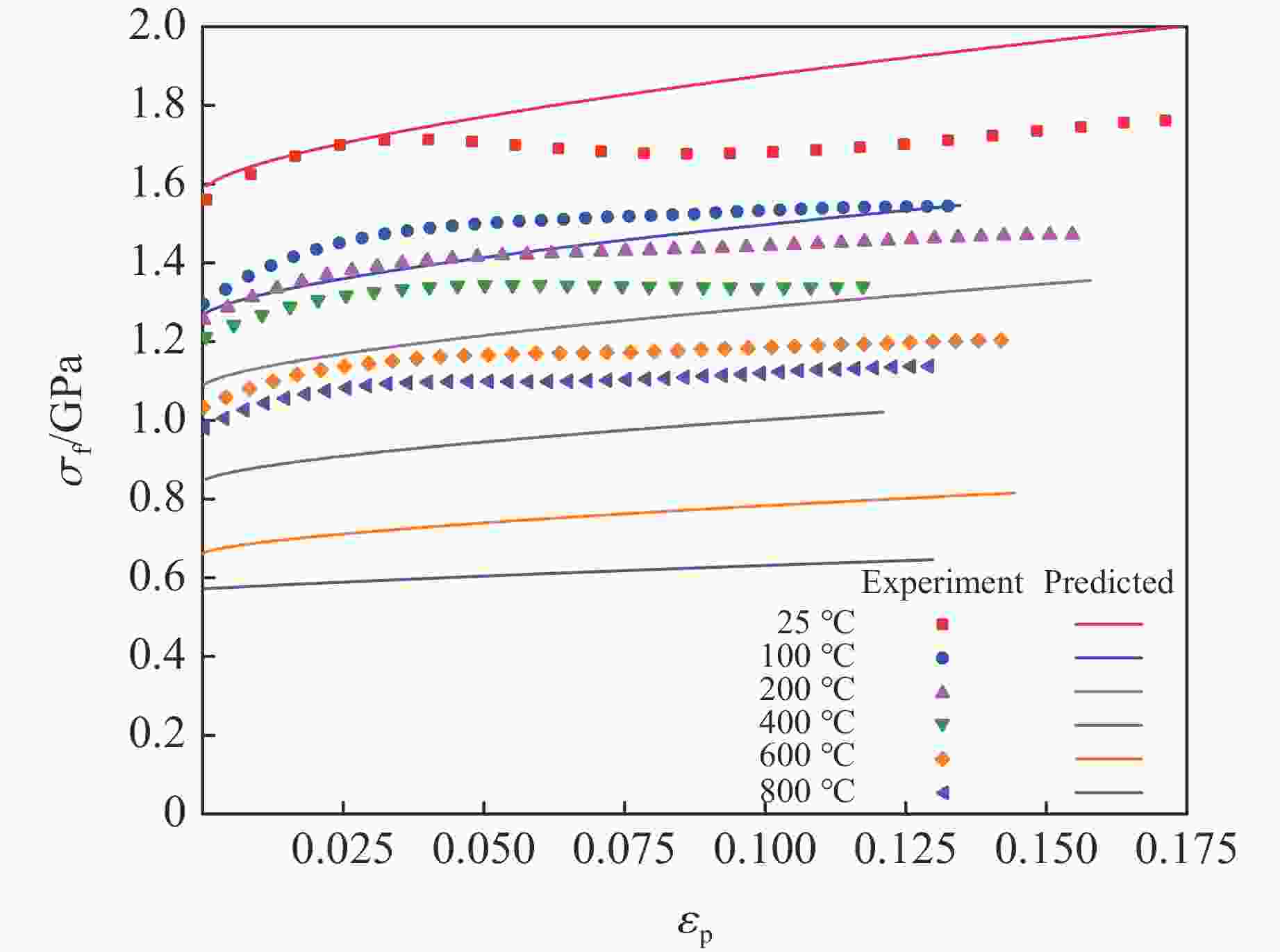
摘要: 采用分离式霍普金森压杆实验技术，研究了钛合金Ti6Al4V在温度为25～800 °C、应变速率为2000～7000 s−1的冲击压缩下的动态力学行为和微观组织演变，分析了其力学响应的温度依赖性和应变率敏感性，构建了可准确表征材料塑性流动行为的修正Johnson-Cook模型。结果表明，Ti6Al4V具有显著的应变硬化、应变率强化、应变率增塑和温度软化效应。随着加载温度和应变率的升高，材料的应变硬化效应减弱。温度敏感性随加载温度的升高而显著降低。应变率敏感性因子与加载温度呈负相关，随真实应变的增大呈下降趋势。高温高应变率下细小等轴α相、拉长型α相和块状α相取代初始等轴α相成为Ti6Al4V微观组织的典型特征。考虑率-温耦合作用和绝热温升影响的修正Johnson-Cook模型能够准确地预测Ti6Al4V的塑性流动应力-应变响应。Abstract: The dynamic mechanical behavior and microstructure evolution of titanium alloy Ti6Al4V under shock compression at temperatures ranging from 25 ℃ to 800 ℃ and strain rates from 2000 s−1 to 7000 s−1 were studied by using a split Hopkinson pressure bar. The temperature dependence and strain rate sensitivity of the material’s mechanical response were analyzed, and a modified Johnson-Cook model that could accurately characterize the plastic flow behavior of the material was developed. The results show that Ti6Al4V exhibited significant strain hardening, strain rate strengthening, strain rate plasticity, and temperature softening effects. With increasing loading temperature and strain rate, the material’s strain hardening effect is weakened. The temperature sensitivity is significantly decreased with increasing loading temperature. The strain rate sensitivity factor is negatively correlated with the loading temperature, and it shows a downward trend as the true strain increased. At high temperatures and high strain rates, fine equiaxial α phase, elongated α phase, and massive α phase replace the initial equiaxial α phase as the typical microstructure features of Ti6Al4V. The modified Johnson-Cook model that considers the effect of rate-temperature coupling and adiabatic temperature rise can accurately predict the plastic flow stress-strain response of Ti6Al4V.
-
图 1 钛合金Ti6Al4V的初始金相组织(a)、晶粒尺寸分布(b)以及EDS (c)
Figure 1. Original microstructure (a), grain size distribution (b) and EDS (c) of titanium alloy Ti6Al4V
图 3 Ti6Al4V试样在不同温度和应变率条件下的真实应力-应变曲线
Figure 3. True stress-strain curves of Ti6Al4V specimens at different temperatures and strain rates
图 4 率-热影响下Ti6Al4V的动态屈服强度
Figure 4. Dynamic yield strength of Ti6Al4V under the influence of strain rate and temperature
图 5 绝热温升随加载温度和应变率的变化
Figure 5. Variations of adiabatic temperature rise with loading temperature and strain rate
图 6 ΔT和T+ΔT对试样工程应变的影响
Figure 6. Influence of ΔT and T+ΔT on the engineering strain of specimens
图 7 不同温度和应变率下Ti6Al4V的微观组织
Figure 7. Microstructures of Ti6Al4V at different temperatures and strain rates
图 8 不同加载温度下温度敏感性因子随应变率的变化（ε=0.02）
Figure 8. Variation of temperature sensitivity factor with strain rate at different temperatures (ε=0.02)
图 9 7000 s−1时应变率敏感性因子随真实应变的变化
Figure 9. Variation of strain rate sensitivity factor with true strain at different temperatures (
${\dot \varepsilon }_0 $ = 7000 s−1)
图 10 实验数据与J-C修正模型预测值的对比
Figure 10. Comparison between experimental data and J-C modified model predictions
图 11 100 ℃、7000 s−1条件下等温曲线与绝热曲线的对比
Figure 11. Comparison of isothermal curve and adiabatic curve at 100 ℃ and 7000 s−1
图 12 Ti6Al4V在不同加载条件下的实验数据与模型预测对比
Figure 12. Comparison of experimental data and model prediction results of Ti6Al4V under different loading conditions
图 13 不同加载条件下修正模型与实验数据的相关度
Figure 13. Correlation degree between the modified model and experimental data under different loading conditions
图 14 不同加载条件下修正模型的平均相对误差
Figure 14. Average relative error of the modified model under different loading conditions
表 1 修正J-C本构模型参数的拟合结果
Table 1. Results of parameter fitting of modified J-C constitutive model
A/MPa B/MPa n C1 C2 a b c d λ/℃−1 894 721 0.138 0.031 0.104 1.082 0.00935 0.02 0.00286 0.004 
下载: 导出CSV
-
[1] 姜紫薇, 杨东, 陈建彬. 面向高速切削的钛合金Ti-6Al-4V动态本构模型: 综述 [J]. 航空材料学报, 2023, 43(4): 55–67. doi: 10.11868/j.issn.1005-5053.2022.000169JIANG Z W, YANG D, CHEN J B. Dynamic constitutive model of titanium alloy Ti-6Al-4V for high speed cutting: a review [J]. Journal of Aeronautical Materials, 2023, 43(4): 55–67. doi: 10.11868/j.issn.1005-5053.2022.000169 [2] WANG B, XIAO X R, ASTAKHOV V P, et al. The effects of stress triaxiality and strain rate on the fracture strain of Ti6Al4V [J]. Engineering Fracture Mechanics, 2019, 219: 106627. doi: 10.1016/j.engfracmech.2019.106627 [3] LONGÈRE P, DRAGON A. Dynamic vs. quasi-static shear failure of high strength metallic alloys: experimental issues [J]. Mechanics of Materials, 2015, 80: 203–218. doi: 10.1016/j.mechmat.2014.05.001 [4] ZHANG J, TAN C W, REN Y, et al. Adiabatic shear fracture in Ti-6Al-4V alloy [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(11): 2396–2401. doi: 10.1016/S1003-6326(11)61026-1 [5] 张炜琪, 许泽建, 孙中岳, 等. Ti-6Al-4V在高应变率下的动态剪切特性及失效机理 [J]. 爆炸与冲击, 2018, 38(5): 1137–1144. doi: 10.11883/bzycj-2017-0107ZHANG W Q, XU Z J, SUN Z Y, et al. Dynamic shear behavior and failure mechanism of Ti-6Al-4V at high strain rates [J]. Explosion and Shock Waves, 2018, 38(5): 1137–1144. doi: 10.11883/bzycj-2017-0107 [6] ZHOU L B, SHIMIZU J, MUROYA A, et al. Material removal mechanism beyond plastic wave propagation rate [J]. Precision Engineering, 2003, 27(2): 109–116. doi: 10.1016/S0141-6359(02)00124-1 [7] 陈敏. TC4钛合金力学性能测试及动态材料模型研究 [D]. 南京: 南京航空航天大学, 2012: 20–30.CHEN M. Research on mechanical properties test and dynamic material model of Ti6Al4V titanium alloy [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012: 20–30. [8] 周琳, 王子豪, 文鹤鸣. 简论金属材料JC本构模型的精确性 [J]. 高压物理学报, 2019, 33(4): 042101. doi: 10.11858/gywlxb.20190721ZHOU L, WANG Z H, WEN H M. On the accuracy of the Johnson-Cook constitutive model for metals [J]. Chinese Journal of High Pressure Physics, 2019, 33(4): 042101. doi: 10.11858/gywlxb.20190721 [9] 刘杨, 李志强, 赵冰, 等. TA32钛合金超塑性变形行为及本构模型 [J]. 稀有金属材料与工程, 2022, 51(10): 3752–3761.LIU Y, LI Z Q, ZHAO B, et al. Superplastic deformation behavior and constitutive model of TA32 titanium alloy [J]. Rare Metal Materials and Engineering, 2022, 51(10): 3752–3761. [10] 桑晔. TC4钛合金薄板高温塑性变形行为及成形性研究 [D]. 长春: 长春工业大学, 2022: 15–16.SANG Y. Research on high temperature plastic deformation behavior and formability of TC4 titanium alloy sheet [D]. Changchun: Changchun University of Technology, 2022: 15–16. [11] 艾建光, 姜峰, 言兰. TC4-DT钛合金材料动态力学性能及其本构模型 [J]. 中国机械工程, 2017, 28(5): 607–616. doi: 10.3969/j.issn.1004-132X.2017.05.017AI J G, JIANG F, YAN L. Dynamic mechanics behavior and constitutive model of TC4-DT titanium alloy materials [J]. China Mechanical Engineering, 2017, 28(5): 607–616. doi: 10.3969/j.issn.1004-132X.2017.05.017 [12] 桂林. 微观组织对TC4钛合金绝热剪切行为的影响 [D]. 沈阳: 沈阳工业大学, 2021: 32–47.GUI L. Effect of microstructure on the adiabatic shear behavior of TC4 titanium alloy [D]. Shenyang: Shenyang University of Technology, 2021: 32–47. [13] 《中国航空材料手册》编辑委员会. 中国航空材料手册-第4卷-钛合金 铜合金 [M]. 2版. 北京: 中国标准出版社, 2002: 104.Editorial Committee of China Aviation Materials Manual. China aeronautical materials manual: volume 4: titanium alloy copper alloy [M]. 2nd ed. Beijing: Standards Press of China, 2002: 104. [14] YADAV R, CHAKLADAR N D, PAUL S. A dynamic recrystallization based constitutive flow model for micro-machining of Ti-6Al-4V [J]. Journal of Manufacturing Processes, 2022, 77: 463–484. doi: 10.1016/j.jmapro.2022.03.040 [15] YANG J Z, WU J J, XIE H N, et al. Mechanism of continuous dynamic recrystallization of Ti-6Al-4V alloy during superplastic forming with sub-grain rotation [J]. Transactions of Nonferrous Metals Society of China, 2023, 33(3): 777–788. doi: 10.1016/S1003-6326(23)66145-X [16] 牛秋林, 陈明, 明伟伟. TC17钛合金在高温与高应变率下的动态压缩力学行为研究 [J]. 中国机械工程, 2017, 28(23): 2888–2892, 2897. doi: 10.3969/j.issn.1004-132X.2017.23.017NIU Q L, CHEN M, MING W W. Study on dynamic compressive mechanics behavior of TC17 titanium alloy at high temperature and high strain rates [J]. China Mechanical Engineering, 2017, 28(23): 2888–2892, 2897. doi: 10.3969/j.issn.1004-132X.2017.23.017 [17] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [J]. Engineering Fracture Mechanics, 1983, 21: 541–548. [18] XU Z J, HUANG F L. Thermomechanical behavior and constitutive modeling of tungsten-based composite over wide temperature and strain rate ranges [J]. International Journal of Plasticity, 2013, 40: 163–184. doi: 10.1016/j.ijplas.2012.08.004 [19] LIANG R Q, KHAN A S. A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures [J]. International Journal of Plasticity, 1999, 15(9): 963–980. doi: 10.1016/S0749-6419(99)00021-2 [20] 李云飞, 曾祥国. TC21钛合金动态拉伸行为的率-热效应及其本构关系 [J]. 稀有金属材料与工程, 2018, 47(6): 1760–1765.LI Y F, ZENG X G. Effect of strain rate and temperature on the dynamic tensile behavior and constitutive model of TC21 titanium alloy [J]. Rare Metal Materials and Engineering, 2018, 47(6): 1760–1765. -
下载:
点击查看大图
计量
- 文章访问数: 238
- HTML全文浏览量: 54
- PDF下载量: 58
