Energy Absorption of Corrugated Multi-Cell Tubes under Axial Compression
-
摘要: 金属薄壁管作为吸能结构被广泛应用于汽车等运载工具中，提高薄壁管的吸能特性对于提升运载工具的被动安全具有重要意义。为此，提出了结合多角和多胞结构的单波纹多胞管和双波纹多胞管，采用数值模拟方法研究了波纹幅值和波纹峰数对吸能性能的影响。研究发现，相比传统方形多胞管，波纹多胞管的能量吸收得到显著提高。双波纹多胞管比单波纹多胞管具有更加稳定的变形和更高的能量吸收。选取吸能最优的结构，研究了加强筋位置和节点强化对吸能性能的影响。结果表明：边对边连接的双波纹多胞管的吸能特性最好；在加强筋处进行节点强化可以进一步提高双波纹多胞管的能量吸收。相比传统方形多胞管，节点强化的双波纹多胞管的能量吸收增加了88.17%，压溃力效率提高了65.91%。节点强化的双波纹多胞管比传统多胞管具有更加优异的吸能特性，作为耐撞性结构具有广阔的应用前景。Abstract: Metal thin-walled tubes are widely used in vehicles as energy absorption structures. Improving the energy absorption characteristics of thin-walled tubes is of great significance for enhancing the passive safety of transportation vehicles. In this paper, a combination of multi-corner and multi-cell structures of single and double corrugated multi-cell tubes were proposed. The influence of corrugation amplitude and corrugation number on the energy absorption characteristics of the corrugated multi-cell tube were studied by numerical method. It was found that the energy absorption of the corrugated multi-cell tube is improved compared with that of traditional square multi-cell tube. In addition, the double corrugated multi-cell tube has a more stable deformation and a higher energy absorption than the single corrugated multi-cell tube. Finally, the optimal structure was selected to study the influence of rib position and node reinforcement. The results show that the edge-to-edge connection has the best energy absorption characteristics, and the node reinforcement at the rib could further improve the energy absorption of the double corrugated multi-cell tube. Compared to traditional square multi-cell tube, the energy absorption of node-strengthened double corrugated multi-cell tube increases by 88.17%, and the crushing force efficiency increases by 65.91%. The node-strengthened double corrugated multi-cell tube has better energy absorption characteristics than traditional square multi-cell tube, leading to broad application prospects as crashworthiness structures.
-
Key words:
- metal thin-walled tube /
- corrugated tube /
- multi-cell tube /
- node reinforcement /
- energy absorption
-
岩体是一种复杂的非均质性天然地质体，在漫长的地质作用下，其内部分布了大量的裂隙、节理以及断层等软弱结构面，软弱结构的存在使得裂隙岩体更易发生围岩破裂失稳等地质灾害，从而造成巨大的经济损失和恶劣的社会影响[1–2]。例如，交通、水利隧道以及矿山巷道等工程施工过程中，围岩发生失稳破坏的本质诱因是岩体内的节理、裂隙等软弱结构面在外界开挖扰动下发生扩展和贯通，从而导致岩体力学强度显著降低，并发生宏观失稳破坏[3–4]。因此，通过预制不同裂隙倾角的岩石，以模拟岩体内节理、裂隙等软弱结构面，开展裂隙岩石在加载过程中的裂纹萌生-扩展-贯通的演化规律以及岩石的宏观力学破坏特征研究，对进一步厘清工程岩体发生失稳破坏的致灾机制、指导地下工程安全建设具有十分重要的工程意义。
近年来，国内外许多学者针对不同裂隙倾角对岩石力学性质的影响开展了大量的室内试验和数值模拟研究，取得了许多成果。易婷等[5]对含有裂隙的岩石开展了单轴压缩试验研究，分析了裂隙倾角对岩石强度以及变形破坏的影响。朱泽奇等[6]运用FLAC数值分析软件，对三峡地区的花岗岩的破坏过程进行了模拟研究，探讨了其在破坏过程中出现的应力集中现象。张仕林等[7]通过ANSYS软件研究了裂隙对红砂岩内裂纹扩展的影响，得出了裂隙试样的力学性质随裂隙张开度的增加呈下降趋势的结论。唐春安等[8]运用RFPA岩石破裂分析软件，对内部含有裂隙的岩石开展了模拟研究，分析了岩石内部微裂纹扩展和应力场的演化特征。上述针对含裂隙岩石力学性能的研究取得了极大的进展，然而，岩石的破坏过程本质上是在外部能量驱动作用下，岩石内部微裂纹逐渐萌生、扩展并相互贯通，最终导致岩石发生宏观破坏。近年来，一些学者尝试从能量转换、结构劣化的角度揭示岩体破坏的本质。对于硬岩在破坏过程中的能量演化机制，众多学者进行了一系列研究。谢和平等[9–10]探讨了岩石在破坏过程中的能量耗散和释放对岩石强度和破坏模式的影响。武晋文等[11]研究了预制裂隙花岗岩的热破裂演化特征，通过高能量、低能量释放率的声发射，揭示了花岗岩发生失稳破坏的特征。孙友杰等[12]对预制裂隙岩石试样开展了单轴压缩试验研究，分析了裂隙试样在受压发生破坏失稳过程中的能量转化关系。上述研究成果对厘清不同裂隙倾角硬岩在受压失稳破坏过程中的能量演化机制发挥了重要的推动作用。
针对含裂隙倾角的岩石的力学性质和能量演化特征，国内外学者已做了相关研究，并取得了丰富的成果。然而，关于裂隙倾角对岩石力学性能、裂纹扩展演化、能量转化以及细观变形破坏特征的影响的报道并不多见。因此，本研究基于颗粒流离散元软件，对不同裂隙倾角的花岗岩开展单轴压缩力学试验模拟，探讨裂隙倾角对岩石力学性质、裂纹扩展以及细观变形破坏的影响规律，分析不同裂隙倾角花岗岩试样在单轴压缩破坏过程中的能量演化特征。研究结果将对地下工程开挖、支护具有重要的现实意义。
1. 含裂隙岩石的数值模型构建
1.1 离散元数值计算模型及方案
近年来，数值计算分析方法在岩石工程领域的应用广泛，借助模拟软件，可以从细观尺度模拟岩石内裂纹的演化过程。颗粒流离散元法可再现颗粒间的相互作用以及微观裂纹的演化特征。为了研究裂隙倾角对岩石力学性能和裂纹扩展的影响，基于颗粒流软件（particle flow code，PFC），构建了裂隙岩石数值计算模型，如图1所示。数值模型的尺寸（长×宽）为100 mm×50 mm，其中：b为裂隙的长度，θ为裂隙的倾斜角度。
1.2 含裂隙岩石细观参数标定
为了较好地模拟岩石材料的力学性能，PFC提供了两种黏结模型：接触黏结模型和平行黏结模型，其中，平行黏结模型更适合岩石内部胶结材料的模拟[13]。采用离散元模拟计算时，不能直接使用岩石的宏观物理力学参数，需要通过反复调整颗粒的平行黏结有效模量、刚度比、线性接触有效模量、正向和切向黏结强度等细观参数来反映岩石的力学特性。耿萍等[14]通过大量的数值试验研究，得到了岩土体的宏观力学强度与细观参数的关系。本研究采用其参数标定方法，利用花岗岩的宏观力学参数（见表1），获取数值计算的细观力学参数（见表2），室内试验和数值计算结果如图2所示。由图2可知，花岗岩完整试样室内试验[15]得到的单轴抗压强度为155.1 MPa，弹性模量为37.63 GPa，数值计算得到的单轴抗压强度为148.6 MPa，弹性模量为37.41 GPa。由此可见，通过参数标定模拟的应力-应变曲线与室内试验结果十分接近。
表 1 岩石的宏观力学参数Table 1. Macromechanical parameters of rocksMaterial Rock density/
(g·cm−3)Compressive
strength/MPaTensile
strength/MPaElastic
modulus/GPaPoisson’s
ratioCohesive
force/MPaFriction
angle/(°)Rock materials[15] 2.63 155.1 11.06 37.63 0.21 Structural plane 0.5 70 表 2 岩石的细观参数Table 2. Mesoscopic parameters of rocksEffective modulus
of parallel
bonding/GPaStiffness
ratioLinear contact
effective
modulus/GPaTangential bonding
strength/MPaNormal bonding
strength/MPaFriction
angle/(°)Frictional
coefficient98.6 1.5 29.2 28 7.6 70 0.5 
2. 单轴压缩下含裂隙岩石的力学性能演化特征
2.1 单轴压缩下裂隙岩石的抗压强度
2.1.1 裂隙岩石的应力-应变关系
根据裂隙岩石单轴压缩数值试验结果，如图3所示，分析不同裂隙倾角下裂隙岩石的应力-应变演化特征，以揭示裂隙倾角对岩石力学性能的影响规律。
图 3 不同裂隙倾角岩石试样的应力-应变关系Figure 3. Stress-strain relationship of rock samples with different crack inclination angles从图3可以明显看出，不同裂隙倾角花岗岩试样在单轴压缩下的力学破坏均经历了压密、弹性、屈服、破坏4个阶段。由应力-应变曲线可知，岩石内裂隙倾角越小，岩石所经历的压密阶段越长。大量研究表明，花岗岩为硬脆岩，在受压过程中其应力-应变曲线具有显著的峰前线弹性特征，即应力-应变曲线呈现出较为明显的线性上升阶段。裂隙倾角对花岗岩试样峰前线弹性特征的影响主要表现为对线性阶段的弹性模量和屈服破坏阶段的峰值应力强度的影响，如图3所示。当裂隙倾角较小时，峰值应力和弹性模量较大；反之，则较小。当裂隙倾角为45°时，岩样的峰值强度下降得较为明显，说明该裂隙倾角下岩样内的损伤较为严重，裂隙两端导致新生裂纹的快速萌生和扩展。当裂隙倾角为75°时，应力-应变曲线在峰前阶段出现明显的应变硬化屈服现象，峰后应力迅速下降，此时岩石的力学强度急剧弱化，表现为明显的脆性破坏特征。
2.1.2 裂隙倾角对岩石抗压强度和弹性模量的影响
为了分析裂隙倾角对岩石力学性能的影响，基于数值计算得到的裂隙岩石强度以及郭奇峰等[16–17]通过室内试验得到的裂隙岩石强度随裂隙倾角的变化规律，如图4所示，通过数值计算得到裂隙岩石的弹性模量随裂隙倾角的变化规律，如图5所示。
图 4 抗压强度与裂隙角度关系曲线Figure 4. Relationship curve between compressive strength and crack inclination angle
图 5 弹性模量与裂隙角度关系曲线Figure 5. Relationship curve between elastic modulus and crack inclination angle由图4可知，裂隙岩石的抗压强度随裂隙倾角的增加呈先减小后增大的变化趋势。当裂隙倾角由0°逐渐增加到60°时，裂隙岩石的强度呈现出线性减弱的趋势；当裂隙倾角由60°增加至75°时，岩石的力学性能表现出增强的趋势。并且，当裂隙倾角由30°增大至60°时，裂隙岩石强度的变化幅度较大，与完整岩石相比，强度下降39.4%～59.6%。将本数值计算结果与文献[16–17]进行对比可知，通过室内试验得到的裂隙岩石强度随裂隙倾角的变化规律与数值计算结果一致，即裂隙岩石强度随裂隙倾角的增加呈现出“V”形变化趋势，当裂隙倾角继续增大时，岩石强度的降低幅度有所减缓。这说明当裂隙倾角在一定范围内时，其对岩石的力学性能产生显著影响，且在该范围内，随着裂隙倾角的增加，岩石力学强度的下降趋势越来越显著；当裂隙倾角超出该范围时，裂隙结构对岩石力学性能的影响程度逐渐弱化。
由图5可知，随着裂隙倾角的逐渐增大，裂隙岩石的弹性模量呈“V”形变化趋势，即随着裂隙倾角的增大，岩石弹性模量先减小后增大。裂隙倾角45°为弹性模量变化的转折点：当倾角从0°增加到45°时，弹性模量逐渐减小；倾角从45°增加到75°时，弹性模量逐渐增大。尽管裂隙岩石的弹性模量随着裂隙倾角的变化呈现“V”形变化趋势，但是变化幅度相对较小。与完整岩石相比，弹性模量的变化范围在1.06%～4.31%之间。由此可见，岩石内单一裂隙结构的存在对岩石的压密阶段和线弹性阶段的影响较弱。
2.2 单轴压缩下含裂隙岩石的破坏特征及裂纹演化规律
2.2.1 含裂隙岩石的力学破坏特征
(1) 基于离散元模拟的裂隙岩石破坏特征
为了研究裂隙倾角对岩石破坏特征的影响，对上述具有不同裂隙倾角的岩石开展单轴压缩数值试验，裂隙岩石在单轴压缩条件下的宏观力学破坏特征如图6所示。
图 6 不同裂隙倾角岩样的典型破坏特征Figure 6. Typical failure characteristics of rock samples with different crack inclination angles由图6可知，在单轴压缩条件下，裂隙倾角对岩石试样的力学破坏特征产生显著的影响，在轴向荷载作用下岩石内不同裂隙倾角产生的破坏模式不同。从图6可以看出裂隙岩石的破坏模式主要分为3类。
第1类：当裂隙倾角为0°时，岩样内的新生裂纹沿着裂隙两端萌生，并沿外荷载方向逐渐扩展并形成贯通裂纹，致使岩样发生剪切破坏，且破碎程度较高。
第2类：当岩石内的裂隙倾角为15°和30°时，试样首先在裂隙端部的软弱部位产生微裂隙，在外部荷载作用下微裂隙沿着破裂面发展并贯通，形成2条宏观破裂带，导致裂隙试样发生宏观竖向劈裂破坏。
第3类：当倾角裂隙为45°、60°和75°时，裂隙岩石的破坏形式主要为“Y”形共轭张拉剪切混合破坏，岩石试样内的新生裂纹在裂隙端部迅速萌生、扩展并形成宏观破裂面，在剪切裂纹周围伴随出现一定区域的张性裂纹破裂带，并且在裂隙试样端部左侧，岩样的破碎程度较高。
(2) 基于离散元模拟的裂隙岩石破坏与室内试验得到的裂隙岩石破坏特征对比
为了验证本数值计算方法的合理性，运用颗粒流离散元软件构建了与文献[18]相同的含裂隙岩石试样模型，数值计算和室内试验得到的裂隙岩石的破坏特征如图7所示。
从图7可以看出：当θ=0°时，翼形裂纹主要沿着裂隙两端萌生，并沿轴向应力加载方向逐渐扩展并形成贯通裂纹；当θ=30°时，裂纹沿着裂隙两端萌生，并逐渐向外扩展延伸，形成宏观拉伸裂纹，并在主裂纹右下端的薄弱处，裂纹产生二次萌生发展；当θ=45°时，岩石内的主裂缝沿着裂隙两端向两边延伸扩展并贯穿岩石底端，岩石内的主裂隙主要呈三角形；当θ=60°时，岩石内的剪切裂缝主要沿着裂隙左端和右端萌生，沿荷载加载方向逐渐发展贯通，并形成宏观破裂面。对比数值计算和室内试验[18]得到的裂隙岩石的破坏特征可知，两者得到的裂隙岩石内的裂纹扩展贯通模式较吻合。数值计算的特点在于可以通过内置Fish语言进行编程，能够轻松地获得岩石内部相关物理力学信息，还能从细观角度揭示裂纹的扩展机理。因此，运用离散元颗粒流软件可以有效地模拟裂隙岩石内裂隙的发展过程以及力学破坏特征。
2.2.2 含裂隙岩石的裂纹演化规律
岩石在经过漫长的地质构造作用后，将产生大量的节理裂隙等复杂地质结构，使得岩石的物理力学性质发生显著的变化[19]。岩石内裂纹的扩展贯通主要分为以下3个过程：(1) 应力加载初期阶段，岩石内部无裂纹扩展，但是裂纹端部破坏区域扩大；(2) 在应力持续作用下，岩石内的裂纹迅速扩展延伸；(3) 裂纹持续扩展，并发展贯通，裂纹的发展过程如图8所示。
为了研究裂隙倾角对岩石内裂纹演化特征的影响规律，对具有不同裂隙倾角的岩石开展单轴压缩数值试验，裂隙岩石在单轴压缩条件下的内部裂纹扩展演化特征如图9所示，其中σc为岩石的单轴抗压强度。由图9可知，受岩石内裂隙倾角的影响，裂纹在岩石内的裂隙周围逐渐萌生并发展贯通。在裂隙岩石内出现较为显著的应力集中现象。当 θ < 30°时，裂纹主要沿着裂隙左端和裂隙中心位置开始扩展，扩展贯通后的裂纹在岩石内部形成显著的宏观破裂带，并且在宏观破裂带附近出现了裂纹汇聚现象，解释了岩石在较小裂隙倾角的影响与内部应力的联合作用下产生相对破碎的原因。当θ ≥ 30°时，裂纹由裂隙两端开始萌生，并逐渐向岩石试样两端发展贯通。裂隙倾角越大，在裂隙周围处产生的新生裂纹越多，其中主要以张拉裂纹为主。随着轴向应力的持续作用，岩石内的宏观裂纹将不再局限于裂隙周围，更多地将在岩石内产生新的张拉裂纹和剪切裂纹，新生的拉剪裂纹将以“弥散”的方式充满整个岩石表面，这也解释了随裂隙倾角的逐渐增加，裂隙岩石的强度不会持续降低，当裂隙倾角增加到一定值时，裂隙岩石的强度会逐渐增强。
图 9 裂隙岩石内微裂纹的演化特征Figure 9. Evolution characteristics of microcracks in fractured rocks在单轴压缩过程中岩石内部将会产生不同类型的微裂纹，为了分析裂隙倾角对岩石内微裂纹类型的影响规律，通过设置Fish语言，统计出岩石内拉剪裂纹的演化特征，如图10所示，其中N为微裂纹数。
图 10 不同裂隙倾角岩石试样的拉剪裂纹演化规律Figure 10. Evolution law of tensile and shear cracks in rock samples with different crack inclination angles对比图10中岩石微裂纹的发展特征曲线可知：在加载初始阶段，岩石内没有微裂纹，随着应力的逐渐增大，微裂纹首先以张拉裂纹的形式生成，随后逐渐生成剪切裂纹，整个过程中以张拉裂纹为主，剪切裂纹的数量相对较少；在微裂纹稳定扩展阶段，张拉裂纹数稳定增加，且增加速率远大于剪切裂纹数。随着裂隙倾角的增加，张拉裂纹出现的时间显著缩短，裂纹总数也显著增加，而剪切裂纹受倾角的影响较小，裂纹数量几乎不受影响。当θ <15°时，张拉裂纹数和剪切裂纹数呈台阶式增长；当θ >15°时，张拉裂纹数和剪切裂纹数呈指数式增长，并且在岩石破裂阶段，裂纹的增长速率最高。当岩石内的裂隙发展贯通后，其受力骨架并未全部破坏，仍具有一定的承载能力，试样在遭受严重破坏后内部的岩石材料仍具有剪切作用，故岩石的破坏特征在宏观上表现为张拉-剪切混合破坏。同时，裂隙岩石内的张拉裂纹数远大于剪切裂纹数，且随着裂隙倾角的增大，两者的差距增大。综合以上分析，裂隙倾角对裂隙岩石内新生裂纹的扩展、拉剪裂纹的增长速率以及裂纹数量均有较大影响。
3. 单轴压缩下含裂隙岩石的能量演化特征
3.1 能量计算
裂隙岩石在单轴压缩下常伴随着宏细观裂纹的萌生、扩展以及贯通。在外部荷载加载过程中，岩石中积累的应变能逐渐释放，相应的应力-应变曲线也会发生显著变化。岩石在加载破坏过程中的弹性应变能Ue和耗散应变能Ud的关系[20]如图11所示。应力-应变曲线可以反映溶蚀岩石内的能量演化过程。
根据热力学第一定律，岩样在加载过程中所做的功W转化为岩石的应变能U
W=U=Ue+Ud (3) 本研究主要针对单轴压缩条件下不同倾角的裂隙岩石，因此，仅有竖向压力对岩石做功，侧向压力σ2=σ3=0，则岩石内各应变能的表达式为
U=∫ε10σ1dε1 (4) Ue=12Ei[σ21+2σ23−2μ(σ23+2σ1σ3)]≈σ212E0 (5) Ud=U−Ue (6) 式中：μ为泊松比；ε1为轴向应变；Ei为岩石卸荷弹性模量，计算时可用初始弹性模量E0代替。
3.2 含裂隙岩石的能量演化特征
岩石的破坏过程是裂纹产生、扩展及贯通的过程，该过程伴随着能量的积聚、耗散与释放，是能量传递与转化的过程[21–22]。不同裂隙倾角的岩石试样在单轴压缩下的能量演化特征如图12所示。
图 12 不同裂隙倾角岩石试样的能量演化特征Figure 12. Energy evolution characteristics of rock samples with different crack inclination angles由图12可知，不同倾角裂隙岩石的能量比曲线近似为S形。基于岩样破坏过程中的能量机制，可将具有不同倾角裂隙的岩石在单轴压缩下的破坏过程分为以下5个阶段。
(1) 初始压密阶段：裂隙岩石在外部荷载的作用下，内部原始裂缝逐渐闭合，岩石结构吸收的能量一部分以弹性能Ue的形式存储起来，一部分则以耗散能Ud的形式用于裂隙的闭合以及结构面的摩擦滑移。
(2) 弹性变形阶段：原生裂隙在外部荷载作用下全部闭合，裂隙岩石可看作弹性压密体，岩石从外界吸收的能量全部以弹性能Ue的形式存储。
(3) 裂纹起裂阶段：裂隙岩石内部微裂纹逐渐萌生，但裂纹的发展处于“平稳”状态。此时，裂隙岩石从外界吸收的能量少部分用作内部微裂纹的萌生和发展，大部分仍以弹性能Ue的形式储存。
(4) 裂纹损伤阶段：此阶段又称岩石内裂纹扩展阶段，此时，裂隙岩石内的微裂纹在外部荷载作用下开始扩展，并且向不同的方向延伸，能量消耗Ud显著增加。
(5) 宏观破裂阶段：裂隙岩石内所积累的应变能瞬间释放，使得裂隙岩石结构面产生宏观裂纹，宏观裂纹扩展贯通，形成宏观的破裂结构面。
3.3 裂隙倾角对能量演化的影响
为了探究裂隙倾角对岩石能量演化特征的影响，分析了裂隙倾角对花岗岩试样的总输入能U、弹性应变能Ue、耗散能Ud的影响。不同裂隙倾角状态下各试样的能量演化特征如图13所示。
图 13 裂隙倾角对能量演化特征影响Figure 13. Effect of crack inclination angle on energy evolution characteristics由图13(a) 可知，不同裂隙倾角下岩石试样的总输入能随轴向应变的增加整体呈阶段性S形增长趋势，主要经历3个阶段：先以上凹形加速增长，随后以近似线性等速增长，最后则以下凹形减速增长。随着裂隙倾角的增加，总输入能的增长率逐渐减小，在相同的轴向应变下，岩石的总输入能随裂隙倾角的增大呈现先减小后增大的变化规律。如图13(b) 所示，在初始压密阶段，不同裂隙倾角下各岩石试样的弹性应变能没有明显差异。在弹性变形阶段，不同裂隙倾角的岩石试样的弹性应变能增长趋势存在明显差异，裂隙倾角越小，弹性应变能的增长速度越高。随着裂隙倾角的增大，弹性应变能呈先降低后增长的变化趋势。在破坏阶段，含裂隙岩石试样内储存的弹性应变能快速释放，裂隙倾角对弹性应变能的释放速度具有显著影响。当裂隙倾角为0°时，弹性应变能的释放速率最大，曲线呈线性垂直下降趋势；随着裂隙倾角的增大，弹性应变能随轴向应变的增加而垂直下降的趋势有所缓和，整体呈缓慢下降趋势。能量耗散是岩石变形破坏的基本特性，其过程是单向的、不可逆的。如图13(c) 所示，在压密和弹性阶段，耗散能较小，且增长速率相对缓慢，裂隙倾角对耗散能的影响较弱。在塑性变形阶段，随着试样内裂纹的萌生、扩展和相互贯通，耗散能迅速增大。由于裂隙的存在对岩样内新生裂纹的起裂以及不稳定扩展有重要影响，因此，裂隙倾角对该阶段岩样耗散能的影响非常显著。随着裂隙倾角的不断增大，花岗岩试样内的耗散能先增大后减小。当试样进入破坏阶段时，试样内的弹性应变能迅速释放，耗散能急剧增加。
3.4 峰值应力处的能量演化特征
图14显示了裂隙岩石试样在峰值应力处的总能量U、弹性应变能Ue及耗散能Ud随裂隙倾角的变化。
图 14 不同裂隙倾角岩石试样在峰值应力处的能量演化特征Figure 14. Energy evolution characteristics of rock samples with different crack inclination angles at peak stress裂隙岩石在受到外部荷载过程中，需要不断从外界吸收能量，这些能量一部分储存为弹性应变能，一部分则用于岩石内微裂纹扩展所需的耗散能。由图14可知，不同裂隙倾角岩石试样在峰值应力处的总能量U、弹性应变能Ue以及耗散应变能Ud随岩石内裂隙倾角的增加呈现先减小后增大的趋势。当θ <60°时，裂隙岩石试样在峰值应力处的各能量随裂隙倾角的增加呈现下降趋势，并且裂隙岩石试样在峰值前的能量耗散现象较为缓和，峰值应力处的耗散能占比为29.26%～25.25%，均值为27.26%；当θ>60°时，岩石试样在峰值应力处的各能量呈上升趋势，裂隙岩石试样在峰值应力处的耗散能有所增强，能量占比为32.28%～33.04%，均值为32.66%。上述现象说明：裂隙倾角对岩石在受压破坏时的储能具有明显的弱化作用，增强了其破坏过程中的能量耗散；当裂隙倾角较大时，裂隙岩石试样在峰值前的损伤持续发展，削弱了其储能能力，增强了其在峰值应力处的耗散能力。
4. 结 论
(1) 裂隙岩石应力-应变曲线峰后均出现明显的应力跌落现象，表现为明显的脆性破坏特征。裂隙倾角对花岗岩试件产生不同程度的初始损伤，随着裂隙倾角的增大，裂隙岩石的峰值强度和弹性模量呈先减小后增大的变化趋势，且峰值强度受到的影响较显著，弹性模量受到的影响较弱。
(2) 裂隙倾角对岩石的破坏模式产生显著影响。当倾角为0°时，主要发生剪切破坏，且破碎程度较高；当倾角增加到30°时，主要发生竖向劈裂破坏，并且在主破裂面附近有较多的次生裂隙；当倾角增加至75°时，由竖向劈裂破坏转变为竖向劈裂与剪切破坏的混合破坏。
(3) 裂隙倾角对岩石内新生裂纹扩展、裂纹类型以及裂纹增长速率具有显著影响。随着裂隙倾角的增大，拉剪裂纹数变化曲线由台阶式增长转变为指数式增长；裂隙倾角越大，岩石内产生的新生裂纹越多，其中主要以张拉裂纹为主，微裂纹主要以“弥散”的方式充满整个岩石。
(4) 含裂隙岩石试样的能量演化趋势大致相同。总输入能经历了上凹形增加、线性匀速增加和下凹形减速增加3个阶段。随着裂隙倾角的增大，试样的总输入能和弹性应变能呈先减小后增大的变化趋势。裂隙倾角越大，耗散能上升越快，但试样破坏时的最终耗散能则越低。裂隙结构的存在对试样受压破坏时的储能极限有明显的弱化作用，削弱了岩石吸收和储存弹性应变能的能力，增强了其在峰值应力处的耗散能力。
-
图 6 不同幅值和波纹峰数的SCMCT的横截面
Figure 6. Cross sections of SCMCT with different amplitudes and corrugation peak numbers
图 7 不同幅值和波纹峰数下SCMCT的变形模式
Figure 7. Deformation modes of SCMCT with different amplitudes and corrugation peak numbers
图 8 不同幅值和波纹峰数下SCMCT的力-位移曲线
Figure 8. Force-displacement curves of SCMCT with different amplitudes and corrugation peak numbers
图 10 As和Ns对SCMCT吸能指标的影响
Figure 10. Effect of As and Ns on energy absorption indexes of SCMCT
图 11 不同幅值和波纹峰数下DCMCT的横截面
Figure 11. Cross sections of DCMCT with different amplitudes and corrugation peak numbers
图 12 不同幅值和波纹峰数下DCMCT的变形模式
Figure 12. Deformation modes of DCMCT with different amplitudes and corrugation peak numbers
图 13 不同幅值和波纹峰数的DCMCT的力-位移曲线
Figure 13. Force-displacement curves of DCMCT with different amplitudes and corrugation peak numbers
图 14 Nd和Ad对DCMCT吸能指标的影响
Figure 14. Effect of Nd and Ad on energy absorption indexes of DCMCT
图 16 加强筋位置对Nd5Ad5变形模式的影响
Figure 16. Influence of rib position on deformation mode of Nd5Ad5
图 17 加强筋位置对Nd5Ad5吸能特性的影响
Figure 17. Influence of rib position on energy absorption characteristics of Nd5Ad5
-
[1] HA N S, LU G X. A review of recent research on bio-inspired structures and materials for energy absorption applications [J]. Composites Part B: Engineering, 2020, 181: 107496. doi: 10.1016/j.compositesb.2019.107496 [2] 贺良国, 赵杰, 谷先广. 基于多胞结构的车身前端轻量化和耐撞性设计 [J]. 汽车工程, 2020, 42(6): 832–839, 846. doi: 10.19562/j.chinasae.qcgc.2020.06.019HE L G, ZHAO J, GU X G. Lightweight and crashworthiness design of vehicle body front-end based on multi-cell structure [J]. Automotive Engineering, 2020, 42(6): 832–839, 846. doi: 10.19562/j.chinasae.qcgc.2020.06.019 [3] 牛枞, 黄晗, 向枳昕, 等. 仿生多胞薄壁管耐撞性分析及优化 [J]. 爆炸与冲击, 2022, 42(10): 105901. doi: 10.11883/bzycj-2021-0527NIU C, HUANG H, XIANG Z X, et al. Crashworthiness analysis and optimization on bio-inspired multi-cell thin-walled tubes [J]. Explosion and Shock Waves, 2022, 42(10): 105901. doi: 10.11883/bzycj-2021-0527 [4] 陈伟东, 门恒, 田晓耕. 具有梯度型刚度折叠收缩管的吸能性能 [J]. 高压物理学报, 2020, 34(5): 055301. doi: 10.11858/gywlxb.20190873CHEN W D, MEN H, TIAN X G. Energy absorption of folded shrink tubes with gradient stiffness [J]. Chinese Journal of High Pressure Physics, 2020, 34(5): 055301. doi: 10.11858/gywlxb.20190873 [5] 门恒, 陈伟东, 田晓耕. 具有刚度梯度折纹管能量吸收 [J]. 机械强度, 2021, 43(3): 651–659. doi: 10.16579/j.issn.1001.9669.2021.03.021MEN H, CHEN W D, TIAN X G. Energy absorption of pre-folded tube with stiffness gradient [J]. Journal of Mechanical Strength, 2021, 43(3): 651–659. doi: 10.16579/j.issn.1001.9669.2021.03.021 [6] MA W, LI Z X, XIE S C. Crashworthiness analysis of thin-walled bio-inspired multi-cell corrugated tubes under quasi-static axial loading [J]. Engineering Structures, 2020, 204: 110069. doi: 10.1016/j.engstruct.2019.110069 [7] WU J C, ZHANG Y, ZHANG F, et al. A bionic tree-liked fractal structure as energy absorber under axial loading [J].Engineering Structures, 2021, 245: 112914. doi: 10.1016/j.engstruct.2021.112914 [8] ZHANG H, SUN W F. Mechanical behavior and crashworthiness assessment of corrugated inner rib reinforced tubular structures [J]. Thin-Walled Structures, 2023, 189: 110894. 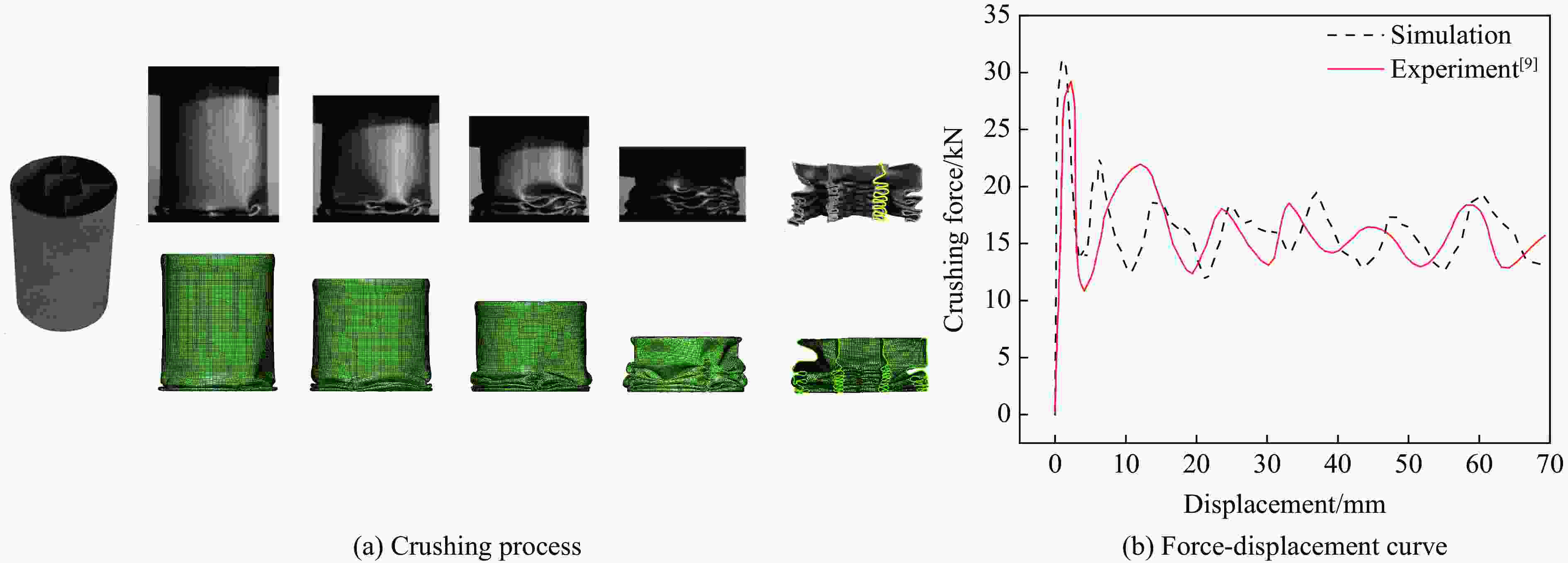doi: 10.1016/j.tws.2023.110894 [9] CHEN T T, ZHANG Y, LIN J M, et al. Theoretical analysis and crashworthiness optimization of hybrid multi-cell structures [J].Thin-Walled Structures, 2019, 142: 116–131. doi: 10.1016/j.tws.2019.05.002 [10] ESTRADA Q, SZWEDOWICZ D, MAJEWSKI T, et al. Effect of discontinuity size on the energy absorption of structural steel beam profiles [J]. Mechanics of Advanced Materials and Structures, 2017, 24(1): 88–94. doi: 10.1080/15376494.2015.1117167 [11] MING S Z, SONG Z B, ZHOU C H, et al. The energy absorption of long origami-ending tubes with geometrical imperfections [J].Thin-Walled Structures, 2021, 161: 107415. doi: 10.1016/j.tws.2020.107415 [12] ZHOU C H, ZHOU Y, WANG B. Crashworthiness design for trapezoid origami crash boxes [J]. Thin-Walled Structures, 2017, 117: 257–267. doi: 10.1016/j.tws.2017.03.022 [13] LIU Z F, HAO W Q, XIE J M, et al. Axial-impact buckling modes and energy absorption properties of thin-walled corrugated tubes with sinusoidal patterns [J]. Thin-Walled Structures, 2015, 94: 410–423. doi: 10.1016/j.tws.2015.05.002 [14] YAMASHITA M, GOTOH M, SAWAIRI Y. Axial crush of hollow cylindrical structures with various polygonal cross-sections: numerical simulation and experiment [J]. Journal of Materials Processing Technology, 2003, 140(1): 59–64. doi: 10.1016/S0924-0136(03)00821-5 [15] ZHANG X, HU H H. Crushing analysis of polygonal columns and angle elements [J]. International Journal of Impact Engineering, 2010, 37(4): 441–451. doi: 10.1016/j.ijimpeng.2009.06.009 [16] TANG Z L, LIU S T, ZHANG Z H. Energy absorption properties of non-convex multi-corner thin-walled columns [J]. Thin-Walled Structures, 2012, 51: 112–120. doi: 10.1016/j.tws.2011.10.005 [17] LI Z X, MA W, XU P, et al. Crushing behavior of circumferentially corrugated square tube with different cross inner ribs [J].Thin-Walled Structures, 2019, 144: 106370. doi: 10.1016/j.tws.2019.106370 [18] DENG X L, LIU W Y, JIN L. On the crashworthiness analysis and design of a lateral corrugated tube with a sinusoidal cross-section [J]. International Journal of Mechanical Sciences, 2018, 141: 330–340. doi: 10.1016/j.ijmecsci.2018.03.001 [19] EYVAZIAN A, HABIBI M K, HAMOUDA A M, et al. Axial crushing behavior and energy absorption efficiency of corrugated tubes [J]. Materials & Design, 2014, 54: 1028–1038. doi: 10.1016/j.matdes.2013.09.031 [20] DENG X L, LIU W Y. Experimental and numerical investigation of a novel sandwich sinusoidal lateral corrugated tubular structure under axial compression [J]. International Journal of Mechanical Sciences, 2019, 151: 274–287. doi: 10.1016/j.ijmecsci.2018.11.010 [21] WANG Z G, LIU J F, YAO S. On folding mechanics of multi-cell thin-walled square tubes [J]. Composites Part B: Engineering, 2018, 132: 17–27. doi: 10.1016/j.compositesb.2017.07.036 [22] HA N S, PHAM T M, TRAN T T, et al. Mechanical properties and energy absorption of bio-inspired hierarchical circular honeycomb [J]. Composites Part B: Engineering, 2022, 236: 109818. doi: 10.1016/j.compositesb.2022.109818 [23] GONG C, BAI Z H, WANG Y L, et al. On the crashworthiness performance of novel hierarchical multi-cell tubes under axial loading [J]. International Journal of Mechanical Sciences, 2021, 206: 106599. doi: 10.1016/j.ijmecsci.2021.106599 [24] WANG J, ZHANG Y, HE N, et al. Crashworthiness behavior of Koch fractal structures [J]. Materials & Design, 2018, 144: 229–244. doi: 10.1016/j.matdes.2018.02.035 [25] ZHANG J, XIE S C, ZHOU H, et al. Study and optimization of energy absorption characteristics of a new concave polygon tube [J].Structures, 2023, 53: 1030–1045. doi: 10.1016/j.istruc.2023.04.129 [26] DENG X L, QIN S G, HUANG J L. Crashworthiness analysis of gradient hierarchical multicellular columns evolved from the spatial folding [J]. Materials & Design, 2022, 215: 110435. 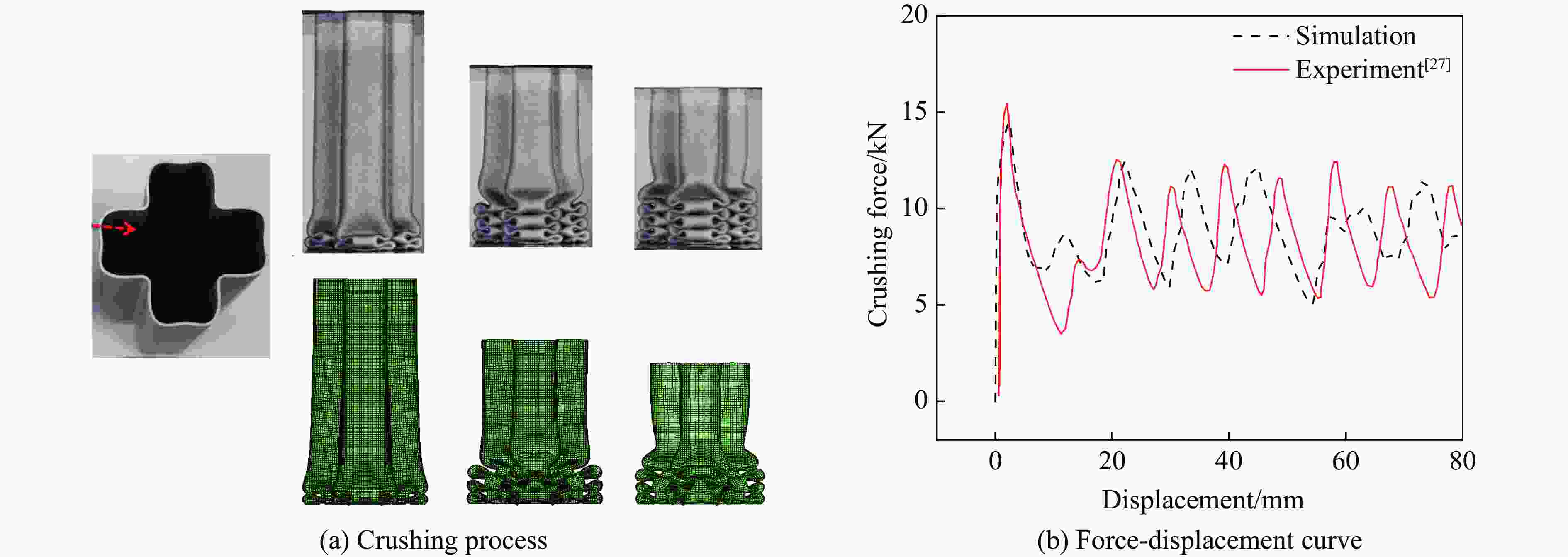doi: 10.1016/J.MATDES.2022.110435 [27] WU S Y, SUN G Y, WU X, et al. Crashworthiness analysis and optimization of Fourier varying section tubes [J]. International Journal of Non-Linear Mechanics, 2017, 92: 41–58. doi: 10.1016/j.ijnonlinmec.2017.03.001 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 209
- HTML全文浏览量: 79
- PDF下载量: 42
