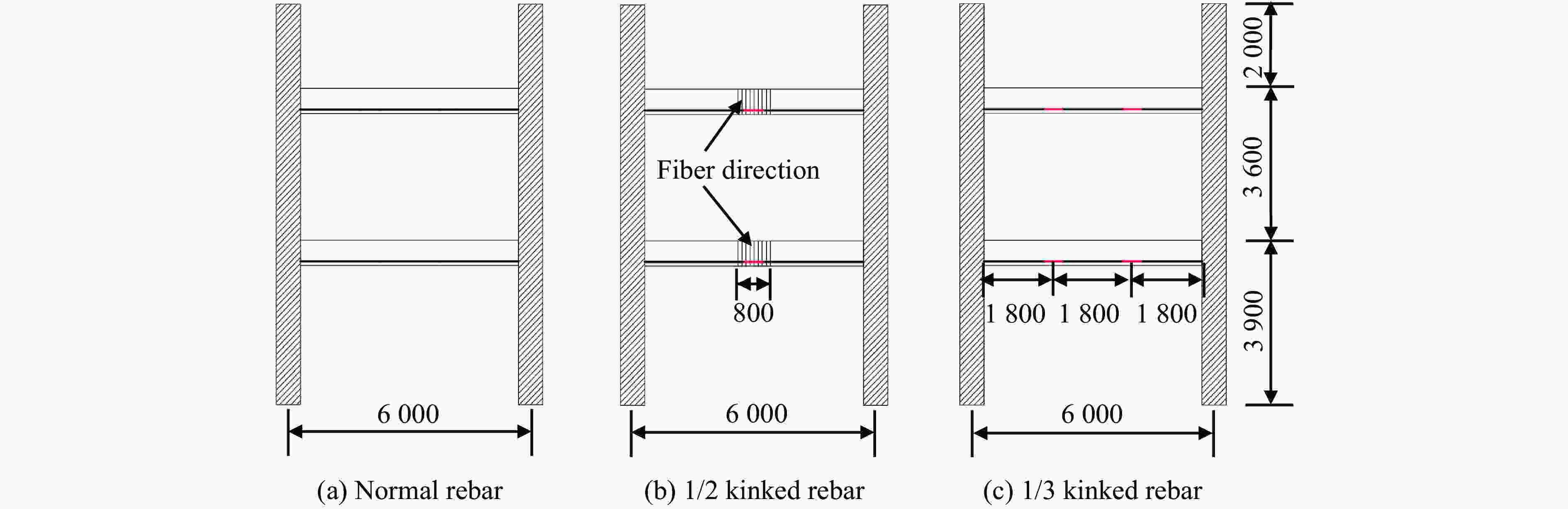
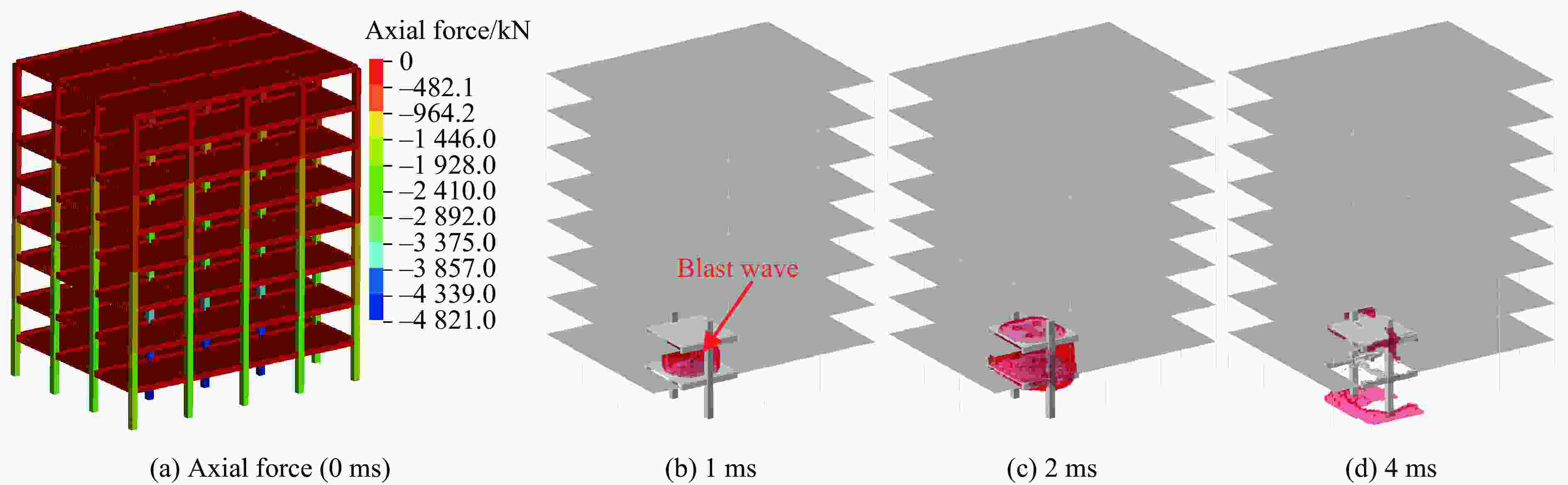
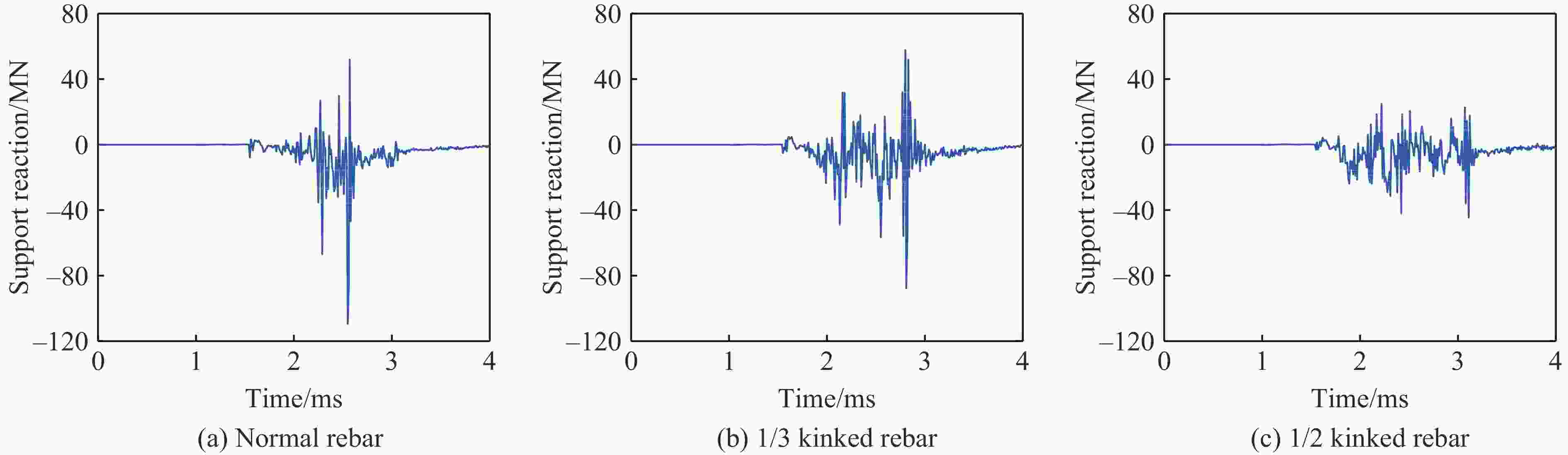
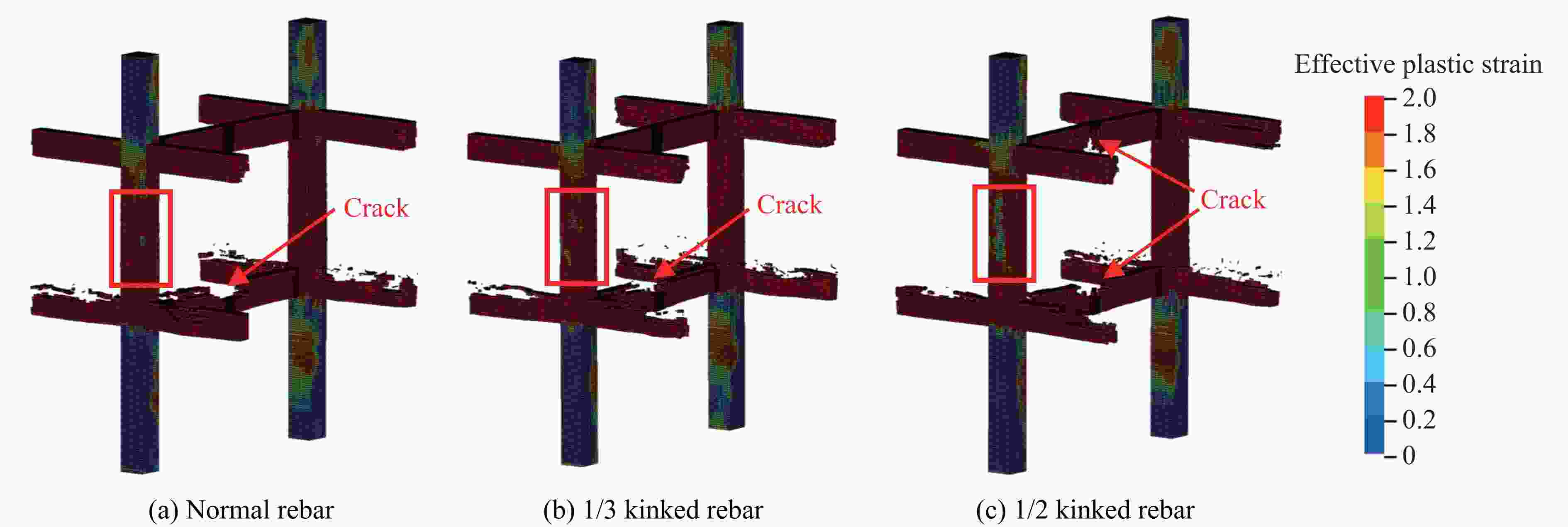
Numerical Simulation on Internal Explosion Resistance of Concrete Frame Structures with Kinked Rebar
-
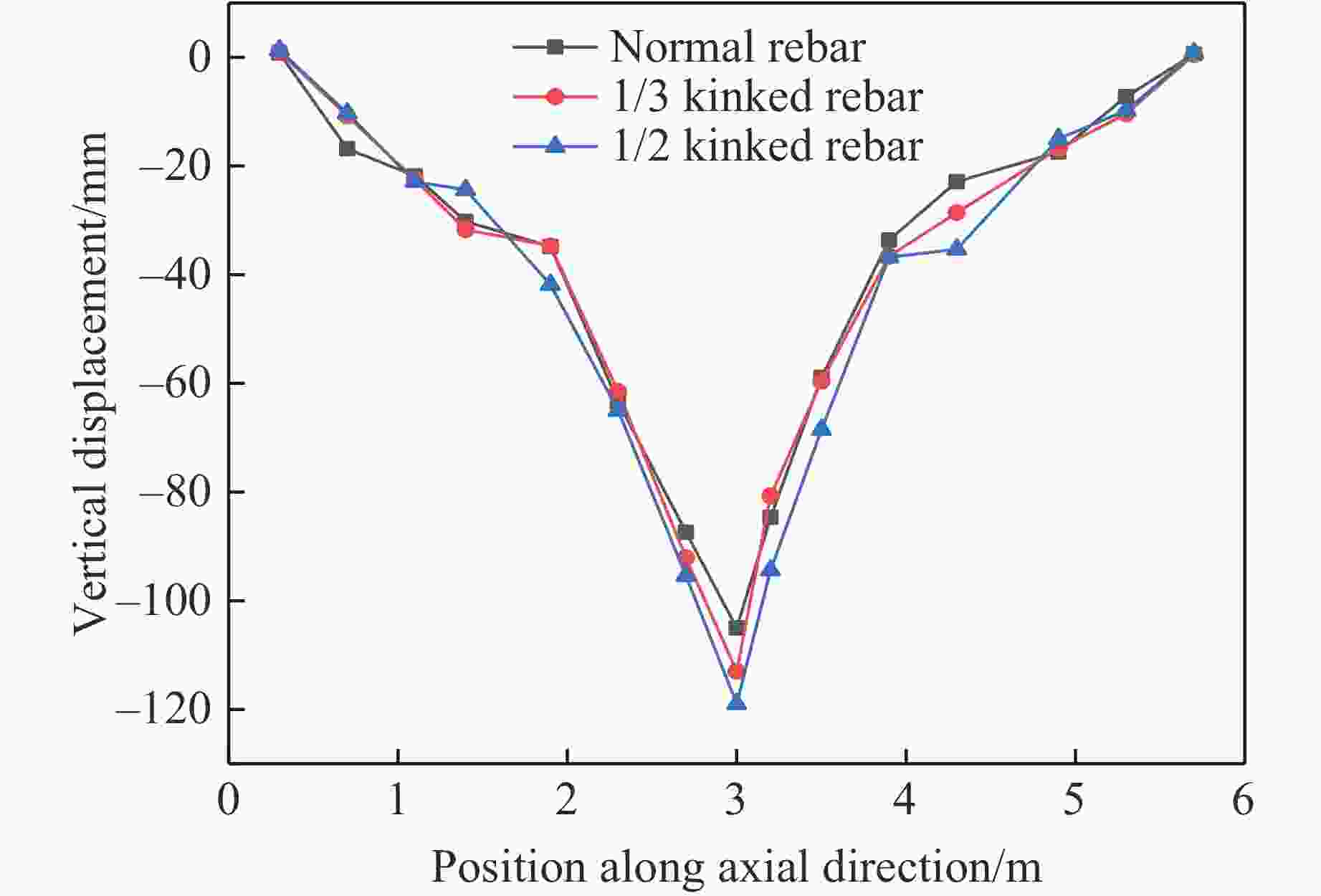
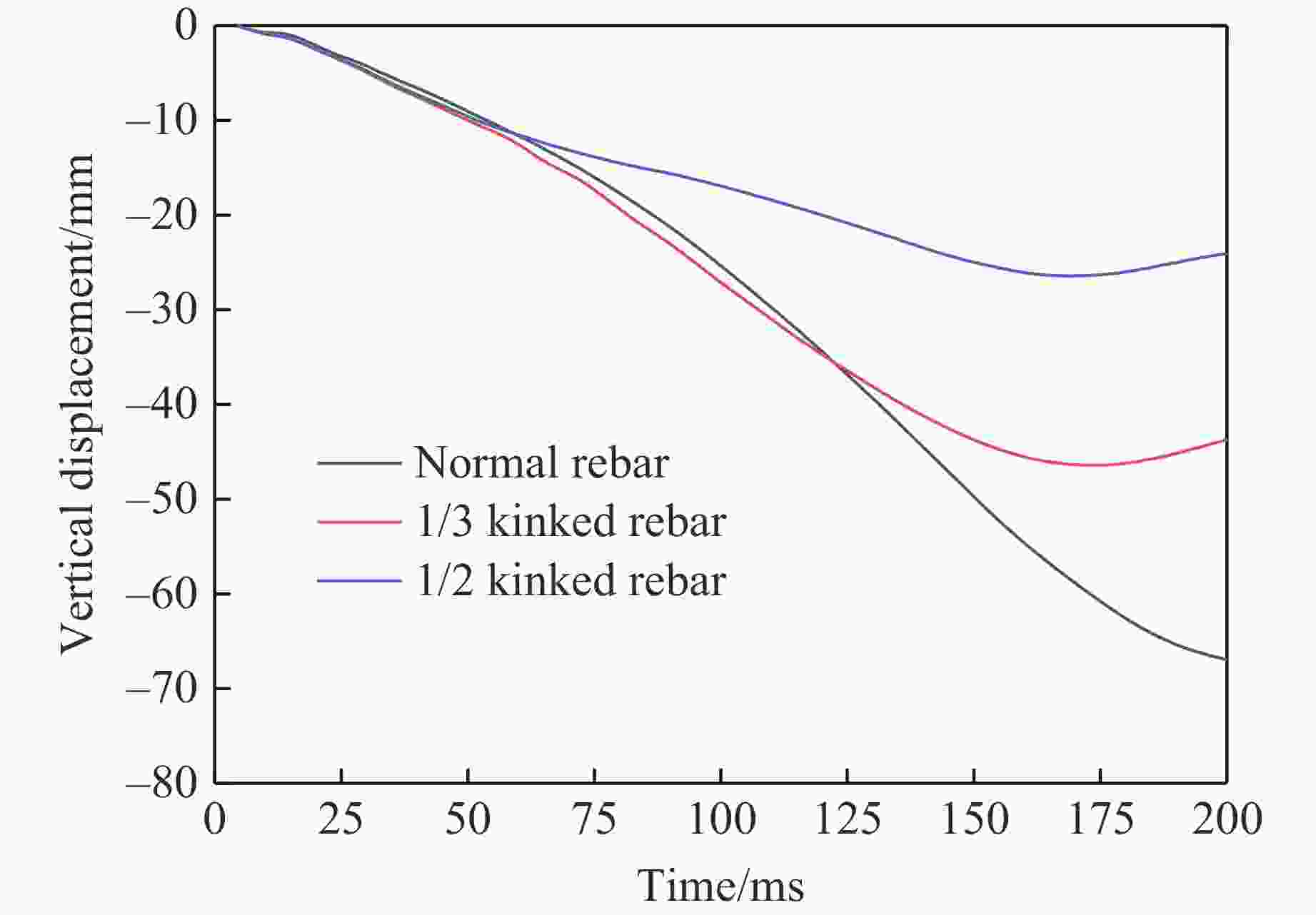
摘要: 人工塑性铰在框架结构抗震研究中已经得到广泛应用，其能够控制梁塑性铰出现的位置，避免框架结构在地震中出现梁柱节点破坏而发生连续倒塌，实现“强柱弱梁”的设计目标。一种新型起波钢筋构造的人工塑性铰为结构抗爆设计提供了新的思路。现有的结构静载试验表明，起波钢筋兼具优异的变形性能和较强的极限承载力。采用简化混合建模的方法，基于有限元分析软件ANSYS/LS-DYNA，对采用不同起波配筋方案的钢筋混凝土框架结构进行数值模拟。研究结果表明：在爆炸荷载作用下，起波配筋梁能有效地吸收冲击力，降低支座反力，推迟反力峰值出现时间，保护梁柱节点，将破坏限制在梁板构件，从而防止结构发生连续倒塌。Abstract: Artificial plastic hinges have been widely used in the seismic research of frame structures, which can control the location of the beam plastic hinges and avoid the continuous collapse of the frame structure due to the damage of beam-column joints in earthquakes. The design goal of “strong column weak beam” can be achieved. An artificial plastic hinge with kinked rebar provides a new idea for structural blast resistance. Established structural static load tests have shown that the kinked rebar has excellent deformation performance. The ultimate load capacity of beam with kinded rebar is not reduced. With the software ANSYS/LS-DYNA and the hybrid finite element modeling approach, a numerical simulation study of reinforced concrete frame structures with different kinked rebar schemes was carried out. The results showed that the beam with kinked rebar can absorb the impact energy, reduce the support reaction, delay the peak reaction force, protect the beam-column joints, limit the damage to beam-slab members, and prevent the continuous collapse of frame structre.
-
Key words:
- impact loading /
- internal explosion /
- kinked rebar /
- frame structure /
- finite element analysis
-
图 12 HRB400起波钢筋的等效应力-应变关系
Figure 12. Equivalent stress-strain relation of HRB400 kinked rebar
表 1 钢筋和混凝土材料参数
Table 1. Rebar and concrete material parameter
Concrete (K&C) Rebar (*MAT_PLASTIC_KINMATIC) ρ0/(kg·m−3) μ fc/MPa ρ0/(kg·m−3) μ E/GPa fy/MPa C/s−1 P εf 2 400 0.2 36 7 800 0.2 206 320 40 5 0.14 
下载: 导出CSV
表 2 空气材料参数
Table 2. Air material parameters
ρ0/(kg·m−3) C0 C1 C2 C3 C4 C5 C6 E0/(J·m−3) V0 1.29 0 0 0 0 0.4 0.4 0 2.5$ \times $105 1
下载: 导出CSV
表 3 TNT材料参数
Table 3. TNT material parameters
ρ0/(kg·m−3) D/(m·s−1) pCJ/GPa A/GPa B/GPa R1 R2 $\omega $ E0/(J·m−3) V0 1 630 6 930 21 373.8 3.747 4.15 0.9 0.35 7$ \times $109 1
下载: 导出CSV
-
[1] Federal Emergency Management Agency (FEMA). Primer to design safe school projects in case of terrorist attacks and school shootings [M]. Washington: Building Performance Assessment Team, 2012. [2] FENG P, QIANG H, QIN W, et al. A novel kinked rebar configuration for simultaneously improving the seismic performance and progressive collapse resistance of RC frame structures [J]. Engineering Structures, 2017, 147: 752–767. doi: 10.1016/j.engstruct.2017.06.042 [3] 樊源, 陈力, 任辉启, 等. 起波配筋RC梁抗爆作用机理及抗力动力系数的理论计算方法 [J]. 爆炸与冲击, 2019, 39(3): 035102. doi: 10.11883/bzycj-2018-0181FAN Y, CHEN L, REN H Q, et al. Blast-resistant mechanism of RC beam with kinked rebar and calculation method of dynamic resistance coefficient [J]. Explosion and Shock Waves, 2019, 39(3): 035102. doi: 10.11883/bzycj-2018-0181 [4] 刘思嘉, 陈力, 曹铭津, 等. 起波钢筋高速动态拉伸力学性能研究 [J]. 爆炸与冲击, 2022, 42(5): 053101. doi: 10.11883/bzycj-2021-0328LIU S J, CHEN L, CAO M J, et al. Study on mechanical properties of the kinked rebar under high speed dynamic tension [J]. Explosion and Shock Waves, 2022, 42(5): 053101. doi: 10.11883/bzycj-2021-0328 [5] 陈力, 任辉启, 樊源, 等. 强动载作用下起波配筋梁抗力性能的试验研究 [J]. 土木工程学报, 2021, 54(10): 1–8. doi: 10.15951/j.tmgcxb.2021.10.001CHEN L, REN H Q, FAN Y, et al. Experimental study on the resistance of RC beam with kinked rebar under severe dynamic loading [J]. China Civil Engineering Journal, 2021, 54(10): 1–8. doi: 10.15951/j.tmgcxb.2021.10.001 [6] 李世强. 爆炸荷载下RC框架结构连续性倒塌数值分析 [D]. 内蒙古: 内蒙古科技大学, 2017.LI S Q. Numerical analysis of progressive collapse of RC frame structure under blast loading [D]. Inner Mongolia: Inner Mongolia University of Science and Technology, 2017. [7] MKRTYCHEV O, DUDAREVA M S, ANDREEV M. Verification of the reinforced concrete column bar model based on the test results [C]//MATEC Web of Conferences. EDP Sciences, 2018, 251: 04014. [8] BULUSHEV S V, DUDAREVA M S. Nonlinear models of reinforced concrete beam elements with the actual reinforcement [C]//IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2020, 753(3): 032040. [9] LU J X, WU H, FANG Q. Progressive collapse of murrah federal building: revisited [J]. Journal of Building Engineering, 2022, 57: 104939. doi: 10.1016/j.jobe.2022.104939 [10] CHEN G Q, LU J X, WU H. Dynamic behavior and retrofitting of RC frame building under vehicular bomb explosion [J]. Engineering Failure Analysis, 2023, 143: 106925. doi: 10.1016/j.engfailanal.2022.106925 [11] 高超, 宗周红, 伍俊. 爆炸荷载下钢筋混凝土框架结构倒塌破坏试验研究 [J]. 土木工程学报, 2013, 46(7): 9–20. doi: 10.15951/j.tmgcxb.2013.07.012GAO C, ZONG Z H, WU J. Experimental study on progressive collapse failure of RC frame structures under blast loading [J]. China Civil Engineering Journal, 2013, 46(7): 9–20. doi: 10.15951/j.tmgcxb.2013.07.012 [12] Comite Euro-International du Beton. CEB-FIP model code 1990: design code [M]. London: Thomas Telford Publishing, 1993. [13] MALVAR L J, CRAWFORD J E. Dynamic increase factors for concrete [R]. Naval Facilities Engineering Service Center, 1998. [14] 陈肇元. 爆炸荷载下的混凝土结构性能与设计 [M]. 北京: 中国建筑工业出版社, 2015.CHEN Z Y. Performance and design of concrete structures under explosive loads [M]. Beijing: China Architecture and Building Press, 2015. [15] HALLQUIST J O. LS-DYNA keyword user’s manual r11 [M]. California: Livermore Software Technology Corporation, 2018. [16] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010 [S]. 北京: 中国建筑工业出版社, 2015.Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for design of concrete structures: GB 50010—2010 [S]. Beijing: China Architecture and Building Press, 2015. [17] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete [J]. Journal of Structural Engineering, 1988, 114(8): 1804–1826. doi: 10.1061/(ASCE)0733-9445(1988)114:8(1804) [18] 中华人民共和国住房和城乡建设部. 高层建筑混凝土结构技术规程: JGJ 3—2010 [S]. 北京: 中国建筑工业出版社, 2010.Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical specification for concrete structures of tall building: JGJ 3—2010 [S]. Beijing: China Architecture and Building Press, 2010. [19] 中华人民共和国住房和城乡建设部. 建筑抗震设计规范: GB 50011—2010 [S]. 北京: 中国建筑工业出版社, 2010.Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for seismic design of building: GB 50011—2010 [S]. Beijing: China Architecture and Building Press, 2010. [20] 张梦琳. FRP加固人防墙抗冲击性能试验研究与有限元分析 [D]. 青岛: 青岛理工大学, 2022.ZHANG M L. Experimental study and finite element analysis on impact resistance of civil air defense wall strengthened with FRP [D]. Qingdao: Qingdao University of Technology, 2022. [21] 高蒙. 配置局部起波钢筋的混凝土梁受力性能试验研究 [D]. 南京: 东南大学, 2016.GAO M. Experimental study on mechanical behavior of concrete beams reinforced with V-shaped rebar [D]. Nanjing: Southeast University, 2016. -
下载:
点击查看大图
图(17) / 表(4)
计量
- 文章访问数: 107
- HTML全文浏览量: 23
- PDF下载量: 23
