Electric Explosion Early Process Analysis of Metal Bridge Foil Based on an Electromagnetic-Thermal-Mechanical Model
-
摘要: 金属桥箔的电爆炸过程对电炮、冲击片雷管等的性能影响极为关键。这一过程中物质性质变化、几何构型和动力学过程非常复杂，早期的大量理论模拟工作均采用极为简化的物理模型。为此，建立了描述爆炸箔早期行为的三维电磁-热-固体力学耦合求解全物理模型，模拟爆炸箔在大电流加载下的早期受热膨胀过程，并对早期膨胀过程中桥箔上的磁场、电流、温度等演化进行分析，观察到电流在构型和电阻率两种因素影响下的角扩散和线扩散现象，模拟得到的桥区温度场分布与参考文献中的实验图像及模拟结果定性符合。Abstract: The electrical explosion of metal bridge foil is a key physical process in many fields, e.g. electric guns and slapper detonator. Due to the complexity of material properties, dynamic processes, and effects of geometric configurations, a large amount of earlier theoretical simulations used simplified physical models. In this paper, a three-dimensional electromagnetic-thermal-mechanical model was established. which was a full physical model describing the early behavior of explosive foil. The early thermal expansion process of the explosive foil under large current loading was simulated, and the evolution of magnetic field, current, temperature, expansion speed of the foil was analyzed. The phenomena of angular and linear current diffusions induced by the configuration and the resistivity were observed in the simulation. The temperature distribution in the bridge region obtained from the simulation is qualitatively consistent with experiment and simulation results of literature.
-
Key words:
- explosive foil /
- slapper detonator /
- magnetic fluid /
- multi-field coupling
-
图 4 爆炸箔几何1/2模型示意图（单位：mm）
Figure 4. Schematic diagram of the 1/2 model of explosion foil (Unit: mm)
图 6 表面磁场强度分布
Figure 6. Magnetic field intensity distribution of upper and lower surfaces
图 11 不同时刻的磁场强度分布
Figure 11. Magnetic field intensity distribution at different instants
-
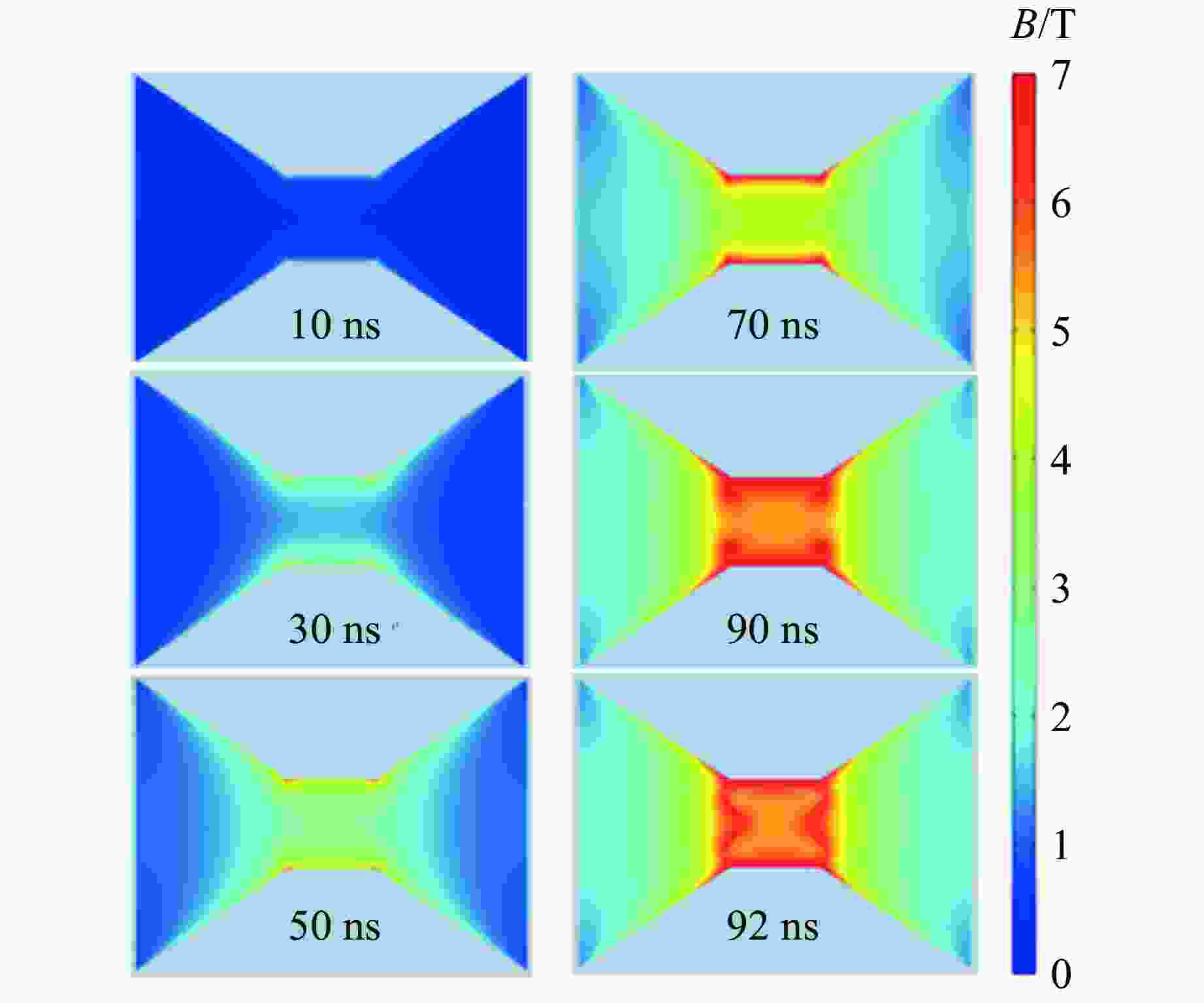
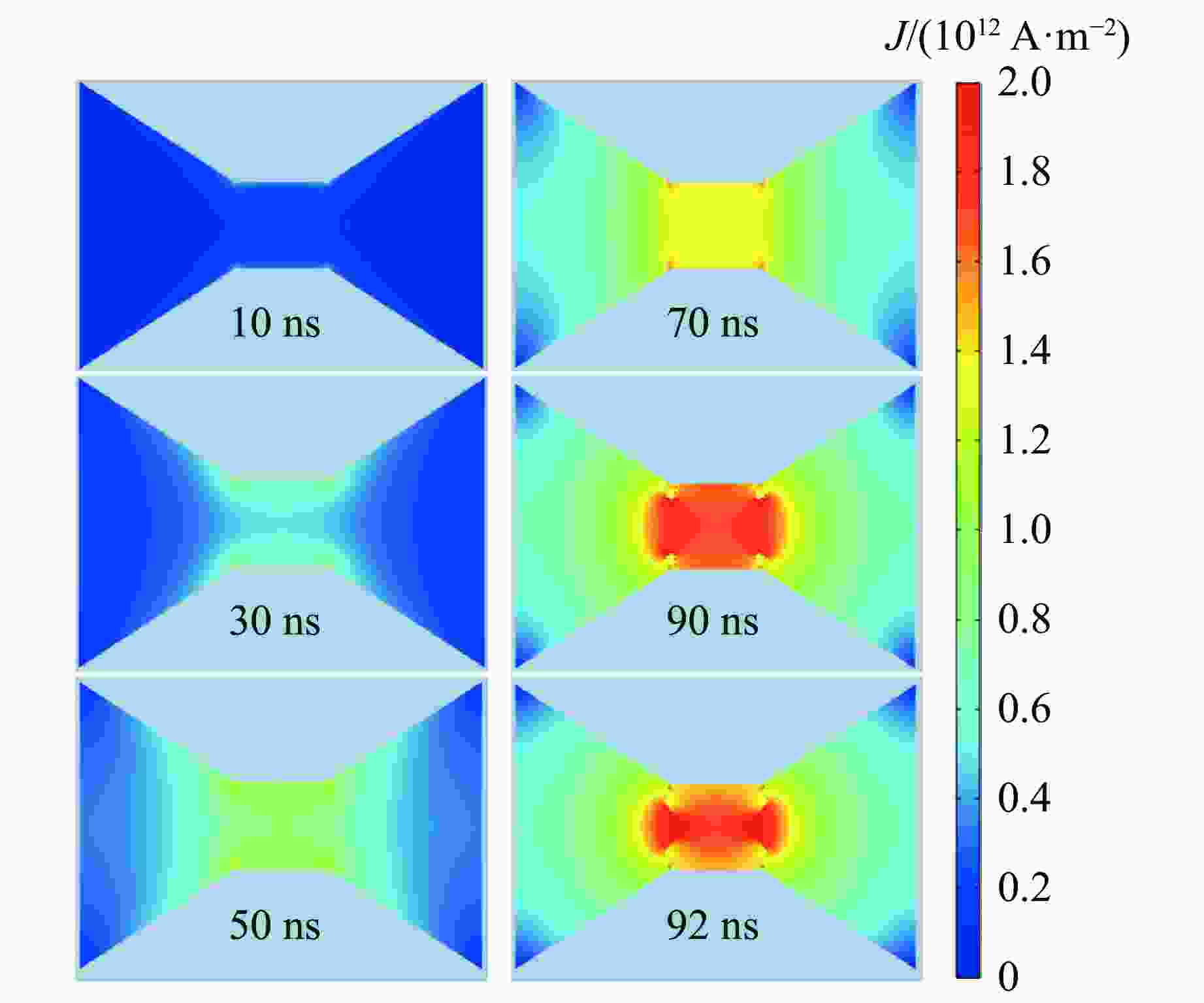
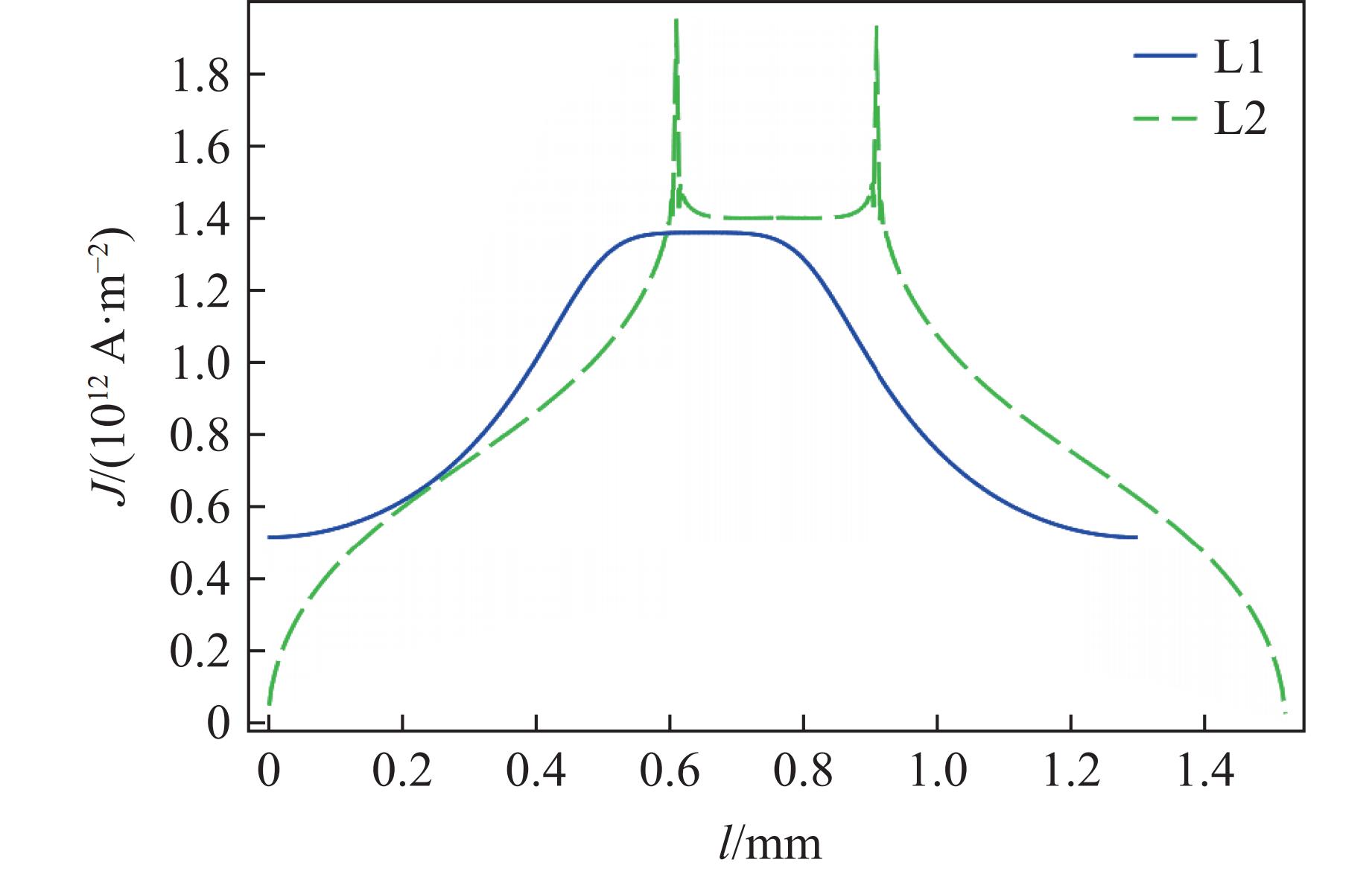
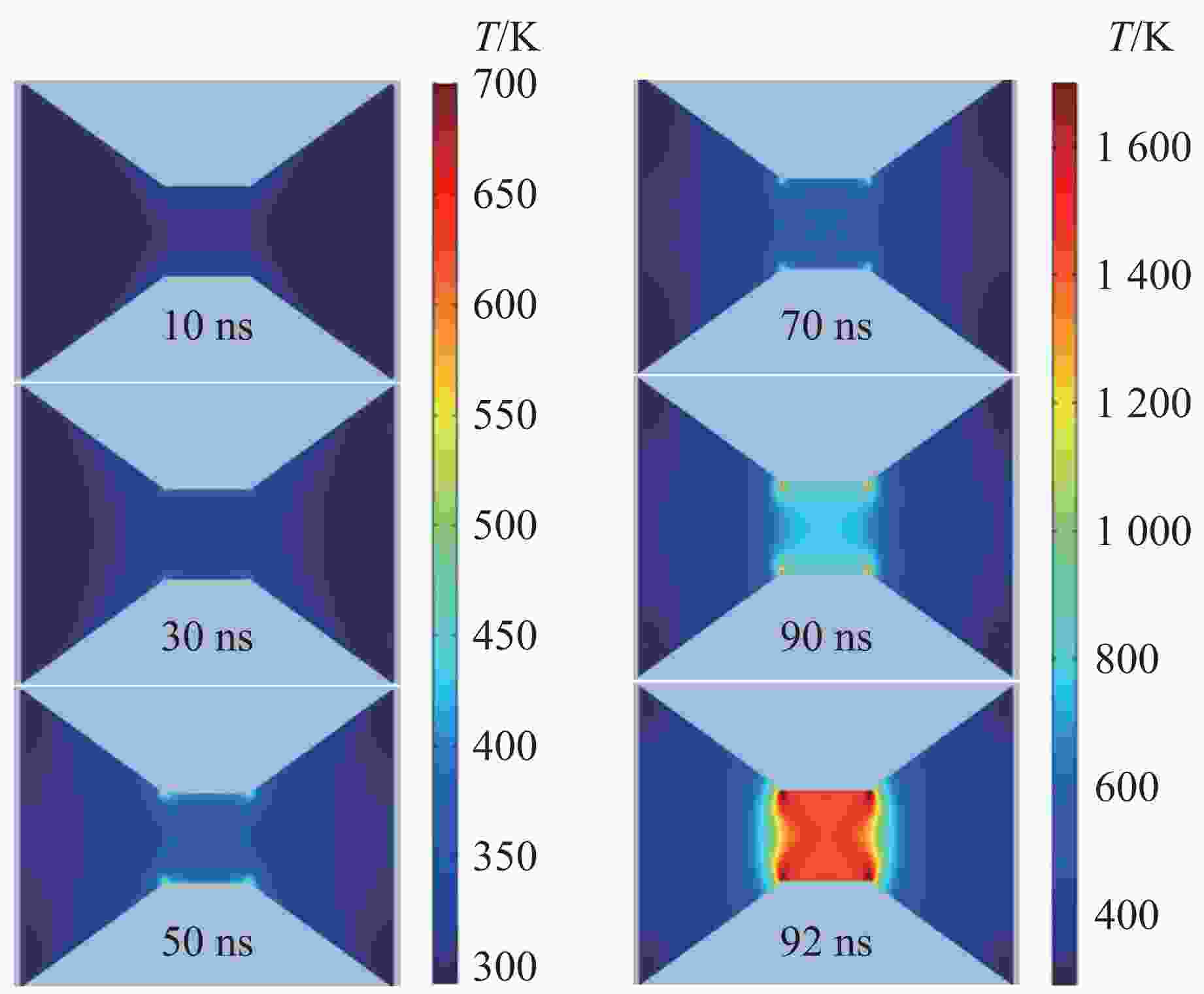
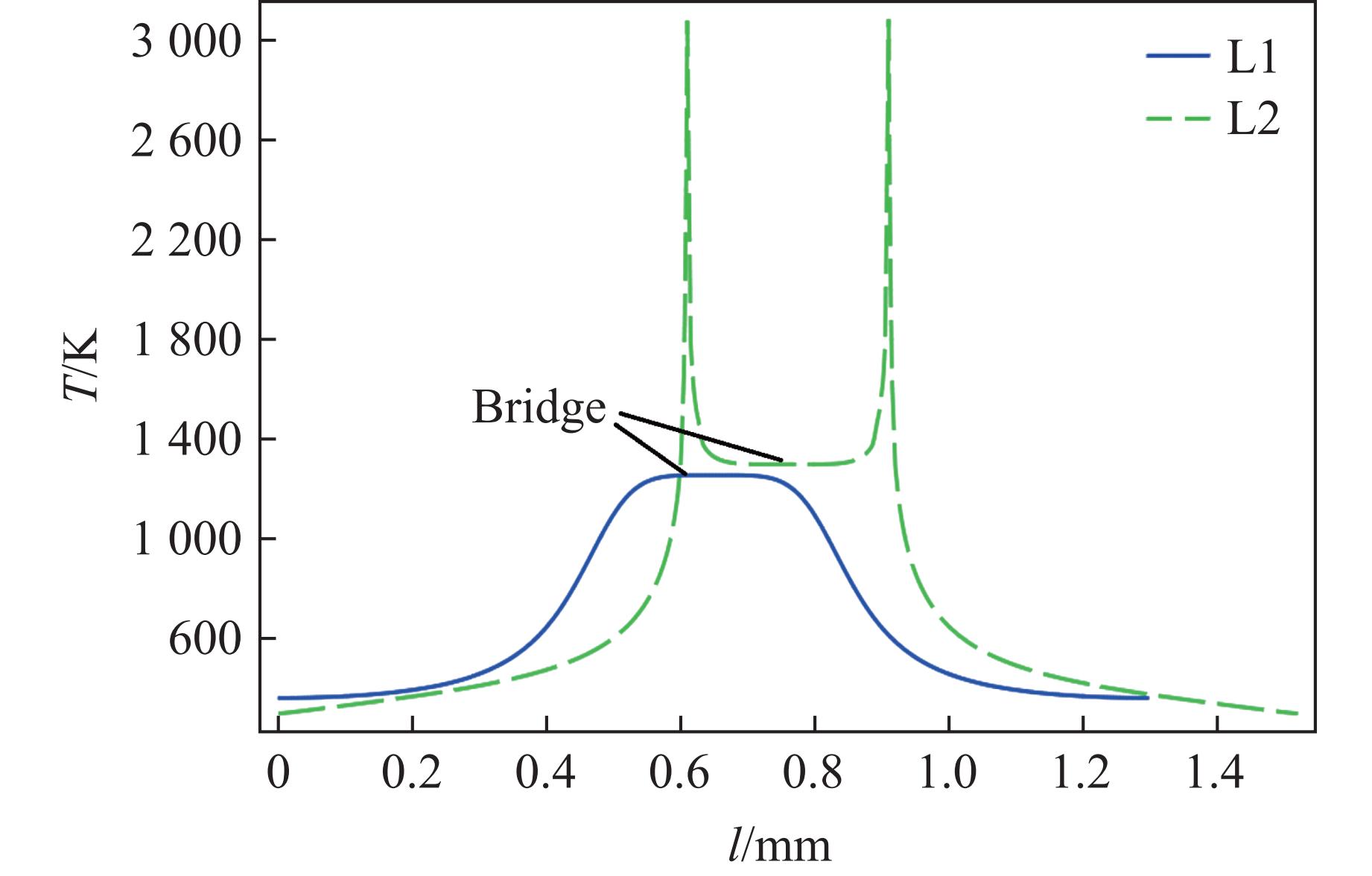
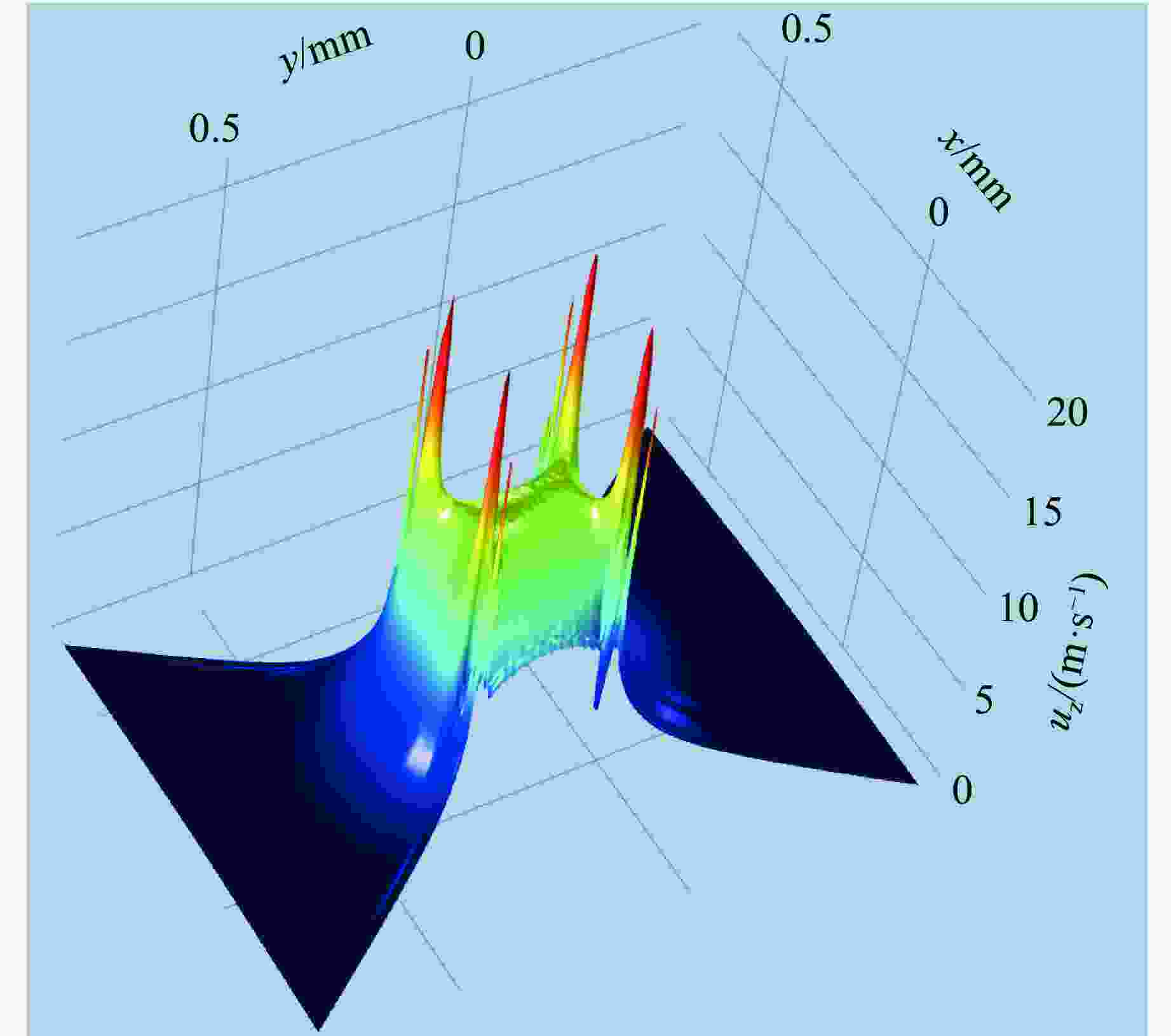
[1] GUENTHER A H, WUNSCH D C, SOAPES T D, et al. Acceleration of thin plates by exploding foil techniques [M]//CHACE W G, MOORE H K. Exploding Wires. Boston: Springer, 1962: 279–298. [2] KELLER D V, PENNING J R JR. Exploding foil-the production of plane shock waves and the acceleration of thin plates [M]//CHACE W G, MOORE H K. Exploding Wires. Boston: Springer, 1962: 263–277. [3] 罗斌强, 张旭平, 郝龙, 等. 7 km/s以上超高速发射技术研究进展 [J]. 爆炸与冲击, 2021, 41(2): 021401. doi: 10.11883/bzycj-2020-0307LUO B Q, ZHANG X P, HAO L, et al. Advances on the techniques of ultrahigh-velocity launch above 7 km/s [J]. Explosion and Shock Waves, 2021, 41(2): 021401. doi: 10.11883/bzycj-2020-0307 [4] WANG G J, HE J, ZHAO J H, et al. The techniques of metallic foil electrically exploding driving hypervelocity flyer to more than 10 km/s for shock wave physics experiments [J]. Review of Scientific Instruments, 2011, 82(9): 095105. doi: 10.1063/1.3633773 [5] CUTTING J L, LEE R S, HONGIN R I. Slapper detonator perfonnance: UCRL-IDl 17787 [R]. USA: Lawrence Livermore National Labratory, 1994. [6] 王桂吉, 蒋吉昊, 邓向阳, 等. 电爆炸驱动小尺寸冲击片实验与数值计算研究 [J]. 兵工学报, 2008, 29(6): 657–661. doi: 10.3321/j.issn:1000-1093.2008.06.004WANG G J, JIANG J H, DENG X Y, et al. Experiments and numerical simulation of small-scale slapper driven by electrical explosion [J]. Acta Armamentarii, 2008, 29(6): 657–661. doi: 10.3321/j.issn:1000-1093.2008.06.004 [7] 张玉若, 梁车平, 程涛, 等. 爆炸箔换能元失效模式分析 [J]. 火工品, 2018(4): 5–7. doi: 10.3969/j.issn.1003-1480.2018.04.002ZHANG Y R, LIANG C P, CHENG T, et al. Experimental study on failure mode of exploding foil [J]. Initiators & Pyrotechnics, 2018(4): 5–7. doi: 10.3969/j.issn.1003-1480.2018.04.002 [8] 秦国圣, 张蕊, 王寅, 等. 多点阵列冲击片雷管仿真与试验研究 [J]. 兵工学报, 2016, 37(Suppl 2): 81–85.QIN G S, ZHANG R, WANG Y, et al. Numerical simulation and experimental study of multi-point array EFI [J]. Acta Armamentarii, 2016, 37(Suppl 2): 81–85. [9] 先明春, 谢浚尧, 王成玲, 等. 考虑压缩空气边界的爆炸箔起爆器飞片运动模型 [J]. 爆破器材, 2023, 52(2): 1–7. doi: 10.3969/j.issn.1001-8352.2023.02.001XIAN M C, XIE J Y, WANG C L, et al. A Motion model of flyer in exploding foil initiator considering compressed air boundary [J]. Explosive Materials, 2023, 52(2): 1–7. doi: 10.3969/j.issn.1001-8352.2023.02.001 [10] 侯新朋, 彭志凌, 宋进宇, 等. 桥区结构对爆炸箔起爆器发火性能的影响 [J]. 兵器装备工程学报, 2022, 43(5): 103–107, 113. doi: 10.11809/bqzbgcxb2022.05.017HOU X P, PENG Z L, SONG J Y, et al. Influence of bridge structure on ignition performance of exploding foil detonator [J]. Journal of Ordnance Equipment Engineering, 2022, 43(5): 103–107, 113. doi: 10.11809/bqzbgcxb2022.05.017 [11] LOGAN J D, LEE R S, WEINGART R C, et al. Calculation of heating and burst phenomena in electrically exploded foils [J]. Journal of Applied Physics, 1977, 48(2): 621–628. doi: 10.1063/1.323646 [12] 董玉斌, 李献文, 董维申. 电加热金属箔爆炸的有限元法计算 [J]. 爆炸与冲击, 1981, 1(1): 28–36.DONG Y B, LI X W, DONG W S. A finite-element method calculation of electrically heated bursting metallic foils [J]. Explosion and Shock Waves, 1981, 1(1): 28–36. [13] OSHER J E, BARNES G, CHAU H H, et al. Operating characteristics and modeling of the LLNL 100-kV electric gun [J]. IEEE Transactions on Plasma Science, 1989, 17(3): 392–402. doi: 10.1109/27.32247 [14] SAXENA A K, KAUSHIK T C, GUPTA S C. Shock experiments and numerical simulations on low energy portable electrically exploding foil accelerators [J]. Review of Scientific Instruments, 2010, 81(3): 033508. doi: 10.1063/1.3327818 [15] 罗斌强. 金属箔电爆炸及其在冲击动力学中的应用 [D]. 合肥: 中国科学技术大学, 2012.LUO B Q. Electrical explosion of metallic foils and its applications in dynamic mechanics [D]. Hefei: University of Science and Technology of China, 2012. [16] 贺佳, 罗斌强, 庞树财, 等. 微型爆炸箔电爆炸过程的数值模拟 [J]. 高压物理学报, 2017, 31(1): 21–26.HE J, LUO B Q, PANG S C, et al. Numerical simulation of electrical explosion of micro-exploding foil [J]. Chinese Journal of High Pressure Physics, 2017, 31(1): 21–26. [17] LUO B Q, SUN C W, ZHAO J H, et al. Unified numerical simulation of metallic foil electrical explosion and its applications [J]. IEEE Transactions on Plasma Science, 2013, 41(1): 49–57. doi: 10.1109/TPS.2012.2227827 [18] NEAL W, GARASI C. High fidelity studies of exploding foil initiator bridges, part 3: ALEGRA MHD simulations [J]. AIP Conference Proceedings, 2017, 1793: 080008. doi: 10.1063/1.4971614 [19] 苏谦, 褚恩义, 解瑞珍, 等. 九点爆炸箔电爆炸性能试验与仿真模拟 [J]. 火工品, 2019(5): 15–18. doi: 10.3969/j.issn.1003-1480.2019.05.004SU Q, CHU E Y, XIE R Z, et al. Experimental study and simulation on the electrical explosion performance of nine-point explosive foil [J]. Initiators & Pyrotechnics, 2019(5): 15–18. doi: 10.3969/j.issn.1003-1480.2019.05.004 [20] 钱石川, 甘强, 任志伟, 等. 爆炸箔起爆器发火阈值影响因素的数值模拟 [J]. 含能材料, 2018, 26(3): 248–254. doi: 10.11943/j.issn.1006-9941.2018.03.008QIAN S C, GAN Q, REN Z W, et al. Numerical simulation of the factors affecting the ignition threshold of an exploding foil initiator [J]. Chinese Journal of Energetic Materials, 2018, 26(3): 248–254. doi: 10.11943/j.issn.1006-9941.2018.03.008 [21] 伍俊英, 于红新, 汪龙, 等. 金属桥箔水中电爆炸流场数值模拟研究 [J]. 兵工学报, 2016, 37(Suppl 1): 51–56.WU J Y, YU H X, WANG L, et al. Numerical simulation of electric exploding of metal bridge foil in water [J]. Acta Armamentarii, 2016, 37(Suppl 1): 51–56. [22] 王亮, 邹苑楠, 蒋小华, 等. 短脉冲电流作用下铜微桥箔的电热分析 [J]. 含能材料, 2013, 21(4): 500–505. doi: 10.3969/j.issn.1006-9941.2013.04.019WANG L, ZOU Y N, JIANG X H, et al. Thermal-electric analysis of small-scale copper bridge foils excited by short pulse currents [J]. Chinese Journal of Energetic Materials, 2013, 21(4): 500–505. doi: 10.3969/j.issn.1006-9941.2013.04.019 [23] 曹始发, 黄寅生. 小飞片冲击起爆HNS-IV的临界速度的研究 [J]. 计算机仿真, 2016, 33(4): 23–26, 149. doi: 10.3969/j.issn.1006-9348.2016.04.006CAO S F, HUANG Y S. Research on threshold velocity of shock initiation of HNS-IV by small flyer [J]. Computer Simulation, 2016, 33(4): 23–26, 149. doi: 10.3969/j.issn.1006-9348.2016.04.006 -
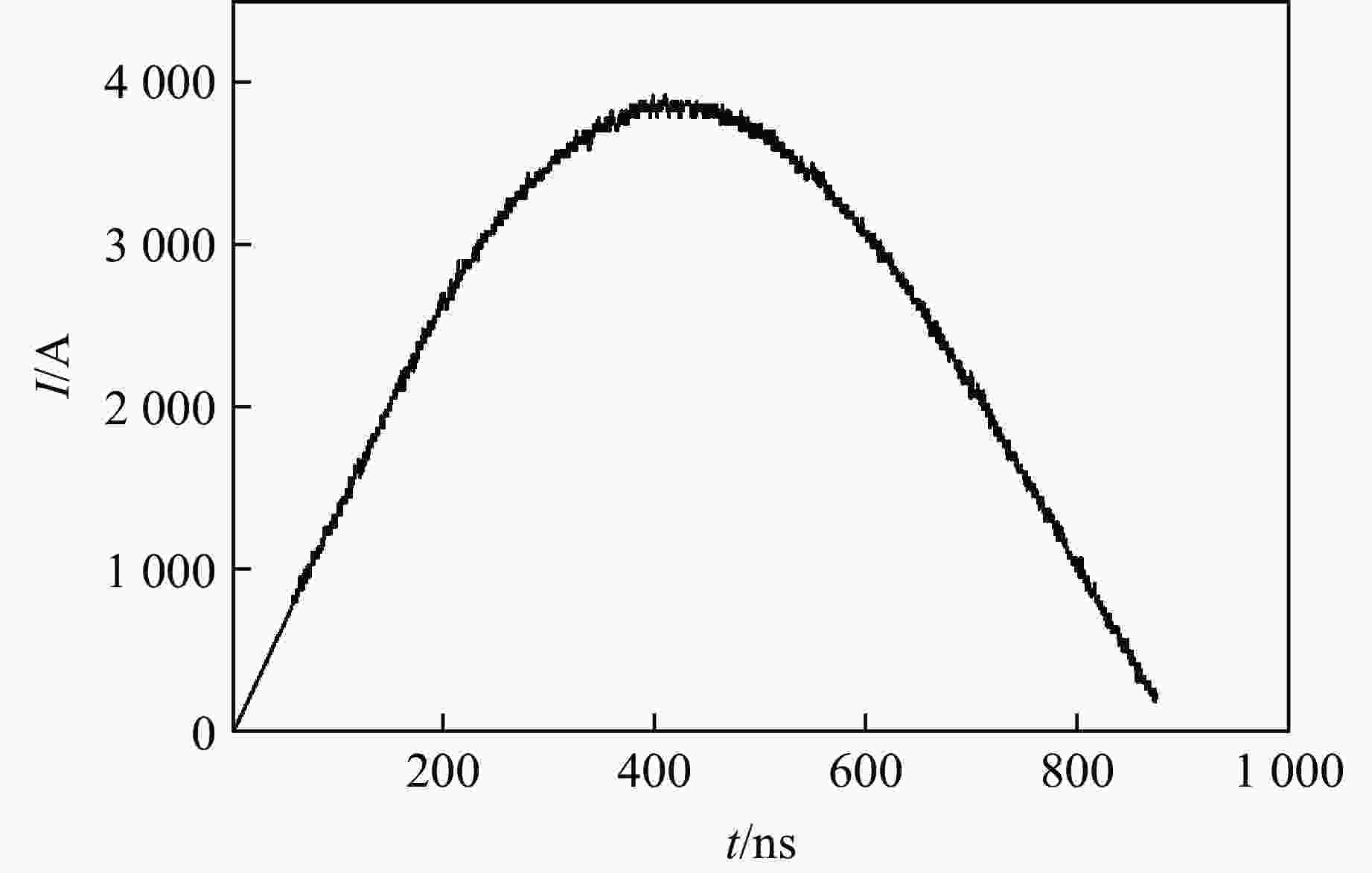
下载:
点击查看大图
图(17)
计量
- 文章访问数: 109
- HTML全文浏览量: 39
- PDF下载量: 31
