基于正交试验法的气泡帷幕削波特性研究

杜明燃; 陈宇航; 陆少锋; 梁进; 李基锐; 王尹军; 王天照; 陈智凡

doi:10.11858/gywlxb.20230684

基于正交试验法的气泡帷幕削波特性研究

doi: 10.11858/gywlxb.20230684

杜明燃^{1, 2,},
陈宇航¹,
陆少锋^{2, 3},
梁进^{2, 3},
李基锐^{2, 3},
王尹军⁴,
王天照¹,
陈智凡¹

1.
安徽理工大学化学工程学院, 安徽淮南　232001
2.
广西壮族自治区水下破岩工程研究中心, 广西南宁　530200
3.
广西新港湾工程有限公司, 广西南宁　530200
4.
矿冶科技集团有限公司, 北京　100160

基金项目: 安徽省高校科学研究项目（KJ2021A0431）；广西重点研发计划(桂科AB22035001)；安徽省自然科学基金（1908085QA33）；安徽理工大学引进人才科研启动基金（11881）

详细信息

作者简介:
杜明燃（1987－），男，博士，副教授，主要从事炸药性能和爆破技术研究. E-mail：dumingranaust@163.com

中图分类号: O389; TD235
计量
- 文章访问数: 127
- HTML全文浏览量: 42
- PDF下载量: 27
出版历程
- 收稿日期: 2023-06-20
- 修回日期: 2023-07-03
- 网络出版日期: 2023-11-26
- 刊出日期: 2023-12-15

Bubble Curtain Clipping Characteristics Based on Orthogonal Test Method

DU Mingran^{1, 2
,},
CHEN Yuhang¹,
LU Shaofeng^{2, 3},
LIANG Jin^{2, 3},
LI Jirui^{2, 3},
WANG Yinjun⁴,
WANG Tianzhao¹,
CHEN Zhifan¹

1.
School of Chemical Engineering, Anhui University of Science and Technology, Huainan 232001, Anhui, China
2.
Research Institution of Underwater Rock-Cutting Engineering at Guangxi Zhuang Autonomous Region, Nanning 530200, Guangxi, China
3.
Guangxi New Harbor Engineering Co., Ltd., Nanning 530200, Guangxi, China
4.
BGRIMM Technology Group, Beijing 100160, China

摘要

摘要: 气泡帷幕削波技术的影响因素众多。为了得到气泡帷幕在实际工程应用中的最佳组合方案，利用AUTODYN软件设计3因素3水平正交试验，以冲击波峰值压力的平均削减率作为评价指标，研究了气泡帷幕层数、气泡帷幕爆心距和药包深度对气泡帷幕削波效果的影响和敏感性。结果表明：气泡帷幕的削波能力存在极大值，此后继续增加气泡帷幕层数反而会出现负效应；气泡帷幕层数对气泡帷幕削波效应的影响最大，药包深度次之，气泡帷幕爆心距的影响最小；气泡帷幕爆心距越小，药包深度越大，气泡帷幕的削波效果越好；气泡帷幕层数为2层，气泡帷幕爆心距为1 m，药包深度为10.5 m时，削波效果最好。
- 水下爆炸 /
- 气泡帷幕 /
- 正交试验 /
- 峰值压力 /
- 敏感性
Abstract: There are many influencing factors of bubble curtain clipping technology. In order to obtain the optimal combination of bubble curtain in engineering applications, AUTODYN software was used to design a three factor and three level orthogonal test. The average reduction rate of shock wave peak pressure was used as an evaluation index to study the influence and sensitivity of the number of bubble curtain layers, the burst distance of the bubble curtain and the charge depth on the bubble curtain clipping effect. The results indicate that the clipping ability of the bubble curtain has a great value, and there will be a negative effect if the number of bubble curtain layers continues to increase. The number of bubble curtain layers has the greatest effect on the clipping ability, followed by the charge depth, and the effect of bubble curtain explosion center distance is the smallest. The smaller the burst center distance and the greater the depth of the packet, the better the bubble curtain chipping effect. When the number of bubble curtain layers is 2, the bubble curtain burst distance is 1 m, and the charge depth is 10.5 m, the clipping effect is the best.
- underwater explosion /
- bubble curtain /
- orthogonal test /
- peak pressure /
- sensitivity

HTML全文

图 1 数值计算模型示意图

Figure 1. Schematic diagram of the numerical simulation model

下载: 全尺寸图片幻灯片

图 2 气泡帷幕试验布局

Figure 2. Layout of the bubble curtain test

下载: 全尺寸图片幻灯片

图 3 设置1层气泡帷幕时测点C₁和C₂处的压力时程曲线

Figure 3. Shock wave pressure-time curves at measurement points C₁ and C₂ for one layer of bubble curtain

下载: 全尺寸图片幻灯片

图 4 无气泡帷幕时冲击波压力时程曲线

Figure 4. Time course curves of shock wave pressure without bubble curtain

下载: 全尺寸图片幻灯片

图 5 有气泡帷幕时的冲击波压力时程曲线

Figure 5. Time course curves of shock wave pressure with bubble curtain

下载: 全尺寸图片幻灯片

图 6 水平与指标的关系

Figure 6. Relationship between level and indicators

下载: 全尺寸图片幻灯片

表 1 炸药的材料参数

Table 1. Material parameters of explosive

ρ/(g·cm⁻³)	D/(km·s⁻¹)	p_C-J/GPa	A/GPa	B/GPa	R₁	R₂	ω	E/(kJ·g⁻¹)
1.30	4.5	9.80	214.4	0.182	4.15	0.95	0.15	4.19

下载: 导出CSV

表 2 水的材料参数

Table 2. Material parameters of water

ρ/(g·cm⁻³)	A₁/GPa	A₂/GPa	A₃/GPa	B₀	B₁	T₁/GPa	T₂/GPa	ω
1.000	2.2	9.54	14.57	0.28	0.28	2.2	0	0.150

下载: 导出CSV

表 3 不同气泡帷幕层数下水下爆炸冲击波峰值压力

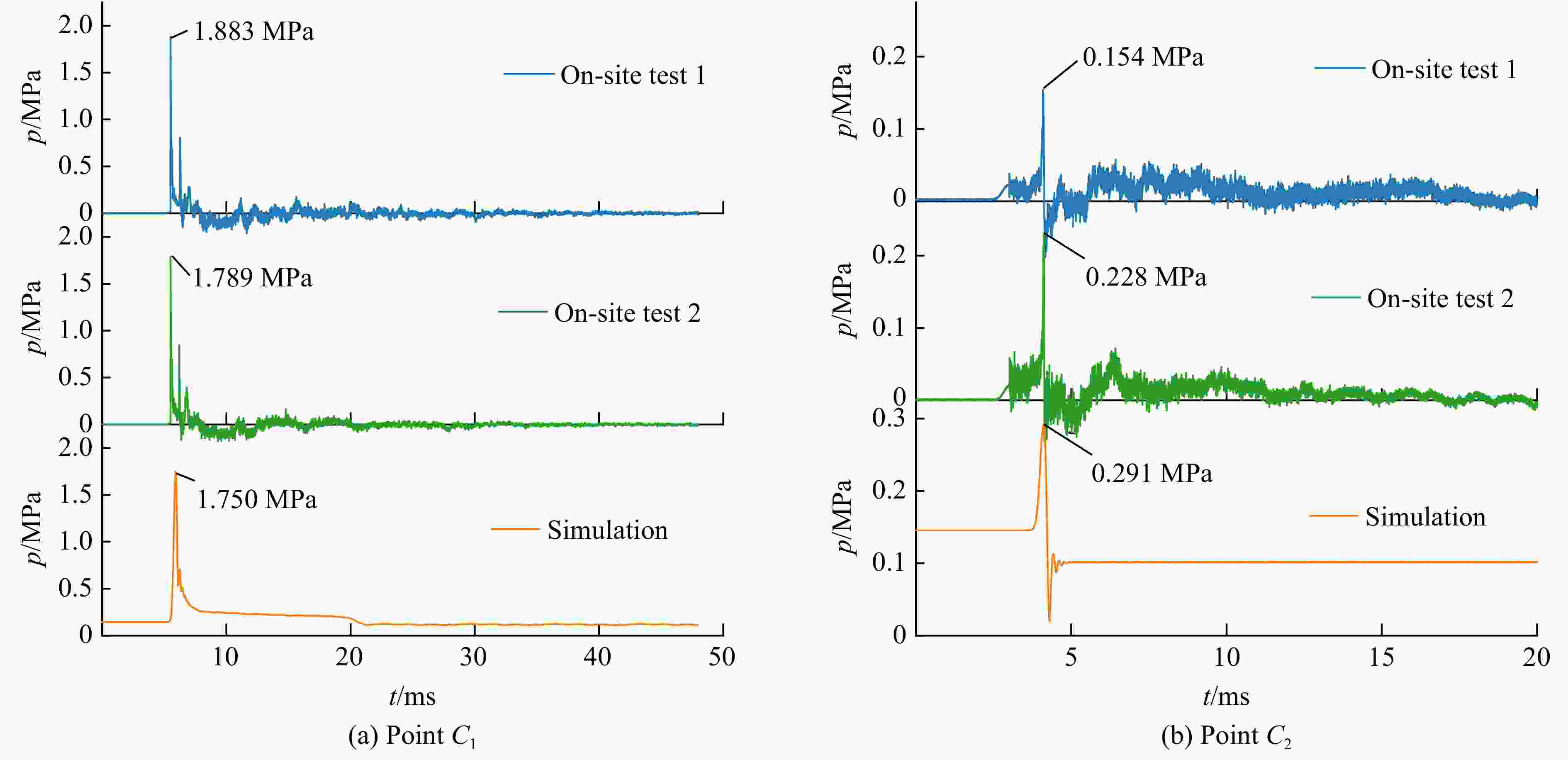
Table 3. Peak pressure of underwater blast shock wave for different bubble curtain layers

Test No.	N	On-site test			Simulation
		p_max/MPa		δ/%	p_max/MPa		δ/%
		C₁	C₂	δ/%	C₁	C₂	δ/%
1	1	1.883	0.154	91.82	1.750	0.291	83.37
2	1	1.789	0.228	87.26	1.750	0.291	83.37
3	2	1.675	0.157	90.63	1.750	0.116	93.37
4	2	1.486	0.108	92.73	1.750	0.116	93.37
5	3	1.862	0.247	86.73	1.750	0.248	85.83
6	3	1.764	0.196	88.89	1.750	0.248	85.83

下载: 导出CSV

表 4 正交试验设计因素和水平

Table 4. Orthogonal test design factors and levels

Level	Factor
Level	N	D/m	H/m
1	1	1	2.5
2	2	3	6.5
3	3	5	10.5

下载: 导出CSV

表 5 正交试验方案

Table 5. Orthogonal test protocols

No.	Level			Test programme	No.	Level			Test programme
No.	N	D	H	Test programme	No.	N	D	H	Test programme
1	1	1	1	A₁B₁C₁	6	2	3	1	A₂B₃C₁
2	1	2	2	A₁B₂C₂	7	3	1	3	A₃B₁C₃
3	1	3	3	A₁B₃C₃	8	3	2	1	A₃B₂C₁
4	2	1	2	A₂B₁C₂	9	3	3	2	A₃B₃C₂
5	2	2	3	A₂B₂C₃

下载: 导出CSV

表 6 空白对照组数据

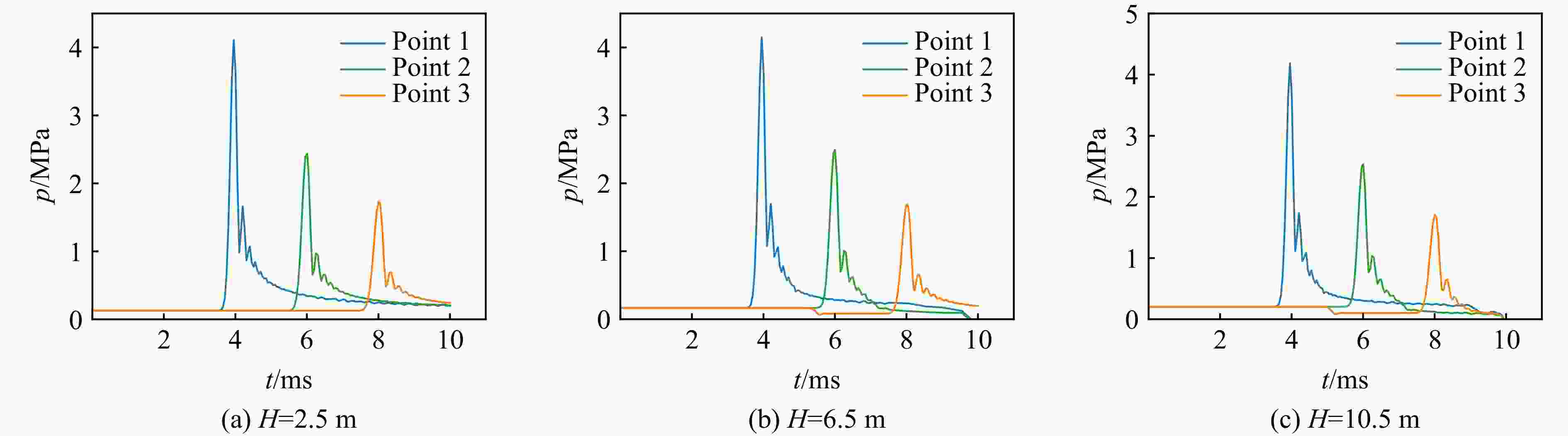
Table 6. Data of blank control group

No.	H/m	Point	p_max/MPa	t_p/ms	No.	H/m	Point	p_max/MPa	t_p/ms
1	2.5	1	4.108	3.952	3	10.5	1	4.187	3.954
		2	2.456	6.001			2	2.533	6.001
		3	1.531	8.006			3	1.708	8.002
2	6.5	1	4.148	3.954
		2	2.494	6.002
		3	1.688	8.016

下载: 导出CSV

表 7 正交试验数据

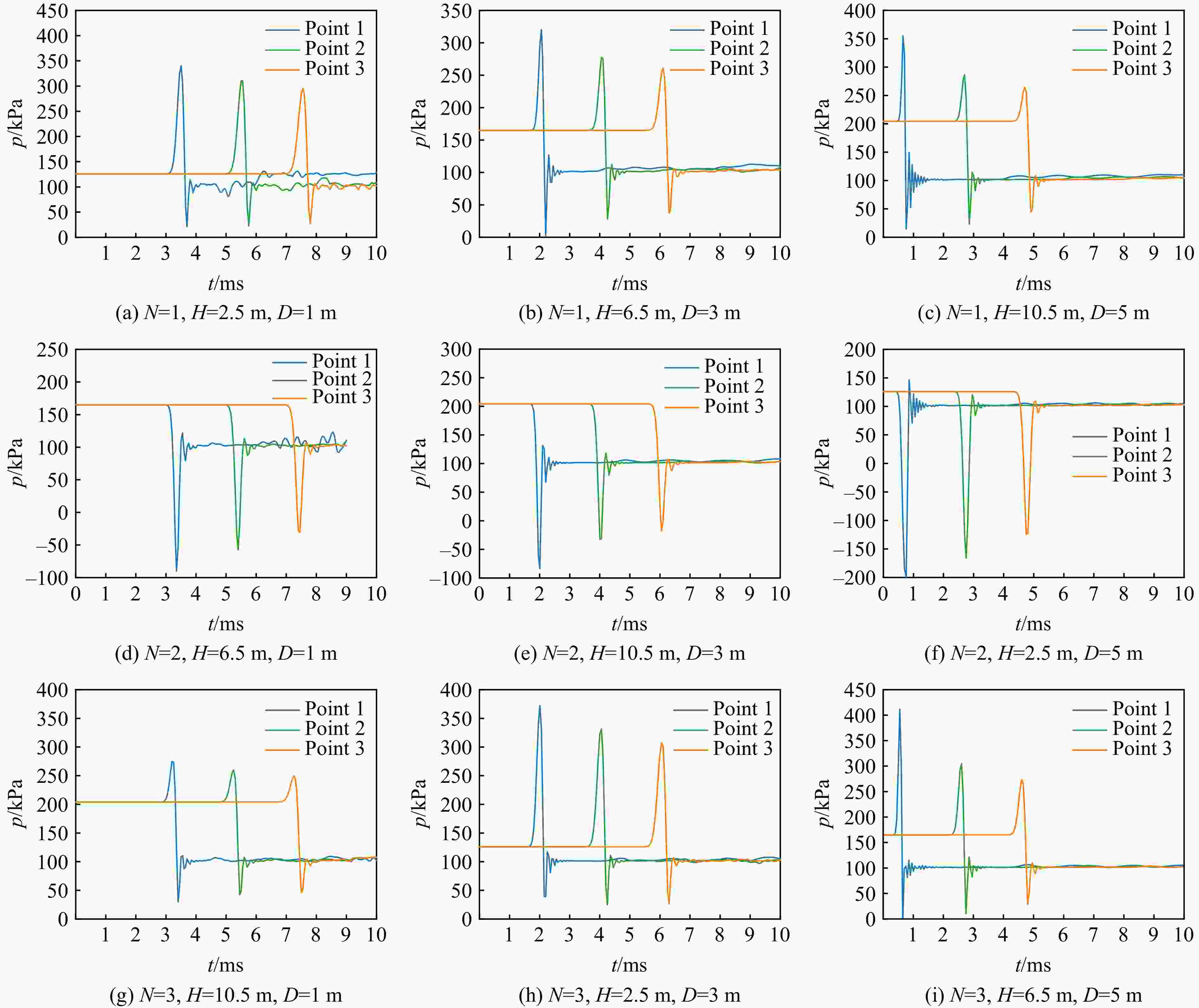
Table 7. Orthogonal test data

Test No.	Programme	N	D/m	H/m	p_max/MPa			δ/%
Test No.	Programme	N	D/m	H/m	Point 1	Point 2	Point 3	δ/%
1	A₁B₁C₁	1	1	2.5	0.341	0.314	0.295	86.55
2	A₁B₂C₂	1	3	6.5	0.320	0.278	0.261	88.56
3	A₁B₃C₃	1	5	10.5	0.355	0.286	0.264	88.26
4	A₂B₁C₂	2	1	6.5	0.122	0.113	0.106	95.42
5	A₂B₂C₃	2	3	10.5	0.132	0.118	0.107	95.31
6	A₂B₃C₁	2	5	2.5	0.146	0.121	0.109	94.80
7	A₃B₁C₃	3	1	10.5	0.275	0.260	0.250	89.51
8	A₃B₂C₁	3	3	2.5	0.372	0.332	0.308	85.77
9	A₃B₃C₂	3	5	6.5	0.412	0.305	0.274	87.20

下载: 导出CSV

表 8 极差分析结果

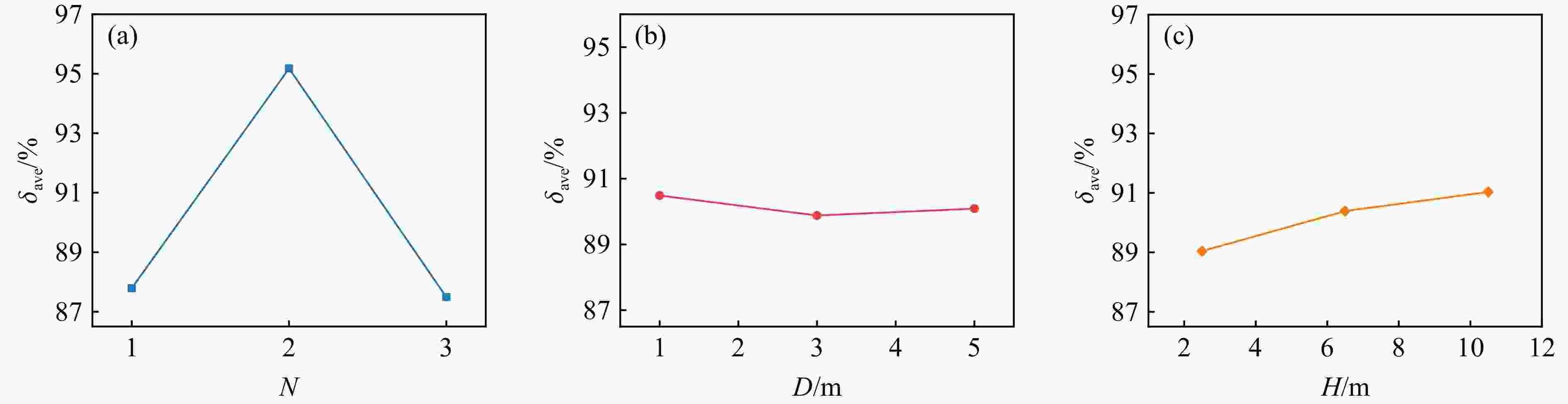
Table 8. Results of the variance analysis

Factor	K₁	K₂	K₃	k₁	k₂	k₃	R
N	263.37	285.53	262.48	87.79	95.18	87.49	7.68
D	271.48	269.64	270.26	90.49	89.88	90.09	0.61
H	267.12	271.18	273.08	89.04	90.39	91.03	1.99

下载: 导出CSV

表 9 方差分析结果

Table 9. Results of variance analysis

Sources of variance	S	f	$ \bar S $	F	Significance-effect
N	113.68	2	56.84	38.81	Yes
D	3.48	2	1.74	1.19	No
H	6.18	2	3.09	2.11	No
Error	2.93	2	1.46
Sum	126.27	8

下载: 导出CSV

参考文献(28)

[1]	高明涛, 李昕, 周晶. 水下钻孔爆破水中冲击波的数值模拟研究 [J]. 水电能源科学, 2009, 27(4): 138–141. doi: 10.3969/j.issn.1000-7709.2009.04.043 GAO M T, LI X, ZHOU J. Numerical simulation of shock wave in water of underwater drilling blasting [J]. Water Resources and Power, 2009, 27(4): 138–141. doi: 10.3969/j.issn.1000-7709.2009.04.043
[2]	杨建, 刘静, 张登泰, 等. 气泡帷幕对港口水域爆破波的削弱 [J]. 中国水运, 2020, 20(10): 90–92. YANG J, LIU J, ZHANG D T, et al. Weakening of blast waves in port waters by air bubble curtains [J]. China Water Transport, 2020, 20(10): 90–92.
[3]	司剑峰. 深水钻孔爆破的冲击波衰减规律及防护研究 [D]. 武汉: 武汉科技大学, 2021. SI J F. Research on attenuation law of shock wave and protection in deep-water drilling and blasting [D]. Wuhan: Wuhan University of Science and Technology, 2021.
[4]	俞统昌, 王晓峰, 王建灵. 炸药的水下爆炸冲击波性能 [J]. 含能材料, 2003, 11(4): 182–186. doi: 10.3969/j.issn.1006-9941.2003.04.002 YU T C, WANG X F, WANG J L. Underwater shockwave performance of explosives [J]. Energetic Materials, 2003, 11(4): 182–186. doi: 10.3969/j.issn.1006-9941.2003.04.002
[5]	伍俊, 杨益, 庄铁栓. 水中爆炸作用机理及毁伤效应研究综述 [J]. 火炸药学报, 2016, 39(1): 1–13. doi: 10.14077/j.issn.1007-7812.2016.01.001 WU J, YANG Y, ZHUANG T S. A review of research on action mechanism and damage effect of underwater explosion [J]. Chinese Journal of Explosives & Propellants, 2016, 39(1): 1–13. doi: 10.14077/j.issn.1007-7812.2016.01.001
[6]	陈岩武, 孙远翔, 王成. 水下爆炸载荷下舰船双层底部结构的毁伤特性 [J]. 兵工学报, 2023, 44(3): 670–681. doi: 10.12382/bgxb.2022.0390 CHEN Y W, SUN Y X, WANG C. Damage characteristics of ship’s double bottom structure subjected to underwater explosion [J]. Acta Armamentarii, 2023, 44(3): 670–681. doi: 10.12382/bgxb.2022.0390
[7]	赵为, 梁作民, 郭成喜. 水下近场爆破安全控制 [J]. 水运工程, 2007, 33(9): 159–164. doi: 10.3969/j.issn.1002-4972.2007.09.038 ZHAO W, LIANG Z M, GUO C X. Safety control of underwater near-site explosion [J]. Port & Waterway Engineering, 2007, 33(9): 159–164. doi: 10.3969/j.issn.1002-4972.2007.09.038
[8]	张轶凡, 刘亮涛, 王金相, 等. 水下爆炸冲击波和气泡载荷对典型圆柱壳结构的毁伤特性 [J]. 兵工学报, 2023, 44(2): 345–359. doi: 10.12382/bgxb.2021.0598 ZHANG Y F, LIU L T, WANG J X, et al. Damage characteristics of underwater explosion shock wave and bubble load on typical cylindrical shell structure [J]. Acta Armamentarii, 2023, 44(2): 345–359. doi: 10.12382/bgxb.2021.0598
[9]	王高辉, 高政, 卢文波, 等. 考虑初始应力的混凝土重力坝水下爆炸毁伤特性研究 [J]. 振动与冲击, 2022, 41(11): 133–140. doi: 10.13465/j.cnki.jvs.2022.11.017 WANG G H, GAO Z, LU W B, et al. Damage characteristics of underwater explosion of concrete gravity dam considering initial stress [J]. Journal of Vibration and Shock, 2022, 41(11): 133–140. doi: 10.13465/j.cnki.jvs.2022.11.017
[10]	张志波, 李春军, 李红勇, 等. 气泡帷幕在水下爆破减震工程中的应用 [J]. 爆破, 2003, 20(2): 75–76, 89. doi: 10.3963/j.issn.1001-487X.2003.02.028 ZHANG Z B, LI C J, LI H Y, et al. Application of air bubble purdah in the damping measure in the underwater blasting [J]. Blasting, 2003, 20(2): 75–76, 89. doi: 10.3963/j.issn.1001-487X.2003.02.028
[11]	刘欣, 顾文彬, 陈学平. 气泡帷幕对水中冲击波衰减特性的数值模拟研究 [J]. 爆破, 2015, 32(3): 79–84. doi: 10.3963/j.issn.1001-487X.2015.03.014 LIU X, GU W B, CHEN X P. Numerical simulation study of attenuation characteristics of water shock wave under bubble curtain [J]. Blasting, 2015, 32(3): 79–84. doi: 10.3963/j.issn.1001-487X.2015.03.014
[12]	胡伟才, 吴立, 舒利, 等. 不同设置方式下气泡帷幕对水中冲击波衰减特性的影响 [J]. 科学技术与工程, 2018, 18(17): 33–38. doi: 10.3969/j.issn.1671-1815.2018.17.006 HU W C, WU L, SHU L, et al. Influence of water shock wave on attenuation characteristics under bubble curtain with different settings [J]. Science Technology and Engineering, 2018, 18(17): 33–38. doi: 10.3969/j.issn.1671-1815.2018.17.006
[13]	李泽华, 白春华, 刘庆明, 等. 气泡帷幕减弱水中冲击波强度的研究 [J]. 中国安全科学学报, 1999, 10(5): 72–76. doi: 10.16265/j.cnki.issn1003-3033.1999.05.015 LI Z H, BAI C H, LIU Q M, et al. Study on weakening the shock wave in water by bubble heavy curtain [J]. China Safety Science Journal, 1999, 10(5): 72–76. doi: 10.16265/j.cnki.issn1003-3033.1999.05.015
[14]	谢达建, 吴立, 洪江, 等. 气泡帷幕对水下爆破冲击波的削弱作用研究 [J]. 人民长江, 2018, 49(8): 72–77. doi: 10.16232/j.cnki.1001-4179.2018.08.014 XIE D J, WU L, HONG J, et al. Study on weakening effect of bubble curtain on water shock wave in underwater blasting [J]. Yangtze River, 2018, 49(8): 72–77. doi: 10.16232/j.cnki.1001-4179.2018.08.014
[15]	陆少锋, 梁进, 覃才勇, 等. 供风量对水下爆炸冲击波气泡帷幕消波效应的影响 [J]. 工程爆破, 2022, 28(5): 143–148. doi: 10.19931/j.EB.20210013 LU S F, LIANG J, QIN C Y, et al. Influence of air supply rate on wave attenuation effect of bubble curtain for underwater explosion shock wave [J]. Engineering Blasting, 2022, 28(5): 143–148. doi: 10.19931/j.EB.20210013
[16]	胡亮亮, 黄瑞源, 李世超, 等. 水下爆炸冲击波数值仿真研究 [J]. 高压物理学报, 2020, 34(1): 015102. doi: 10.11858/gywlxb.20190773 HU L L, HUANG R Y, LI S C, et al. Shock wave simulation of underwater explosion [J]. Chinese Journal of High Pressure Physics, 2020, 34(1): 015102. doi: 10.11858/gywlxb.20190773
[17]	刘世聪, 王秋生, 娄浩然. 装药深度及空气域尺寸对水下爆炸的影响分析 [J]. 水下无人系统学报, 2019, 27(6): 664–672. doi: 10.11993/j.issn.2096-3920.2019.06.010 LIU S C, WANG Q S, LOU H R. Effects of charge depth and air domain size on underwater explosion [J]. Journal of Unmanned Undersea Systems, 2019, 27(6): 664–672. doi: 10.11993/j.issn.2096-3920.2019.06.010
[18]	黄洪, 卢熹, 王健. 柱形装药水下爆炸近场冲击波数值仿真 [J]. 水下无人系统学报, 2021, 29(4): 471–476. doi: 10.11993/j.issn.2096-3920.2021.04.015 HUANG H, LU X, WANG J. Near field shock wave numerical simulation of cylindrical charge underwater explosion [J]. Journal of Unmanned Undersea Systems, 2021, 29(4): 471–476. doi: 10.11993/j.issn.2096-3920.2021.04.015
[19]	鲁天龙. 气泡帷幕周围流场运动特性数值模拟研究 [D]. 长沙: 长沙理工大学, 2020. LU T L. Numerical simulation of flow field motion characteristics around bubble curtain [D]. Changsha: Changsha University of Technology, 2020.
[20]	王思, 胡晶, 张雪东, 等. 不同水深水下爆炸数值及离心试验研究 [J]. 哈尔滨工业大学学报, 2020, 52(6): 78–84. doi: 10.11918/202001082 WANG S, HU J, ZHANG X D, et al. Numerical analysis and centrifugal test of underwater explosion effect at different water depths [J]. Journal of Harbin Institute of Technology, 2020, 52(6): 78–84. doi: 10.11918/202001082
[21]	盛振新, 刘荣忠, 郭锐. 壳体厚度和爆炸深度对水下爆炸冲击波的影响 [J]. 火炸药学报, 2011, 34(3): 45–47, 64. doi: 10.3969/j.issn.1007-7812.2011.03.012 SHENG Z X, LIU R Z, GUO R. Effect of shell thickness and explosion depth on underwater explosive shock wave [J]. Chinese Journal of Explosives & Propellants, 2011, 34(3): 45–47, 64. doi: 10.3969/j.issn.1007-7812.2011.03.012
[22]	陈兴, 周兰伟, 李福明, 等. 爆炸深度对装药水下载荷的影响 [J]. 兵器装备工程学报, 2021, 42(8): 79–84. doi: 10.11809/bqzbgcxb2021.08.013 CHEN X, ZHOU L W, LI F M, et al. Research on influence of depth of charge on underwater explosion load [J]. Journal of Ordnance Equipment Engineering, 2021, 42(8): 79–84. doi: 10.11809/bqzbgcxb2021.08.013
[23]	尹岳降, 李瑞泽, 陈明, 等. 基于正交试验法的爆破块度分布影响因素敏感性分析 [J]. 爆破, 2019, 36(4): 37–42. doi: 10.3963/j.issn.1001-487X.2019.04.005 YIN Y J, LI R Z, CHEN M, et al. Sensitivity analysis of influencing factors of blasting fragmentation distribution based on orthogonal experiment method [J]. Blasting, 2019, 36(4): 37–42. doi: 10.3963/j.issn.1001-487X.2019.04.005
[24]	张世豪, 韩晶, 焦国太, 等. 单个装药混凝土爆破毁伤效果敏感性分析 [J]. 工程爆破, 2014, 20(3): 5–9. doi: 10.3969/j.issn.1006-7051.2014.03.002 ZHANG S H, HAN J, JIAO G T, et al. Sensitivity analysis of blasting damage effect in concrete based on single charge [J]. Engineering Blasting, 2014, 20(3): 5–9. doi: 10.3969/j.issn.1006-7051.2014.03.002
[25]	史秀志, 王怀勇, 刘金明, 等. 基于粗糙集的影响爆破振动特征参量因素的敏感性分析 [J]. 爆破器材, 2009, 38(2): 1–4, 7. doi: 10.3969/j.issn.1001-8352.2009.02.001. SHI X Z, WANG H Y, LIU J M, et al. Sensitivity analysis of the factors impact of blasting vibration characteristic parameters based on rough set theory [J]. Explosive Materials, 2009, 38(2): 1–4, 7. doi: 10.3969/j.issn.1001-8352.2009.02.001.
[26]	胡玉林, 姜俊杰, 罗健琛, 等. 基于多因素方差分析探究灌水施肥量对番茄产量的影响 [J]. 浙江农业科学, 2023, 64(5): 1042–1045. doi: 10.16178/j.issn.0528-9017.20230126 HU Y L, JIANG J J, LUO J C, et al. Exploring the effect of irrigation and fertilizer application on tomato yield based on multi-factor analysis of variance [J]. Journal of Zhejiang Agricultural Sciences, 2023, 64(5): 1042–1045. doi: 10.16178/j.issn.0528-9017.20230126
[27]	刘世涛, 郝兵元, 杨冉, 等. 基于方差分析法坚硬顶板下矿压显现分析 [J]. 煤炭技术, 2022, 41(7): 20–23. doi: 10.13301/j.cnki.ct.2022.07.005 LIU S T, HAO B Y, YANG R, et al. Analysis of mineral pressure under rigid top plate based on variance analysis [J]. Coal Technology, 2022, 41(7): 20–23. doi: 10.13301/j.cnki.ct.2022.07.005
[28]	王志建, 龙顺忠, 李颖宏. 基于正交试验的感应控制参数组合优化 [J]. 浙江大学学报(工学版), 2023, 57(6): 1128–1136. doi: 10.3785/j.issn.1008-973X.2023.06.008 WANG Z J, LONG S Z, LI Y H. Combination optimization of induction control parameters based on orthogonal test [J]. Journal of Zhejiang University (Engineering Science), 2023, 57(6): 1128–1136. doi: 10.3785/j.issn.1008-973X.2023.06.008