Numerical Simulation of Magnetically Driven Sample Experiment
-
摘要: 采用二维磁驱动数值模拟程序对磁驱动样品实验进行了模拟研究。数值模拟结果表明，二维磁驱动数值模拟程序模拟的样品/窗口界面速度（或飞片/窗口界面速度）与实验测量速度基本一致。磁驱动样品实验的结构系数与样品材料、阴阳极之间的初始间隙、电极板宽度等负载初始结构相关，不随磁驱动样品实验的演化过程而改变。样品材料不同，结构系数不同。对于同一样品材料，在其他初始条件相同的情况下，电极板越宽，结构系数越大。二维磁驱动数值模拟程序能够正确模拟磁驱动样品实验，是磁驱动样品物性研究的重要工具。
-
关键词:
- 二维磁驱动数值模拟程序 /
- 磁驱动样品实验 /
- 磁流体力学 /
- 结构系数
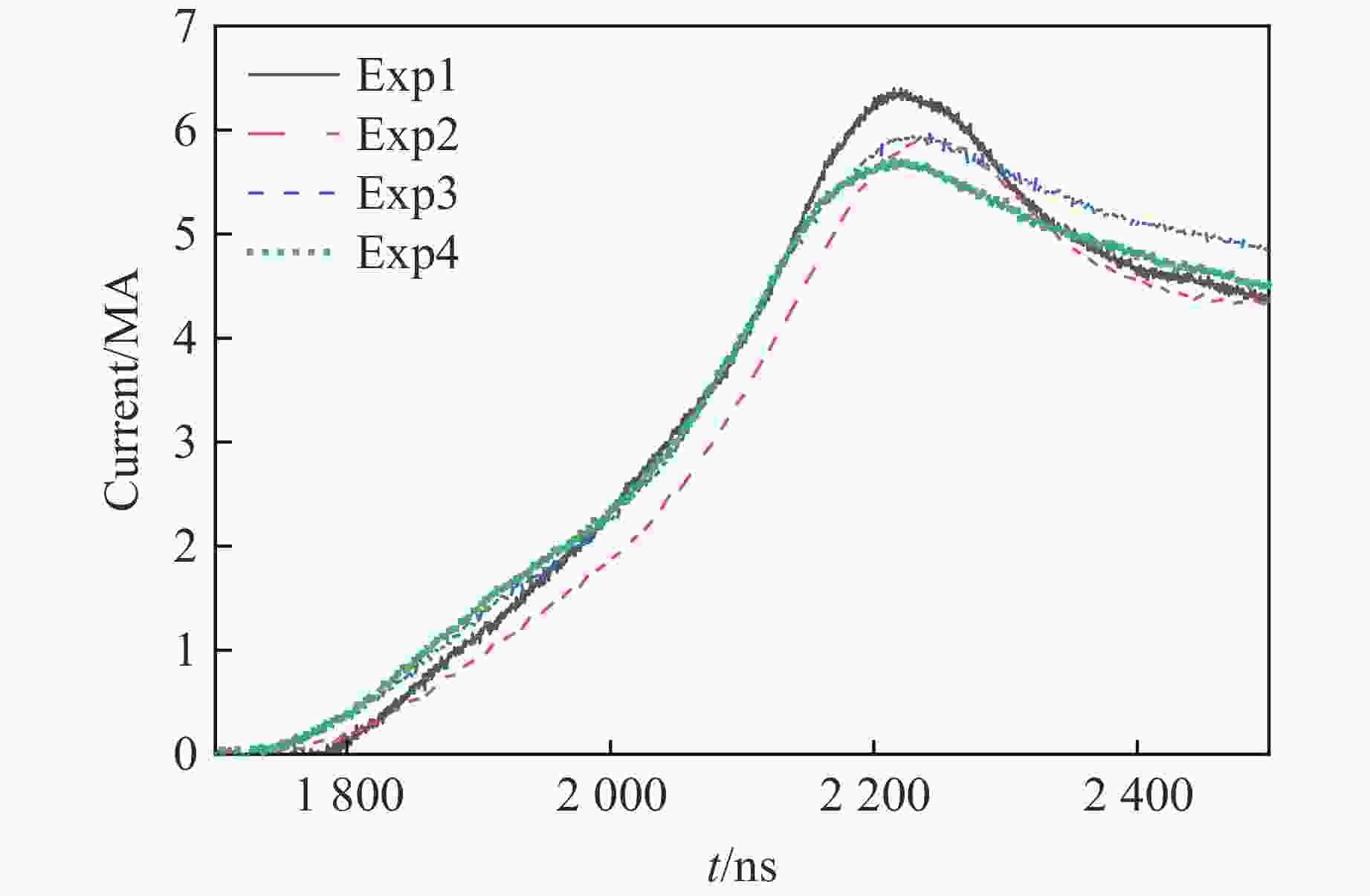
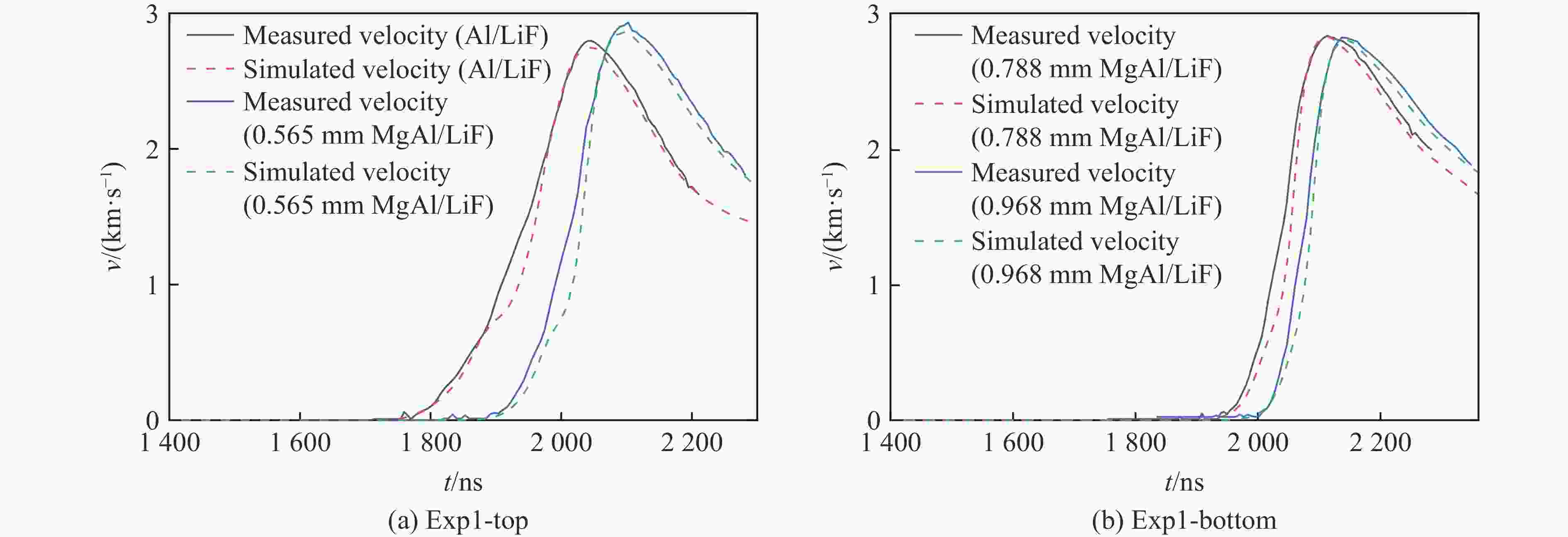
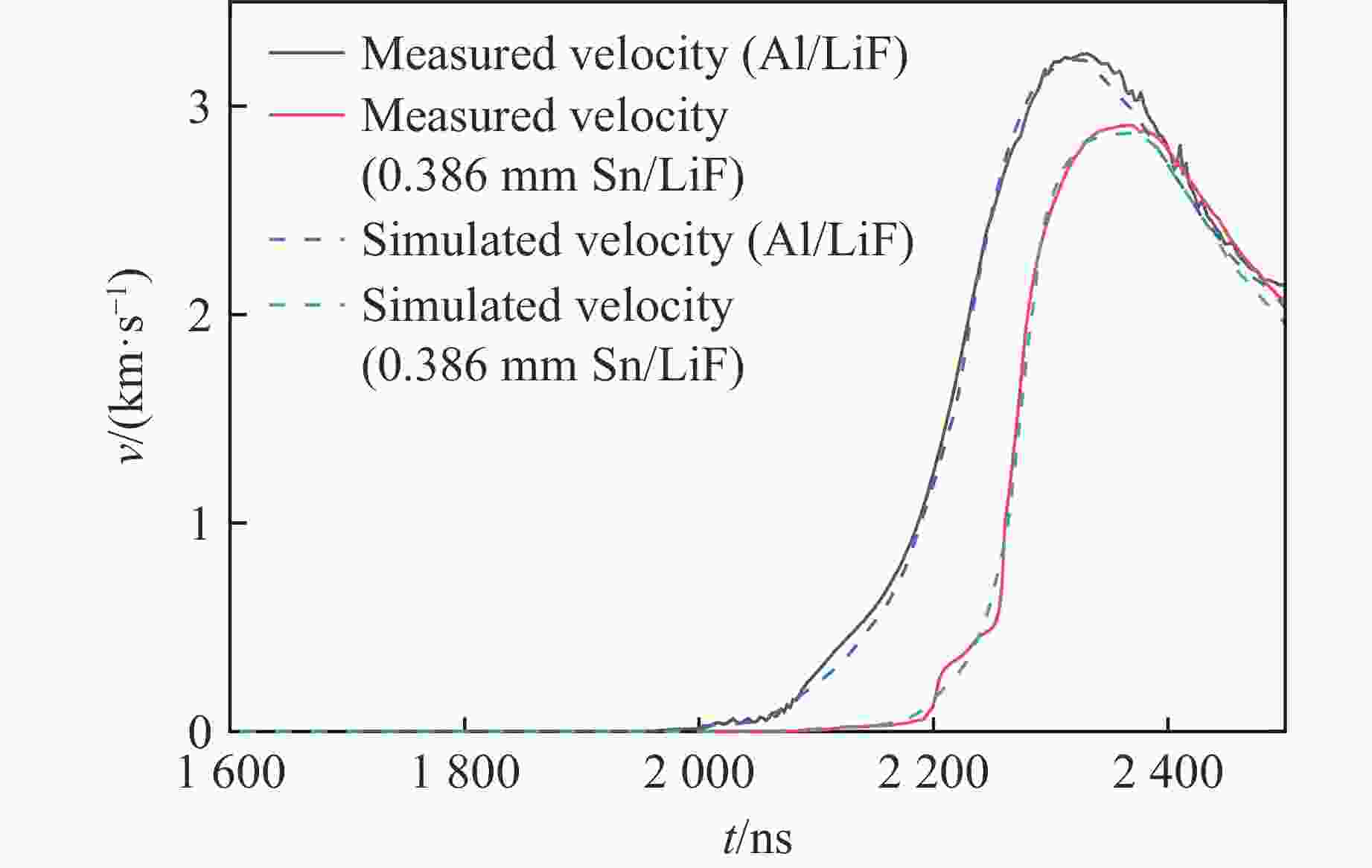
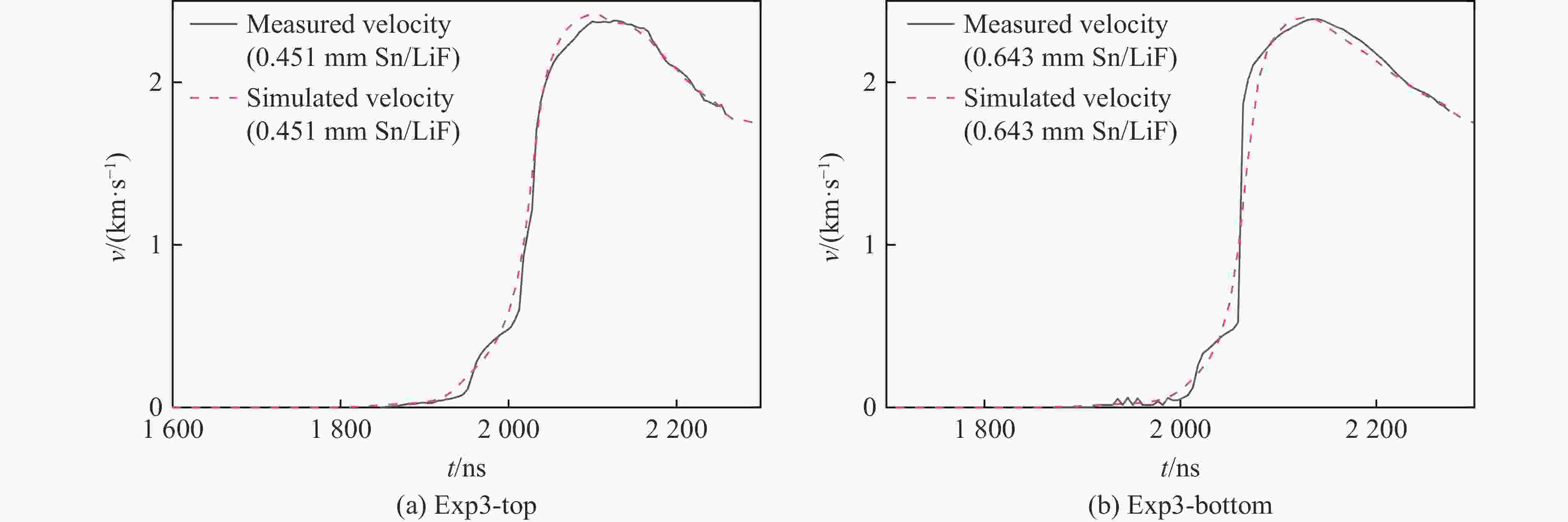
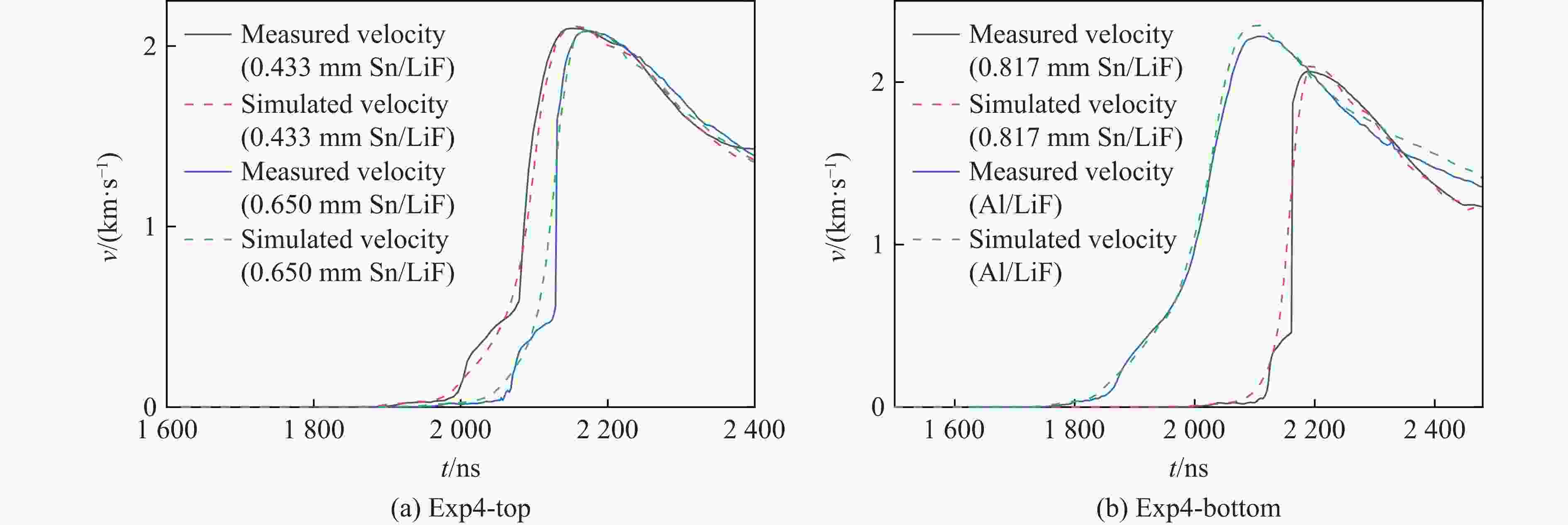
Abstract: The magnetically driven sample experiments which were carried out in an intense pulsed power device were simulated and analyzed by two-dimensional magnetically driven simulation code (MDSC2), and the structure coefficient of magnetically driven sample experiments was studied and analyzed. The numerical results show that MDSC2 can correctly simulate experiments of magnetically driven samples such as tin and magnesium-aluminum alloy. The simulated sample/window interface velocity (or flyer plate/window interface velocity) is basically consistent with the experimental measured one. The structure coefficients of magnetically driven samples are usually different when the magnetically driven sample experiments are different. The structure coefficient of magnetically driven sample experiment is related to the initial conditions such as the sample material and the width of the electrode plate but not to the initial thickness of the sample material. Under the same initial conditions, such as the thickness of the flyer plate, the material of the flyer plate, the material of the sample, the initial gap between the cathode and the anode, the wider the electrode plate, the larger the structure coefficient of the magnetic drive sample experiment. MDSC2 can correctly simulate the magnetically driven sample experiments, which makes MDSC2 an important tool for the study of magnetically driven sample experiments. -
图 1 磁驱动样品实验负载结构示意图
Figure 1. Load configuration of magnetically driven sample experiments
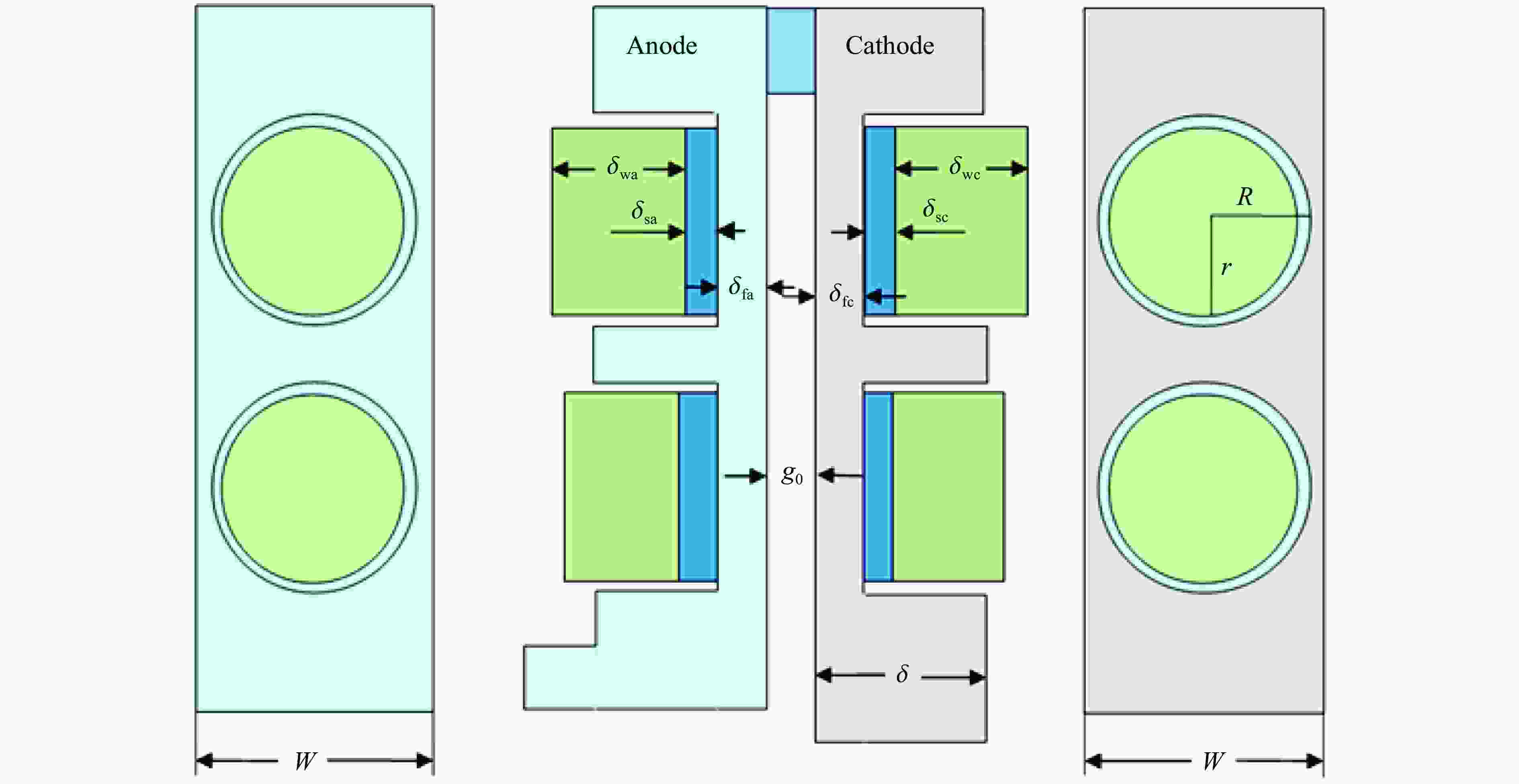
表 1 磁驱动样品实验负载参数
Table 1. Load parameters for magnetically driven sample experiments
Exp. No. Sample material δfa/mm δsa/mm δwa/mm δfc/mm δsc/mm δwc/mm g0/mm W/mm Exp1-top MgAl 0.970 0 8 0.983 0.565 8 1.200 13 Exp1-bottom MgAl 0.984 0.968 8 0.988 0.788 8 1.200 13 Exp2-top Sn 1.000 0.386 8 1.000 0 8 1.200 11 Exp2-bottom Sn 1.000 0.386 8 1.000 0 8 1.200 11 Exp3-top Sn 0.993 0.417 8 0.990 0.451 8 1.200 13 Exp3-bottom Sn 0.993 0 8 0.990 0.643 8 1.200 13 Exp4-top Sn 0.995 0.433 8 0.998 0.650 8 1.175 15 Exp4-bottom Sn 0.990 0.817 8 0.991 0 8 1.175 15 
下载: 导出CSV
表 2 磁驱动样品实验的结构系数
Table 2. Structure coefficients of magnetically driven sample experiments
Exp. No. Sample material δsa/mm δsc/mm g0/mm W/mm f Exp1-top MgAl 0 0.565 1.200 13 0.78 Exp1-bottom MgAl 0.968 0.788 1.200 13 0.78 Exp2-top Sn 0.386 0 1.200 11 0.84 Exp2-bottom Sn 0.386 0 1.200 11 0.84 Exp3-top Sn 0.417 0.451 1.200 13 0.85 Exp3-bottom Sn 0 0.643 1.200 13 0.85 Exp4-top Sn 0.433 0.650 1.175 15 0.88 Exp4-bottom Sn 0.817 0 1.175 15 0.88
下载: 导出CSV
-
[1] KNUDSON M D, HANSON D L, BAILEY J E, et al. Equation of state measurements in liquid deuterium to 70 GPa [J]. Physical Review Letters, 2001, 87(22): 225501. doi: 10.1103/PhysRevLett.87.225501 [2] KNUDSON M D, LEMKE R W, HAYES D B, et al. Near-absolute Hugoniot measurements in aluminum to 500 GPa using a magnetically accelerated flyer plate technique [J]. Journal of Applied Physics, 2003, 94(7): 4420–4431. doi: 10.1063/1.1604967 [3] KNUDSON M D, HANSON D L, BAILEY J E, et al. Use of a wave reverberation technique to infer the density compression of shocked liquid deuterium to 75 GPa [J]. Physical Review Letters, 2003, 90(3): 035505. doi: 10.1103/PhysRevLett.90.035505 [4] KNUDSON M D, HANSON D L, BAILEY J E, et al. Principal Hugoniot, reverberating wave, and mechanical reshock measurements of liquid deuterium to 400 GPa using plate impact techniques [J]. Physical Review B, 2004, 69(14): 144209. doi: 10.1103/PhysRevB.69.144209 [5] LEMKE R W, KNUDSON M D, BLISS D E, et al. Magnetically accelerated, ultrahigh velocity flyer plates for shock wave experiments [J]. Journal of Applied Physics, 2005, 98(7): 073530. doi: 10.1063/1.2084316 [6] VOGLER T J, AO T, ASAY J R. High-pressure strength of aluminum under quasi-isentropic loading [J]. International Journal of Plasticity, 2009, 25(4): 671–694. doi: 10.1016/j.ijplas.2008.12.003 [7] REISMAN D B, TOOR A, CAUBLE R C, et al. Magnetically driven isentropic compression experiments on the Z accelerator [J]. Journal of Applied Physics, 2001, 89(3): 1625–1633. doi: 10.1063/1.1337082 [8] LEMKE R W, KNUDSON M D, HALL C A, et al. Characterization of magnetically accelerated flyer plates [J]. Physics of Plasmas, 2003, 10(4): 1092–1099. doi: 10.1063/1.1554740 [9] LEMKE R W, KNUDSON M D, DAVIS J P. Magnetically driven hyper-velocity launch capability at the Sandia Z accelerator [J]. International Journal of Impact Engineering, 2011, 38(6): 480–485. doi: 10.1016/j.ijimpeng.2010.10.019 [10] DAVIS J P, BROWN J L, KNUDSON M D, et al. Analysis of shockless dynamic compression data on solids to multi-megabar pressures: application to tantalum [J]. Journal of Applied Physics, 2014, 116(20): 204903. doi: 10.1063/1.4902863 [11] KAN M X, ZHANG Z H, XIAO B, et al. Simulation of magnetically driven flyer plate experiments with an improved magnetic field boundary formula [J]. High Energy Density Physics, 2018, 26: 38–43. doi: 10.1016/j.hedp.2017.12.002 [12] 阚明先, 蒋吉昊, 王刚华, 等. 衬套内爆ALE方法二维MHD数值模拟 [J]. 四川大学学报(自然科学版), 2007, 44(1): 91–96. doi: 10.3969/j.issn.0490-6756.2007.01.020KAN M X, JIANG J H, WANG G H, et al. ALE simulation of 2D MHD for liner [J]. Journal of Sichuan University (Natural Science Edition), 2007, 44(1): 91–96. doi: 10.3969/j.issn.0490-6756.2007.01.020 [13] 阚明先, 王刚华, 赵海龙, 等. 磁驱动飞片二维磁流体力学数值模拟 [J]. 强激光与粒子束, 2013, 25(8): 2137–2141. doi: 10.3788/HPLPB20132508.2137KAN M X, WANG G H, ZHAO H L, et al. Two-dimensional magneto-hydrodynamic simulations of magnetically accelerated flyer plates [J]. High Power Laser and Particle Beams, 2013, 25(8): 2137–2141. doi: 10.3788/HPLPB20132508.2137 [14] 杨龙, 李平, 王刚华, 等. 固体套筒内爆非冲击压缩研究 [J]. 高压物理学报, 2016, 30(4): 344–352. doi: 10.11858/gywlxb.2016.04.012YANG L, LI P, WANG G H, et al. Research on the shockless compression of the solid liner implosion [J]. Chinese Journal of High Pressure Physics, 2016, 30(4): 344–352. doi: 10.11858/gywlxb.2016.04.012 [15] 阚明先, 王刚华, 刘利新, 等. 带窗口磁驱动准等熵压缩实验模拟 [J]. 强激光与粒子束, 2021, 33(5): 055001. doi: 10.11884/HPLPB202133.200329KAN M X, WANG G H, LIU L X, et al. Simulation of magnetically driven quasi-isentropic compression experiments with windows [J]. High Power Laser and Particle Beams, 2021, 33(5): 055001. doi: 10.11884/HPLPB202133.200329 -
下载:
点击查看大图
图(6) / 表(2)
计量
- 文章访问数: 166
- HTML全文浏览量: 89
- PDF下载量: 37
