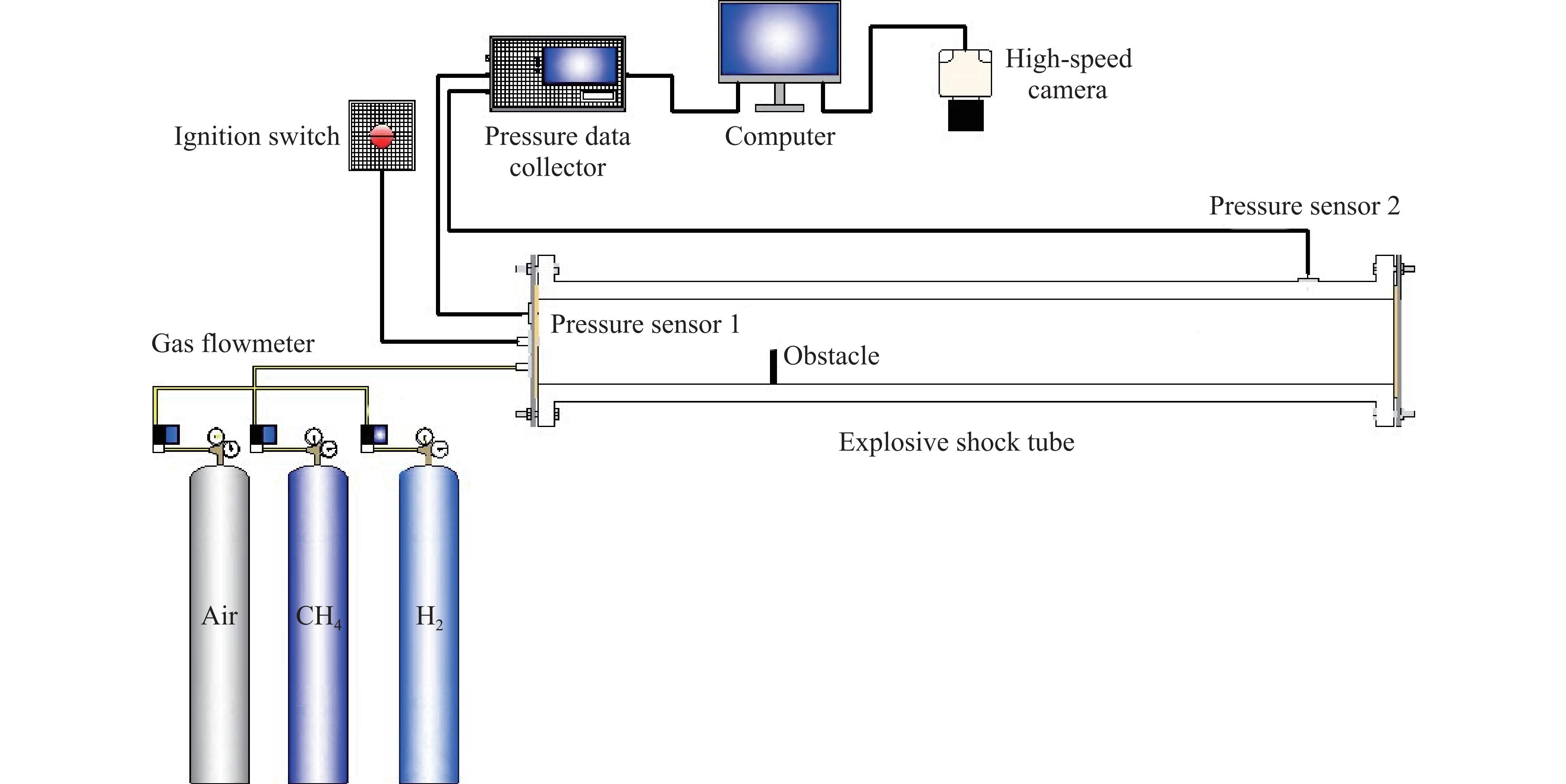
Effect of Various Material Obstacles on the Promoting Explosion of Methane-Hydrogen Premixed Gas
-
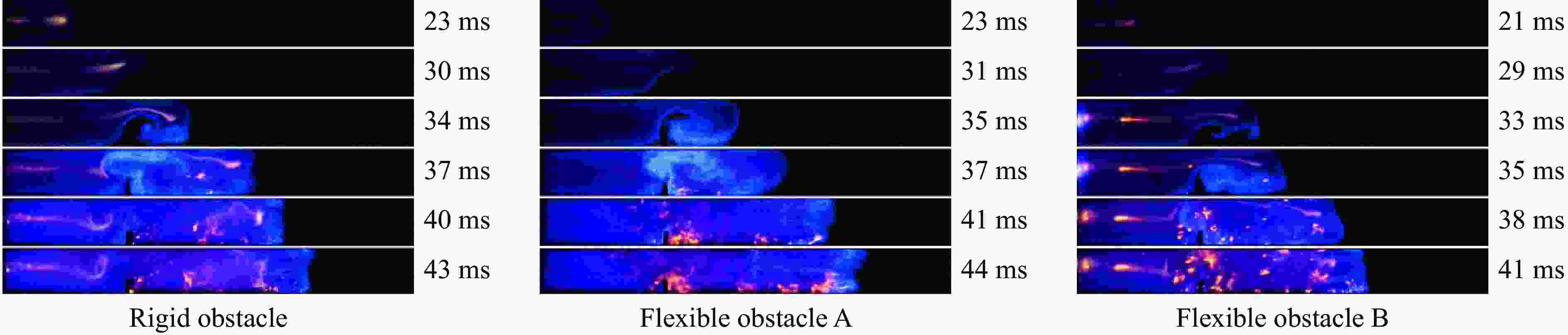
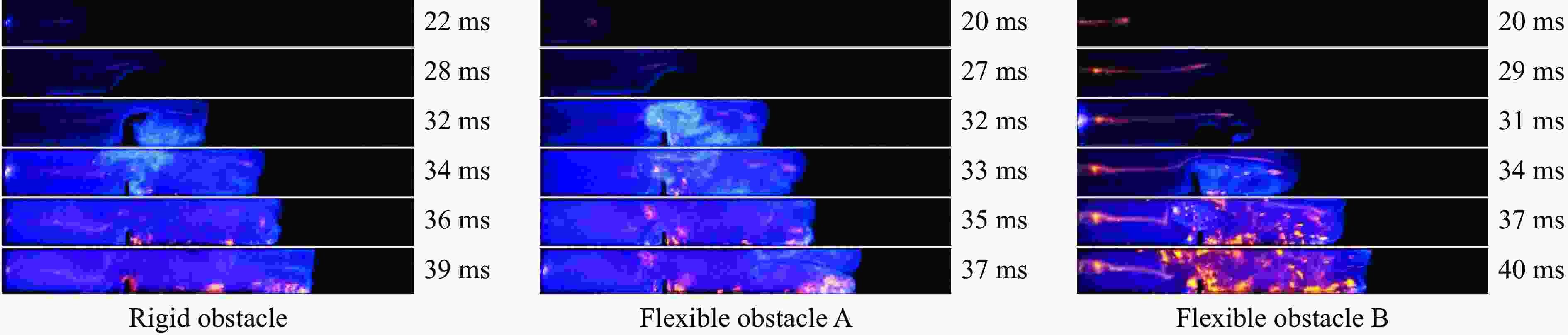
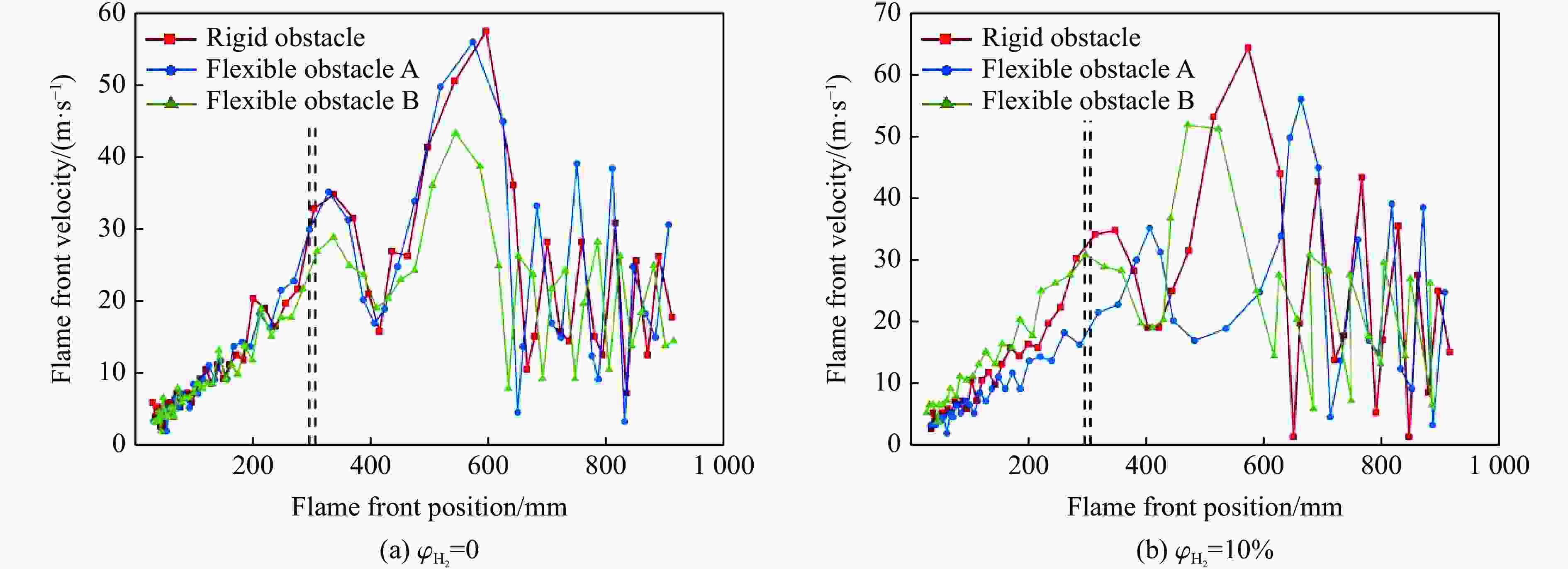
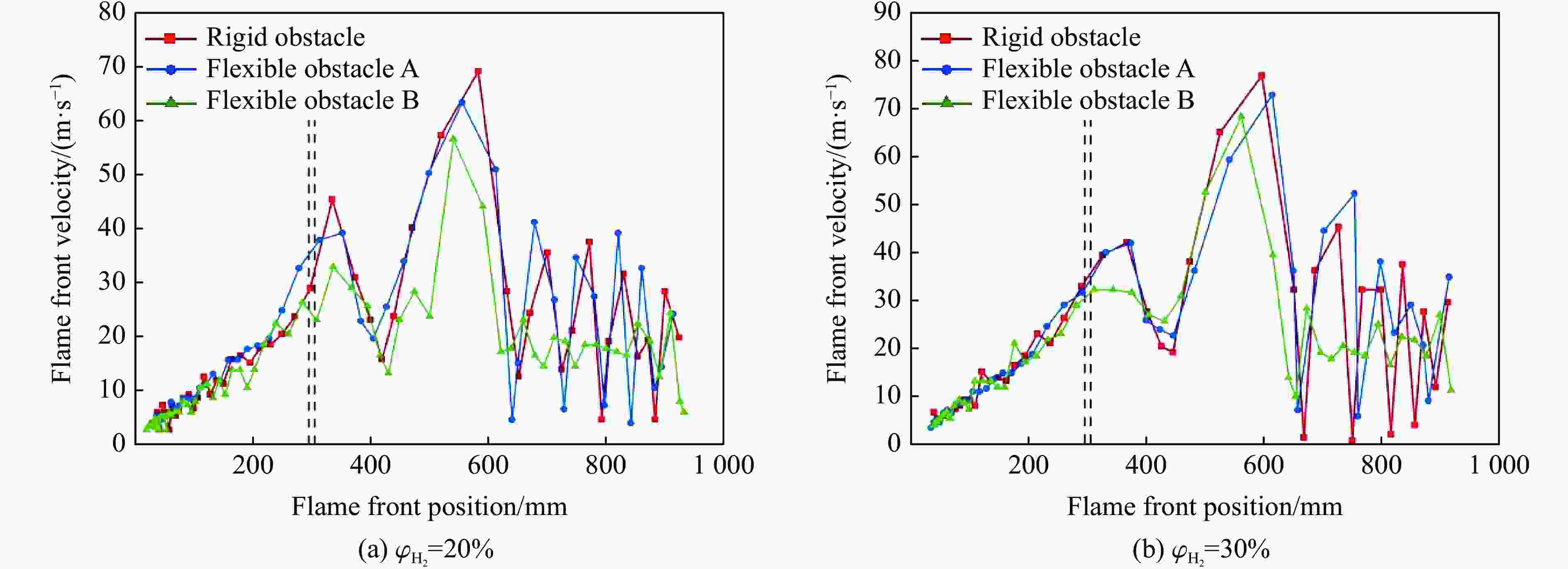
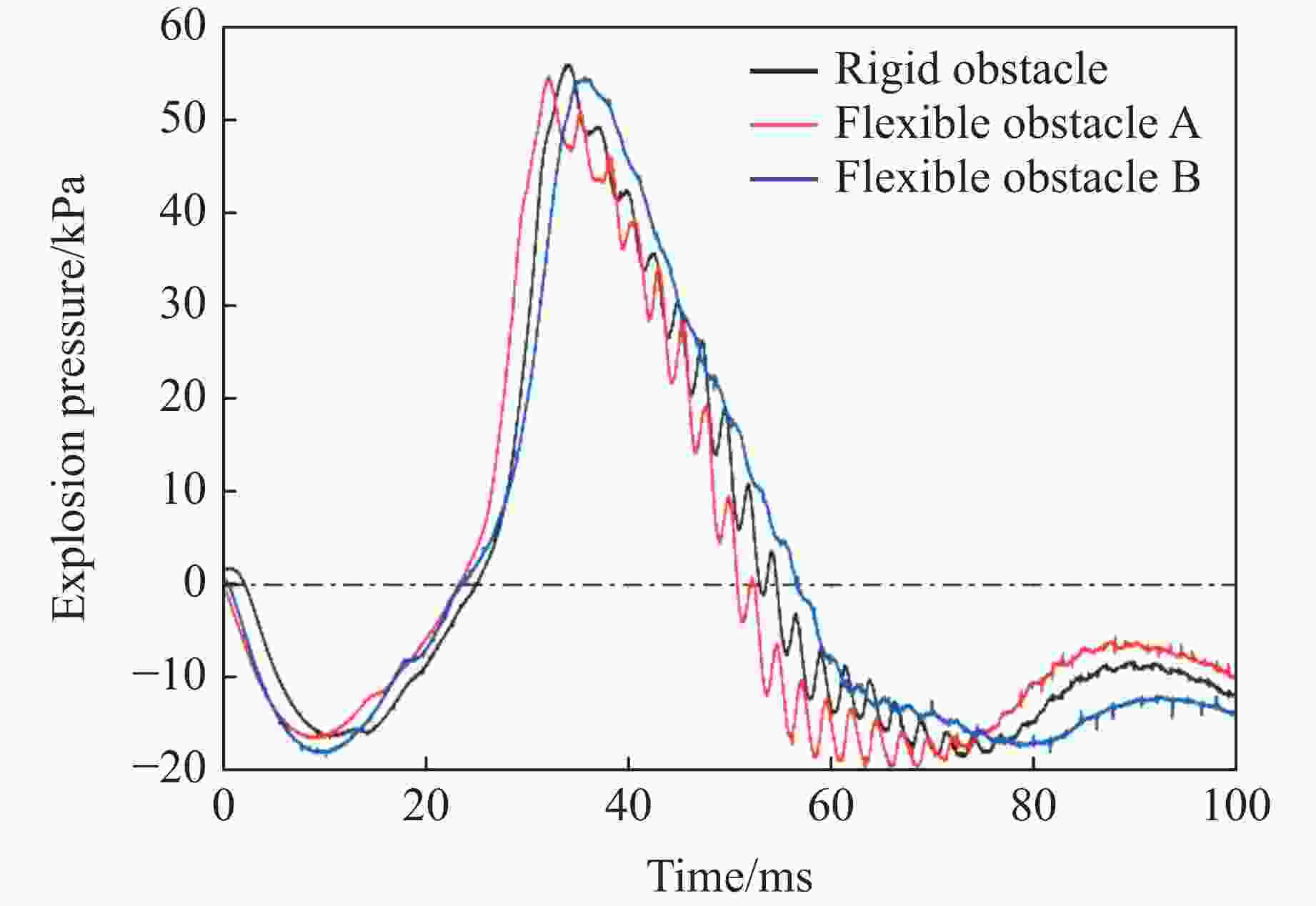
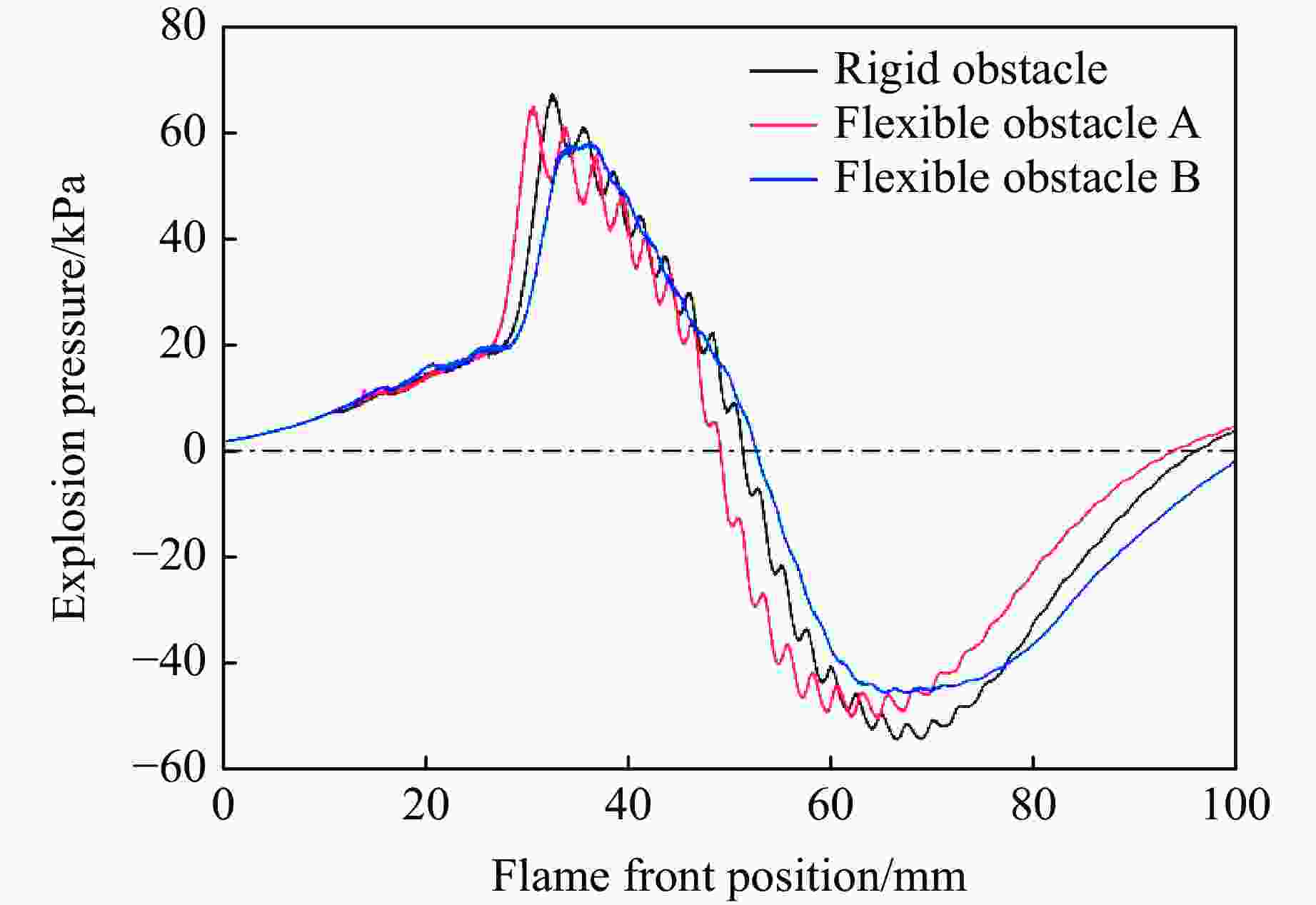
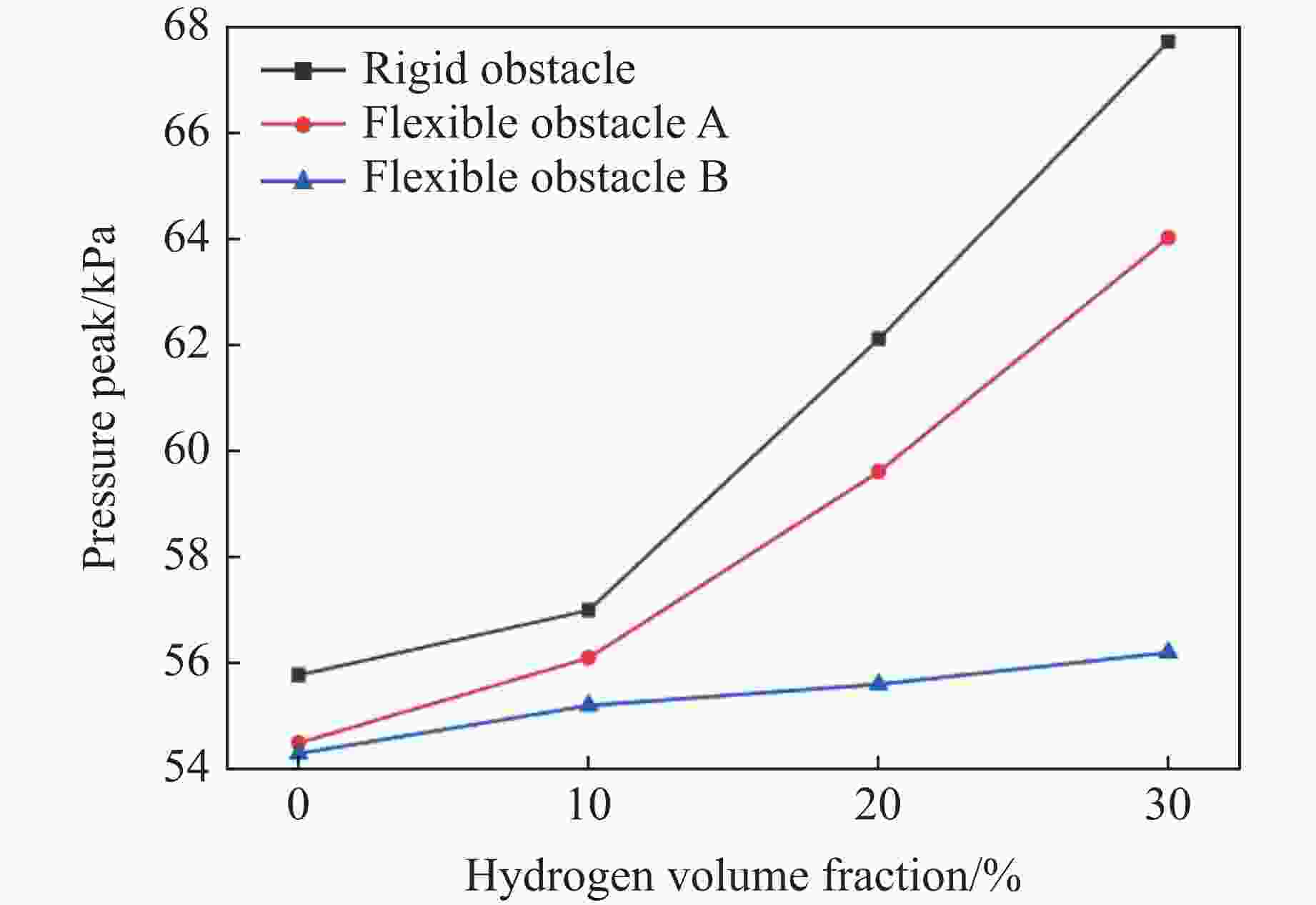
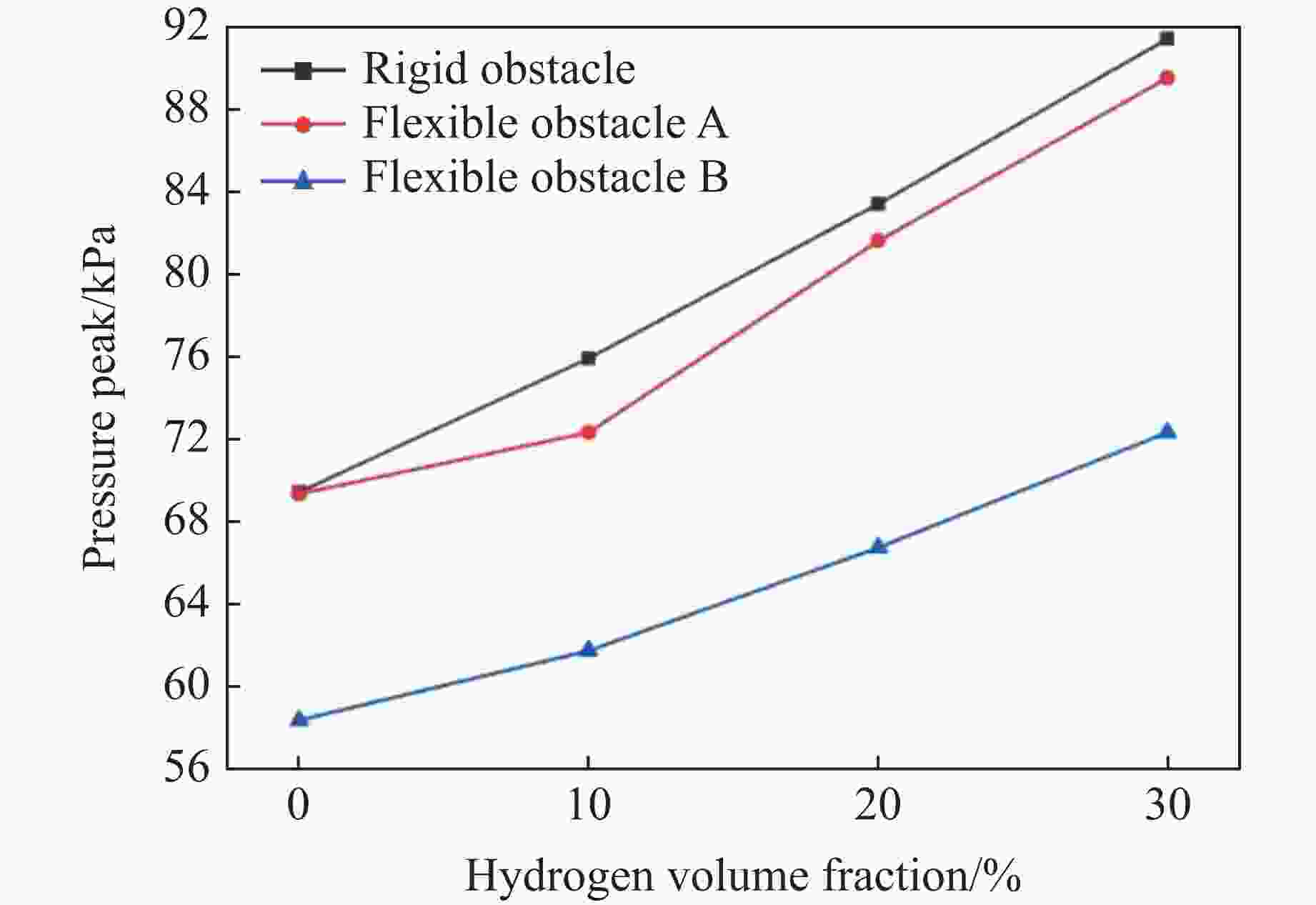
摘要: 选取3种不同弯曲强度障碍物进行氢气-甲烷混合气体爆炸影响实验研究，以探究不同环境下的促爆危险性。实验过程中采集爆炸管道内火焰图像以及上下游压力。通过分析火焰图像以及爆炸压力数据后发现，爆炸后膨胀燃气推动流场加速在障碍物后方产生涡流，流场在不同材质障碍物后产生不同的涡流强度，导致燃气后期火焰峰值速度差异以及管道内爆炸超压差异。实验证明了促爆强度与障碍物材质的相关性。在本研究中，促爆强度与障碍物弯曲强度成正比，在氢气加入后，燃气基础反应加快，3种材质障碍物管道内爆炸压力峰值开始产生明显差异。通过上述结果可以得出，环境内障碍物以及粗糙壁面会影响燃气促爆效果，由于材料本身特性影响而产生差异，并且这种差异受燃气自身燃烧速率的影响。Abstract: Three obstacles with different levels of bending strength was selected for experimental research on the impact of hydrogen-methane mixed gas explosions in order to explore the varying environmental hazards of explosion promotion. During the experiment, the images of the flame in the explosion pipeline and the upstream and downstream pressure were collected. Through the analysis of flame images and explosion pressure data, the flow field accelerated by expanding gas after explosion generates eddy currents behind obstacles, and the flow field produces different eddy currents behind obstacles of different materials, which result in the difference of peak flame velocity of gas in the later stage and the difference of explosion overpressure in pipelines. This proves the correlation between the intensity of promoting explosions and the material of obstacles. In the experiments conducted in this paper, there is a proportional relationship between the intensity of promoting explosions and the bending strength of the obstacle. Moreover, after hydrogen was added, the reaction of the gas base was accelerated and the peak explosion pressure in the obstacle pipes of the three materials began to produce obvious differences. It can be concluded that obstacles and rough walls in the environment will affect the gas explosion effect, and the difference is caused by the characteristics of the material itself, and the difference is affected by the combustion rate of the gas itself.
-
Key words:
- gas explosion /
- obstacle /
- promoting explosion experiment /
- premixed gas
-
图 2 3种障碍物：刚性障碍物、柔性障碍物A和柔性障碍物B
Figure 2. Three types of obstacle：rigid obstacle，flexible obstacle A and flexible obstacle B
图 3 管道内火焰图像（
$\varphi_{{\mathrm{H}}_2} $ =0）Figure 3. Images of flame in pipeline (
$\varphi_{{\mathrm{H}}_2} $ =0)
图 4 管道内火焰图像（
$\varphi_{{\mathrm{H}}_2} $ =10%）Figure 4. Images of flame in pipeline (
$\varphi_{{\mathrm{H}}_2} $ =10%)
图 5 管道内火焰图像（
$\varphi_{{\mathrm{H}}_2} $ =20%）Figure 5. Images of flame in pipeline (
$\varphi_{{\mathrm{H}}_2} $ =20%)
图 6 管道内火焰图像（
$\varphi_{{\mathrm{H}}_2} $ =30%）Figure 6. Images of flame in pipeline (
$\varphi_{{\mathrm{H}}_2} $ =30%)
图 9
$\varphi_{{\mathrm{H}}_2} $ =0时管道内上游的压力-时间曲线Figure 9. Pipeline upstream pressure-time curves of
$\varphi_{{\mathrm{H}}_2} $ =0
图 10
$\varphi_{{\mathrm{H}}_2} $ =0时管道内下游压力-时间曲线Figure 10. Pipeline downstream pressure-time curves of
$\varphi_{{\mathrm{H}}_2} $ =0
图 11 管道内上游的压力峰值-氢气体积分数曲线
Figure 11. Upstream pressure peak-hydrogen volume fraction curves in pipeline
图 12 管道内下游的压力峰值-氢气体积分数曲线
Figure 12. Downstream pressure peak-hydrogen volume fraction curves in pipeline
表 1 预混气体的组分
Table 1. Premixed gas components
${\varphi _{{{\mathrm{H}}_2}}} $/% ${\varPhi _{{{\mathrm{H}}_2}}} $/% ${\varPhi _{{{\mathrm{CH}}_4}}} $/% $\varPhi _{{\mathrm{Air}}}$/% 0 0 9.50 90.50 10 1.02 9.18 89.80 20 2.20 8.80 89.00 30 3.58 8.53 88.07 
下载: 导出CSV
表 2 障碍物参数
Table 2. Obstacle parameter
Obstacle Material Dimensions Mean density/
(g·cm−3)Average elastic modulus/MPa Rigid obstacle Polymethyl methacrylate 100 mm×10 mm
×
30 mm1.190 2800.0 Flexible obstacle A Foamed silicone gel 1.920 31.3 Flexible obstacle B Polyurethane foam 0.699 7.4
下载: 导出CSV
-
[1] STARR A, LEE J, NG H D. Detonation limits in rough walled tubes [J]. Proceedings of the Combustion Institute, 2015, 35(2): 1989–1996. doi: 10.1016/j.proci.2014.06.130 [2] ShCHELKIN K I, TROSHIN Y K. Non-stationary phenomena in the gaseous detonation front [J]. Combustion and Flame, 1963, 7: 143–151. doi: 10.1016/0010-2180(63)90172-X [3] SHCHELKIN K I. Instability of combustion and detonation of gases [J]. Soviet Physics Uspekhi, 1966, 8(5): 780–797. doi: 10.1070/PU1966v008n05ABEH003038 [4] MOEN I O, DONATO M, KNYSTAUTAS R, et al. Flame acceleration due to turbulence produced by obstacles [J]. Combustion and Flame, 1980, 39(1): 21–32. doi: 10.1016/0010-2180(80)90003-6 [5] NA’INNA A M, PHYLAKTOU H N, ANDREWS G E. The acceleration of flames in tube explosions with two obstacles as a function of the obstacle separation distance [J]. Journal of Loss Prevention in the Process Industries, 2013, 26(6): 1597–1603. doi: 10.1016/j.jlp.2013.08.003 [6] FAIRWEATHER M, HARGRAVE G K, IBRAHIM S S, et al. Studies of premixed flame propagation in explosion tubes [J]. Combustion and Flame, 1999, 116(4): 504–518. doi: 10.1016/S0010-2180(98)00055-8 [7] YU M G, ZHENG K, CHU T K. Gas explosion flame propagation over various hollow-square obstacles [J]. Journal of Natural Gas Science and Engineering, 2016, 30: 221–227. doi: 10.1016/j.jngse.2016.02.009 [8] WEN X P, YU M G, JI W T, et al. Methane-air explosion characteristics with different obstacle configurations [J]. International Journal of Mining Science and Technology, 2015, 25(2): 213–218. doi: 10.1016/j.ijmst.2015.02.008 [9] WEN X P, YU M G, LIU Z C, et al. Large eddy simulation of methane-air deflagration in an obstructed chamber using different combustion models [J]. Journal of Loss Prevention in the Process Industries, 2012, 25(4): 730–738. doi: 10.1016/j.jlp.2012.04.008 [10] MASRI A R, IBRAHIM S S, NEHZAT N, et al. Experimental study of premixed flame propagation over various solid obstructions [J]. Experimental Thermal and Fluid Science, 2000, 21(1/2/3): 109–106. doi: 10.1016/S0894-1777(99)00060-6 [11] JOHANSEN C T, CICCARELLI G. Modeling the initial flame acceleration in an obstructed channel using large eddy simulation [J]. Journal of Loss Prevention in the Process Industries, 2013, 26(4): 571–585. doi: 10.1016/j.jlp.2012.12.005 [12] JOHANSEN C T, CICCARELLI G. Visualization of the unburned gas flow field ahead of an accelerating flame in an obstructed square channel [J]. Combustion and Flame, 2009, 156(2): 405–416. doi: 10.1016/j.combustflame.2008.07.010 [13] CICCARELLI G, JOHANSEN R T, PARRAVANI R. The role of shock-flame interactions on flame acceleration in an obstacle laden channel [J]. Combustion and Flame, 2010, 157(11): 2125–2136. doi: 10.1016/j.combustflame.2010.05.003 [14] SALAMANDRA G D, BAZHENOVA T V, NABOKO I M. Formation of detonation wave during combustion of gas in combustion tube [J]. Symposium (International) on Combustion, 1958, 7(1): 851–855. doi: 10.1016/S0082-0784(58)80128-9 [15] ZHANG B, LIU H, LI Y C. The effect of instability of detonation on the propagation modes near the limits in typical combustible mixtures [J]. Fuel, 2019, 253: 305–310. doi: 10.1016/j.fuel.2019.05.006 [16] SULAIMAN S Z, KASMANI R M, MUSTAFA A, et al. Effect of obstacle on deflagration to detonation transition (DDT) in closed pipe or channel-an overview [J]. Jurnal Teknologi, 2013, 66(1): 49–52. doi: 10.11113/jt.v66.1326 [17] OGAWA T, GAMEZO V N, ORAN E S. Flame acceleration and transition to detonation in an array of square obstacles [J]. Journal of Loss Prevention in the Process Industries, 2013, 26(2): 355–362. doi: 10.1016/j.jlp.2011.12.009 [18] ZHANG B, LIU H, YAN B J. Investigation on the detonation propagation limit criterion for methane-oxygen mixtures in tubes with different scales [J]. Fuel, 2019, 239: 617–622. doi: 10.1016/j.fuel.2018.11.062 [19] BANG B H, AHN C S, KIM Y T, et al. Deflagration-to-detonation transition in pipes: the analytical theory [J]. Applied Mathematical Modelling, 2019, 66: 332–343. doi: 10.1016/j.apm.2018.09.023 [20] KIVERIN A D, YAKOVENKO I S. Estimation of critical conditions for deflagration-to-detonation transition in obstructed channels filled with gaseous mixtures [J]. Mathematical Modelling of Natural Phenomena, 2018, 13(6): 54. doi: 10.1051/mmnp/2018071 [21] COATES A M, MATHIAS D L, CANTWELL B J. Numerical investigation of the effect of obstacle shape on deflagration to detonation transition in a hydrogen-air mixture [J]. Combustion and Flame, 2019, 209: 278–290. doi: 10.1016/j.combustflame.2019.07.044 [22] LEAL C A, SANTIAGO G F. Do tree belts increase risk of explosion for LPG spheres? [J]. Journal of Loss Prevention in the Process Industries, 2004, 17(3): 217–224. doi: 10.1016/j.jlp.2004.02.003 [23] BAKKE J R, WINGERDEN K V, HOORELBEKE P, et al. A study on the effect of trees on gas explosions [J]. Journal of Loss Prevention in the Process Industries, 2010, 23(6): 878–884. doi: 10.1016/j.jlp.2010.08.007 [24] LI Q, LU S X, XU M J, et al. Comparison of flame propagation in a tube with a flexible/rigid obstacle [J]. Energy & Fuels, 2016, 30(10): 8720–8726. doi: 10.1021/acs.energyfuels.6b01594 [25] LI Q, CICCARELLI G, SUN X X, et al. Flame propagation across a flexible obstacle in a square cross-section channel [J]. International Journal of Hydrogen Energy, 2018, 43(36): 17480–17491. doi: 10.1016/j.ijhydene.2018.07.077 [26] LI Q, SUN X X, WANG X, et al. Experimental study of flame propagation across flexible obstacles in a square cross-section channel [J]. International Journal of Hydrogen Energy, 2019, 44(7): 3944–3952. doi: 10.1016/j.ijhydene.2018.12.085 [27] 李权. 管道内障碍物对氢-空气预混火焰传播动力学影响研究 [D]. 合肥: 中国科学技术大学, 2019. [28] YU M G, ZHENG K, ZHENG L G, et al. Effects of hydrogen addition on propagation characteristics of premixed methane/air flames [J]. Journal of Loss Prevention in the Process Industries, 2015, 34: 1–9. doi: 10.1016/j.jlp.2015.01.017 [29] YU S W, DUAN Y L, LONG F Y, et al. The influence of flexible/rigid obstacle on flame propagation and blast injuries risk in gas explosion [J]. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 2023, 45(2): 4520–4536. -
下载:
点击查看大图
计量
- 文章访问数: 100
- HTML全文浏览量: 26
- PDF下载量: 20
