Experimental Investigation of Plate Driven by HNS-Based PBX Explosive and Equation of State Parameters Determination for Explosive Detonation Products
-
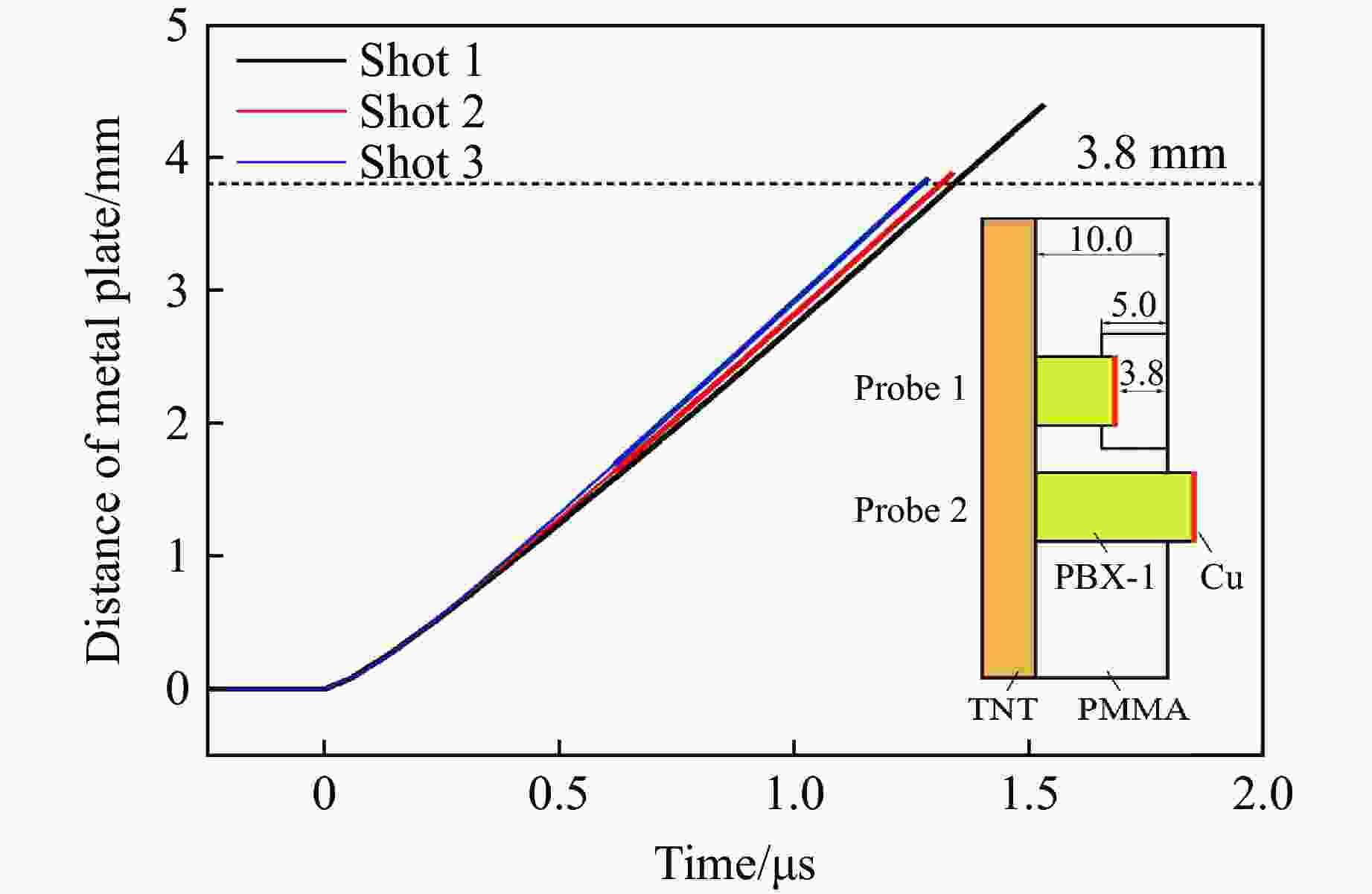
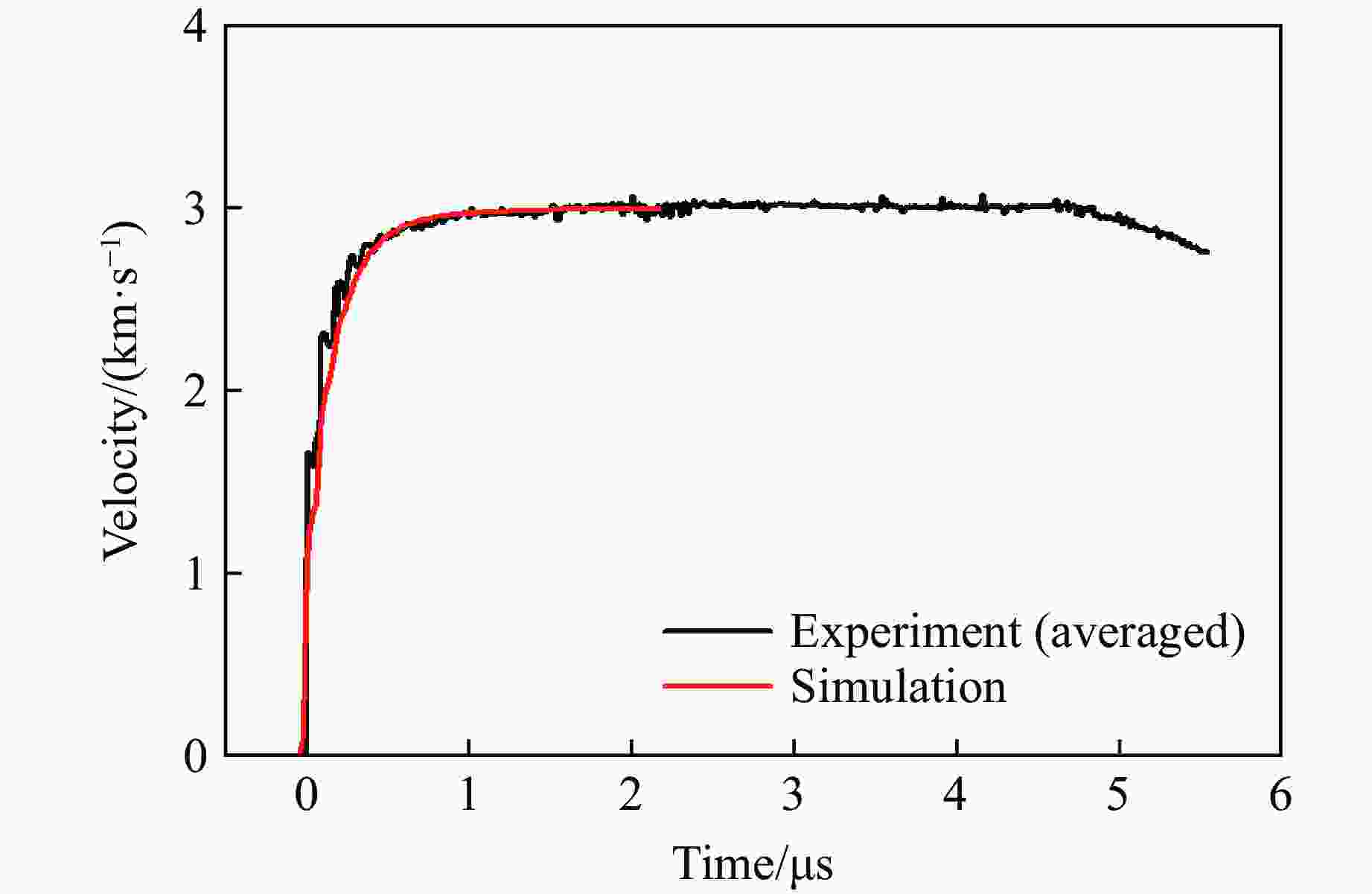
摘要: 为确定六硝基茋基PBX-1炸药产物的状态方程参数，采用平面波透镜加载和激光干涉测速技术，测量了在长度不同、直径为6 mm的PBX-1炸药药柱爆轰驱动下金属平板的自由面速度变化历程。实验结果表明：PBX-1炸药的爆轰波传播速度约为6798.2 m/s，且炸药的长径比对驱动平板的有效装药量有显著影响；与长径比为1的情况相比，长径比为2时PBX-1炸药驱动平板的有效装药量更小，导致金属平板的最大运动速度降低，但是在驱动平板过程中，金属平板受平面波透镜加载边界的影响较小。基于实验数据，开展了长径比为2的PBX-1炸药爆轰驱动平板的数值模拟，确定了PBX-1炸药爆轰产物的状态方程参数，计算得到的平板自由面速度变化历程与实验结果吻合较好。研究结果可为冲击片雷管的可靠性评估提供重要的基础参数。Abstract: To determine the parameters of equation of state for detonation products of the HNS-based explosive PBX-1, the plane wave lens and the photonic Doppler velocimetry (PDV) were used to measure the free surface velocity histories of metal plates driven by the PBX-1 explosives. The explosive samples had diameters of 6 mm and different lengths. According to the experimental results, the detonation velocity of PBX-1 is about 6798.2 m/s, and the effective explosive volume is obviously affected by the ratio of length to diameter of explosive sample. Compared with the sample with the ratio equal to 1, the effective explosive volume of the sample with the ratio equal to 2, leads to a lower maximum plate velocity. The plate driven by the longer explosive sample is less affected by the initiation boundary of plane wave lens. Therefore, the experimental result obtained by the longer explosive sample was used to determine the detonation products’ parameters of equation of state by numerical simulation. The simulation showed that the simulated free surface velocity history is in good agreement with the experimental result. The obtained detonation products’ parameters of equation of state provides fundamental data for reliability assessment of slapper detonator.
-
随着空间科学研究的发展，为进一步开展空间碎片毁伤效应、防护结构以及超高速碰撞等研究工作，提出了10 km/s以上的超高速发射需求。国内外常用的发射技术（设备）包括：二级/三级轻气炮、磁驱动飞片、聚能射流、等离子体加速器、激光驱动飞片装置等[1-6]。其中二级轻气炮是目前应用最广泛、技术最为成熟的发射设备。然而，受到炮体材料性能的限制，二级轻气炮的稳定发射速度基本都低于8 km/s，如果超过该速度，发射管将发生严重的烧蚀破坏[7]。虽然有些发射技术能够实现8 km/s以上的超高速发射，但是这些发射技术要么难以控制弹丸的质量和形状，要么只能发射很薄的飞片状弹丸或质量很小的弹丸[8]，因此将其应用到超高速碰撞实验研究中受到了一定的限制。在20世纪60年代，内爆驱动式超高速发射技术已经实现了2 g弹丸12.2 km/s的发射速度[9-10]；进入21世纪后，加拿大麦吉尔大学[1, 11-13]又实现了15 g弹丸7.5 km/s左右的发射速度，这是一项发射质量和速度都超过二级轻气炮的超高速发射技术，能够满足空间碎片撞击的研究需求。
内爆驱动式超高速发射技术（国外有Explosive hypervelocity launcher[9]、Explosively driven gun[10]、Implosion-driven launcher[11-13]等不同说法，国内也有炸药爆轰驱动高速激波管发射技术[14]、炸药驱动枪[15]等不同名称，本文以Implosion-driven launcher说法为准，简称内爆发射器）是一种利用炸药爆炸线性挤压压缩管内轻质气体，通过被压缩的轻质气体驱动弹丸的一种发射技术[11]，作用过程与二级轻气炮中活塞压缩高压轻质气体类似，不同的是其活塞速度为炸药爆速。国内一些文献中对该技术进行了相关介绍，但尚未见相关实验和仿真研究报道[14-15]。
为了掌握内爆发射技术，获得10 km/s以上的发射能力，通过与加拿大麦吉尔大学的Higgins教授合作，以8 mm口径内爆发射装置为研究对象，对内爆发射器的发射能力和研究方法进行了初步探索，开展了内爆发射器内弹道分析和结构设计，并利用AUTODYN软件对设计结构进行了初步仿真分析，最终针对典型状态开展了初步验证实验。
1. 内爆发射器工作原理
内爆发射器主要由炸药线性压缩段、高压段和发射管组成，其中炸药线性压缩段包括外壳、装药、压缩管、驱动气体等，发射器的结构如图1所示，作用过程如图2所示。左端炸药起爆后，压缩管向内塌缩，形成锥形结构，当炸药爆轰波传播时，锥形结构向右运动并压缩驱动气体。该过程与二级轻气炮中活塞压缩高压轻质气体类似，因此该锥形结构可看成虚拟活塞，当冲击波到达弹丸底部时，高压驱动气体开始推动弹丸加速运动。
2. 内爆发射过程的仿真分析
设计了内径16 mm、长度500 mm的压缩管和内径8 mm、长度300 mm的发射管组成的内爆发射器，高压段采用锥段连接压缩管和发射管，锥段半锥角度为5°。采用AUTODYN软件对该内爆发射器的工作过程进行了仿真计算。
2.1 仿真模型及方法
采用有限元中的流固耦合方法进行仿真。将模型分为Euler模型和Lagrange模型两个部分：Euler模型包括填充的氦气、压缩管、装药以及周围空气介质；Lagrange模型包括压缩段外壳、高压段、发射管以及弹丸。外壳、高压段、压缩管、发射管均采用4340钢。本构模型采用Johnson Cook模型，状态方程为Linear。装药采用爆速为7 km/s左右的季戊四醇四硝酸酯（PETN），状态方程为JWL；驱动气体为氦气，采用理想气体状态方程；弹丸本构模型为Steinberg Guinan，状态方程为Shock。材料参数均选自AUTUDYN数据库。
为了使弹丸能够约束初始状态的高压氦气，在弹丸与高压气体交界处增加一层Lagrange网格。该网格与高压段和弹丸均采用共节点的方式固定，并将该部分的材料失效应变设置为0.5，当达到失效应变时自动删除该部分的网格，使其不会对弹丸发射造成过大影响。
2.2 仿真计算相关参数
针对弹丸材料和充气压力两个参数，共进行4个状态的仿真计算，相关参数以及各状态下获得的弹丸出炮口速度见表1。
表 1 不同弹丸材料和充气压力下仿真计算参数Table 1. Simulation parameters of launchers with different projectile materials and filling pressureNo. Material of projectile Filling pressure/MPa Diameter of launch tube/mm Diameter of pump tube/mm Muzzle velocity/（km·s–1） 1 Aluminum alloy 4 8 16 8.62 2 Aluminum alloy 5 8 16 9.17 3 Aluminum alloy 6 8 16 9.25 4 Magnesium alloy 5 8 16 10.66 2.3 仿真结果
2.3.1 内爆发射器工作过程
图3给出了内爆式超高速发射装置发射铝弹丸的仿真结果，其中弹丸尺寸为
$\varnothing$ 8 mm × 4 mm，质量为0.55 g。零时刻从装药的左端面开始点火，装药爆炸后开始挤压压缩管形成锥形活塞，并在氦气（初始压力5 MPa）中形成压力达到500 MPa左右的冲击波向右传播，外壳达到失效应变后被删除，如图3(b)所示，压力超过1 GPa时显示为红色；在55 μs左右，冲击波到达弹丸底部反射，形成峰值压力高达5 GPa的气体推动弹丸加速运动；70 μs左右炸药爆轰结束；在108 μs左右弹丸离开发射管，达到最高发射速度。2.3.2 不同初始充气压力下弹丸的发射速度
图4给出了充气压力分别为4、5和6 MPa状态下铝弹丸的速度-时间历程。从速度-时间曲线上可以看到，弹丸加速过程有较为明显的二次冲击加载。初始冲击加载是由先导冲击波到达弹丸底部产生的；二次冲击加载是弹丸底部反射的冲击波到达左端后再次反射冲击波，该冲击波追赶上弹丸产生的。从表1中的数据可知，4、5和6 MPa充气压力下弹丸的出炮口速度分别为8.62、9.17和9.25 km/s。可以看到，炮口速度随充气压力的增加而增加，但增加幅度缩小。可能是由于当充气压力从5 MPa增加至6 MPa时，压缩管、高压段内壁的膨胀显著增加，削弱了驱动压力增加的增速效果。
图 4 不同充气压力下铝弹丸的速度-时间历史Figure 4. Velocity-time history of aluminum projectiles with different filling pressure2.3.3 不同弹丸材料的发射速度
根据建立的仿真模型对尺寸为
$\varnothing$ 8 mm × 4 mm的铝合金弹丸和镁合金弹丸进行发射过程的计算，初始填充5 MPa氦气，计算结果如图5所示。0.55 g铝合金弹丸的最终发射速度为9.17 km/s；0.37 g镁合金弹丸的发射速度为10.66 km/s，比铝合金弹丸速度高1.49 km/s。
图 5 不同材料弹丸速度-时间历史Figure 5. Velocity-time history of projectiles with different materials3. 实验设计及结果
3.1 发射器结构
发射器总长度为914 mm，最大部位直径为81.4 mm，主要包括发射管、发射管护套、高压段、外壳、压缩管、弹丸和装药等。其中：发射管内径为8 mm，长度为304 mm；压缩管内径为16 mm，长度为495 mm。装药为柱壳装药，厚度约为5 mm，装药量约为300 g，采用两层以黑索金（RDX）为基底的片状挠性炸药包裹而成，挠性炸药的爆速为7.1 km/s。弹丸直径为8 mm，高度为4 mm。弹丸材料有两种，分别是铝合金和镁合金，其中铝合金弹丸质量约为0.55 g，镁合金弹丸质量约为0.37 g，安装完成后的发射器如图6所示。
3.2 实验装置总体布局
实验装置布局如图7所示。实验装置主要包括发射器、测试系统、真空系统和防护系统等。发射器放置在厚壁防护筒内，防止爆炸产生的碎片向外飞散，损伤实验装置和设备。采用激光测速系统和靶网测速装置等测量弹丸的发射速度，并采用序列激光阴影成像仪拍摄模型的飞行姿态和形貌。实验中发射器压缩管内充5 MPa氦气，从端面起爆装药。
3.3 实验结果与分析
共开展了7次实验，其中铝合金弹丸实验3次，镁合金弹丸实验4次，具体实验参数如表2所示。
表 2 内爆发射器实验相关参数Table 2. Parameters of the implosion-driven launchers in testsNo. Material of projectile Mass of projectile/g Filling pressure/MPa Diameter of launch tube/mm Diameter of pump tube/mm Maximum velocity/（km·s–1） ILT04 Aluminum alloy 0.55 5 8 16 7.26 ILT07 6.96 ILT14 7.95 ILT08 Magnesium alloy 0.37 5 8 16 9.73 ILT09 10.28 ILT11 9.36 ILT12 9.77 3.3.1 回收发射器
实验后的发射器压缩管和外壳完全碎裂，高压段外壳明显膨胀变形并出现裂纹，回收的典型发射器装置如图8所示。
3.3.2 铝合金弹丸速度测试结果
3次铝合金弹丸实验结果如图9所示，其中横坐标为测点位置离炮口的距离，纵坐标为测得的速度，各次实验测得的最大速度见表2。其中，实验中测得的弹丸最高出炮口速度为7.95 km/s，比仿真预测速度9.17 km/s低1.22 km/s，相对偏差为15.3%。实验速度偏低可能是许多因素共同影响的结果，例如装置加工误差、装药松紧程度、发射管与弹丸有摩擦阻力等，而仿真状态则相对理想，没有考虑这些因素的影响。另外，实验中弹丸的速度也有1 km/s左右的偏差，挠性炸药装填、装药爆轰的圆周同步性、发射管与弹丸的配合程度等问题都会对实际发射速度造成一定影响，导致重复实验出现一定的偏差。
图 9 0.55 g铝合金弹丸速度测试结果Figure 9. Experimental muzzle velocities of 0.55 g aluminum projectile3.3.3 镁合金弹丸速度测试结果
4次镁合金有效实验获得的速度结果如图10所示，实验测得的最大速度见表2。4次实验获得的最高发射速度与仿真预测速度10.66 km/s非常接近，相对偏差为3.7%。镁合金弹丸在实验中的速度偏差为1 km/s左右，产生偏差的原因可能与铝合金弹丸相同。
图 10 0.37 g镁合金弹丸速度测试结果Figure 10. Experimental muzzle velocities of 0.37 g magnesium projectile3.3.4 弹丸成像结果
通过超高速八序列激光阴影成像仪拍摄弹丸在实验过程中的飞行情况，图11为3次实验拍摄的照片，其中ILT11、ILT12为镁合金弹丸，ILT14为铝合金弹丸。在图11中可以看到，实验过程中的弹丸仍保持为一个整体弹丸，但存在一定程度变形，其中实验ILT12的弹丸变形非常明显。发生变形的原因可能是材料强度不够，也可能是发射器结构存在一定的缺陷，有待进一步深入研究。
图 11 弹丸序列激光阴影成像结果Figure 11. Projectile photos shot by sequence laser shadowgraph imager4. 结 论
通过与加拿大麦吉尔大学合作，初步设计了8 mm口径内爆式超高速发射器结构，采用AUTODYN软件对内爆式超高速发射器内弹道进行数值模拟，所获得的发射器作用过程中弹底压力最高可达5 GPa，并计算了铝合金弹丸和镁合金弹丸的发射速度。最终通过开展验证实验，证明了设计的内爆发射技术能够将尺寸为
$\varnothing$ 8 mm × 4 mm、质量为0.37 g的柱状镁合金弹丸发射到10.28 km/s，将尺寸为$\varnothing$ 8 mm × 4 mm、质量为0.55 g的柱状铝合金弹丸发射到7.95 km/s。实验获得的发射速度与数值仿真结果吻合较好。实验结果也证明了内爆式超高速发射技术的可行性，在空间碎片的撞击与防护方面具有较强的应用前景。利用超高速八序列激光阴影成像仪拍摄弹丸的飞行情况，获得了弹丸发射后的形状，发现发射后的弹丸是一个整体弹丸，但与原始柱形结构相比，存在不同程度的变形。未来将深入探索提高内爆发射器速度的方法，分析弹丸发生变形的原因，并在保持弹丸初始形状的发射器结构设计等方面开展进一步的研究工作。感谢中国空气动力研究与发展中心的罗庆、龙耀、宋强、周毅、覃金贵、李俊玲、姜林、邹胜宇、李文光、廖强、刘晓龙、廖富强、丁建文等同事在实验过程中提供的无私帮助。
-
图 1 PBX-1炸药爆轰驱动平板的实验装置
Figure 1. Experimental device of plate driven by PBX-1 explosive
图 4 探头1测得的平板位移-时间曲线（内插图中的单位为mm）
Figure 4. Displacement-time curves of metal plate measured by probe 1(Unit in inset figure is mm)
图 5 炸药长径比为1时的稀疏波轮廓线
Figure 5. Rarefaction profile for the explosive whose length equal to diameter
图 6 探头2测得的平板自由面速度曲线对比
Figure 6. Comparison of free surface velocity profiles of plate obtained by probe 2
图 8 不同网格尺寸条件下计算得到的铜板速度-时间曲线
Figure 8. Simulated velocity-time curves of plate for different mesh sizes of copper
图 9 数值模拟与实验获得的PBX-1炸药爆轰驱动下平板的自由面速度随时间的变化曲线
Figure 9. Free surface velocity-time curves of plate driven by PBX-1 explosive obtained by simulation and experiment
表 1 PBX-1炸药样品与金属平板的实测参数
Table 1. Measured parameters of PBX-1 explosive samples and metal plates
Shot No. Probe No. Explosive sample length/mm Explosive initial density/(g·cm−3) Plate thickness/mm 1 1 6.00 1.582 0.19 2 11.98 1.580 0.19 2 1 6.01 1.585 0.18 2 12.03 1.586 0.19 3 1 6.02 1.585 0.19 2 11.99 1.588 0.19 
下载: 导出CSV
表 2 实验测得的平板最大速度
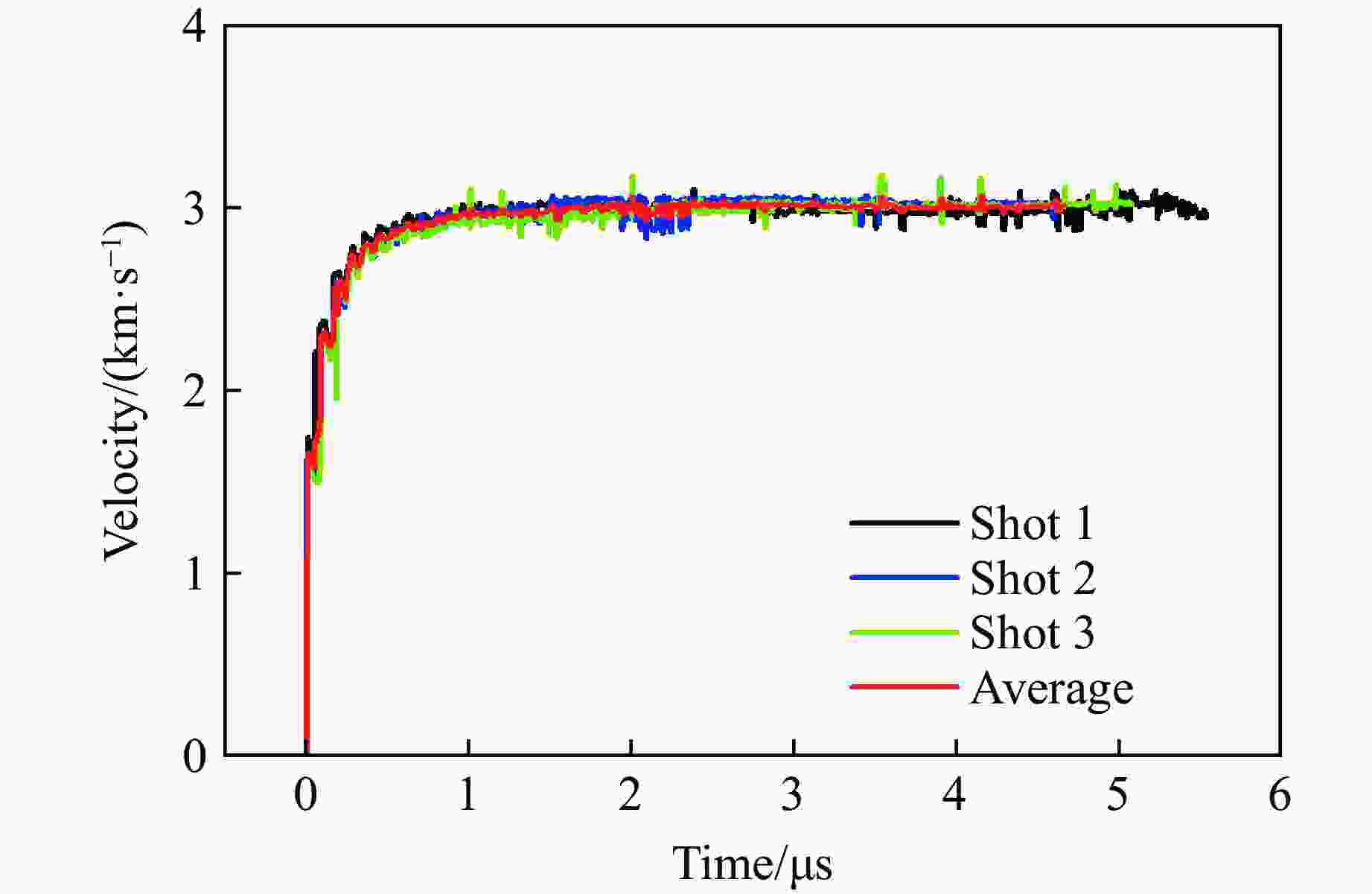
Table 2. Measured maximum velocity of plate
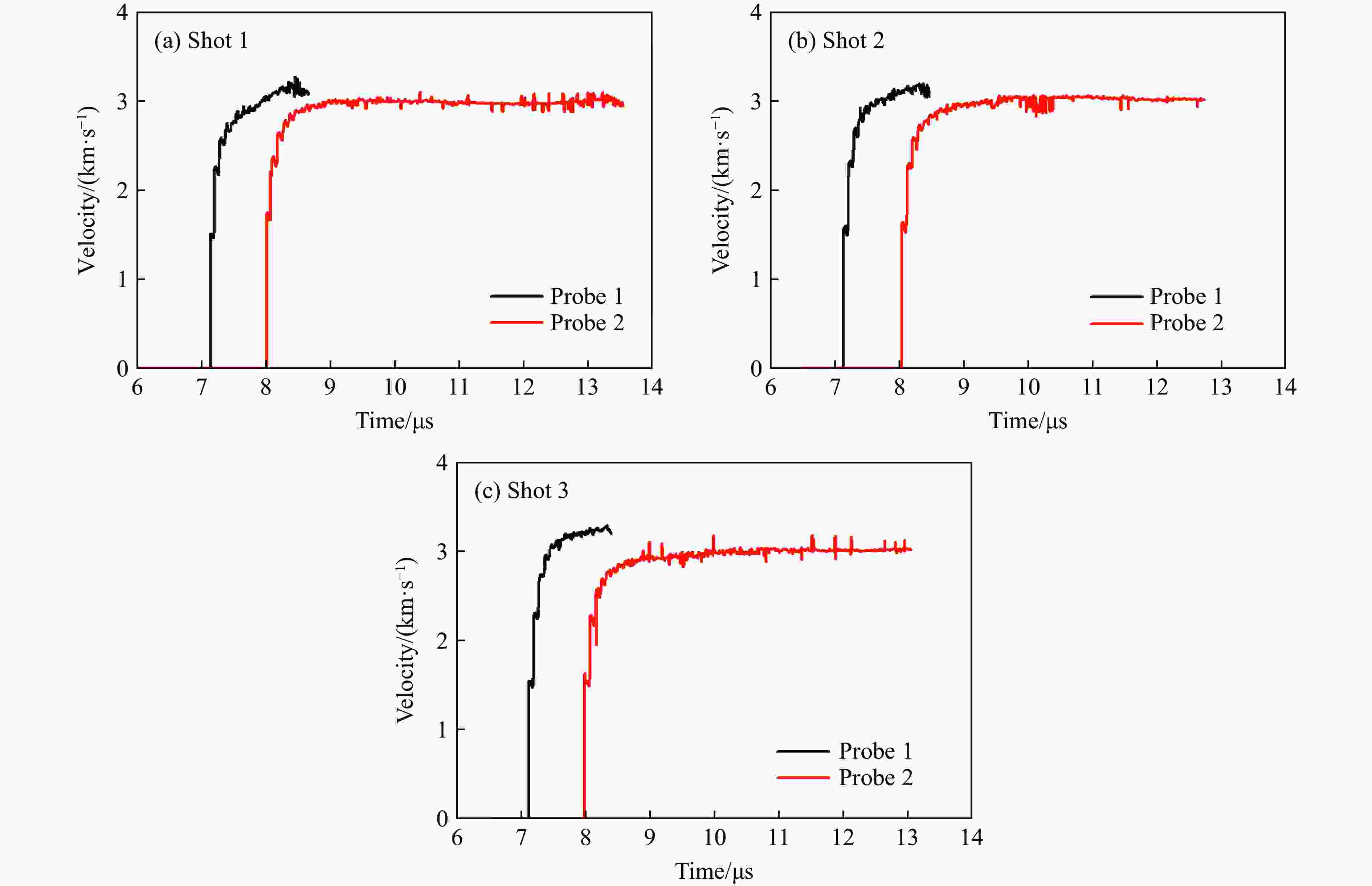
Shot No. Maximum velocity/(m∙s−1) Probe 1 Probe 2 1 3163.6 3004.6 2 3167.4 3050.1 3 3246.8 3016.0
下载: 导出CSV
表 3 速度起跳时间与爆轰波传播速度计算结果
Table 3. Starting points and the calculated results of detonation velocity
Shot No. Starting point of velocity/μs Time delay/μs Difference of explosive
samples’ length/mmDetonation velocity/
(m·s−1)Probe 1 Probe 2 1 7.130 8.010 0.880 5.98 6795.5 2 7.129 8.030 0.901 6.02 6681.5 3 7.116 7.979 0.863 5.97 6917.7
下载: 导出CSV
ρ0/(g·cm−3) C/(km·s−1) S1 S2 S3 γ0 a 8.90 3.958 1.497 0 0 2.0 0
下载: 导出CSV
表 5 PBX-1炸药爆轰产物JWL状态方程参数
Table 5. Parameters of JWL equation of state for detonation product of PBX-1 explosive
A/GPa B/GPa C/GPa R1 R2 ω E0/GPa pJ/GPa DJ/(km·s−1) 694.26 17.28 1.23 5.6 1.4 0.45 7.0 18.9 6.798
下载: 导出CSV
-
[1] 谭凯元, 韩勇, 罗观, 等. HMX基PBX的作功能力及其JWL状态方程 [J]. 火炸药学报, 2013, 36(3): 42–45.TAN K Y, HAN Y, LUO G, et al. Power ability and JWL equation of state of a HMX-based PBX [J]. Chinese Journal of Explosive & Propellants, 2013, 36(3): 42–45. [2] YANG Y, DUAN Z P, LI S R, et al. Evaluation of the detonation characteristics of aluminized DNAN-based melt-cast explosive by the detonation cylinder test [J]. Propellants, Explosives, Pyrotechnics, 2022, 47(4): e202100344. [3] LIU Y, WANG H F, BAI F, et al. A new equation of state for detonation products of RDX-Based aluminized explosives [J]. Propellants, Explosives, Pyrotechnics, 2019, 44(10): 1293–1301. doi: 10.1002/prep.201800126 [4] CHIQUETE C, JACKSON S I, ANDERSON E K, et al. Detonation performance experiments and modeling for the DAAF-based high explosive PBX 9701 [J]. Combustion and Flame, 2021, 223: 382–397. doi: 10.1016/j.combustflame.2020.10.009 [5] JACKSON S I. Scaled cylinder test experiments with insensitive PBX 9502 explosive [C]//15th International Detonation Symposium, 2014: 171–180. [6] WELLE E J, TAPPAN A S, PAHL R J, et al. Diameter effects on detonation performance of HNS and CL-20 [C]//Proceedings of the 13th International Detonation Symposium. Norfolk: Sandia National Laboratories, 2006. [7] 陈清畴, 蒋小华, 李敏, 等. HNS-Ⅳ炸药的点火增长模型 [J]. 爆炸与冲击, 2012, 32(3): 328–332.CHEN Q C, JIANG X H, LI M, et al. Ignition and growth reactive flow model for HNS-Ⅳexplosive [J]. Explosion and Shock Waves, 2012, 32(3): 328–332. [8] 刘丹阳, 陈朗, 杨坤, 等. CL-20基炸药爆轰产物JWL状态方程实验标定方法研究 [J]. 兵工学报, 2016, 37(Suppl 1): 141–145.LIU D Y, CHEN L, YANG K, et al. Calibration method of parameters in JWL equation of state for detonation products of CL-20-based explosives [J]. Acta Armamentarii, 2016, 37(Suppl 1): 141–145. [9] 杨洋, 段卓平, 张连生, 等. 两种DNAN基含铝炸药的爆轰性能 [J]. 含能材料, 2019, 27(8): 679–684.YANG Y, DUAN Z P, ZHANG L S, et al. Detonation performance of two DNAN based aluminized explosives [J]. Chinese Journal of Energetic Materials, 2019, 27(8): 679–684. [10] 郭向利, 韩勇, 刘世俊, 等. TATB基含铝炸药作功能力的试验研究 [J]. 火炸药学报, 2015, 38(3): 81–85. doi: 10.14077/j.issn.1007-7812.2015.03.016GUO X L, HAN Y, LIU S J, et al. Experimental study on work ability of TATB-based aluminized explosives [J]. Chinese Journal of Explosives & Propellants, 2015, 38(3): 81–85. doi: 10.14077/j.issn.1007-7812.2015.03.016 [11] PACHMÁŇ J, KÜNZEL M, NĚMEC O, et al. Characterization of Al plate acceleration by low power photonic Doppler velocimetry (PDV) [C]//Proceedings of the 40th International Pyrotechnics Society Seminar. Denver: IPSUSA Seminars (International Pyrotechnics Society), 2014. [12] 虞德水, 赵锋, 谭多望, 等. JOB-9003和JB-9014炸药平面爆轰驱动飞片的对比研究 [J]. 爆炸与冲击, 2006, 26(2): 140–144.YU D S, ZHAO F, TAN D W, et al. Experimental studies on detonation driving behavior of JOB-9003 and JB-9014 slab explosives [J]. Explosion and Shock Waves, 2006, 26(2): 140–144. [13] 向梅, 饶国宁, 彭金华. 复合装药结构爆轰驱动飞片作用数值模拟 [J]. 火工品, 2010(6): 1–4. doi: 10.3969/j.issn.1003-1480.2010.06.001XIANG M, RAO G N, PENG J H. The numerical simulation on driven metallic flyer plate rule for the composite charge structure [J]. Initiators & Pyrotechnics, 2010(6): 1–4. doi: 10.3969/j.issn.1003-1480.2010.06.001 [14] COOK M A. The science of high explosives [M]. New York: Reinhold, 1958. [15] 孙承纬, 卫玉章, 周之奎. 应用爆轰物理 [M]. 北京: 国防工业出版社, 2000: 467–472.SUN C W, WEI Y Z, ZHOU Z K. Applied detonation physics [M]. Beijing: National Defense Industry Press, 2000: 467–472. [16] MARSH S P. LASL shock Hugoniot data [M]. Berkeley: University of California Press, 1980. [17] 温丽晶, 段卓平, 张震宇, 等. 采用遗传算法确定炸药爆轰产物JWL状态方程参数 [J]. 爆炸与冲击, 2013(Suppl 1): 130–134.WEN L J, DUAN Z P, ZHANG Z Y, et al. Determination of JWL-EOS parameters for explosive detonation products using genetic algorithm [J]. Explosion and Shock Waves, 2013(Suppl 1): 130–134. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 207
- HTML全文浏览量: 87
- PDF下载量: 36
