基于重大事故场景的受限空间内燃气泄漏情景模拟及泄爆优化研究

金友平; 帅健; 王文想; 徐后佳

doi:10.11858/gywlxb.20230658

基于重大事故场景的受限空间内燃气泄漏情景模拟及泄爆优化研究

doi: 10.11858/gywlxb.20230658

金友平^{1, 2,},
帅健^{1, 3,*, ,},
王文想²,
徐后佳^{1, 3}

1.
中国石油大学（北京）安全与海洋工程学院, 北京　102249
2.
深圳市燃气集团股份有限公司, 广东深圳　518049
3.
油气生产安全与应急技术应急管理部重点实验室, 北京　102249

基金项目: 国家自然科学基金（51806247）；中国石油大学（北京）科研基金（2462022YXZZ002）

详细信息

作者简介:
金友平（1996－），男，硕士研究生，主要从事城镇燃气泄漏后果研究. E-mail：jinyouping2@163.com

通讯作者:
帅　健（1963－），男，博士，教授，主要从事油气管道安全管理研究. E-mail：shuaij@cup.edu.cn

中图分类号: O382.1; TE88
计量
- 文章访问数: 193
- HTML全文浏览量: 40
- PDF下载量: 29
出版历程
- 收稿日期: 2023-05-08
- 修回日期: 2023-06-12
- 网络出版日期: 2023-12-08
- 刊出日期: 2023-12-15

Leakage Characteristics of Flammable Gas in Confined Space and the Optimum Design of Explosion Venting: Numerical Simulation on Basis of the Major Accident

JIN Youping^{1, 2
,},
SHUAI Jian^{1, 3,*
, ,},
WANG Wenxiang²,
XU Houjia^{1, 3}

1.
College of Safety and Ocean Engineering, China University of Petroleum (Beijing), Beijing 102249, China
2.
Shenzhen Gas Co. Ltd., Shenzhen 518049, Guangdong, China
3.
Key Laboratory of Oil and Gas Safety and Emergency Technology, Ministry of Emergency Management, Beijing 102249, China

摘要

摘要: 为研究受限空间内燃气泄漏的情景并探究泄爆优化后的效果，基于FLACS软件构建了受限空间内重大燃气事故场景，模拟了燃气在受限空间内的泄漏扩散和爆炸，分析了泄爆口在受限空间内的泄爆效果。结果表明：燃气在管道封闭段泄漏时，云团沿着管外壁向外扩散形成内凹的不规则形状，障碍物使扩散速度加快；燃气泄漏产生的冲击波最大超压高达660.7 kPa，可使周边建筑物受到严重破坏，并且受限空间开口端一侧的建筑物破坏程度高于密闭端一侧建筑物；泄爆口安装在火焰发展轴向位置时泄爆效果最佳，空间内的最大爆炸压力可降至312.4 kPa，降幅达52.70%，若将泄爆口设置在受限空间侧面，离点火源位置越近，泄爆效果越佳；增大泄爆口的长宽比进而提高泄爆面积可使受限空间内的最大爆炸压力显著降低，长宽比为34∶1时，最大爆炸压力降至15.4 kPa，降幅达97.65%；降低泄爆口开启压力可有效降低受限空间内的最大爆炸压力，当泄爆开启压力降至50 kPa时，最大爆炸压力降低至351.0 kPa，降幅达46.87%。
- 受限空间 /
- 燃气 /
- 情景模拟 /
- 泄爆优化 /
- FLACS /
- 泄漏扩散 /
- 爆炸冲击波
Abstract: In order to study the gas leakage in a confined space and the effect of venting methods on the subsequent explosion, a major gas accident scene in confined space was constructed based on FLACS software. The leakage, diffusion, and explosion behavior of the leaked gas in the confined space was investigated, and the venting effect on the subsequent explosion was analysed. The results showed that the leaked gas cloud from the closed section of the pipeline diffuses outward along the outer wall of the pipeline, forming an irregular concave shape, and the diffusion speed will be accelerated when encountering obstacles. The maximum overpressure of leaked gas cloud is 660.7 kPa, which can seriously damage the surrounding buildings, and the degree of damage to the buildings at the open end of the restricted space is higher than that at the closed end. When the outlet is installed in the axial position of the flame development, the pressure-venting effect is the best. The maximum explosion pressure in the confined space can be reduced to 312.4 kPa, a reduction of 52.70%. If the outlet is placed on the side of the confined space, the closer it is to the ignition source, the better the venting effect will be. The maximum explosion pressure in the confined space can be significantly reduced by increasing the length-to-width ratio of the outlet to expand the explosion area. When the length-to-width ratio is 34∶1, the maximum explosion pressure is reduced to 15.4 kPa, a reduction of 97.65%. Reducing the outlet opening pressure can effectively reduce the maximum explosion pressure in the confined space. For the outlet opening pressure at 50 kPa, the maximum explosion pressure is reduced to 351.0 kPa, a reduction of 46.87%.
- confined space /
- gas /
- scenario simulation /
- explosion relief optimization /
- FLACS /
- leakage and diffusion /
- blast shock wave

HTML全文

图 1 事故报告场景图与FLACS事故场景建模

Figure 1. Accident report scene diagram and FLACS accident scene modeling diagram

下载: 全尺寸图片幻灯片

图 2 0.4 MPa下燃气扩散浓度随时间的变化

Figure 2. Change of gas diffusion concentration over time at 0.4 MPa

下载: 全尺寸图片幻灯片

图 3 最大爆炸火焰形态的时空演化

Figure 3. Spatial and temporal evolution of maximum explosion flame morphology

下载: 全尺寸图片幻灯片

图 4 最大爆炸超压时空演化云图

Figure 4. Space-time evolution of maximum explosion overpressure

下载: 全尺寸图片幻灯片

图 5 受限空间内不同测点爆炸压力随时间的变化

Figure 5. Variation of explosion pressure with time at different measuring points in confined space

下载: 全尺寸图片幻灯片

图 6 涉事故建筑物四周爆炸压力随时间的变化

Figure 6. Variation of explosion pressure around the involved building over time

下载: 全尺寸图片幻灯片

图 7 泄爆口设置示意图

Figure 7. Schematic diagram of burst outlet setting

下载: 全尺寸图片幻灯片

图 8 不同泄爆口位置下最大爆炸火焰的二维面视图

Figure 8. Two-dimensional view of the maximum explosion flame under different outlet location conditions

下载: 全尺寸图片幻灯片

图 9 不同泄爆口位置下最大爆炸超压二维面视图

Figure 9. Two-dimensional view of maximum explosion overpressure under different outlet location conditions

下载: 全尺寸图片幻灯片

图 10 不同泄爆口位置下测点MP1（密闭端）的爆炸压力和爆炸火焰速度随时间的变化

Figure 10. Variations of explosion pressure and explosion flame velocity at the measuring point MP1 (closed end) with time under different outlet location conditions

下载: 全尺寸图片幻灯片

图 11 不同泄爆口位置下测点MP6（开口端）的爆炸压力和爆炸火焰速度随时间的变化

Figure 11. Variations of explosion pressure and explosion flame velocity at the measuring point MP6 (open end) with time under different outlet location conditions

下载: 全尺寸图片幻灯片

图 12 整个模拟空间中最大爆炸压力随泄爆口位置的变化

Figure 12. Variation of the maximum explosion pressure in the entire simulation space with the outlet location

下载: 全尺寸图片幻灯片

图 13 不同泄爆口长宽比下最大爆炸火焰的三维分布

Figure 13. Three-dimensional distribution of maximum explosion flame under different length-to-width ratios of the outlet

下载: 全尺寸图片幻灯片

图 14 不同泄爆口长宽比下测点MP1（密闭端）的爆炸压力和爆炸火焰速度随时间的变化

Figure 14. Variations of explosion pressure and explosion flame velocity at the measuring point MP1 (closed end) with time under different length-to-width ratios of the outlet

下载: 全尺寸图片幻灯片

图 15 不同泄爆口长宽比下测点MP6（开口端）的爆炸压力和爆炸火焰速度随时间的变化

Figure 15. Variations of explosion pressure and explosion flame velocity at the measuring point MP6 (open end) with time under different length-to-width ratios of the outlet

下载: 全尺寸图片幻灯片

图 16 整个模拟空间中最大爆炸压力随泄爆口长宽比的变化

Figure 16. Variation of the maximum explosion pressure in the whole simulation space with the length-to-width ratio of the outlet

下载: 全尺寸图片幻灯片

图 17 不同泄爆口开启压力下最大爆炸火焰的三维云图

Figure 17. 3D nephogram of the maximum explosion flame under different opening pressures of the outlet

下载: 全尺寸图片幻灯片

图 18 不同泄爆口开启压力下测点MP1（密闭端）的爆炸压力和爆炸火焰速度随时间的变化

Figure 18. Variations of explosion pressure and explosion flame velocity at the measuring point MP1 (closed end) with time under different opening pressures of the outlet

下载: 全尺寸图片幻灯片

图 19 不同泄爆口开启压力下测点MP6（开口端）的爆炸压力和爆炸火焰速度随时间的变化

Figure 19. Variations of explosion pressure and explosion flame velocity at the measuring point MP6 (open end) with time under different opening pressures of the outlet

下载: 全尺寸图片幻灯片

图 20 整个模拟空间中最大爆炸压力随泄爆口开启压力的变化

Figure 20. Variation of the maximum explosion pressure in the whole simulation space with the opening pressure of the outlet in the entire simulation space

下载: 全尺寸图片幻灯片

参考文献(21)

[1]	孟伟, 何卫, 李璐伶, 等. 城镇燃气行业发展现状与关键前沿技术 [J]. 油气储运, 2022, 41(6): 673–681. MENG W, HE W, LI L L, et al. Current status and key advanced technologies of urban gas industry development [J]. Oil & Gas Storage and Transportation, 2022, 41(6): 673–681.
[2]	单克. 基于数据统计及情景模拟的燃气管道定量风险评价方法研究 [D]. 北京: 中国石油大学(北京), 2019. SHAN K. Research on quantitative risk assessment method of gas pipeline based on data statistics and scenario simulation [D]. Beijing: China University of Petroleum (Beijing), 2019.
[3]	李亚勋. 公共管廊泄漏事故情景构建与应急管理研究 [D]. 北京: 中国石油大学(北京), 2018. LI Y X. Research on the scenario construction of leakage accidents and emergency management of common corridors in chemical industry park [D]. Beijing: China University of Petroleum (Beijing), 2018.
[4]	刘少杰. 城市油气管道爆燃事故风险演化及应急决策研究[D]. 青岛: 中国石油大学(华东), 2017. LIU S J. Study on explosion accident risk evolution and emergency decision for urban oil and gas pipeline [D]. Qingdao: China University of Petroleum (East China), 2017.
[5]	胡盛. 大型甲类仓库典型危险化学品爆炸灾害效应时空演化规律及防控策略[D]. 广州: 华南理工大学, 2020. HU S. Temporal and spatial evolution laws of explosive hazards of typical chemicals and pre-control strategies in large warehouses [D]. Guangzhou: South China University of Technology, 2020.
[6]	梅苑, 帅健, 李云涛, 等. 不同泄漏条件下输油管道泄漏事故后果研究 [J]. 石油与天然气化工, 2021, 50(3): 127–133. doi: 10.3969/j.issn.1007-3426.2021.03.021 MEI Y, SHUAI J, LI Y T, et al. Study on the consequences of oil pipeline leakage under different leakage conditions [J]. Chemical Engineering of Oil and Gas, 2021, 50(3): 127–133. doi: 10.3969/j.issn.1007-3426.2021.03.021
[7]	石剑云, 潘科. 开窗条件对室内天然气扩散影响的模拟研究 [J]. 大连交通大学学报, 2020, 41(6): 86–90. doi: 10.13291/j.cnki.djdxac.2020.06.016 SHI J Y, PAN K. Simulation study on the effect of window opening conditions on indoor natural gas diffusion [J]. Journal of Dalian Jiaotong University, 2020, 41(6): 86–90. doi: 10.13291/j.cnki.djdxac.2020.06.016
[8]	董浩宇. 地下综合管廊燃气爆炸灾害效应时空演化规律及防控策略 [D]. 广州: 华南理工大学, 2020. DONG H Y. Law of temporal and spatial evolution of gas explosion hazard and prevention and controlling in utility tunnel [D]. Guangzhou: South China University of Technology, 2020.
[9]	HANSEN O R, JOHNSON D M. Improved far-field blast predictions from fast deflagrations, DDTs and detonations of vapour clouds using FLACS CFD [J]. Journal of Loss Prevention in the Process Industries, 2015, 35: 293–306. doi: 10.1016/j.jlp.2014.11.005
[10]	HOLBORN P G, BENSON C M, INGRAM J M. Modelling hazardous distances for large-scale liquid hydrogen pool releases [J]. International Journal of Hydrogen Energy, 2020, 45(43): 23851–23871. doi: 10.1016/j.ijhydene.2020.06.131
[11]	LV D, TAN W, LIU L Y, et al. Research on maximum explosion overpressure in LNG storage tank areas [J]. Journal of Loss Prevention in the Process Industries, 2017, 49: 162–170. doi: 10.1016/j.jlp.2017.06.010
[12]	WAN S, YU M, ZHENG K, et al. Influence of side venting position on methane/air explosion characteristics in an end-vented duct containing an obstacle [J]. Experimental Thermal and Fluid Science, 2018, 92: 202–210. doi: 10.1016/j.expthermflusci.2017.11.022
[13]	CHAO J, BAUWENS C R, DOROFEEV S B. An analysis of peak overpressures in vented gaseous explosions [J]. Proceedings of the Combustion Institute, 2011, 33(2): 2367–2374. doi: 10.1016/j.proci.2010.06.144
[14]	KASMANI R M, ANDREWS G E, PHYLAKTOU H N. Experimental study on vented gas explosion in a cylindrical vessel with a vent duct [J]. Process Safety & Environmental Protection, 2013, 91(4): 245–252.
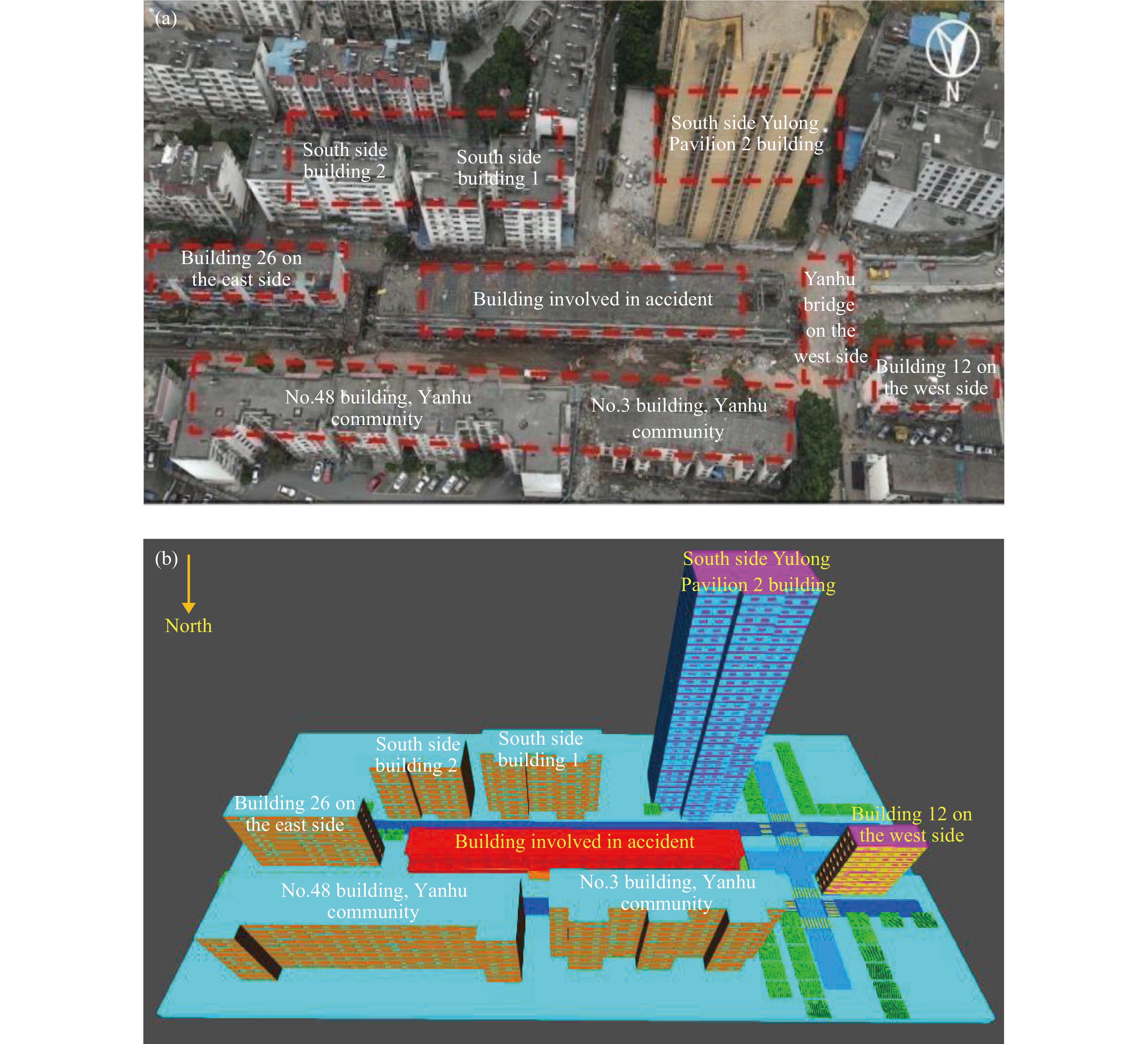
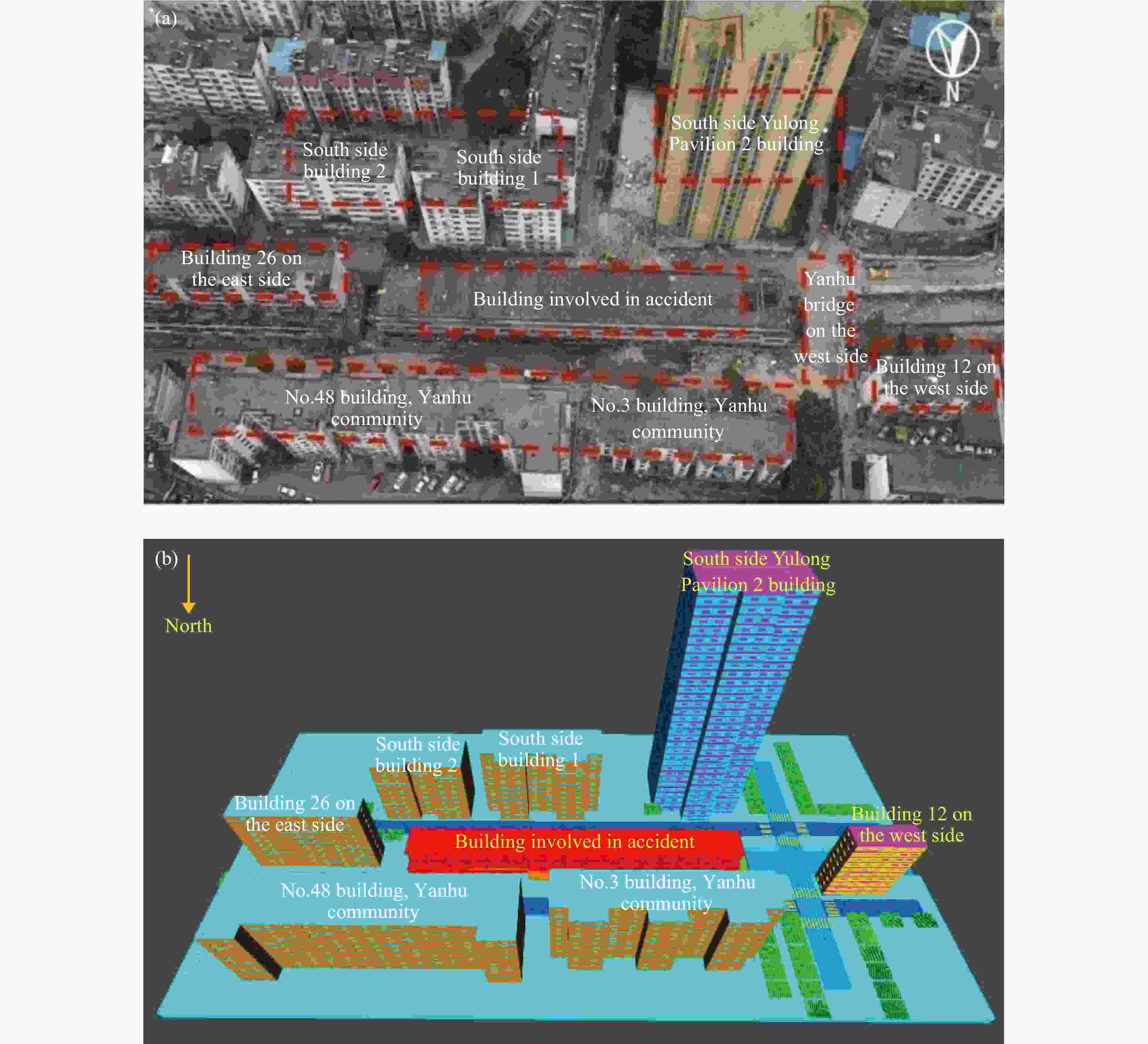
[15]	湖北省十堰市张湾区艳湖社区集贸市场“6·13”重大燃气爆炸事故调查报告[R]. 武汉: 湖北省应急管理厅, 2021. Investigation report of “June 13” gas explosion accident in Yanhu community market, Zhangwan district, Shiyan city, Hubei province [R]. Wuhan: Hubei Provincial Emergency Management Department, 2021.
[16]	董玉华, 周敬恩, 高惠临, 等. 长输管道稳态气体泄漏率的计算 [J]. 油气储运, 2002, 21(8): 11–15. DONG Y H, ZHOU J E, GAO H L, et al. Calculation of steady-state gas leakage rate in long distance pipeline [J]. Oil & Gas Storage and Transportation, 2002, 21(8): 11–15.
[17]	DONG Y H, GAO H L, ZHOU J E, et al. Evaluation of gas release rate through holes in pipelines [J]. Journal of Loss Prevention in the Process Industries, 2002, 15(6): 423–428. doi: 10.1016/S0950-4230(02)00041-4
[18]	赵雪娥, 孟亦飞, 刘秀玉. 燃烧与爆炸理论 [M]. 北京: 化学工业出版社, 2010: 134−135.
[19]	霍春勇, 董玉华, 余大涛, 等. 长输管线气体泄漏率的计算方法研究 [J]. 石油学报, 2004, 25(1): 101–105. HUO C Y, DONG Y H, YU D T, et al. Study on calculation method of gas leakage rate in long distance pipeline [J]. Acta Petrolei Sinica, 2004, 25(1): 101–105.
[20]	朱渊, 杨强, 左腾腾, 等. 基于FLACS的清管作业接收筒燃爆事故后果模拟及分析 [J]. 安全与环境学报, 2018, 18(5): 1762–1767. doi: 10.13637/j.issn.1009-6094.2018.05.019 ZHU Y, YANG Q, ZUO T T, et al. Simulation and analysis of the fire and explosion accident consequence of receiving tubes in pigging operation based on FLACS [J]. Journal of Safety and Environment, 2018, 18(5): 1762–1767. doi: 10.13637/j.issn.1009-6094.2018.05.019
[21]	潘旭海. 燃烧爆炸理论及应用 [M]. 北京: 化学工业出版社, 2015: 137−140. PAN X H. Theory and application of combustion and explosion [M]. Beijing: Chemical Industry Press, 2015: 137−140.