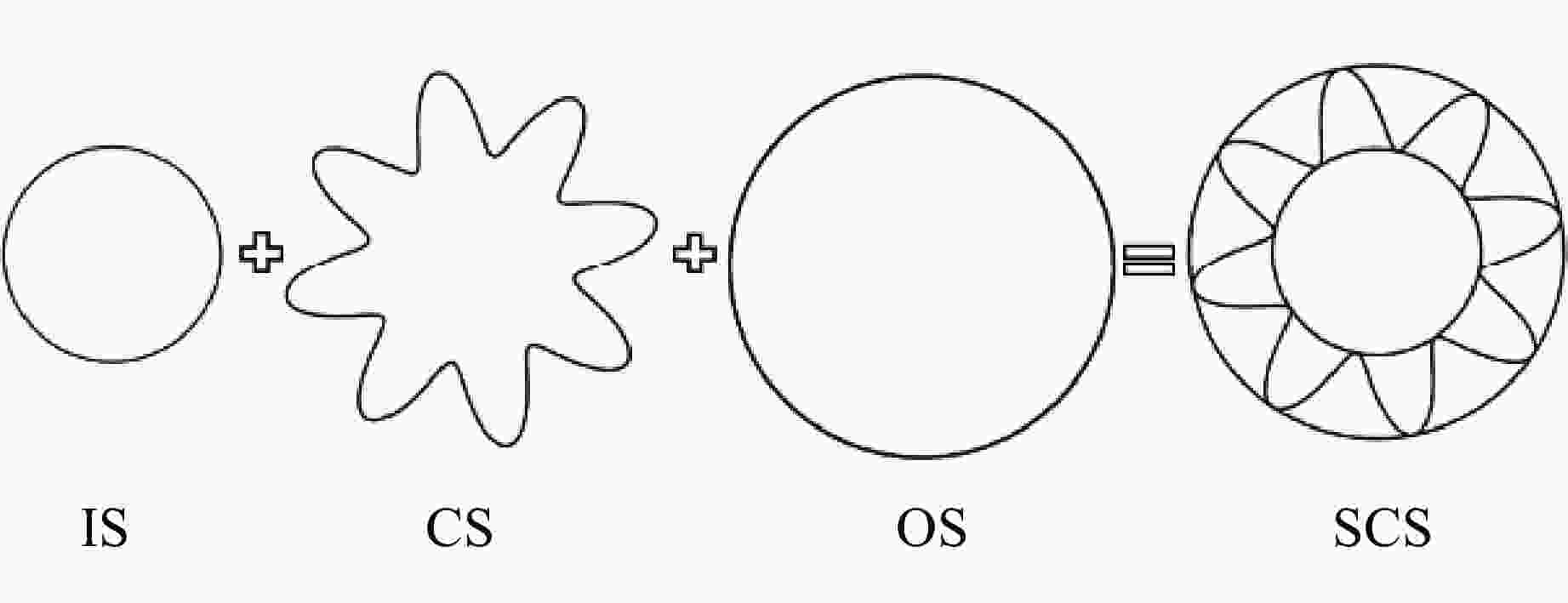
Quasi-Static Axial Energy Absorption Characteristics and Optimization of Sunflower-Like Sandwich Cylindrical Shells
-
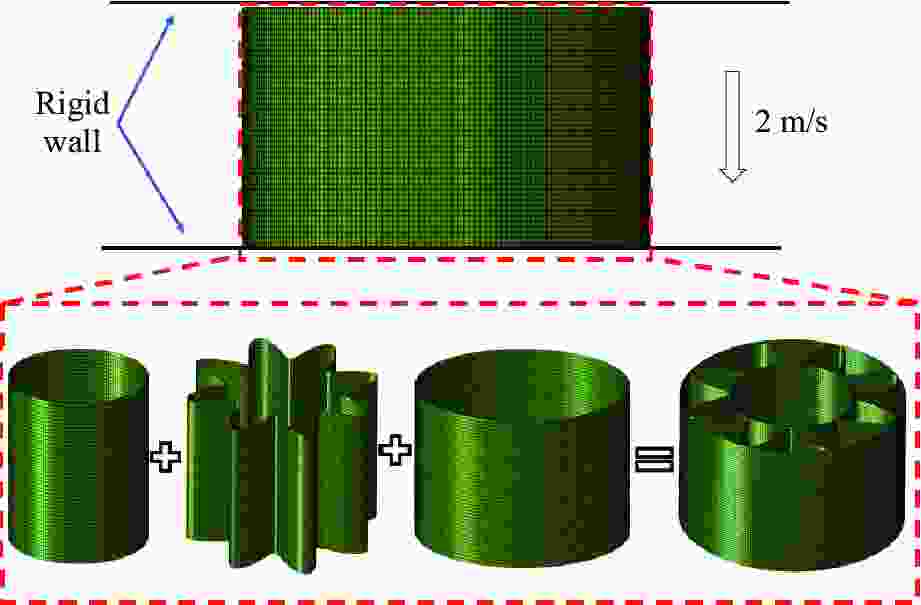
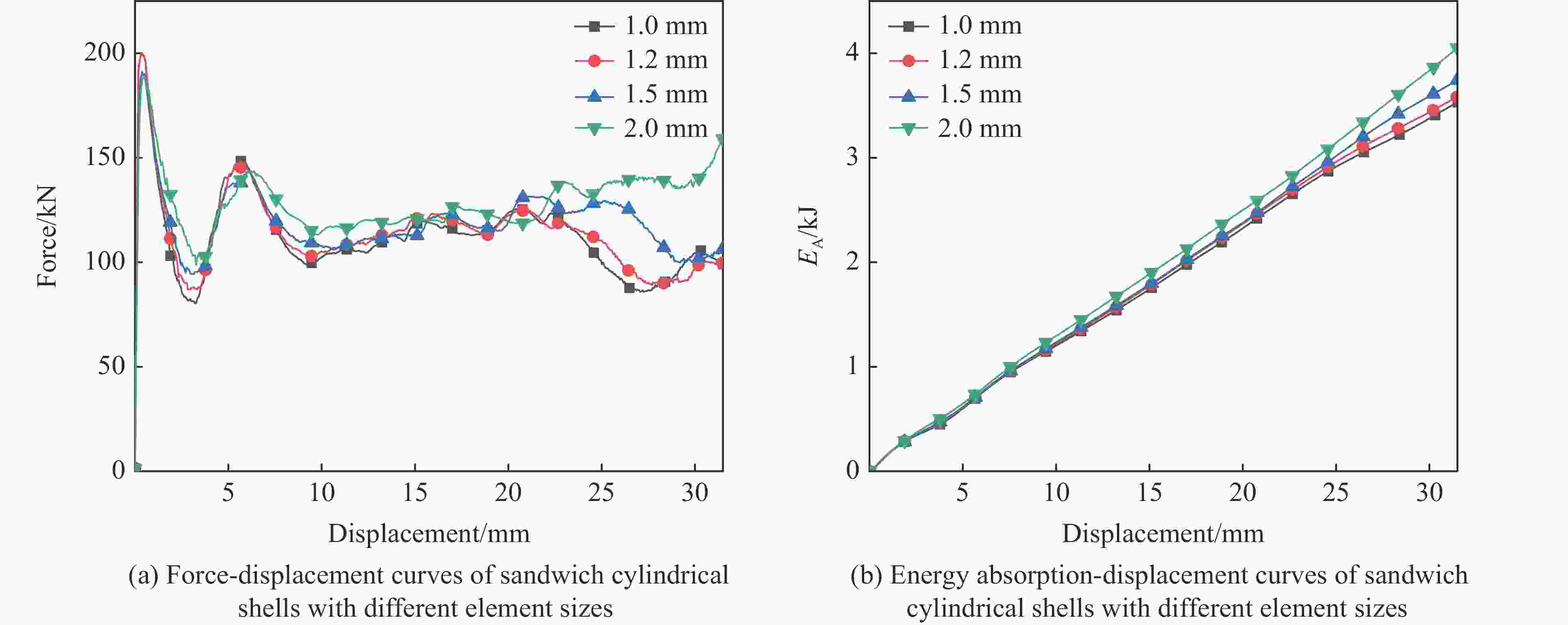
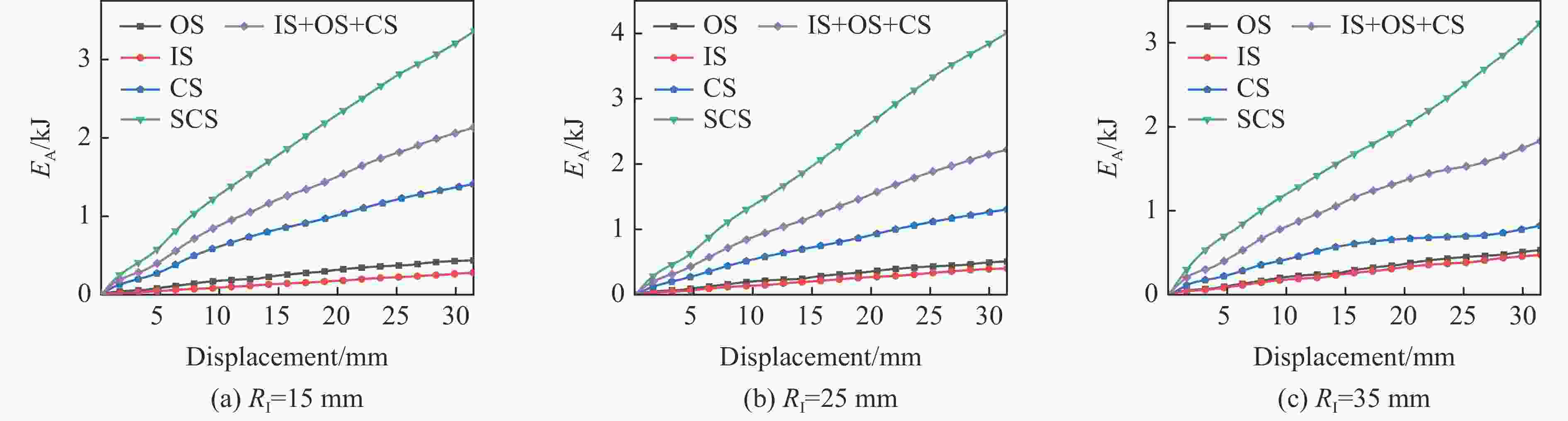
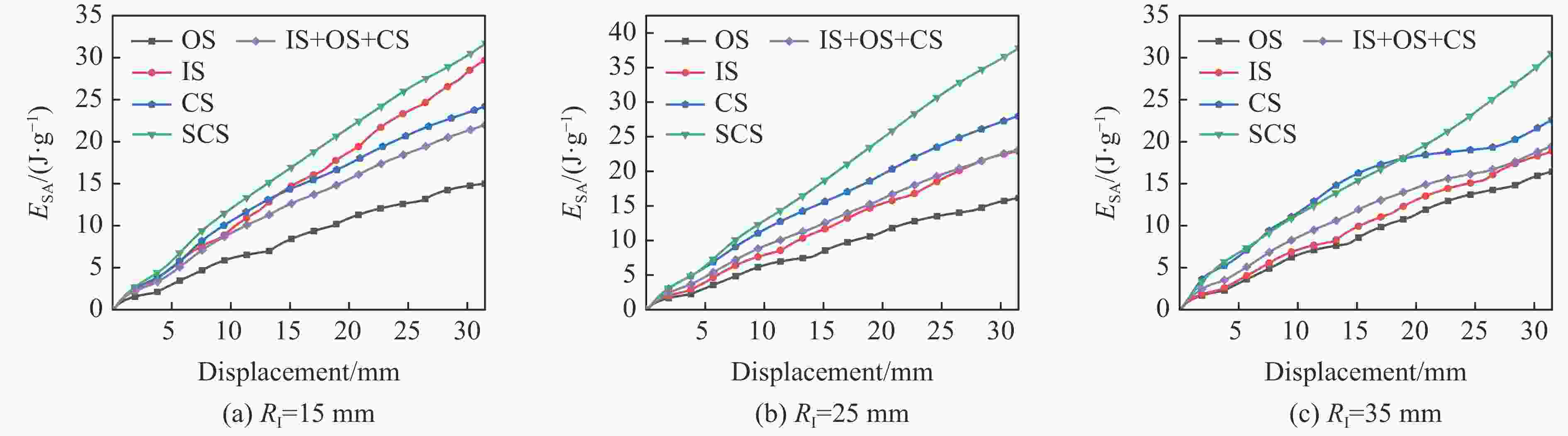
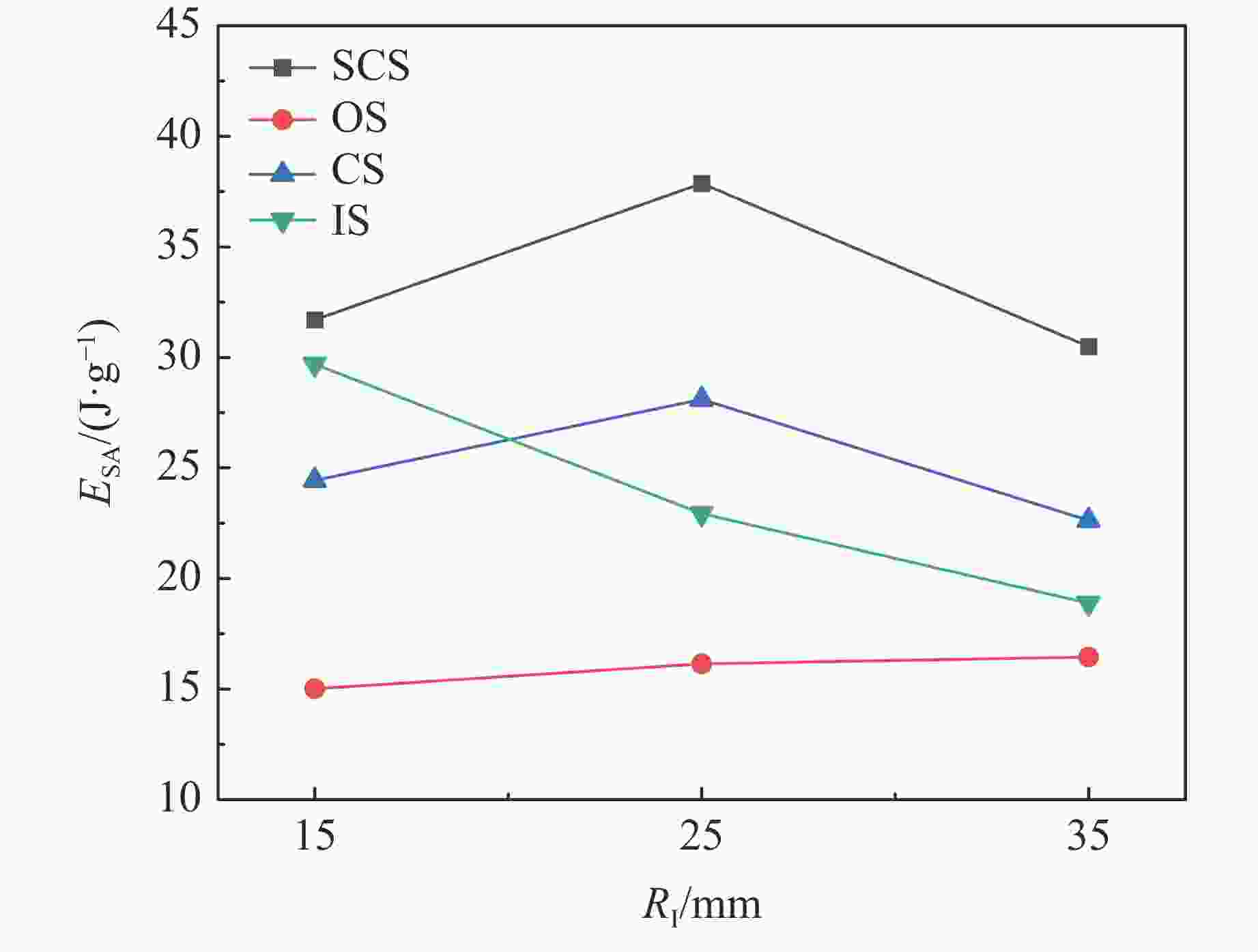
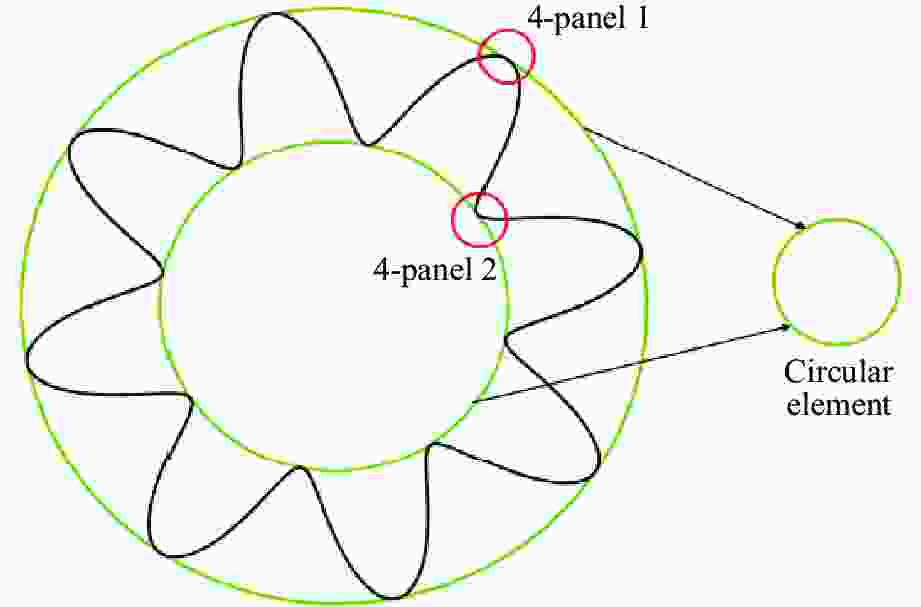
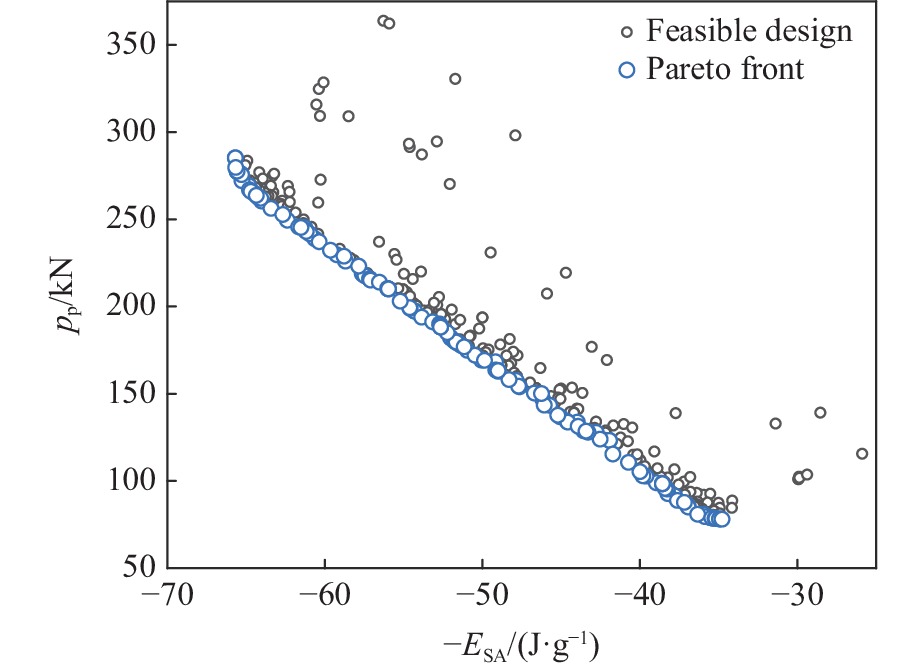
摘要: 采用实验、理论和数值模拟方法研究了类向日葵夹芯圆柱壳在准静态轴向加载下的吸能特性。首先,对3种内径的夹芯圆柱壳及其构件进行了准静态轴向压缩实验和数值模拟。结果表明:所有夹芯圆柱壳的比吸能和压溃力效率都大于其各个组成构件以及构件之和;芯壳的波浪形结构比圆柱壳结构具有更好的能量吸收能力;圆柱壳和波浪形曲线芯壳的联合使用可以有效地提高薄壁金属结构的吸能效率。其次,基于简化的超级折叠单元理论,推导了夹芯圆柱壳的轴向平均压溃力的理论公式。理论预测的平均压溃力与实验结果及数值模拟结果间的相对误差均在10%以内。最后,以比吸能最大和峰值压溃力最小为目标,进行了类向日葵夹芯圆柱壳吸能特性的多目标优化设计,得到了夹芯圆柱壳比吸能和峰值压溃力的Pareto前沿,优化后的夹芯圆柱壳的比吸能和平均压溃力均有提高,与此同时,质量减小。Abstract: Experiments, theoretical analysis, and numerical simulations were conducted to investigate the energy absorption characteristics of sunflower-like sandwich cylindrical shells under quasi-static axial loading. Firstly, quasi-static axial compression experiments and numerical simulations were conducted for sandwich cylindrical shells with three inner diameters and for their components. It was found that the specific energy absorptions and crushing force efficiencies of all sandwich cylindrical shells are greater than those of their individual components, and those of the sums of the individual components. The combination of cylindrical shell and corrugated core shell can effectively improve the energy absorption efficiency of thin-walled metal structure. Then, the theoretical formula of the axial average crushing force for the sandwich cylindrical shell was derived based on the simplified super folding element theory. The axial average crushing force predicted by the theoretical model was compared with the experimental and simulation results. It was found that the errors are within 10%. Finally, a multi-objective optimization design, with the objectives of maximum specific energy absorption and minimum peak crushing force for the sunflower-like sandwich cylindrical shell, was carried out. The Pareto front of specific energy absorption and peak crushing force of the sandwich cylindrical shell was obtained. The optimized sandwich cylindrical shell structure was improved in terms of specific energy absorption, average crushing force, and mass.
-
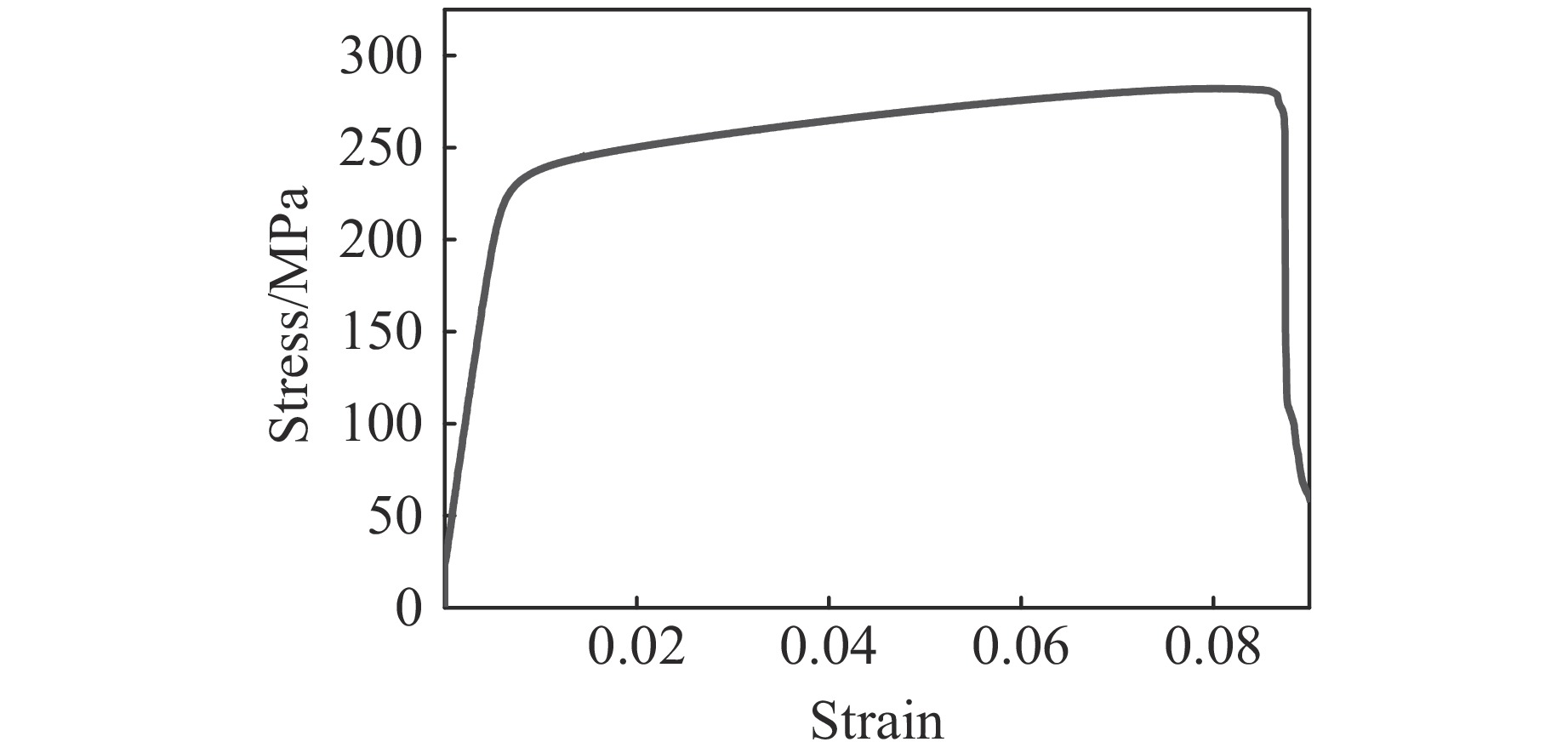
表 1 AA6061铝合金的材料属性
Table 1. Material properties of AA6061 aluminium alloy
Density/(kg·m−3) Young’s modulus/GPa Initial yield stress/MPa Ultimate strength/MPa Poison’s ratio 2.7×103 68.2 227 282 0.3 表 2 夹芯圆柱壳及其构件的壁厚和质量
Table 2. Wall thickness and mass of sandwich cylindrical shells and its components
Item t/mm m/kg RI=15 mm RI=25 mm RI=35 mm RI=15 mm RI=25 mm RI=35 mm SCS 1.00 1.08 1.11 0.102 0.103 0.103 IS 0.96 0.98 1.04 0.010 0.018 0.025 CS 0.96 1.04 1.10 0.058 0.046 0.037 OS 0.92 1.06 1.08 0.029 0.032 0.032 表 3 实验和有限元模拟获得的夹芯圆柱壳及其构件的SEA对比
Table 3. SEA comparison of experiments and finite element simulaitons of sandwich cylindrical shells and its components
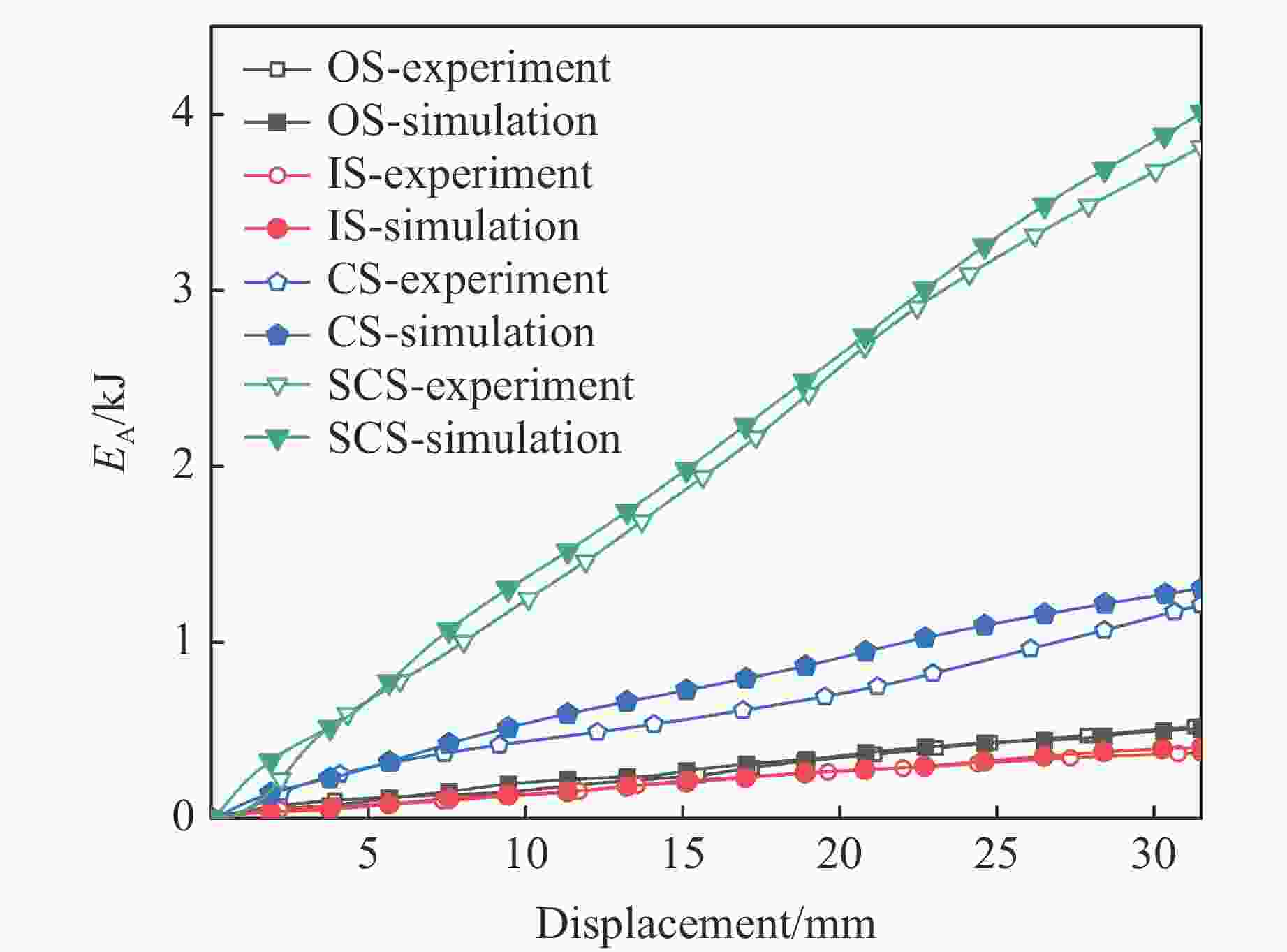
Name ESA for RI=15 mm ESA for RI=25 mm ESA for RI=35 mm Exp./(J·g−1) Sim./(J·g−1) Error/% Exp./(J·g−1) Sim./(J·g−1) Error/% Exp./(J·g−1) Sim./(J·g−1) Error/% SCS 34.82 31.70 −8.95 37.14 37.87 1.93 32.91 30.50 −7.91 IS 30.43 29.69 −2.43 21.16 22.93 7.73 18.54 18.89 1.84 OS 15.23 15.01 −1.46 16.49 16.14 −2.17 15.48 16.45 5.93 CS 21.18 24.44 13.36 26.12 28.10 7.05 23.85 22.63 −5.39 表 4 内径为25 mm的夹芯圆柱壳及其构件的能量吸收性能指标
Table 4. Energy absorption performance indicators of sandwich cylindrical shell with the inner diameter of 25 mm and its components
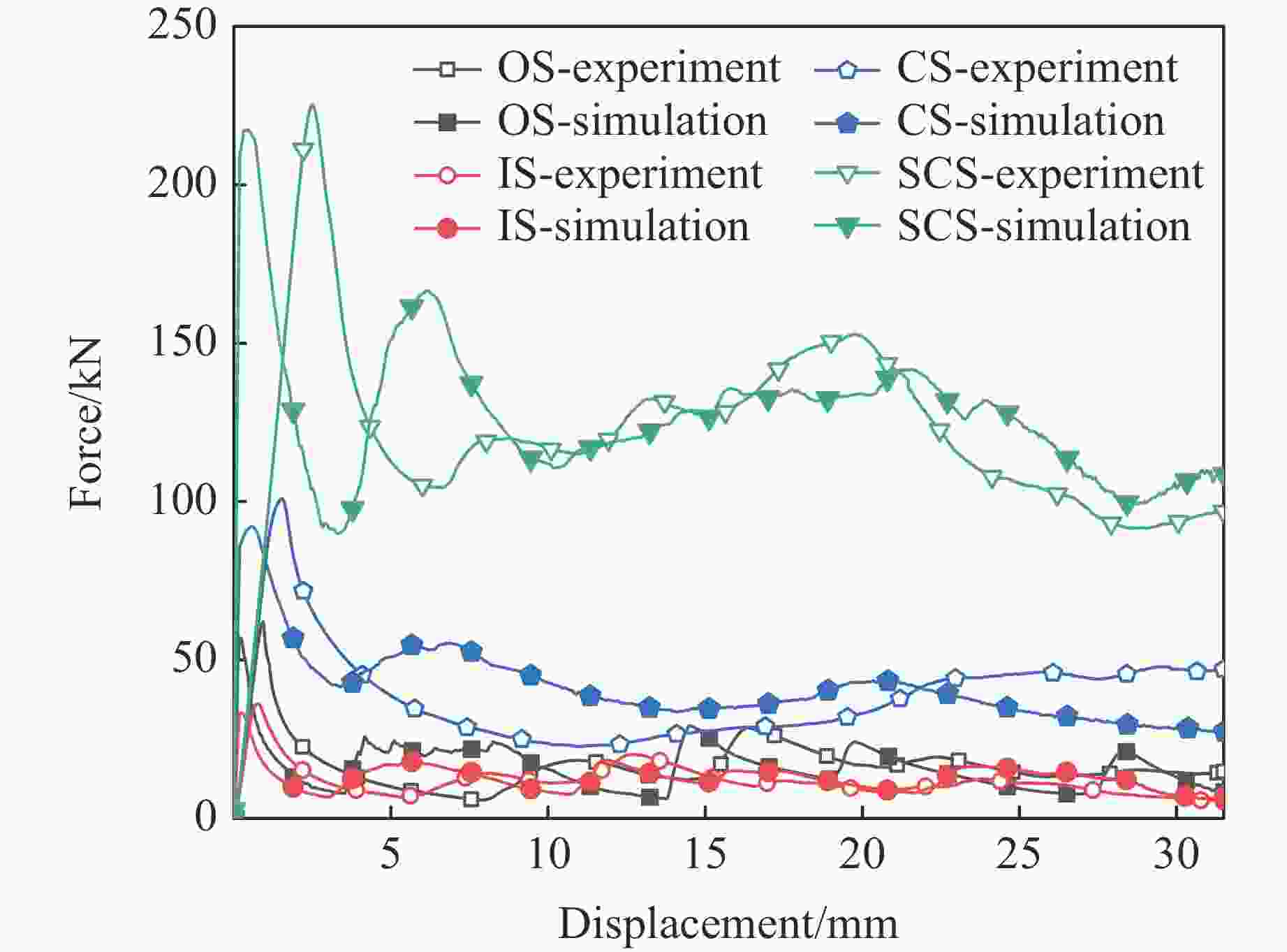
Item m/kg EA/kJ ESA/(J·g−1) pp/kN ηc SCS 0.106 4.02 37.87 217.36 0.59 IS 0.018 0.40 22.93 33.27 0.38 OS 0.032 0.51 16.14 57.10 0.28 CS 0.047 1.69 28.11 92.15 0.45 表 5 理论预测与实验及模拟结果的对比
Table 5. Comparison of theoretical predictions with experiments and simulations
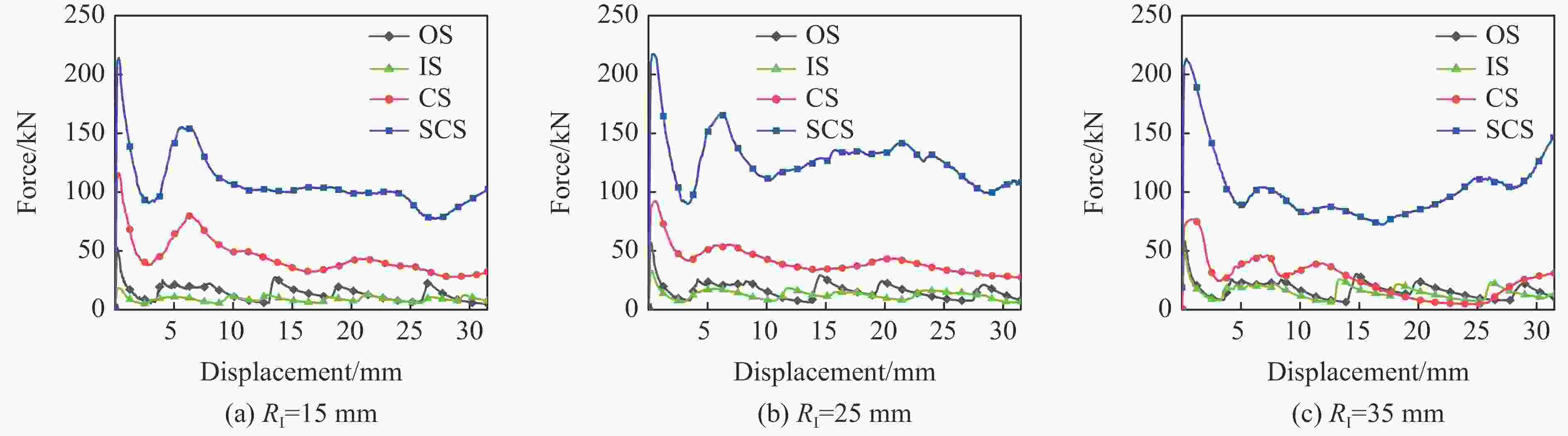
RI/mm t/mm pm/kN Error/% Theory Sim. Exp. Theory relative to simulation Theory relative to experiment 15 1.00 109.1 106.8 112.2 2.15 −2.76 25 1.08 115.1 121.2 121.2 −5.03 −5.03 35 1.11 116.5 114.2 107.7 2.01 8.17 表 6 夹芯圆柱壳的样本点及响应值
Table 6. Sample points and response values of sandwich cylindrical shells
No. RI/mm RO/mm t/mm pp/kN ESA/(J·g−1) 1 23.05 37.05 0.816 154.1 43.7 2 23.58 46.00 1.079 273.3 41.6 3 32.00 38.11 0.763 129.5 40.4 4 27.79 36.53 0.711 119.2 41.9 5 26.74 43.37 0.974 217.1 42.5 6 31.47 42.32 0.868 170.9 40.5 7 28.32 44.42 1.500 360.6 58.7 8 28.84 44.95 0.658 142.6 34.7 9 22.00 38.63 1.237 269.4 52.7 10 22.53 41.79 0.921 208.2 40.6 11 30.95 41.26 1.289 262.3 53.8 12 25.16 39.68 0.553 104.7 33.3 13 24.63 43.89 0.605 132.9 30.4 14 29.89 37.58 1.184 213.8 51.7 15 25.68 36.00 1.342 249.7 60.6 16 29.37 40.74 0.500 91.6 30.7 17 30.42 45.47 1.132 258.8 47.3 18 24.11 42.84 1.395 337.4 52.7 19 27.26 40.21 1.447 307.0 62.0 20 26.21 39.16 1.026 203.3 48.0 表 7 夹芯圆柱壳近似模型的预测精度评估
Table 7. Evaluation of prediction accuracy of the approximation models for sandwich cylindrical shell
Model R2 P Q pp ESA pp ESA pp ESA KRG 0.9742 0.9687 0.0458 0.0520 0.1501 0.1354 RBF 0.9951 0.9737 0.0198 0.0476 0.0683 0.1088 RSM 0.9993 0.9718 0.0076 0.0494 0.0171 0.1137 表 8 NSGA-Ⅱ算法参数设置
Table 8. Parameters of NSGA-Ⅱ algorithm
Population size Number of iterations Crossover probability Crossover distribution index Mutation distribution index 12 40 0.9 10 20 表 9 优化获得的PCF和 SEA 与有限元结果对比
Table 9. PCF and SEA comparison between optimization results and finite element results
pp/kN ESA/(J·g−1) Error/% Optimization Simulation Optimization Simulation pp ESA 204.1 206.2 53.7 52.2 1.0 2.9 表 10 优化前后模拟结果的对比
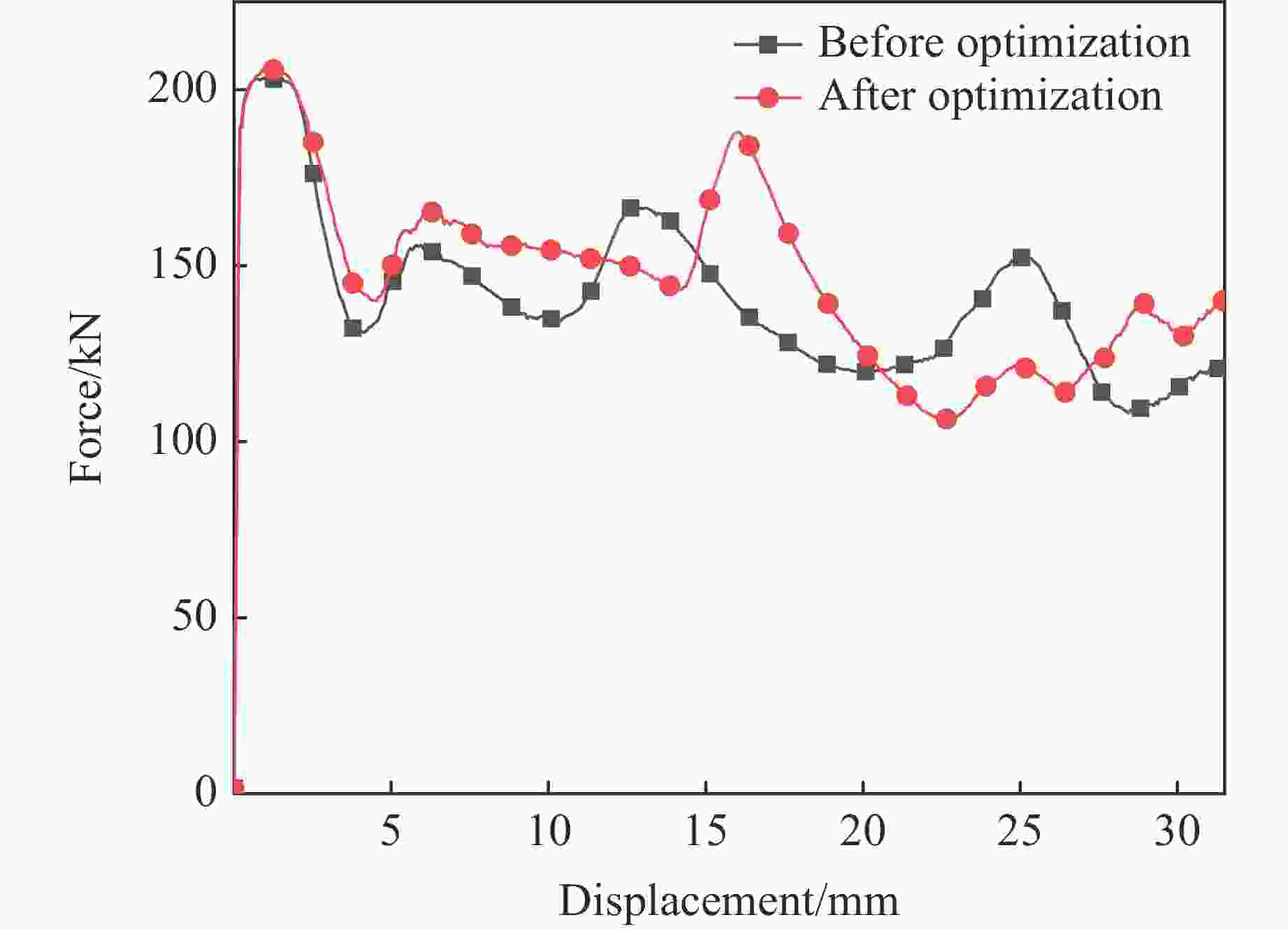
Table 10. Comparison of simulation results before and after optimization
Case pp/kN ESA/(J·g−1) pm/kN m/kg Before optimization 203.3 48.0 140.0 0.092 After optimization 206.2 52.2 146.2 0.088 Change/% 1.43 8.75 4.43 −4.35 -
[1] JOHNSON W, SODEN P D, AL-HASSANI S T S. Inextensional collapse of thin-walled tubes under axial compression [J]. The Journal of Strain Analysis for Engineering Design, 1977, 12(4): 317–330. doi: 10.1243/03093247V124317 [2] ANDREWS K R F, ENGLAND G L, GHANI E. Classification of the axial collapse of cylindrical tubes under quasi-static loading [J]. International Journal of Mechanical Sciences, 1983, 25(9/10): 687–696. [3] 李志斌, 虞吉林, 郑志军, 等. 薄壁管及其泡沫金属填充结构耐撞性的实验研究 [J]. 实验力学, 2012, 27(1): 77–86.LI Z B, YU J L, ZHENG Z J, et al. An experimental study on the crashworthiness of thin-walled tubes and their metallic foam-filled structures [J]. Journal of Experimental Mechanics, 2012, 27(1): 77–86. [4] ALI M, OHIOMA E, KRAFT F, et al. Theoretical, numerical, and experimental study of dynamic axial crushing of thin walled pentagon and cross-shape tubes [J]. Thin-Walled Structures, 2015, 94: 253–272. doi: 10.1016/j.tws.2015.04.007 [5] 荆友录, 温卫东, 魏民祥. 不同截面结构薄壁直梁的轴向耐撞性研究 [J]. 机械科学与技术, 2009, 28(4): 455–459. doi: 10.3321/j.issn:1003-8728.2009.04.008JING Y L, WEN W D, WEI M X. A study of the axial crashworthiness of thin-walled straight beams with different shapes [J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(4): 455–459. doi: 10.3321/j.issn:1003-8728.2009.04.008 [6] VINAYAGAR K, SENTHIL KUMAR A. Crashworthiness analysis of double section bi-tubular thin-walled structures [J]. Thin-Walled Structures, 2017, 112: 184–193. doi: 10.1016/j.tws.2016.12.008 [7] ZHENG G, WU S Z, SUN G Y, et al. Crushing analysis of foam-filled single and bitubal polygonal thin-walled tubes [J]. International Journal of Mechanical Sciences, 2014, 87: 226–240. doi: 10.1016/j.ijmecsci.2014.06.002 [8] GOEL M D. Deformation, energy absorption and crushing behavior of single-, double- and multi-wall foam filled square and circular tubes [J]. Thin-Walled Structures, 2015, 90: 1–11. doi: 10.1016/j.tws.2015.01.004 [9] CHEN H C, ZHANG Y, LIN J M, et al. Crushing responses and optimization of novel sandwich columns [J]. Composite Structures, 2021, 263: 113682. doi: 10.1016/j.compstruct.2021.113682 [10] 马梦娇, 刘志芳, 李世强. 波纹芯层夹芯管的轴向压缩吸能特性与多目标优化 [J]. 高压物理学报, 2022, 36(6): 064201.MA M J, LIU Z F, LI S Q. Energy absorption and multi-objective optimization for sandwich tubes with a corrugated core under axial compression [J]. Chinese Journal of High Pressure Physics, 2022, 36(6): 064201. [11] 葛平政, 张勇. 新颖波纹截面薄壁圆管的耐撞性 [J]. 华侨大学学报(自然科学版), 2016, 37(5): 531–535.GE P Z, ZHANG Y. Crashworthiness of novel thin-walled circular tube with novel corrugated cross section [J]. Journal of Huaqiao University (Natural Science), 2016, 37(5): 531–535. [12] 闫栋, 王根伟, 宋辉, 等. 类向日葵夹芯圆柱壳径向冲击数值模拟 [J]. 高压物理学报, 2020, 34(5): 054201.YAN D, WANG G W, SONG H, et al. Numerical simulation of radial impact on sunflower-like sandwich cylindrical shell [J]. Chinese Journal of High Pressure Physics, 2020, 34(5): 054201. [13] YIN H F, WEN G L, HOU S J, et al. Crushing analysis and multiobjective crashworthiness optimization of honeycomb-filled single and bitubular polygonal tubes [J]. Materials & Design, 2011, 32(8/9): 4449−4460. [14] ZHANG Y, XU X, WANG J, et al. Crushing analysis for novel bio-inspired hierarchical circular structures subjected to axial load [J]. International Journal of Mechanical Sciences, 2018, 140: 407–431. doi: 10.1016/j.ijmecsci.2018.03.015 [15] LI W W, LUO Y H, LI M, et al. A more weight-efficient hierarchical hexagonal multi-cell tubular absorber [J]. International Journal of Mechanical Sciences, 2018, 140: 241–249. doi: 10.1016/j.ijmecsci.2018.03.006 [16] CHEN W G, WIERZBICKI T. Relative merits of single-cell, multi-cell and foam-filled thin-walled structures in energy absorption [J]. Thin-Walled Structures, 2001, 39(4): 287–306. doi: 10.1016/S0263-8231(01)00006-4 [17] ABRAMOWICZ W, JONES N. Dynamic axial crushing of square tubes [J]. International Journal of Impact Engineering, 1984, 2(2): 179–208. doi: 10.1016/0734-743X(84)90005-8 [18] LANGSETH M, HOPPERSTAD O S, HANSSEN A G. Crash behaviour of thin-walled aluminium members [J]. Thin-Walled Structures, 1998, 32(1/2/3): 127–150. [19] ZHANG Y, CHEN T T, XU X, et al. Out-of-plane mechanical behaviors of a side hierarchical honeycomb [J]. Mechanics of Materials, 2020, 140: 103227. doi: 10.1016/j.mechmat.2019.103227 [20] TRAN T, HOU S J, HAN X, et al. Crushing analysis and numerical optimization of angle element structures under axial impact loading [J]. Composite Structures, 2015, 119: 422–435. doi: 10.1016/j.compstruct.2014.09.019 [21] LI Z C, RAKHEJA S, SHANGGUAN W B. Study on crushing behaviors of foam-filled thin-walled square tubes with different types and number of initiators under multiple angle loads [J]. Thin-Walled Structures, 2019, 145: 106376. doi: 10.1016/j.tws.2019.106376 -






 下载:
下载: