Crashworthiness Evaluation of Star-Shaped Hybrid Multi-Cell Tubes under Multiple Impact Angles
-
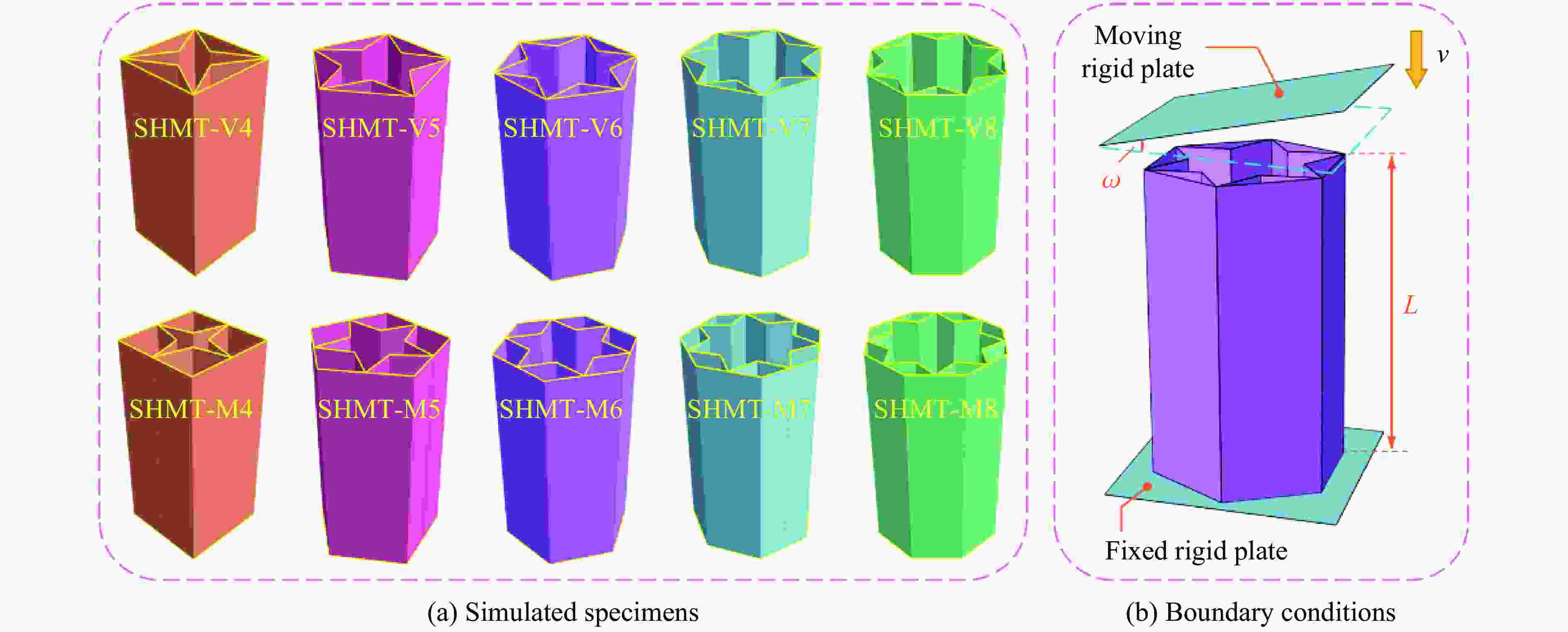
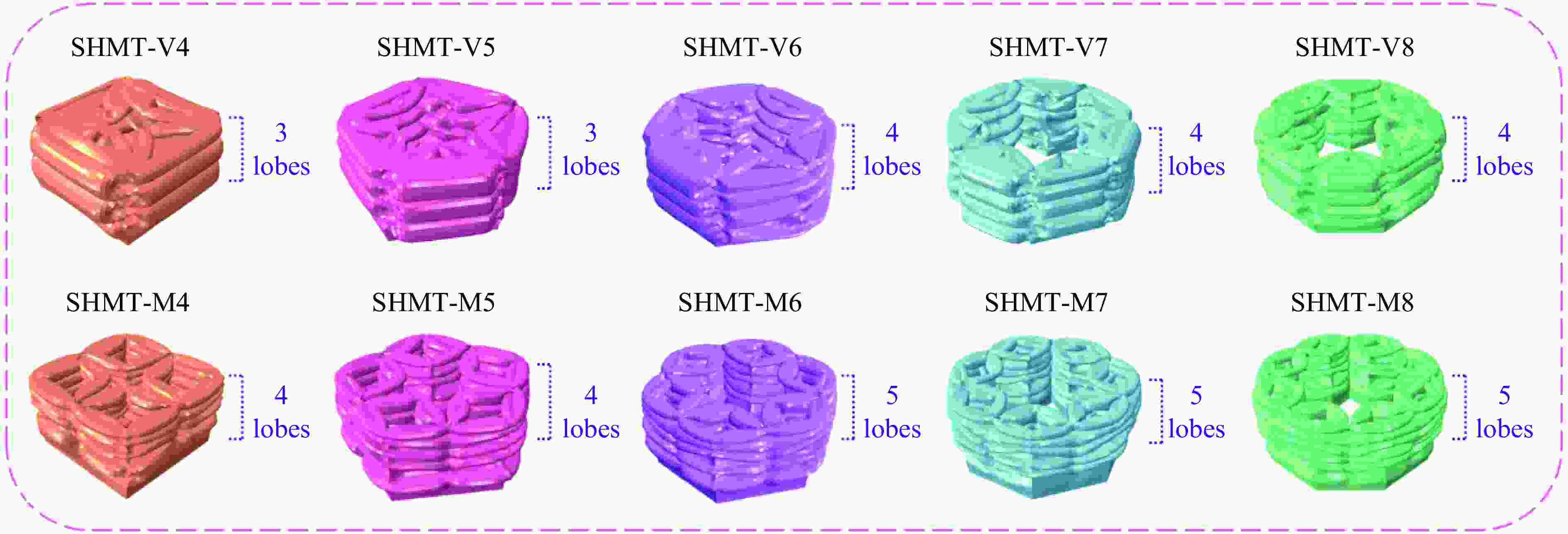
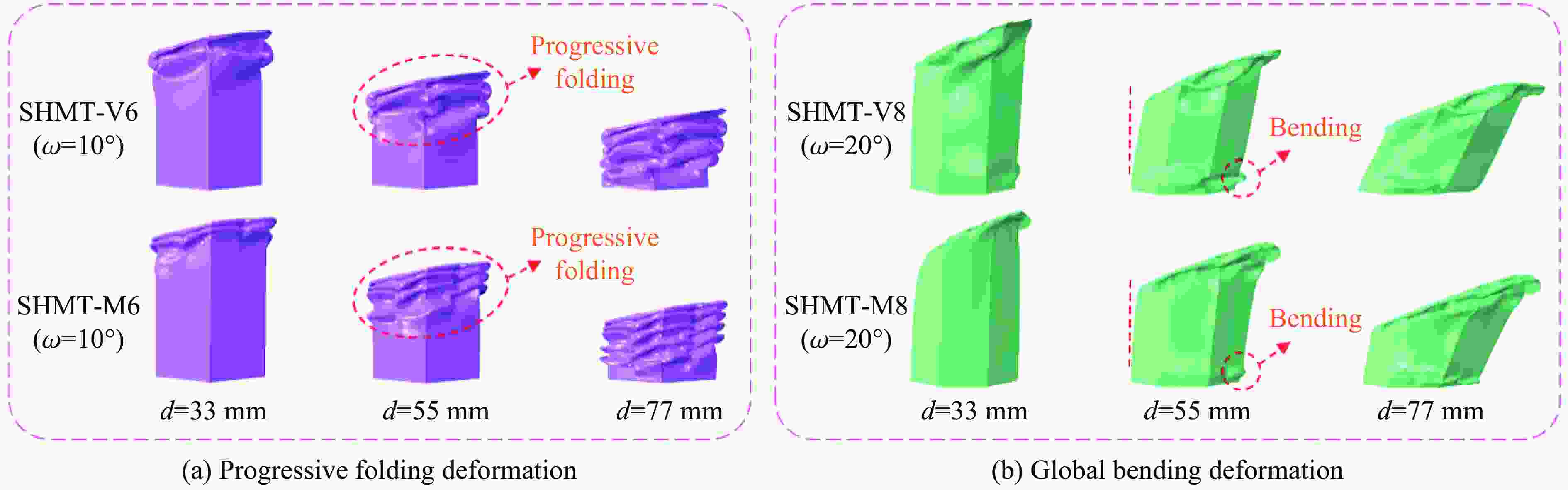
摘要: 基于混合截面的设计思路，针对星形混合多胞管（star-shaped hybrid multi-cell tube，SHMT）提出了10种截面设计方案。通过数值模拟的方式，深入分析了SHMT在多种冲击角度下的耐撞性。研究发现，混合截面的连接方式以及多边形边数均对星形混合多胞管的吸能性能产生重要影响。在轴向冲击下，采用顶点连接的SHMT（SHMT-V）对于多边形边数的变化较为敏感，八边形SHMT-V（SHMT-V8）的比吸能高达24.31 J/g，相比于四边形SHMT-V（SHMT-V4）提高了71.86%；采用中点连接的SHMT（SHMT-M）拥有更强的力学响应，其碰撞力性能比SHMT-V高30%以上。在斜向冲击下，SHMT的承载能力随着冲击角度的增加而减小，截面不同的SHMT的耐撞性能表现出较大的不确定性。采用优劣解距离法对SHMT的综合耐撞性进行了评估。结果表明，八边形SHMT-M（SHMT-M8）是最优的截面设计方案。研究成果可为薄壁结构的实际应用与耐撞性优化设计提供指导。Abstract: Based on the hybrid cross-section design, 10 kinds of cross-section design of star-shaped hybrid multi-cell tube (SHMT) were proposed. The crashworthiness of SHMT under multiple impact angles was studied by numerical simulation. It is found that the connection mode of hybrid cross-section and the number of polygonal edges N have important influences on the energy absorption of SHMT. Under axial impact, SHMT with vertex connection (SHMT-V) is more sensitive to N. The specific absorption energy of octagonal SHMT-V (SHMT-V8) reaches 24.31 J/g, which is 71.86% higher than that of quadrangular SHMT-V (SHMT-V4). SHMT with midpoint connection (SHMT-M) has stronger mechanical response, and its crushing force is more than 30% higher than that of SHMT-V. Under oblique impact, the load-carrying capacity of SHMT decreases with the increase of the impact angle, and the crashworthiness of SHMT shows great uncertainty. Technique for order preference by similarity to ideal solution method (TOPSIS) was used to evaluate the crashworthiness of SHMT. The results show that SHMT-M8 is the optimal cross-section design. The research results of this paper can provide guidance for practical application and crashworthiness optimization design of thin-walled structures.
-
图 2 有限元模型的模拟试件与边界条件
Figure 2. Simulated specimens and boundary conditions of finite element model
图 5 实验与有限元模拟的结果对比
Figure 5. Comparison of experimental and finite element simulation results
图 6 星形混合多胞管在轴向冲击下的碰撞力-位移曲线和能量吸收曲线
Figure 6. Force-displacement curves and
$ {E}_{\mathrm{A}} $ -displacement curves of SHMT under axial impact
图 7 星形混合多胞管在斜向冲击下的碰撞力-位移曲线
Figure 7. Force-displacement curves of SHMT under oblique impact
图 8 SHMT-V4与SHMT-M4的变形过程比较
Figure 8. Comparison of deformation process between SHMT-V4 and SHMT-M4
图 9 轴向冲击下星形混合多胞管压溃后的变形情况
Figure 9. Deformations of SHMT after collapse under axial impact
图 10 斜向冲击下星形混合多胞管的变形过程比较
Figure 10. Comparison of deformation process of SHMT under oblique impact
图 12 多种冲击角度下星形混合多胞管的
$ {P}_{\mathrm{p}} $ Figure 12.
$ {P}_{\mathrm{p}} $ of SHMT under multiple impact angles
图 13 多种冲击角度下星形混合多胞管的
$ {P}_{\mathrm{m}} $ Figure 13.
$ {P}_{\mathrm{m}} $ of SHMT under multiple impact angles
图 14 SHMT-V与SHMT-M的
$ \eta $ 比较Figure 14. Comparison of
$ \eta $ between SHMT-V and SHMT-M
图 15 SHMT-V与SHMT-M的
$ {E}_{\mathrm{S}\mathrm{A}} $ 比较Figure 15. Comparison of
$ {E}_{\mathrm{S}\mathrm{A}} $ between SHMT-V and SHMT-M表 1 星形混合多胞管的几何参数
Table 1. Geometric parameters of SHMT
Specimens $ {l}_{1} $/mm $ {l}_{2} $/mm $ t $/mm Specimens $ {l}_{1} $/mm $ {l}_{2} $/mm $ t $/mm SHMT-V4 28.28 48.99 1.06 SHMT-M4 20.00 48.99 1.26 SHMT-V5 23.51 40.72 1.02 SHMT-M5 19.02 40.72 1.14 SHMT-V6 20.00 34.64 1.00 SHMT-M6 17.32 34.64 1.08 SHMT-V7 17.36 30.06 0.99 SHMT-M7 15.64 30.06 1.04 SHMT-V8 15.31 26.51 0.98 SHMT-M8 14.14 26.51 1.02 
下载: 导出CSV
表 2 星形混合多胞管的数值矩阵
Table 2. Numerical matrix of SHMT
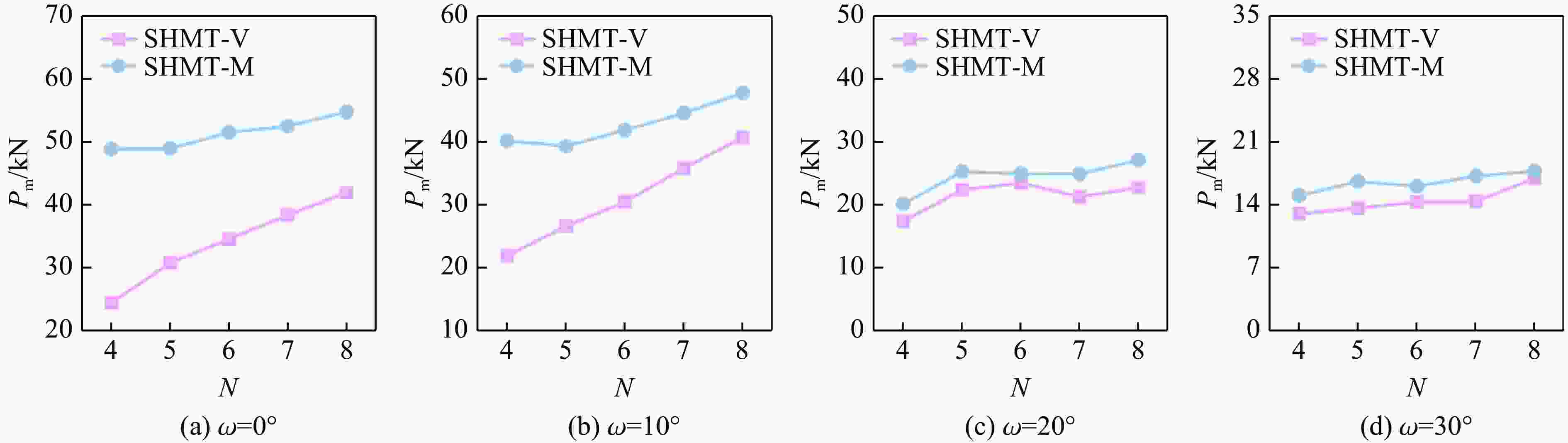
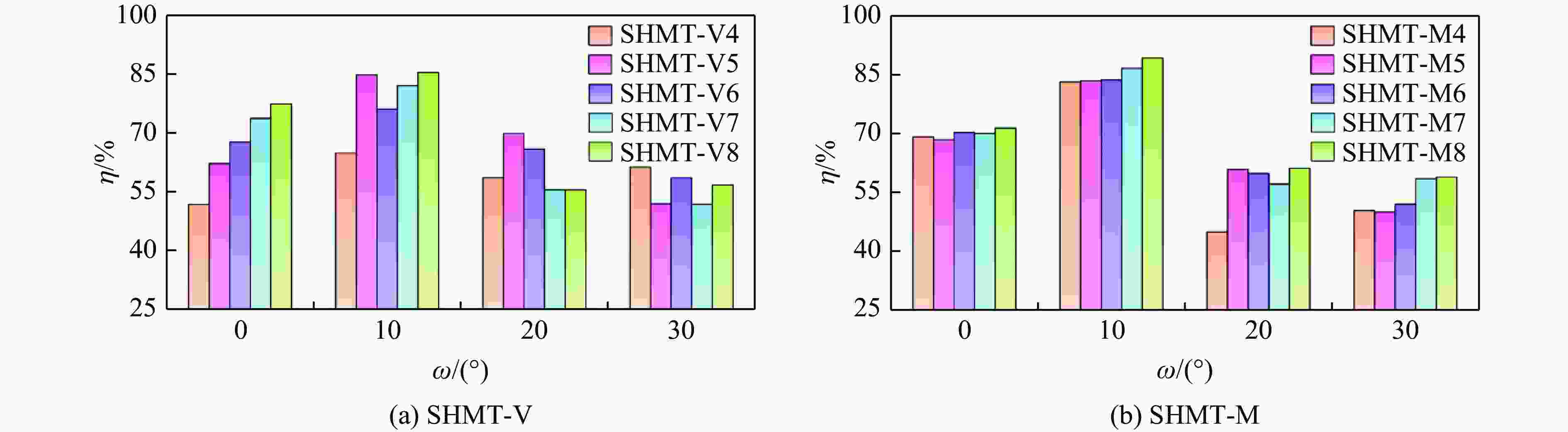
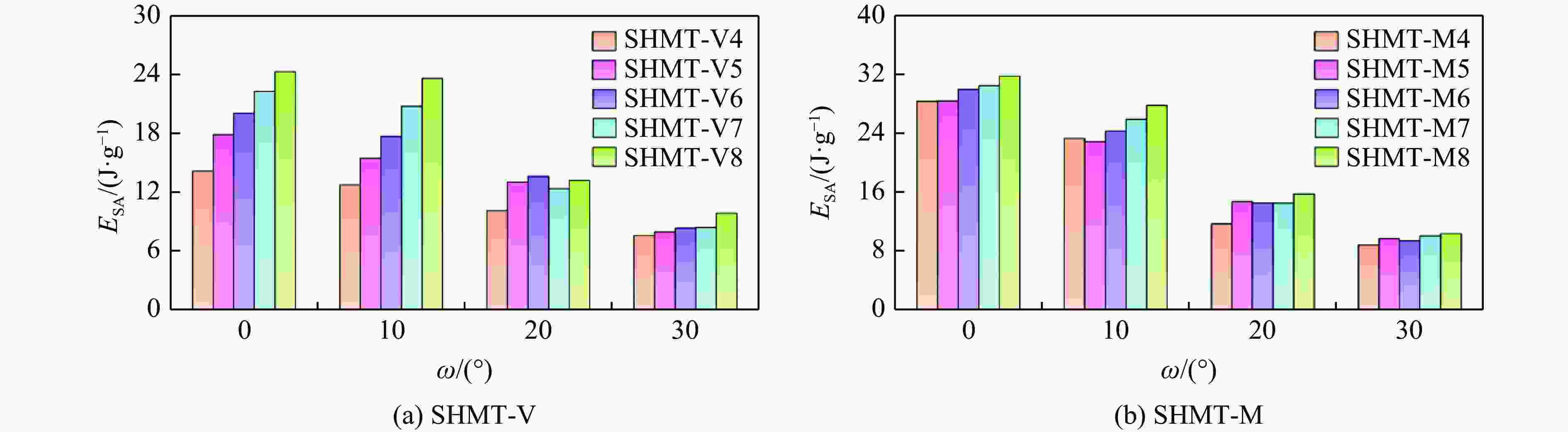
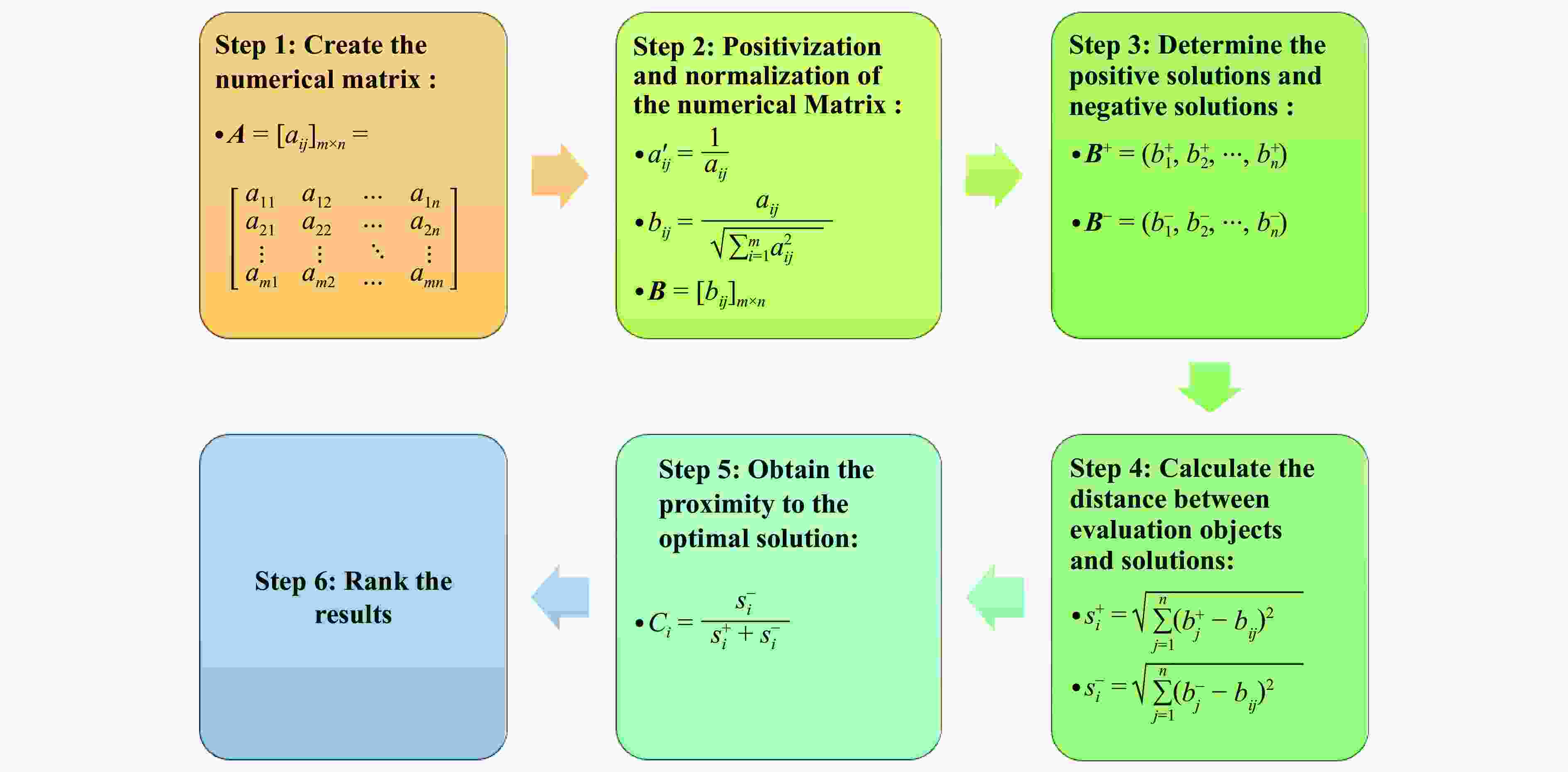
Specimens ${P}{_{\mathrm{p} } }$/kN $ \eta $/% ${E}{_{\mathrm{S}\mathrm{A} } }$/(J·g−1) ω=0° ω=10° ω=20° ω=30° ω=0° ω=10° ω=20° ω=30° ω=0° ω=10° ω=20° ω=30° SHMT-V4 47.07 33.69 29.58 21.20 51.82 64.91 58.62 61.32 14.14 12.71 10.07 7.55 SHMT-V5 49.46 31.36 31.99 26.21 62.18 84.83 69.89 51.94 17.88 15.44 12.99 7.90 SHMT-V6 50.99 40.00 35.53 24.38 67.73 76.10 65.92 58.58 20.05 17.67 13.59 8.28 SHMT-V7 52.01 43.64 38.32 27.70 73.71 82.07 55.51 51.85 22.27 20.77 12.35 8.36 SHMT-V8 54.08 47.61 40.89 29.82 77.44 85.44 55.52 56.75 24.31 23.63 13.18 9.82 SHMT-M4 70.56 48.26 44.72 29.78 69.20 83.21 44.99 50.41 28.33 23.29 11.65 8.72 SHMT-M5 71.45 47.08 41.52 33.13 68.43 83.46 60.83 50.03 28.39 22.83 14.68 9.62 SHMT-M6 73.30 50.00 41.66 30.83 70.26 83.70 59.88 52.06 29.94 24.29 14.49 9.32 SHMT-M7 74.90 51.42 43.56 29.39 70.05 86.65 57.17 58.48 30.45 25.89 14.45 9.98 SHMT-M8 76.61 53.53 44.22 30.10 71.45 89.23 61.17 58.92 31.76 27.75 15.70 10.30
下载: 导出CSV
表 3 TOPSIS方法得出的评估结果
Table 3. Evaluation results obtained using TOPSIS method
Specimens ${S}_{i}^+$ ${S}_{i}^-$ ${C}{_{i} }$ Rank Specimens ${S}_{i}^+$ ${S}_{i}^-$ ${C}{_{i} }$ Rank SHMT-V4 0.3867 0.3093 0.4444 9 SHMT-M4 0.3388 0.2666 0.4404 10 SHMT-V5 0.2970 0.3169 0.5162 5 SHMT-M5 0.3020 0.3000 0.4983 7 SHMT-V6 0.2688 0.2760 0.5066 6 SHMT-M6 0.2974 0.3186 0.5172 4 SHMT-V7 0.2809 0.2578 0.4786 8 SHMT-M7 0.2968 0.3426 0.5358 2 SHMT-V8 0.2716 0.3003 0.5250 3 SHMT-M8 0.3018 0.3873 0.5620 1
下载: 导出CSV
-
[1] YAO R Y, PANG T, HE S Y, et al. A bio-inspired foam-filled multi-cell structural configuration for energy absorption [J]. Composites Part B: Engineering, 2022, 238: 109801. doi: 10.1016/j.compositesb.2022.109801 [2] ZHANG J X, GUO H Y, DU J L, et al. Splitting and curling collapse of metal foam core square sandwich metal tubes: experimental and theoretical investigations [J]. Thin-Walled Structures, 2021, 169: 108346. doi: 10.1016/j.tws.2021.108346 [3] 邓敏杰, 刘志芳. 仿马尾草薄壁结构的设计与耐撞性研究 [J]. 高压物理学报, 2022, 36(3): 034202.DENG M J, LIU Z F. Design and crashworthiness study based on horsetail bionic thin-walled structure [J]. Chinese Journal of High Pressure Physics, 2022, 36(3): 034202. [4] SAN HA N, PHAM T M, HAO H, et al. Energy absorption characteristics of bio-inspired hierarchical multi-cell square tubes under axial crushing [J]. International Journal of Mechanical Sciences, 2021, 201: 106464. doi: 10.1016/j.ijmecsci.2021.106464 [5] ZHANG J X, YE Y, ZHU Y Q, et al. On axial splitting and curling behaviour of circular sandwich metal tubes with metal foam core [J]. International Journal of Solids and Structures, 2020, 202: 111–125. doi: 10.1016/j.ijsolstr.2020.06.021 [6] PANG T, ZHENG G, FANG J G, et al. Energy absorption mechanism of axially-varying thickness (AVT) multicell thin-walled structures under out-of-plane loading [J]. Engineering Structures, 2019, 196: 109130. doi: 10.1016/j.engstruct.2019.04.074 [7] ZHANG J X, DU J L, GUO H Y, et al. Splitting and curling performance of metal foam-filled circular tubes [J]. Acta Mechanica, 2022, 233(2): 535–559. doi: 10.1007/s00707-021-03116-z [8] WANG Z G, ZHANG J, LI Z D, et al. On the crashworthiness of bio-inspired hexagonal prismatic tubes under axial compression [J]. International Journal of Mechanical Sciences, 2020, 186: 105893. doi: 10.1016/j.ijmecsci.2020.105893 [9] ZHANG Y, HE N, SONG X Y, et al. On impacting mechanical behaviors of side fractal structures [J]. Thin-Walled Structures, 2020, 146: 106490. doi: 10.1016/j.tws.2019.106490 [10] DENG X L, LIU W Y, LIN Z Q. Experimental and theoretical study on crashworthiness of star-shaped tubes under axial compression [J]. Thin-Walled Structures, 2018, 130: 321–331. doi: 10.1016/j.tws.2018.06.002 [11] WANG Z G, LIU J F, YAO S. On folding mechanics of multi-cell thin-walled square tubes [J]. Composites Part B: Engineering, 2018, 132: 17–27. doi: 10.1016/j.compositesb.2017.07.036 [12] LI Z X, MA W, YAO S G, et al. Crashworthiness performance of corrugation-reinforced multicell tubular structures [J]. International Journal of Mechanical Sciences, 2021, 190: 106038. doi: 10.1016/j.ijmecsci.2020.106038 [13] ALBAK E İ. Crashworthiness design and optimization of nested structures with a circumferentially corrugated circular outer wall and inner ribs [J]. Thin-Walled Structures, 2021, 167: 108219. doi: 10.1016/j.tws.2021.108219 [14] CHEN B C, ZOU M, LIU G M, et al. Experimental study on energy absorption of bionic tubes inspired by bamboo structures under axial crushing [J]. International Journal of Impact Engineering, 2018, 115: 48–57. doi: 10.1016/j.ijimpeng.2018.01.005 [15] GONG C, BAI Z H, WANG Y L, et al. On the crashworthiness performance of novel hierarchical multi-cell tubes under axial loading [J]. International Journal of Mechanical Sciences, 2021, 206: 106599. doi: 10.1016/j.ijmecsci.2021.106599 [16] ZOU M, XU S C, WEI C G, et al. A bionic method for the crashworthiness design of thin-walled structures inspired by bamboo [J]. Thin-Walled Structures, 2016, 101: 222–230. doi: 10.1016/j.tws.2015.12.023 [17] WU J C, ZHANG Y, ZHANG F, et al. A bionic tree-liked fractal structure as energy absorber under axial loading [J]. Engineering Structures, 2021, 245: 112914. doi: 10.1016/j.engstruct.2021.112914 [18] CHEN T T, ZHANG Y, Lin J M, et al. Theoretical analysis and crashworthiness optimization of hybrid multi-cell structures [J]. Thin-Walled Structures, 2019, 142: 116–131. doi: 10.1016/j.tws.2019.05.002 [19] WANG J, ZHANG Y, HE N, et al. Crashworthiness behavior of Koch fractal structures [J]. Materials & Design, 2018, 144: 229–244. [20] TIAN K, ZHANG Y, YANG F, et al. Enhancing energy absorption of circular tubes under oblique loads through introducing grooves of non-uniform depths [J]. International Journal of Mechanical Sciences, 2020, 166: 105239. doi: 10.1016/j.ijmecsci.2019.105239 [21] SONG J F, XU S C, ZHOU J F, et al. Experiment and numerical simulation study on the bionic tubes with gradient thickness under oblique loading [J]. Thin-Walled Structures, 2021, 163: 107624. doi: 10.1016/j.tws.2021.107624 [22] TABACU S. Analysis of circular tubes with rectangular multi-cell insert under oblique impact loads [J]. Thin-Walled Structures, 2016, 106: 129–147. doi: 10.1016/j.tws.2016.04.024 [23] TRAN T N, BAROUTAJI A. Crashworthiness optimal design of multi-cell triangular tubes under axial and oblique impact loading [J]. Engineering Failure Analysis, 2018, 93: 241–256. doi: 10.1016/j.engfailanal.2018.07.003 [24] HUANG H, XU S C. Crashworthiness analysis and bionic design of multi-cell tubes under axial and oblique impact loads [J]. Thin-Walled Structures, 2019, 144: 106333. doi: 10.1016/j.tws.2019.106333 [25] YU X H, QIN Q H, ZHANG J X, et al. Crushing and energy absorption of density-graded foam-filled square columns: experimental and theoretical investigations [J]. Composite Structures, 2018, 201: 423–433. doi: 10.1016/j.compstruct.2018.06.053 [26] NIKKHAH H, GUO F L, CHEW Y, et al. The effect of different shapes of holes on the crushing characteristics of aluminum square windowed tubes under dynamic axial loading [J]. Thin-Walled Structures, 2017, 119: 412–420. doi: 10.1016/j.tws.2017.06.036 -
下载:
点击查看大图
计量
- 文章访问数: 277
- HTML全文浏览量: 76
- PDF下载量: 51
