Design and Mechanical Properties of Star-Shaped Structure with Double Stress Plateaus
-
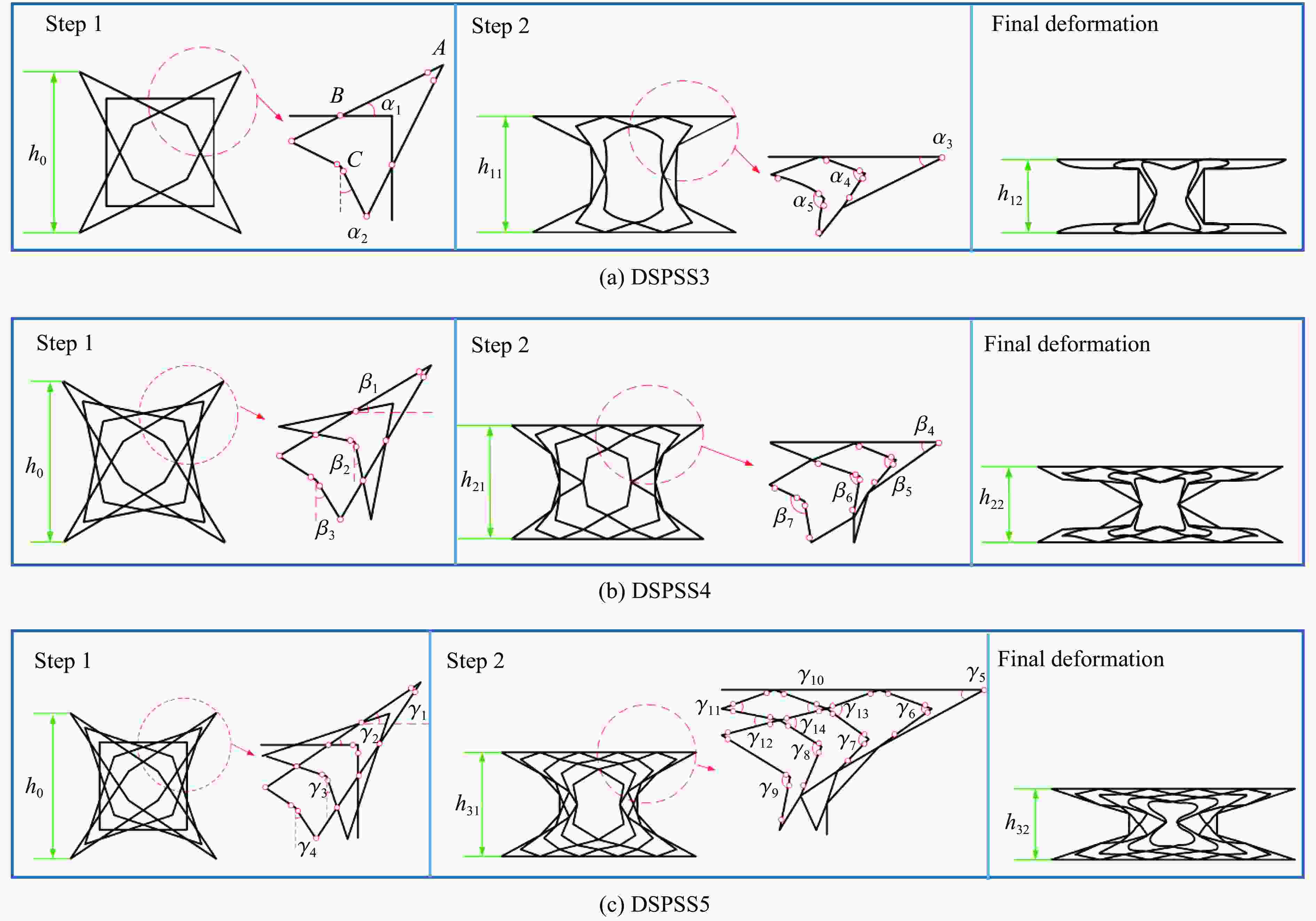
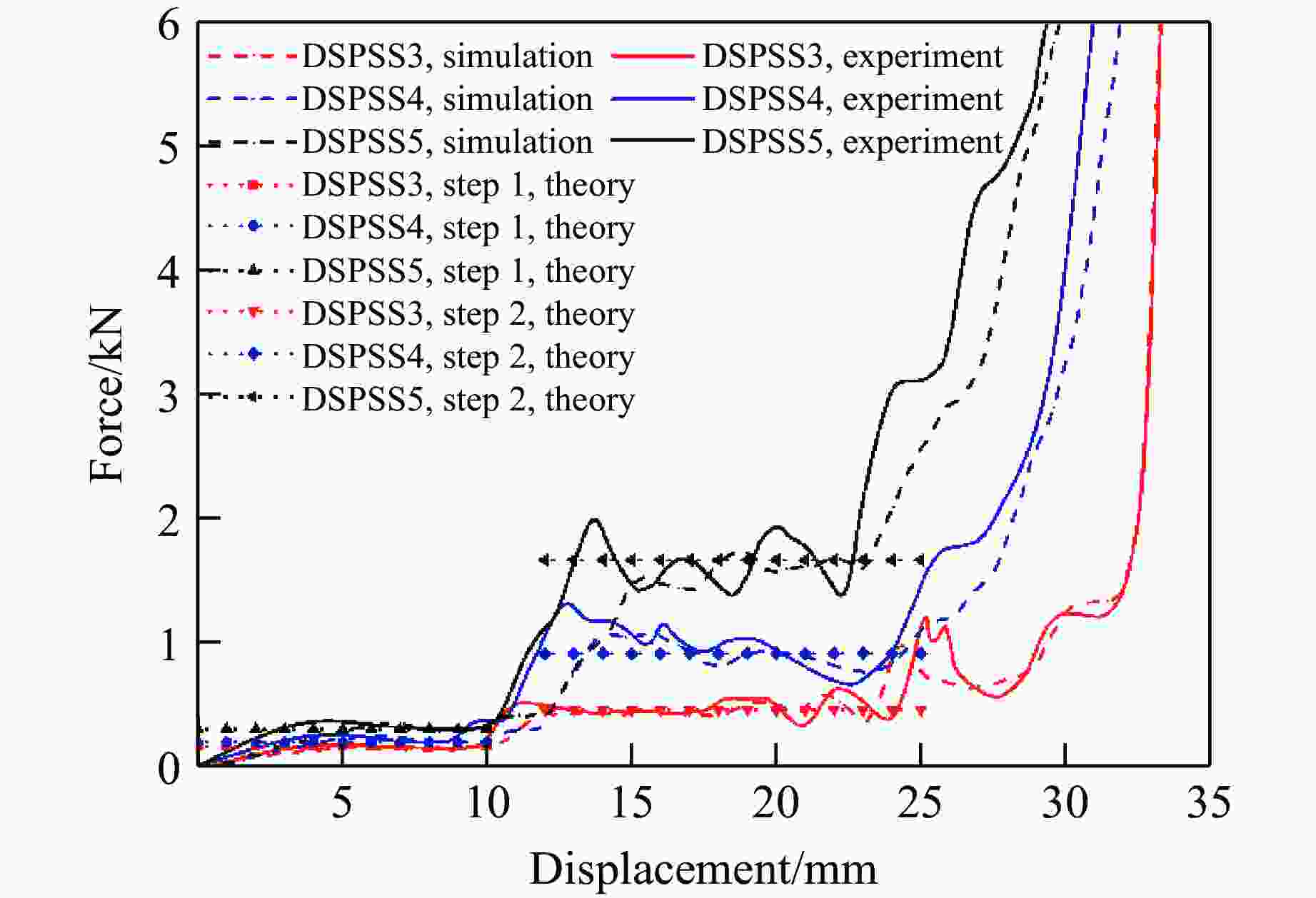
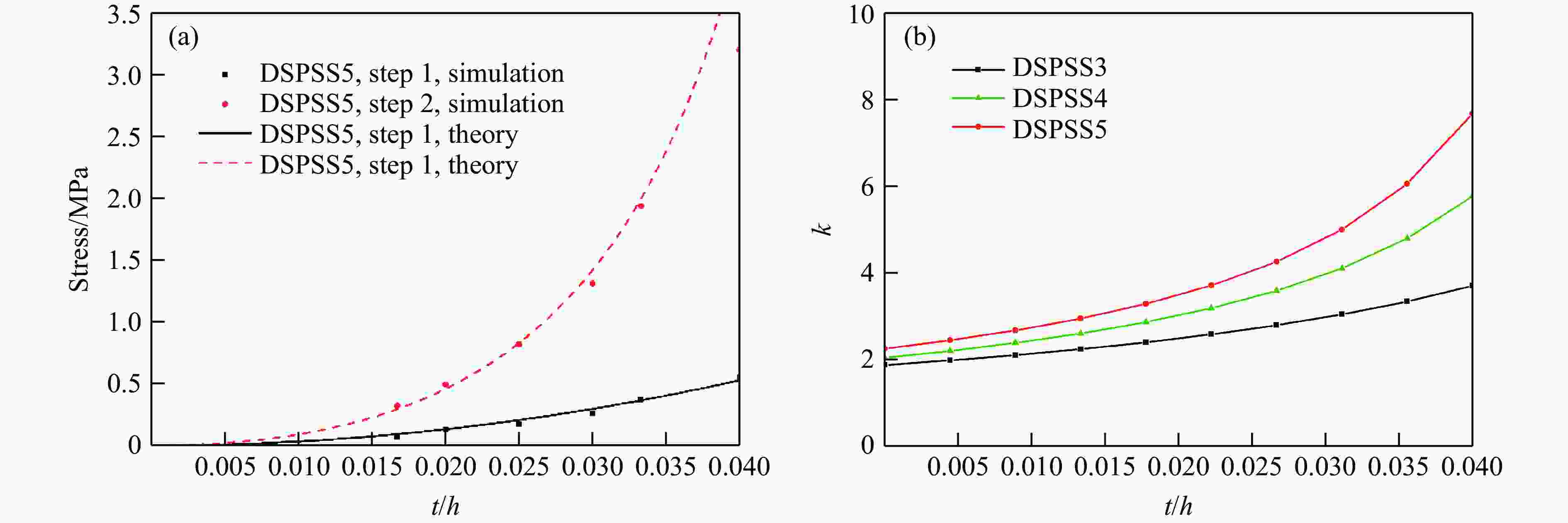
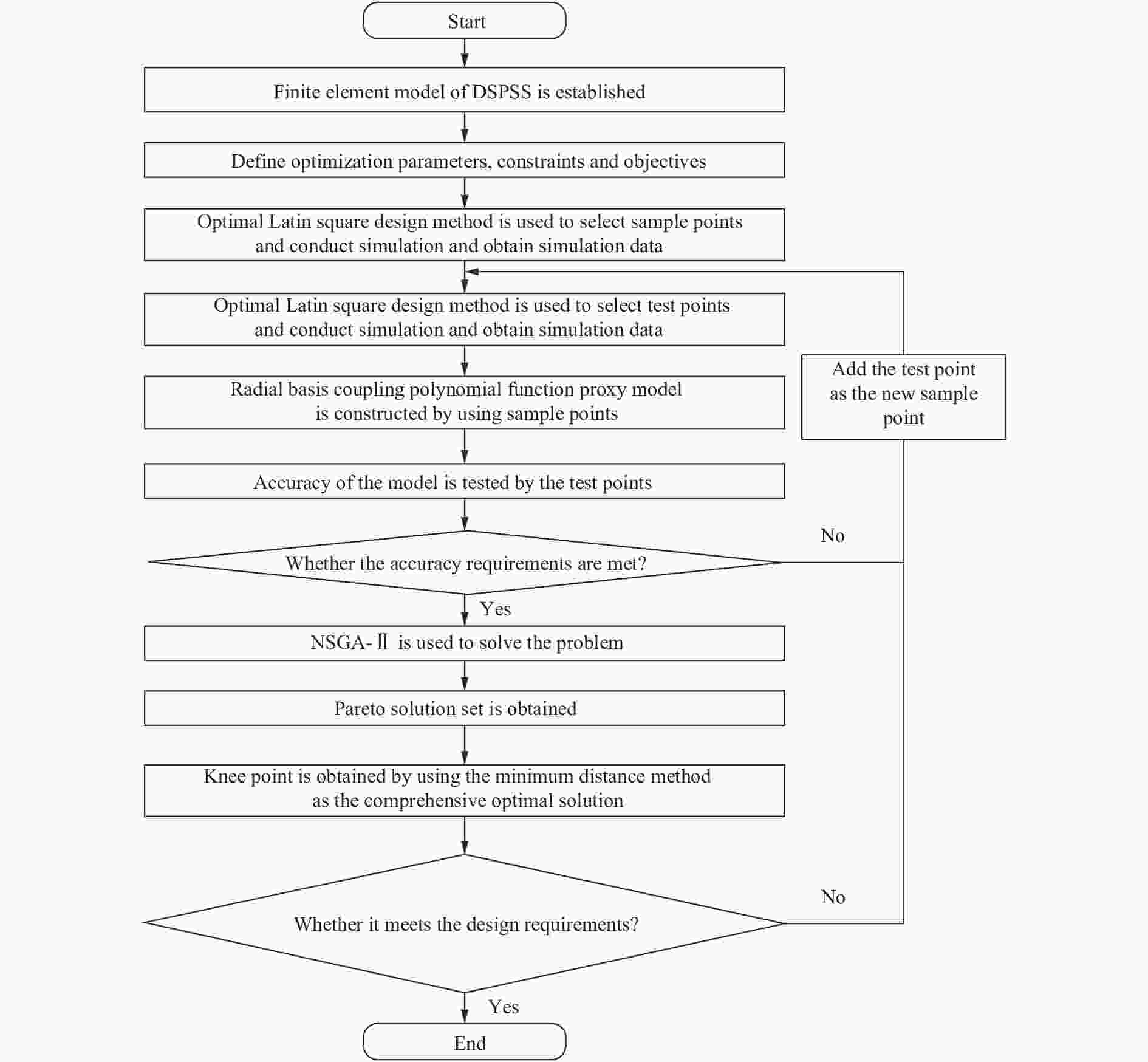
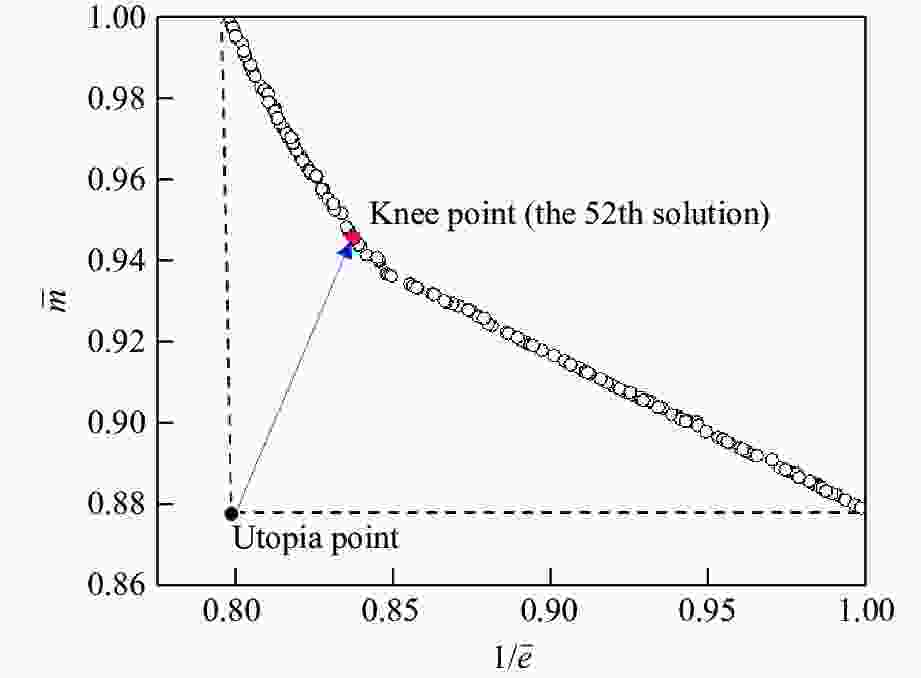
摘要: 为实现多孔格栅类结构平台应力和能量吸收的可调控，提出了一种双应力平台星形结构的设计方法，设计并制备了3种双应力平台星形结构。采用实验、理论分析与数值模拟相结合的方法研究了结构在面内压缩载荷下的力学行为和能量吸收性能。结果表明，双应力平台星形结构的载荷-位移曲线呈现两个明显的平台阶段，结构的几何参数和肋板数对结构变形的稳定性以及平台应力的大小存在显著影响。平台应力的理论预测结果与实验、数值模拟结果吻合较好。通过调整相应的设计参数，能够有效地调控结构在压缩过程中的平台应力和能量吸收能力。为了进一步提高双应力平台星形结构的能量吸收性能，以结构的质量和比吸能为设计变量，进行了多目标优化。采用基于径向基耦合多项式函数代理模型和遗传算法（NSGA-Ⅱ），使结构比吸能最大化的同时质量最小化。与最初设计的结构相比，优化后结构的质量减小了6.0%，比吸能提高了21.5%。Abstract: To achieve the tunable plateau stress and energy absorption in porous grid structures, a design method for star-shaped structures with double stress plateaus was proposed. Three kinds of star-shaped structures with double stress plateaus were designed and fabricated. The mechanical behavior and energy absorption properties under in-plane compressive load were investigated through experimental tests, theoretical analysis and numerical simulations. It was shown that the star-shaped structures with double stress plateaus exhibit two distinct plateau steps in the load-displacement curves. The geometric parameters of the structure and the number of ribs have a significant effect on the structural deformation stability and the plateau stress. The theoretical predictions, experimental results and numerical simulations were in good agreement with each other. The plateau stress and energy absorption capacity of star-shaped structures can be effectively controlled by tuning the corresponding design parameters. To further improve the energy absorption capacity of the star-shaped structure with double stress plateaus, a multi-objective optimization method was performed using the mass and specific absorption energy of the structure as design variables. The radial basis coupling polynomial function proxy model and genetic algorithm (NSGA-Ⅱ) were used to maximize the specific energy absorption and minimize the mass of the structure. Compared to the original structure, the optimized structure has a 6.0% reduction in mass and a 21.5% increase in specific energy absorption.
-
图 2 双应力平台星形结构的 (a) 载荷-位移曲线、 (b) 实验变形、 (c) 模拟变形
Figure 2. (a) Load-displacement curves, (b) experimental deformation, and (c) simulated deformation of star structure with double stress plateau
图 3 DSPSS3的 (a) 载荷-位移曲线和 (b) 能量时程曲线
Figure 3. (a) Load-displacement curves and (b) time history of energy of DSPSS3
图 4 3种双应力平台星形结构变形
Figure 4. Deformations of three star-shaped structures with double stress plateaus
图 5 实验、数值模拟与理论预测结果的对比
Figure 5. Comparison of experimental results, numerical simulation and theoretical prediction
图 6 (a) 模拟与理论预测的DSPSS5的平台应力， (b) 平台应力比值随
$ t/{h_{}} $ 的变化Figure 6. (a) Simulation and theoretical prediction of plateau stress of DSPSS5, (b) variation of plateau stress ratio with
$ t/{h_{}} $ 
图 9 DSPSS3最优结构与初始结构的力-位移曲线
Figure 9. Force-displacement curves of the optimal structure and the initial structure of DSPSS3
表 1 27组试验设计样本点及其响应值
Table 1. Design sample points and their response values of 27 group experimental tests
No. a/mm b/mm $\overline m $ $\overline e$ 1 0 11.61 0.52 0.49 2 0.97 5.81 0.77 0.14 3 1.94 26.13 1.13 0.96 4 2.90 16.45 0.97 1.15 5 3.87 0.97 0.82 0.34 6 5.81 10.65 0.93 1.07 7 7.74 4.84 0.88 0.65 8 9.68 14.52 1.07 0.76 9 11.61 8.71 1.01 0.88 10 13.55 2.90 0.96 0.71 11 15.48 12.58 1.15 0.50 12 17.42 6.77 1.09 0.86 13 19.35 0 1.07 0.89 14 23.23 3.87 1.10 0.40 15 28.06 1.94 1.25 0.42 16 5.25 2.73 0.79 0.54 17 8.18 16.36 1.07 1.17 18 13.64 8.18 1.04 0.84 19 8.57 4.29 0.89 0.61 20 17.14 8.57 1.12 0.60 21 3.33 3.33 0.77 0.29 22 6.67 13.33 0.99 0.93 23 12.86 12.86 1.10 0.63 24 10.00 10.00 1.00 1.00 25 3.45 15.25 0.94 1.20 26 18.14 7.31 1.11 0.80 27 20.71 4.31 1.11 0.26 
下载: 导出CSV
表 2 4组检验点的参数、响应及相对误差
Table 2. Parameters, responses and relative errors of four test points
No. a/mm b/mm ${\overline m {_{\rm{RBF} } }}$ ${\overline e {_{\rm{RBF} } }}$ ${\overline m {_{\rm{FEA} } }}$ ${\overline e {_{\rm{FEA} } }}$ $\delta{_ {\overline m}}$/% $\delta {_{\overline e}}$/% 1 4.78 19.04 1.0501 1.2601 1.0481 1.269 0 −0.19 0.71 2 8.57 6.46 0.9189 0.7180 0.9131 0.7292 −0.63 1.50 3 12.86 15.14 1.1264 0.6601 1.1262 0.6300 −0.39 −4.50 4 18.01 7.11 1.1084 0.8011 1.1141 0.8406 0.51 4.90
下载: 导出CSV
-
[1] YU X L, ZHOU J, LIANG H Y, et al. Mechanical metamaterials associated with stiffness, rigidity and compressibility: a brief review [J]. Progress in Materials Science, 2018, 94: 114–173. doi: 10.1016/j.pmatsci.2017.12.003 [2] LV W T, LI D, DONG L. Study on mechanical properties of a hierarchical octet-truss structure [J]. Composite Structures, 2020, 249(8): 112640. [3] WANG Z G, LI Z D, SHI C, et al. Mechanical performance of vertex-based hierarchical vs square thin-walled multi-cell structure [J]. Thin Walled Structures, 2019, 134: 102–110. doi: 10.1016/j.tws.2018.09.017 [4] WEN G L, CHEN G X, LONG K, et al. Stacked-origami mechanical metamaterial with tailored multistage stiffness [J]. Research Square, 2021, 212(11): 110203. [5] LU H, WANG X P, CHEN T N. Design and quasi-static responses of a hierarchical negative Poisson’s ratio structure with three plateau stages and three-step deformation [J]. Composite Structures, 2022, 291(2): 115591. [6] ZHANG Z W, TIAN R L, ZHANG X L, et al. A novel butterfly-shaped auxetic structure with negative Poisson’s ratio and enhanced stiffness [J]. Journal of Materials Science, 2021, 56(25): 1–18. [7] FU Y M, YU T B, WANG X. Study on a Chiral structure with tunable Poisson’s ratio [J]. Materials, 2021, 14(12): 3338. doi: 10.3390/ma14123338 [8] WANG H, LU Z X, YANG Z Y, et al. In-plane dynamic crushing behaviors of a novel auxetic honeycomb with two plateau stress regions [J]. International Journal of Mechanical Sciences, 2019, 151: 746–759. doi: 10.1016/j.ijmecsci.2018.12.009 [9] WANG H, HE Y, YU A, et al. Origami-inspired structures with programmable multi-step deformation [J]. Mechanics of Advanced Materials and Structures, 2022, 137(18): 2133197. [10] AN M R, WANG L, LIU H T, et al. In-plane crushing response of a novel bidirectional re-entrant honeycomb with two plateau stress regions [J]. Thin-Walled Structures, 2022, 170: 108530. [11] LIU H T, WANG L. Design 3D improved star-shaped honeycomb with different tip angles from 2D analytical star-shaped model [J]. Composite Structures, 2022, 283(5): 115154. [12] LI X, FAN R, FAN Z J, et al. Programmable mechanical metamaterials based on hierarchical rotating structures [J]. International Journal of Solids and Structures, 2021, 216(1): 145–155. [13] WEI L L, ZHAO X, YU Q, et al. A novel star auxetic honeycomb with enhanced in-plane crushing strength [J]. Thin-Walled Structures, 2020, 149(19): 106623. [14] HECTOR K W, RESTREPO D, BONILLA C T, et al. Mechanics of chiral honeycomb architectures with phase transformations [J]. Journal of Applied Mechanics, 2019, 86(11): 111014. doi: 10.1115/1.4044024 [15] MENG Z Q, LIU M C, ZHANG Y F, et al. Multi-step deformation mechanical metamaterials [J]. Journal of the Mechanics and Physics of Solids, 2020, 144: 104095. doi: 10.1016/j.jmps.2020.104095 [16] AHMAD Z, THAMBIRATNAM D P. Crushing response of foam-filled conical tubes under quasi-static axial loading [J]. Materials & Design, 2009, 30(7): 2393–2403. [17] 王中钢. 轻质蜂窝结构力学 [M] 北京: 科学出版社, 2019. [18] ABRAMOWICZ W, WIERZBICKI T. Axial crushing of multicorner sheet metal columns [J]. Journal of applied mechanics, 1989, 56(1): 113–120. [19] MICHAEL M. Choosing basis functions and shape parameters for radial basis function methods [J]. SIAM Undergraduate Research Online, 2011, 4(4): 190–209. -
下载:
点击查看大图
计量
- 文章访问数: 295
- HTML全文浏览量: 142
- PDF下载量: 41
