聚脲/铝分层复合结构的抗爆性能研究

姜策; 肖李军; 宋卫东

doi:10.11858/gywlxb.20230610

聚脲/铝分层复合结构的抗爆性能研究

doi: 10.11858/gywlxb.20230610

北京理工大学爆炸科学与技术国家重点实验室, 北京　100081

基金项目: 国家自然科学基金（11972092）

详细信息

作者简介:
姜　策（1998－），男，硕士研究生，主要从事材料与结构冲击动力学研究. E-mail：jiangce199805@163.com

通讯作者:
宋卫东（1975－），男，博士，教授，主要从事材料与结构冲击动力学研究. E-mail：swdgh@bit.edu.cn

中图分类号: O383.1
计量
- 文章访问数: 179
- HTML全文浏览量: 72
- PDF下载量: 55
出版历程
- 收稿日期: 2023-02-13
- 修回日期: 2023-03-20
- 网络出版日期: 2023-06-19
- 刊出日期: 2023-06-05

Blast Resistance of Polyurea/Aluminum Composite Structures

State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China

摘要

摘要: 为研究聚脲/铝分层复合结构的抗爆性能，对在空爆载荷下的聚脲/铝结构进行了数值模拟，并与文献中的试验结果进行对比，验证数值模型的准确性。在此基础上研究了等质量条件下，复合结构层数、复合结构中金属铝的体积分数以及聚脲层位置对靶板中心点挠度的影响，分析爆炸过程中结构的能量吸收特点。结果表明：在等质量下，聚脲/铝分层复合结构存在最优的结构设计；在所讨论的结构中，除铝体积分数为90%的4层结构外，其他结构的抗爆性能均优于均质铝板，铝体积分数为10%的一层结构的抗爆炸性能最好；聚脲涂覆位置影响结构的抗爆性能，且聚脲涂覆在背爆面时抗冲击性能更优；铝板的内能吸收是复合结构能量吸收的主要部分，铝板的内能吸收比例随着铝体积分数的增加先减小后增大。研究结果可为聚脲/铝复合结构的抗爆设计提供参考。
- 聚脲涂覆铝板 /
- 爆炸载荷 /
- 层级结构 /
- 有限元模拟 /
- 能量吸收
Abstract: Numerical simulations of polyurea/aluminum structures under blast loading were carried out to study the blast resistant performance of polyurea/aluminum composite (PAC) structures. The accuracy of the numerical models was verified by the test results in related literature. Under the condition of equal masses, the effects of structural layer number, volume fraction of metal aluminum in the structure, and position of polyurea layer on the blast resistant performance of PAC structures were investigated. Meanwhile, the energy absorption characteristics of PAC structures were analyzed. The results show that the PAC hierarchical structure is the best structure design under the same mass. Except for the four-layer structure with 90% aluminum volume fraction, the other structures exhibit better performance than the homogeneous aluminum counterpart. The single-layer structure with 10% aluminum volume fraction presents the most excellent blast resistance. For polyurea-coated structures, the shock resistance of polyurea coating on the rear surface of the structure opposite to explosion is superior. Internal energy absorption of aluminum plates provide the most contribution to the overall energy absorption. The proportion of internal energy absorption of aluminum layers first decreases, and then increases with the enhancement of aluminum volume fraction. The research results can provide a reference for the anti-explosion design of PAC structures.
- polyurea coated aluminum plate /
- blast load /
- layered structure /
- finite element simulation /
- energy absorption

HTML全文

图 1 1/4有限元模型

Figure 1. A quarter of the finite element model

下载: 全尺寸图片幻灯片

图 2 数值模拟与试验结果的对比

Figure 2. Comparison between numerical simulation and experimental results

下载: 全尺寸图片幻灯片

图 3 具有不同铝体积分数的复合板

Figure 3. Composite plates with different aluminum volume fractions

下载: 全尺寸图片幻灯片

图 4 等质量均质铝的变形和挠度曲线

Figure 4. Deformation and deflection curve of homogeneous aluminum with equal mass

下载: 全尺寸图片幻灯片

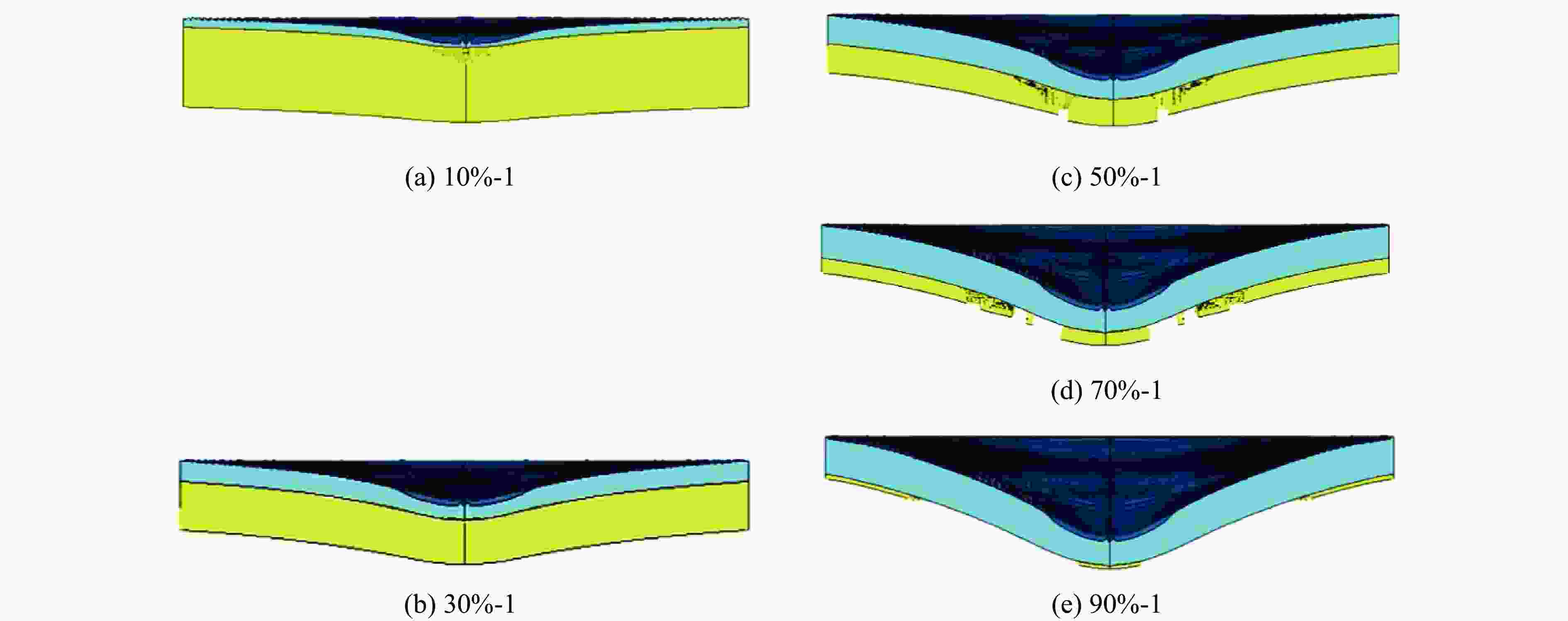
图 5 具有不同铝体积分数的靶板的最大挠度：(a) 10%-1（0.77 cm），(b) 30%-1 （1.64 cm），(c) 50%-1（2.52 cm），(d) 70%-1 （3.41 cm），(e) 90%-1（4.17 cm）

Figure 5. Maximum deflection of plates with different volume fractions of aluminum: (a) 10%-1 (0.77 cm), (b) 30%-1 (1.64 cm), (c) 50%-1 (2.52 cm), (d) 70%-1 (3.41 cm), (e) 90%-1 (4.17 cm)

下载: 全尺寸图片幻灯片

图 6 多层板的变形

Figure 6. Deformation of multilayer plates

下载: 全尺寸图片幻灯片

图 7 不同结构的最大挠度

Figure 7. Maximum deflection for different structures

下载: 全尺寸图片幻灯片

图 8 聚脲涂覆不同位置的最大挠度

Figure 8. Maximum deflection at different positions of polyurea coatings

下载: 全尺寸图片幻灯片

图 9 50%-1结构的能量曲线

Figure 9. Energy curves of 50%-1 structure

下载: 全尺寸图片幻灯片

图 10 具有不同铝体积分数的多层结构的能量曲线

Figure 10. Energy curves of multilayer structures with different aluminum volume fractions

下载: 全尺寸图片幻灯片

图 11 不同铝体积分数结构的能量吸收

Figure 11. Energy absorption of structures with different aluminum volume fractions

下载: 全尺寸图片幻灯片

表 1 铝材料参数

Table 1. Material parameters of aluminum

Material	A/MPa	B/MPa	n	c	m
LY12	370	339	0.369	0.0083	1

E/GPa	ν	ρ/(g·cm^–³)	c_p/(J·kg^–1·K^–1)	T_m/K	T_r/K
73	0.33	2.76	960	893	293

下载: 导出CSV

表 2 聚脲材料参数

Table 2. Material parameters of polyurea

C₁₀/MPa	C₀₁/MPa	C₁₁/MPa	C₂₀/MPa	C₀₂/MPa	C₃₀/MPa
4.5	0.7	−0.03	−0.02	0.001	0.002

下载: 导出CSV

表 3 试验模拟工况

Table 3. Experiment and simulation cases

Method	Structures	Explosion distance/cm	Deformation /cm
Experiment 1^[18]	5.5 mm Al	8.5	6.31
Simulation 1	5.5 mm Al	8.5	6.91
Experiment 2^[18]	4.0 mm PU+4.0 mm Al	10.0	5.94
Simulation 2	4.0 mm PU+4.0 mm Al	10.0	5.08

下载: 导出CSV

表 4 模拟工况

Table 4. Simulation cases

Specimen No.	Volume fraction of Al/%	Number of layers (Al)	Thickness (Al)/cm	Thickness (PU)/cm	Total thickness/cm	Total mass/g	Mass (Al)/g	Mass (PU)/g
10%-1	10	1	0.41×1	3.68×1	4.09	821.3	186.7	634.6
10%-2		2	0.21×2	1.84×2
10%-3		3	0.14×3	1.23×3
10%-4		4	0.10×4	0.92×4
30%-1	30	1	0.96×1	2.23×1	3.19	821.3	436.5	384.8
30%-2		2	0.48×2	1.12×2
30%-3		3	0.32×3	0.74×3
30%-4		4	0.24×4	0.56×4
50%-1	50	1	1.30×1	1.30×1	2.60	821.3	596.2	225.1
50%-2		2	0.65×2	0.65×2
50%-3		3	0.43×3	0.43×3
50%-4		4	0.33×4	0.33×4
70%-1	70	1	1.55×1	0.66×1	2.21	821.3	706.9	114.4
70%-2		2	0.76×2	0.33×2
70%-3		3	0.52×3	0.22×3
70%-4		4	0.39×4	0.17×4
90%-1	90	1	1.73×1	0.19×1	1.92	821.3	788.3	33.0
90%-2		2	0.87×2	0.10×2
90%-3		3	0.58×3	0.06×3
90%-4		4	0.43×4	0.05×4

下载: 导出CSV

表 5 模拟工况

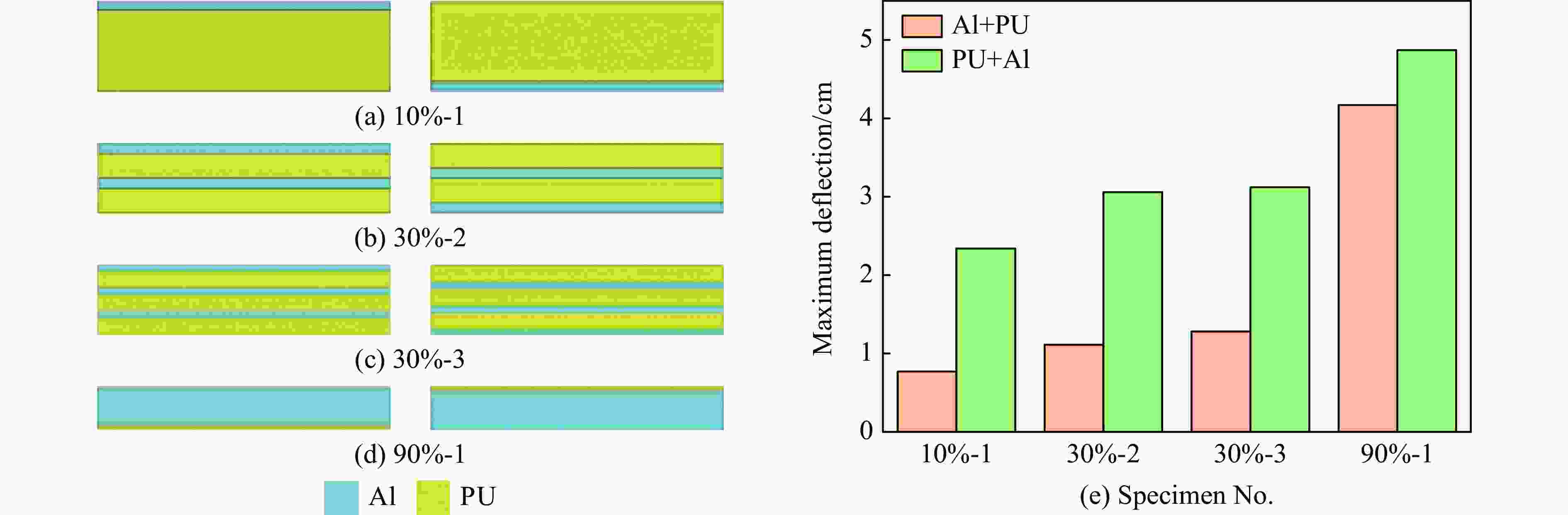
Table 5. Simulation cases

Specimen No.	Structures	Number of layers (Al)	Total thickness/cm	Thickness (Al)/cm	Thickness (PU)/cm	Mass (Al)/g	Mass (PU)/g
10%-1	Al+PU	1	4.09	0.41×1	3.68×1	186.7	634.6
10%-1	PU+Al	1	4.09	0.41×1	3.68×1	186.7	634.6
30%-2	Al+PU	2	3.19	0.48×2	1.12×2	436.5	384.8
30%-2	PU+Al	2	3.19	0.48×2	1.12×2	436.5	384.8
30%-3	Al+PU	3	3.19	0.32×3	0.74×3	436.5	384.8
30%-3	PU+Al	3	3.19	0.32×3	0.74×3	436.5	384.8
90%-1	Al+PU	1	1.92	1.73×1	0.19×1	788.3	33.0
90%-1	PU+Al	1	1.92	1.73×1	0.19×1	788.3	33.0

下载: 导出CSV

参考文献(19)

[1]	JIANG Y X, ZHANG B Y, WEI J S, et al. Study on the impact resistance of polyurea-steel composite plates to low velocity impact [J]. International Journal of Impact Engineering, 2019, 133: 103357.
[2]	CHU D Y, LI Z J, YAO K L, et al. Studying the strengthening mechanism and thickness effect of elastomer coating on the ballistic-resistance of the polyurea-coated steel plate [J]. International Journal of Impact Engineering, 2022, 163: 104181.
[3]	MOHOTTI D, FERNANDO P L N, WEERASINGHE D, et al. Evaluation of effectiveness of polymer coatings in reducing blast-induced deformation of steel plates [J]. Defence Technology, 2021, 17(6): 1895–1904. doi: 10.1016/j.dt.2020.11.009
[4]	XIA Y, SHI Z T, ZHOU Q, et al. Numerical investigation on polyurea coated aluminum plate subjected to low velocity impact [J]. International Journal of Impact Engineering, 2023, 177: 104516.
[5]	SI P, LIU Y, YAN J B, et al. Effect of polyurea layer on ballistic behavior of ceramic/metal armor [J]. Structures, 2023, 48: 1856−1867.
[6]	WU G, WANG X, WANG Y T, et al. Bioinspired nacre-like steel-polyurea composite plate subjected to projectile impact [J]. Materials & Design, 2022, 224: 111371.
[7]	LIU Q, GUO B Q, CHEN P W, et al. Experimental investigation blast resistance of CFRP/polyurea composite plates under blast loading [J]. Thin-Walled Structures, 2022, 181: 110149.
[8]	甘云丹, 宋力, 杨黎明. 弹性体涂覆钢板抗冲击性能的数值模拟 [J]. 兵工学报, 2009, 30(Suppl 2): 15–18. GAN Y D, SONG L, YANG L M. Numerical simulation for anti-blast performances of steel plate coated with elastomer [J]. Acta Armamentaria, 2009, 30(Suppl 2): 15–18.
[9]	LI Y Q, CHEN C H, HOU H L, et al. The influence of spraying strategy on the dynamic response of polyurea-coated metal plates to localized air blast loading: experimental investigations [J]. Polymers, 2019, 11(11): 1888. doi: 10.3390/polym11111888
[10]	HOU H L, CHEN C H, CHENG Y S, et al. Effect of structural configuration on air blast resistance of polyurea-coated composite steel plates: experimental studies [J]. Materials & Design, 2019, 182: 108049.
[11]	王喜梦, 刘均, 陈长海, 等. 近距空爆载荷下钢板/聚脲复合结构动响应特性仿真 [J]. 中国舰船研究, 2021, 16(2): 116–124. doi: 10.19693/j.issn.1673-3185.01833 WANG X M, LIU J, CHEN C H, et al. Simulation on dynamic response characteristics of steel/polyurea composite structures under close-range air blast loading [J]. Chinese Journal of Ship Research, 2021, 16(2): 116–124. doi: 10.19693/j.issn.1673-3185.01833
[12]	王逸平, 汪维, 杨建超, 等. 钢板/POZD复合结构在近距空爆载荷下的抗爆性能 [J]. 高压物理学报, 2023, 37(1): 014104. WANG Y P, WANG W, YANG J C, et al. Research on blast resistant performance of steel/pozd composite structures under close-range airblast load [J]. Chinese Journal of High Pressure Physics, 2023, 37(1): 014104.
[13]	ZHANG L, WANG X, JI C, et al. Effect of polyurea coating with different mechanical properties on blast resistance of aluminum alloy circular tube structures: experiments vs. numerical simulations [J]. Thin-Walled Structures, 2023, 183: 110361.
[14]	LIANG M Z, ZHOU M, QI Z Z, et al. Failure mode and blast resistance of polyurea coated metallic cylinders under internal multi-field coupled loading [J]. Thin-Walled Structures, 2023, 184: 110522.
[15]	CHEN C H, WANG X M, HOU H L, et al. Effect of strength matching on failure characteristics of polyurea coated thin metal plates under localized air blast loading: experiment and numerical analysis [J]. Thin-Walled Structures, 2020, 154: 106819.
[16]	ROLAND C M, TWIGG J N, VU Y, et al. High strain rate mechanical behavior of polyurea [J]. Polymer, 2007, 48(2): 574–578. doi: 10.1016/j.polymer.2006.11.051
[17]	XUE L, MOCK W JR, BELYTSCHKO T. Penetration of dh-36 steel plates with and without polyurea coating [J]. Mechanics of Materials, 2010, 42(11): 981–1003. doi: 10.1016/j.mechmat.2010.08.004
[18]	朱学亮. 聚脲金属复合结构抗冲击防护性能研究[D]. 北京: 北京理工大学, 2016: 56−58 ZHU X L. Study on impact and blast resistance of polyurea metal composite structure [D]. Beijing: Beijing Institute of Technology, 2016: 56−58.
[19]	JIA Z, YU Y, HOU S Y, et al. Biomimetic architected materials with improved dynamic performance [J]. Journal of the Mechanics and Physics of Solids, 2019, 125: 178–197. doi: 10.1016/j.jmps.2018.12.015