Research on Dynamic Mechanical Properties of Two-Phase Composites Based on Convolutional Neural Network
-
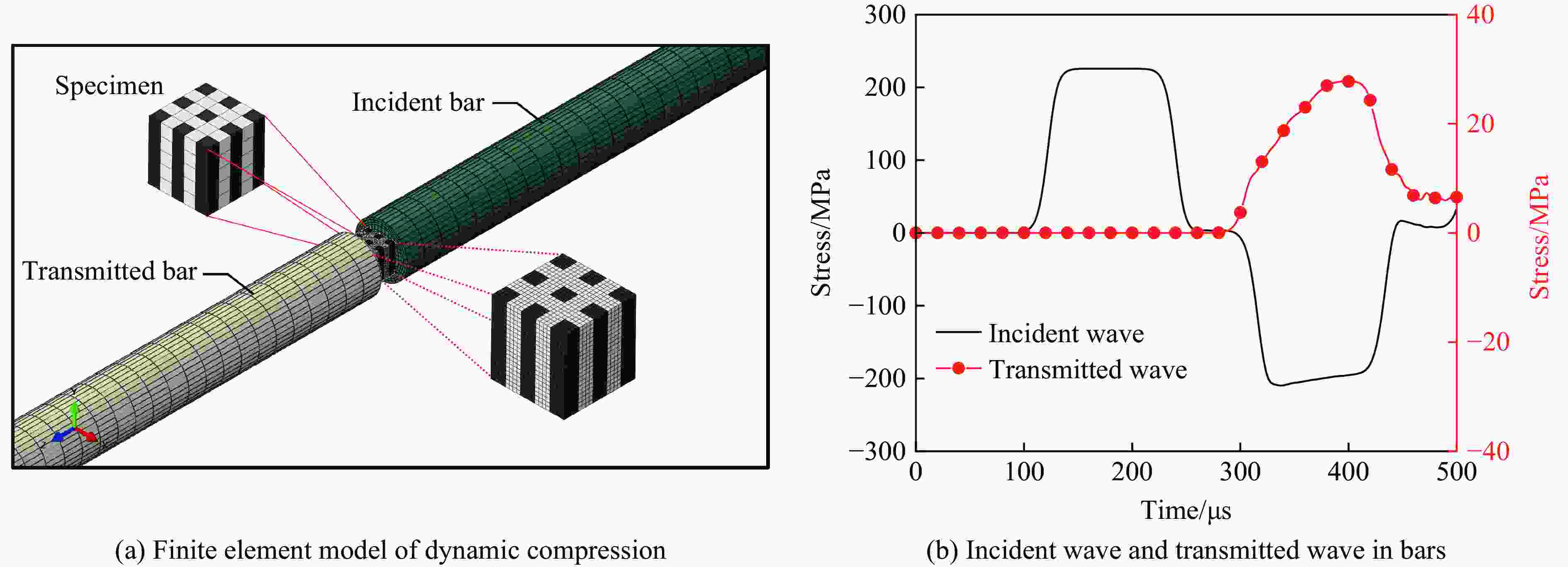
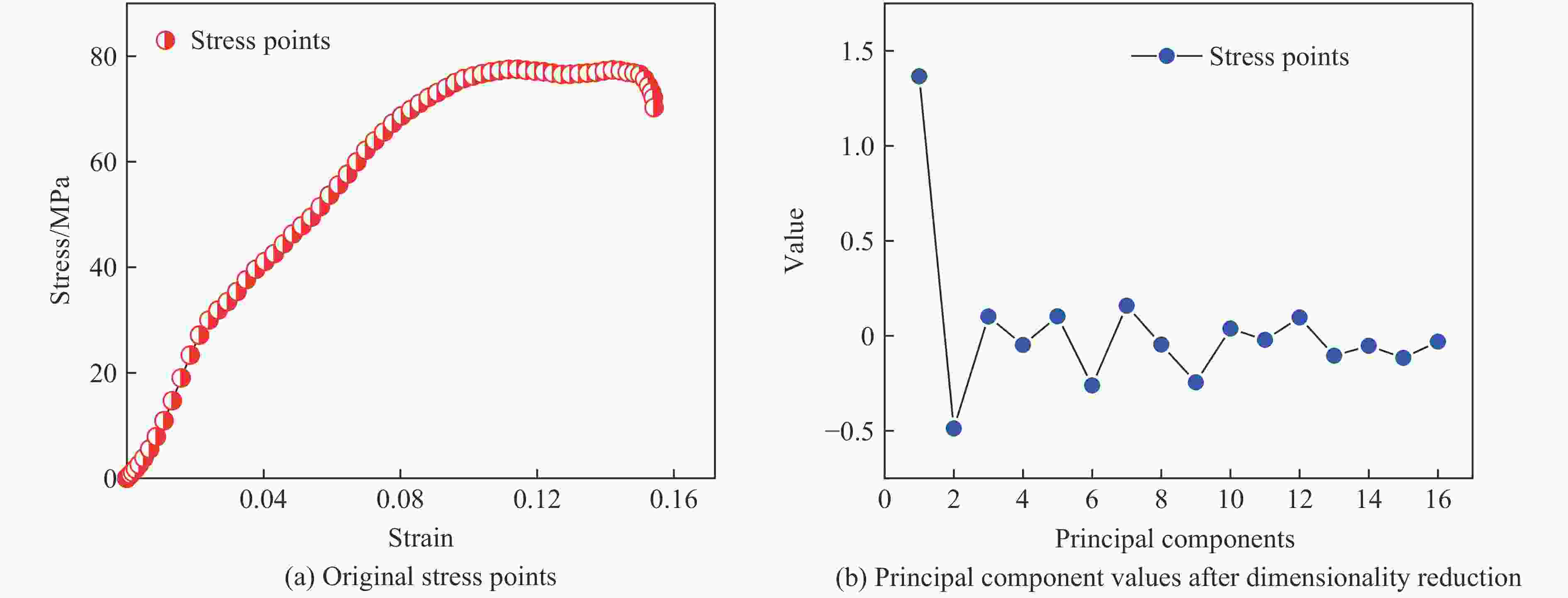
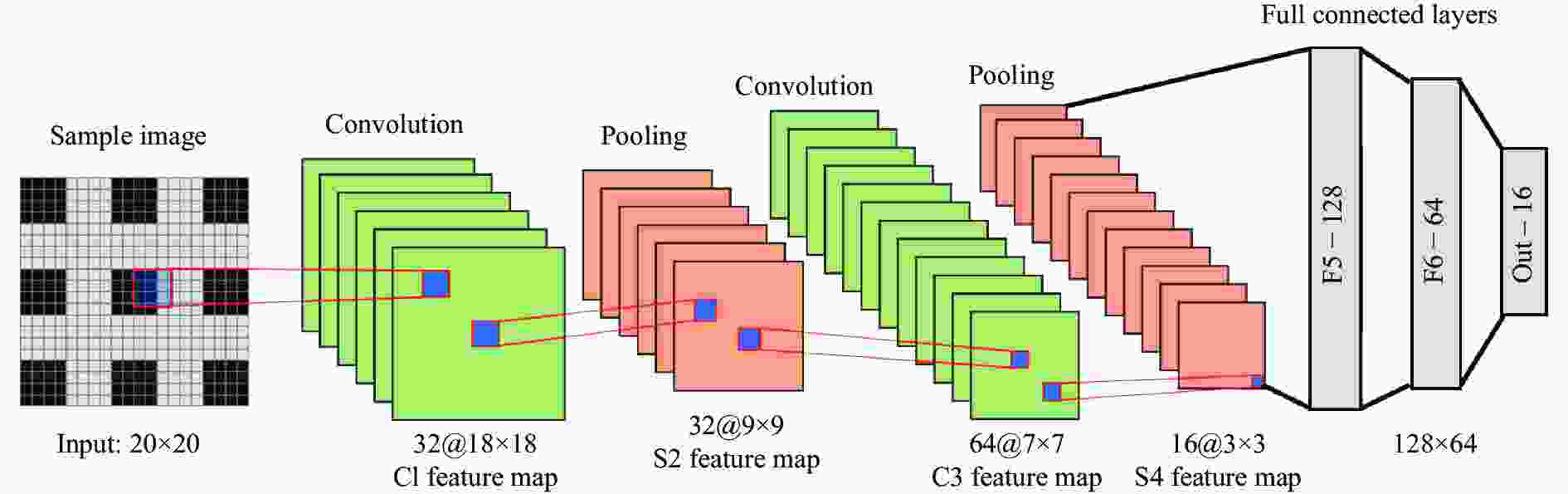
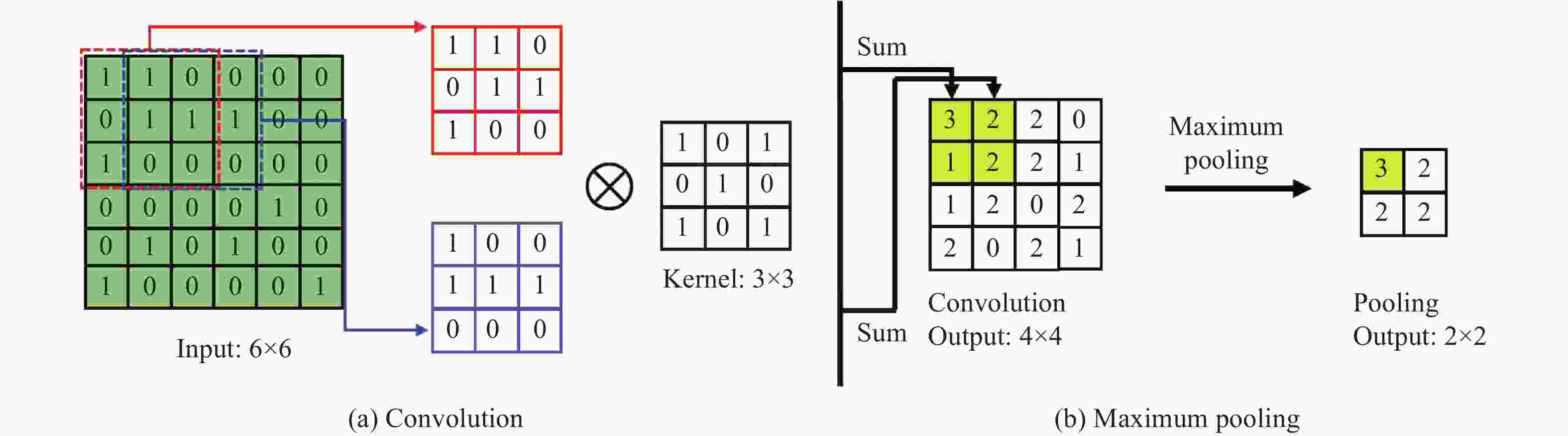
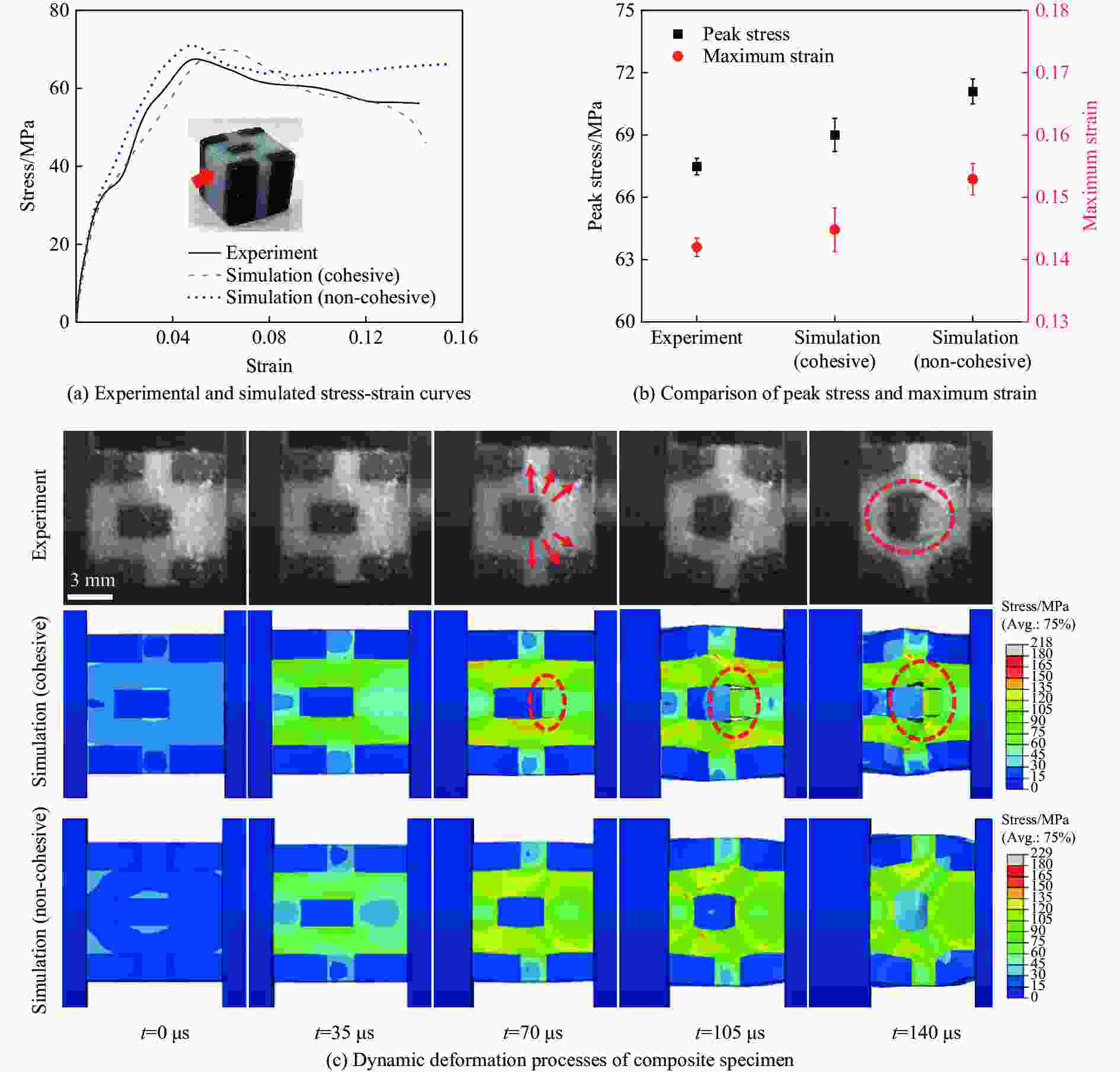
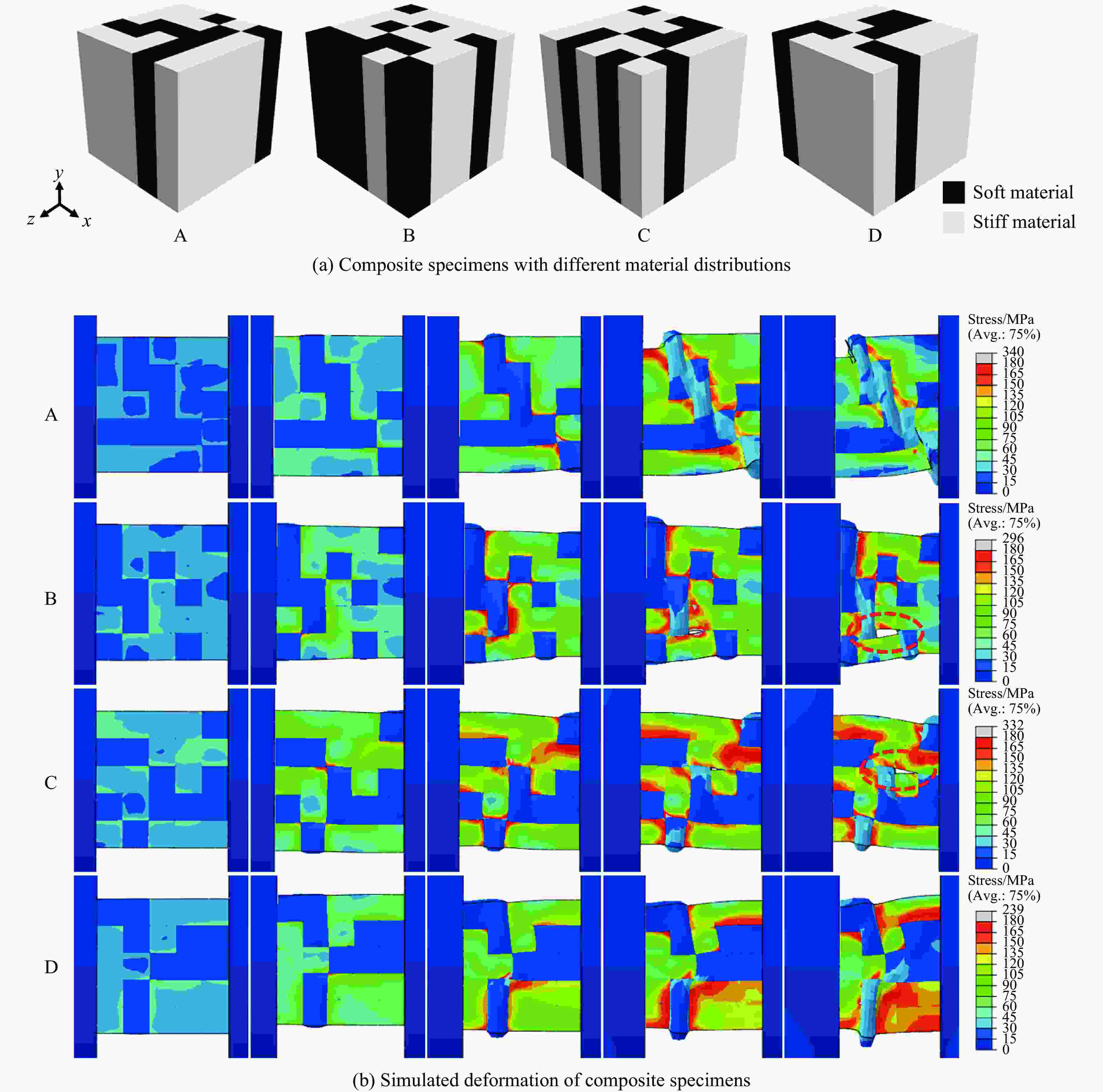
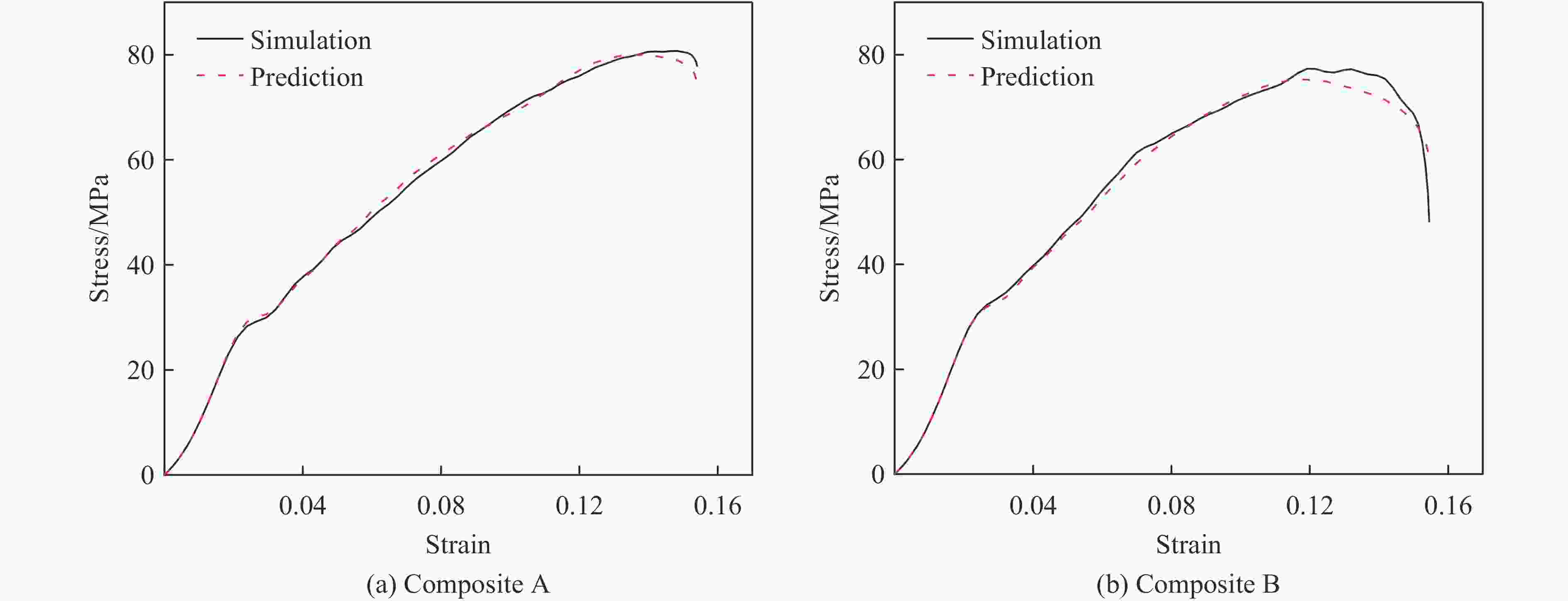
摘要: 增材制造技术促进了复合材料的发展，也拓宽了复合结构的设计空间，然而基于增材制造的复合材料动态力学性能研究仍然面临研究方法欠缺、设计过程复杂等问题。利用分离式霍普金森压杆实验技术和ABAQUS有限元模拟，研究光固化3D打印两相复合材料的动态力学行为，结合主成分分析法建立复合结构的数据集，通过高性能的卷积神经网络学习复合材料结构与应力-应变曲线的关系。结果表明，含有界面单元的有限元模型更适用于模拟复合材料的动态力学响应，通过超参数的设置可以提高卷积神经网络的预测性能，训练完成的卷积神经网络能够根据结构快速预测复合材料的动态应力-应变曲线。此研究对机器学习在复合材料动态力学性能设计与应用具有一定的借鉴意义。Abstract: Additive manufacturing technology has promoted the development of composite materials and broadened the design space of composite structures. However, the dynamic mechanical properties of composite materials based on additive manufacturing still face problems such as lack of research methods and complex design processes. The split Hopkinson pressure bar (SHPB) experimental technique and ABAQUS finite element simulation were used to study the dynamic mechanical behavior of two-phase composites printed by light-cured 3D, combined with the principal component analysis (PCA) to establish composite structure datasets, and the relationship between the composite structures and the stress-strain curves were learned through a high-performance convolutional neural network (CNN). The research results showed that the finite element model containing interface elements was more suitable for simulating the dynamic mechanical response of composites, and the predictive performance of CNN could be improved by setting hyperparameters. Based on the structure, the trained CNN could quickly predict the dynamic stress-strain curve of the composites. This study provides a reference for the design and application of machine learning in the dynamic performance of composites.
-
近年来，燃气管道用户逐年增加，越来越多的人工煤气和液化石油气被天然气取代，中国的城镇燃气普及率已超过97.9%，大部分中小城市都已铺设了大量的城镇燃气管道[1]。由于城镇燃气管道铺设在城市的密集型地区，管道穿越地下受限空间的可能性较大。十堰“6 • 13”重大燃气爆炸事故的发生引起了社会和政府对受限空间内燃爆事故的高度关注。该事故发生后，政府机构、燃气公司均加大力度对城镇燃气管道穿越地下受限空间的情况进行了全面排查。因此，有必要对燃气在受限空间内的事故情景进行模拟，掌握燃气泄漏规律，并分析泄爆优化效果。
国内已有多位学者对城镇燃气管道泄漏情景、大型储罐泄漏情景、封闭空间等不同的事故场景进行了模拟，从不同的角度对发生的事故进行分析，并提出了不同的防控措施。单克[2]基于FLACS软件对美国曼哈顿燃气管道泄漏爆炸进行情景模拟，分析了在不同的内压、管径、风速、点火时间下燃气管道泄漏爆炸冲击波的影响范围，结合失效概率，提出了量化的燃气管道风险管控措施。李亚勋[3]基于FLACS软件构建了化工园区内的公共管廊乙烯管道和丙烯管道泄漏情景，分别模拟了气体泄漏扩散、蒸气云爆炸、喷射火的事故情景，根据模拟结果提出了泄漏事故发生后的应急管理方法。刘少杰[4]构建了青岛“11 • 22”输油管道爆炸事故情景，根据实际情况对管道泄漏进行了扩散蒸气云爆炸模拟，分析了不同油品种类和泄漏时长下的爆炸冲击波影响范围。胡盛[5]对大型甲类仓库内的危险化学品爆炸灾害进行了情景模拟，分析了戊烷气云爆炸后的超压、压力上升速度、火焰传播速度以及爆炸温度的时空分布，基于爆炸模拟结果探究了调整堆垛数量和堆垛层数、改变泄压板数量及其位置时的泄爆效果。梅苑等[6]计算了在不同泄漏孔径和泄漏时长下的输油管道泄漏事故范围，发现泄漏时间对流淌火的影响受流淌火稳定时的燃烧时间的限制，而池火受泄漏时间的影响较大。在泄爆措施效果方面，学者们主要对泄爆口的形状和大小进行了研究。石剑云等[7]分析了开窗条件对室内天然气泄漏扩散的影响，运用数值模拟软件Fluent对不同泄漏口尺寸、窗户类型、门窗启闭及通风条件下的天然气泄漏后果进行分析，发现当门窗关闭的情况下，天然气的浓度上升速率和泄漏口面积成正比。董浩宇[8]对综合管廊中通风口的长宽比、通风口泄压板的开启压力进行了分析，发现通风口的设置对管廊最大爆炸超压峰值和温度峰值的削减作用显著，通风口安装泄压板时的超压峰值比无泄压板时更大。
国外学者也对油气管道泄漏爆炸情景进行了大量的模拟工作，应用的主流软件是FLACS。Hansen等[9]利用FLACS软件预测了蒸气云快速发生爆燃事故的影响范围，并且在DNV（Det Norske Veritas）的试验场进行了全尺寸实验验证，实验结果与FLACS数值模拟结果较为吻合。Holborn等[10]利用FLACS软件模拟了大规模液氢池释放，分析其行为并预测了不同环境条件和不同释放场景下形成的液氢池大小、顺风危险距离和氢-空气云的可燃质量。Lv等[11]模拟了液化天然气储罐泄漏下的最大爆炸超压，针对管道连接处和罐顶处泄漏场景进行了模拟研究。Wan等[12]通过实验研究了直管中有侧向泄爆口时甲烷-空气预混气体的爆炸火焰传播特性，发现减小点火源与泄爆口之间的距离可以显著增强泄爆效果。Chao等[13]通过实验分析了圆柱形容器内点火位置对甲烷气体爆炸超压峰值的影响，发现中部会出现“双峰值”现象。Kasmani等[14]通过缩比实验，发现泄爆口的开启压力与爆炸火焰速度及最大爆炸超压具有一定的非线性关系。
综合以上国内外研究可以看出，目前，油气燃爆事故情景模拟主要使用主流软件FLACS，它适用于不同情景下的燃爆事故，模拟结果与实际事故场景具有较高的吻合度，但缺少根据事故情景模拟结果探讨泄爆口对燃爆的泄爆效果。为此，本研究将以十堰重大燃气爆炸事故为背景，借助FLACS软件对该事故场景进行还原构建，根据三维泄漏爆炸模拟结果设计泄爆优化方案，以期更直观科学地掌握事故发生的过程与危害，防止此类事故再次发生，从而为提出泄爆防控措施提供参考依据。
1. 三维模型建立
根据事故报告中的场景图[15]，采用FLACS子模块前处理器CASD对该事故场景进行全尺寸1∶1还原建模，如图1所示。
图 1 事故报告场景图与FLACS事故场景建模Figure 1. Accident report scene diagram and FLACS accident scene modeling diagram地面长、宽、高分别为230、150、4 m，地面中间开凿一条地下河道作为燃气聚集的受限空间，空间尺寸大小与事故场景中的河道大小一致，为了更接近实际情况，地下受限空间上方设置一块300 kPa的泄压板。地下河道上方为涉事故建筑物，一共有17间两层的商铺，墙体厚度均设置为0.3 m。涉事故建筑物东边为一栋居民楼（26号楼），与涉事故建筑物之间的距离为10 m，东边用盖板进行封闭。涉事故建筑物西边为一座艳湖桥，西边河道下方未进行封闭，在涉事故建筑物下方建成一个半密闭的狭长形受限空间。涉事故建筑物南北之间搭建了居民小区楼，其中南侧玉龙阁2栋为最高楼，楼层高度达105 m。借助高德地图对楼宇之间的距离进行测量，并且构建了道路两侧的树木和道路交通线，以此还原事故场景。在几何模型中设置了27个监测点，其中MP1～MP12以30 m间隔均匀分布在地下河道和涉事故建筑物二层内，MP13～MP24以30 m间隔均匀分布在涉事故建筑物南北两侧道路中，MP25～MP27分布在涉事故建筑物东侧。
2. 情景参数设置
在燃气管道泄漏扩散研究中，第一步是计算气体泄漏速率。目前，燃气管道泄漏速率计算模型主要有小孔模型、大孔模型、管道模型[16]。本研究中，城镇燃气管道发生泄漏的位置较为隐蔽，泄漏发生在地下受限空间密闭端一侧，且以腐蚀小孔为主，泄漏孔径较小。根据文献[16]，当泄漏孔径小于30 mm时采用小孔模型最佳，为此采用小孔模型计算，计算公式[16-19]为
Q={Aorp[MkRT(2k+1)(k+1)/(k−1)]1/2p0p>(2k+1)k/(k−1)C0Aorp{2MRTkk−1[(p0p)2/k−(p0p)(k+1)/k]}1/2p0p⩽(2k+1)k/(k−1) (1) 式中：p0为环境压力，Pa；p为管道内的气体压力，Pa；k为等熵指数，即比定压热容与比定容热容的比值，对于甲烷，取1.369；Q为气体泄漏速率，kg/s；C0为气体排放系数，对于雷诺数Re>30000的非临界流，取0.61，其他情况可取1.0；Aor为泄漏孔面积，m2；M为气体分子量，kg/mol，对于甲烷取0.0171；R为摩尔气体常数，8.3145 J/(mol·K)；T为管道内的气体温度，K。计算泄漏速率时，需先判断气体流动是亚声速流动
(p0p>(2k+1)k/(k−1)) 还是声速流动(p0p⩽(2k+1)k/(k−1)) 。该事故管道材质为无缝钢管，管径为57 mm，管道埋深为1.5 m，温度为293 K，设泄漏孔径为30 mm。将燃气管道压力0.4 MPa代入小孔模型中，计算得到燃气管道泄漏速率为0.509 kg/s。最后，将计算出的泄漏速率代入FLACS软件中模拟燃气泄漏扩散场景。基于FLACS的燃气燃爆数值模拟能够呈现复杂的非稳态湍流流动。初始边界条件：在受限空间开口端方向上设置平面波（Plane_Wave）边界，其他方向均设置欧拉（Euler）边界。模拟过程中，各个状态参数遵循质量守恒方程、动量守恒方程、能量守恒方程3个基本方程[20]，即
\left\{ {\begin{array}{*{20}{l}} {\dfrac{{\partial p}}{{\partial t}}+\nabla \cdot \rho \mathop {\boldsymbol{u}} = 0} \\ {\rho \dfrac{{\partial \mathop {\boldsymbol{u}} }}{{\partial t}}+(\mathop {\boldsymbol{u}} \cdot \nabla )\mathop {\boldsymbol{u}}+\nabla p - \rho g = \mathop {\boldsymbol{f}} +\nabla \cdot \boldsymbol {\tau} } \\ {\dfrac{\partial }{{\partial t}}(\rho h)+\nabla \cdot \rho h\mathop {\boldsymbol{u}} = \dfrac{{\rm d}p}{{\rm d}t}+q+\nabla \cdot k_0\nabla T+\nabla \cdot \displaystyle\sum\limits_i {p{h_i}{D_i}\nabla {Y_i} - \nabla {q\rm_r}} } \end{array}} \right. (2) 式中：
\rho 为流体密度，kg/m3；t 为时间，s；{\boldsymbol{u}} 为流场矢量速度，m/s；p 为流场压力，Pa；g为重力加速度，m/s2；{\boldsymbol{f}} 为所受力的矢量和，N；h 为流体总焓，J/mol；{h}_{i} 为流场中组分i 的焓，J/mol；k0为系数；{Y}_{i} 为流场中组分i的质量浓度，kg/m3；{D}_{i} 为组分i的相对分子质量；\boldsymbol {\tau} 为速度流场的黏性应力张量；{q}_{\rm r} 为热辐射通量；q 为流体燃烧反应放出的热量，J。3. 三维模拟结果分析
3.1 泄漏扩散模拟结果分析
将已建立的模型导入FLACS中的Run Manager模块进行计算，通过后处理器Flowvis 5对燃气泄漏扩散可视化，抽取相应的二维或三维图进行分析，由于燃气爆炸极限范围为5%～15%，因此重点对燃气在5%～15%的扩散浓度范围进行分析。图2提取了燃气管道压力为0.4 MPa时燃气泄漏扩散随时间变化的二维图，其中左图为xy地下河道位置俯视图，右图为xz横向剖面图。
图 2 0.4 MPa下燃气扩散浓度随时间的变化Figure 2. Change of gas diffusion concentration over time at 0.4 MPa通过模拟发现，燃气在地下受限空间泄漏时，一部分气体从泄漏源位置开始释放，由于在泄漏初始阶段燃气具有一定的初速度，因此初始阶段燃气沿着泄漏口方向扩散。因为燃气的密度比空气的密度小，所以气体逐渐向上扩散，在上方遇到受限壁面后发生聚集，扩散过程中遇到障碍物使气体紊流程度加大。随着燃气不断地从管道内泄漏扩散，地下河道内密闭端一侧的燃气浓度逐渐增大，t=60 s时，密闭端一侧浓度已达到爆炸上限，靠近泄漏源一侧的壁面扩散范围更大，在xy平面内形成内凹不规则形状，在xz横向剖面上方的燃气浓度明显大于下方，并且逐渐向开口端一侧扩散。随着燃气继续泄漏，受限空间内气体浓度逐渐增大，聚集程度进一步提高。t=150 s时，受限空间上方燃气浓度已接近爆炸上限，一部分气体已扩散至开口端一侧方向上，扩散出的气体由于被外界空气稀释，浓度降低到爆炸下限，但由于持续的泄漏，不断有气体从受限空间内冒出补充，导致开口处的一部分气体依旧处于爆炸极限范围内。最终，爆炸性气体在受限空间内从密闭端一侧逐渐向开口端一侧扩散，扩散遇到障碍物使气体紊流程度进一步加大，密闭端一侧的燃气聚集程度大于开口端一侧，受限空间上方的燃气浓度大于下方的燃气浓度，燃气在外界释放的爆炸性气体范围逐渐扩大。
3.2 爆炸模拟结果分析
将扩散后的模型导入FLACS爆炸模块，得到燃气爆炸事故情景模拟。对该重大爆炸事故情景中的爆炸火焰和爆炸超压进行分析，图3显示了爆炸模拟过程中最大爆炸火焰的时空演化情况，其中w为最大燃烧产物的质量分数。可以发现，燃气爆炸火焰从点火源开始发展，1550.15 ms内燃爆火焰还位于地下受限空间内，从密闭端不断孕育加速向开口端前进。经过约100 ms后，燃爆火焰从开口端冒出，并且由于到达开口端后火焰形态不受限制而发生急剧膨胀变形。在密闭端由于燃爆压力达到河道上部泄压板的压力，泄压板被气压打开，从而在1799.93 ms时观察到一部分爆炸火焰从密闭端冒出。最终，燃爆火焰在受限空间外不断发生膨胀并摧毁周围建筑物，从而可能导致次生、衍生灾害。
图 3 最大爆炸火焰形态的时空演化Figure 3. Spatial and temporal evolution of maximum explosion flame morphology对燃气爆炸冲击波超压进行分析，结合冲击波超压对建筑物的破坏准则[21]，设爆炸超压的梯度范围为5～300 kPa，图4显示了在该爆炸压力梯度下建筑物表面受到的最大冲击波超压（pmax）时空演化云图。爆炸初期（1351.01 ms以内），爆炸超压处于萌芽阶段，从密闭端开始发展，逐渐延伸至开口端，涉事故建筑物还未到达破坏阶段。随后，爆炸超压进入迅速升压阶段，1608.40 ms时地下受限空间内的爆炸超压均达到200～300 kPa，导致空间内立柱发生倒塌，一层地面楼板设置的300 kPa泄压板地面和河道内四周钢筋混凝土结构均遭到破坏。当冲击波到达开口端后，会产生爆炸压力衰减，并且以开口端为中心向四周逐渐衰减，靠近开口端一侧的居民小区大部分门窗玻璃遭到破坏，同时部分墙体和开口端一侧河道地面产生裂缝。随着爆炸超压的进一步发展，在涉事故建筑物密闭端一侧也遭受相应的破坏，爆炸超压也向四周辐射。最终，涉事故建筑物二层被破坏，内部大部分隔墙发生垮塌，导致建筑物房间内部人员死亡；四周居民小区门窗和地面物品均遭到严重破坏，并且开口端一侧的破坏程度重于密闭端一侧。根据FLACS后处理器数据得出河道内部爆炸超压最高达660.7 kPa。对比事故报告中对该事故破坏情况的定性描述[15]以及网络媒体对该事故发生后的详细报道，结果显示，本研究的爆炸情景模拟结果与事故报告及实际情况基本一致，验证了情景模拟的准确性。
进一步提取出该爆炸模拟过程中地下河道内部监测点和涉事故建筑物四周的爆炸压力随时间的变化情况，如图5和图6所示，其中MP1～MP6分别为地下受限空间内从密闭端至开口端的监测点。由图5可知，受限空间内部压力大于涉事故建筑物四周的压力，密闭端一侧的内部最大压力大于开口端一侧，并且越接近密闭端，压力振荡幅度越大。对于涉事故建筑物四周，密闭和开口轴向两侧压力明显大于涉事故建筑物两侧压力，并且开口端一侧压力要稍高于密闭端一侧压力。这是由于受限空间轴向两侧位于爆炸冲击波发展中心线上，而涉事故建筑物两侧受到建筑物墙面的约束，导致受限空间轴向两侧压力大于涉事故建筑物两侧压力；受限空间开口端的爆炸冲击波受到的约束较弱，密闭端超压在冲击上方地面时压力有所衰减，致使开口端一侧的爆炸超压稍高于密闭端一侧。
图 5 受限空间内不同测点爆炸压力随时间的变化Figure 5. Variation of explosion pressure with time at different measuring points in confined space
图 6 涉事故建筑物四周爆炸压力随时间的变化Figure 6. Variation of explosion pressure around the involved building over time4. 数值模拟泄爆优化方案设计
基于已建立的数值模型进行泄爆优化设计，主要通过设置不同的泄爆口开展泄爆方案设计。通过分析泄爆口的位置、泄放面积以及开启压力对爆炸的泄放效果，获取最佳的泄爆方案。
图7为泄爆口设置示意图，其中：在涉事故建筑物北侧2 m设置一个长为2 m、宽为1 m的泄爆口，如图7(a)所示；在涉事故建筑物东侧设置一块长为10 m、宽为1 m的泄压板，如图7(b)所示。其他参数设置与事故爆炸模拟保持一致，具体工况如下。
(1) 泄爆口位置不同：保持泄爆口的尺寸（长10 m、宽1 m）不变，泄爆口分别设置在东侧位置（火焰发展轴向）、北侧2 m、北侧28 m、北侧54 m、北侧80 m、北侧106 m。
(2) 泄爆口泄放面积不同：保持泄爆口起始位置（北侧2 m）不变，通过改变泄爆口的长度来改变泄放面积，泄爆口的长度分别设置为2、10、18、26、34 m。
(3) 泄爆口开启压力不同：将泄爆口位置设置在涉事故建筑物东侧，保持泄爆口尺寸（长为10 m、宽为1 m）不变，在泄爆口表面安装一块泄压板，泄压板的单位面积质量为10 kg/m2，起始孔隙率为零，最终孔隙率为1，泄压板开启压力分别设置为50、100、200、300 kPa。
5. 泄爆口在受限空间内的泄爆效果分析
5.1 泄爆口位置
将不同泄爆口位置工况下的模拟文件导入FLACS，提取不同泄爆口位置下的最大爆炸火焰分布，如图8所示。观察图8可知，燃气在受限空间内发生燃爆后，爆炸火焰在泄爆口位置发生急剧膨胀，并从泄爆口迅速向外喷射。当泄爆口设置在狭长受限空间内火焰发展轴向并靠近点火源时，如图8(a)所示，在火焰发展初期，一部分火焰就从轴向泄爆口释放，泄放出的火焰遇到建筑物后向敞开区域散去。当泄爆口设置在北侧位置时，如图8(b)～图8(f)所示，泄爆口越远离点火源，泄放出的火焰范围越大，泄放出的火焰冲击强度越小。这是由于火焰在密闭点火端处于初期发展阶段，若此时将火焰泄放出来，则会抑制火焰的轴向发展，越远离密闭点火端泄放，爆炸火焰发展得越充分，更多的可燃气体被点燃，致使更多的爆炸产物从泄爆口释放，火焰范围越大。当泄爆口接近开口端时，其爆炸强度已有一定程度的衰减，若此时泄放出来，则爆炸火焰冲击强度将有所减弱。
图 8 不同泄爆口位置下最大爆炸火焰的二维面视图Figure 8. Two-dimensional view of the maximum explosion flame under different outlet location conditions分析在不同泄爆口位置上产生的最大爆炸超压，如图9所示。当泄爆口设置在东侧位置时，地面上大于5 kPa的可见范围最小，产生的爆炸超压最小。当泄爆口在北侧位置上时，越远离点火源，产生的爆炸超压越大，泄爆效果越差。泄爆口在东侧位置时的爆炸超压变化幅度比西侧大。显然，随着泄爆口远离点火源，东侧密闭端的爆炸超压与壁面的反射叠加现象更强烈，导致其爆炸超压更大。
图 9 不同泄爆口位置下最大爆炸超压二维面视图Figure 9. Two-dimensional view of maximum explosion overpressure under different outlet location conditions提取地下河道受限空间内密闭端和开口端监测点测得的爆炸压力和爆炸火焰速度，如图10和图11所示。可以看出：不同泄爆口位置工况下，密闭端的爆炸压力变化趋势相同，将泄爆口设置在东侧时，密闭端的爆炸压力最小，将泄爆口设置在北侧越靠近点火源时，密闭端的爆炸压力越小；密闭端的爆炸火焰速度变化趋势则显著不同，泄爆口越接近点火源，爆炸火焰速度峰值越小，波动幅度越小。对于开口端，不同泄爆口位置工况下，爆炸压力和爆炸火焰速度在短时间内都出现短暂的上升，仍然是泄爆口位于东侧或北侧离点火源近时爆炸压力峰值和爆炸火焰速度峰值最小，并且爆炸压力出现负压现象，爆炸火焰速度最终趋于零。
图 10 不同泄爆口位置下测点MP1（密闭端）的爆炸压力和爆炸火焰速度随时间的变化Figure 10. Variations of explosion pressure and explosion flame velocity at the measuring point MP1 (closed end) with time under different outlet location conditions
图 11 不同泄爆口位置下测点MP6（开口端）的爆炸压力和爆炸火焰速度随时间的变化Figure 11. Variations of explosion pressure and explosion flame velocity at the measuring point MP6 (open end) with time under different outlet location conditions对模拟空间区域内的最大爆炸压力进行对比分析，如图12所示。泄爆口设置在东侧（火焰发展轴向）时泄爆效果最佳，最大爆炸压力降至312.4 kPa，降幅达52.70%；在火焰发展轴向无法设置泄爆口的情况下，可将泄爆口设置在狭长受限空间侧面，且离点火密闭端越近，泄爆效果越佳。
图 12 整个模拟空间中最大爆炸压力随泄爆口位置的变化Figure 12. Variation of the maximum explosion pressure in the entire simulation space with the outlet location5.2 泄爆口面积
不同泄爆口长宽比下的最大爆炸火焰三维云图如图13所示。从模拟效果图中可以观察到，随着侧边泄爆口面积的增大，泄爆出的火焰体积增大，并且侧边泄爆会削弱开口端的泄爆强度。例如：在泄爆面积较小（长宽比为2∶1）的工况下，开口端的泄爆火焰高度最高；随着泄爆面积逐渐增大，从泄爆口喷射出的火焰范围越来越大，大部分燃爆火焰从泄爆口泄放，从而降低了受限空间内轴向火焰冲击强度。
图 13 不同泄爆口长宽比下最大爆炸火焰的三维分布Figure 13. Three-dimensional distribution of maximum explosion flame under different length-to-width ratios of the outlet受限空间内密闭端和开口端的爆炸压力和爆炸火焰速度随时间的变化如图14和图15所示。从爆炸压力时程曲线中可以看出，随着泄爆口面积的增大，密闭端的爆炸压力下降，并且下降幅度逐渐增大，可见，泄爆口面积越大，密闭端爆炸压力下降得越快。密闭端的爆炸火焰速度也发生急剧地下降，加大了火焰速度峰值的削减程度，最后降低到一个较低的水平。
图 14 不同泄爆口长宽比下测点MP1（密闭端）的爆炸压力和爆炸火焰速度随时间的变化Figure 14. Variations of explosion pressure and explosion flame velocity at the measuring point MP1 (closed end) with time under different length-to-width ratios of the outlet
图 15 不同泄爆口长宽比下测点MP6（开口端）的爆炸压力和爆炸火焰速度随时间的变化Figure 15. Variations of explosion pressure and explosion flame velocity at the measuring point MP6 (open end) with time under different length-to-width ratios of the outlet对比图14和图15还可以看出，对于开口端，其爆炸压力时程曲线与封闭端相似，爆炸压力和爆炸火焰速度均有所削减，但爆炸压力随着泄爆面积的进一步加大，降低幅度不明显。开口端的爆炸火焰速度均在短时间内达到峰值，且都随着泄爆面积的增大而降低。分析原因可知，通过加大泄爆口长度的方式增大泄爆面积时，受限空间内的高压从更大的泄爆口释放，并且安装在侧面狭长形的泄爆口形状与受限空间内的火焰传播方向一致，使得爆炸火焰没有足够的距离来充分发展，最终导致爆炸火焰速度在密闭端和开口端均有所削减。
对比不同泄爆面积工况下整个模拟空间中的最大爆炸压力，如图16所示，可以看出：随着泄爆面积的增大，空间内的最大爆炸压力显著降低；当长宽比为34∶1时，泄爆面积增大17倍，最大爆炸压力降至15.4 kPa，降幅达97.65%。因此设置泄爆口时，可通过增加泄爆口的长宽比来增大泄爆面积，从而减轻受限空间内爆炸超压带来的危害。
图 16 整个模拟空间中最大爆炸压力随泄爆口长宽比的变化Figure 16. Variation of the maximum explosion pressure in the whole simulation space with the length-to-width ratio of the outlet5.3 泄爆口开启压力
由以上分析可知，将泄爆口设置在受限空间火焰发展轴向上时，爆炸压力的降低幅度最大。然而，在一些受限空间内，为了满足安全要求，往往会在泄爆口设置一块泄压板，防止受限空间内的有毒有害气体从泄爆口逸出。为此，对泄爆口设置在模型东侧位置上的泄压板的开启压力进行分析。
图17显示了泄压板开启压力分别为50、100、200、300 kPa时的最大爆炸火焰三维可视云图。随着开启压力的升高，爆炸火焰从泄爆口泄放的范围扩大，这是由于增大泄爆口开启压力会导致火焰的成长时间更长，进而使爆炸火焰持续发展，当爆炸压力达到泄爆口开启压力时，泄压板被瞬间冲破，爆炸火焰从泄爆口中喷出，冲毁泄爆口周围的墙面，导致爆炸火焰从泄爆口喷射出的影响范围增大。
图 17 不同泄爆口开启压力下最大爆炸火焰的三维云图Figure 17. 3D nephogram of the maximum explosion flame under different opening pressures of the outlet不同泄爆口开启压力下密闭端和开口端的爆炸压力和爆炸火焰速度随时间的变化如图18和图19所示。在密闭端，不同泄爆口开启压力下，爆炸压力变化趋势相同，随着泄爆口开启压力的增大，密闭端的爆炸压力增大，但增大的幅度不明显，这是由于密闭端的泄爆口开启压力达到封闭前的压力时再增加泄爆口开启压力对爆炸压力没有太大的影响。在密闭端，爆炸火焰速度峰值随着泄爆口开启压力的增大而明显增大，这是由于泄爆口开启压力的增大促进了爆炸火焰的发展，致使泄爆口泄放时火焰速度增大得较快。随着密闭端泄爆口开启压力的增大，开口端的爆炸压力和爆炸火焰速度的变化不明显，说明密闭端泄爆口的开启压力对开口端的影响较小。
图 18 不同泄爆口开启压力下测点MP1（密闭端）的爆炸压力和爆炸火焰速度随时间的变化Figure 18. Variations of explosion pressure and explosion flame velocity at the measuring point MP1 (closed end) with time under different opening pressures of the outlet
图 19 不同泄爆口开启压力下测点MP6（开口端）的爆炸压力和爆炸火焰速度随时间的变化Figure 19. Variations of explosion pressure and explosion flame velocity at the measuring point MP6 (open end) with time under different opening pressures of the outlet不同泄爆口开启压力下整个模拟空间中的最大爆炸压力如图20所示。随着泄爆口开启压力的增大，整个空间内的最大爆炸压力逐渐增大；当泄爆口的开启压力为50 kPa时，最大爆炸压力降低至351.0 kPa，降幅达46.87%。由此可知，若要有效地防控爆炸压力带来的危害，在泄爆口处设置泄压板时，需要考虑泄爆口开启压力的影响，并且尽可能地降低泄爆口开启压力，以有效地降低爆炸压力。
图 20 整个模拟空间中最大爆炸压力随泄爆口开启压力的变化Figure 20. Variation of the maximum explosion pressure in the whole simulation space with the opening pressure of the outlet in the entire simulation space6. 结 论
对受限空间内城镇燃气泄漏重大事故爆炸场景进行全尺寸动态模拟，并对泄爆口进行泄爆优化分析，得出以下结论。
(1) 燃气从地下河道密闭端一侧泄漏并且沿着管道壁面逐渐向外扩散形成内凹的不规则形状，遇到障碍物后扩散加速，受限空间内上方的燃气浓度大于下方燃气浓度。燃爆火焰从点火源开始发展，通过密闭端孕育加速，向开口端前进，到达开口端后，火焰发生急剧膨胀变形，摧毁周围建筑物。爆炸冲击波从密闭端一侧开始发展，到达开口端后以开口端为中心向四周逐渐递减辐射，最终爆炸冲击波破坏涉事故建筑物二层，其内部的大部分隔墙垮塌，四周居民小区的门窗和地面物品均遭到严重破坏，并且开口端一侧的破坏程度重于密闭端一侧，最大超压高达660.7 kPa。
(2) 当泄爆口安装在火焰发展轴向位置时，泄爆效果最佳，空间内的最大爆炸压力降至312.4 kPa，降幅达52.70%；在火焰发展轴向位置无法设置泄爆口的情况下，将泄爆口设置在狭长受限空间的侧面，离点火密闭端越近，泄爆效果越佳。
(3) 随着泄爆口面积的增大，受限空间内的最大爆炸压力显著降低。当泄爆口的长宽比为34∶1时，最大爆炸压力降至15.4 kPa，降幅达97.65%。适当增加泄爆口面积可减轻受限空间内爆炸超压带来的危害。
(4) 随着泄爆口开启压力的增大，受限空间内的最大爆炸压力增大。泄爆开启压力为50 kPa时，最大爆炸压力降至351.0 kPa，降幅达46.87%。降低泄爆开启压力也可有效降低爆炸压力。
(5) 通过分析泄爆口位置、面积和泄爆开启压力可知，设计泄爆方案时应先尽可能地增加泄爆面积，其次考虑将泄爆位置应该安装在狭长受限空间轴向位置，最后尽可能地降低泄爆开启压力。
-
表 1 软材料的超弹性本构模型参数
Table 1. Hyperelastic constitutive model parameters for soft material
{C{_{10} }} {C{_{01} }} {C{_{20} }} {C{_{11} }} {C{_{02} } } −270 290 −1 150 −3 180 2 350 
下载: 导出CSV
表 2 不同CNN架构的性能比较
Table 2. Performance comparison of different CNN architecture
No. CNN architecture Total parameters Validation loss Training time/s 1 Conv(32, 3)+Conv(32, 3)+FC(128, 64) 23344 0.064 131 2 Conv(32, 5)+Conv(32, 5)+FC(128, 64) 39728 0.066 163 3 Conv(32, 3)+Conv(64, 3)+FC(128, 64) 36816 0.059 167 4 Conv(64, 3)+Conv(64, 3)+FC(128, 64) 55696 0.057 181 5 Conv(32, 3)+Conv(64, 3)+FC(256, 128, 64) 78032 0.060 223 6 Conv(32, 3)+Conv(64, 3)+FC(256, 128, 64, 32) 79600 0.068 249
下载: 导出CSV
-
[1] ZHAO T, YU Y Y, ZHANG Y Y, et al. Lightweight and dual-functional composites with stiff-soft microstructure for energy absorption and thermal insulation [J]. Composites Communications, 2021, 26: 100778. doi: 10.1016/j.coco.2021.100778 [2] SARVESTANI H Y, VAN EGMOND D A, ESMAIL I, et al. Bioinspired stochastic design: tough and stiff ceramic systems [J]. Advanced Functional Materials, 2022, 32(6): 2108492. doi: 10.1002/adfm.202108492 [3] WANG J, HU D Y, ZHANG Z Q, et al. Anti-impact performance of bionic tortoiseshell-like composites [J]. Composite Structures, 2023, 303: 116315. doi: 10.1016/j.compstruct.2022.116315 [4] PILANIA G, WANG C C, JIANG X, et al. Accelerating materials property predictions using machine learning [J]. Scientific Reports, 2013, 3(1): 2810. [5] YANG K K, WU Z, ARNOLD F H. Machine-learning-guided directed evolution for protein engineering [J]. Nature Methods, 2019, 16(8): 687–694. doi: 10.1038/s41592-019-0496-6 [6] LIU X, ATHANASIOU C E, PADTURE N P, et al. A machine learning approach to fracture mechanics problems [J]. Acta Materialia, 2020, 190: 105–112. doi: 10.1016/j.actamat.2020.03.016 [7] MAZHNIK E, OGANOV A R. Application of machine learning methods for predicting new superhard materials [J]. Journal of Applied Physics, 2020, 128(7): 075102. doi: 10.1063/5.0012055 [8] WEN C, ZHANG Y, WANG C X, et al. Machine learning assisted design of high entropy alloys with desired property [J]. Acta Materialia, 2019, 170: 109–117. doi: 10.1016/j.actamat.2019.03.010 [9] BESSA M A, GLOWACKI P. Bayesian machine learning in metamaterial design: fragile becomes supercompressible [J]. Advanced Materials, 2019, 31(48): 1904845. doi: 10.1002/adma.201904845 [10] MAO Y W, HE Q, ZHAO X H. Designing complex architectured materials with generative adversarial networks [J]. Science Advances, 2020, 6(17): 4169. doi: 10.1126/sciadv.aaz4169 [11] REN F, WARD L, WILLIAMS T, et al. Accelerated discovery of metallic glasses through iteration of machine learning and high-throughput experiments [J]. Science Advances, 2018, 4(4): 1566. doi: 10.1126/sciadv.aaq1566 [12] CHAN H, CHERUKARA M, LOEFFLER T D, et al. Machine learning enabled autonomous microstructural characterization in 3D samples [J]. NPJ Computational Materials, 2020, 6(1): 1. doi: 10.1038/s41524-019-0267-z [13] BESSA M A, BOSTANABAD R, LIU Z, et al. A framework for data-driven analysis of materials under uncertainty: countering the curse of dimensionality [J]. Computer Methods in Applied Mechanics and Engineering, 2017, 320: 633–667. doi: 10.1016/j.cma.2017.03.037 [14] ANKENMAN B, NELSON B, STAUM J. Stochastic kriging for simulation metamodeling [J]. Operations Research, 2009, 58(2): 371−382. [15] MOZAFFAR M, BOSTANABAD R, CHEN W, et al. Deep learning predicts path-dependent plasticity [J]. Proceedings of the National Academy of Sciences, 2019, 116(52): 26414–26420. doi: 10.1073/pnas.1911815116 [16] LIU Z L, WU C T. Exploring the 3D architectures of deep material network in data-driven multiscale mechanics [J]. Journal of the Mechanics and Physics of Solids, 2019, 127: 20–46. doi: 10.1016/j.jmps.2019.03.004 [17] GU G X, CHEN C T, BUEHLER M J. De novo composite design based on machine learning algorithm [J]. Extreme Mechanics Letters, 2018, 18: 19–28. doi: 10.1016/j.eml.2017.10.001 [18] GU G X, CHEN C T, RICHMOND D J, et al. Bioinspired hierarchical composite design using machine learning: simulation, additive manufacturing, and experiment [J]. Materials Horizons, 2018, 5(5): 939–945. doi: 10.1039/C8MH00653A [19] YU C H, QIN Z, BUEHLER M J. Artificial intelligence design algorithm for nanocomposites optimized for shear crack resistance [J]. Nano Futures, 2019, 3(3): 035001. doi: 10.1088/2399-1984/ab36f0 [20] YANG C, KIM Y, RYU S, et al. Prediction of composite microstructure stress-strain curves using convolutional neural networks [J]. Materials & Design, 2020, 189: 108509. doi: 10.1016/j.matdes.2020.108509 [21] WANG P F, JIANG H B, XU S L, et al. Dynamic plastic instability of ring-shaped aluminum alloy with different interface behaviors [J]. International Journal of Impact Engineering, 2021, 155: 103898. doi: 10.1016/j.ijimpeng.2021.103898 [22] WANG P F, JIANG H B, LIU M, et al. Toughening mechanisms for the dynamic perforation behavior of laminar aluminum alloy with lubricated frictional interfaces [J]. Materials & Design, 2022, 224: 111268. [23] CHEN X, SHI X Z, ZHOU J, et al. High strain rate compressive strength behavior of cemented paste backfill using split Hopkinson pressure bar [J]. International Journal of Mining Science and Technology, 2021, 31(3): 387–399. doi: 10.1016/j.ijmst.2021.03.008 [24] WANG L L. Foundations of stress waves [M]. Amsterdam: EIsevier Science Ltd, 2007. [25] 宋力, 胡时胜. SHPB 数据处理中的二波法与三波法 [J]. 爆炸与冲击, 2005, 25(4): 368–373. doi: 10.3321/j.issn:1001-1455.2005.04.014SONG L, HU S S. Two wave and three wave method in SHPB data processing [J]. Explosion and Shock Waves, 2005, 25(4): 368–373. doi: 10.3321/j.issn:1001-1455.2005.04.014 [26] ZHANG H, ZHANG J. Static and dynamic sealing performance analysis of rubber d-ring based on FEM [J]. Journal of Failure Analysis and Prevention, 2016, 16(1): 165–172. doi: 10.1007/s11668-016-0066-5 [27] 孟祥生, 武晓东, 张海广. 3D打印浆砌层合结构复合材料层间断裂韧性的数值模拟 [J]. 高压物理学报, 2020, 34(4): 044206. doi: 10.11858/gywlxb.20190827MENG X S, WU X D, ZHANG H G. Numerical simulation on interlaminar fracture toughness of 3D printed mortar laminated composites [J]. Chinese Journal of High Pressure Physics, 2020, 34(4): 044206. doi: 10.11858/gywlxb.20190827 [28] WANG P F, ZHANG X, ZHANG H, et al. Energy absorption mechanisms of modified double-aluminum layers under low-velocity impact [J]. International Journal of Applied Mechanics, 2015, 7(6): 1550086. doi: 10.1142/S1758825115500866 [29] WEI Z Q, XU X H. Gradient design of bio-inspired nacre-like composites for improved impact resistance [J]. Composites Part B: Engineering, 2021, 215: 108830. doi: 10.1016/j.compositesb.2021.108830 [30] GU G X, TAKAFFOLI M, BUEHLER M J. Hierarchically enhanced impact resistance of bioinspired composites [J]. Advanced Materials, 2017, 29(28): 1700060. doi: 10.1002/adma.201700060 [31] DU PASQUIER C, CHEN T, TIBBITS S, et al. Design and computational modeling of a 3D printed pneumatic toolkit for soft robotics [J]. Soft Robotics, 2019, 6(5): 657–663. doi: 10.1089/soro.2018.0095 [32] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks [J]. Communications of the ACM, 2017, 60(6): 84–90. doi: 10.1145/3065386 [33] LI T T, CHEN Y Y, HU X Y, et al. Exploiting negative Poisson’s ratio to design 3D-printed composites with enhanced mechanical properties [J]. Materials & Design, 2018, 142: 247–258. doi: 10.1016/j.matdes.2018.01.034 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 398
- HTML全文浏览量: 112
- PDF下载量: 50
