高应变率加载下FCC金属晶体取向对孔洞增长的影响

米星宇; 钟政; 蒋招绣; 王永刚

doi:10.11858/gywlxb.20220711

高应变率加载下FCC金属晶体取向对孔洞增长的影响

doi: 10.11858/gywlxb.20220711

宁波大学冲击与安全工程教育部重点实验室, 浙江宁波　315211

基金项目: 国家自然科学基金（11972202）；宁波市重大科技任务攻关项目（2022Z188）；宁波市自然科学基金（202002N3133）

详细信息

作者简介:
米星宇（1996-），男，硕士研究生，主要从事金属层裂损伤演化研究. E-mail：dazz12345@sina.com

通讯作者:
王永刚（1976-），男，博士，教授，主要从事冲击动力学研究. E-mail：wangyonggang@nbu.edu.cn

中图分类号: O521.2; O347.3
计量
- 文章访问数: 238
- HTML全文浏览量: 85
- PDF下载量: 40
出版历程
- 收稿日期: 2022-12-25
- 修回日期: 2023-03-07
- 网络出版日期: 2023-04-11
- 刊出日期: 2023-04-05

Effect of FCC Metal Crystal Orientation on Void Growth under High Strain Rate Loading

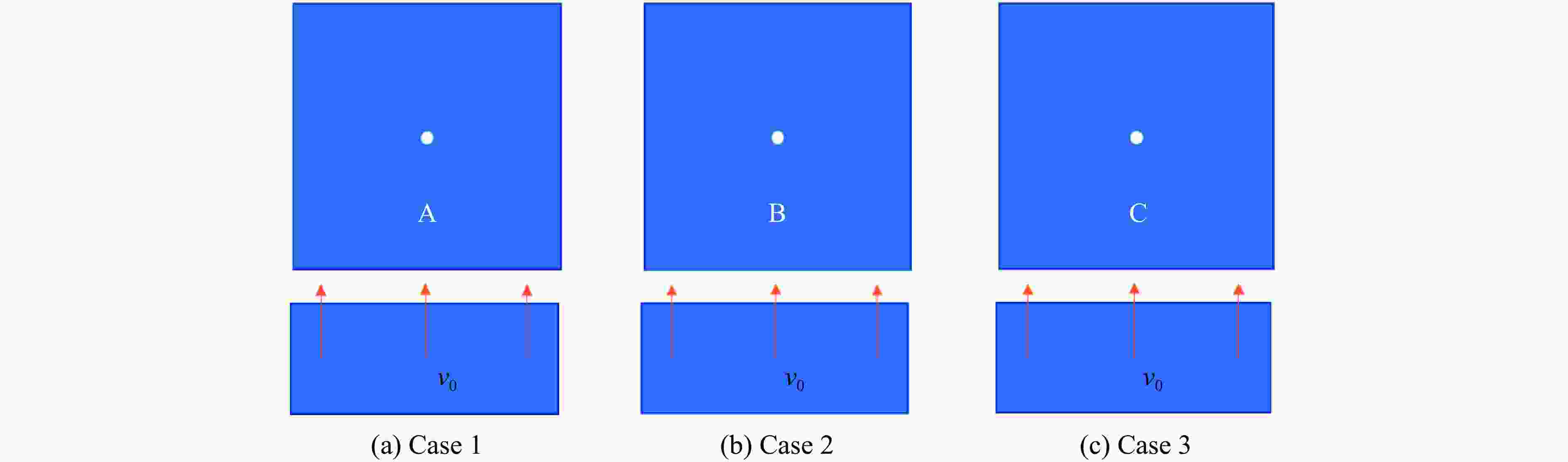
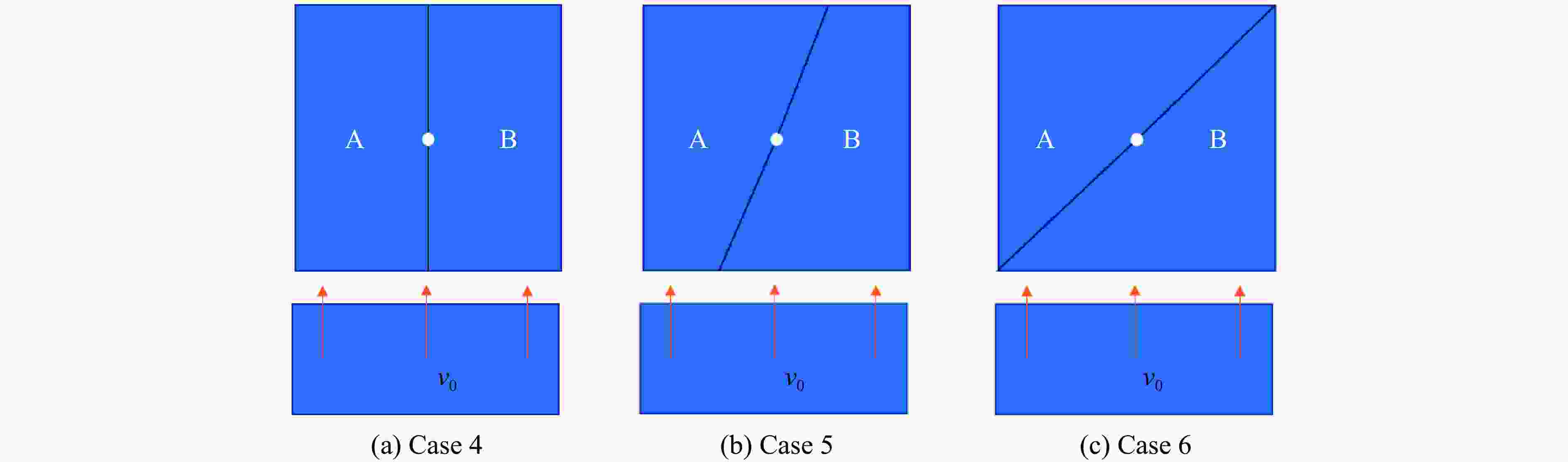
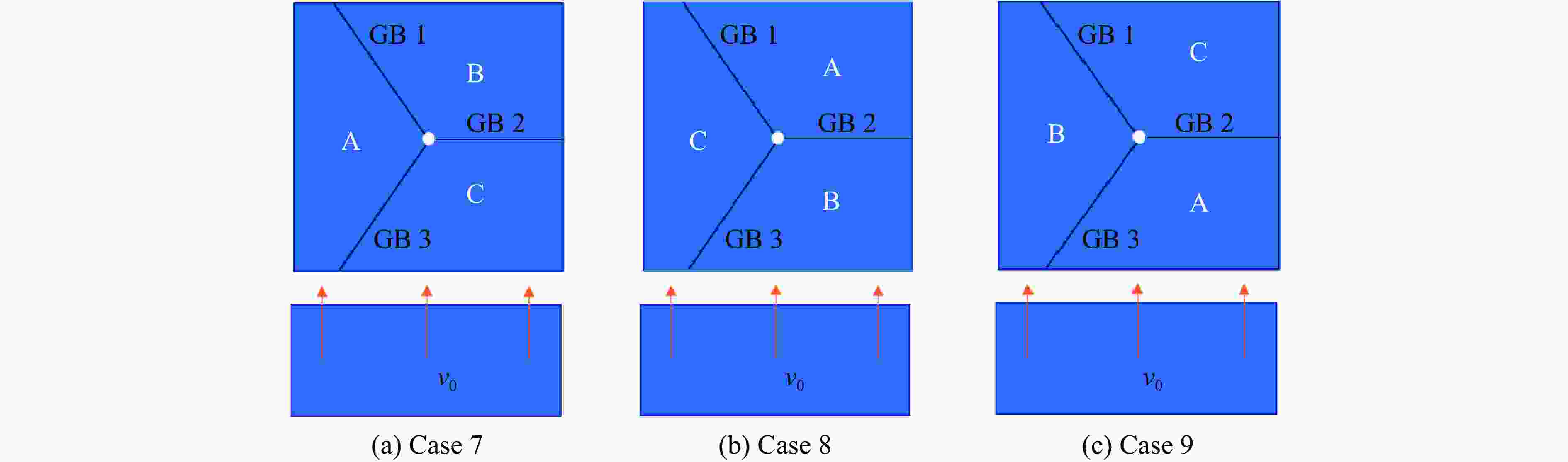
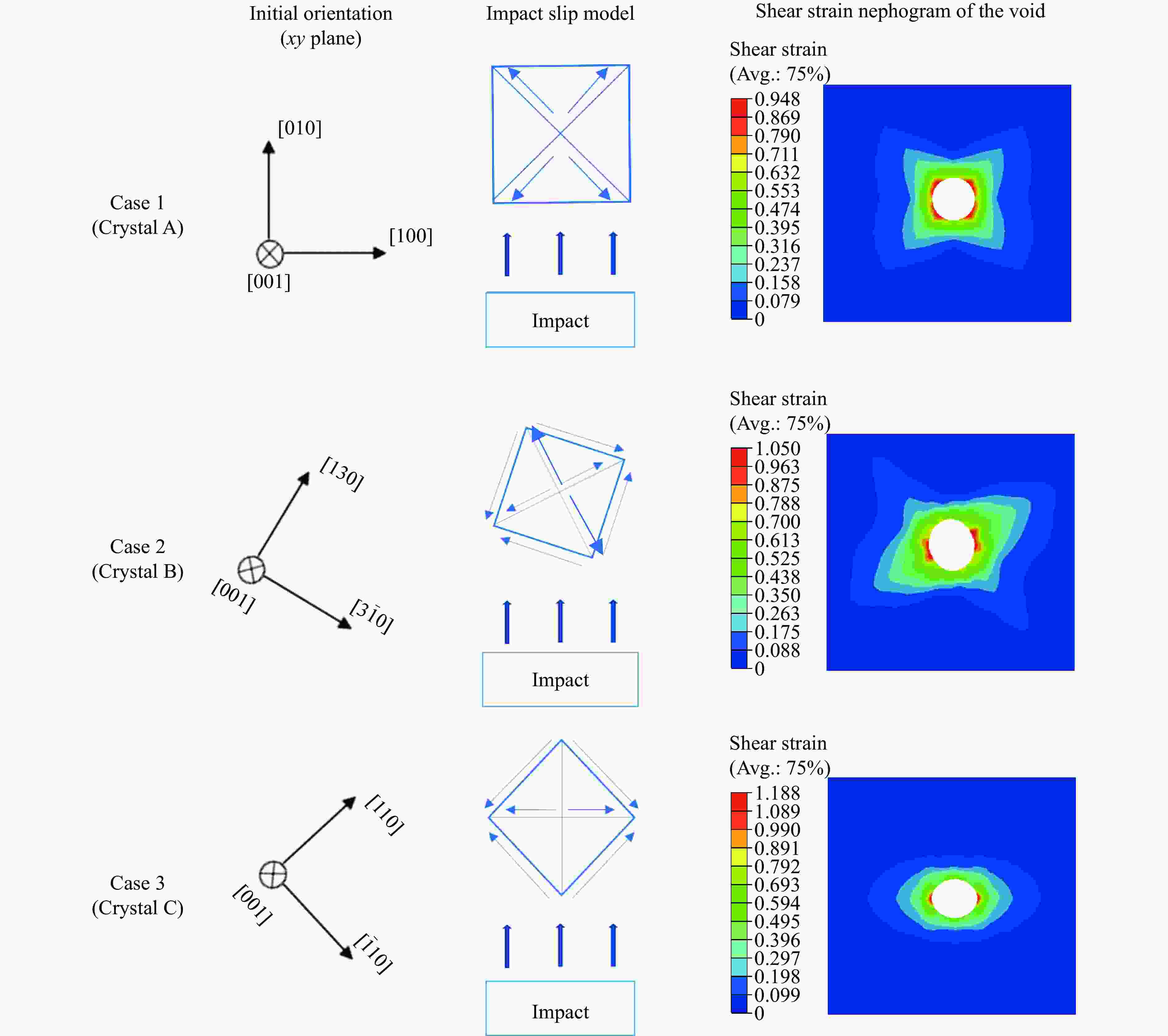
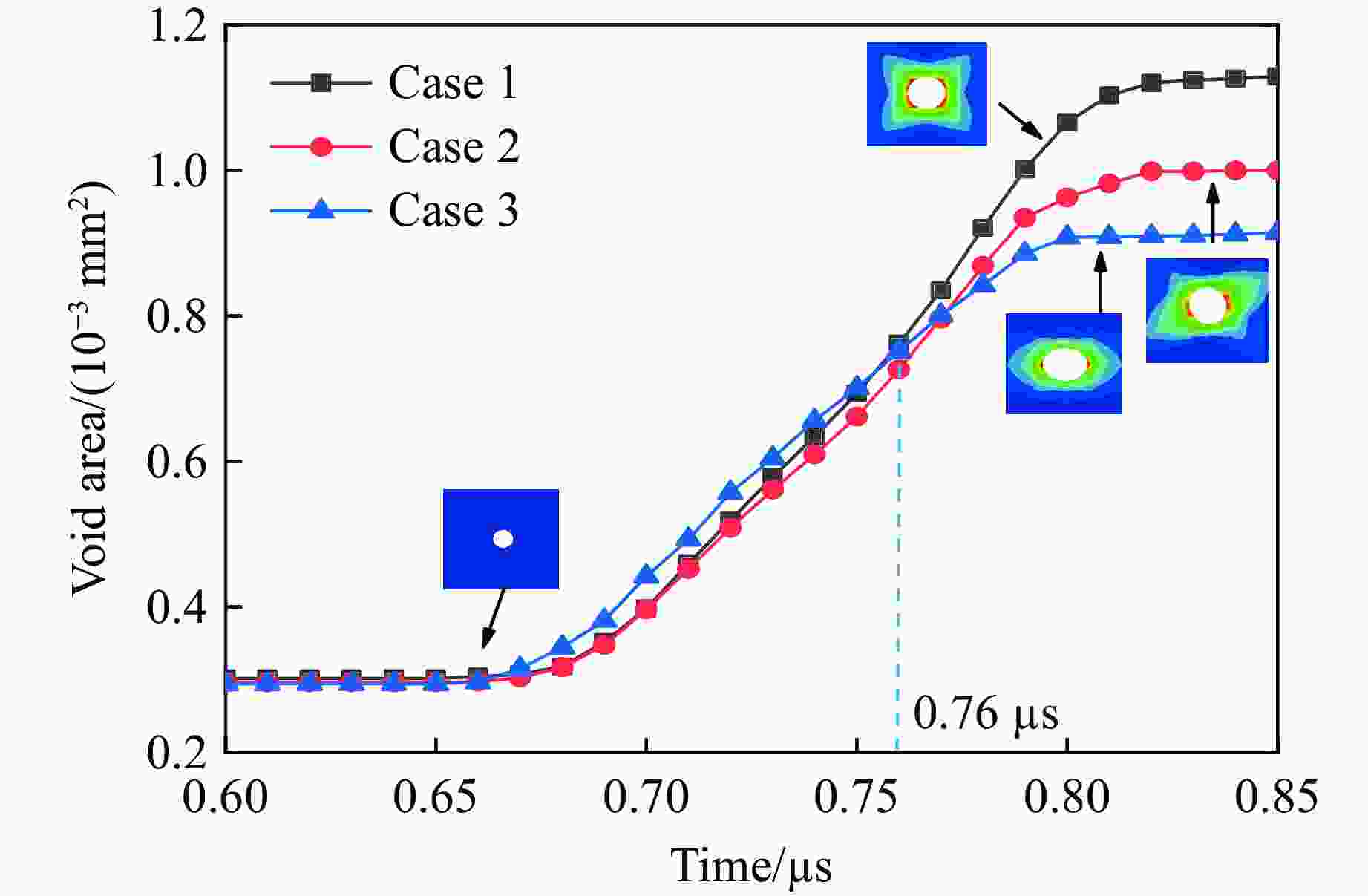
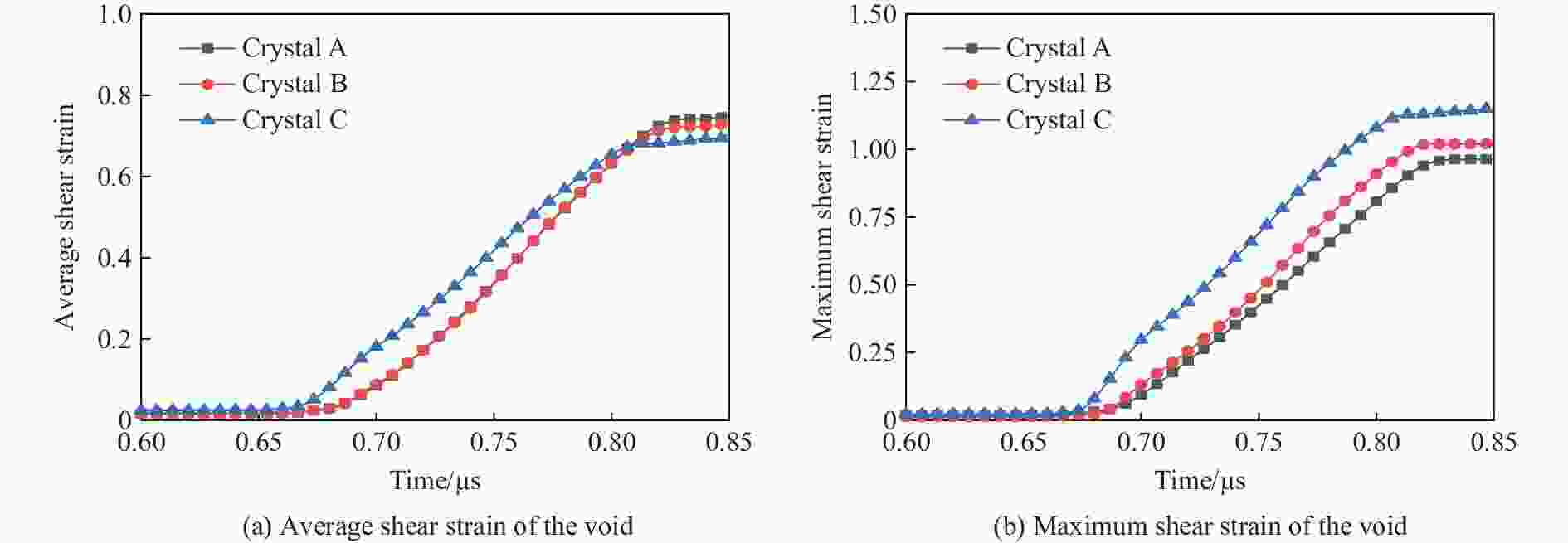
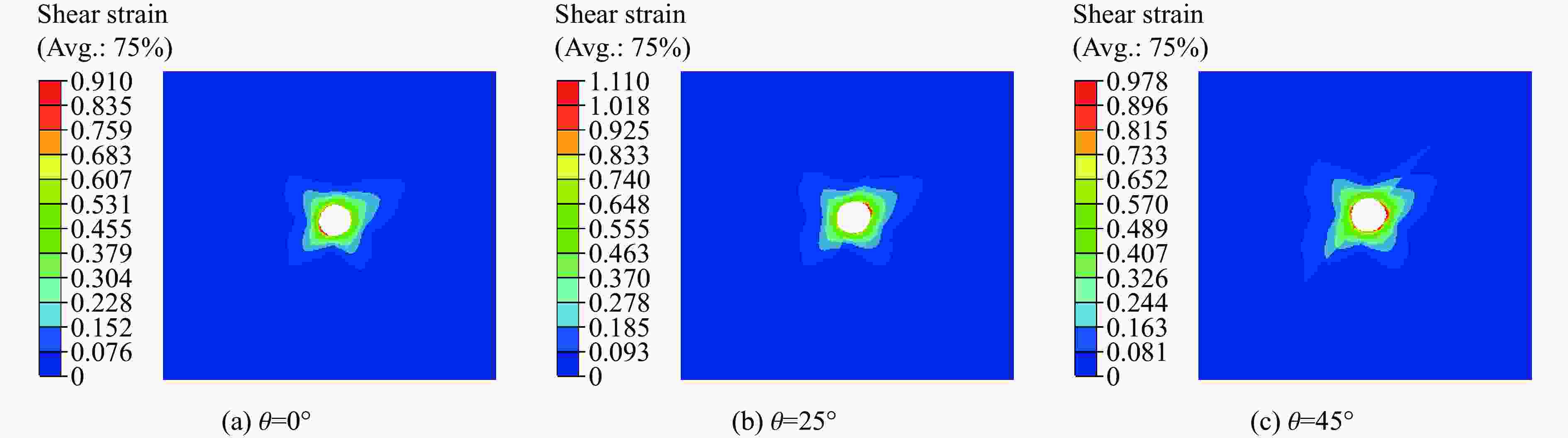
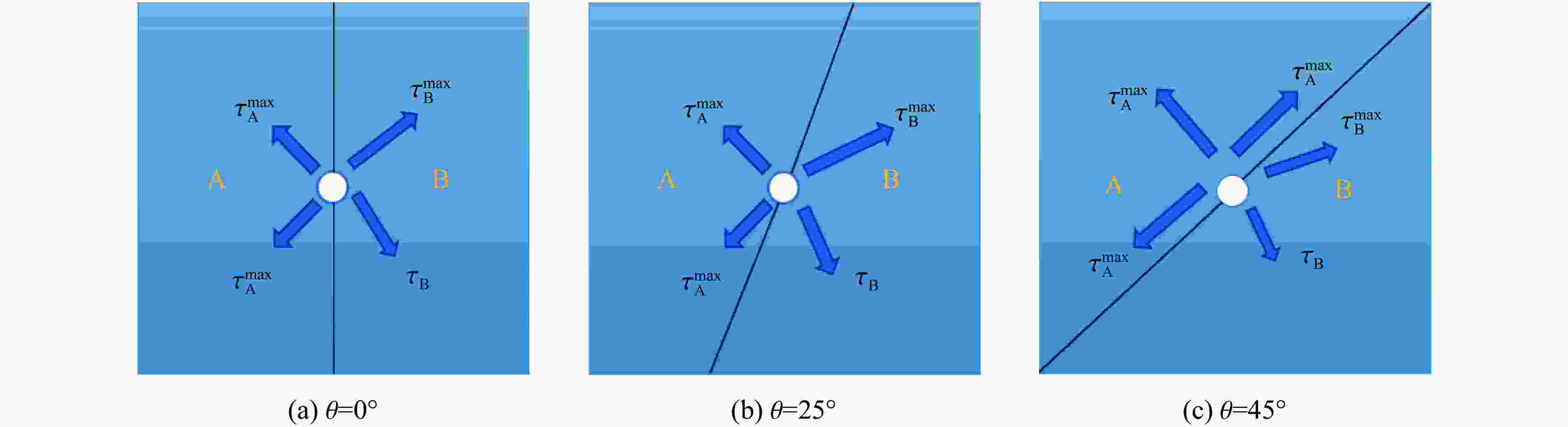
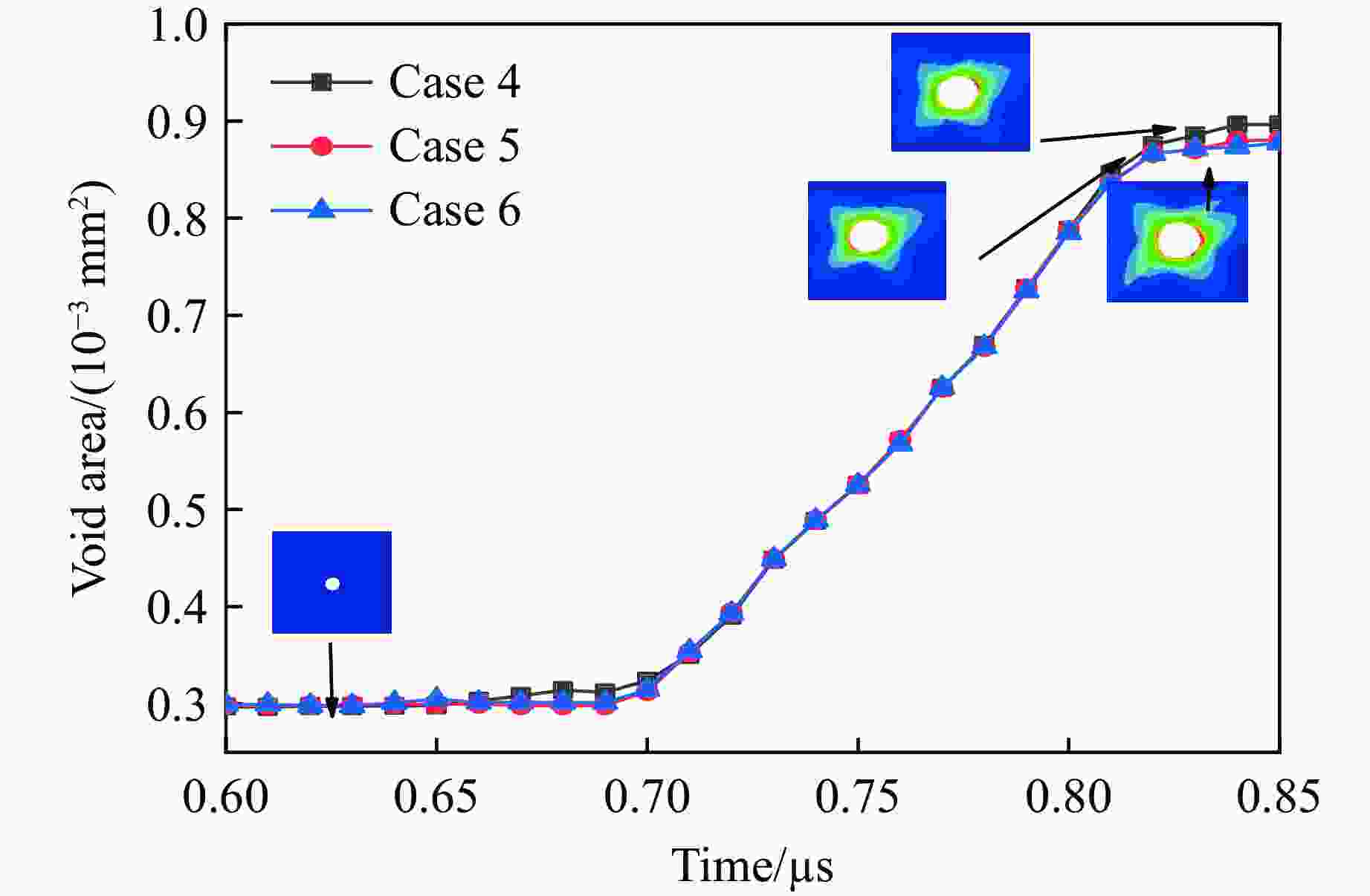
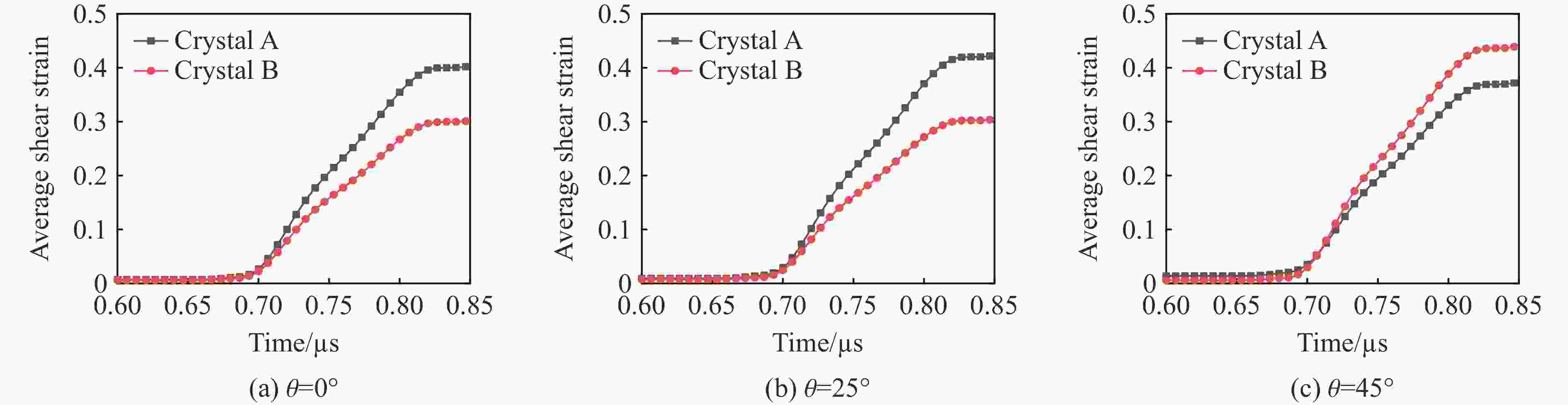
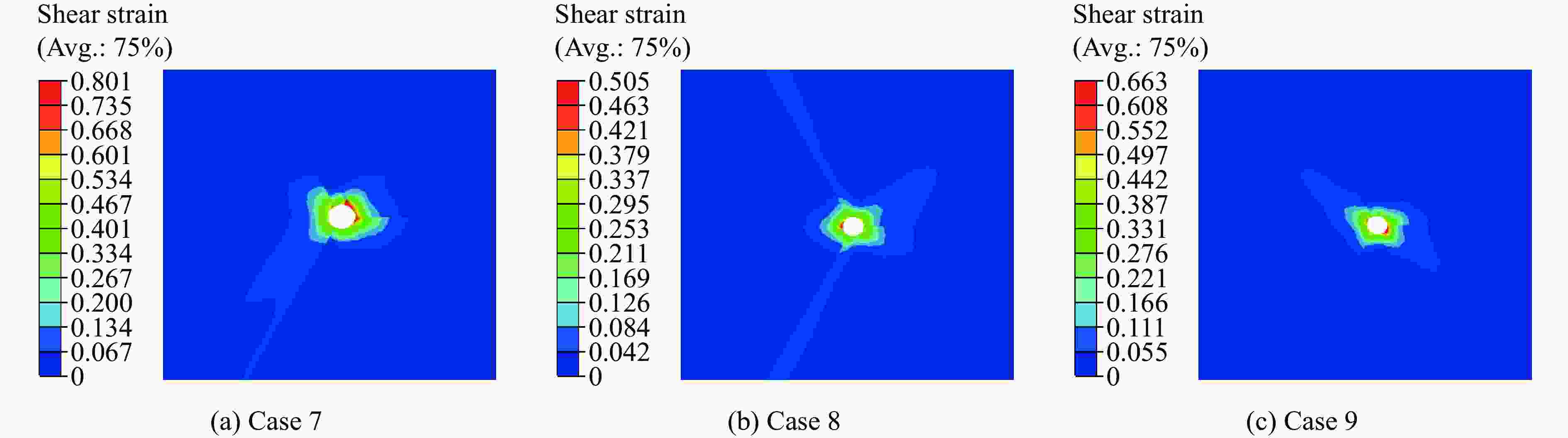
Key Laboratory of Shock and Safety Engineering, Ministry of Education, Ningbo University, Ningbo 315211, Zhejiang, China

摘要

摘要: 采用率相关的晶体塑性本构模型研究了冲击荷载作用下晶体取向对面心立方金属内部孔洞增长的影响。利用VUMAT子程序，将率相关晶体塑性本构模型嵌入ABAQUS有限元软件中，分析了单晶晶内孔洞、双晶晶界孔洞和三角晶界孔洞的增长行为，结果显示：孔洞的变形模式与晶体取向、晶界位置（冲击加载方向与晶界的相对方位）、加载方向相关，晶体的滑移线模型与晶界位置之间的关系可以反映孔洞增长方向。对于晶内孔洞，加载方向越接近[011]，孔洞开始增长变形时间越晚，但孔洞的总体增长变形越大；加载方向越接近[111]，孔洞开始增长变形时间越早，但孔洞的总体增长变形越小。对于晶界处孔洞，晶界位置影响孔洞的部分变形，但不会影响总体变形。晶体受冲击之后，若孔洞增长方向沿晶内，则晶界会促进孔洞沿晶内增长；若增长方向沿晶界，则晶界会促进孔洞沿晶界方向增长，抑制其向晶内增长。
- 晶体塑性 /
- 晶体取向 /
- 晶内孔洞 /
- 晶界孔洞
Abstract: The effect of crystal orientation on the void growth in face centered cubic (FCC) metal under impact loading was studied by adopting rate-dependent crystal plastic constitutive model. VUMAT subroutine was used to embed the rate-dependent crystal plastic constitutive model into the ABAQUS finite element software, and the growth behavior of a single crystal inner void, a bicrystal boundary void and a triangular boundary void was analyzed. The results showed that the void deformation pattern is related to three factors: crystal orientation, grain boundary position (relative orientation of impact loading direction and grain boundary) and loading direction. The relation between the crystal slip line model and grain boundary position can reflect the void growth direction. For intracrystalline voids, the closer the loading direction is to [011], the later the beginning of void deformation is, the greater the overall void deformation is. The closer the loading direction is to [111], the earlier the void starts to deform, the smaller the overall void deformation. For voids at grain boundaries, the location of grain boundaries affect part of the deformation of voids, but not the overall deformation. When the deformation direction of the crystal after the impact is intracrystalline, the grain boundary promotes the growth of voids along the intracrystalline. When the deformation direction is along the grain boundary, the grain boundary promotes the growth of voids along the grain boundary, and inhibits their growth into the crystal.
- crystal plasticity /
- crystal orientation /
- intragranular pore /
- grain boundary pore

HTML全文

图 1 软回收靶板的金相图像^[17]

Figure 1. Metallography of soft recovery target plate^[17]

下载: 全尺寸图片幻灯片

图 2 单晶加载工况

Figure 2. Single crystal loading conditions

下载: 全尺寸图片幻灯片

图 3 双晶晶界加载工况

Figure 3. Bicrystal grain loading conditions

下载: 全尺寸图片幻灯片

图 4 三角晶界加载工况

Figure 4. Triangular grain loading conditions

下载: 全尺寸图片幻灯片

图 5 FCC晶胞的滑移面和滑移线分布

Figure 5. Slip surface and slip line distribution of FCC cells

下载: 全尺寸图片幻灯片

图 6 初始滑移系和孔洞的剪切应变

Figure 6. Initial slip systems and shear strain nephograms of the voids

下载: 全尺寸图片幻灯片

图 7 晶内孔洞面积变化曲线

Figure 7. Area-time curves of voids in single crystal

下载: 全尺寸图片幻灯片

图 8 孔洞区域滑移剪切应变-时间曲线

Figure 8. Shear strain-time curves of the voids

下载: 全尺寸图片幻灯片

图 9 双晶晶界孔洞累积剪切应变云图

Figure 9. Shear strain nephograms of grain boundary voids of bicrystals

下载: 全尺寸图片幻灯片

图 10 双晶晶界剪切应力分布

Figure 10. Shear stress distributions of bicrystals grain boundaries

下载: 全尺寸图片幻灯片

图 11 双晶晶界处的孔洞面积-时间曲线

Figure 11. Void area-time curves at the grain boundary of bicrystals

下载: 全尺寸图片幻灯片

图 12 晶界位置不同时孔洞的剪切应变

Figure 12. Shear strain of voids at different grain boundary locations

下载: 全尺寸图片幻灯片

图 13 三角晶界孔洞剪切应变云图

Figure 13. Shear strain nephograms of triangular grain boundary voids

下载: 全尺寸图片幻灯片

图 14 三角晶界加载模型

Figure 14. Triangular grain boundary loading models

下载: 全尺寸图片幻灯片

图 15 三角晶界孔洞的剪切应力分布

Figure 15. Shear stress distributions of triangular grain boundary voids

下载: 全尺寸图片幻灯片

图 16 三角晶界处的孔洞面积-时间曲线

Figure 16. Void area-time curves at the triangular grain boundaries

下载: 全尺寸图片幻灯片

图 17 3种工况中沿晶内的剪切应变

Figure 17. Intragranular shear strain under three conditions

下载: 全尺寸图片幻灯片

图 18 晶体区域以及不同区域处的剪切应变

Figure 18. Crystal areas and shear strain in different areas

下载: 全尺寸图片幻灯片

表 1 晶体取向

Table 1. Grain orientation

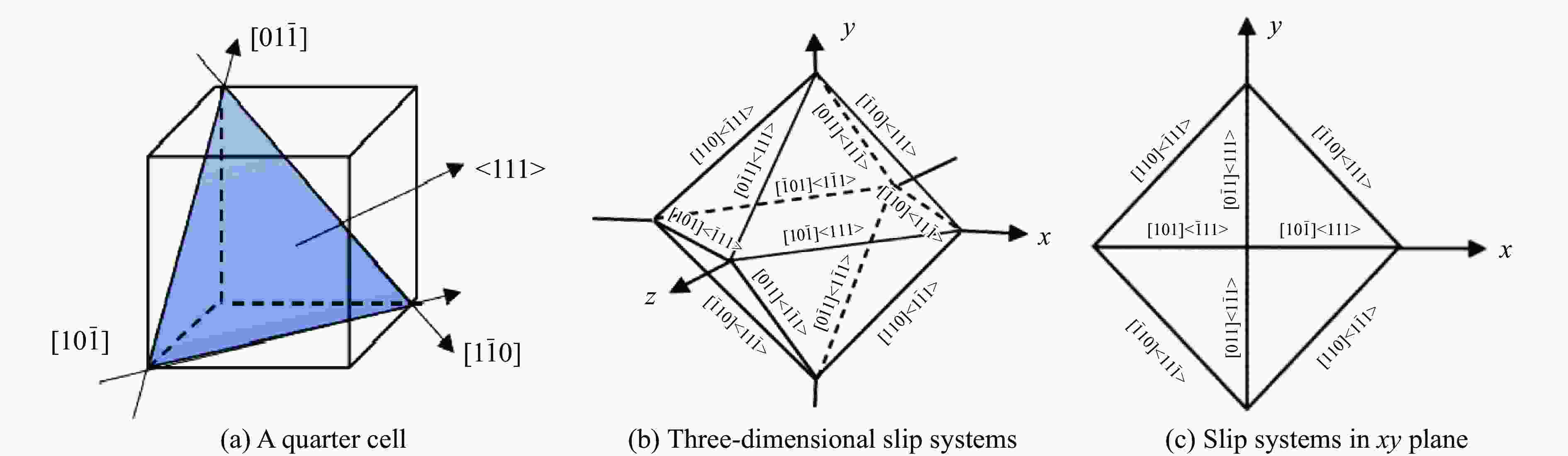
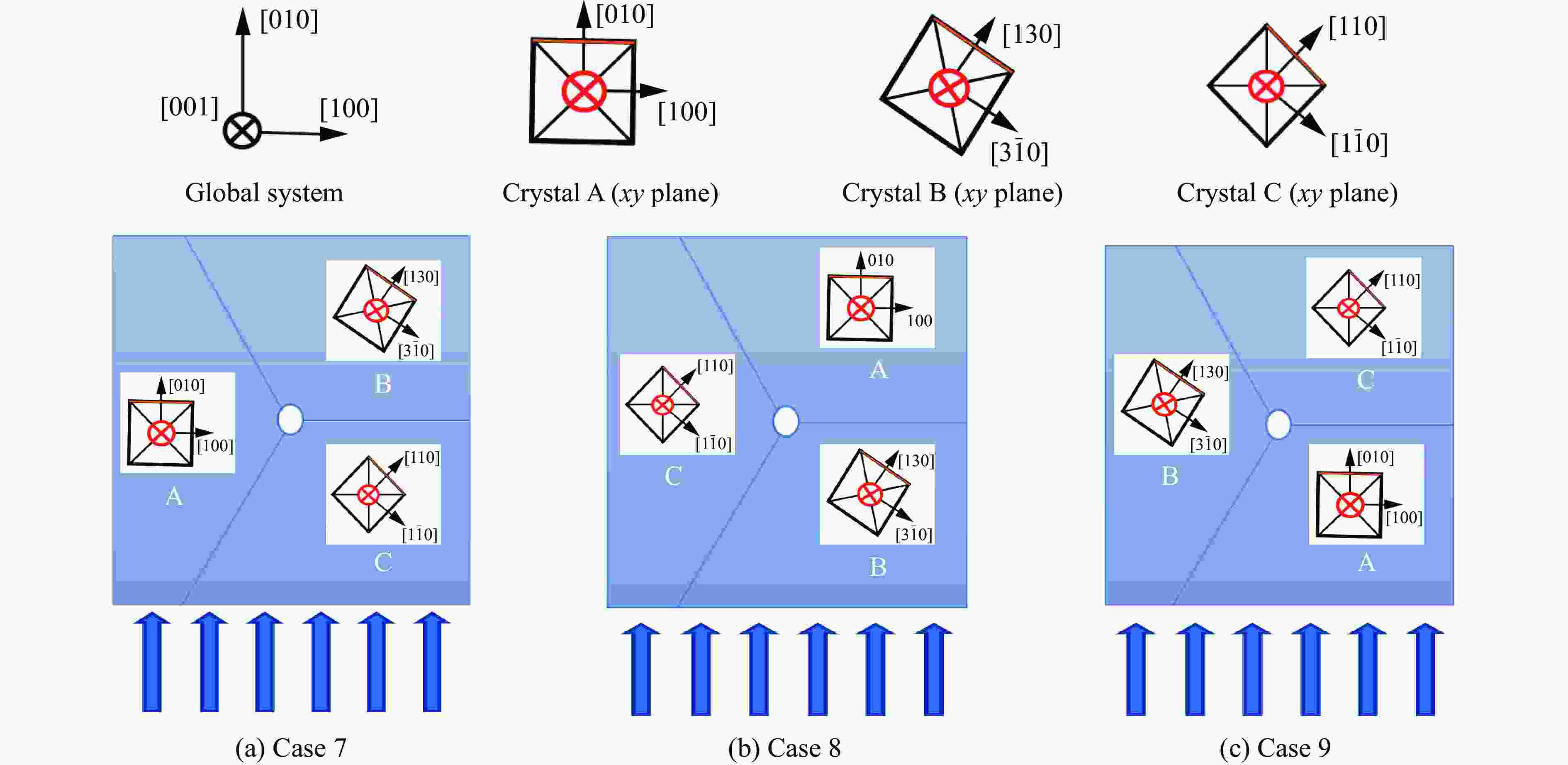
Grain	Miller-Bravais indices (y-x)	Orientation of crystal (Main loading direction)	Orientation of crystal (xy plane)	Angle/(°)
A	(011)$ [100] $	(011)	(010)	0
B	(131)$[ 3\bar10]$	(131)	(130)	18.4
C	(111)$ [\bar 110] $	(111)	(110)	45.0

下载: 导出CSV

表 2 金属铝的12条滑移系晶面指数和晶向指数

Table 2. Initial orientations of 12 slip systems of aluminum metal

$ \alpha $	n^α	m^α	$ \alpha $	n^α	m^α	$ \alpha $	n^α	m^α	$ \alpha $	n^α	m^α
1	(111)	$ \left[ {\bar 101} \right] $	4	($1\bar 11 $)	$ \left[ {\bar 101} \right] $	7	($ \bar 111 $)	$ \left[ {0\bar 11} \right] $	10	($ 11\bar 1 $)	$ \left[ {\bar 110} \right] $
2	(111)	$ \left[ {0\bar 11} \right] $	5	($ 1\bar 11 $)	$ \left[ {011} \right] $	8	($ \bar 111 $)	$ \left[ {101} \right] $	11	($ 11\bar 1 $)	$ \left[ {101} \right] $
3	(111)	$ \left[ {\bar 110} \right] $	6	($ 1\bar 11 $)	$ \left[ {110} \right] $	9	($ \bar 111 $)	$ \left[ {110} \right] $	12	($ 11\bar 1 $)	$ \left[ {011} \right] $

下载: 导出CSV

表 3 金属铝的晶体塑性有限元本构参数

Table 3. Plastic finite element constitutive parameters of aluminum metal crystals

ρ/(kg·m⁻³)	C₁₁/GPa	C₁₂/GPa	C₄₄/GPa	τ⁰/MPa	τ^s/MPa	h⁰/MPa	q	$\dot a$/s^–1
2700	108	62	28.3	21	61	60	1.4	0.001

下载: 导出CSV

参考文献(21)

[1]	ANTOUN T, CURRAN D R, RAZORENOV S V, et al. Spall fracture [M]. New York: Springer, 2003.
[2]	KANEL G I. Spall fracture: methodological aspects, mechanisms and governing factors [J]. International Journal of Fracture, 2010, 163(1/2): 173–191. doi: 10.1007/s10704-009-9438-0
[3]	林茜, 谢普初, 胡建波, 等. 不同晶粒度高纯铜层裂损伤演化的有限元模拟 [J]. 物理学报, 2021, 70(20): 204601. doi: 10.7498/aps.70.20210726 LIN Q, XIE P C, HU J B, et al. Numerical simulation on dynamic damage evolution of high pure copper with different grain sizes [J]. Acta Physica Sinica, 2021, 70(20): 204601. doi: 10.7498/aps.70.20210726
[4]	张凤国, 刘军, 何安民, 等. 层裂损伤孔洞增长模型参数的确定方法及其应用 [J]. 物理学报, 2020, 69(20): 204601. doi: 10.7498/aps.69.20200527 ZHANG F G, LIU J, HE A M, et al. Method of determining parameters of void growth damage model and its application to simulation of spall test [J]. Acta Physica Sinica, 2020, 69(20): 204601. doi: 10.7498/aps.69.20200527
[5]	JIANG Z X, ZHONG Z, XIE P C, et al. Characteristics of the damage evolution and the free surface velocity profile with dynamic tensile spallation [J]. Journal of Applied Physics, 2022, 131(12): 125104. doi: 10.1063/5.0082361
[6]	邓小良, 祝文军, 贺红亮, 等. 沿<111>晶向冲击加载下铜中纳米孔洞增长的塑性机制研究 [J]. 高压物理学报, 2007, 21(1): 59–65. doi: 10.11858/gywlxb.2007.01.010 DENG X L, ZHU W J, HE H L, et al. Plasticity mechanism associated with nano-void growth under impact loading along <111> direction in copper [J]. Chinese Journal of High Pressure Physics, 2007, 21(1): 59–65. doi: 10.11858/gywlxb.2007.01.010
[7]	SUN X Y, XU G K, LI X Y, et al. Mechanical properties and scaling laws of nanoporous gold [J]. Journal of Applied Physics, 2013, 113(2): 023505. doi: 10.1063/1.4774246
[8]	RUESTES C J, BRINGA E M, STUKOWSKI A, et al. Plastic deformation of a porous bcc metal containing nanometer sized voids [J]. Computational Materials Science, 2014, 88: 92–102. doi: 10.1016/j.commatsci.2014.02.047
[9]	RUESTES C J, BRINGA E M, STUKOWSKI A, et al. Atomistic simulation of the mechanical response of a nanoporous body-centered cubic metal [J]. Scripta Materialia, 2013, 68(10): 817–820. doi: 10.1016/j.scriptamat.2013.01.035
[10]	RODRIGUEZ-NIEVA J F, RUESTES C J, TANG Y, et al. Atomistic simulation of the mechanical properties of nanoporous gold [J]. Acta Materialia, 2014, 80: 67–76. doi: 10.1016/j.actamat.2014.07.051
[11]	TANG T, KIM S, HORSTEMEYER M F. Molecular dynamics simulations of void growth and coalescence in single crystal magnesium [J]. Acta Materialia, 2010, 58(14): 4742–4759. doi: 10.1016/j.actamat.2010.05.011
[12]	ZHANG Y Q, JIANG S Y, ZHU X M, et al. Orientation dependence of void growth at triple junction of grain boundaries in nanoscale tricrystal nickel film subjected to uniaxial tensile loading [J]. Journal of Physics and Chemistry of Solids, 2016, 98: 220–232. doi: 10.1016/j.jpcs.2016.07.018
[13]	XIANG M Z, HU H B, CHEN J, et al. Molecular dynamics simulations of micro-spallation of single crystal lead [J]. Modelling and Simulation in Materials Science and Engineering, 2013, 21(5): 055005. doi: 10.1088/0965-0393/21/5/055005
[14]	XIANG M Z, HU H B, CHEN J. Spalling and melting in nanocrystalline Pb under shock loading: molecular dynamics studies [J]. Journal of Applied Physics, 2013, 113(14): 144312. doi: 10.1063/1.4799388
[15]	SHAO J L, WANG C, WANG P, et al. Atomistic simulations and modeling analysis on the spall damage in lead induced by decaying shock [J]. Mechanics of Materials, 2019, 131: 78–83. doi: 10.1016/j.mechmat.2019.01.012
[16]	WANG K, ZHANG F G, HE A M, et al. An atomic view on spall responses of release melted lead induced by decaying shock loading [J]. Journal of Applied Physics, 2019, 125(15): 155107. doi: 10.1063/1.5081920
[17]	陈伟. 晶粒尺寸对高纯铝动态力学行为与层裂特性的影响 [D]. 宁波: 宁波大学, 2020. CHEN W. Effect of grain size on dynamic fracture behavior and spallation characteristics of high-purity aluminum [D]. Ningbo: Ningbo University, 2020.
[18]	HILL R, RICE J R. Constitutive analysis of elastic-plastic crystals at arbitrary strain [J]. Journal of the Mechanics and Physics of Solids, 1972, 20(6): 401–413. doi: 10.1016/0022-5096(72)90017-8
[19]	李宏伟, 杨合, 孙志超. 率相关晶体塑性在有限元应用中的关键技术 [J]. 塑性工程学报, 2008, 15(1): 7–13. LI H W, YANG H, SUN Z C. Key problems for rate-dependent crystal plasticity applied in finite element simulation [J]. Journal of Plasticity Engineering, 2008, 15(1): 7–13.
[20]	刘周攀. FCC金属滑移变形和损伤劣化的晶体塑性有限元分析 [D]. 南宁: 广西大学, 2019. LIU Z P. The analysis on slip deformation and damage behavior of FCC metals based on crystal plasticity finite element model [D]. Nanning: Guangxi University, 2019.
[21]	王琦, 黄庆学, 马立东. 纯铝弯曲的单晶体塑性有限元模拟 [J]. 太原科技大学学报, 2014, 35(2): 119–122. doi: 10.3969/j.issn.1673-2057.2014.02.009 WANG Q, HUANG Q X, MA L D. Aluminum bending of crystal plasticity finite element simmulation [J]. Journal of Taiyuan University of Science and Technology, 2014, 35(2): 119–122. doi: 10.3969/j.issn.1673-2057.2014.02.009