Analysis of Propagation Characteristics of SH Waves in Upper Soil and Lower Rock Strata
-
摘要: 为研究爆破地震波在层状地层的传播规律,选取平面SH(水平剪切)波作为研究对象,基于弹性波动理论,建立了一般层状地层的刚度矩阵和动力平衡方程,分析了土层与基岩的阻抗比、土层厚度、入射波频率和入射波角度对地表速度与土岩地层界面速度的比值(|u1/u2|)的影响。结果表明:|u1/u2|的各个峰值随着入射波频率的增大而减小,且第2个峰值明显小于第1个峰值,实际工程中应重点关注土层的一阶卓越频率;随着土层阻抗的增大,高频部分的响应越来越强烈,且受入射角的影响也越来越大;当土层较薄时,|u1/u2|高频部分的响应比较明显,但随着土层厚度增加,高频部分的响应越来越小,说明土层的高频滤波作用随着厚度的增加而增强。Abstract: In order to study the propagation law of blasting seismic waves in general strata induced by underground engineering constructions, shear horizontal (SH) waves were selected as the research object and the stiffness matrix and dynamic balance equation of general layered strata were established based on elastic wave theory. The propagation law of plane SH waves in the soil-rock stratum was studied, and the influence of soil-rock impedance ratio, thickness of soil layers, frequency and incident angle of incident waves on the ratio of ground velocity to soil-rock interface velocity |u1/u2| was analyzed. Results show that the peak |u1/u2| decreases with the increase of the frequency of incident waves, and the secondary peak is obviously smaller than the first peak. In practical engineering, the focus is on the first predominant frequency of the soil layer; as the impedance of the soil layer increases, the high-frequency response becomes stronger and stronger, and it is also increasingly affected by the incident angle. When the soil layer is thin, the high-frequency response of |u1/u2| is more obvious, but it becomes smaller and smaller as the thickness increases. This indicates that the high frequency filtering effect of the soil layer increases with the increase of the thickness.
-
目前,钻爆法广泛应用于地下工程建设中,在实现经济、便捷、高效施工的同时,其产生的爆破地震效应也是公认的爆破“公害”之首[1-2]。为保证爆破施工邻近建(构)筑物的安全正常运行,研究爆破地震波的传播规律具有重要的工程应用价值。
对于爆破地震波的传播规律,学者们已开展了大量研究工作。胡国忠[3]运用地震波理论对监测资料进行分析,研究了地下工程爆破开挖时地面爆破的振动特性。王玉杰等[4]研究了完整花岗岩体中爆破地震波的传播规律。董永香等[5]通过实验和数值模拟方法,分析了不同组成的多层介质对应力波传播特性的影响。Smerzini等[6]研究了平面和柱面水平剪切(shear horizontal,SH)波入射地下结构的动力响应特性及其对地面位移的影响。王猛等[7]通过爆炸力学理论和数值计算方法,研究了炸药在土岩介质中爆炸的动力响应规律。王超等[8]基于模拟、实测数据验证和量纲分析方法,研究了不同埋深隧道爆破地震波在邻近地表一定范围内的反射叠加规律和地表振动速度衰减规律。张震等[9]、高文学等[10]、汪平等[11]通过数值模拟与现场监测相结合的方法,研究了浅埋隧道爆破振动的传播规律。陈学军等[12]运用萨道夫斯基修正公式对采集的数据进行研究,探讨了不同情况下爆破振动强度的衰变规律以及振动对岩溶塌陷的影响。Jayasinghe等[13]根据现场试验,分析了应力波在土壤和岩石中以及土壤与岩石之间的界面上的传播规律。朱斌等[14]进行了下穿预埋燃气管道的现场爆破试验,通过应变及爆破应力波理论分析了爆破过程中爆破地震波的传播特点。高启栋等[15]通过理论和数值模拟,对考虑爆源特征的岩石爆破诱发地震波的波形进行了研究。王秉相等[16]使用PFC3D软件研究了应力波在散体颗粒中的传播规律和影响因素。王桂林等[17]以重庆市某管廊甲烷爆炸案例为背景,研究了爆炸作用下地面压强与位移的响应特性。
总体来看,现今关于爆破地震波在一般地层传播规律的研究主要集中在现场监测及数值模拟方面,以现今的技术手段测定土层和岩石内部场分布仍然比较困难。考虑到研究平面SH波在一般地层的传播规律具有重要意义,本研究试图建立地面振动与土层内部振动的关系,选取爆破地震波中的平面SH波作为研究对象,基于弹性波动理论,建立半空间上层状地层的刚度矩阵及动力平衡方程组,分析土层与基岩的阻抗比、土层厚度、入射波频率和入射波角度对地表速度与土岩地层界面速度的比值的影响,以期为后续类似工程提供参考。
1. SH波入射作用下上土下岩的动力刚度矩阵建立
1.1 SH波入射作用下单层土的动力刚度矩阵
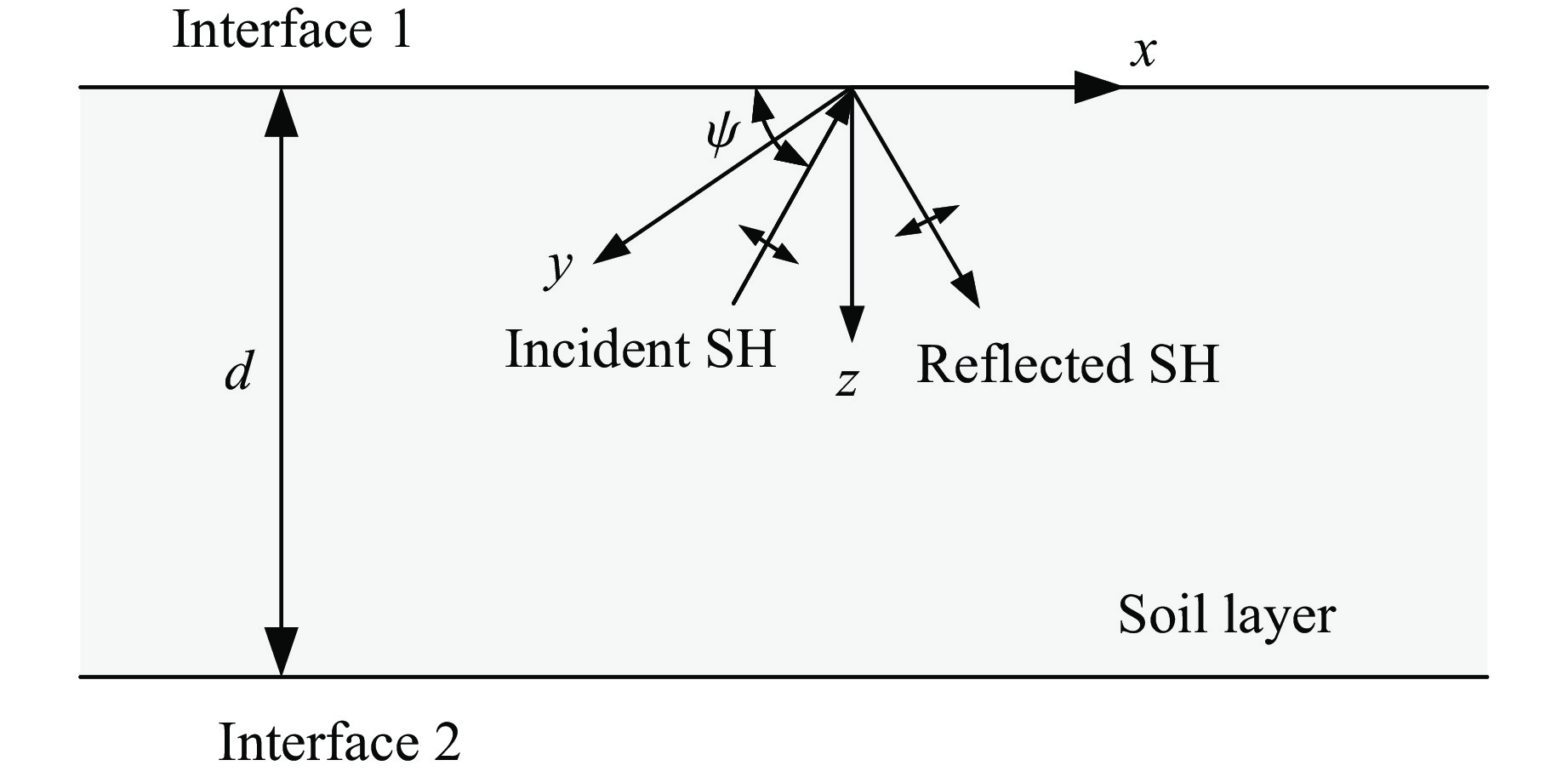
如图1所示,根据弹性波动理论,SH入射波的位移函数可写为
w(i)(z,x)=Aexp[ik′(zsinψ−xcosψ)+iωt] (1) 反射SH波的位移函数可以表示为
w(f)(z,x)=Bexp[ik′(−zsinψ−xcosψ)+iωt] (2) 式中:A、B分别为入射波和反射波的幅值;
k′ 为波数,k′=ω/cs ,cs 为波速,ω为频率;ψ为入射波传播方向与x轴的夹角,即入射角;上标“(i)”表示入射,“(f)”表示反射。为了便于建立一般性位移场,引入
mx=cosψ, c=cs/mx, ζ=√1/m2x−1 ,k=ω/c,ω=2πf ,f为入射波频率。根据文献[18]中构造的土层和基岩的动力刚度矩阵,土层内总位移场的表达式为
w(z,x)=w(i)(z,x)+w(f)(z,x)=[Aexp(iω√1−m2xcsz)+Bexp(−iω√1−m2xcsz)]exp(−iωmxcsx+iωt) = [Aexp(ikζz)+Bexp(−ikζz)]exp(−ikx+iωt) = u(z)exp(−ikx+iωt) (3) 由广义胡克定律可得
τyz(z,x)=ikζG[Aexp(ikζz)−Bexp(−ikζz)]exp(−ikx+iωt) (4) 式中:
τyz(z,x) 为点(z, x)处的剪应力,G为土层的剪切模量。土层顶面和底面的位移和应力幅值为
(w1τyz1)=(11ikζG−ikζG)(AB) (5) (w2τyz2)=(exp(ikζd)exp(−ikζd)ikζGexp(ikζd)−ikζGexp(−ikζd))(AB) (6) 式中:下标1和2分别表示顶面和底面。
联立式(5)和式(6)即可得到顶底面的转换矩阵
(w2τyz2)=(cos(kζd)1kζGsin(−kζd)−kζGsin(kζd)cos(kζd))(w1τyz1) (7) 令
Q1=−τyz1 ,Q2=τyz2 ,Q1 、Q2 分别为土层上、下界面外荷载幅值,可得到该土层的动力刚度矩阵(Q1Q2)=kζGsin(kζd)(cos(kζd)−1−1cos(kζd))(w1w2) (8) 1.2 SH波入射作用下半空间上的层状地层的动力刚度矩阵
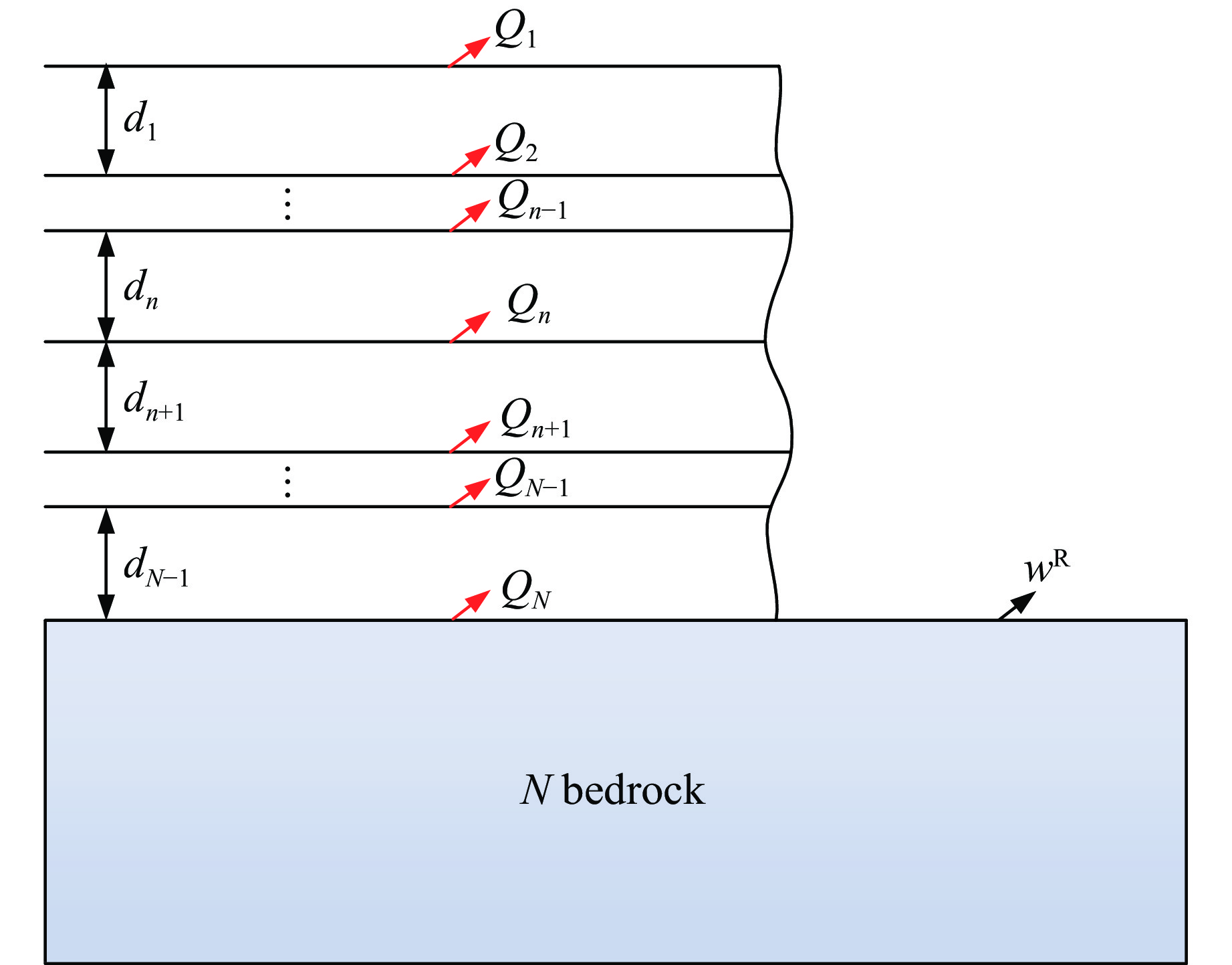
地层往往具有上土下岩的特点,并且土层常为多层层状分布,为了进一步推广适用范围,建立了更具一般性的层状地层的动力刚度矩阵。假设n–1层土层(每层的材料参数为常数)置于基岩上(用N表示)。从土层表面至基岩顶,对各地层界面依次编号,如图2所示。
根据式(3),第n层土层的上、下界面位移幅值可表示为
(wn−1wn) = (11exp(ikζndn)exp(ikζndn))(AnBn) (9) 根据式(4),第n层土层的上、下界面应力幅值为
(τn−1τn) = (ikζnGn−ikζnGnikζnGnexp(ikζndn)−ikζnGnexp(ikζndn))(AnBn) (10) 令
Q1=−τn−1 ,Q2=τn ,由式(8)可知第n层上、下界面的力-位移关系为(Qn−1Qn) = kζnGnsin(kζndn)(cos(kζndn)−1−1cos(kζndn))(wn−1wn) (11) 土层n的刚度矩阵可写为
Ken = kζnGnsin(kζndn)(cos(kζndn)−1−1cos(kζndn))=(kζnGncot(kζndn)−kζnGncsc(kζndn)−kζnGncsc(kζndn)kζnGncot(kζndn)) (12) 在半无限基岩上表面施加荷载,只会产生去波(辐射条件),在式(4)中令A=0,
Q0=−τyz1 (下标0代表半空间自由表面),消去B后得到Q0=ikζRGRwR (13) 对于无阻尼体系,半空间的动力刚度系数为
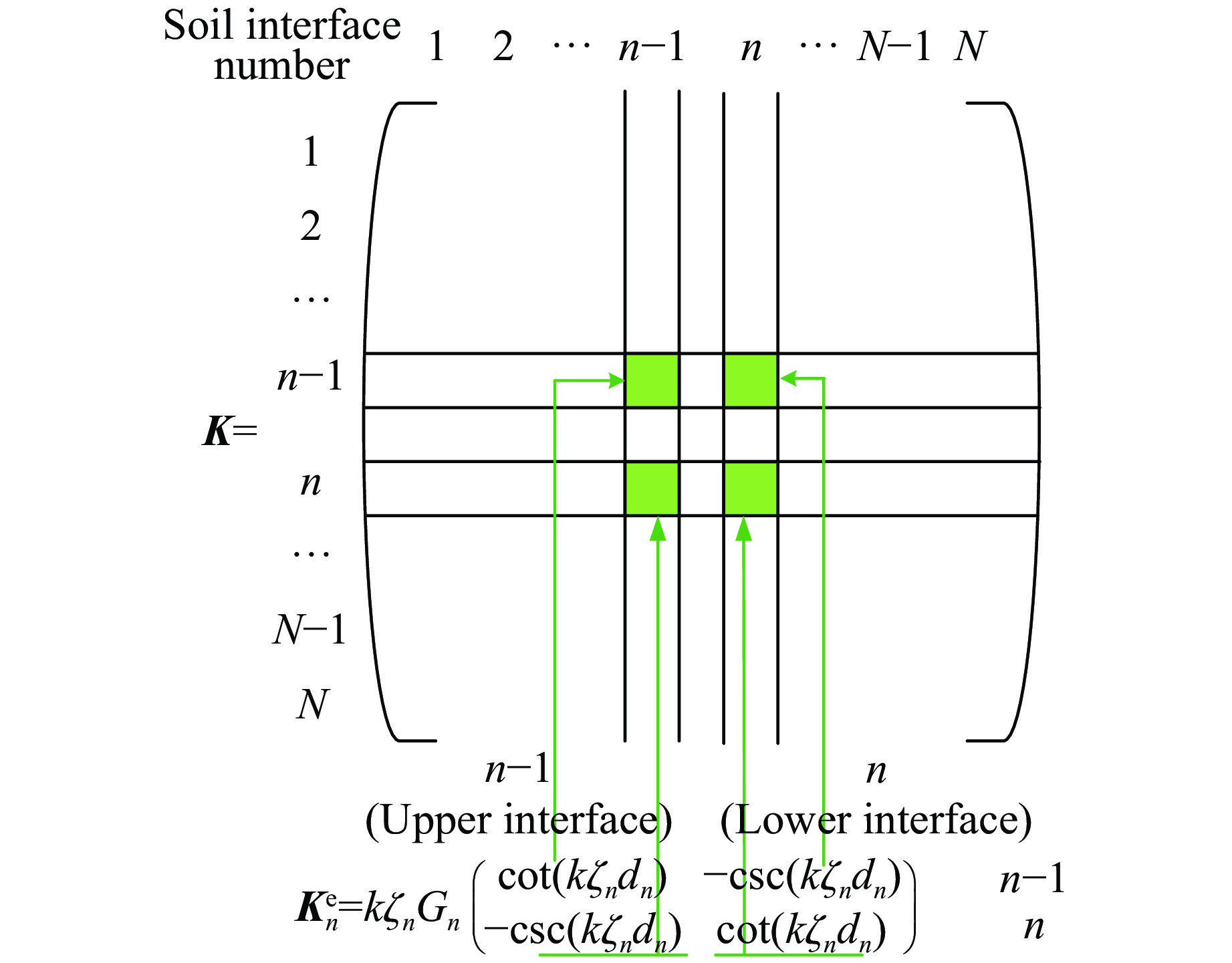
KR=ikζRGR 。整体刚度矩阵组装:将各层土单元刚度矩阵
Ken 的子块按照该层顶底界面对号入座置于总刚度矩阵的相应位置,从而直接形成总刚度矩阵K,如图3所示。K=kζ1G1[D1−Y1−Y1D1+p2D2−p2Y2−p2Y2p2D2+p3D3⋱pN−2DN−2+pN−1DN−1−pN−1YN−1−pN−1YN−1pN−1DN−1+pNDN−pNYN−pNYNpNDN+pR] (14) 式中:
pn=ζnGnζ1G1 ,pR=ζRGRζ1G1 ,Di=cot(kζidi) ,Yi=csc(kζidi) ,Qn 为土层界面外荷载幅值。令
W=[w0,w1,w2,⋯,wN−2,wN−1,wN]T ,Q=[Q0,Q1,Q2,⋯,QN−2,QN−1,QN]T ,则层状地层的动力平衡方程可写为KW=Q (15) 2. 上土下岩地层的波传播规律分析
2.1 SH波入射作用下上土下岩地层的动力刚度矩阵
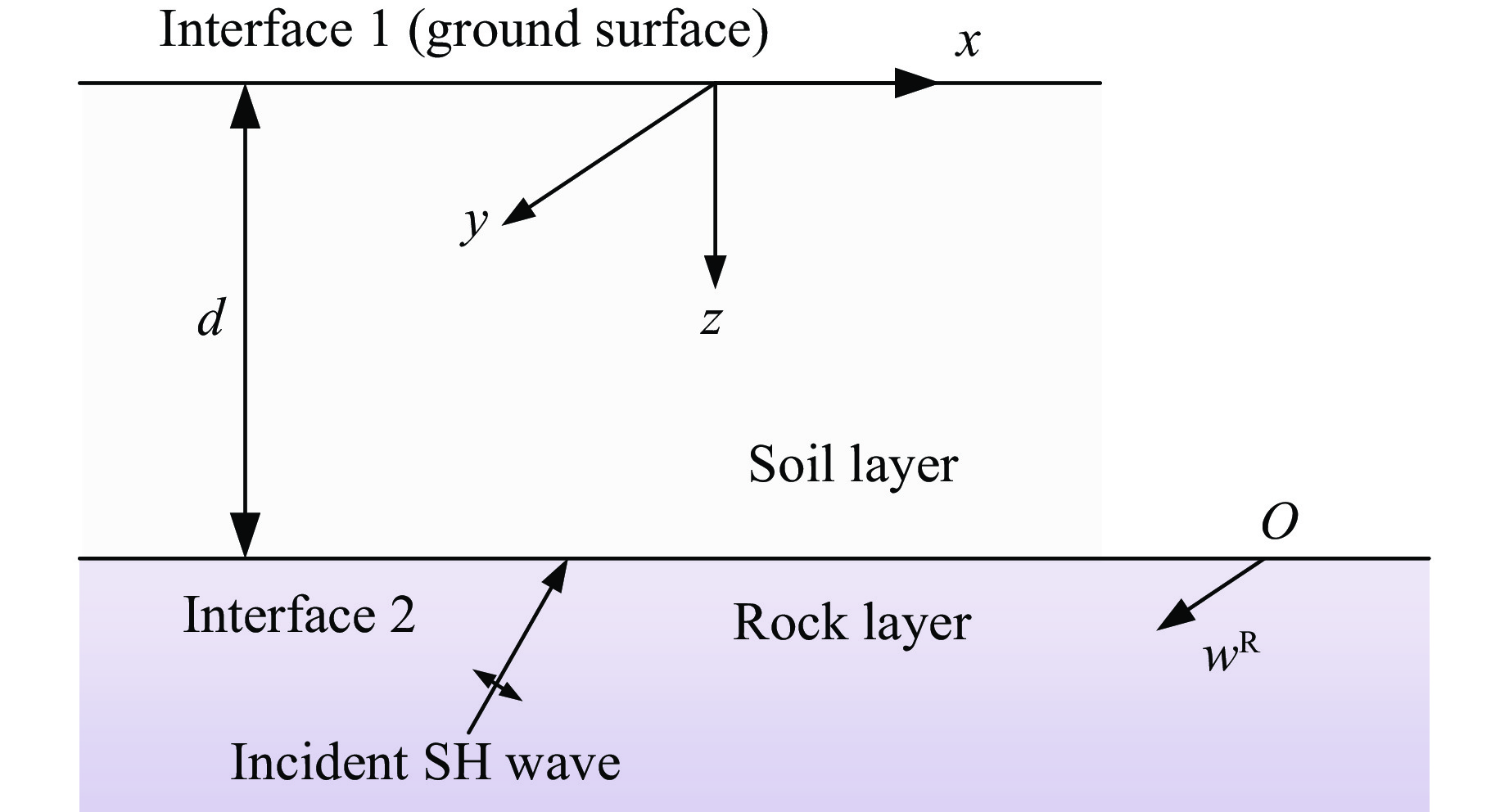
上土下岩地层简化为无限基岩上覆盖一层厚度为d的土层,如图4所示。
通过式(15)可得该模型的动力刚度矩阵
(cos(kζd)−1−1cos(kζd)+ipsin(kζd))(w1w2) = (0Q2) (16) 式中:
p = ζRGR/(ζG) ,Q2=ikζRGRwR ,ζR 和GR 为基岩的物理力学参数。w1wR=1cos(kζd)+ipsin(kζd) (17) w2wR=11+iptan(kζd) (18) 进一步得到地表速度与土岩地层界面位移的比值
|w1wR|=1√cos2(kζd)+sin2(kζd)p2 (19) |w2wR|=1√1+tan2(kζd)p2 (20) 由式(19)和式(20)得到
|w1w2|=√p2+tan2(kζd)√p2cos2(kζd)+sin2(kζd) (21) 将位移场公式(式(3))对时间求导,可以得到地表速度与土岩地层界面速度的比值
|u1/u2| =|w1/w2| 。2.2 参数分析
2.2.1 阻抗比和入射角对
|u1/u2| 的影响波阻抗是抗拒应力波通过的能力,也是应力波扫越一定介质的能力。为了开展更具一般性的讨论,选取入射波频率f为0~200 Hz[19],定义土层与基岩的阻抗比
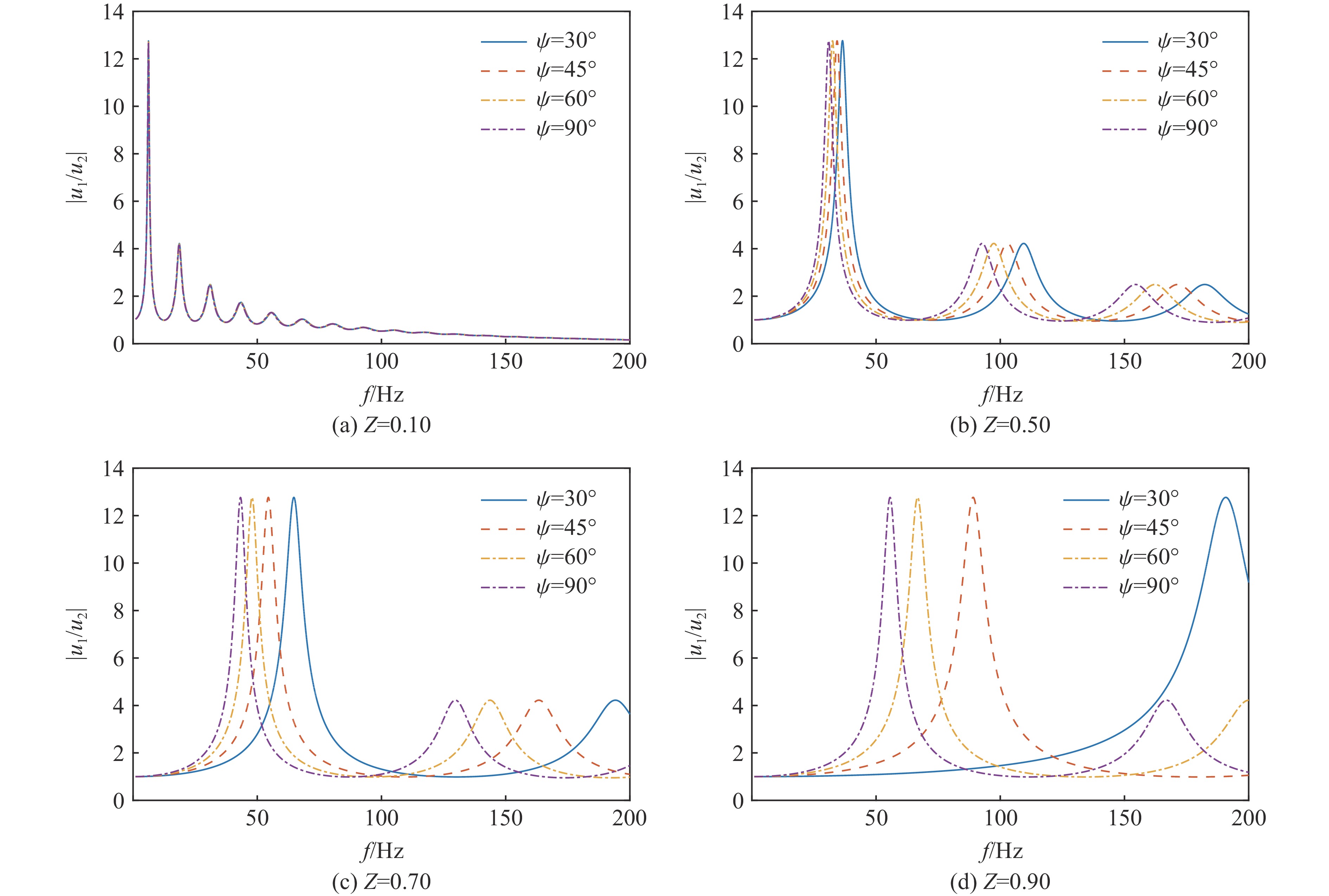
Z=(ρc)s/(ρc)R ,Z分别为0.10、0.50、0.70、0.90的情况下,入射角ψ为30°、45°、60°、90°时,绘制|u1/u2| -f曲线,如图5所示。由图5(a)可知:当Z比较小时,
|u1/u2| 的峰值随着频率的增加缓慢减小,约60 Hz时峰值由大于1向小于1转变,并且SH波的入射角对峰值几乎没有影响。由图5(a)~图5(d)可知,随着Z的增大,不同入射角下SH波对应的峰值开始慢慢地向高频分散开来,并且入射角较小的SH波向高频方向移动的速度大于入射角较大的SH波。这说明波阻抗较大的土层在高频波作用下的动力响应更加剧烈,并且速度对入射角的敏感性比峰值更强。2.2.2 不同土层厚度下入射角对
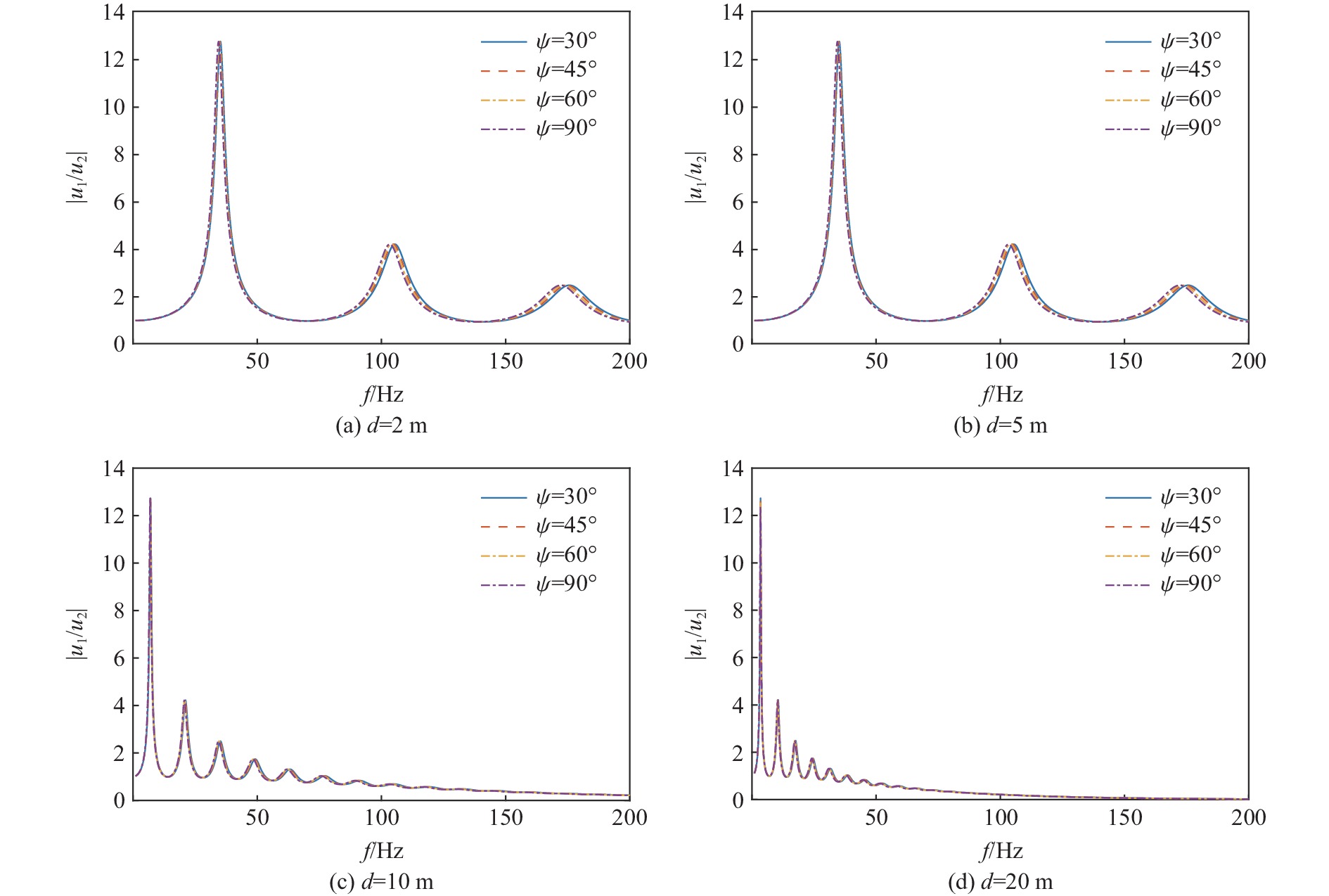
|u1/u2| 的影响当土层与基层的阻抗比Z=0.19,入射波频率f为0~200 Hz,上覆土层厚度d为2、5、10、20 m,入射角为30°、45°、60°、90°时,
|u1/u2| -f曲线如图6所示。对比图6(a)~图6(d)可以看出:当覆盖土层厚度不同时,
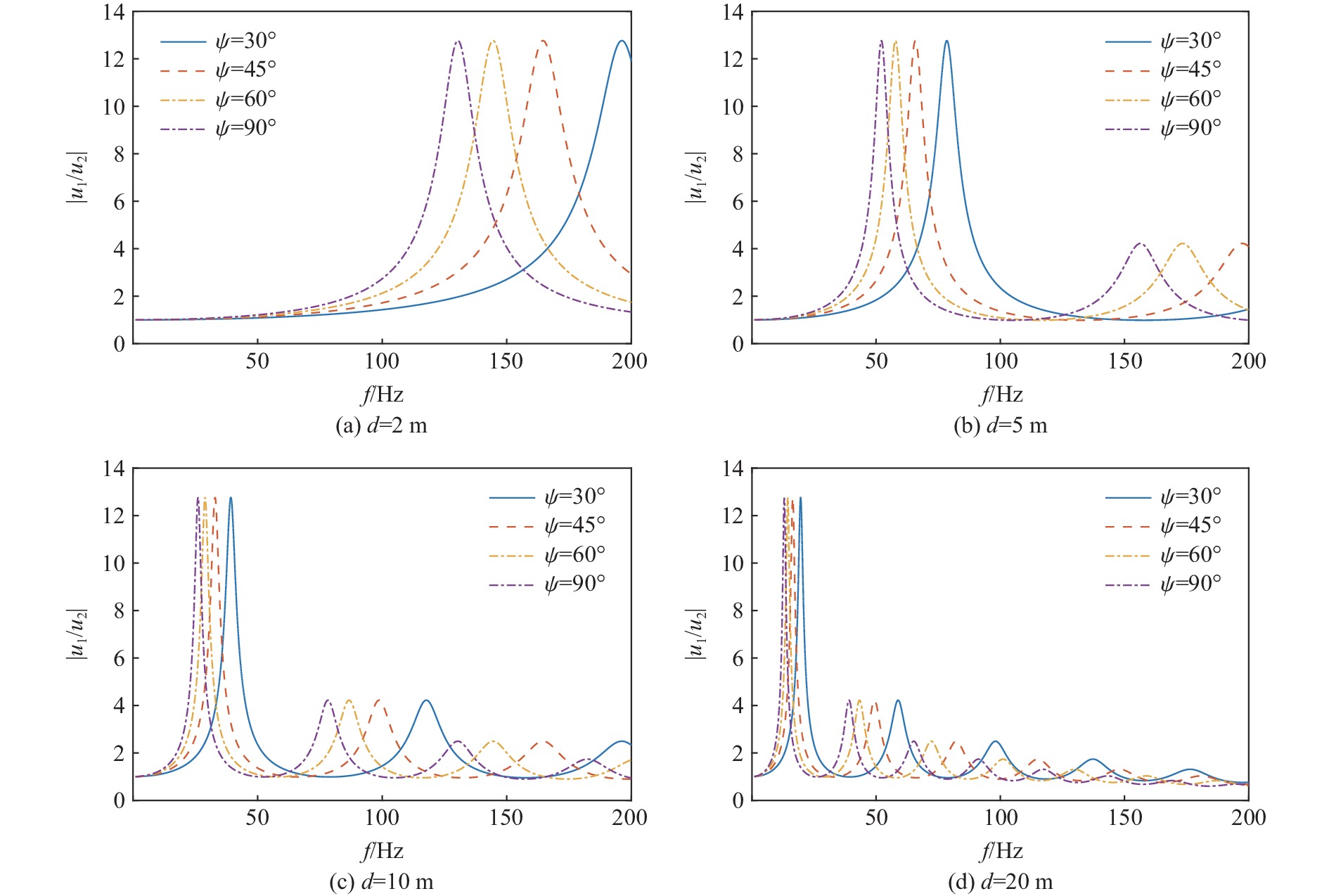
|u1/u2| 的峰值均随着入射波频率f的增大而减小,并逐渐趋于零,入射角对|u1/u2| 峰值的影响较小;随着覆盖土层厚度的增加,高频波对应的|u1/u2| 峰值逐渐向低频方向移动,随着低频波对|u1/u2| 峰值影响的增强,高频波的影响越来越弱。这说明覆盖的土层越厚,土层的固有频率响应峰值个数越多,且峰值越向低频集中,高频波对|u1/u2| 的影响程度越弱。当土层与基层的阻抗比Z=0.70,入射波频率f为0~200 Hz,上覆土层厚度d为2、5、10、20 m,入射角为30°、45°、60°、90°时,
|u1/u2| -f曲线如图7所示。从图7可以看出:当土层厚度较小时,土层的固有频率由高频波控制,但是随着土层厚度的增加,高频固有频率对应的峰值逐渐向低频区移动,即低频固有频率对|u1/u2| 的影响越来越大。从波的入射角来看,当土层厚度较小时,图7(a)中4个峰值频率为130.6、144.6、163.9、196.3 Hz,不同入射角对应的|u1/u2| 的最大峰值频率分布范围较大,且主要处于较高的频率;随着土层厚度的增加,如图7(d)所示,4个峰值频率为12.7、12.7、16.4、19.6 Hz,不同入射角对应的|u1/u2| 的最大峰值频率分布范围变窄,即入射波角度的影响程度慢慢减弱。这说明:当土层与基岩的阻抗比Z较大且土层厚度较薄时,高频波和入射角对|u1/u2| 的影响较大;随着覆盖土层厚度的增加,不同入射角下的土层固有频率响应峰值向低频移动且相互靠近,即高频波和入射角对|u1/u2| 的影响程度逐渐减弱。3. 结 论
选取平面SH爆破地震波,基于波动理论及单层土,建立了一般状况下层状土-基岩地层的刚度矩阵和动力平衡方程组。整体而言,地表速度与土岩地层界面速度的比值
|u1/u2| 的各个峰值随着入射波频率的增加而减小,且第2个峰值明显小于第1个峰值,说明实际工程中需要重点关注|u1/u2| 的第1个峰值对应的频率,即土层的一阶卓越频率。随着土层阻抗的增大,高频部分的响应越来越强烈,受入射角的影响也越来越弱。当土层较薄时,|u1/u2| 的高频部分的响应比较明显,但是随着土层厚度的增加,高频部分的响应越来越弱,说明土层的高频滤波作用随着厚度的增加而增强。 -
-
[1] 张永兴, 张远华. 隧道爆破开挖条件下地表建筑振动速度响应研究 [J]. 地震工程与工程振动, 2010, 30(6): 112–119. doi: 10.13197/j.eeev.2010.06.007ZHANG Y X, ZHANG Y H. Research on vibration velocity responses of surface building under the condition of blasting excavation in tunnel [J]. Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(6): 112–119. doi: 10.13197/j.eeev.2010.06.007 [2] 路世伟. 露天转地下开采边坡爆破振动传播特性及安全判据研究 [D]. 武汉: 中国地质大学(武汉), 2017.LU S W. Propagation characteristics of blasting vibration in slopes subjected to open-pit to underground mining and safety criterion [D]. Wuhan: China University of Geosciences (Wuhan), 2017. [3] 胡国忠. 城市地下工程爆破的地面爆破震动效应及其震动强度预测 [D]. 重庆: 重庆大学, 2005.HU G Z. Forecast on intensity of vibration and study on effect of ground blast induced vibration of underground engineering in city [D]. Chongqing: Chongqing University, 2005. [4] 王玉杰, 梁开水, 田新邦. 周宁水电站地下厂房开挖爆破地震波衰减规律的研究 [J]. 岩石力学与工程学报, 2005, 24(22): 4111–4114. doi: 10.3321/j.issn:1000-6915.2005.22.017WANG Y J, LIANG K S, TIAN X B. Study on redundant regulation of underground digging blasting vibration of Zhouning hydropower station [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(22): 4111–4114. doi: 10.3321/j.issn:1000-6915.2005.22.017 [5] 董永香, 黄晨光, 段祝平. 多层介质对应力波传播特性影响分析 [J]. 高压物理学报, 2005, 19(1): 59–65. doi: 10.11858/gywlxb.2005.01.011DONG Y X, HUANG C G, DUAN Z P. Analysis on the influence of multi-layered media on stress wave propagation [J]. Chinese Journal of High Pressure Physics, 2005, 19(1): 59–65. doi: 10.11858/gywlxb.2005.01.011 [6] SMERZINI C, AVILÉS J, PAOLUCCI R, et al. Effect of underground cavities on surface earthquake ground motion under SH wave propagation [J]. Earthquake Engineering & Structural Dynamics, 2009, 38(12): 1441–1460. doi: 10.1002/eqe.912 [7] 王猛, 马天宝, 宁建国. 炸药混凝土中爆炸能量释放规律的研究 [J]. 高压物理学报, 2012, 26(5): 517–522. doi: 10.11858/gywlxb.2012.05.006WANG M, MA T B, NING J G. Research of energy release law of explosive blasting in concrete [J]. Chinese Journal of High Pressure Physics, 2012, 26(5): 517–522. doi: 10.11858/gywlxb.2012.05.006 [8] 王超, 周传波, 路世伟, 等. 城市暗挖隧道爆破地震波传播规律研究 [J]. 科学技术与工程, 2017, 17(6): 158–162. doi: 10.3969/j.issn.1671-1815.2017.06.028WANG C, ZHOU C B, LU S W, et al. Propagation pattern of blasting vibration in the surrounding rock of metro tunnel [J]. Science Technology and Engineering, 2017, 17(6): 158–162. doi: 10.3969/j.issn.1671-1815.2017.06.028 [9] 张震, 周传波, 路世伟, 等. 超浅埋地铁站通道爆破暗挖地表振动传播特征 [J]. 中南大学学报(自然科学版), 2017, 48(8): 2119–2125. doi: 10.11817/j.issn.1672-7207.2017.08.020ZHANG Z, ZHOU C B, LU S W, et al. Propagation characteristics of ground vibration induced by subsurface blasting excavation in an ultra-shallow buried underpass [J]. Journal of Central South University (Science and Technology), 2017, 48(8): 2119–2125. doi: 10.11817/j.issn.1672-7207.2017.08.020 [10] 高文学, 颜鹏程, 李志星, 等. 浅埋隧道爆破开挖及其振动效应研究 [J]. 岩石力学与工程学报, 2011, 30(Suppl 2): 4153–4157.GAO W X, YAN P C, LI Z X, et al. Blasting excavation and vibration effects of shallow tunnel excavation [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Suppl 2): 4153–4157. [11] 汪平, 吉凌. 浅埋地铁隧道爆破振动速度传播规律及预测 [J]. 工程爆破, 2021, 27(2): 108–113, 134. doi: 10.19931/j.EB.20200222WANG P, JI L. Propagation law and prediction of blasting vibration velocity of shallow buried subway tunnel [J]. Engineering Blasting, 2021, 27(2): 108–113, 134. doi: 10.19931/j.EB.20200222 [12] 陈学军, 余思喆, 宋宇, 等. 采矿爆破振动波在岩溶区的传播影响因素分析 [J]. 地质力学学报, 2018, 24(5): 692–698. doi: 10.12090/j.issn.1006-6616.2018.24.05.070CHEN X J, YU S Z, SONG Y, et al. Analysis of factors influencing the propagation of mining blasting vibration wave in karst area [J]. Journal of Geomechanics, 2018, 24(5): 692–698. doi: 10.12090/j.issn.1006-6616.2018.24.05.070 [13] JAYASINGHE B, ZHAO Z Y, CHEE A G T, et al. Attenuation of rock blasting induced ground vibration in rock-soil interface [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2019, 11(4): 770–778. doi: 10.1016/j.jrmge.2018.12.009 [14] 朱斌, 蒋楠, 贾永胜, 等. 下穿燃气管道爆破振动效应现场试验研究 [J]. 岩石力学与工程学报, 2019, 38(12): 2582–2592. doi: 10.13722/j.cnki.jrme.2019.0183ZHU B, JIANG N, JIA Y S, et al. Field experiment on blasting vibration effect of underpass gas pipelines [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(12): 2582–2592. doi: 10.13722/j.cnki.jrme.2019.0183 [15] 高启栋, 卢文波, 冷振东, 等. 考虑爆源特征的岩石爆破诱发地震波的波型与组分分析 [J]. 岩土力学, 2021, 42(10): 2830–2844. doi: 10.16285/j.rsm.2021.0108GAO Q D, LU W B, LENG Z D, et al. Analysis of wave-type and seismic component induced by rock blasting considering source characteristics [J]. Rock and Soil Mechanics, 2021, 42(10): 2830–2844. doi: 10.16285/j.rsm.2021.0108 [16] 王秉相, 程普锋, 郑宇轩, 等. 应力波在散体颗粒中的传播规律 [J]. 高压物理学报, 2020, 34(4): 044202. doi: 10.11858/gywlxb.20200508WANG B X, CHENG P F, ZHENG Y X, et al. Attenuation law of stress wave in granular particles [J]. Chinese Journal of High Pressure Physics, 2020, 34(4): 044202. doi: 10.11858/gywlxb.20200508 [17] 王桂林, 欧阳啸天, 翟俊, 等. 浅埋三舱管廊甲烷爆炸的地面响应规律 [J]. 高压物理学报, 2021, 35(1): 015202. doi: 10.11858/gywlxb.20200616WANG G L, OUYANG X T, ZHAI J, et al. Ground response law of methane explosion in shallow buried three-cabin pipe gallery [J]. Chinese Journal of High Pressure Physics, 2021, 35(1): 015202. doi: 10.11858/gywlxb.20200616 [18] WOLF J P. Dynamic soil-structure interaction [M]. Englewood Cliffs: Prentice-Hall, 1985. [19] 周俊汝. 爆破地震波传播过程中振动主频的衰减规律研究 [D]. 武汉: 武汉大学, 2017.ZHOU J R. Study on attenuation of dominant frequency of blast-induced vibration [D]. Wuhan: Wuhan University, 2017. -








 下载:
下载:
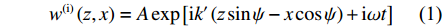
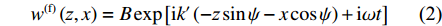
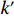
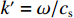
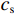
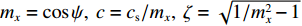
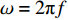
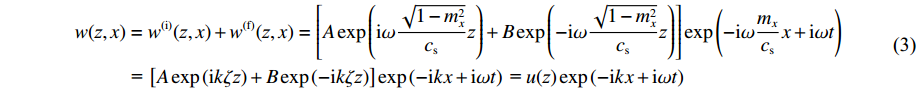
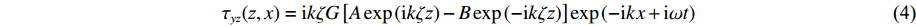
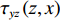
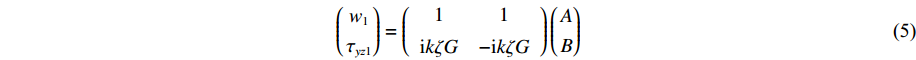
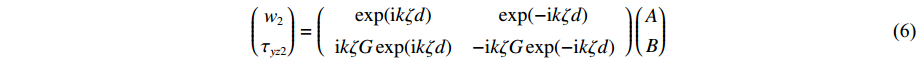
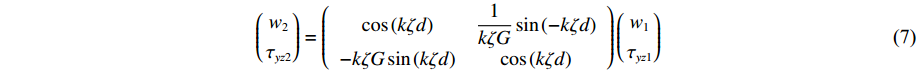
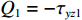
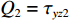
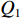
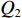
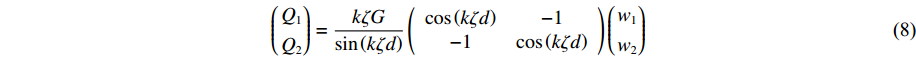

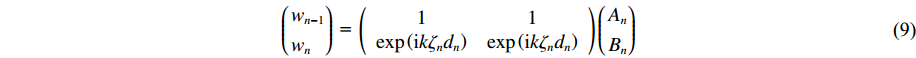
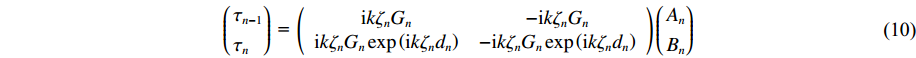
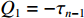
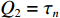
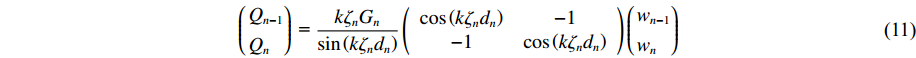
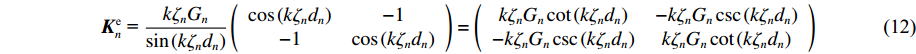
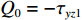
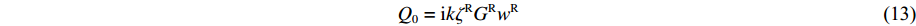
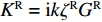
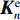

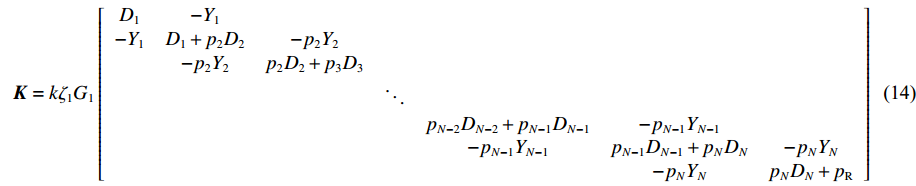
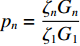
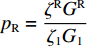
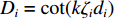
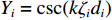
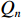
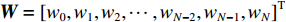
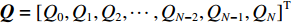
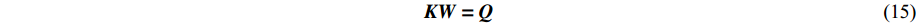

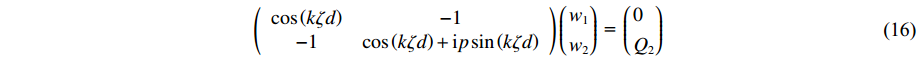
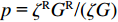
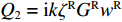
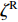
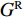
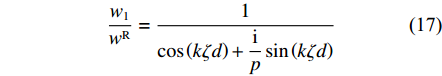
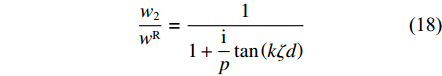
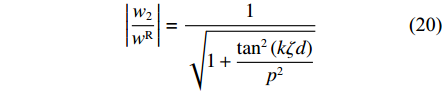
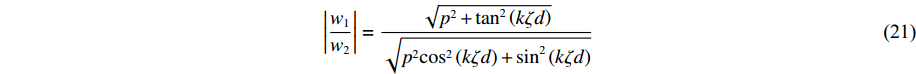
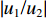
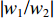
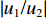
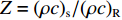
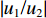

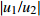
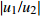
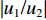
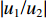
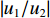

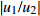
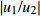
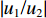
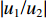
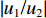
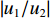
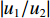
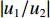
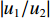
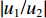
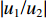
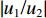
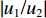

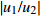
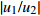
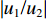
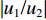
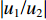

 下载:
下载: