压力和碳含量调控BC<i><sub>x</sub></i>O化合物物理性质的机理研究

刘超; 应盼

doi:10.11858/gywlxb.20210792

压力和碳含量调控BC_xO化合物物理性质的机理研究

doi: 10.11858/gywlxb.20210792

刘超^{1, 2,},
应盼^3,*, ,

1.
江西理工大学材料冶金化学学部，江西赣州　341000
2.
燕山大学亚稳材料制备技术与科学国家重点实验室，河北秦皇岛　066004
3.
燕山大学理学院河北省微结构材料物理重点实验室，河北秦皇岛　066004

基金项目: 国家自然科学基金（12064013）；江西省自然科学基金（20202BAB214010）；亚稳材料制备技术与科学国家重点实验室开放课题（201906）；赣州市科技创新人才计划（202060）；江西理工大学清江青年优秀人才支持计划（JXUSTQJYX2020002）

详细信息

作者简介:
刘　超（1989－），男，博士，讲师，主要从事新型轻质高硬化合物的理论设计与热压合成研究.E-mail：liuchao198967@126.com

通讯作者:
应　盼（1991－），男，博士，讲师，主要从事新型亚稳材料的结构设计与高压合成研究.E-mail：yingpan@ysu.edu.cn

中图分类号: O481.1; O482.1
计量
- 文章访问数: 1227
- HTML全文浏览量: 717
- PDF下载量: 39
出版历程
- 收稿日期: 2021-05-12
- 修回日期: 2021-05-26

Mechanism of Pressure and Carbon Content Regulating Physical Properties of BC_xO Compounds

LIU Chao^{1, 2
,},
YING Pan^{3,*
, ,}

1.
Faculty of Materials Metallurgy and Chemistry, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China
2.
State Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao 066004, Hebei, China
3.
Hebei Key Laboratory of Microstructural Material Physics, School of Science, Yanshan University, Qinhuangdao 066004, Hebei, China

摘要

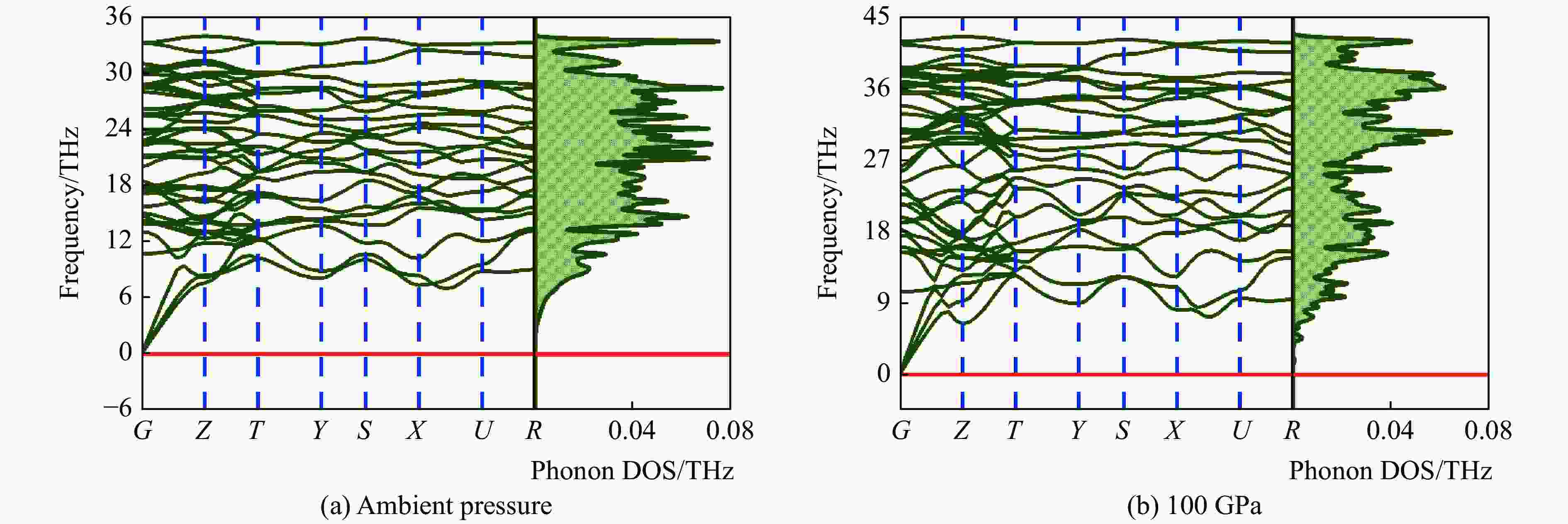
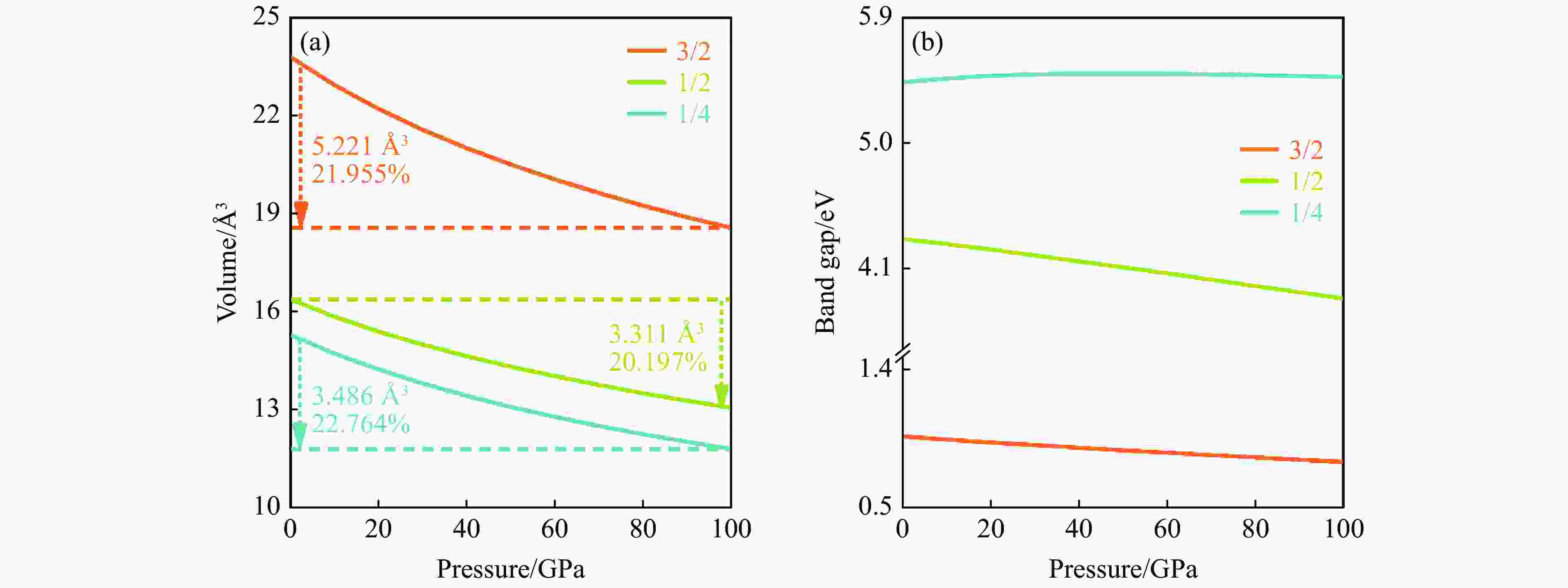
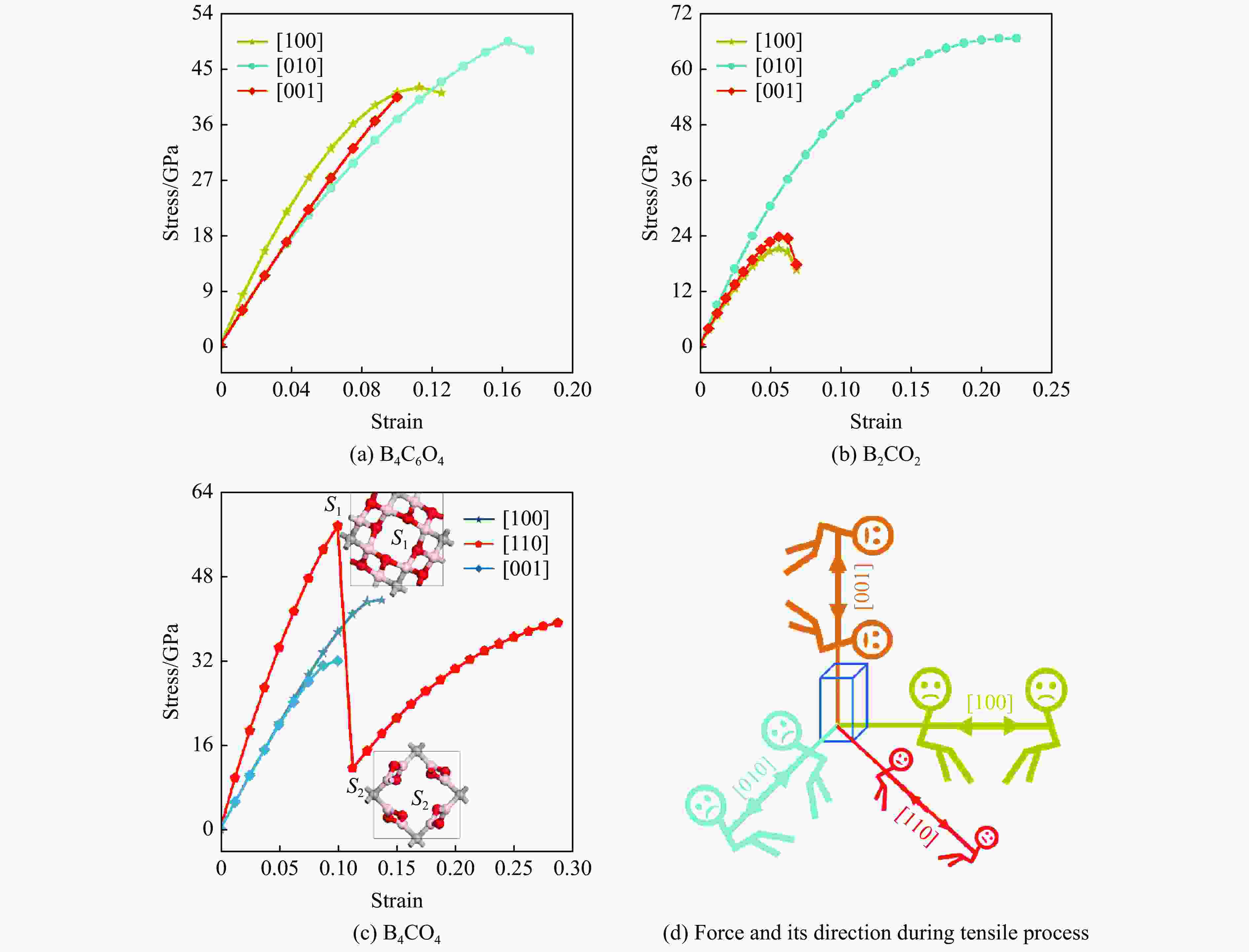
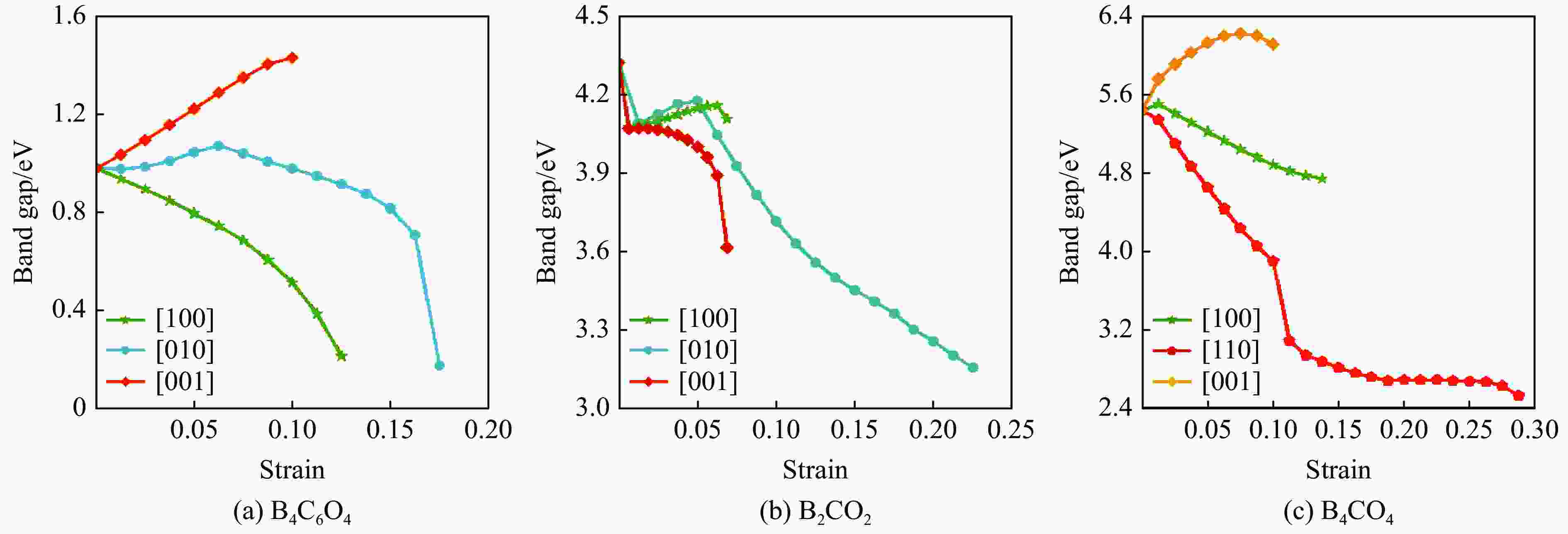
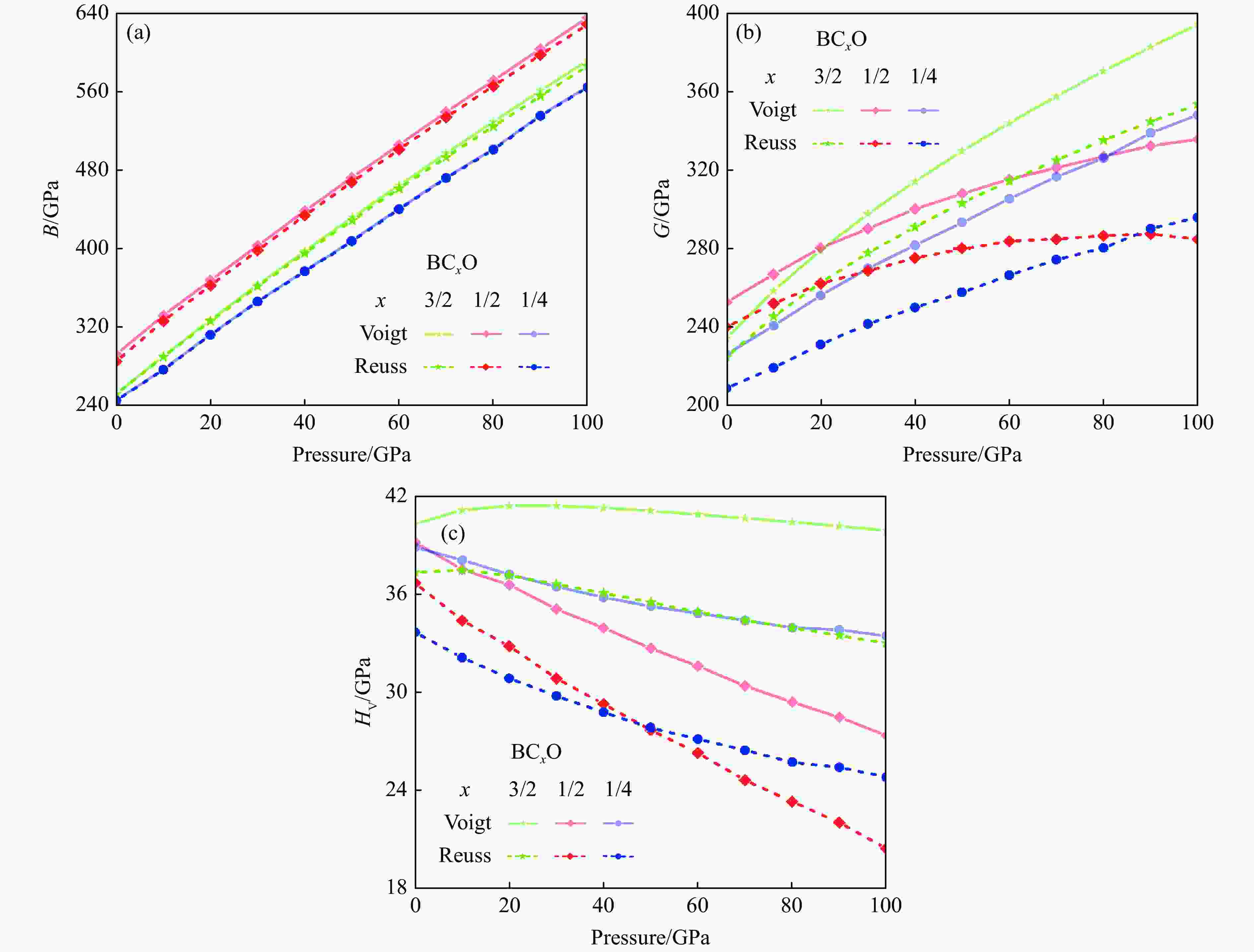
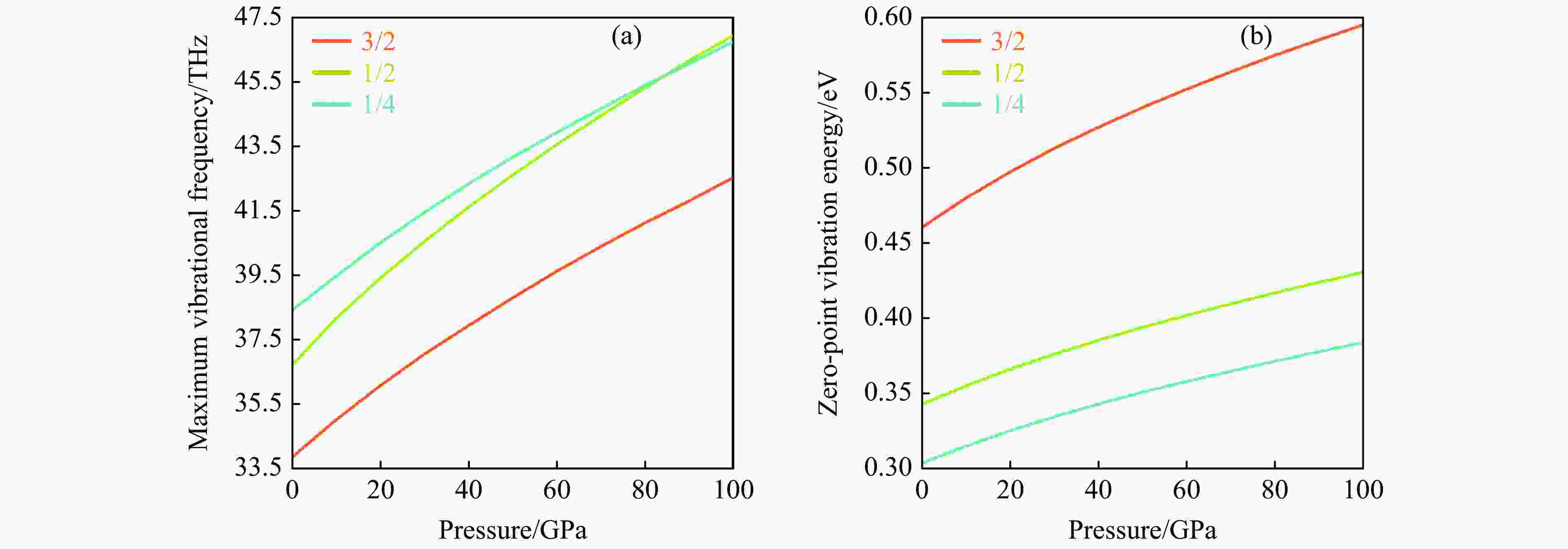
摘要: 结合粒子群优化算法生成的候选结构和第一性原理的稳定性分析，预测出新型B-C-O化合物B₄C₆O₄。B₄C₆O₄具有带隙宽度约2.25 eV的直接带隙半导体属性。研究同属BC_xO系列，且结构具有相似性的B₄C₆O₄、B₂CO₂和B₄CO₄，发现C含量的降低会导致体系带隙增大，三者的分子式体积随C含量的降低而降低，且100 GPa的高压对三者体积均形成高达20%的压缩。高压导致B₂CO₂和B₄C₆O₄的带隙持续降低，而B₄CO₄的带隙先升后降。应力-应变模拟结果表明，3种BC_xO（x = 3/2, 1/2, 1/4）化合物均具有较高的极限拉伸应力，同时应力引起的应变会影响3种BC_xO化合物的带隙。力学性能研究表明，3种BC_xO化合物均具有高弹性模量和高硬度等特点。常压下BC_xO的最高声子振动频率均高于30 THz，且由高到低分别为B₄CO₄、B₂CO₂、B₄C₆O₄，压力作用使该体系结构的键能持续增强。
- 高压 /
- 碳含量 /
- 稳定性 /
- 力学性质 /
- 电学性质
Abstract: A novel B-C-O compound, B₄C₆O₄, was predicted by combining the candidate structure generated by the particle swarm optimization algorithm and first-principles stability analysis. B₄C₆O₄ has a direct bandgap semiconductivity characteristic with a bandgap width of about 2.25 eV. B₄C₆O₄, B₂CO₂ and B₄CO₄ have similar structures and belong to the BC_xO series. It was found that the decrease of carbon content led to the increase of the band gap of the system, and the molecular formula volume decreased synchronically with the decrease of carbon content, and the high pressure of 100 GPa compressed the volume of the three as high as 20%. The band gaps of B₂CO₂ and B₄C₆O₄ continue to decrease due to the effect of high pressure, while the band gap of B₄CO₄ rise first and then fall. The stress-strain simulation results showed that the three BC_xO compounds (x = 3/2, 1/2, 1/4) all have high ultimate tensile stress, and the strain would affect the band gaps of the three BC_xO compounds. The mechanical properties of three BC_xO compounds showed that they all had high modulus of elasticity and hardness. The highest phonon vibration frequencies of BC_xO under chamber pressure are higher than 30 THz, and the relationship is B₄CO₄ > B₂CO₂ > B₄C₆O₄. The effect of high pressure will cause the continuous enhancement of the bond energy of the system.
- high pressure /
- carbon content /
- stability /
- mechanical properties /
- electrical properties

HTML全文

图 1 常压下B₄C₆O₄结构（2 × 2 × 2）的超胞模型

Figure 1. Structure graphs for B₄C₆O₄ (2 × 2 × 2) supercell at ambient pressure

下载: 全尺寸图片幻灯片

图 2 常压和100 GPa下B₄C₆O₄的声子散射谱和声子态密度

Figure 2. Phonon dispersion spectrum and phonon density of states of B₄C₆O₄ at ambient pressure and 100 GPa

下载: 全尺寸图片幻灯片

图 3 B₄C₆O₄在恒温273 K和常压下的分子动力学模拟

Figure 3. Molecular dynamics simulation for B₄C₆O₄ at 273 K and ambient pressure

下载: 全尺寸图片幻灯片

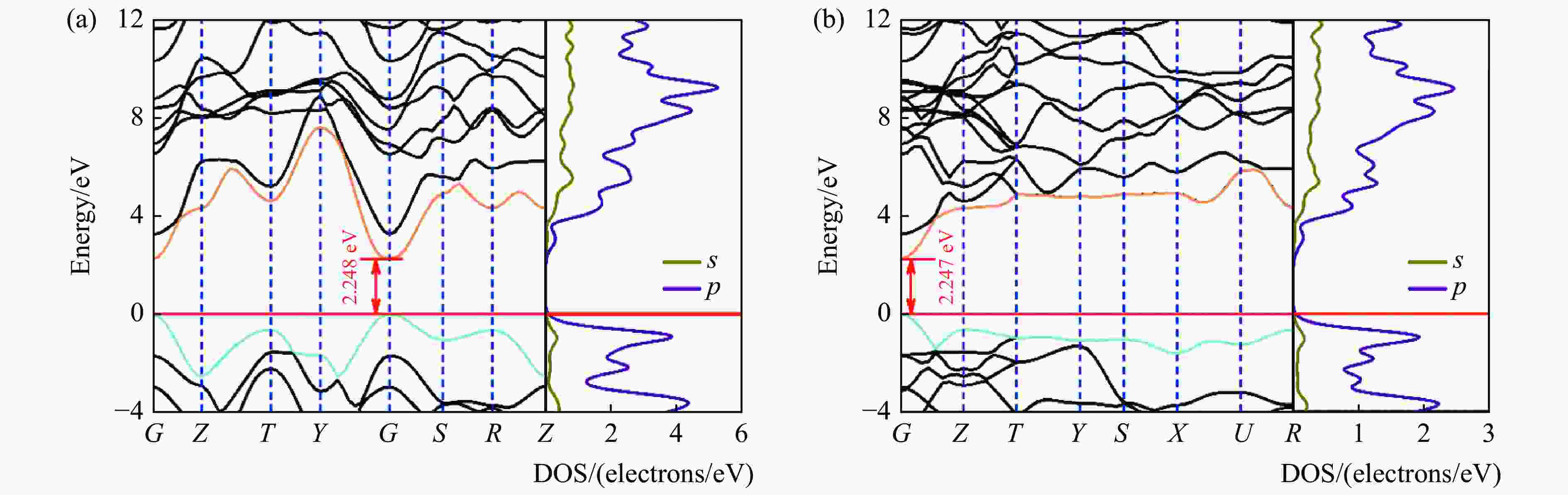
图 4 基于HSE06计算得到的常压下B₄C₆O₄的电子能带结构和态密度：(a)原胞，(b)单胞（水平红线、暗青色曲线和金色曲线分别代表费米能级、VBM和CBM）

Figure 4. Calculated electronic band structures and density of states of B₄C₆O₄ phases via HSE06 with primitive cell (a) and unit cell (b) at ambient pressure (The horizontal red line, dark cyan curve and gold curve represent the Fermi energy level, VBM and CBM, respectively.)

下载: 全尺寸图片幻灯片

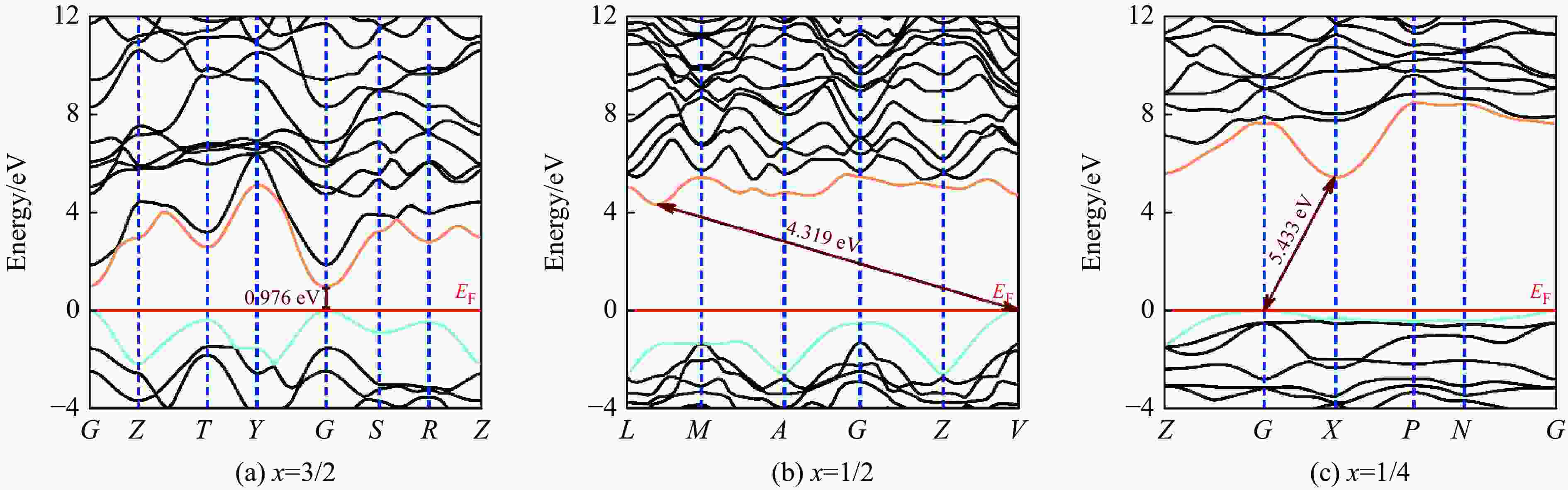
图 5 基于PBE计算常压下BC_xO原胞结构的电子能带结构和态密度（水平红线、暗青色曲线和金色曲线分别代表费米能级E_F、VBM和CBM）

Figure 5. Calculated electronic band structures and density of states of three BC_xO phases with primitive cell via PBE at ambient pressure (The horizontal red line, dark cyan curve and gold curve represent the Fermi energy level E_F, VBM and CBM, respectively.)

下载: 全尺寸图片幻灯片

图 6 基于PBE泛函和原胞模型计算的BC_xO（x = 3/2, 1/2, 1/4）的归一化体积(a)和带隙(b)与压力的关系

Figure 6. Relationship of the normalized volume (a) and the calculated electronic band gaps (b) of BC_xO (x = 3/2, 1/2, 1/4) with pressure based on PBE funtional and primitive cell

下载: 全尺寸图片幻灯片

图 7 模拟得到的3种BC_xO沿特定方向的拉伸应力-应变关系

Figure 7. Simulated tensile stress-strain relationship along the specific direction for three BC_xO phases

下载: 全尺寸图片幻灯片

图 8 模拟得到的3种BC_xO在沿特定方向拉伸过程中的电阻-应变关系

Figure 8. Simulated gap-strain relationship along the specific direction for three BC_xO phases during the tensile process

下载: 全尺寸图片幻灯片

图 9 3种BC_xO（x = 3/2, 1/2, 1/4）的体积模量(a)、剪切模量(b)、硬度(c)与压力的关系

Figure 9. Relationship of bulk modulus (a), shear modulus (b), and hardness (c) with pressure for BC_xO (x = 3/2, 1/2, 1/4)

下载: 全尺寸图片幻灯片

图 10 BC_xO（x = 3/2, 1/2, 1/4）的最大声子振动频率(a)和零点振动能(b)与压力的关系

Figure 10. Relationship of maximum vibrational frenquency (a), and zero-point vibration energy (b) with pressure for BC_xO (x = 3/2, 1/2, 1/4)

下载: 全尺寸图片幻灯片

表 1 常压下B₄C₆O₄的原子坐标

Table 1. Atomic Wyckoff positions of B₄C₆O₄ at ambient pressure

Atom	Wyckoff site	x	y	z
B	4d	0.299	0.500	0.267
C1	2b	0	0.500	0.991
C2	4c	0.250	0.250	0.491
O	4e	0	0.279	0.746

下载: 导出CSV

表 2 常压和100 GPa下B₄C₆O₄的弹性常数

Table 2. Elastic parameters of B₄C₆O₄ at ambient pressure and 100 GPa 　GPa

Pressure	C₁₁	C₁₂	C₁₃	C₂₂	C₂₃
Ambient	693.28	15.78	77.13	542.70	167.35
100	1394.79	146.17	335.20	974.72	497.69

Pressure	C₃₃	C₄₄	C₅₅	C₆₆
Ambient	516.07	255.45	197.31	222.21
100	1000.58	517.68	363.80	292.39

下载: 导出CSV

表 3 恒温常压条件下B₄C₆O₄在分子动力学过程中的动态结构信息

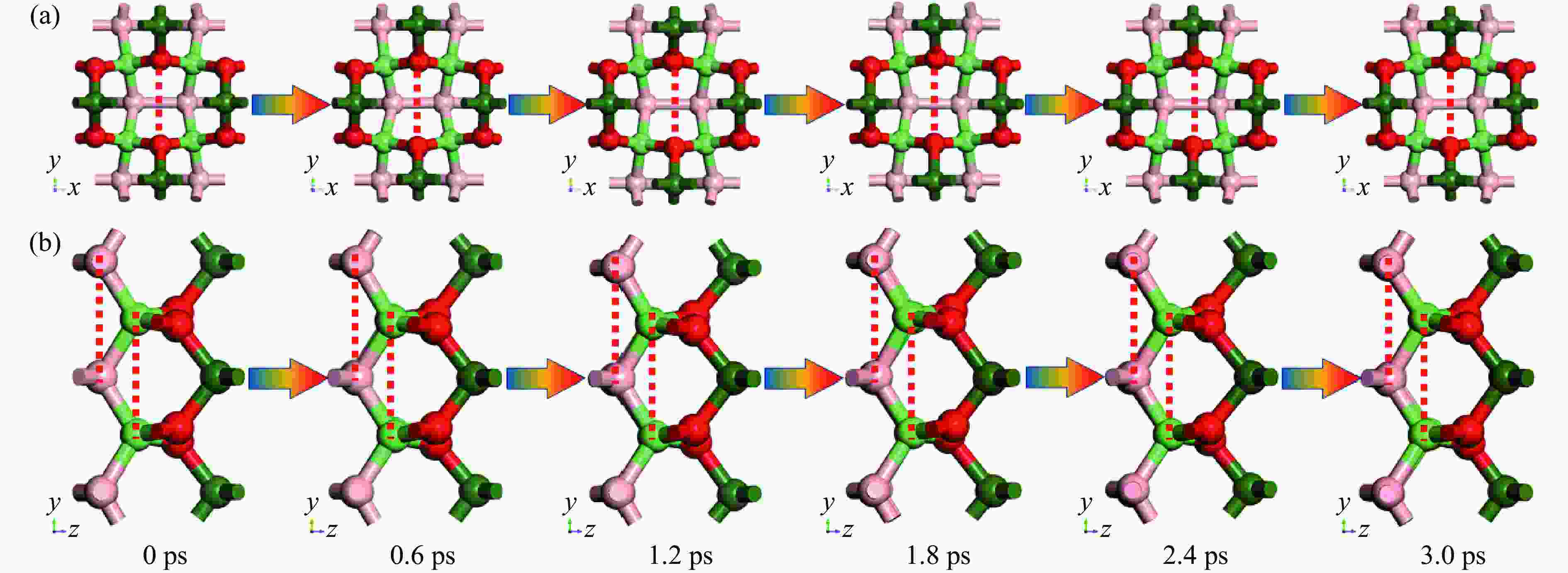
Table 3. Structural information of B₄C₆O₄ during molecular dynamics under constant temperature and ambient pressure

Time/ps	$\,\rho $/(g·cm⁻³)	B―B bond length/Å	Atom distance/Å
Time/ps	$\,\rho $/(g·cm⁻³)	B―B bond length/Å	C2―C2	O―O	B―B
0	3.130	1.842	2.720	3.038	2.757
0.6	3.175	1.776	2.677	3.013	2.775
1.2	3.137	1.869	2.697	3.026	2.722
1.8	3.066	1.827	2.741	3.010	2.810
2.4	3.123	1.846	2.711	3.063	2.806
3.0	3.128	1.884	2.738	3.033	2.798

下载: 导出CSV

参考文献(44)

[1]	XU B, TIAN Y J. Superhard materials: recent research progress and prospects [J]. Science China Materials, 2015, 58(2): 132–142. doi: 10.1007/s40843-015-0026-5
[2]	刘银娟, 贺端威, 王培, 等. 复合超硬材料的高压合成与研究 [J]. 物理学报, 2017, 66(3): 038103. doi: 10.7498/aps.66.038103 LIU Y J, HE D W, WANG P, et al. Syntheses and studies of superhard composites under high pressure [J]. Acta Physica Sinica, 2017, 66(3): 038103. doi: 10.7498/aps.66.038103
[3]	KIDALOV S V, SHAKHOV F M, DAVIDENKO V M, et al. Synthesis and properties of superhard crystalline materials in boron-carbon-nitrogen system [J]. Technical Physics Letters, 2011, 37(3): 247–249. doi: 10.1134/S1063785011030266
[4]	SOLOZHENKO V L, KURAKEVYCH O O, ANDRAULT D, et al. Ultimate metastable solubility of boron in diamond: synthesis of superhard diamondlike BC₅ [J]. Physical Review Letters, 2009, 102(1): 015506. doi: 10.1103/PhysRevLett.102.015506
[5]	ZININ P V, MING L C, ISHII H A, et al. Phase transition in BC_x system under high-pressure and high-temperature: synthesis of cubic dense BC₃ nanostructured phase [J]. Journal of Applied Physics, 2012, 111(11): 114905. doi: 10.1063/1.4723275
[6]	KOBAYASHI M, HIGASHI I, BRODHAG C, et al. Structure of B₆O boron-suboxide by Rietveld refinement [J]. Journal of Materials Science, 1993, 28(8): 2129–2134. doi: 10.1007/BF00367573
[7]	ENDO T, SATO T, SHIMADA M. High-pressure synthesis of B₂O with diamond-like structure [J]. Journal of Materials Science Letters, 1987, 6(6): 683–685. doi: 10.1007/BF01770925
[8]	ZHAO Y, HE D W, DAEMEN L L, et al. Superhard B-C-N materials synthesized in nanostructured bulks [J]. Journal of Materials Research, 2002, 17(12): 3139–3145. doi: 10.1557/JMR.2002.0454
[9]	SOLOZHENKO V L, ANDRAULT D, FIQUET G, et al. Synthesis of superhard cubic BC₂N [J]. Applied Physics Letters, 2001, 78(10): 1385–1387. doi: 10.1063/1.1337623
[10]	KNITTLE E, KANER R B, JEANLOZ R, et al. High-pressure synthesis, characterization, and equation of state of cubic C-BN solid solutions [J]. Physical Review B, 1995, 51(18): 12149–12156. doi: 10.1103/PhysRevB.51.12149
[11]	LIU L Y, HU M, ZHAO Z S, et al. Superhard conductive orthorhombic carbon polymorphs [J]. Carbon, 2020, 158: 546–552. doi: 10.1016/j.carbon.2019.11.024
[12]	李子鹤, 刘超, 马梦东, 等. 新型超硬C₅N晶体结构及性能的第一性原理研究 [J]. 高压物理学报, 2018, 32(1): 010103. doi: 10.11858/gywlxb.20170606 LI Z H, LIU C, MA M D, et al. Structure and properties of novel superhard C₅N: a first-principles study [J]. Chinese Journal of High Pressure Physics, 2018, 32(1): 010103. doi: 10.11858/gywlxb.20170606
[13]	LUO X G, GUO X J, XU B, et al. Body-centered superhard BC₂N phases from first principles [J]. Physical Review B, 2007, 76(9): 094103. doi: 10.1103/PhysRevB.76.094103
[14]	LIU A Y, COHEN M L. Prediction of new low compressibility solids [J]. Science, 1989, 245(4920): 841–842. doi: 10.1126/science.245.4920.841
[15]	GARVIE L A J, HUBERT H, PETUSKEY W T, et al. High-pressure, high-temperature syntheses in the B-C-N-O system [J]. Journal of Solid State Chemistry, 1997, 133(2): 365–371. doi: 10.1006/jssc.1997.7583
[16]	BOLOTINA N B, DYUZHEVA T I, BENDELIANI N A. Atomic structure of boron suboxycarbide B(C,O)_0.155 [J]. Crystallography Reports, 2001, 46(5): 734–740. doi: 10.1134/1.1405858
[17]	LI Y W, LI Q, MA Y M. B₂CO: a potential superhard material in the B-C-O system [J]. EPL (Europhysics Letters), 2011, 95(6): 66006. doi: 10.1209/0295-5075/95/66006
[18]	ZHANG M G, YAN H Y, ZHENG B B, et al. Influences of carbon concentration on crystal structures and ideal strengths of B₂C_xO compounds in the B-C-O system [J]. Scientific Reports, 2015, 5: 15481. doi: 10.1038/srep15481
[19]	LIU C, ZHAO Z S, LUO K, et al. Superhard orthorhombic phase of B₂CO compound [J]. Diamond and Related Materials, 2017, 73: 87–92. doi: 10.1016/j.diamond.2016.07.010
[20]	QIAO L P, JIN Z, YAN G Y, et al. Density-functional-studying of oP8-, tI16-, and tP4-B₂CO physical properties under pressure [J]. Journal of Solid State Chemistry, 2019, 270: 642–650. doi: 10.1016/j.jssc.2018.12.012
[21]	LIU C, CHEN M W, HE J L, et al. Superhard B₂CO phases derived from carbon allotropes [J]. RSC Advances, 2017, 7(82): 52192–52199. doi: 10.1039/c7ra09277f
[22]	YAN H Y, ZHANG M G, WEI Q, et al. A new orthorhombic ground-state phase and mechanical strengths of ternary B₂CO compound [J]. Chemical Physics Letters, 2018, 701: 86–92. doi: 10.1016/j.cplett.2018.04.041
[23]	CHEN M W, LIU C, LIU M L, et al. Exploring the electronic, mechanical, and anisotropy properties of novel tetragonal B₂CO phase [J]. Journal of Materials Research, 2019, 34(21): 3617–3626. doi: 10.1557/jmr.2019.271
[24]	WANG S N, OGANOV A R, QIAN G R, et al. Novel superhard B-C-O phases predicted from first principles [J]. Physical Chemistry Chemical Physics, 2016, 18(3): 1859–1863. doi: 10.1039/c5cp05367f
[25]	NURUZZAMAN M, ALAM M A, SHAH M A H, et al. Investigation of thermodynamic stability, mechanical and electronic properties of superhard tetragonal B₄CO₄ compound: ab initio calculations [J]. Computational Condensed Matter, 2017, 12: 1–8. doi: 10.1016/j.cocom.2017.05.005
[26]	ZHENG B B, ZHANG M G, WANG C J. Exploring the mechanical anisotropy and ideal strengths of tetragonal B₄CO₄ [J]. Materials, 2017, 10(2): 128. doi: 10.3390/ma10020128
[27]	QIAO L P, JIN Z. Two B-C-O compounds: structural, mechanical anisotropy and electronic properties under pressure [J]. Materials, 2017, 10(12): 1413. doi: 10.3390/ma10121413
[28]	LIU C, CHEN M W, YANG Y, et al. Theoretical exploring the mechanical and electrical properties of tI12-B₆C₄O₂ [J]. Computational Materials Science, 2018, 150: 259–264. doi: 10.1016/j.commatsci.2018.04.020
[29]	刘超, 陈明伟, 梁彤祥. B-C-O化合物硬质结构的理论设计与性质研究[M]. 北京: 冶金工业出版社, 2020.
[30]	WANG Y C, LV J, ZHU L, et al. Crystal structure prediction via particle-swarm optimization [J]. Physical Review B, 2010, 82(9): 094116. doi: 10.1103/PhysRevB.82.094116
[31]	WANG Y C, LV J, ZHU L, et al. CALYPSO: a method for crystal structure prediction [J]. Computer Physics Communications, 2012, 183(10): 2063–2070. doi: 10.1016/j.cpc.2012.05.008
[32]	WANG H, WANG Y C, LV J, et al. CALYPSO structure prediction method and its wide application [J]. Computational Materials Science, 2016, 112: 406–415. doi: 10.1016/j.commatsci.2015.09.037
[33]	CLARK S J, SEGALL M D, PICKARD C J, et al. First principles methods using CASTEP [J]. Zeitschrift für Kristallographie-Crystalline Materials, 2005, 220(5/6): 567–570. doi: 10.1524/zkri.220.5.567.65075
[34]	PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865–3868. doi: 10.1103/PhysRevLett.77.3865
[35]	VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J]. Physical Review B, 1990, 41(11): 7892–7895. doi: 10.1103/PhysRevB.41.7892
[36]	PARLINSKI K, LI Z Q, KAWAZOE Y. First-principles determination of the soft mode in cubic ZrO₂ [J]. Physical Review Letters, 1997, 78(21): 4063–4066. doi: 10.1103/PhysRevLett.78.4063
[37]	MOUHAT F, COUDERT F X. Necessary and sufficient elastic stability conditions in various crystal systems [J]. Physical Review B, 2014, 90(22): 224104. doi: 10.1103/PhysRevB.90.224104
[38]	BROQVIST P, ALKAUSKAS A, PASQUARELLO A. Defect levels of dangling bonds in silicon and germanium through hybrid functionals [J]. Physical Review B, 2008, 78(7): 075203. doi: 10.1103/PhysRevB.78.075203
[39]	KRUKAU A V, VYDROV O A, IZMAYLOV A F, et al. Influence of the exchange screening parameter on the performance of screened hybrid functionals [J]. Journal of Chemical Physics, 2006, 125(22): 224106. doi: 10.1063/1.2404663
[40]	刘超. AlX化合物结构与性质的第一性原理研究[M]. 北京: 冶金工业出版社, 2020.
[41]	DIAS R P, SILVERA I F. Observation of the Wigner-Huntington transition to metallic hydrogen [J]. Science, 2017, 355(6326): 715–718. doi: 10.1126/science.aal1579
[42]	MA Y M, EREMETS M, OGANOV A R, et al. Transparent dense sodium [J]. Nature, 2009, 458(7235): 182–185. doi: 10.1038/nature07786
[43]	WU Z J, ZHAO E J, XIANG H P, et al. Crystal structures and elastic properties of superhard IrN₂ and IrN₃ from first principles [J]. Physical Review B, 2007, 76(5): 054115. doi: 10.1103/PhysRevB.76.054115
[44]	TIAN Y J, XU B, ZHAO Z S. Microscopic theory of hardness and design of novel superhard crystals [J]. International Journal of Refractory Metals and Hard Materials, 2012, 33: 93–106. doi: 10.1016/j.ijrmhm.2012.02.021