First-Principles Calculation on Crystal Structure and Elastic Properties of Py-FeO2, Py-FeOOH and ε-FeOOH under High Pressures
-
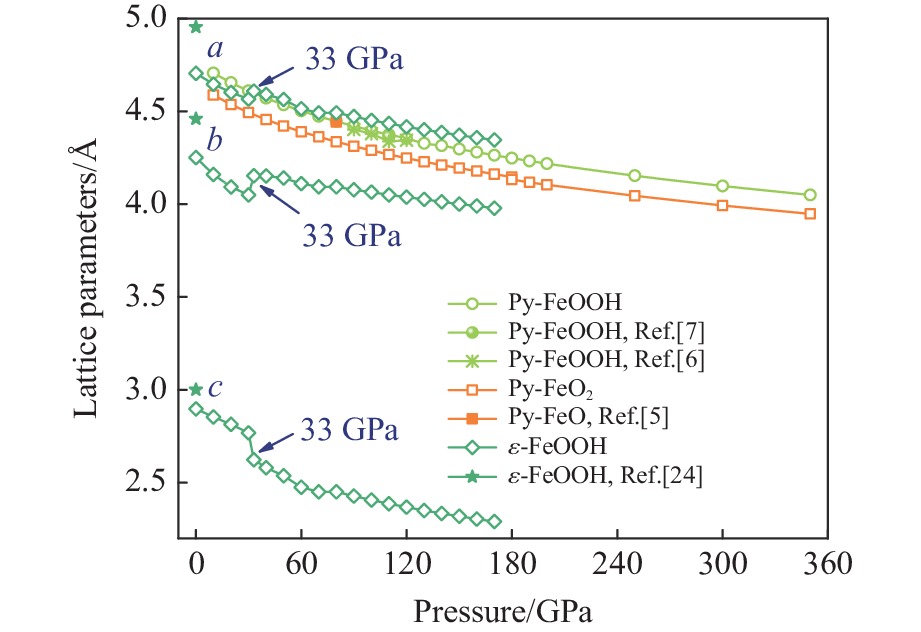
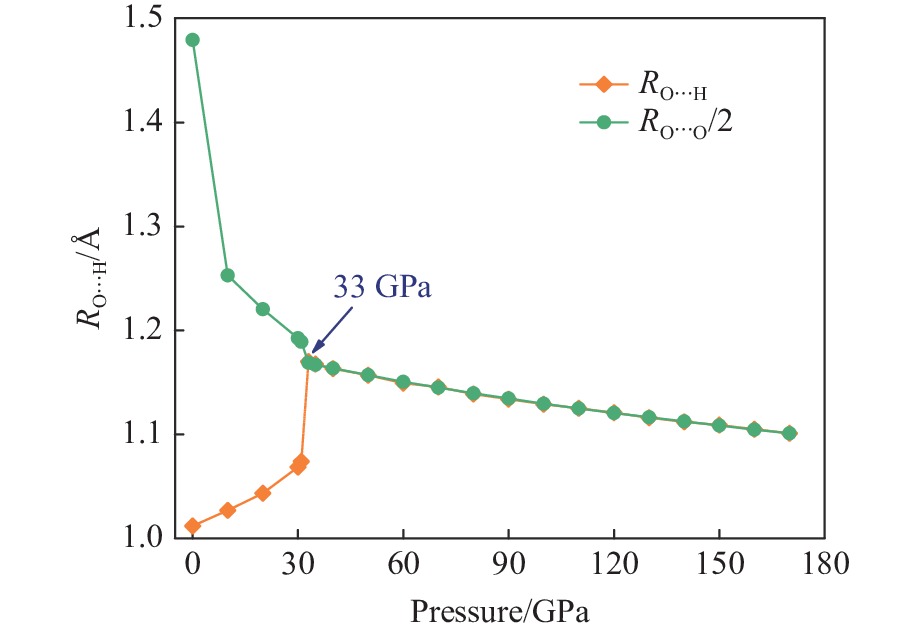
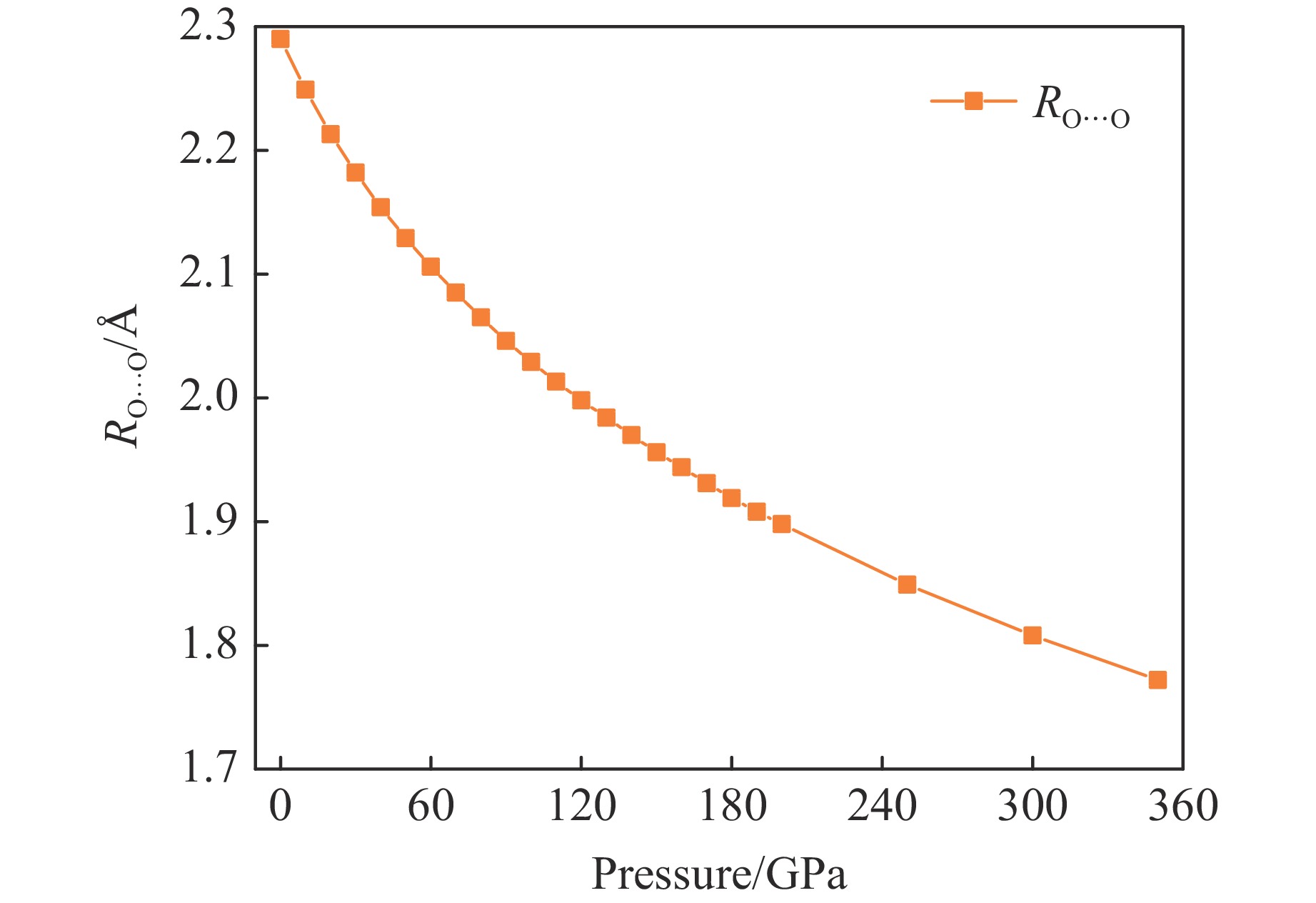
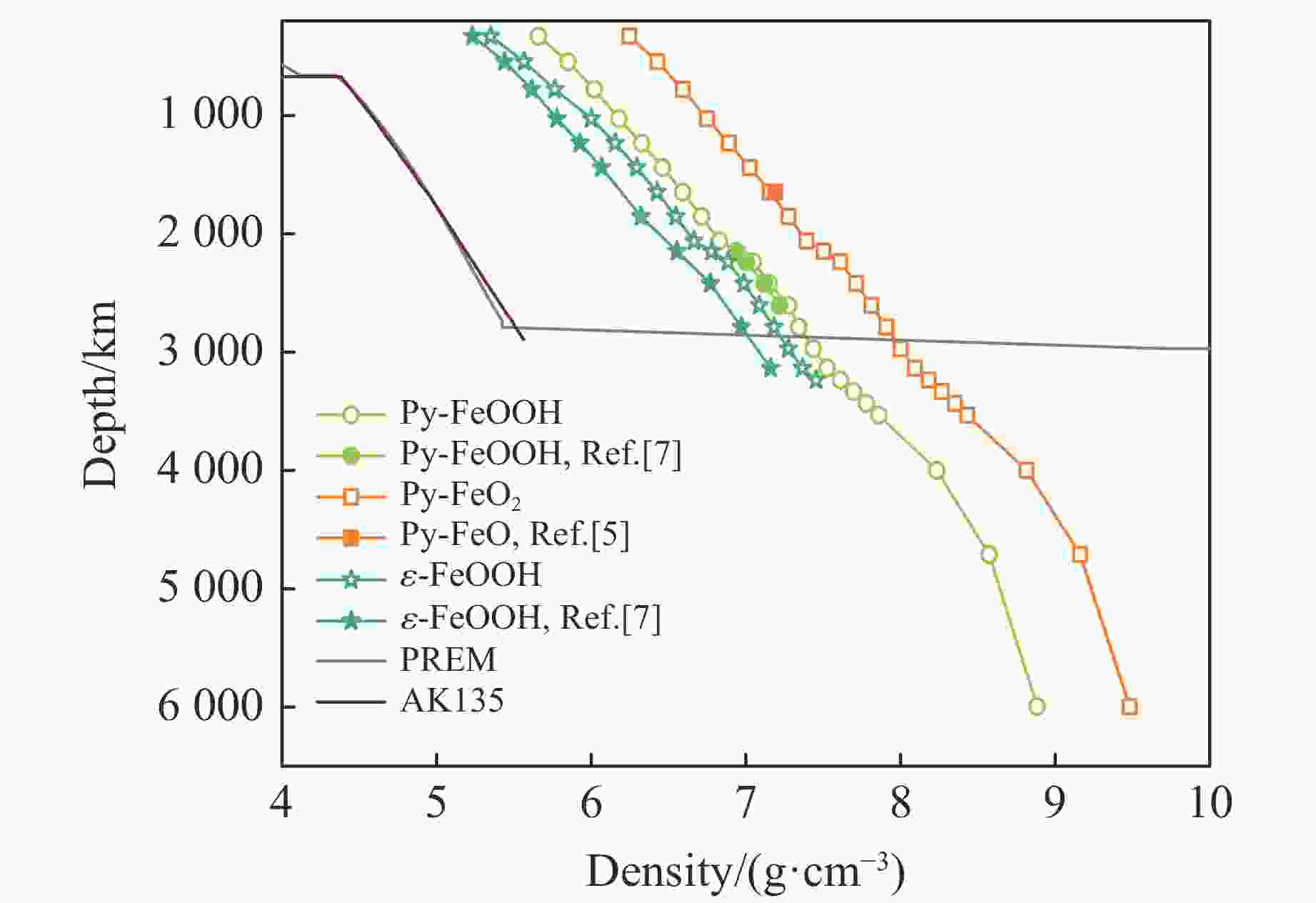
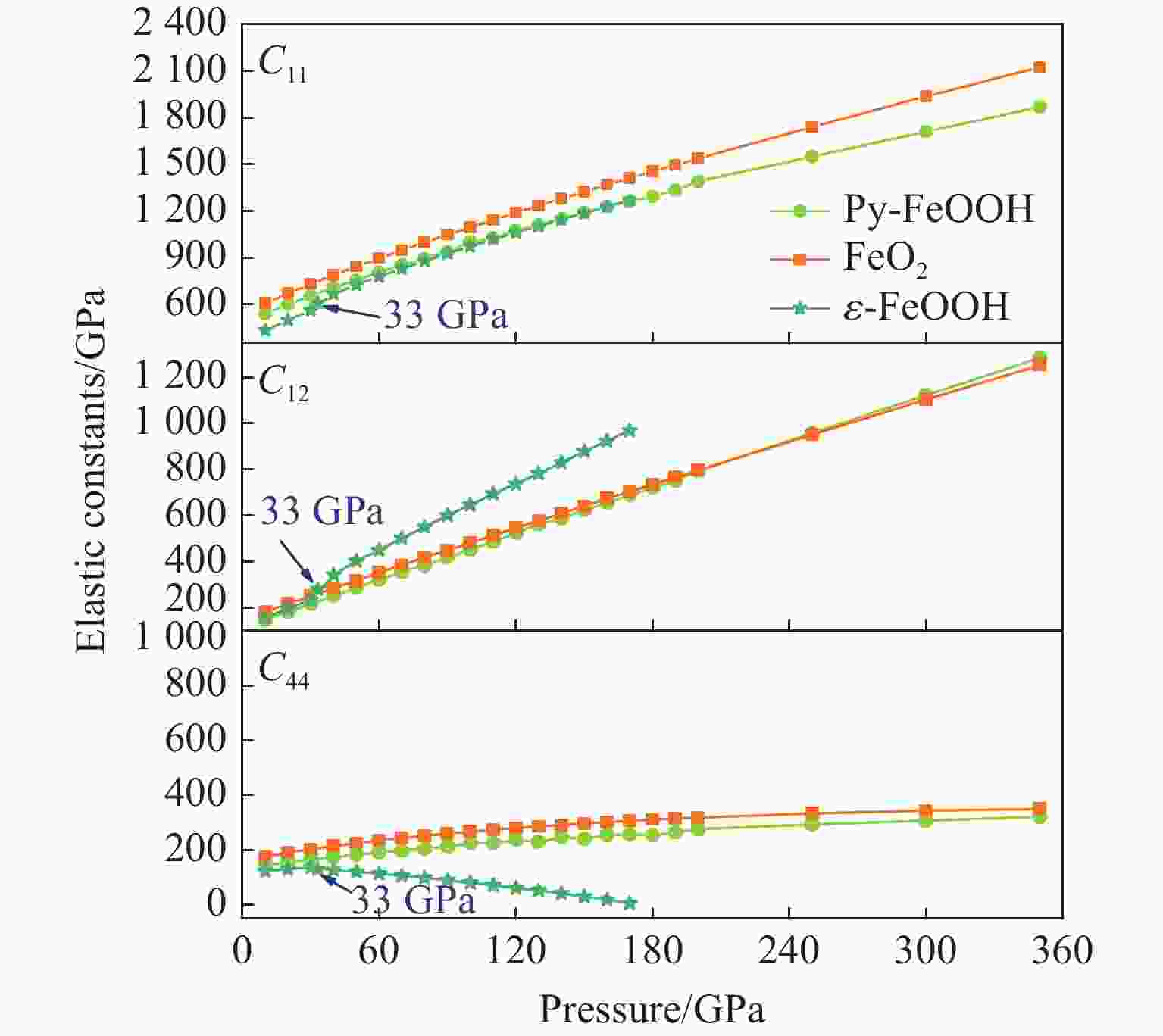
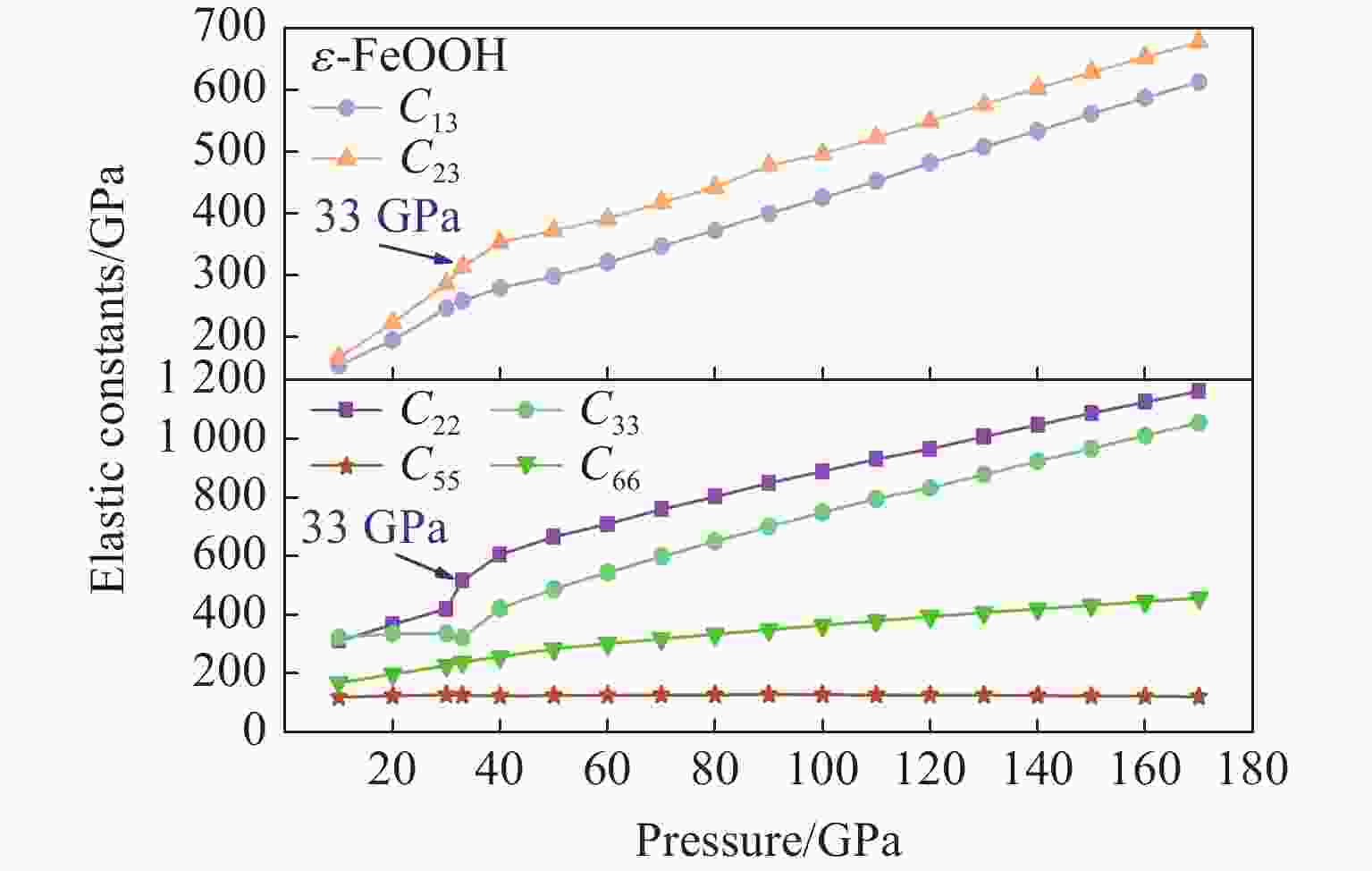
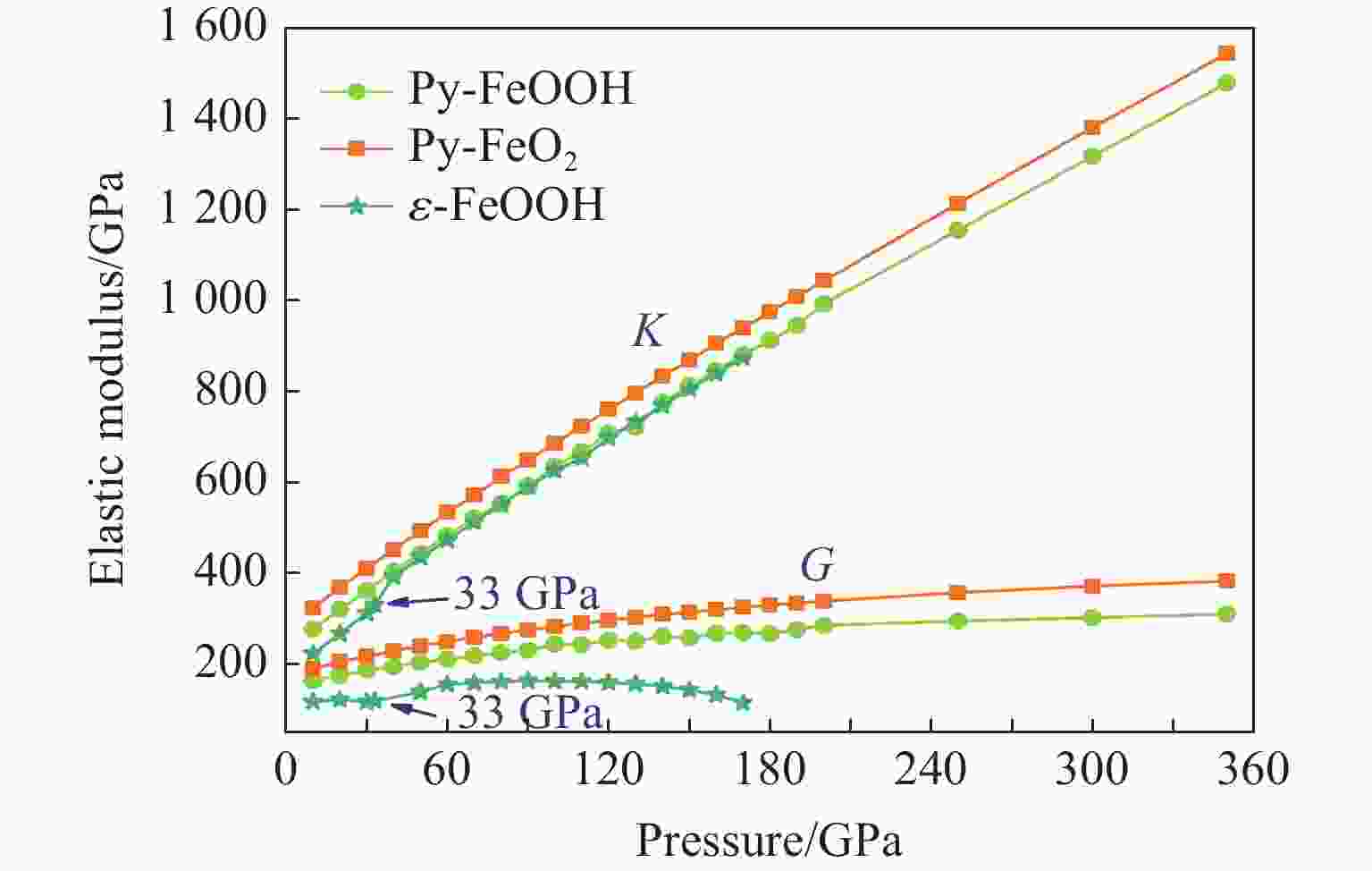
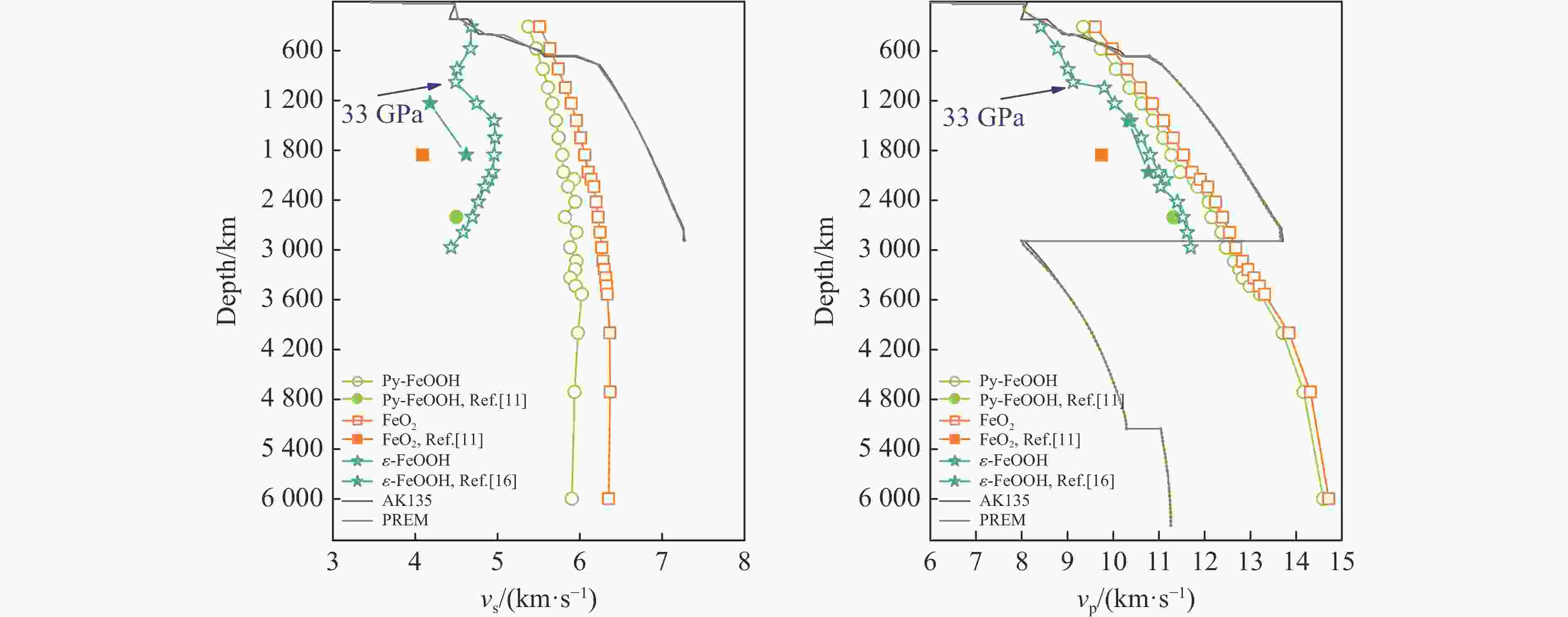
摘要: Py-FeO2、Py-FeOOH和ε-FeOOH是地幔及核幔边界的重要成分,其在高温高压下的物性演化特征对了解地幔物质组成和结构及动力学过程有重要意义,为此利用第一性原理方法计算了 0~350 GPa条件下Py-FeO2和Py-FeOOH以及0~170 GPa条件下ε-FeOOH的晶体结构与弹性性质。Py-FeO2和Py-FeOOH的晶格常数随压强的增加呈逐渐减小趋势,而ε-FeOOH的晶格常数随压强增加而减小,其中c轴更容易被压缩。Py-FeO2、Py-FeOOH和ε-FeOOH的晶胞密度随压强增加而增大,按照密度由大到小依次为Py-FeO2、Py-FeOOH、ε-FeOOH。3相的体积模量随压强的增加线性增加,Py-FeO2和Py-FeOOH的剪切模量随压强的增加线性增加。对比体积模量可知,Py-FeO2的体积模量最高,Py-FeOOH和ε-FeOOH的体积模量在高压下几乎一致;而Py-FeO2的剪切模量最大,ε-FeOOH的剪切模量最小。Py-FeO2、Py-FeOOH和ε-FeOOH的压缩波速随压强的增加而增加,Py-FeO2的剪切波速随压强的增加而增加。Py-FeOOH的剪切波速在0~2000 km深度范围内随深度增加而减小,在2000~6000 km深度范围内变化较小(在5.8~6.0 km/s之间);ε-FeOOH的剪切波速在33 GPa(约900 km深度)发生突变。3相中ε-FeOOH的波速最低,而Py-FeO2的波速最高。综合计算结果表明,Py-FeO2和Py-FeOOH具有高密度、低波速的特点,与地幔超低速区的性质一致。Py-FeO2和Py-FeOOH在形成之后可能富集下沉到核幔边界,成为超低速区的来源。ε-FeOOH在超过33 GPa压强条件下发生的氢键对称化给ε-FeOOH的结构带来显著变化,同时氢键对称化会影响原子间相互作用,进而影响ε-FeOOH的弹性性质以及地震波速。Abstract: Py-FeO2, Py-FeOOH and ε-FeOOH are important components of mantle and core-mantle boundary. Their physical evolution characteristics at high temperature and high pressure are important for understanding the composition, structure and dynamic process of mantle. The crystal structures and elastic properties of Py-FeO2 and Py-FeOOH at 0−350 GPa and ε-FeOOH at 0−170 GPa were calculated by first principles in this study. The Py-FeO2 and Py-FeOOH belong to the cubic crystal system, their lattice constants decrease gradually with increasing pressure. The ε-FeOOH belongs to orthorhombic crystal system, and its lattice constants decrease with increasing pressure, however, a and b axes bump up at 33 GPa, while c axis swoop at 33 GPa. The cell densities of Py-FeO2, Py-FeOOH and ε-FeOOH increase with pressure, and the relative cell density among these three phases is Py-FeO2 > Py-FeOOH > ε-FeOOH. The bulk moduli of Py-FeO2, Py-FeOOH and ε-FeOOH increase linearly with pressure, and the shear moduli of Py-FeO2 and Py-FeOOH increase linearly with pressure, but the shear modulus of ε-FeOOH mutates at 33 GPa. Py-FeO2 has the highest bulk modulus, and Py-FeOOH and ε-FeOOH have almost the same bulk modulus at high pressures. In addition, Py-FeO2 has the largest shear modulus, and ε-FeOOH has the smallest shear modulus. The compression wave velocities of Py-FeO2, Py-FeOOH and ε-FeOOH decrease gradually with the increasing pressure, while the shear wave velocities of Py-FeO2 increase gradually with the increasing pressure. The shear wave velocity of Py-FeOOH decreases with the increasing depth in the range of 0−2000 km, and the variation is small in the range of 2000−6000 km (5.8 km/s < vs < 6.0 km/s). The shear wave velocities of ε-FeOOH mutate at 33 GPa (about 900 km depth). The wave velocity of ε-FeOOH is the lowest, while that of Py-FeO2 is the highest. Based on comprehensive theoretical calculations, it is found that Py-FeO2 and Py-FeOOH have the high density and low wave velocity characteristics, which are consistent with the properties of the mantle ultra-low velocity zone (ULVZs). Py-FeO2 and Py-FeOOH may enrich and sink to the core-mantle boundary after formation, becoming the source of the ULVZs. The hydrogen bond symmetry of ε-FeOOH under 33 GPa may affect the crystal structure of ε-FeOOH, the atomic interactions of ε-FeOOH, and then the elastic properties and seismic wave velocity of ε-FeOOH.
-
Key words:
- ε-FeOOH /
- Py-FeOOH /
- Py-FeO2 /
- crystal structure /
- elastic properties /
- first-principles calculation
-
表 1 Py-FeO2、Py-FeOOH和ε-FeOOH的晶格参数和体积模量
Table 1. Lattice parameters and bulk moduli of Py-FeO2, Py-FeOOH and ε-FeOOH
Garnet Pressure & Temperature a/Å b/Å c/Å V·Z –1/Å3 Bulk modulus Method Ref. Py-FeO2 70 GPa, 0 K 4.3370 20.391 Sim. This study 76 GPa 4.3310 20.308 Sim. Ref.[5] 76 GPa 4.4420 20.745 Exp. Ref.[5] Maximum deviation/% 2.4 1.7 Py-FeOOH 120 GPa, 0 K 4.3540 20.635 Sim. This study 120 GPa, 0 K 21.110 Sim. Ref.[7] 119 GPa, 2300 K 4.3447 20.503 Exp. Ref.[6] 119 GPa, 300 K 4.3626 20.758 Exp. Ref.[7] Maximum deviation/% 0.4 2.3 ε-FeOOH 0 GPa, 0 K 4.7054 4.2510 2.8970 28.970 172 Sim. This study 28.900 187 Sim. Ref.[25] 0 GPa, 300 K 4.9540 4.4540 3.0001 33.100 126 Exp. Ref.[23] 0.001 GPa, 300 K 4.9544 4.4594 2.9999 33.139 135 Exp. Ref.[24] 4.937 4.432 2.994 32.636 Exp. Ref.[18] Maximum deviation/% 4.8 4.7 3.4 14.0 32 -
[1] SCHMIDT M W, POLI S. 4.19-devolatilization during subduction [J]. Treatise on Geochemistry (2nd ed), 2014, 4: 669–701. doi: 10.1016/B978-0-08-095975-7.00321-1 [2] POLI S, SCHMIDT M W. Petrology of subducted slabs [J]. Annual Review of Earth & Planetary Sciences, 2002, 30: 207–235. [3] LIN Y H, HU Q Y, MENG Y, et al. Evidence for the stability of ultrahydrous stishovite in Earth’s lower mantle [J]. Proceedings of the National Academy of Sciences, 2019, 117(1): 184–189. [4] LI Y, VOADLO L, SUN T, et al. The Earth’s core as a reservoir of water [J]. Nature Geoscience, 2020, 13(6): 1–6. [5] HU Q Y, KIM D Y, YANG W G, et al. FeO2 and FeOOH under deep lower-mantle conditions and Earth’s oxygen-hydrogen cycles [J]. Nature, 2016, 534(7606): 241–244. doi: 10.1038/nature18018 [6] HU Q Y, KIM D Y, LIU J, et al. Dehydrogenation of goethite in Earth’s deep lower mantle [J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(7): 1498. doi: 10.1073/pnas.1620644114 [7] NISHI M, KUWAYAMA Y, TSUCHIYA J, et al. The pyrite-type high-pressure form of FeOOH [J]. Nature, 2017, 547(7662): 205–208. doi: 10.1038/nature22823 [8] BO G J, KIM D Y, JI H S. Metal-insulator transition and the role of electron correlation in FeO2 [J]. Physical Review B, 2017, 95: 075144. doi: 10.1103/PhysRevB.95.075144 [9] ZHANG X L, NIU Z W, TANG M, et al. First-principles thermoelasticity and stability of pyrite-type FeO2 under high pressure and temperature [J]. Journal of Alloys & Compounds, 2017, 719: 42–46. [10] HUANG S X, QIN S, WU X. Elasticity and anisotropy of the pyrite-type FeO2H-FeO2 system in Earth’s lowermost mantle [J]. Journal of Earth Science, 2019, 30: 1293–1301. [11] LIU J, HU Q Y, KIM D Y, et al. Hydrogen-bearing iron peroxide and the origin of ultralow-velocity zones [J]. Nature, 2017, 551(7681): 494–497. doi: 10.1038/nature24461 [12] YUAN L, OHTANI E, IKUTA D, et al. Chemical reactions between Fe and H2O up to megabar pressures and implications for water storage in the Earth’s mantle and core [J]. Geophysical Research Letters, 2018, 45(3): 1330–1338. doi: 10.1002/2017GL075720 [13] ZHUANG Y K, CUI Z X, ZHANG D Z, et al. Experimental evidence for partially dehydrogenated ε-FeOOH [J]. Crystals, 2019, 9(7): 356. doi: 10.3390/cryst9070356 [14] DENG J, KARKI B B, GHOSH D B, et al. First-principles study of FeO2Hx solid and melt system at high pressures: implications for ultralow-velocity zones [J]. Journal of Geophysical Research: Solid Earth, 2019, 124(5): 4566–4575. [15] HOU M Q, HE Y, JANG B G, et al. Superionic iron oxide-hydroxide in Earth’s deep mantle [J]. Nature Geoscience, 2021, 14: 174–178. doi: 10.1038/s41561-021-00696-2 [16] THOMPSON E C, CAMPBELL A J, TSUCHIYA J. Elastic properties of the pyrite-type FeOOH-AlOOH system from first principles calculations [J]. Geochemistry Geophysics Geosystems, 2021. [17] BENDELIANI N A, BANEYEVA M I, PORYVKIN D S. Synthesis of new modification of FeO(OH), stable at high pressurere [J]. Geochemistry International, 1972, 9: 589–590. [18] PERNET M, JOUBERT J C, BERTHET-COLOMINAS C. Etude par diffraction neutronique de la forme haute pression de FeOOH [J]. Solid State Communications, 1975, 17(12): 1505–1510. doi: 10.1016/0038-1098(75)90983-7 [19] CHENAVAS J, JOUBERT J C, CAPPONI J J, et al. Synthese de nouvelles phases denses d'oxyhydroxydes M3+OOH des metaux de la premiere serie de transition, en milieu hydrothermal à tres haute pression [J]. Journal of Solid State Chemistry, 1973, 6(1): 1–15. doi: 10.1016/0022-4596(73)90199-0 [20] BOLOTINA N B, MOLCHANOV V N, DYUZHEVA T I, et al. Single-crystal structures of high-pressure phases FeOOH, FeOOD, and GaOOH [J]. Crystallography Reports, 2008, 53(6): 960–965. doi: 10.1134/S1063774508060084 [21] MAJZLAN J, GREVEL K D, NAVROTSKY A. Thermodynamics of Fe oxides: Part Ⅱ. enthalpies of formation and relative stability of goethite (α-FeOOH), lepidocrocite (γ-FeOOH), and maghemite (γ-Fe2O3) [J]. American Mineralogist, 2003, 88(5/6): 855–859. doi: 10.2138/am-2003-5-614 [22] GLEASON A E, JEANLOZ R, KUNZ M. Pressure-temperature stability studies of FeOOH using X-ray diffraction [J]. American Mineralogist, 2008, 93(11/12): 1882–1885. doi: 10.2138/am.2008.2942 [23] SUZUKI A. High-pressure X-ray diffraction study of ε-FeOOH [J]. Physics and Chemistry of Minerals, 2009, 37(3): 153–157. [24] SUZUKI A. Pressure-volume-temperature equation of state of ε-FeOOH to 11 GPa and 700 K [J]. Journal of Mineralogical and Petrological Sciences, 2016, 111(6): 420–424. doi: 10.2465/jmps.160719c [25] OTTE K, ENTCHEVA R, SCHMAHL W W, et al. Pressure-induced structural and electronic transitions in FeOOH from first principles [J]. Physical Review B, 2009, 80(20): 205116. doi: 10.1103/PhysRevB.80.205116 [26] GLEASON A E, QUIROGA C E, SUZUKI A, et al. Symmetrization driven spin transition in ε-FeOOH at high pressure [J]. Earth and Planetary Science Letters, 2013, 379: 49–55. doi: 10.1016/j.jpgl.2013.08.012 [27] THOMPSON E C, CAMPBELL A J, TSUCHIYA J. Elasticity of ε-FeOOH: seismic implications for Earth’s lower mantle [J]. Journal of Geophysical Research: Solid Earth, 2017, 122(7): 5038–5047. doi: 10.1002/2017JB014168 [28] THOMPSON E C, DAVIS A H, NIGEL M B, et al. Phase transitions in ε-FeOOH at high pressure and ambient temperature [J]. American Mineralogist, 2020, 105(12): 1769–1777. doi: 10.2138/am-2020-7468 [29] HU Y, KIEFER B, PLONKA A, et al. Compressional behavior of end-member and aluminous iron-bearing diopside at high pressure from single-crystal X-ray diffraction and first principles calculations [J]. Physics and Chemistry of Minerals, 2019, 46(10): 977–986. doi: 10.1007/s00269-019-01056-8 [30] MONSERRAT B, MARTINEZ-CANALES M, NEEDS R J, et al. Helium-iron compounds at terapascal pressures [J]. Physical Review Letters, 2018, 121(1): 015301. doi: 10.1103/PhysRevLett.121.015301 [31] KVASHNIN A G, KRUGLOV I A, SEMENOK D V, et al. Iron superhydrides FeH5 and FeH6: stability, electronic properties, and superconductivity [J]. The Journal of Physical Chemistry C, 2018, 122(8): 4731–4736. doi: 10.1021/acs.jpcc.8b01270 [32] ZHANG J, HAO B, ZHANG X, et al. The influence of microstructure and emissivity of NiO-Doped Fe3O4 spinel structure on near-and middle-infrared radiation [C]//LI B, LI J, IKHMAYIES S, et al. Characterization of Minerals, Metals, and Materials, 2019: 69−77 . [33] CUI W Y, ZHANG Y B, CHEN J H, et al. Comparative study on surface structure, electronic properties of sulfide and oxide minerals: a first-principles perspective [J]. Minerals, 2019, 9(6): 329. doi: 10.3390/min9060329 [34] LU L, YU S. Metal distribution in iron-nickel sulfide mineral pentlandite: first-principles study [J]. Chemical Physics Letters, 2019, 736: 136786. doi: 10.1016/j.cplett.2019.136786 [35] DENG Z, TONG X, HUANG L, et al. Density functional theory study of H2O adsorption on different sphalerite surfaces [J]. Physicochemical Problems of Mineral Processing, 2019, 55(1): 82–88. [36] KUROKI Y, KAWANO S, IIKUBO S, et al. First-principles study of chemical driving force for face centered cubic to hexagonal close packed martensitic transformation in hydrogen-charged iron [J]. Metallurgical and Materials Transactions A, 2019, 50: 3019–3023. [37] SANTOS P, COUTINHO J, ÖBERG S. First-principles calculations of iron-hydrogen reactions in silicon [J]. Journal of Applied Physics, 2018, 123(24): 245703. doi: 10.1063/1.5039647 [38] SONG Y L, HE K H, SUN J, et al. Effects of iron spin transition on the electronic structure, thermal expansivity and lattice thermal conductivity of ferropericlase: a first principles study [J]. Scientific Reports, 2019, 9(1): 4172. doi: 10.1038/s41598-019-40454-4 [39] LEONOV I, ROZENBERG G K, ABRIKOSOV I A. Charge disproportionation and site-selective local magnetic moments in the post-perovskite-type Fe2O3 under ultra-high pressures [J]. NPJ Computational Materials, 2019, 5(1): 1–7. doi: 10.1038/s41524-019-0225-9 [40] CLARK S J, SEGALLII M D, PICKARDII C J, et al. First principles methods using CASTEP [J]. Zeitschrift fur Kristallographie-Crystalline Materials, 2005, 220: 567–570. doi: 10.1524/zkri.220.5.567.65075 [41] LIU L, YANG L X, YANG G S, et al. The effect of Fe on crystal structure and elasticity superhydous phase H under high pressure by first-principles calculations [J]. Annals of Geophysics, 2020, 63(6): PE672. [42] LIU L, YI L, LIU H, et al. First principles calculation of the nonhydrostatic effects on structure and Raman frequency of 3C-SiC [J]. Scientific Reports, 2018, 8(1): 11279. doi: 10.1038/s41598-018-29666-2 [43] LIU L, YI L, LIU H, et al. The structure and elasticity of phase B silicates under high pressure by first principles simulation [J]. Physics B, 2018, 27(4): 047402. [44] GONCHAROV A F, STRUZHKIN V V, SOMAYAZULU M S, et al. Compression of ice to 210 gigapascals: infrared evidence for a symmetric hydrogen-bonded phase [J]. Science, 1996, 273(5272): 218–220. doi: 10.1126/science.273.5272.218 [45] TSUCHIYA J. First-principles study of hydrogen bond symmetrization of phase D under high pressure [J]. American Mineralogist, 2005, 90(1): 44–49. doi: 10.2138/am.2005.1628 [46] SANO-FURUKAWA A, KOMATSU K, VANPETEGHEM C B, et al. Neutron diffraction study of δ-AlOOD at high pressure and its implication for symmetrization of the hydrogen bond [J]. American Mineralogist, 2008, 93(10): 1558–1567. doi: 10.2138/am.2008.2849 [47] ERREA I, CALANDRA M, PICKARD C J, et al. Quantum hydrogen-bond symmetrization in the superconducting hydrogen sulfide system [J]. Nature, 2016, 532: 81–84. doi: 10.1038/nature17175 [48] TSUCHIYA J, TSUCHIYA T. First-principles prediction of a high-pressure hydrous phase of AlOOH [J]. Physical Review B, 2011, 83(5): 054115. doi: 10.1103/PhysRevB.83.054115 [49] HILL R. The elastic behaviour of a crystalline aggregate [J]. Proceedings of the Physical Society, 1952, 65(5): 349–354. doi: 10.1088/0370-1298/65/5/307 [50] NYE J F. Physical properties of crystals: their representation by tensors and matrices [M]. Oxford: Clarendon Press, 1957. -






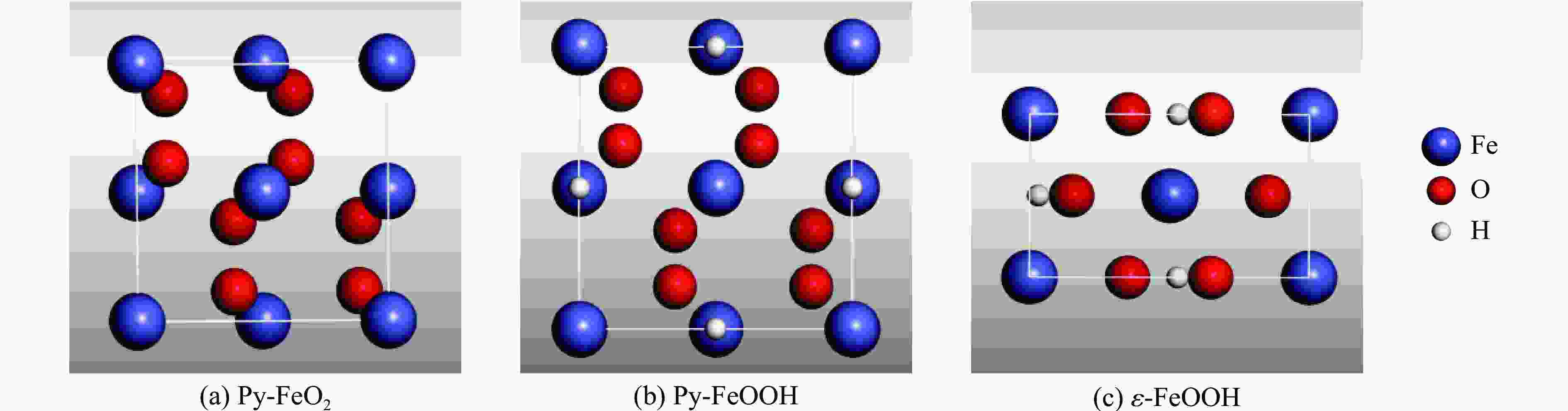
 下载:
下载: