New Developments of Hydrogen-Based High-Temperature Superconductors under High Pressure
-
摘要: 富氢材料被认为是室温超导体的最佳候选体系,是物理学、材料科学等多学科的热点研究领域之一。理论和实验研究发现的新型共价氢化物H3S和笼状氢化物LaH10的超导转变温度(Tc)均超过 200 K,进一步推动了对富氢化合物超导电性的探索。最近,通过高压实验合成的碳质硫氢化物在288 K的室温下实现了零电阻,让人们看到了室温超导的曙光。本文结合课题组在此领域的主要成果,介绍了3类典型富氢化合物的结构及超导特性,包括近期首次在层状氢化物中发现的具有类五角石墨烯结构的富氢超导体HfH10,其超导转变温度高达213~234 K。Abstract: Hydrogen-rich materials are considered to be the most potential candidates for room-temperature superconductors, yielding a research hotspot in physics, material science and so on. Remarkably, the new covalent hydride H3S and clathrate like LaH10, exhibit record high superconducting transition temperature (Tc) above 200 K both found theoretically and experimentally, which further promotes the study on the superconductivity of hydrogen-rich compounds. Very recently, the successful experimental discovery of high-temperature superconductivity at 288 K in a carbonaceous sulfur hydride system at high pressure shows the light for achieving room-temperature superconductors. In this paper, we introduce the structures and superconductivities of three typical hydrogen-rich compounds, including HfH10, a "pentagraphenelike" superconductor exhibiting an extraordinarily high Tc of around 213–234 K at 250 GPa, which was recently discovered for the first time in layered structure hydrides.
-
Key words:
- high pressure /
- hydrogen-rich material /
- layered hydrides /
- superconductivity
-
Ceramic materials have been increasingly used in armors, personal armor system, aeronautic engineering and vehicle engineering due to its excellent ballistic performance. An understanding of the response and failure of ceramic materials under impact loading is of great significance for the design and assessment of military hardware and protective structures.
As ballistic tests are expensive to perform and time consuming, numerical simulations have been widely employed in the design and optimization of ceramic armors. However, the accuracy of numerical simulations depends on the dynamic constitutive model for ceramic materials to a large extent. To this end, many models have been put forward[1-8]. Fahrenthold[1] proposed a continuum damage model for fracture of brittle solids under dynamic loading in which Weibull strength distribution was employed to account for the effects of flaw size distribution on the damage accumulation rate. The model was used to compute the depth of penetration in a steel plate impacted by a sphere of alumina without being applied to simulate the behavior of ceramic armors subjected to projectile impact. Rajendran[2] modeled the impact behavior of AD85 ceramic under multiaxial loading by assuming an existing distribution of micro-cracks and employing a criterion for crack growth based on theories of dynamic fracture mechanics. The strength of the intact material was rate dependent, and the inelastic deformation was modeled using an elastic-plastic cracking rule. The model predictions were found to be in good agreement with the test data obtained from plate impact tests. The most widely used constitutive model for ceramic materials in many commercial codes is the Johnson-Holmquist model (JH-2)[3]. The model employs two strength surfaces to describe the pressure-dependent compressive strength of the intact and failed materials, respectively. However, in the model strain rate effect is described by the same form of function adopted in the constitutive models for metals and concrete materials, which has been found to be inconsistent with the dynamic mechanical behavior in recent studies[9-12]. Furthermore, tensile softening cannot be accurately predicted, and no differentiation was made between the effects of strain rate and inertia (containment).
The main objective of this paper is to establish a macroscopic dynamic constitutive model for ceramic materials by closely following the previous work on concrete[9] and on the basis of the experimental observations for some ceramic materials. Various equations of the constitutive model are given and compared with some available experimental data for ceramic materials in terms of pressure-volumetric response, quasi-static strength surface and strain rate effect. Furthermore, the model is also verified against the data for triaxial test by single element simulation approach.
1. A Macroscopic Constitutive Model for Ceramics
A dynamic macroscopic constitutive model for ceramic materials is developed in the following sections based on the computational constitutive model for concrete subjected to dynamic loadings[9] with some modifications being made. There are two points which should be highlighted here, namely, (1) the pressure-volumetric response is described by polynomial equation and the phase transition (e.g. AlN ceramics) as the pressure increases to a certain value is considered; (2) a hyperbolic tangent function is employed to describe the pressure dependent shear strength surfaces of ceramic materials which level out at very high pressures.
1.1 Equation of State
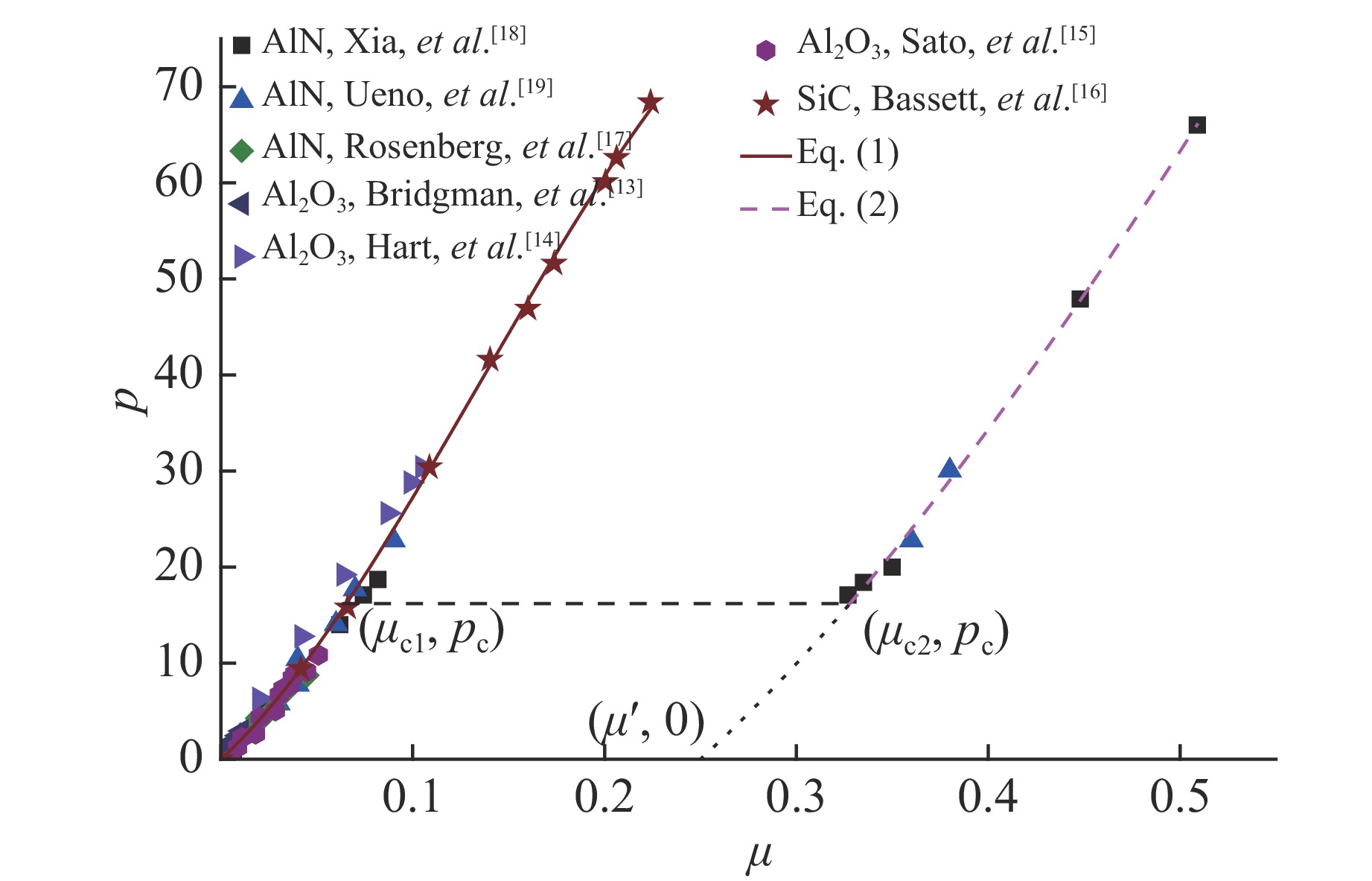
Ceramics are complex granular materials, which contain a large number of micro cracks and voids just as concrete material. On the one hand, it has been observed experimentally that the volumetric strains of Al2O3 and SiC increase with increasing pressure[13-16] and the equation of state for this category of ceramic materials can be expressed as polynomial equation, viz.
{p=K1μ+K2μ2+K3μ3μ=V0/V−1=ρ/ρ0−1 (1) where p is pressure;
$\mu $ is volumetric strain; K1, K2, K3 are bulk moduli for ceramic material;${\rho _0} = 1/{V_0}$ and$\rho = 1/V$ indicate initial and current densities of ceramic material, respectively. On the other hand, the pressure-volumetric response of AlN has been observed experimentally to be quite different[17-19] and a phase transformation occurs from wurtzite structure to salt structure as pressure reaches a critical value. Thus, the equation of state for such ceramics as AlN can be written in the following form, namelyp={K1μ+K2μ2+K3μ3μ<μc1pcμc1⩽μ⩽μc2K4(μ−μ′)+K5(μ−μ′)2+K6(μ−μ′)3μ>μc2 (2) where pc represents a constant pressure at which phase transformation occurs; K4, K5, K6 are bulk moduli for ceramic material after the phase transformation;
$\mu '$ is an offset in volumetric strain due to phase transformation;${\mu _{{\rm{c}}1}}$ and${\mu _{{\rm{c}}2}}$ are volumetric strains at the beginning and end of phase transformation, respectively. For μ < 0, ceramic material is under tension condition. Thus, one obtainsp=K1μ (3) 1.2 Strength Model
On the basis of the previous studies on concrete[9-10] and the experimental observations for ceramic materials[17, 20-24], it is suggested that the strength surface of ceramic materials can be cast into the following form, i.e.
Y={3(p+ftt)r(θ,e)p<0[3ftt+(fcc−3ftt)×3p/fcc]r(θ,e)0⩽p⩽fc/3[fcc+Bf′ctanh(p/f′c−fcc/(3f′c))]r(θ,e)p>fc/3 (4) in which Y is shear strength;
${f_{{\rm{cc}}}} = f_{\rm{c}}'{\psi _{\rm{c}}}{\eta _{\rm{c}}}$ and${f_{{\rm{tt}}}} = {f_{\rm{t}}}{\psi _{\rm{t}}}{\eta _{\rm{t}}}$ are respective dynamic strengths of ceramic materials in uniaxial compression and tension, which take account of shear damage in the form of damage shape functions ($\eta $ ) and strain rate effects by dynamic increase factor (DIF); B is an empirical constant;$r\left( {\theta,e} \right)$ represents Lode effect. The dynamic increase factor in compression (ψc) can be obtained by the following equation[9-10], viz.ψc=fcdf′c=(ψt−1)ftf′c+1 (5) where fcd and
${f_{\rm{c}}'} $ are the dynamic and static uniaxial compressive strength, respectively, ft is the static uniaxial tensile strength, and ψt represents the dynamic increase factor in tension which is expressed as followsψt=ftdft={(FmWy−1)tanh[(lg˙ε˙ε0−Wx)S]+1}Wy (6) in which ftd is the dynamic uniaxial tensile strength, parameters Wx, Fm, Wy and S are constants to be determined experimentally,
$\dot \varepsilon $ is the strain rate,${\dot \varepsilon _0}$ is the reference strain rate usually taken to be${\dot \varepsilon _0}$ = 1.0 s−1.The multi-axial tests of ceramics show that the effective strain at maximum load (
${\varepsilon _{\max }}$ ) increases almost linearly with increasing pressure. Furthermore, these tests also show ceramic compressive strength has no significant influence on this behavior. According to Eq.(18) in Ref.[9], the failure strain of ceramic is written asεf=εmλm(˙ε˙ε0)0.02=1λm0.0065max[1,1+λs(pfc−13)](˙ε˙ε0)0.02 (7) where
${\varepsilon _{\rm{f}}}$ is the failure strain of ceramic material,${\varepsilon _{\rm{m}}}$ is the strain corresponding to the maximum compressive strength,${\lambda _{\rm{m}}}$ is the shear damage at which strength reaches its maximum value under compression, and${\lambda _{\rm{s}}}$ is an empirical constant.The residual strength of the crushed ceramics is still high under the confining pressure. The residual strength surface for ceramic materials can be obtained from Eq.(4) by setting ftt = 0 and fcc =
$f_{\rm{c}}'$ × r, namelyY={3p×r(θ,e)0<p⩽f′c×r/3[f′c×r+Bf′ctanh(pf′c−f′c×r3f′c)]×r(θ,e)p>f′c×r/3 (8) where r is a constant,
$f_{\rm c}'$ × r represents the residual strength of concrete under quasi-static uniaxial compression. Meanwhile, the initial yield strength of concrete under quasi-static uniaxial compression is defined as$f_{\rm c}'$ × l.2. Verification of the Newly-Developed Constitutive Model
The present model is verified against some available experimental data in terms of pressure-volumetric response, quasi-static strength surface and strain rate effect.
Values of various parameters in equation of state can be determined by hydrostatic compression experiment and they are listed in Table 1. For Al2O3 and SiC ceramic materials, the relationship between pressure and volumetric strain (Eq.(1)) can be rewritten as
Table 1. Values of parameters for BeO in the present modelEquation of state parameters Constitutive model parameters K1/GPa K2/GPa K3/GPa ρc/(kg·m−3) Fm Wx Wy S 181.5 1 207.9 −2 991 3 030 3 3.8 2 1.25 Constitutive model parameters ${f_{{\rm{c}}}'}$/GPa ft/GPa B G/GPa λm λs l r 1.5 0.15 1.2 125 0.3 7.5 0.8 0.3 p=1.815×1011μ+1.208×1012μ2−2.991×1012μ3 (9) and, for AlN ceramic material, the relationship between pressure and volumetric strain (Eq.(2)) can be recast into the following form
p={1.815×1011μ+1.208×1012μ2−2.991×1012μ3μ<0.0671.668×10100.067⩽μ⩽0.3301.819×1011(μ−0.250)+3.556×1011(μ−0.250)2−2.830×1011(μ−0.250)3μ>0.330 (10) Fig.1 shows comparison of the present model predictions (Eq.(9) and Eq.(10)) with the experimental data for Al2O3 and SiC[13-16] and for AlN[17-19]. It can be seen from Fig.1 that good agreement is obtained.
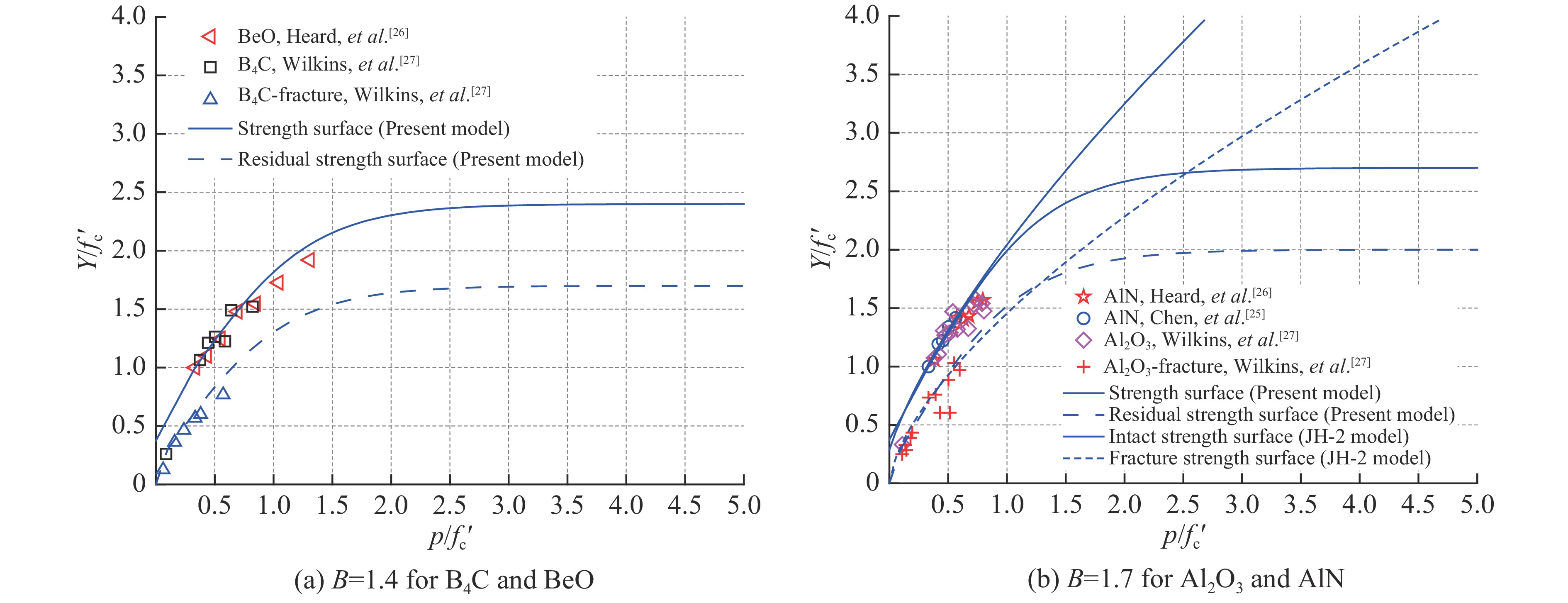
Fig.2(a) and Fig.2(b) show comparisons between the present model predictions (Eq.(4) with B = 1.4 for B4C and BeO and Eq.(9) with B = 1.7 for Al2O3 and AlN) and the test data[25-27] for the strength surfaces. The strength surfaces of Al2O3 and AlN obtained from the JH-2 model[28] are also shown in Fig.2(b). It is clear from Fig.2 that the present model predictions are in good agreement with available test results for ceramic materials. It is also clear from Fig.2(b) that the JH-2 model produces similar results to those of the present model for relatively low pressures whilst for higher pressure the present model levels out and the JH-2 model increases with increasing pressure.
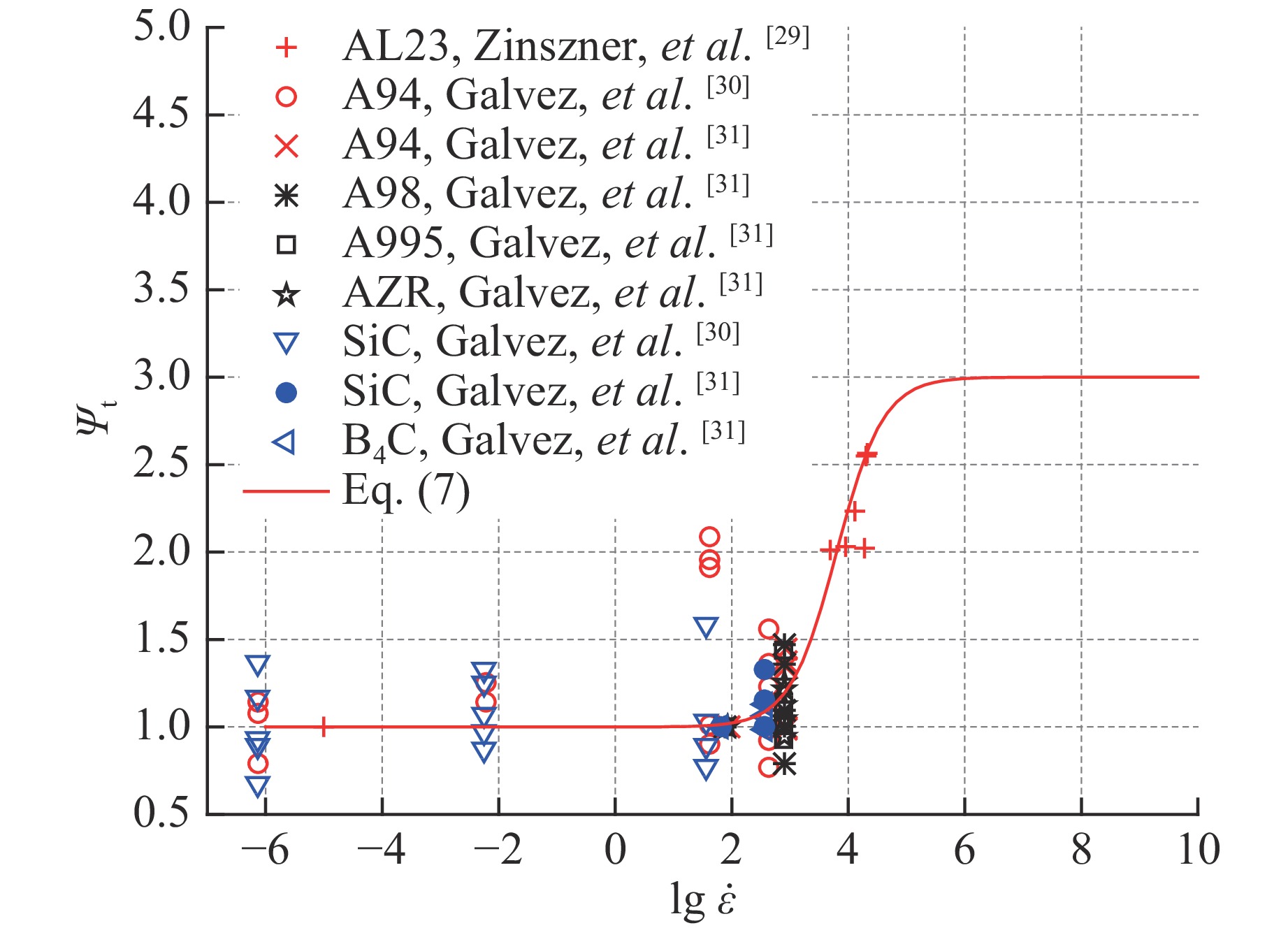
Values of parameters Fm, Wx and S in Eq.(6) for the dynamic increase factor in tension can be determined from tensile test data for ceramic materials at different strain rates. Fig.3 shows comparisons between the present model predictions (Eq.(6) with Fm = 3, Wx = 3.8 and S = 1.25) and available experimental data[29-31] for different ceramic materials at different strain rates. It is evident from Fig.3 that reasonable agreement is obtained.
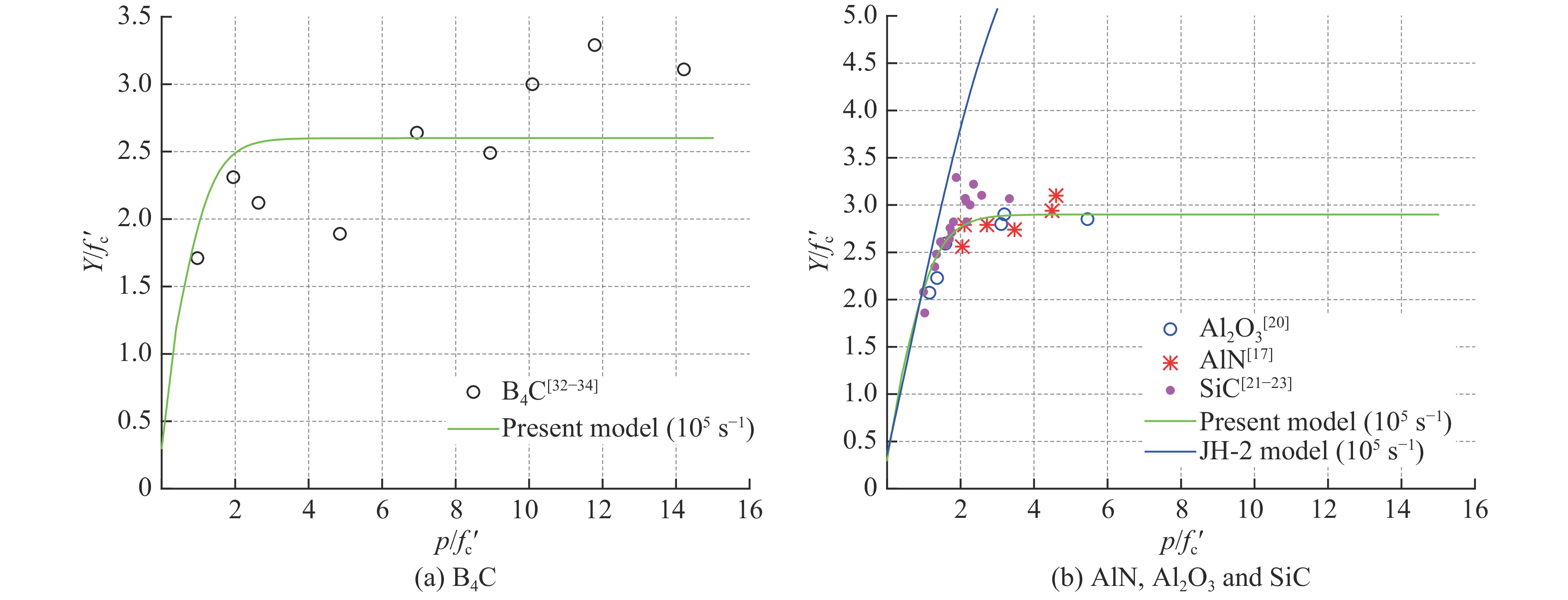
Fig.4(a) and Fig.4(b) show comparisons between the theoretically predicted strength surfaces (Eq.(4)) and some experimental data obtained from plate impact tests on B4C[32-34], AlN[17], Al2O3[20] and SiC[21-23]. In the calculations, a strain rate of 105 s−1 is taken which is of a typical value in a plate impact test. Also shown in Fig.4(b) are the predictions from the JH-2 model. It is clear from Fig.4(a) that reasonable agreement is obtained between the present model predictions and the tests results for B4C which are somehow scattered whilst good agreement is achieved between Eq.(4) and the test data for AlN, Al2O3 and SiC as can be seen from Fig.4(b). It is also clear from Fig.4(b) that the JH-2 model has failed to predict the dynamic mechanical behavior of ceramic materials at higher confining pressure.
Fig.5 shows comparison of the present model predictions and the experimental data obtained from SHPB (split Hopkinson pressure bar) tests[25]. Also shown in the figure are the predictions from the JH-2 model. In the tests, confining pressures of up to 230 MPa were applied, and a constant strain rate was employed (i.e. 500 s−1). The solid line indicates theoretically predicted quasi-static strength surface, and the broken line designates dynamic strength surface from the present model with a strain rate of 500 s−1. As can be seen from Fig.5 that a good agreement is obtained between the present model predictions and the experimental data whilst the JH-2 model underestimates the strength surface of AlN ceramic under the strain rate of 500 s−1. It should be stressed here that the present model predicts that the quasi-static and dynamic strength surfaces are parallel to each other, which has been confirmed/verified by the experimental data. It leads to further support for the accuracy and validity of the present constitutive model for ceramics.
 Figure 5. Comparison between the experimental data[25] and the predictions by the present model of strength varies with pressure at different strain rates of AlN
Figure 5. Comparison between the experimental data[25] and the predictions by the present model of strength varies with pressure at different strain rates of AlNTo demonstrate the quasi-static behavior of the present constitutive model, numerical tests are performed to evaluate stress-strain relationships for ceramics under various loading conditions, which includes: (a) triaxial compression with different confining pressures, (b) uniaxial tension, (c) biaxial tension and (d) triaxial tension. The numerical tests are carried out using single element simulation approach. Table 1 lists the values of various parameters in the present constitutive model for BeO ceramic. Table 2 and Table 3 list the values of various parameters for AlN ceramic employed in the present model and JH-2 model, respectively. Parameters in the present model are clearly defined in the previous paragraphs, and in JH-2 model. K1, K2, K3 are bulk moduli, and ρc is the density for ceramic material; a, b, C, m, n are strength surface parameters; pHEL, σHEL and μHEL are respectively the pressure, the equivalent stress and the volumetric strain at HEL (Hugoniot elastic limit); T is the maximum tensile hydrostatic pressure the material can withstand; β is strain rate parameter; d1, d2 are damage parameters.
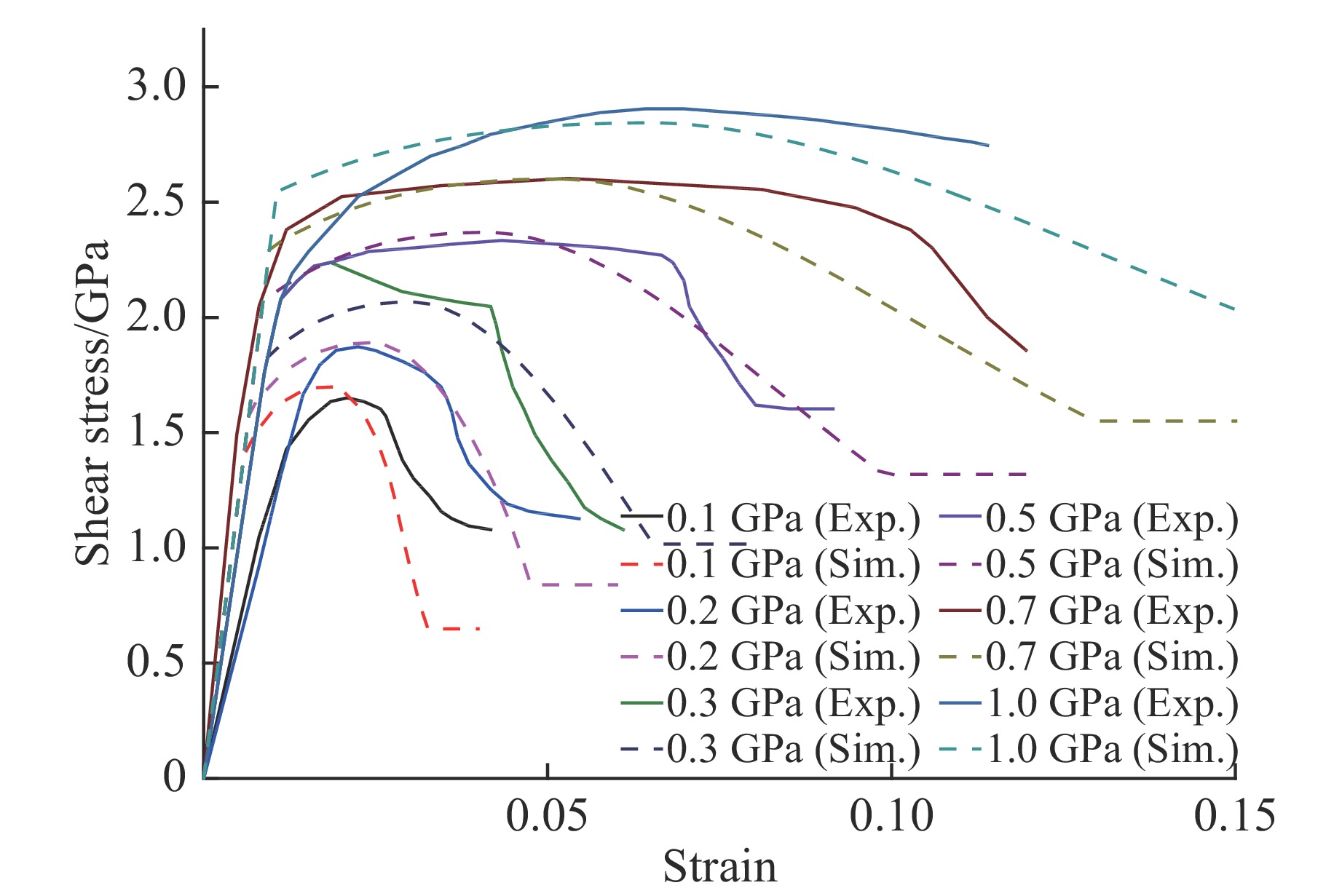
Table 2. Values of parameters for AlN in the present modelEquation of state parameters Constitutive model parameters ρc/(kg·m−3) K1/GPa K2/GPa K3/GPa K4/GPa K5/GPa K6/GPa Fm Wx Wy 3 229 181.5 1 207.9 −2 991 181.9 335.6 −283 3 3.8 2 Constitutive model parameters ${f_{{\rm{c}}}'}$/GPa ft/GPa B G/GPa S λm λs l r 3 0.3 1.7 127 1.25 0.3 7.5 0.8 0.3 Table 3. Values of various parameters for AlN ceramic (JH-2 model)Equation of state parameters Constitutive model parameters ρc/(kg·m−3) K1/GPa K2/GPa K3/GPa a b C n m 3 229 201 260 0 1.36 1.0 0.013 0.75 0.65 Constitutive model parameters HEL/GPa pHEL/GPa σHEL/GPa μHEL T/GPa β d1 d2 9.0 5.0 6.0 0.024 2 0.32 1.0 0.02 1.85 Fig.6 shows the comparison of the numerically predicted stress-strain curves and the experimental data for BeO under triaxial compression with confinement pressures ranging from 0.1 GPa up to 1.0 GPa, as reported by Heard and Cline[26]. It is clear from Fig.6 that the numerical results are in reasonable agreement with the experimental observations.
 Figure 6. Comparison of stress-strain curves for BeO under triaxial compression between the present model and experimental data[22]
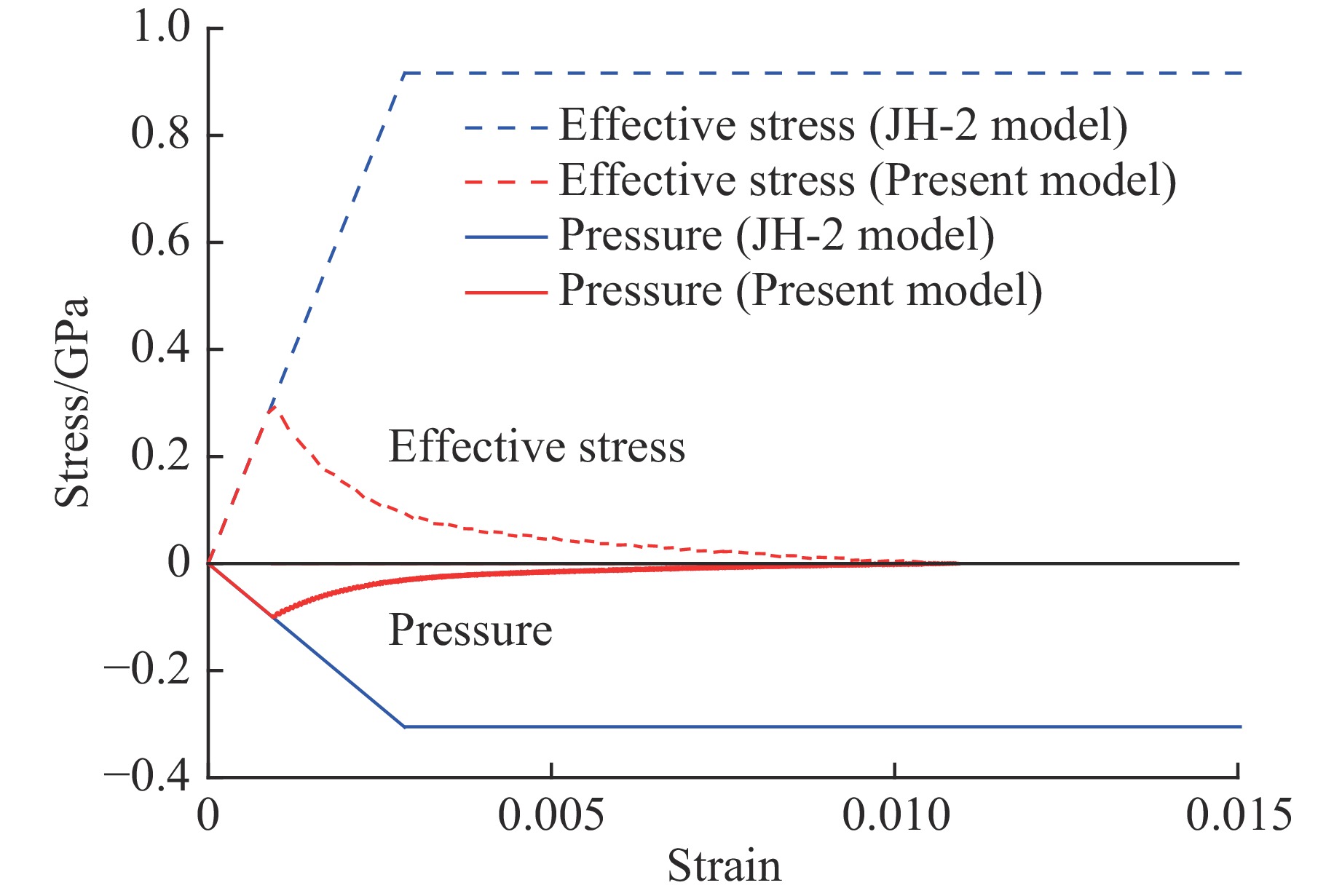
Figure 6. Comparison of stress-strain curves for BeO under triaxial compression between the present model and experimental data[22]Fig.7 shows variations of pressure and effective stress with maximum principal strain of AlN under quasi-static uniaxial tension. It is evident from Fig.7 that the numerical results from the present model give an elastic-brittle softening response of AlN under uniaxial tension with a principal tensile strength of 0.3 GPa for AlN. It is also evident from the figure that the mechanic behavior of the ceramic under uniaxial tension predicted numerically by the JH-2 model is elastic-perfectly plastic with the minimum pressure of 0.31 GPa and the maximum effective stress of 0.93 GPa, which are obviously not in compliance with the actual tensile behavior of the ceramic.
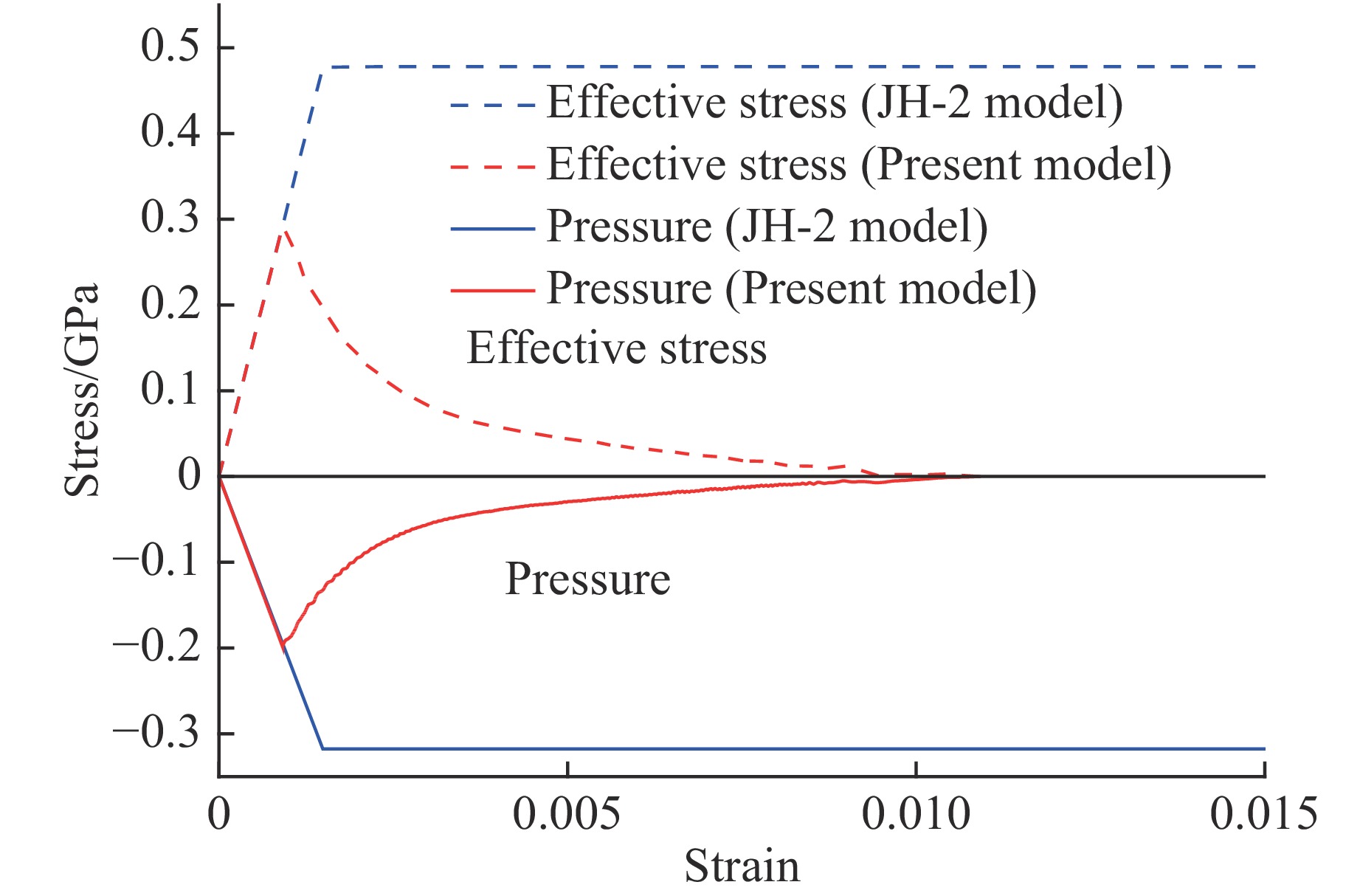
Fig.8 shows variations of pressure and effective stress with maximum principal strain of AlN under quasi-static biaxial tension. Elastic-brittle softening response of the ceramic is predicted numerically using the present model under biaxial tension with a principal tensile strength of 0.3 GPa. On the other hand, an elastic-perfectly plastic response of the ceramic under biaxial tension predicted numerically by the JH-2 model have the minimum pressure of 0.31 GPa and the maximum effective stress of 0.48 GPa.
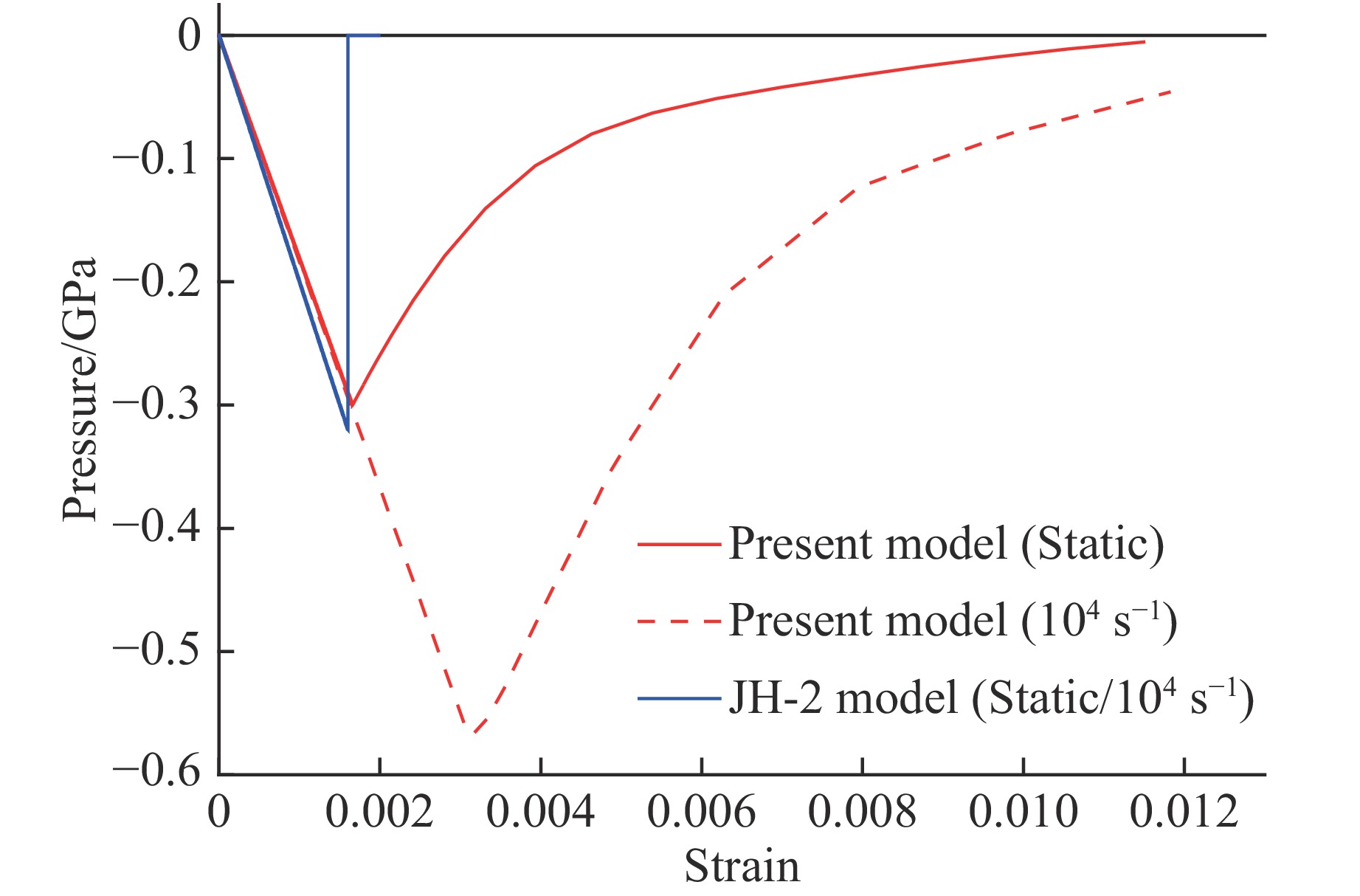
Fig.9 shows numerically predicted relationship between pressure and the maximum principal strain of AlN under both quasi-static triaxial tension. It can be seen from the figure that the present model predicts the elastic-brittle softening response of AlN under triaxial tension with quasi-static principal tensile strength of 0.3 GPa. Whilst the material is no longer able to withstand any loads after the maximum pressure reached according to the JH-2 model predictions. Furthermore, no strain rate effect is found under hydrostatic tension in the JH-2 model since it hasn’t taken into account the strain rate effect in tension.
3. Penetration of AD99.7/RHA Target
Numerical simulations are conducted in this section for the penetration of AD99.7/RHA target struck by flat-nosed projectiles as reported by Lundberg[35]. In the experiments, long tungsten projectiles with length-to-diameter ratio 15 were fired against the unconfined alumina with steel backing. The tests were carried out in three different scales with projectile lengths 30, 75 and 150 mm (corresponding diameters 2, 5 and 10 mm), respectively. The impact velocities were 1 500 m/s and 2 500 m/s. Fig.10 shows the schematic diagrams of the geometric dimensions of the projectile-target combination. Table 4, Table 5 and Table 6 list the values of various parameters for AD99.7 ceramic material in the present model, tungsten alloy and RHA materials in the JC model. Parameters A1 in the JC model is the initial yield strength under reference strain rate and reference temperature; B1, N1 are respectively the strain hardening modulus and index; C1 is strain rate hardening parameter; M1 is temperature softening index;
${\dot \varepsilon _0}$ is the reference strain rate; cp is heat capacity; Tm and Tr are the ambient temperature and the reference temperature (melting point), respectively; D1, D2, D3, D4 and D5 are failure criteria parameters; Cs is the intercept of shock wave velocity-particle velocity (us-up) curve; S1, S2, S3 are us-up curveslope coefficient; γ0 is Grüneisen parameter, A0 is the first order volume correction of γ0.Table 4. Values of various parameters for AD99.7 ceramic[35] (The present model)Equation of state parameters Constitutive model parameters ρc/(kg·m−3) K1/GPa K1/GPa K3/GPa Fm Wx Wy S 3 809 181.5 1 207.9 −2 991 3 3.8 2 1.25 Constitutive model parameters ${f_{{\rm{c}}}'}$/GPa ft/GPa B G/GPa λm λs l r 3 0.3 1.4 135 0.3 7.5 0.8 0.3 Table 5. Values of various parameters for tungsten alloy[35] (JC model)Constitutive model parameters ρc/(kg·m−3) G/GPa A1/GPa B1/GPa N1 C1 M1 ${\dot \varepsilon_{_0}}$/s−1 17 600 122 1.506 0.177 0.12 0.016 1.0 1.0 Constitutive model parameters cp/(J·kg−1·K−1) Tm/K Tr/K D1 D2 D3 D4 D5 134 1 723 300 2.0 0 0 0 0 Equation of state parameters Cs/(m·s−1) S1 S2 S3 γ0 A0 4 029 1.23 0 0 1.54 0.4 Table 6. Values of various parameters for RHA[35] (JC model)Constitutive model parameters ρc/(kg·m−3) G/GPa A1/GPa B1/GPa N1 C1 M1 ${\dot \varepsilon _{_{0}}}$/s−1 7 800 77 0.792 0.51 0.26 0.014 1.03 1.0 Constitutive model parameters cp/(J·kg−1·K−1) Tm/K Tr/K D1 D2 D3 D4 D5 477 1 793 294 0.05 3.44 −2.12 0.002 0.61 Equation of state parameters Cs/(m·s−1) S1 S2 S3 γ0 A0 4 569 1.49 0 0 2.17 0.460 Fig.11 shows the comparison of total penetration depth between the numerical predictions and the experimental data[35]. PT represents the sum of thickness of the ceramic and penetration depth in the RHA back plate, and Lp is the length of the projectile. In the figure, the solid symbols indicate the experimental data and the hollow symbols represent the numerical results by the present model proposed in this paper. The data of different scales under the impact velocity of 1 500 m/s and 2 500 m/s are designated by square and triangle, respectively. For comparison, the numerical results obtained by Lundberg[35] with JH-2 model are also shown in Fig.11. The solid and broken lines represent the numerical results by JH-2 model at 1 500 m/s and 2 500 m/s respectively. It can be seen from Fig.11 that the numerical results from the present model are in good agreement with the experimental data. As can be seen from the figure that the numerical results for impact velocity of 1 500 m/s are in good agreement with the test data, whilst the results for impact velocity of 2 500 m/s are below the experimental observations[35]. Thus, the JH-2 model has failed to produce consistent results as compared to the experiments.
 Figure 11. Comparison between the numerical results and the test data for the depth of penetration in AD99.7/RHA targets by flat-nosed tungsten alloy penetrators[35]
Figure 11. Comparison between the numerical results and the test data for the depth of penetration in AD99.7/RHA targets by flat-nosed tungsten alloy penetrators[35]4. Conclusions
A dynamic macroscopic constitutive model for ceramic materials has been developed by closely following the previous work on concrete. The model captures the basic features of the mechanical response of ceramic materials including pressure hardening behavior, strain rate effects, strain softening behavior, path dependent behavior (Lode angle), and failure in both low and high confining pressures. In particular, a new function is used to characterize the pressure dependent shear strength surface of ceramic materials which levels out at very high pressures, and strain rate effect is taken into consideration by dynamic increase factor which excludes inertial effect.
The present model has been compared with some available experimental data for ceramic materials. It transpires that the present model predictions are in good agreement with the experimental observations in terms of pressure-volumetric response, triaxial compression, quasi-static strength surface, dynamic strength surface, strain rate effect and depth of penetration. It also transpires that the present model is much more improved than the JH-2 model.
-
图 2 (a)Fm
${\overline{3}} $ m-LaH10结构中的H32笼状结构[17],(b)P63/mmc-CeH9结构中的H29笼状结构[44],(c)各二元富氢化物中的最近邻氢原子距离与金属氢中最近邻氢原子距离的比较[44]Figure 2. (a) The H32 cage in Fm
${\overline{3}} $ m-LaH10[17], (b) the H29 cage in P63/mmc-CeH9[44], (c) the evolution of nearest-neighbor H-H distances in polyhydrides and atomic metallic H2 as a function of pressure[44]表 1 3类高Tc氢化物中氢的结构类型、金属的原子半径、电负性、价电子排布、晶体结构对称性以及对应压力点下超导电性的对比[33]
Table 1. Comparison of structural types, atomic radius, electronegativity, electronic configuration, crystal structure symmetry and superconductivity of H in three types of high Tc hydrides[33]
Hydrogenic
motifsHydrides Atomic
radius/ÅElectronegativity Electronic
configurationSpace group Tc/K H3S 1.84 2.58 [Ne] 3s23p4 Im${\overline{3}} $m 204a (200 GPa)[13],
203b (155 GPa)[28]H3Se 1.98 2.55 [Ne] 3d104s24p4 Im${\overline{3}} $m 110a (200 GPa)[52] LaH10 1.88 1.10 [Xe] 5d16s2 Fm${\overline{3}} $m 288a (200 GPa)[18],
250–260b
(170–200 GPa)[31, 30]YH10 1.81 1.22 [Kr] 4d15s2 Fm${\overline{3}} $m 303a (400 GPa)[18] ThH10 1.80 1.30 [Rn] 6d27s2 Fm${\overline{3}} $m 241a (100 GPa)[19],
161b (174 GPa)[32]HfH10 1.56 1.30 [Xe] 4f145d26s2 P63/mmc 234c (250 GPa) ZrH10 1.60 1.33 [Kr] 4d25s2 P63/mmc 220c (250 GPa) ScH10 1.61 1.36 [Ar] 3d14s2 P63/mmc 158c (250 GPa) LuH10 1.73 1.27 [Xe] 4f145d16s2 P63/mmc 152c (200 GPa) Note : (1) The superscript “a” denotes the calculated Tc with fixed $\;\mu ^*$ = 0.1 ($\;\mu ^*$ is the coulomb parameter);
(2) The superscript “b” denotes the experimental Tc in previous work;
(3) The superscript “c” denotes the obtained Tc using G-K equation with $\;\mu ^*$ = 0.1. -
[1] BEDNORZ J G, MÜLLER K A. Possible high Tc superconductivity in the Ba-La-Cu-O system [J]. Zeitschrift für Physik B Condensed Matter, 1986, 64(2): 189–193. doi: 10.1007/BF01303701 [2] GAO L, XUE Y Y, CHEN F, et al. Superconductivity up to 164 K in HgBa2Ca m-1CumO2 m+2+ δ (m = 1, 2, and 3) under quasihydrostatic pressures [J]. Physical Review B, 1994, 50(6): 4260–4263. doi: 10.1103/PhysRevB.50.4260 [3] WU G, XIE Y L, CHEN H, et al. Superconductivity at 56 K in samarium-doped SrFeAsF [J]. Journal of Physics: Condensed Matter, 2009, 21(14): 142203. doi: 10.1088/0953-8984/21/14/142203 [4] WIGNER E, HUNTINGTON H B. On the possibility of a metallic modification of hydrogen [J]. Journal of Chemical Physics, 1935, 3(12): 764–770. doi: 10.1063/1.1749590 [5] BARDEEN J, COOPER L N, SCHRIEFFER J R. Theory of superconductivity [J]. Physical Review, 1957, 108(5): 1175–1204. doi: 10.1103/PhysRev.108.1175 [6] DALLADAY-SIMPSON P, HOWIE R T, GREGORYANZ E. Evidence for a new phase of dense hydrogen above 325 gigapascals [J]. Nature, 2016, 529(7584): 63–67. doi: 10.1038/nature16164 [7] LOUBEYRE P, OCCELLI F, DUMAS P. Synchrotron infrared spectroscopic evidence of the probable transition to metal hydrogen [J]. Nature, 2020, 577(7792): 631–635. doi: 10.1038/s41586-019-1927-3 [8] ASHCROFT N W. Hydrogen dominant metallic alloys: high temperature superconductors? [J]. Physical Review Letters, 2004, 92(18): 187002. doi: 10.1103/PhysRevLett.92.187002 [9] DUAN D F, LIU Y X, MA Y B, et al. Structure and superconductivity of hydrides at high pressures [J]. National Science Review, 2017, 4(1): 121–135. doi: 10.1093/nsr/nww029 [10] DUAN D F, YU H Y, XIE H, et al. Ab initio approach and its impact on superconductivity [J]. Journal of Superconductivity and Novel Magnetism, 2019, 32(1): 53–60. doi: 10.1007/s10948-018-4900-8 [11] EREMETS M I, TROJAN I A, MEDVEDEV S A, et al. Superconductivity in hydrogen dominant materials: silane [J]. Science, 2008, 319(5869): 1506–1509. doi: 10.1126/science.1153282 [12] GONCHARENKO I, EREMETS M I, HANFLAND M, et al. Pressure-induced hydrogen-dominant metallic state in aluminum hydride [J]. Physical Review Letters, 2008, 100(4): 045504. doi: 10.1103/PhysRevLett.100.045504 [13] DUAN D F, LIU Y X, TIAN F B, et al. Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity [J]. Scientific Reports, 2014, 4: 6968. doi: 10.1038/srep06968 [14] DUAN D F, HUANG X L, TIAN F B, et al. Pressure-induced decomposition of solid hydrogen sulfide [J]. Physical Review B, 2015, 91(18): 180502. doi: 10.1103/PhysRevB.91.180502 [15] WANG H, TSE J S, TANAKA K, et al. Superconductive sodalite-like clathrate calcium hydride at high pressures [J]. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109(17): 6463–6466. doi: 10.1073/pnas.1118168109 [16] LI Y W, HAO J, LIU H Y, et al. Pressure-stabilized superconductive yttrium hydrides [J]. Scientific Reports, 2015, 5: 9948. doi: 10.1038/srep09948 [17] LIU H Y, NAUMOV I I, HOFFMANN R, et al. Potential high-Tc superconducting lanthanum and yttrium hydrides at high pressure [J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(27): 6990–6995. doi: 10.1073/pnas.1704505114 [18] PENG F, SUN Y, PICKARD C J, et al. Hydrogen clathrate structures in rare earth hydrides at high pressures: possible route to room-temperature superconductivity [J]. Physical Review Letters, 2017, 119(10): 107001. doi: 10.1103/PhysRevLett.119.107001 [19] KVASHNIN A G, SEMENOK D V, KRUGLOV I A, et al. High-temperature superconductivity in a Th-H system under pressure conditions [J]. ACS Applied Materials & Interfaces, 2018, 10(50): 43809–43816. doi: 10.1021/acsami.8b17100 [20] JIN X L, MENG X, HE Z, et al. Superconducting high-pressure phases of disilane [J]. Proceedings of the National Academy of Sciences of the United States of America, 2010, 107(22): 9969–9973. doi: 10.1073/pnas.1005242107 [21] TROYAN I, GAVRILIUK A, RÜFFER R, et al. Observation of superconductivity in hydrogen sulfide from nuclear resonant scattering [J]. Science, 2016, 351(6279): 1303–1306. doi: 10.1126/science.aac8176 [22] DUAN D F, TIAN F B, LIU Y X, et al. Enhancement of Tc in the atomic phase of iodine-doped hydrogen at high pressures [J]. Physical Chemistry Chemical Physics, 2015, 17(48): 32335–32340. doi: 10.1039/C5CP05218A [23] DUAN D F, HUANG X L, TIAN F B, et al. Predicted formation of H $$ in solid halogen polyhydrides at high pressures [J]. The Journal of Physical Chemistry A, 2015, 119(45): 11059–11065. doi: 10.1021/acs.jpca.5b08183[24] SHAO Z J, HUANG Y P, DUAN D F, et al. Stable structures and superconductivity of an At-H system at high pressure [J]. Physical Chemistry Chemical Physics, 2018, 20(38): 24783–24789. doi: 10.1039/C8CP04317E [25] WANG L Y, DUAN D F, YU H Y, et al. High-pressure formation of cobalt polyhydrides: a first-principle study [J]. Inorganic Chemistry, 2018, 57(1): 181–186. doi: 10.1021/acs.inorgchem.7b02371 [26] SHAO Z J, DUAN D F, MA Y B, et al. Ternary superconducting cophosphorus hydrides stabilized via lithium [J]. NPG Computational Materials, 2019, 5(1): 104. doi: 10.1038/s41524-019-0244-6 [27] SONG H, DUAN D F, CUI T, et al. High-Tc state of lanthanum hydrides [J]. Physical Review B, 2020, 102(1): 014510. doi: 10.1103/PhysRevB.102.014510 [28] DROZDOV A P, EREMETS M I, TROYAN I A, et al. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system [J]. Nature, 2015, 525(7567): 73–76. doi: 10.1038/nature14964 [29] EINAGA M, SAKATA M, ISHIKAWA T, et al. Crystal structure of the superconducting phase of sulfur hydride [J]. Nature Physics, 2016, 12(9): 835–838. doi: 10.1038/nphys3760 [30] SOMAYAZULU M, AHART M, MISHRA A K, et al. Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures [J]. Physical Review Letters, 2019, 122(2): 027001. doi: 10.1103/PhysRevLett.122.027001 [31] DROZDOV A P, KONG P P, MINKOV V S, et al. Superconductivity at 250 K in lanthanum hydride under high pressures [J]. Nature, 2019, 569(7757): 528–531. doi: 10.1038/s41586-019-1201-8 [32] SEMENOK D V, KVASHNIN A G, IVANOVA A G, et al. Superconductivity at 161 K in thorium hydride ThH10: synthesis and properties [J]. Materials Today, 2020, 33: 36–44. doi: 10.1016/j.mattod.2019.10.005 [33] XIE H, YAO Y S, FENG X L, et al. Hydrogen pentagraphenelike structure stabilized by hafnium: a high-temperature conventional superconductor [J]. Physical Review Letters, 2020, 125(21): 217001. doi: 10.1103/PhysRevLett.125.217001 [34] STROBEL T A, GANESH P, SOMAYAZULU M, et al. Novel cooperative interactions and structural ordering in H2S-H2 [J]. Physical Review Letters, 2011, 107(25): 255503. doi: 10.1103/PhysRevLett.107.255503 [35] HUANG X L, WANG X, DUAN D F, et al. High-temperature superconductivity in sulfur hydride evidenced by alternating-current magnetic susceptibility [J]. National Science Review, 2019, 6(4): 713–718. doi: 10.1093/nsr/nwz061 [36] ALEXANDER F, GONCHAROV S S, LOBANOV V B, et al. Stable high-pressure phases in the H-S system determined by chemically reacting hydrogen and sulfur [J]. Physical Review B, 2017, 95(14): 140101. doi: 10.1103/PhysRevB.95.140101 [37] PAPACONSTANTOPOULOS D A, KLEIN B M, MEHL M J, et al. Cubic H3S around 200 GPa: an atomic hydrogen superconductor stabilized by sulfur [J]. Physical Review B, 2015, 91(18): 184511. doi: 10.1103/PhysRevB.91.184511 [38] QUAN Y D, PICKETT W E. Van hove singularities and spectral smearing in high-temperature superconducting H3S [J]. Physical Review B, 2016, 93(10): 104526. doi: 10.1103/PhysRevB.93.104526 [39] HEIL C, BOERI L. Influence of bonding on superconductivity in high-pressure hydrides [J]. Physical Review B, 2015, 92(6): 060508. doi: 10.1103/PhysRevB.92.060508 [40] GE Y F, ZHANG F, YAO Y G. First-principles demonstration of superconductivity at 280 K in hydrogen sulfide with low phosphorus substitution [J]. Physical Review B, 2016, 93(22): 224513. doi: 10.1103/PhysRevB.93.224513 [41] SNIDER E, DASENBROCK-GAMMON N, MCBRIDE R, et al. Room-temperature superconductivity in a carbonaceous sulfur hydride [J]. Nature, 2020, 586(7829): 373–377. doi: 10.1038/s41586-020-2801-z [42] SUN Y, TIAN Y F, JIANG B W, et al. Computational discovery of a dynamically stable cubic SH3-like high-temperature superconductor at 100 GPa via CH4 intercalation [J]. Physical Review B, 2020, 101: 174102. doi: 10.1103/PhysRevB.101.174102 [43] CUI W W, BI T G, SHI J M, et al. Route to high-Tc superconductivity via CH4-intercalated H3S hydride perovskites [J]. Physical Review B, 2020, 101(13): 134504. doi: 10.1103/PhysRevB.101.134504 [44] LI X, HUANG X L, DUAN D F, et al. Polyhydride CeH9 with an atomic-like hydrogen clathrate structure [J]. Nature Communications, 2019, 10(1): 3461. doi: 10.1038/s41467-019-11330-6 [45] ZHOU D, SEMENOK D V, DUAN D F, et al. Superconducting praseodymium superhydrides [J]. Science Advances, 2020, 6(9): eaax6849. doi: 10.1126/sciadv.aax6849 [46] ZHOU D, SEMENOK D V, XIE H, et al. High-pressure synthesis of magnetic neodymium polyhydrides [J]. Journal of the American Chemical Society, 2020, 142(6): 2803–2811. doi: 10.1021/jacs.9b10439 [47] SHAO Z J, DUAN D, MA Y, et al. Unique phase diagram and superconductivity of calcium hydrides at high pressures [J]. Inorganic Chemistry, 2019, 58(4): 2558–2564. doi: 10.1021/acs.inorgchem.8b03165 [48] WU G, HUANG X L, XIE H, et al. Unexpected calcium polyhydride CaH4: a possible route to dissociation of hydrogen molecules [J]. The Journal of Chemical Physics, 2019, 150(4): 044507. doi: 10.1063/1.5053650 [49] PÉPIN C M, GENESTE G, DEWAELE A, et al. Synthesis of FeH5: a layered structure with atomic hydrogen slabs [J]. Science, 2017, 357(6349): 382–385. doi: 10.1126/science.aan0961 [50] ZHONG X, WANG H, ZHANG J R, et al. Tellurium hydrides at high pressures: high-temperature superconductors [J]. Physical Review Letters, 2016, 116(5): 057002. doi: 10.1103/PhysRevLett.116.057002 [51] ZHOU D W, JIN X L, MENG X, et al. Ab initio study revealing a layered structure in hydrogen-rich KH6 under high pressure [J]. Physical Review B, 2012, 86(1): 014118. doi: 10.1103/PhysRevB.86.014118 [52] ZHANG S, WANG Y, ZHANG J, et al. Phase diagram and high-temperature superconductivity of compressed selenium hydrides [J]. Scientific Reports, 2015, 5(3): 1–6. -







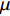

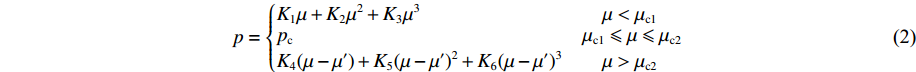
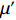

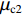
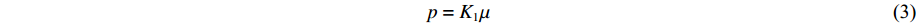

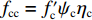
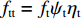
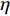

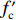
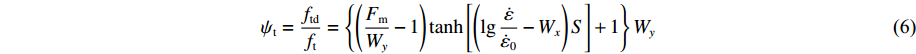
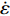
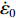
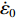
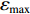
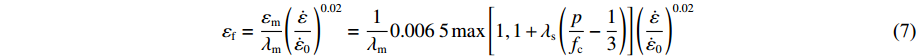
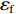
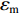
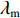

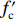
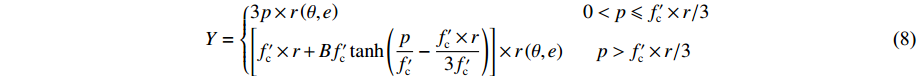

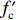
 DownLoad:
DownLoad:
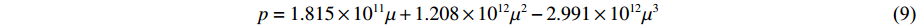


 DownLoad:
DownLoad:






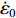






 下载:
下载: