高压下新型双“A”层MAX相V<sub>2</sub>Ga<sub>2</sub>C 的密度泛函理论研究

王腾飞; 李小雷; 李露; 李东; 王军凯

doi:10.11858/gywlxb.20200658

高压下新型双“A”层MAX相V₂Ga₂C 的密度泛函理论研究

doi: 10.11858/gywlxb.20200658

河南理工大学材料科学与工程学院，河南焦作　454003

基金项目: 国家自然科学基金（51001042）；河南省科技攻关计划（212102210589）；省部共建耐火材料与冶金国家重点实验室开放基金（G201904）；河南理工大学博士基金（B2019-40）

详细信息

作者简介:
王腾飞（1996－），男，硕士研究生，主要从事功能陶瓷材料研究. E-mail：212006010027@home.hpu.edu.cn

通讯作者:
李小雷（1968－），男，博士，教授，主要从事功能陶瓷材料和超硬材料研究. E-mail：lixl@hpu.edu.cn

中图分类号: O521.2; O413.1
计量
- 文章访问数: 3723
- HTML全文浏览量: 1628
- PDF下载量: 33
出版历程
- 收稿日期: 2020-12-21
- 修回日期: 2020-12-31

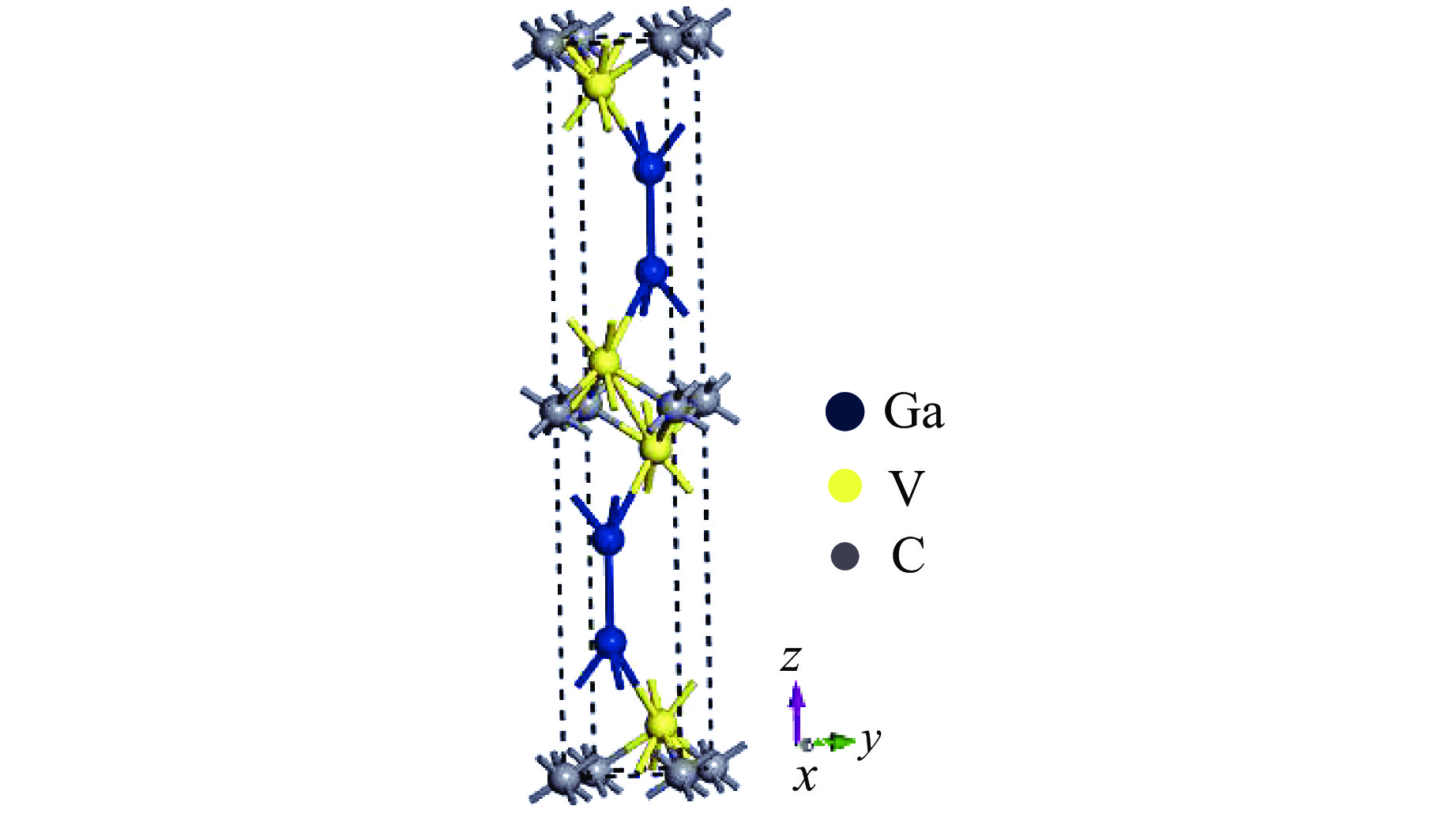
Density Functional Theory of New Double “A” Layer MAX Phase V₂Ga₂C under High Pressure

School of Materials Science and Engineering, Henan Polytechnic University, Jiaozuo 454003, Henan, China

摘要

摘要: 基于密度泛函理论的第一性原理，研究了压强对双“A”层MAX相V₂Ga₂C晶体结构、弹性和电子性质的影响，并利用玻恩稳定准则预测了V₂Ga₂C力学稳定状态下的压强范围。计算结果表明：在0～70 GPa下，V₂Ga₂C的晶体结构处于力学稳定状态；随着压强的增大，V₂Ga₂C的晶格常数和体积均有不同程度的缩小，a轴随压强的增大收缩得最快，晶胞体积收缩了24%左右；随着压强的增加，V₂Ga₂C材料的维氏硬度从0 GPa压强下的18.23 GPa减小为70 GPa压强下的2.30 GPa，在20.15 GPa时从脆性材料转变为韧性材料；V₂Ga₂C的态密度和能带结构等电子性质随压强的变化较小，即压强对V₂Ga₂C的电子性质影响不大。
- MAX相 /
- V₂Ga₂C /
- 高压 /
- 力学稳定性 /
- 弹性性质 /
- 电子性质
Abstract: The structural, elastic and electronic properties of double “A” layer MAX phase V₂Ga₂C under high pressure were studied by the first-principles calculations of density functional theory, and the stable state of V₂Ga₂C was predicted by using the Born stability criteria. The results show that V₂Ga₂C crystal structure at the state of mechanical stability within the pressure range of 0–70 GPa. With the increase of pressure, the lattice parameters and volumes of V₂Ga₂C decreased. V₂Ga₂C is more compressible in the a-axis direction than c-axis direction, and the volume shrinks by about 24%. With increasing pressure, Vickers hardness of V₂Ga₂C material decreased from 18.23 GPa (0 GPa) to 2.30 GPa (70 GPa), and from brittle material transform into ductile material at 20.15 GPa. With the change of pressure, the electronic properties have changed slightly such as density of states and band structures, which have almost no effect on the electronic properties of V₂Ga₂C.
- MAX phase /
- V₂Ga₂C /
- high pressure /
- mechanical stability /
- elastic property /
- electronic property

HTML全文

月球在形成或演化过程中经历了一个或一系列灾难性热事件，导致大部分挥发分丢失^[1]，其中最轻的元素氢在形成月球的大撞击事件中几乎完全丢失(H₂O的质量分数≤10^-9)^[2-3]。然而，随着原位分析技术(如二次离子探针、傅里叶转换红外光谱等)的分析精度和检出限等能力的提高，近年来人们在来自月球深部的返回样品(火山玻璃、磷灰石、橄榄石熔体包裹体等)中发现了大量的水(质量分数达4×10^-6~7.5×10^-3)^[4-14]。例如：采用二次离子探针技术，Saal等^[4]测得月球火山玻璃中水含量(质量分数)为4×10^-6~4.6×10^-5，推测去气作用前原始玄武质岩浆中的水含量约为7.45×10^-4；Boyce等^[5]测得月球玄武岩14053中磷灰石的水含量为0.16%~0.24%，基于结晶模型推测其母岩浆中的水含量为0.01%~0.02%；采用纳米离子探针技术，Hauri等^[8]测得橄榄石熔体包裹体中水含量为6.15×10^-4~1.41×10^-3，推测原始月幔中水含量为7.9×10^-5~4.09×10^-4。

来自月球深部的返回样品可能经历了复杂的地质过程，在利用这些样品推算月幔原始岩浆的水含量时需要特别小心。例如，火山玻璃样品在上升过程中经历了极强烈的脱水过程(95%~98%的水在此期间丢失)^[4]，利用火山玻璃中的水含量反推原始岩浆的水含量时，严重依赖岩浆来源深度、岩浆上升速率、矿物-熔体之间的配分系数等，而人们对月球内部岩浆上升模型仍未有准确限定。Saal等^[4]所建立的模型只考虑了岩浆喷发前的去气作用，忽略了在玻璃形成和生长阶段的去气作用。月球玄武岩中的磷灰石是岩浆结晶分异的产物，准确估算喷发前玄武质岩浆的水含量需要确定水在磷灰石-硅酸盐熔体之间的配分系数。遗憾的是，由于对月幔熔融硅酸盐组分的约束甚少，Boyce等^[5]只能采用水在磷灰石-玄武岩熔体之间的配分系数粗略估算深部水含量。

熔体包裹体是被封存在矿物中的原始岩浆珠滴，是反映原始岩浆信息最直接的"见证人"^[15]。由于熔体被其宿主矿物所包裹，人们常认为熔体包裹体是封闭体系。然而事实上橄榄石熔体包裹体极易与围岩岩浆发生物质交换^[16-18]，如Portnyagin等^[16]将几乎无水的橄榄石熔体包裹体置于富水环境(200 MPa，1 140 ℃)仅两天时，通过橄榄石扩散进入熔体包裹体的水的质量分数高达2.5%；火星陨石GRV 020090中橄榄石熔体包裹体核部水含量(1.7×10^-4)远低于边部(5.337×10^-3)，这也是由于水通过橄榄石扩散进入熔体包裹体造成的^[18]。因此，准确限定月幔条件下水在橄榄石中的扩散速率，将有助于更加可靠地通过橄榄石熔体包裹体限定月幔原始岩浆的水含量。

目前，含水橄榄石研究主要集中在橄榄石中水对熔融温度、电导率、板块运动等的影响^[19-21]，而对于月幔条件下水在橄榄石中的高压扩散缺乏系统研究。本工作旨在利用高温高压实验技术，开展不同月幔氧逸度、压力和温度条件下水在橄榄石中的扩散研究，为准确理解月球深部水提供热力学基础数据。

1. 实验与分析方法

1.1 高温高压扩散实验

实验初始样品为辽宁蛟河橄榄石(内部无明显裂隙或包裹体)。首先，利用中国科学院地质与地球物理研究所的日本电子JXA-8100型电子探针对橄榄石的化学成分进行测量(电子束斑直径约5 μm，加速电压15 kV，电子束流20 nA，平均计数时间20 s)，确定橄榄石的化学组成为(Mg_0.9Fe_0.1)₂SiO₄。然后，采用电子背散射衍射(Electron Backscatter Diffraction，EBSD)技术对晶体进行准确定向。该实验在北京大学造山带与地壳演化教育部重点实验室的场发射扫描电镜(FEI-Quanta650FEG)能谱与电子背散射衍射系统(Oxford-EDS+EBSD)上开展(倾斜角度70°，工作距离15~25 mm，加速电压20 kV，电子束流5.5 nA)，利用HKL Channel 5 Oxford Instruments软件对实验数据进行处理。之后使用划片切割机对样品进行定向切割，并用金刚石研磨膏将样品抛光(至表面粗糙度0.5 μm)，抛光后橄榄石的晶体尺寸见表 1。最后，在日本冈山大学气体混合炉KANHTAL1760中对样品进行退火处理，以干燥样品，并使晶体结构中的点缺陷浓度接近高温高压实验中的浓度水平^[22]。为了防止高温下Fe²⁺被氧化成Fe³⁺，在密闭的高温炉中通入Ar+1%H₂混合气体，退火温度为1 200 ℃，退火时间为12 h。为检验退火后样品中的Fe²⁺是否被氧化成Fe³⁺，对样品开展穆斯堡尔谱分析(放射源为⁵⁷Co，强度为0.925×10⁸ Bq，测试温度为293 K，用α-Fe箔做多普勒速度标定)，如图 1所示。结果显示，样品中的铁为二价，并未发生高温氧化。此外，利用红外光谱仪测得橄榄石样品的初始水含量几乎为零。

表 1 水在橄榄石中扩散的实验条件及样品尺寸

Table 1. Experimental conditions of water diffusion in olivine and crystal sizes of samples

Sample	Pressure/GPa	Temperature/℃	Duration/h	Buffer	Capsule	Size before hydration[100]×[010]×[001]/(mm×mm×mm)	Size for FTIR measurement[100]×[010]×[001]/(mm×mm×mm)
Ol-5-3	1.5	900	5	NNO	Ni	2.90×1.80×1.64	2.90×0.30^*×1.64
Ol-7-1	2.5	900	5	NNO	Ni	2.44×2.10×2.09	2.44×0.36^*×2.09
Ol-7-2	3.0	900	5	NNO	Ni	1.86×2.08×2.41	1.86×0.21^*×2.41
No.1-2	2.5	900	5	IW	Fe	2.42×2.47×1.65	2.42×0.22^*×1.65
No.2-3	2.5	1 050	2/3	IW	Fe	1.87×2.08×2.44	1.87×0.16^*×2.44
No.1-3	2.5	1 200	1/3	IW	Fe	2.31×2.33×1.75	2.31×0.33^*×1.75
Note: The asterisk symbols represent sample thickness; NNO and IW stand for nickel-nickel oxide and iron-wüstite, respectively.

下载: 导出CSV

| 显示表格

图 1 退火后橄榄石的穆斯堡尔谱(293 K)

Figure 1. Mössbauer spectrum of olivine recovered from annealing experiment (293 K)

下载: 全尺寸图片幻灯片

扩散实验在中国科学院地质与地球物理研究所高压实验室的Mavo Press LPC 250-300/50活塞圆筒压机上开展。实验温度为900~1 200 ℃，压力为1.5~3.0 GPa，共完成6次实验。实验采用1/2英寸样品组装，用Ni管或Fe管作为样品仓分别模拟氧化和还原环境。样品仓直径为5 mm，高10 mm。在样品仓底部铺一层NiO或FeO粉末，将定向切割的晶体放入样品仓中，周围填满橄榄石粉末(粒度≤5 μm)，并加入过量的蒸馏水(见图 2)。氧逸度(f_O₂)采用O'Neill等^[23-24]的计算公式进行计算(见表 2)。利用S型热电偶(Pt_0.9Rh_0.1-Pt)测温，测温点位于样品仓顶端，样品仓内的最大温差小于25 ℃^[25]。实验的降温速率为150~200 ℃/min，快速降温有利于防止羟基缺陷作为流体包裹体析出以及次生含水相形成^[26]。为了降低快速降压对样品完整性的影响，压力在几小时内卸载完成。尽管如此，部分实验样品依然发生破碎。

图 2 实验组装示意

Figure 2. Schematic illustration of experimental assembly

下载: 全尺寸图片幻灯片

表 2 水沿橄榄石各晶轴的扩散速率

Table 2. Diffusion coefficients of water along each axis in olivines

Sample	Pressure/GPa	Temperature/℃	lg f_O₂	Duration/h	C₀/10^-5	D_[100]/(10^-12 m²·s^-1)	D_[001]/(10^-12 m²·s^-1)
Ol-5-3	1.5	900	-12.0	5	2.7	2.15	0.35
Ol-7-1	2.5	900	-12.0	5	6.0	2.35	0.26
Ol-7-2	3.0	900	-12.0	5	7.1	0.70	0.40
No.1-2	2.5	900	-16.7	5	10.3	0.31	0.16
No.2-3	2.5	1 050	-14.1	2/3	13.1	ND	3.50
No.1-3	2.5	1 200	-11.9	1/3	12.5	8.50	6.75
Note: (1) lg f_O₂ was calculated using O'Neill's equation^[23] for NNO and O'Neill and Pownceby's equation^[24] for IW; (2) ND means "not detected", and D_[010] in all samples were not detected.

下载: 导出CSV

| 显示表格

实验结束后将样品仓切开，置于110 ℃干燥箱中12 h，质量明显减少(通常有1~20 mg的差异)，表明实验过程中水是过量的。每个回收样品仓中的氧化还原缓冲对依然存在，保证实验在限定的氧化还原条件下进行。利用金刚石研磨膏对回收的橄榄石晶体进行双面抛光(至表面粗糙度0.5 μm)，将其置于丙酮溶液中浸泡24 h，彻底清除表面污染。开展傅里叶转换红外(Fourier Transform Infrared，FTIR)光谱测量的橄榄石样品尺寸列于表 1。

1.2 傅里叶转换红外光谱

利用中国科学院地质与地球物理研究所的Bruker Vertex 70 V红外光谱仪，在透射模式下对样品中的羟基进行非偏振红外光谱测量。仪器配有MCT(Mercury Cadmium Telluride)探测器和一台红外显微镜(Bruker Hyperion 2000)。采用硅碳棒光源和KBr分束器产生非偏振红外辐射。扩散剖面沿样品中心进行测量，玻璃刀口光栅产生尺寸为280 μm×200 μm的矩形光束，步长为40~50 μm，扫描次数为512，分辨率为8 cm^-1，测量波段为3 000~4 000 cm^-1，每个剖面在测量前都进行一次背景测量，以扣除背景干扰。所有红外光谱都进行了背景扣除、基线校正以及归一化处理(1 cm)。对于非偏振红外光谱，采用Paterson^[27]的方法计算水含量(C_OH，即质量分数)，即

${C_{{\rm{OH}}}} = \frac{{{\chi _i}}}{{150\xi }}\int {\frac{{k\left( \nu \right)}}{{3780 - \nu }}} {\rm{d}}\nu$

(1)

式中：χ_i为矿物i的密度因子，对于含铁的橄榄石，χ_Ol=2.695×10^-3；ξ为取向因子；k(ν)为厚度归一化后每个波数的吸光度；积分区域为3 610~3 150 cm^-1。对于非偏振红外分析(未定向样品)，ξ=1/3；对于非偏振光源下定向后的[100]-[001]平面，ξ=1/2；对于偏振光源下定向后的晶体，ξ=1。本实验计算所得C_OH的相对误差约为15%。

1.3 扩散分析

扩散速率由水含量和扩散距离计算得到。本研究中所有实验均在水不完全饱和的条件下开展。当样品中心的C_OH不超过溶解度的10%时，样品的扩散剖面可以利用菲克第二定律计算

${C_{{\rm{OH}}}}\left( x \right) = {C_0}\left( {{\rm{erfc}}\frac{x}{{2\sqrt {{D_i}t} }} + {\rm{erfc}}\frac{{X - x}}{{2\sqrt {{D_i}t} }}} \right)$

(2)

式中：C_OH(x)为距样品某边缘x处的水含量，x的单位为m；X为样品宽度，单位m；t为时间，单位s；erfc(x)为余误差函数；C₀为样品边缘处的水含量，即最大水含量；D_i为实验条件下平行于i(i=[100]，[010]，[001])轴的扩散速率，单位m²/s。在测量扩散剖面时，应尽量减少不同方向扩散的重叠影响。因此，当测量某一个方向上的扩散数据时，通常沿样品中心进行。

计算得到的扩散速率代表化学扩散速率D_exch，根据Kohlstedt等^[28]的计算公式，得到氧化还原机制下的化学扩散速率D_exch，即

${D_{{\rm{exch}}}} = 2{D_{\rm{p}}}{D_{\rm{H}}}/\left( {{D_{\rm{p}}} + {D_{\rm{H}}}} \right)$

(3)

式中：D_p为极化子扩散速率，D_H为氢离子扩散速率。由于D_p＞＞D_H，则

${D_{{\rm{exch}}}} \approx 2{D_{\rm{H}}}$

(4)

需要指出的是，前人将水在橄榄石中的扩散机制分为氧化还原机制和空位缺陷机制^{[22, 26, 28-30]}。本实验条件满足氧化还原机制，因此本研究仅在氧化还原机制下讨论。

2. 实验结果

2.1 红外光谱

由于本扩散实验回收的橄榄石晶体大都平行于(100)面破裂，因此只得到沿[100]和[001]两个轴扩散的非偏振红外实验数据。图 3为回收样品的非偏振红外光谱。扩散进入橄榄石中的水以羟基(质子H与硅酸盐骨干中的O原子结合)为主要存在形式(以下涉及的水代指H)。羟基的红外吸收峰分为两组：较高波数的Group Ⅰ (3 450~3 620 cm^-1)和较低波数的Group Ⅱ (3 200~3 450 cm^-1)^[31]。这两组峰对应4种主要的OH结合机制。(1) Group Ⅰ：Si空位([SiO₄]^4-↔[(OH)₄]^4-)，吸收峰主要位于3 613、3 580、3 566、3 555和3 480 cm^-1；Ti⁴⁺相关(M²⁺+Si⁴⁺↔Ti⁴⁺+2H⁺)，吸收峰主要位于3 572和3 525 cm^-1。(2) Group Ⅱ：M空位(M为橄榄石晶体结构中的阳离子Mg²⁺、Fe²⁺等，M²⁺↔2H⁺)，吸收峰主要位于3 160和3 220 cm^-1；Me³⁺相关(Fe³⁺、Al³⁺等，Me³⁺+H⁺↔2Mg²⁺)，吸收峰主要位于3 300~3 400 cm^-1^{[29-30, 32-41]}。本实验测得羟基的吸收峰主要位于3 610、3 599、3 572、3 568、3 502、3 444、3 417、3 356和3 329 cm^-1，对应的羟基的结合机制如表 3所示。

图 3 橄榄石[100]轴边缘处非偏振红外光谱(所有光谱都进行了归一化处理)

Figure 3. Unpolarized IR spectra of olivines (at the rim) along [100] axis (All the spectra are normalized to 1 cm of thickness)

下载: 全尺寸图片幻灯片

表 3 回收橄榄石样品中的红外羟基波数和羟基结合机制

Table 3. Hydroxyl band positions in all recovered olivines and hydroxyl incorporation mechanisms

Hydroxyl band positions/cm^-1						Band assignments
Ol-5-3	Ol-7-1	Ol-7-2	No.1-2	No.2-3	No.1-3	Band assignments
3 182						M site
3 197	3 224					M site
3 232						M site
3 263	3 263
3 329			3 329		3 321	Me³⁺ site
3 356	3 356	3 352	3 352	3 356	3 344	Me³⁺ site
	3402	3 398	3 390	3 394		Ti⁴⁺
3 417	3 421	3 425	3 410	3 410
			3 433
3 448	3 456	3 452	3 452	3 444		Si site
3 487	3 483		3 475	3 479	3 475
3 502			3 494	3 506
	3 510		3 514
3 525				3 521		Ti⁴⁺
				3 545
	3 568	3 568	3 556	3 568	3 560	Si site
3 572			3 575			Ti⁴⁺
					3 591
			3 599	3 599	3 602
				3 610		Si site
3 629

下载: 导出CSV

| 显示表格

2.2 扩散剖面

沿橄榄石晶体[100]轴测量的非偏振红外光谱如图 4所示，可见羟基在边缘处的红外吸收最强，向中心逐渐降低。利用扩散定律对橄榄石晶体沿不同轴向的红外数据进行拟合(见图 5)，可以看出绝大部分实验数据能够被扩散定律较好地拟合，只有边缘位置的少量数据点落在拟合线之外，可能是淬火导致边缘出现微小裂隙造成的。扩散过程中的活化能由阿伦尼乌斯方程计算得到，即

${D_i} = {D_{i0}}\exp \left( { - {Q_i}/RT} \right)$

(5)

图 4 Ol-5-3橄榄石晶体中平行[100]轴的非偏振红外光谱(900 ℃、1.5 GPa、5 h、NNO；主要的羟基峰位于3 610、3 599、3 572、3 568、3 502、3 444、3 417、3 356和3 329 cm^-1；所有光谱都进行了归一化处理)

Figure 4. Unpolarized infrared spectra as a function of wavenumber and position along the [100] axis in sample Ol-5-3 (900 ℃, 1.5 GPa, 5 h, NNO.The major hydroxyl absorption bands are located at 3 610, 3 599, 3 572, 3 568, 3 502, 3 444, 3 417, 3 356 and 3 329 cm^-1.All the spectra are normalized to 1 cm of thickness.)

下载: 全尺寸图片幻灯片

图 5 Ol-7-1橄榄石晶体(2.5 GPa、900 ℃、NNO、样品尺寸2.44 mm×0.36 mm×2.09 mm)中水沿[100]和[001]轴的扩散剖面(相应的化学扩散速率标记在图中，黑色圆点为实验数据，实线为根据扩散定律拟合的扩散剖面)

Figure 5. Hydroxyl content as a function of position parallel to [100] and [001] crystallographic axes in sample Ol-7-1 (2.5 GPa, 900 ℃, 5 h, buffered by NNO, size 2.44 mm×0.36 mm×2.09 mm.Diffusion coefficients are shown in each plot.Black points are IR data, and the solid lines are fitted diffusion profiles.)

下载: 全尺寸图片幻灯片

式中：D_i0为指前因子；Q_i为扩散的活化能；R为摩尔气体常数，R=8.314 J/(mol·K)；T为温度，单位K。根据(5)式计算得到本实验在2.5 GPa压力下平行于橄榄石晶体[100]轴的活化能和指前因子分别为159.45 kJ/mol和10^-5.12 m²/s，平行于[001]轴的活化能和指前因子分别为182.94 kJ/mol和10^-4.22 m²/s，与前人报道的结果(平行[100]轴和平行[001]轴的活化能分别为145~210 kJ/mol和110~258 kJ/mol；平行[100]轴和平行[001]轴的指前因子分别为10^-1.4~10^-5 m²/s和10^-3.3~10^-6m²/s)一致^{[22, 26, 28, 42-43]}。

3. 讨论

3.1 氧逸度对扩散速率的影响

如前所述，月幔(温度、压力、氧逸度)条件下水在橄榄石中的扩散研究极为匮乏，而且现有低压实验数据存在较大争议。Mackwell等^[26]在1 000 ℃、0.3 GPa条件下分别以NNO和IW为氧化还原缓冲对得到水沿橄榄石[100]晶向的扩散速率，分别为D_[100](NNO)=(2±1)×10^-10 m²/s，D_[100](IW)=(4±1)×10^-10 m²/s，表明在高氧逸度条件下水在橄榄石中的扩散比低氧逸度条件下稍慢些。然而，Demouchy等^[43]利用相同的氧化还原缓冲对在1 000 ℃、1.5 GPa条件下得到水沿[100]晶向的扩散速率，分别为D_[100](NNO)=(7±0.2)×10^-13 m²/s，D_[100](IW)=(4±1)×10^-13 m²/s，沿[010]晶向的扩散速率，分别为D_[010](NNO)=D_[010](IW)=(3±0.2)×10^-13 m²/s，与Mackwell等^[26]的结论相反。

本实验选用NNO和IW两种氧化还原缓冲对对氧逸度加以限制，得到在2.5 GPa、900 ℃条件下水沿橄榄石[100]和[001]晶向的扩散速率：D_[100](NNO)=2.35×10^-12 m²/s，D_[001](NNO)=0.26×10^-12 m²/s；D_[100](IW)=0.305×10^-12 m²/s，D_[001](IW)=0.16×10^-12 m²/s。实验结果表明，氧逸度越高，水在橄榄石中的扩散速率越大，与Demouchy等^[43]的结论一致。

3.2 压力对扩散速率的影响

在氧化还原机制下，前人针对水在橄榄石中扩散的研究仅有压力为0.3 GPa时的数据^{[26, 28]}。Mackwell等^{[26, 28]}的数据显示，氧化还原机制下沿[100]轴的扩散速率明显大于[001]轴。本研究结果也支持这一结论。此外，本研究的高压数据表明，随着压力的升高，沿不同晶轴的扩散速率降低，且[100]和[001]两轴的扩散速率差异变小，即水在橄榄石中扩散的各向异性减弱(见图 6)。

图 6 水沿橄榄石[100]和[001]轴的扩散速率与压力的关系

Figure 6. Diffusion coefficients along [100] and [001] axes as a function of pressure in olivines

下载: 全尺寸图片幻灯片

3.3 温度对扩散速率的影响

Mackwell等^{[26, 28]}发现在压力为0.3 GPa、氧化还原缓冲对为IW的条件下温度具有促进扩散的作用，即随着温度升高，沿各晶轴的扩散速率均增大。本实验的高压(2.5 GPa)数据也支持温度促进扩散这一结论(见图 7)。此外，从图 7可以看出，除了Kohlstedt等^[28]报道的[001]轴扩散速率受温度的影响较小以外，其余数据均有相似的lg D-10⁴T^-1斜率。由于压力越高，扩散越慢，因此本实验的高压(2.5 GPa)数据远小于前人在0.3 GPa压力条件下得到的数据。

图 7 水沿橄榄石[100]、[010]、[001]轴的扩散速率与温度的关系

Figure 7. Diffusion coefficients along [100], [010] and [001] axes as a function of temperature in olivines

下载: 全尺寸图片幻灯片

3.4 月幔深部水的指示意义

月幔占月球绝大部分的体积和质量^[44-46]，根据前人所建立的模型，月幔的温度和压力范围为500~1 120 ℃、0.4~4.3 GPa^[47-48]。本研究选取的实验条件为900~1 200 ℃、1.5~3.0 GPa，基本覆盖月幔的温度和压力变化范围。本研究结果表明，即使在未完全饱和条件下，橄榄石中的水含量也达到10^-4以上(如No.2-3橄榄石中，C₀=1.31×10^-4)。高温高压模拟实验和遥感数据均证实橄榄石是月幔最主要的组成矿物^[49-55]，因此橄榄石可能是月球深部水的重要储库。

熔体包裹体通常被认为是封闭体系，因此人们常利用橄榄石熔体包裹体中的水含量反演行星深部水含量^{[8, 13]}。事实上，包裹体从深部到达月表需要经历岩浆运移和快速喷发两个过程。目前研究认为，月球深部相对还原(IW-1)^[56]，包裹体在岩浆房中的移动非常缓慢，蒙伟娟等^[57]通过模拟得到地幔柱上升速度为0.47~2.75 m/a。地震波数据显示，在月球500 km深度存在月震波速不连续面^[58]，此深度或许代表了月球岩浆房最深位置。基于以上前提，本实验数据表明，在500 km不连续界面的温度压力条件下，水从直径为0.5~1 mm、含有熔体包裹体的橄榄石晶体^[16]中沿轴向完全扩散出去的时间(在1 200 ℃、2.5 GPa条件下，沿[100]轴为8~33 h，沿[001]轴为10~42 h)远远小于岩浆从该处运移至月表的时间(以百万年计)。因此，在岩浆运移过程中，橄榄石熔体包裹体中的水能够与外界熔体达到充分平衡，此时熔体包裹体中的水含量与深部熔体无异。

在岩浆喷发过程中，假设喷发深度为50 km(月壳厚度)，岩浆上升速度为0.1~6 m/s^{[22, 59-60]}，熔体包裹体需要2 h~6 d到达月表。熔体中的水在此过程中不断丢失，产生一定的浓度梯度，使得橄榄石熔体包裹体中的水发生扩散。在喷发条件下，水同样从直径为0.5~1 mm、含有熔体包裹体的橄榄石中沿轴向完全扩散出去的时间极短(在1 000 ℃、0.3 GPa条件下，沿[100]轴为20~82 min，沿[001]轴为14~57 h)，在此过程中包裹体中的水可能拥有足够时间因扩散作用而丢失。因此，Hauri等^[8]测得的橄榄石熔体包裹体的水含量(6.15×10^-4~1.41×10^-3)很可能是下限值。

4. 结论

在本实验的温度和压力(900~1 200 ℃，1.5~3.0 GPa)条件下，得到以下结论：

(1) 水在橄榄石中的扩散行为表现出各向异性，即沿[100]轴的扩散速率较高，沿[001]轴的扩散速率较低；

(2) 在相同温压条件下，在氧逸度较高的环境下水在橄榄石中的扩散速率相对于氧逸度较低的环境下高；

(3) 水在橄榄石中的扩散速率与压力呈负相关，且随着压力的升高，水在橄榄石中沿不同晶轴的扩散速率差异减小，即各向异性减弱；

(4) 随着温度的升高，水沿着橄榄石各晶轴的扩散速率均增大；

(5) 橄榄石可能是月球深部水的重要储库；

(6) 岩浆喷发过程中，水因扩散作用丢失，由此推测前人根据橄榄石熔体包裹体所测得的水含量很可能仅是下限值。

根据中国探月计划三期，"嫦娥五号"将于2017年底实现月球采样返回，中国将成为世界上第3个能返回月球样品的国家。届时科学家们将对珍贵的月球样品开展多方位的全面分析，尽可能挖掘其中蕴含的宝贵信息。扩散速率等热动力学参数是理解月球深部挥发分演化的物理基础，橄榄石熔体包裹体是携带深部信息的重要载体，然而在根据它限定原始岩浆中水及其他挥发分含量时需要非常谨慎，本研究为准确推演月球演化历史提供基础科学依据。

图 1 V₂Ga₂C的晶体结构

Figure 1. Crystal structure of V₂Ga₂C

下载: 全尺寸图片幻灯片

图 2 V₂Ga₂C的相对晶格参数和相对体积随压强的变化

Figure 2. Pressure dependence of relative lattice parameters and relative unit cell volume for V₂Ga₂C

下载: 全尺寸图片幻灯片

图 3 压强与B_H/G_H之间的关系

Figure 3. Pressure dependence of B_H/G_H

下载: 全尺寸图片幻灯片

图 4 V₂Ga₂C材料的维氏硬度随压强的变化

Figure 4. Pressure dependence of Vickers hardness for V₂Ga₂C

下载: 全尺寸图片幻灯片

图 5 不同压强下V₂Ga₂C的能带结构

Figure 5. Pressure dependence of electronic band structures for V₂Ga₂C

下载: 全尺寸图片幻灯片

图 6 不同压强下V₂Ga₂C的总态密度

Figure 6. Pressure dependence of total state density for V₂Ga₂C

下载: 全尺寸图片幻灯片

表 1 不同压强下V₂Ga₂C的弹性常数

Table 1. Pressure dependences of elastic constants for V₂Ga₂C

Pressure/GPa	C₁₁/GPa	C₃₃/GPa	C₄₄/GPa	C₁₂/GPa	C₁₃/GPa
0	275.07	309.04	88.92	65.69	48.31
10	325.89	437.85	103.70	79.38	101.23
20	392.18	492.57	112.70	113.70	122.66
30	475.27	582.90	99.80	176.94	174.81
40	462.17	636.80	103.00	156.69	180.10
50	524.87	696.25	51.41	228.45	221.66
60	558.67	743.34	29.53	220.05	219.34
70	640.36	854.90	4.53	280.99	275.36
80	618.66	892.67	−84.84	305.13	305.24

下载: 导出CSV

参考文献(19)

[1]	WAI-YIM C, YUXIANG M, ARYAL S, et al. Intrinsic mechanical properties of 20 MAX-phase compounds [J]. Journal of the American Ceramic Society, 2013, 96(7): 2292–2297. doi: 10.1111/jace.12376
[2]	BARSOUM M W. The M_N+1AX_N phases: a new class of solids [J]. Progress in Solid State Chemistry, 2000, 28(1/2/3/4): 201–281. doi: 10.1016/S0079-6786(00)00006-6
[3]	BARSOUM M W, BRODKIN D, EL-RAGHY T. Layered machinable ceramics for high temperature applications [J]. Scripta Materialia, 1997, 36(5): 535–541. doi: 10.1016/S1359-6462(96)00418-6
[4]	SONG G M, LI S B, ZHAO C X, et al. Ultra-high temperature ablation behavior of Ti₂AlC ceramics under an oxyacetylene flame [J]. Journal of the European Ceramic Society, 2011, 31(5): 855–862. doi: 10.1016/j.jeurceramsoc.2010.11.035
[5]	JIAO Z Y, MA S H, WANG T X. High-pressure phase stability, mechanical properties and bonding characteristics of Ti₄GeC₃ compound [J]. Solid State Sciences, 2015, 39: 97–104. doi: 10.1016/j.solidstatesciences.2014.12.003
[6]	HOPFELD M, GRIESELER R, VOGEL A, et al. Tribological behavior of selected M_n+1AX_n phase thin films on silicon substrates [J]. Surface and Coatings Technology, 2014, 257: 286–294.
[7]	HU C F, LAI C C, TAO Q, et al. Mo₂Ga₂C: a new ternary nanolaminated carbide [J]. Chemical Communications, 2015, 51(30): 6560–6563. doi: 10.1039/C5CC00980D
[8]	THORE A, DAHLQVIST M, ALLING B, et al. Phase stability of the nanolaminates V₂Ga₂C and (Mo_{1- x}V_x)₂Ga₂C from first-principles calculations [J]. Physical of Materials Science, 2016, 51(18): 12682–12688.
[9]	FASHANDI H, LAI C C, DAHLPVIST M, et al. Ti₂Au₂C and Ti₃Au₂C₂ formed by soild state reaction of gold with Ti₂AlC and Ti₃AlC₂ [J]. Chemical Communications, 2017, 53(69): 9554–9557. doi: 10.1039/C7CC04701K
[10]	THORE A, DAHLQVIST M, ALLING B, et al. Temperature dependent phase stability of nanolaminated ternaries from first-principles calculations [J]. Computational Materials Science, 2014, 91(2): 251–257.
[11]	金森, 周爱国, 胡前库, 等. 三元碳化物Mo₂Ga₂C及其二维衍生物的研究进展 [J]. 硅酸盐通报, 2020, 39(3): 866–872. JIN S, ZHOU A G, HU Q K, et al. Progress in ternary carbide Mo₂Ga₂C and its two-dimensional derivatives [J]. Bulletin of the Chinese Ceramic Society, 2020, 39(3): 866–872.
[12]	CLARK S J, SEGALL M D, PICKARD C J, et al. First principles methods using CASTEP [J]. Zeitschrift für Kristallographie-Crystalline Materials, 2005, 220(5): 567–570.
[13]	SEGALL M D, LINDAN P J D, PROBERT M J, et al. First-principles simulation: ideas, illustrations and the CASTEP code [J]. Journal of Physics Condensed Matter, 2002, 14(11): 2717–2744. doi: 10.1088/0953-8984/14/11/301
[14]	CHEN Z Y, ALBRIGHT P C, SENGERS J V. Crossover from singular critical to regular classical thermodynanic behavior of fluids [J]. Physical Review A, 1990, 41(6): 3161–3177. doi: 10.1103/PhysRevA.41.3161
[15]	PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865. doi: 10.1103/PhysRevLett.77.3865
[16]	KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Physical Review B, 1999, 59(3): 1758–1775. doi: 10.1103/PhysRevB.59.1758
[17]	PUGH S F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals [J]. Philosophical Magazine, 1954, 45(367): 823–843.
[18]	HUANG X, NAUMOV I I, RABE K M. Phonon anomalies and elastic constants of cubic NiAl from first principles [J]. Physical Review B, 2004, 70(6): 064301.
[19]	HILL R. The elastic behaviour of a crystalline aggregate [J]. Proceedings of the Physical Society, 1952, 65(5): 349–354. doi: 10.1088/0370-1298/65/5/307