Space Conversion Model of Peak Overpressure in Near-Earth Air Blast Shockwave with Cylindrical Charge
-
摘要: 为研究近地空爆冲击波峰值超压空间数值关系，基于镜像法、角等分和超压归一化思想，确定了冲击波空间传播界线，建立了混合流场中超压的理论计算方法。首先，利用三波点轨迹与爆高水平线交点、虚拟爆源、真实爆心三者连线构成的几何约束以及马赫反射终点条件，确定了冲击波流场分布界限。其次，等分测点角度，并基于超压归一化值分段线性假设构建归一化值方程。然后将归一化值方程扩展为圆柱装药长径比、爆高、当量、测点角度和比例距离的函数。最后，基于控制变量法，利用符合经验公式和实爆结果的圆柱装药近地空爆AUTODYN-2D数值模型的计算结果代入上述函数求解。结果表明：以长径比、比例爆高、比例距离和测点角度为输入参数的峰值超压空间转换模型可描述圆柱装药近地空爆峰值超压的空间数值关系，转换效果良好。Abstract: The shockwave overpressure is one of the main damage elements of the high energy warhead, and many researchers have paid great attention on it. The spatial propagation boundary of shockwave is determined based on the method of image, division angle and overpressure normalization, and the theoretical calculation method of overpressure in mixed flow field is also established. Firstly, the boundary of shockwave flow field distribution is determined by using the terminal condition of Mach reflection and the geometric constraints formed by connecting three points, including the intersection of triple point trajectory and the horizontal line of height of burst (HOB), the imaginary burst point and real blast center. Secondly, the angle of measuring point (AMP) is equalized and the normalized value equation is constructed based on the piecewise linear assumption of the normalized value of overpressure. Then, the normalized value equation is extended to the functions of the length diameter ratio (k) of cylindrical charge, HOB, equivalent, AMP and scaled distance. Finally, based on the control variable method, the above function is solved by using the calculated results of AUTODYN-2D numerical model of near-earth air blast with cylindrical charge in accordance with the empirical equations and the real explosion results. The results show that the spatial conversion model of peak overpressure with k, scaled HOB, scaled distance and AMP as input parameters can describe the spatial numerical relation of peak overpressure of cylindrical charge in near-earth air blast, and the conversion effect is well.
-
图 1 近地爆炸冲击波近距离传播流场示意图
Figure 1. Near-earth blast shockwave propagation flow field at close range
图 2 近地爆炸冲击波远距离传播流场示意图
Figure 2. Near-earth blast shockwave propagation flow field over long distance
图 6 不同比例爆高时峰值超压的归一化值
Figure 6. Normalized value of peak overpressure under different scaled height of burst (HOB)
图 7 相对于长径比（k）1.0的变量
Figure 7. Variables that relative to the length diameter ratio (k) of 1.0
A/GPa B/GPa R1 R2 $\omega $ E/(GJ·m−3) 371.2 3.231 4.15 0.95 0.3 7 
下载: 导出CSV
表 2 实爆及数值模拟结果对比
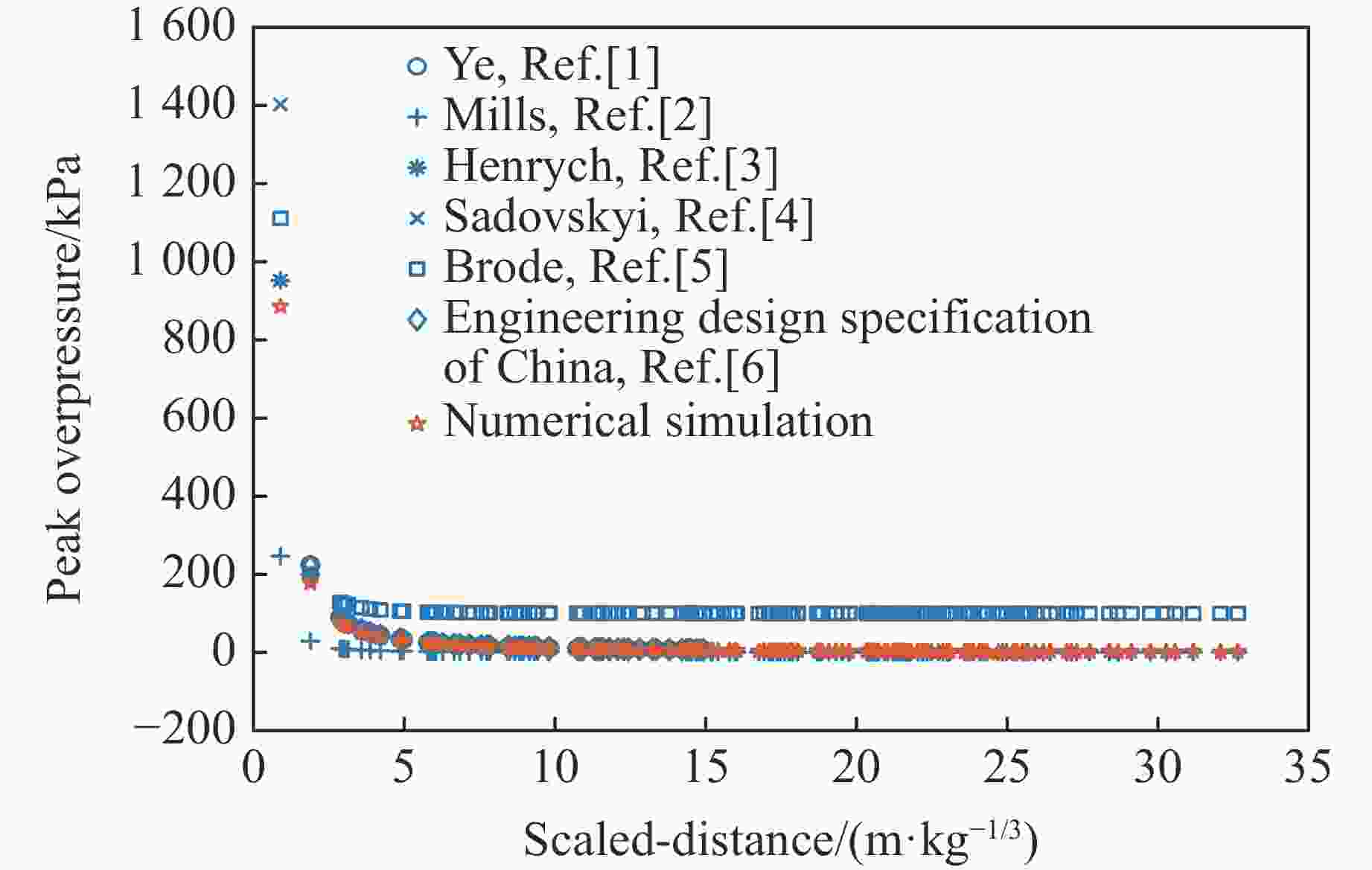
Table 2. Real blast and numerical simulation results
Case No. Scaled distance/(m·kg−1/3) Peak overpressure/kPa Error/% Real blast Numerical simulation 1 3.2 111.8 102.017 −8.75 2 4.2 69.8 64.177 −8.06 3 5.1 47.6 44.663 −6.17 4 6.0 39.3 33.311 −15.24
下载: 导出CSV
表 3 系数汇总表
Table 3. Summary of coefficients
No. $\theta $/(°) A1 A2 A3 1 0 70.08 764.30 −69.75 2 15 175.40 −38.19 677.70 3 30 137.30 −161.10 1177.00 4 45 67.84 317.10 370.50 5 60 68.28 330.50 315.00 6 75 75.65 315.50 216.10 7 90 99.50 123.10 503.60
下载: 导出CSV
表 4 模型计算结果对比
Table 4. Comparison of model calculation results
m/kg k HOB/m Scaled distance/
(kg·m−1/3)Peak overpressure/kPa Error/% Test value (90°) Test value (0°) Predicted value 20 1.0 1.5 2.58 143.8 221.1 191.3 13.5 3.32 90.3 110.6 92.7 16.2
下载: 导出CSV
-
[1] 叶晓华. 军事爆破工程[M]. 北京: 解放军出版社, 1995: 216–219.YE X H. Military blasting engineering [M]. Beijing: PLA Press, 1995: 216–219. [2] TOLBA A F F. Response of FRP-retrofitted reinforced concrete panels to blast loading [D]. Ottawa, Canada: Charleton University, 2002. [3] HENRYCH J. 爆炸动力学及其应用 [M]. 熊建国, 译. 北京: 科学出版社, 1987: 127.HENRYCH J. The dynamics of explosion and its use [M]. Translated by XIONG J G. Beijing: Science Press, 1987: 127. [4] SADOVSKYI M A. Mechanical action of air shock waves of explosion, based on experimental data [M]. Moscow: Izd Akad Nauk SSSR, 1952: 1–2. [5] BRODE H L. Numerical solutions of spherical blast wave [J]. Journal of Applied Physics, 1955, 26(6): 766. doi: 10.1063/1.1722085 [6] 李翼祺, 马素贞. 爆炸力学 [M]. 北京: 科学出版社, 1992.LI Y Q, MA S Z. Mechanics of explosion [M]. Beijing: Science Press, 1992. [7] 郭炜, 俞统昌, 金朋刚. 三波点的测量与实验技术研究 [J]. 火炸药学报, 2007, 30(4): 55–57, 61. doi: 10.3969/j.issn.1007-7812.2007.04.014GUO W, YU T C, JIN P G. Test of triple point and study on its test technology [J]. Chinese Journal of Explosives & Propellants, 2007, 30(4): 55–57, 61. doi: 10.3969/j.issn.1007-7812.2007.04.014 [8] 徐彬, 张寒虹, 陈志坚, 等. 球面激波在固壁的马赫反射 [J]. 爆炸与冲击, 1988, 8(1): 25–28.XU B, ZHANG H H, CHEN Z J, et al. Mach reflection of spherical shock wave on rigid wall [J]. Explosion and Shock Waves, 1988, 8(1): 25–28. [9] 赵升, 恽寿榕, 陈权,等. 马赫反射效应在炸药爆轰合成金刚石中的应用 [J]. 高压物理学报, 1997, 11(2): 110–116. doi: 10.11858/gywlxb.1997.02.006ZHAO S, YUN S R, CHEN Q, et al. Using Mach reflection effect in synthesis of ultrafine diamond by detonation wave method [J]. Chinese Journal of High Pressure Physics, 1997, 11(2): 110–116. doi: 10.11858/gywlxb.1997.02.006 [10] 徐彬, 陈志坚, 郭长铭. 球面激波在固壁上马赫反射的数值计算及实验研究(I) [J]. 爆炸与冲击, 1987, 7(3): 223–229.XU B, CHEN Z J, GUO C M. Numerical computation and experiments of Mach reflection of spherical shock wave on rigid wall (I) [J]. Explosion and Shock Waves, 1987, 7(3): 223–229. [11] 彭荣强. 几何激波动力学在激波绕射反射和聚焦中的应用 [J]. 四川工业学院学报, 1996, 15(1): 50–54.PENG R Q. Application of geometrical shock dynamics in shock diffraction reflection and focus [J]. Journal of Sichuan Institute of Technology, 1996, 15(1): 50–54. [12] WU Z, GUO J, YAO X, et al. Analysis of explosion in enclosure based on improved method of images [J]. Shock Waves, 2016, 27(2): 1–9. [13] KONG B, LEE K, LEE S, et al. Indoor propagation and assessment of blast waves from weapons using the alternative image theory [J]. Shock Waves, 2016, 26(2): 75–85. doi: 10.1007/s00193-015-0581-4 [14] KONG X S, WU W G, LI J, et al. Experimental investigation on characteristics of blast load in partially confined cabin structure [J]. Journal of Shanghai Jiaotong University, 2013, 18(5): 583–589. doi: 10.1007/s12204-013-1431-0 [15] EHRHARDT L, BOUTILLIER J, MAGNAN P, et al. Evaluation of overpressure prediction models for air blast above the triple point [J]. Journal of Hazardous Materials, 2016, 311(5): 176–185. [16] 易仰贤. 空爆冲击波马赫反射近似计算 [J]. 爆炸与冲击, 1983, 3(2): 44–49.YI Y X. Approximate calculation of Mach reflection of explosive shock waves in air [J]. Explosion and Shock Waves, 1983, 3(2): 44–49. [17] 陈材, 石全, 尤志锋, 等. 圆柱形弹药空气中爆炸相似性规律 [J]. 爆炸与冲击, 2019, 39(9): 092202. doi: 10.11883/bzycj-2018-0255CHEN C, SHI Q, YOU Z F, et al. Similarity law of cylindrical ammunition explosions in air [J]. Explosion and Shock Waves, 2019, 39(9): 092202. doi: 10.11883/bzycj-2018-0255 [18] 耿振刚, 李秀地, 苗朝阳, 等. 温压炸药爆炸冲击波在坑道内的传播规律研究 [J]. 振动与冲击, 2017, 36(5): 23–29.GENG Z G, LI X D, MIAO C Y, et al. Propagation of blast wave of thermobaric explosive inside a tunnel [J]. Journal of Vibration and Shock, 2017, 36(5): 23–29. [19] 徐森, 刘大斌, 彭金华, 等. 药柱冲击波在有机玻璃中的衰减特性研究 [J]. 高压物理学报, 2010, 24(6): 431–437. doi: 10.11858/gywlxb.2010.06.005XU S, LIU D B, PENG J H, et al. Study on the shock wave attenuation of the booster charge in the PMMA gap [J]. Chinese Journal of High Pressure Physics, 2010, 24(6): 431–437. doi: 10.11858/gywlxb.2010.06.005 [20] 张学伦, 张团, 王昭明. 基于AUTODYN爆炸场三波点的数值模拟 [J]. 兵器装备工程学报, 2015, 36(3): 17–19. doi: 10.11809/scbgxb2015.03.005ZHANG X L, ZHANG T, WANG Z M. Numerical simulation on triple point explosion field with AUTODYN [J]. Journal of Ordnance Equipment Engineering, 2015, 36(3): 17–19. doi: 10.11809/scbgxb2015.03.005 [21] 廖真, 唐德高, 李治中, 等. 近地面空中爆炸马赫反射数值模拟研究 [J]. 振动与冲击, 2020, 39(5): 164–169.LIAO Z, TANG D G, LI Z Z, et al. Numerical simulation for Mach reflection in air explosion near ground [J]. Journal of Vibration and Shock, 2020, 39(5): 164–169. [22] 辛春亮, 徐更光, 刘科种, 等. 考虑后燃烧效应的TNT空气中爆炸的数值模拟 [J]. 含能材料, 2008, 16(2): 160–163. doi: 10.3969/j.issn.1006-9941.2008.02.011XIN C L, XU G G, LIU K Z, et al. Numerical simulation of TNT explosion with post-detonation burning effect in air [J]. Chinese Journal of Energetic Materials, 2008, 16(2): 160–163. doi: 10.3969/j.issn.1006-9941.2008.02.011 -
下载:
点击查看大图
图(8) / 表(4)
计量
- 文章访问数: 4230
- HTML全文浏览量: 1422
- PDF下载量: 54
