基于电流密度的分段计算电爆炸模型研究

于红新; 冉汉政; 杜涛; 丰伟

doi:10.11858/gywlxb.20180537

基于电流密度的分段计算电爆炸模型研究

doi: 10.11858/gywlxb.20180537

中国工程物理研究院电子工程研究所, 四川绵阳 621999

基金项目:

中国工程物理研究院电子工程研究所创新发展基金 S20160801

详细信息

作者简介:
于红新(1988-), 男, 硕士, 研究实习员, 主要从事脉冲功率技术研究. E-mail:yuhongxin1221@126.com

中图分类号: TJ450.2;TM133
计量
- 文章访问数: 6107
- HTML全文浏览量: 2762
- PDF下载量: 16
出版历程
- 收稿日期: 2018-04-09
- 修回日期: 2018-05-31

Electrical Explosion Model Based on Current Density in Piecewise Calculation

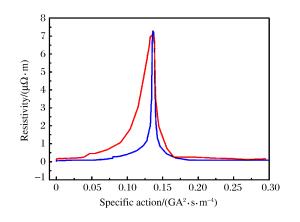
Institute of Electronic Engineering, CAEP, Mianyang 621999, China

摘要

摘要: 瞬态电阻是爆炸丝在电爆炸过程中最重要的参数之一，准确描述爆炸丝电阻的非线性时变特性是电爆炸仿真的关键，决定了电爆炸过程的仿真精度。为解决传统仿真模型精度差的问题，提出了根据电流密度采用分段计算的方法校正传统电阻率-比作用量关系，建立基于电流密度的分段计算电爆炸仿真模型。结果表明，在大脉冲电流条件下，基于电流密度的分段计算电爆炸模型精度较传统的仿真模型精度明显提高，可用于高精度的爆炸丝电爆炸过程研究。
- 爆炸丝 /
- 电流密度 /
- 分段计算 /
- 电阻率 /
- 比作用量
Abstract: Transient resistance is one of the most important parameters in the process of electric explosion.The accurate description of the nonlinear time-varying characteristics of the exploding wire resistance is the key to the simulation of electric explosion, which determines the simulation precision.In order to solve the problem of poor precision associated with traditional simulation model, this paper presents a piecewise calculation method based on current density to correct the relationship between traditional resistivity and specific action, and establishes a piecewise calculation electric explosion simulation model based on the current density.The results show that, under the condition of large pulse current, the precision of the model is higher than that of the traditional simulation model, which can be used to study the electric explosion process with high accuracy.
- exploding wire /
- current density /
- piecewise calculation /
- resistivity /
- specific action

HTML全文

图 1 RLC放电电路

Figure 1. Discharge circuit containing R, L and C parameters

下载: 全尺寸图片幻灯片

图 2 典型的RLC放电电流波形

Figure 2. Typical RLC discharge current waveform

下载: 全尺寸图片幻灯片

图 3 典型电阻率-比作用量曲线

Figure 3. Typical resistivity-specific action curves

下载: 全尺寸图片幻灯片

图 4 不同电流密度下电阻率-比作用量曲线

Figure 4. Resistivity-specific action curves at different current densities

下载: 全尺寸图片幻灯片

图 5 电阻率曲线(1 TA/m²)

Figure 5. Resistivity curve(1 TA/m²)

下载: 全尺寸图片幻灯片

图 6 分段的电阻率-比作用量曲线

Figure 6. Resistivity-specific action curves at different current densities

下载: 全尺寸图片幻灯片

图 7 Saber仿真模型

Figure 7. Simulation model in Saber

下载: 全尺寸图片幻灯片

图 8 实验示意图

Figure 8. Schematic diagram of experimental setup

下载: 全尺寸图片幻灯片

图 9 短路实验电流波形

Figure 9. Current waveform of short-circuit discharge experiment

下载: 全尺寸图片幻灯片

图 10 短路仿真模型

Figure 10. Simulation model of short-circuit

下载: 全尺寸图片幻灯片

图 11 爆炸丝结构示意图

Figure 11. Schematic diagram of exploding wire structure

下载: 全尺寸图片幻灯片

图 12 电流波形

Figure 12. Current waveform

下载: 全尺寸图片幻灯片

图 13 控制电流曲线

Figure 13. Curve of control current

下载: 全尺寸图片幻灯片

图 14 仿真与实验电流波形

Figure 14. Simulation and experimental current waveforms

下载: 全尺寸图片幻灯片

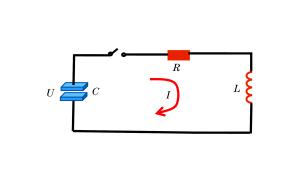
表 1 爆炸丝单点起爆实验与仿真结果

Table 1. Experiment and simulation results of explosive wire with single point initiation

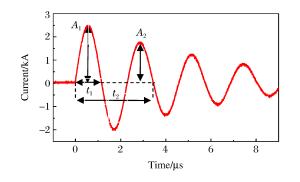
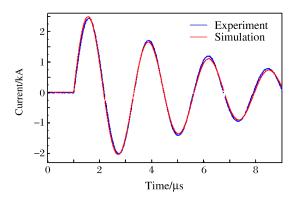
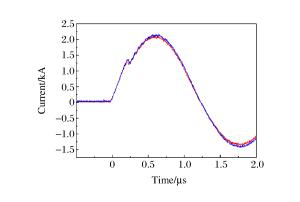
State	Peak current/kA	Error/%	Time of peak current/μs	Error/%	Burst current/kA	Error/%	Burst time/μs	Error/%
Experiment	2.088		0.638		1.315		0.251
Simulation 1	2.066	0.95	0.623	2.35	1.309	0.76	0.253	0.80
Simulation 2	2.138	2.39	0.594	6.90	1.439	9.42	0.243	3.19
Simulation 3	1.936	7.18	0.712	11.60	1.298	1.29	0.225	10.36
Simulation 4	1.600	23.37	0.532	16.61	1.263	3.95	0.206	17.93

下载: 导出CSV

参考文献(11)

[1]	TUCKER T J.Behavior of exploding glod wires[J].Journal of Applied Physics, 1961, 32(10):1894-1900. doi: 10.1063/1.1728259
[2]	TUCKER T J, STANTON P L.Electrical gurney energy: a new concept in modeling of energy transfer from electrically exploded conductors: SAND-75-0244[R].Albuquerque, NM: Sandia National Laboratories, 1975.
[3]	杨汉武, 钟辉煌.PSpice模型用于电爆炸丝的数值模拟[J].国防科技大学学报, 2000, 22(增刊):38-42. http://d.old.wanfangdata.com.cn/Periodical/gfkjdxxb2000Z1011 YANG H W, ZHONG H H.Numerical simulation of electrical exploding wires via PSpice models[J].Journal of National University of Defense Technology, 2000, 22(Suppl):38-42. http://d.old.wanfangdata.com.cn/Periodical/gfkjdxxb2000Z1011
[4]	杨集, 杜涛, 赵翔, 等.基于电容放电单元的爆炸丝起爆特性数值分析[J].太赫兹科学与电子信息学报, 2014, 12(3):461-465. http://d.old.wanfangdata.com.cn/Periodical/xxydzgc201403029 YANG J, DU T, ZHAO X, et al.Numerical analysis of exploding wire initiation characteristic based on capacitor discharge unit[J].Journal of Terahertz Science and Electronic Information Technology, 2014, 12(3):461-465. http://d.old.wanfangdata.com.cn/Periodical/xxydzgc201403029
[5]	LEE R S.Fireset: UCID-21322[R].Livermore, CA: Lawrence Livermore National Laboratory, 1988.
[6]	FURNBERG C M.Computer modeling of detonators[C]//Proceedings of the 37th Midwest Symposium on Circuits and Systems.Piscataway, NJ: Institute of Electrical and Electronics Engineers, 1994, 1: 646-649.
[7]	IVANENKOV G V, STEPNIEWSKI W.Three-temperature model for the dynamics of a plasma produced by exploding metal wires[J].Plasma Physics Reports, 2000, 26(1):21-32. doi: 10.1134/1.952818
[8]	王刚华, 胡熙静.单丝Z箍缩的一维单温辐射磁流体力学计算[J].高压物理学报, 2002, 16(1):57-60. doi: 10.3969/j.issn.1000-5773.2002.01.009 WANG G H, HU X J.One-dimensional simulations of single temperature radiative magnetic field dynamics for liner implosion experiments[J].Chinese Journal of High Pressure Physics, 2002, 16(1):57-60. doi: 10.3969/j.issn.1000-5773.2002.01.009
[9]	张振涛, 汤铁钢, 王健, 等.爆炸丝起爆系统研制[J].高能量密度物理, 2013, 3(1):35-40. http://www.cnki.com.cn/Article/CJFDTOTAL-QJGY201403053.htm ZHANG Z T, TANG T G, WANG J, et al.Development of exploding wire initiation system[J].High Energy Density Physics, 2013, 3(1):35-40. http://www.cnki.com.cn/Article/CJFDTOTAL-QJGY201403053.htm
[10]	TUCKER T J, TOTH R P.EBW1: a computer code for the prediction of the behavior of electrical circuit containing exploding wire elements: SAND-75-0041[R].Albuquerque, NM: Sandia National Laboratories, 1975.
[11]	YING G F, LI X W, JIA S L.Electrical characteristics of microsecond electrical explosion of Cu wires in air under various parameters[J].Transactions on Plasma Science, 2018, 46(4):972-981. doi: 10.1109/TPS.2018.2805351