超声波作用下SiO<sub>2</sub>纳米颗粒的分离

任超宇; 薛鹏程; 焦雄; 王根伟

doi:10.11858/gywlxb.20180526

超声波作用下SiO₂纳米颗粒的分离

doi: 10.11858/gywlxb.20180526

任超宇^{1, 2,},
薛鹏程^{1, 2},
焦雄^{1, 2},
王根伟^{1, 2, 3,*,}

1.
太原理工大学应用力学与生物医学工程研究所, 山西太原 030024
2.
太原理工大学力学学院, 山西太原 030024
3.
力学国家级实验教学示范中心(太原理工大学), 山西太原 030024

基金项目:

国家自然科学基金 11772215

详细信息

作者简介:
任超宇(1991-), 男, 硕士, 主要从事微纳米力学研究.E-mail:15122346848@163.com

通讯作者:
王根伟(1974-), 男, 博士, 硕士生导师, 主要从事纳米结构和纳米复合材料力学研究

中图分类号: O647.4
计量
- 文章访问数: 7419
- HTML全文浏览量: 3241
- PDF下载量: 262
出版历程
- 收稿日期: 2018-03-13
- 修回日期: 2018-03-26

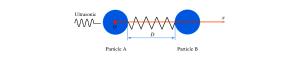
Separation of Two SiO₂ Nanoparticles under Ultrasonic Vibration

REN Chaoyu^{1, 2
,},
XUE Pengcheng^{1, 2},
JIAO Xiong^{1, 2},
WANG Genwei^{1, 2, 3,*
,}

1.
China Institute of Applied Mechanics and Biomedical Engineering, Taiyuan University of Technology, Taiyuan 030024, China
2.
College of Mechanics, Taiyuan University of Technology, Taiyuan 030024, China
3.
National Demonstration Center for Experimental Mechanics Education(Taiyuan University of Technology), Taiyuan 030024, China

摘要

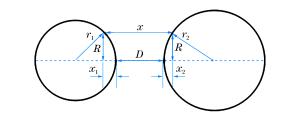
摘要: 在范德华力的作用下，纳米颗粒常常会黏在一起。黏在一起的纳米颗粒的分离提纯是纳米领域亟待解决的难题。研究了超声波作用下受到范德华力的两个SiO₂纳米颗粒的分离。假设颗粒处于空气中且是刚性的，给其中一个颗粒施加超声波振动，计算两个颗粒之间的范德华力和距离变化。结果表明，颗粒粒径比、超声波幅值、超声波周期、超声波平均能量密度对颗粒分离产生不同的影响。
- 范德华力 /
- 超声波 /
- 分离 /
- 纳米颗粒
Abstract: Nanoparticles tend to aggregate due to the van der Waals force, and the separation and purification of these nanoparticles are difficult in nanometer scale.In this study, we focus on the separation of two SiO₂ nanoparticles attracted by van der Waals force.Assuming them as being stiffness particles in air and applying ultrasonic vibration to one of them, we analyzed and calculated the interaction and distance between the two SiO₂ nanoparticles.It is found that the ratio of diameters, the amplitude, the period and the average energy density of the ultrasonic have different effects on their separation.
- van der Waals force /
- ultrasonic vibration /
- separation /
- nanoparticle

HTML全文

图 1 几何关系

Figure 1. Schematic of geometric relations

下载: 全尺寸图片幻灯片

图 2 SiO₂纳米颗粒运动模型

Figure 2. Motion model of SiO₂ nanoparticles

下载: 全尺寸图片幻灯片

图 3 粒径比η对颗粒分离的影响

Figure 3. Influence of diameter ratio η on distance between two particles

下载: 全尺寸图片幻灯片

图 4 超声波振幅H对颗粒分离的影响

Figure 4. Influence of ultrasound amplitude H on distance between two particles

下载: 全尺寸图片幻灯片

图 5 周期T对颗粒分离的影响

Figure 5. Impact of ultrasound period T on distance between two particles

下载: 全尺寸图片幻灯片

图 6 相同超声波平均能量密度ζ下振幅H及周期T对颗粒分离的影响

Figure 6. Impact of ultrasound amplitude and period on distance between two particles with the same average energy density ζ

下载: 全尺寸图片幻灯片

表 1 Lennard-Jones势能参数

Table 1. Parameters of Lennard-Jones interaction potential

Atom type of interaction σ/nm ε/(10^-20 J)

Si-Si 0.330 4.3766

O-O 0.275 0.1104

下载: 导出CSV

表 2 颗粒分离时间随粒径比η的变化关系

Table 2. Relationship of diameter ratio η and separation time of two particles

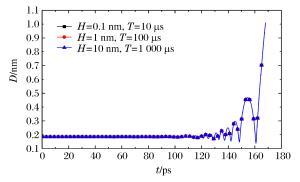
η Separation time/ps

0.1 843

0.5 249

1 180

5 139

10 94

下载: 导出CSV

表 3 颗粒分离时间随振幅H的变化关系

Table 3. Relationship of ultrasound amplitude H and separation time of two particles

H/nm Separation time/ps

0.1 167

0.5 168

1 181

5 164

10 156

下载: 导出CSV

表 4 颗粒分离时间随周期T变化关系

Table 4. Relationship of ultrasound period T and separation time of two particles

T/μs Separation time/ps

0.1 99

1 139

10 164

100 168

下载: 导出CSV

参考文献(13)

[1]	刘维平, 邱定番, 卢惠民.纳米材料制备方法及应用领域[J].化工矿物与加工, 2003, 32(12):1-5. doi: 10.3969/j.issn.1008-7524.2003.12.001 LIU W P, QIU D F, LU H M.Preparation methods of nano-materials and its applications[J].Industrial Minerals & Processing, 2003, 32(12):1-5. doi: 10.3969/j.issn.1008-7524.2003.12.001
[2]	袁文俊, 周勇敏.纳米颗粒团聚的原因及解决措施[J].材料导报, 2008, 22(S3):59-61. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cldb2008z3021 YUAN W J, ZHOU Y M.Reasons for aggregation of nanoparticles and solutions[J].Materials Review, 2008, 22(S3):59-61. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cldb2008z3021
[3]	张璐, 吴晶, 陈慧英.微米及纳米级微粒的分离与操控研究进展[J].内蒙古民族大学学报, 2011, 26(3):262-266. http://www.cqvip.com/QK/97047A/201103/38130386.html ZHANG L, WU J, CHEN H Y.The research progress of the separation and manipulation technologies for micro/nano-scale particles[J].Journal of Inner Mongolia University for Nationalities, 2011, 26(3):262-266. http://www.cqvip.com/QK/97047A/201103/38130386.html
[4]	富玉, 李晓鸥, 李鹤鸣, 等.超声沉降法强化脱除印尼油砂油中机械杂质[J].辽宁石油化工大学学报, 2017, 37(5):17-21. http://www.cqvip.com/QK/98572X/200304/8757544.html FU Y, LI X O, LI H M, et al. Enhanced removal of the mechanical impurities in oil-sands-oil from indonesia by ultrasound-sedimentation method[J].Journal of Liaoning Shihua University, 2017, 37(5):17-21. http://www.cqvip.com/QK/98572X/200304/8757544.html
[5]	赵亚溥.表面与界面物理力学[M].北京:科学出版社, 2012:40-45. ZHAO Y P.Physical mechanics of surface and interfaces[M].Beijing:Science Press, 2012:40-45.
[6]	赵亚溥.纳米与介观力学[M].北京:科学出版社, 2014:256-257. ZHAO Y P.Nano and mesoscopic mechanics[M].Beijing:Science Press, 2014:256-257.
[7]	ISRAELACHVILI J N.Intermolecular and surface forces[M].3rd Ed.Cambridge, Massachusetts:Academic Press, 2011:215-287.
[8]	FU S P, PENG Z, YUAN H, et al.Lennard-Jones type pair-potential method for coarse-grained lipid bilayer membrane simulations in LAMMPS[J].Computer Physics Communications, 2017, 210:193-203. doi: 10.1016/j.cpc.2016.09.018
[9]	XU J, ZHENG B, LIU Y.Solitary wave in one-dimensional buckyball system at nanoscale[J].Scientific Reports, 2016, 6:21052. doi: 10.1038/srep21052
[10]	AHANGARI M G, FEREIDOON A, MASHHADZADEH A H.Interlayer interaction and mechanical properties in multi-layer graphene, boron-nitride, aluminum-nitride and gallium-nitride graphene-like structure:a quantum-mechanical DFT study[J].Superlattices & Microstructures, 2017, 112:30-45. https://www.sciencedirect.com/science/article/pii/S0749603617319572
[11]	OVERSTEEGEN S M, LEKKERKERKER H N W.On the accuracy of the Derjaguin approximation for depletion potentials[J].Physica A:Statistical Mechanics & Its Applications, 2004, 341(1):23-39. https://econpapers.repec.org/RePEc:eee:phsmap:v:341:y:2004:i:c:p:23-39
[12]	ANDRÉ P, BUSSIÈRE W, ROCHETTE D.Transport coefficients of Ag-SiO₂ plasmas[J].Plasma Chemistry & Plasma Processing, 2007, 27(4):381-403. https://www.deepdyve.com/lp/springer-journals/transport-coefficients-of-ag-sio-2-plasmas-welAJfr4wC
[13]	MUNETOH S, MOTOOKA T, MORIGUCHI K, et al.Interatomic potential for Si-O systems using Tersoff parameterization[J].Computational Materials Science, 2007, 39(2):334-339. doi: 10.1016/j.commatsci.2006.06.010